Robust Optimization over Time Problems—Characterization and Literature Review
Abstract
:1. Introduction
2. Robust Optimization over Time
3. Proposed Framework
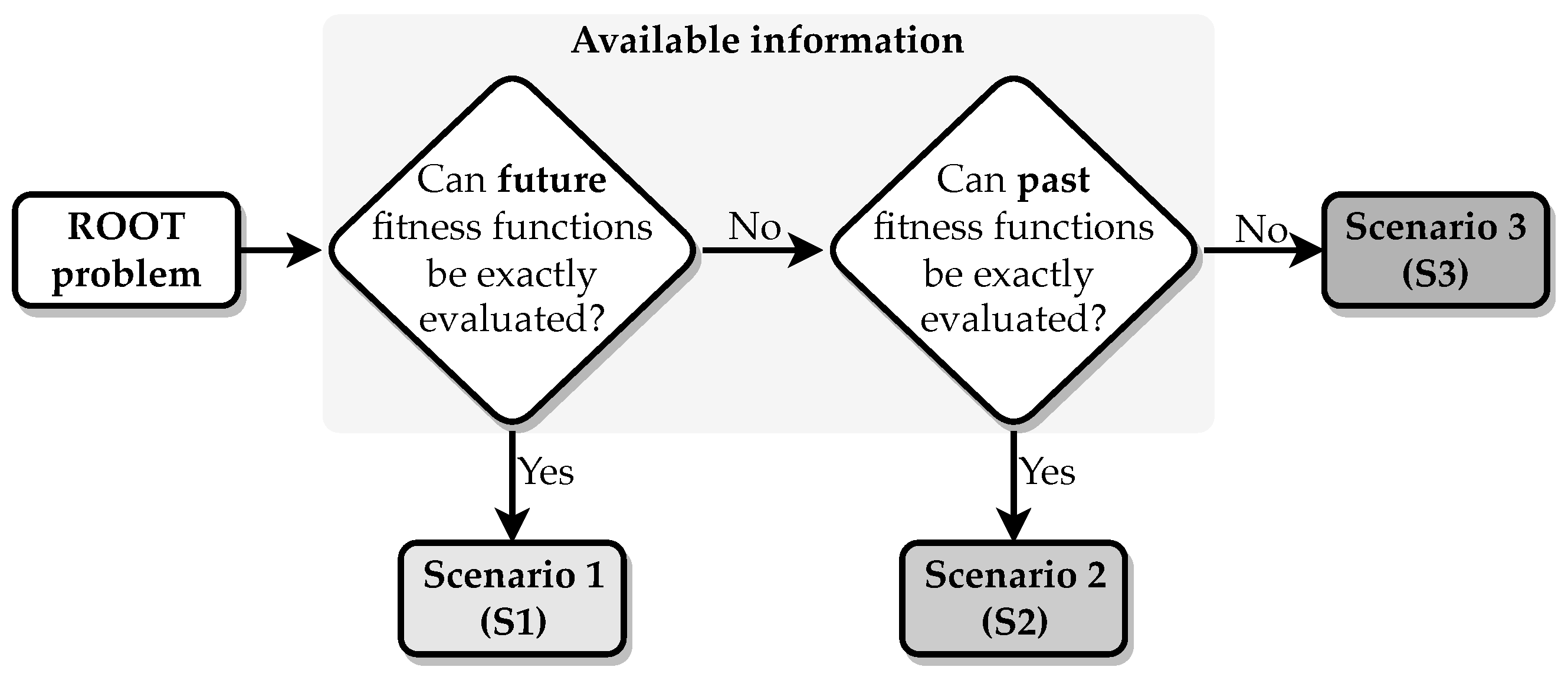
3.1. Dimension 1: Available Information
- Scenario 1 (S1): This is the case of ROOT problems where fitness functions from future environments can be evaluated exactly. Hence, it comprises a family of ROOT problems where the robustness of a solution can be quantified exactly. As mentioned earlier, the only source of uncertainty here is the black-box nature of the environment’s fitness function. So, in this type of ROOT problem, typical TMO algorithms like [4], ref. [14] could be applied without any major adaptation. In other words, problems belonging to this scenario are slightly different from traditional dynamic optimization problems, where tracking the optimum is the main goal. To better visualize this, consider the Averaged Fitness as the robustness definition and as the fitness function guiding the optimizer during the search. Since it is an aggregation of the present and future values of objective functions that can be evaluated exactly, the problem is reduced to a TMO problem with a single, dynamic objective function, i.e., the Averaged Fitness. In the case of robustness defined in terms of Survival Time, it is not trivial to transform problems from this scenario into TMO problems. The difficulty arises because, in theory, the robustness value could be infinite. This is the case of a problem with an endless number of changes (environments) in which it is possible to find a solution that both in the current and future environments maintains a fitness above the threshold V (Equation (3)). If the number of changes has a finite, computationally tractable limit, then it would be possible to construct an objective function that captures this definition in each environment t. Note that here, instead of using an average to aggregate the information from several environments, the values of the objective function are integers. For these reasons, this scenario is suitable for studying how the optimizer part of the algorithm copes with the uncertainty of the black box fitness function.
- Scenario 2 (S2): In this scenario, we consider ROOT problems with unknown future environments, but with past environments that can be evaluated exactly. Hence, the algorithm requires a forecasting model to estimate the future fitness values. Uncertainty is present here due to the future environments and the black box definition of fitness functions. From an experimental perspective, problems in this category are suitable to study forecasting models which help to evaluate future environments.
- Scenario 3 (S3): In this type of ROOT problem, neither the future environments nor the past environments can be evaluated precisely. This implies that algorithms must include mechanisms to not only forecast the future but also to store or approximate the past effectively. It is easy to infer that, of the three scenarios, this one encloses ROOT problems with the highest level of uncertainty. In addition to the performance of the optimizer and the forecasting model, problems in this category are suitable for studying function approximation models that properly represent past environments.
3.2. Dimension 2: Robustness Definition
3.3. Dimension 3: Number of Objectives
3.4. Dimension 4: Search Space Features
3.5. Dimension 5: Problem Source
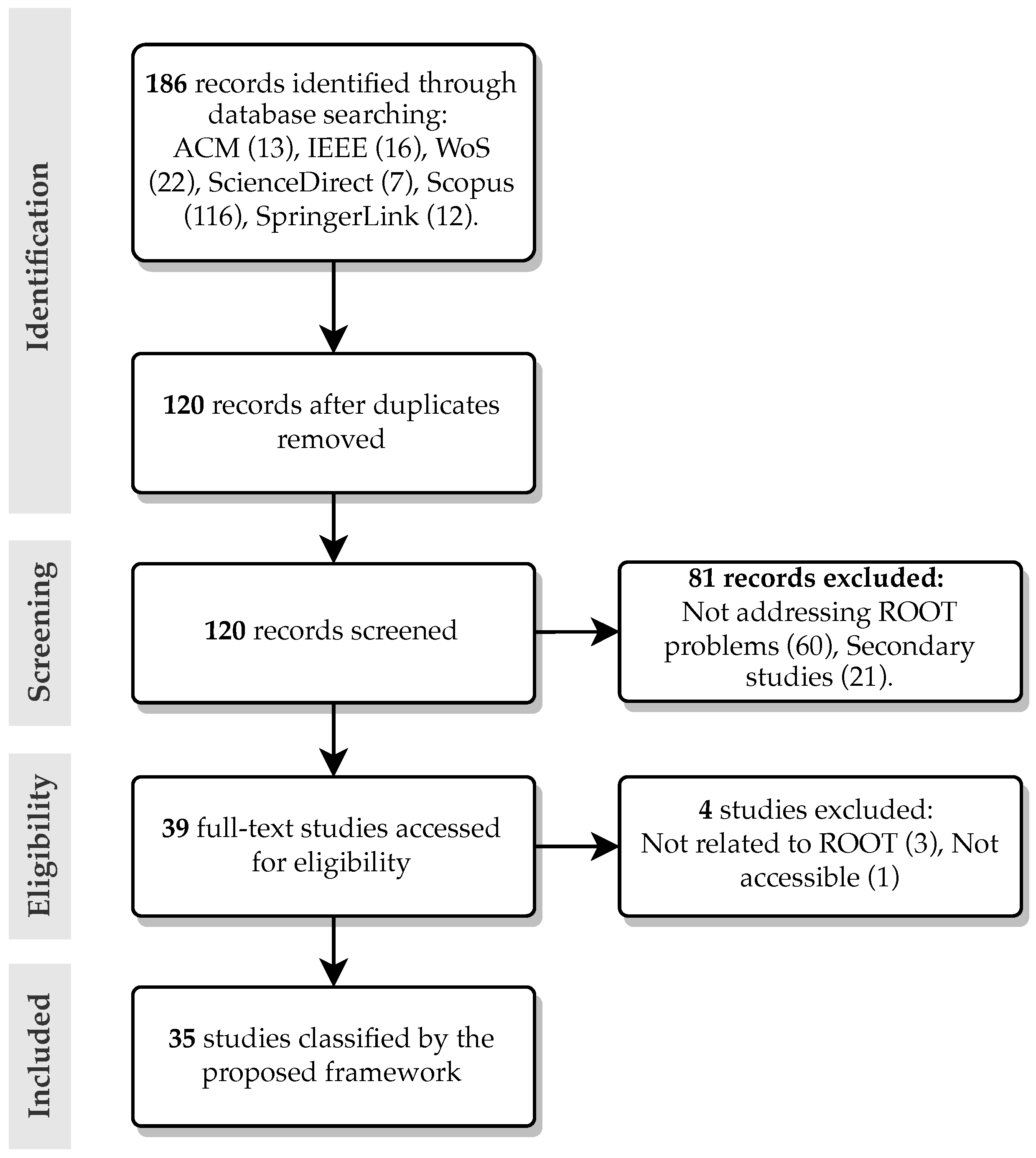
4. Literature Review, Analysis, and Research Opportunities
(“robust optimization over time” OR “robust optimisation over time”)
4.1. Results
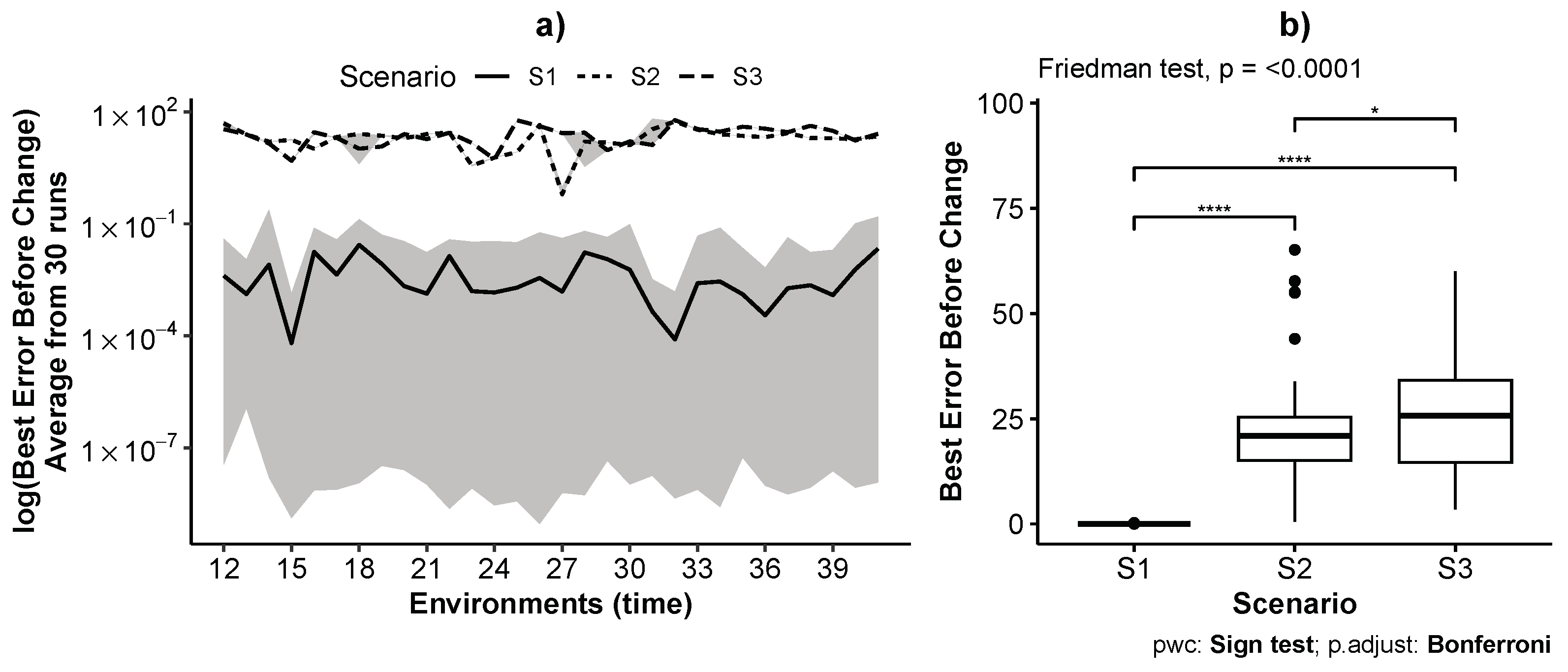
4.2. On the Effect of the Available Information
4.3. Research Opportunities
- 1.
- Defining and/or solving problems with discrete variables, with a moderate or high number of variables, and considering feasible regions unbounded or constrained;
- 2.
- Address more problems of type S2 or S3, rather than those of type S1. Although all three categories of problems have been addressed in the past, some recent contributions focus on the simpler S1 scenario (e.g., where future fitness functions can be accurately evaluated). As was stated earlier, this type of problem is in essence the same as the Tracking Moving Optima if we defined robustness in terms of Average Fitness. In our opinion, the true ROOT problems are those derived from the assumptions defining scenarios S2 and S3;
- 3.
- Exploring alternative robustness definitions. Although alternatives to the typical ones (e.g., Average Fitness and Survival Time) have appeared in recent years, these definitions are very specific to the problem being solved. Thus, there is room to propose alternatives that can efficiently guide the algorithm in the search for robust solutions.
- 4.
- Address more real-world (inspired) problems. Except for just a few works like [25,26,27,28,29,30], the rest were focused on artificial problems. Note that addressing a larger number of real-world problems is a way to increase the number of contributions that exploit the opportunities indicated above. This is because a large number of these problems involve discrete variables, various constraints, uncertainty about the available information, and very specific definitions of robustness.
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Ref. | Source | Year | Scenario | Robust. Def. | N. Object. | Dimen. | Dec. Var. | Feas. Region | Prob. Source |
|---|---|---|---|---|---|---|---|---|---|
| [6] | Conference | 2010 | S3 | A.F. | Single | Low | Contin. | Bounded | Artificial |
| [33] | Conference | 2012 | S1 | Others | Single | Low | Contin. | Constrain. | Artificial |
| [34] | Conference | 2013 | S2 | S.T. | Single | Low | Contin. | Bounded | Artificial |
| [25] | Conference | 2013 | S3 | Others | Single | Low | Contin. | Constrain. | Real-world inspired |
| [13] | Journal | 2013 | S3 | A.F. | Single | Low | Contin. | Bounded | Artificial |
| [21] | Conference | 2014 | S2 | A.F., S.T. | Many | Low | Contin. | Bounded | Artificial |
| [17] | Journal | 2015 | S3 | S.T. | Many | Low | Contin. | Constrain. | Artificial |
| [11] | Journal | 2015 | S3 | A.F., S.T. | Single | Low | Contin. | Bounded | Artificial |
| [35] | Conference | 2015 | S3 | A.F., S.T. | Single | Low | Contin. | Bounded | Artificial |
| [36] | Journal | 2017 | S3 | S.T. | Many | Low | Contin. | Constrain. | Artificial |
| [37] | Journal | 2017 | S3 | S.T. | Many | Low | Contin. | Bounded | Artificial |
| [38] | Conference | 2017 | S1 | A.F., S.T. | Single | Low | Contin. | Bounded | Artificial |
| [26] | Journal | 2018 | S1 | Others | Many | Low | Mixed | Constrain. | Real-world inspired |
| [31] | Conference | 2018 | S3 | A.F. | Single | Low | Contin. | Bounded | Artificial |
| [39] | Conference | 2018 | S1 | Others | Single | Low | Contin. | Bounded | Artificial |
| [40] | Conference | 2019 | S1 | A.F., S.T. | Single | Low | Contin. | Bounded | Artificial |
| [41] | Conference | 2019 | S1 | A.F. | Single | High | Discrete | Constrain. | Real-world inspired |
| [42] | Journal | 2019 | S3 | A.F. | Single | Low | Contin. | Bounded | Artificial |
| [43] | Conference | 2019 | S1 | A.F. | Single | Low | Contin. | Bounded | Artificial |
| [44] | Journal | 2019 | S3 | A.F., S.T. | Many | Low | Contin. | Constrain. | Artificial |
| [45] | Conference | 2019 | S1 | A.F. | Single | Low | Contin. | Bounded | Artificial |
| [27] | Conference | 2019 | S1 | Others | Single | Low | Contin. | Constrain. | Real-world |
| [46] | Journal | 2019 | S3 | S.T. | Single | Low | Contin. | Bounded | Artificial |
| [28] | Conference | 2020 | S1 | A.F. | Single | High | Discrete | Constrain. | Real-world inspired |
| [47] | Journal | 2020 | S1 | A.F., S.T. | Single | Low | Contin. | Bounded | Artificial |
| [32] | Conference | 2020 | S2 | A.F., S.T. | Single | Low | Contin. | Bounded | Artificial |
| [48] | Journal | 2020 | S1 | S.T. | Single | Low | Contin. | Bounded | Artificial |
| [49] | Journal | 2020 | S3 | A.F., S.T. | Many | Low | Contin. | Constrain. | Artificial |
| [29] | Journal | 2020 | S1 | S.T. | Many | Low | Contin. | Bounded | Artificial |
| [50] | Journal | 2020 | S3 | A.F. | Many | Low | Contin. | Constrain. | Real-world |
| [51] | Journal | 2020 | S3 | Others | Single | Low | Contin. | Constrain. | Real-world inspired |
| [30] | Journal | 2021 | S1 | Others | Single | Low | Contin. | Constrain. | Real-world |
| [52] | Journal | 2022 | S3 | S.T. | Single | Low | Contin. | Bounded | Artificial |
| [53] | Journal | 2023 | S3 | S.T. | Single | Low | Contin. | Bounded | Artificial |
| [54] | Journal | 2023 | S3 | S.T. | Many | Low | Contin. | Constrain. | Artificial |
References
- Siddique, N.; Adeli, H. Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing, 1st ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2013. [Google Scholar]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A Survey on Optimization Metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Cruz, C.; González, J.R.; Pelta, D.A. Optimization in Dynamic Environments: A Survey on Problems, Methods and Measures. Soft Comput. 2011, 15, 1427–1448. [Google Scholar] [CrossRef]
- Novoa-Hernández, P.; Corona, C.C.; Pelta, D.A. Self-adaptation in dynamic environments—A survey and open issues. Int. J. Bio-Inspired Comput. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Yang, S.; Branke, J. Evolutionary dynamic optimization: A survey of the state of the art. Swarm Evol. Comput. 2012, 6, 1–24. [Google Scholar] [CrossRef]
- Yu, X.; Jin, Y.; Tang, K.; Yao, X. Robust optimization over time—A new perspective on dynamic optimization problems. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Novoa-Hernández, P.; Puris, A. Robust optimization over time: A review of most relevant contributions. RISTI Rev. Iber. Sist. Tecnol. Inf. 2019, 2019, 156–164. [Google Scholar]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades—Part A. IEEE Trans. Evol. Comput. 2021, 25, 609–629. [Google Scholar] [CrossRef]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A Survey of Evolutionary Continuous Dynamic Optimization Over Two Decades—Part B. IEEE Trans. Evol. Comput. 2021, 25, 630–650. [Google Scholar] [CrossRef]
- Yazdani, D.; Omidvar, M.N.; Yazdani, D.; Branke, J.; Nguyen, T.T.; Gandomi, A.H.; Jin, Y.; Yao, X. Robust Optimization Over Time: A Critical Review. IEEE Trans. Evol. Comput. 2023, 1–21. [Google Scholar] [CrossRef]
- Fu, H.; Sendhoff, B.; Tang, K.; Yao, X. Robust optimization over time: Problem difficulties and benchmark problems. IEEE Trans. Evol. Comput. 2015, 19, 731–745. [Google Scholar] [CrossRef]
- Rao, S. Engineering Optimization: Theory and Practice, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Jin, Y.; Tang, K.; Yu, X.; Sendhoff, B.; Yao, X. A framework for finding robust optimal solutions over time. Memetic Comput. 2013, 5, 3–18. [Google Scholar] [CrossRef]
- Kordestani, J.K.; Ranginkaman, A.E.; Meybodi, M.R.; Novoa-Hernández, P. A novel framework for improving multi-population algorithms for dynamic optimization problems: A scheduling approach. Swarm Evol. Comput. 2019, 44, 788–805. [Google Scholar] [CrossRef]
- Samuelson, L. Game Theory in Economics and Beyond. J. Econ. Perspect. 2016, 30, 107–130. [Google Scholar] [CrossRef]
- Jiang, S.; Zou, J.; Yang, S.; Yao, X. Evolutionary Dynamic Multi-objective Optimisation: A Survey. ACM Comput. Surv. 2022, 55, 1–47. [Google Scholar] [CrossRef]
- Chen, M.; Guo, Y.; Liu, H.; Wang, C. The evolutionary algorithm to find robust pareto-optimal solutions over time. Math. Probl. Eng. 2015, 2015, 1–18. [Google Scholar] [CrossRef]
- Li, X.; Tang, K.; Omidvar, M.; Yang, Z.; Qin, K. Benchmark Functions for the CEC’2013 Special Session and Competition on Large Scale Global Optimization; Technical Report; Evolutionary Computation and Machine Learning Group, RMIT University: Melbourne, Australia, 2013. [Google Scholar]
- Raggl, S.; Beham, A.; Hauder, V.; Wagner, S.; Affenzeller, M. Discrete Real-world Problems in a Black-box Optimization Benchmark. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1745–1752. [Google Scholar] [CrossRef]
- Pelamatti, J.; Brevault, L.; Balesdent, M.; Talbi, E.G.; Guerin, Y. How to Deal with Mixed-Variable Optimization Problems: An Overview of Algorithms and Formulations. In Advances in Structural and Multidisciplinary Optimization; Schumacher, A., Vietor, T., Fiebig, S., Bletzinger, K.U., Maute, K., Eds.; Springer: Cham, Switzerland, 2018; pp. 64–82. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, M.; Fu, H.; Liu, Y. Find robust solutions over time by two-layer multi-objective optimization method. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 1528–1535. [Google Scholar] [CrossRef]
- Novoa-Hernández, P.; Corona, C.C.; Pelta, D.A. A Software Tool for Assisting Experimentation in Dynamic Environments. Appl. Comput. Intell. Soft Comput. 2015, 2015, 302172. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Novoa-Hernández, P.; Corona, C.C.; Pelta, D.A. Self-adaptive, multipopulation differential evolution in dynamic environments. Soft Comput. 2013, 17, 1861–1881. [Google Scholar] [CrossRef]
- Hutterer, S.; Affenzeller, M. Policy function approximation for optimal power flow control issues. In Proceedings of the 1st International Workshop on Simulation for Energy, Sustainable Development and Environment, SESDE 2013, Held at the International Multidisciplinary Modeling and Simulation Multiconference, I3M, Athens, Greece, 25–27 September 2013; pp. 66–70. [Google Scholar]
- Guo, Y.N.; Cheng, J.; Luo, S.; Gong, D.; Xue, Y. Robust Dynamic Multi-Objective Vehicle Routing Optimization Method. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 1891–1903. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, H. A ROOT Approach for Stochastic Energy Management in Electric Bus Transit Center with PV and ESS. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ankrah, R.; Lacroix, B.; McCall, J.; Hardwick, A.; Conway, A.; Owusu, G. Racing Strategy for the Dynamic-Customer Location-Allocation Problem. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Huang, Y.J.; Jin, Y.C.; Hao, K.R. Robust optimization over time for constrained optimization based on swarm intelligence. Kongzhi yu Juece/Control Decision 2020, 35, 740–748. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, H. A Three-Layer Stochastic Energy Management Approach for Electric Bus Transit Centers With PV and Energy Storage Systems. IEEE Trans. Smart Grid 2021, 12, 1346–1357. [Google Scholar] [CrossRef]
- Novoa-Hernández, P.; Pelta, D.A.; Corona, C.C. Approximation Models in Robust Optimization Over Time—An Experimental Study. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Fox, M.; Yang, S.; Caraffini, F. An Experimental Study of Prediction Methods in Robust optimization Over Time. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Fu, H.; Sendhoff, B.; Tang, K.; Yao, X. Characterizing environmental changes in Robust Optimization Over Time. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, CEC 2012, Brisbane, QLD, Australia, 10–15 June 2012. [Google Scholar] [CrossRef]
- Fu, H.; Sendhoff, B.; Tang, K.; Yao, X. Finding Robust Solutions to Dynamic Optimization Problems. In Proceedings of the Applications of Evolutionary Computation; Lecture Notes in Computer Science; Esparcia-Alcázar, A.I., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7835, pp. 616–625. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, Y.; Ding, Y. New performance indicators for robust optimization over time. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 1380–1387. [Google Scholar] [CrossRef]
- Chen, M.R.; Guo, Y.N.; Gong, D.W.; Yang, Z. A novel dynamic multi-objective robust evolutionary optimization method. Zidonghua Xuebao/Acta Autom. Sin. 2017, 43, 2014–2032. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, Y.; Hao, K.; Jin, Y. A multi-objective approach to robust optimization over time considering switching cost. Inf. Sci. 2017, 394–395, 183–197. [Google Scholar] [CrossRef]
- Yazdani, D.; Nguyen, T.T.; Branke, J.; Wang, J. A New Multi-swarm Particle Swarm Optimization for Robust Optimization Over Time. In Proceedings of the Applications of Evolutionary Computation; Squillero, G., Sim, K., Eds.; Springer: Cham, Switzerland, 2017; pp. 99–109. [Google Scholar]
- Yazdani, D.; Branke, J.; Omidvar, M.N.; Nguyen, T.T.; Yao, X. Changing or Keeping Solutions in Dynamic Optimization Problems with Switching Costs. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 1095–1102. [Google Scholar] [CrossRef]
- Adam, L.; Yao, X. A Simple Yet Effective Approach to Robust Optimization Over Time. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 680–688. [Google Scholar] [CrossRef]
- Ankrah, R.; Lacroix, B.; McCall, J.; Hardwick, A.; Conway, A. Introducing the Dynamic Customer Location-Allocation Problem. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019. [Google Scholar] [CrossRef]
- Fei, X.; Branke, J.; Gulpinar, N. New Sampling Strategies When Searching for Robust Solutions. IEEE Trans. Evol. Comput. 2019, 23, 273–287. [Google Scholar] [CrossRef]
- Guzman-Gaspar, J.Y.; Mezura-Montes, E. Differential Evolution Variants in Robust Optimization Over Time. In Proceedings of the 2019 International Conference on Electronics, Communications and Computers (CONIELECOMP), Cholula, Mexico, 27 February–1 March 2019. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, H.; Chen, M.; Cheng, J.; Gong, D. Ensemble prediction-based dynamic robust multi-objective optimization methods. Swarm Evol. Comput. 2019, 48, 156–171. [Google Scholar] [CrossRef]
- Guzmán-Gaspar, J.Y.; Mezura-Montes, E. Robust Optimization Over Time with Differential Evolution using an Average Time Approach. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1548–1555. [Google Scholar] [CrossRef]
- Yazdani, D.; Nguyen, T.; Branke, J. Robust Optimization over Time by Learning Problem Space Characteristics. IEEE Trans. Evol. Comput. 2019, 23, 143–155. [Google Scholar] [CrossRef]
- Essiet, I.; Sun, Y. Tracking variable fitness landscape in dynamic multi-objective optimization using adaptive mutation and crossover operators. IEEE Access 2020, 8, 188927–188937. [Google Scholar] [CrossRef]
- Guzmán-Gaspar, J.Y.; Mezura-Montes, E.; Domínguez-Isidro, S. Differential Evolution in Robust Optimization Over Time Using a Survival Time Approach. Math. Comput. Appl. 2020, 25, 72. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, H.; Chen, M.; Gong, D.; Cheng, S. Grid-based dynamic robust multi-objective brain storm optimization algorithm. Soft Comput. 2020, 24, 7395–7415. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, Y.; Hao, K. Decision-making and multi-objectivization for cost sensitive robust optimization over time. Knowl.-Based Syst. 2020, 199, 105857. [Google Scholar] [CrossRef]
- Hui, Q.; Teng, Y.; Zuo, H.; Chen, Z. Reactive power multi-objective optimization for multi-terminal AC/DC interconnected power systems under wind power fluctuation. CSEE J. Power Energy Syst. 2020, 6, 630–637. [Google Scholar] [CrossRef]
- Fox, M.; Yang, S.; Caraffini, F. A new moving peaks benchmark with attractors for dynamic evolutionary algorithms. Swarm Evol. Comput. 2022, 74, 101125. [Google Scholar] [CrossRef]
- Yazdani, D.; Yazdani, D.; Branke, J.; Omidvar, M.N.; Gandomi, A.H.; Yao, X. Robust Optimization Over Time by Estimating Robustness of Promising Regions. IEEE Trans. Evol. Comput. 2023, 27, 657–670. [Google Scholar] [CrossRef]
- Chen, M.; Guo, Y.; Jin, Y.; Yang, S.; Gong, D.; Yu, Z. An environment-driven hybrid evolutionary algorithm for dynamic multi-objective optimization problems. Complex Intell. Syst. 2023, 9, 659–675. [Google Scholar] [CrossRef]



| Parameter | Values |
|---|---|
| Number of peaks (m) | 5 |
| Dimension (D) | 2 |
| Search space | |
| Number of changes (environments) (N) | 30 |
| Change frequency () | 1000 |
| Change type | Small step (Equation (5)) |
| Peaks’ height range (h) | |
| Height severity () | 5.0 |
| Peaks’ width range (w) | |
| Width severity () | 0.5 |
| Rotation angle range () | |
| Angle severity () | 1.0 |
| Time window (T) | 3 |
| History size (period P) | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novoa-Hernández, P.; Puris, A.; Pelta, D.A. Robust Optimization over Time Problems—Characterization and Literature Review. Electronics 2023, 12, 4609. https://doi.org/10.3390/electronics12224609
Novoa-Hernández P, Puris A, Pelta DA. Robust Optimization over Time Problems—Characterization and Literature Review. Electronics. 2023; 12(22):4609. https://doi.org/10.3390/electronics12224609
Chicago/Turabian StyleNovoa-Hernández, Pavel, Amilkar Puris, and David A. Pelta. 2023. "Robust Optimization over Time Problems—Characterization and Literature Review" Electronics 12, no. 22: 4609. https://doi.org/10.3390/electronics12224609
APA StyleNovoa-Hernández, P., Puris, A., & Pelta, D. A. (2023). Robust Optimization over Time Problems—Characterization and Literature Review. Electronics, 12(22), 4609. https://doi.org/10.3390/electronics12224609













