Comparison of Multi-Object Control Methods Using Multi-Objective Optimization
Abstract
:1. Introduction
1.1. State of Knowledge
1.2. Study Objectives
- The reference to multi-object control processes;
- The formation of various possible optimization goals reflecting the properties of the actual control process;
- A comparison of the sensitivity of individual multi-objective optimization algorithms in various environmental conditions.
1.3. Article Content
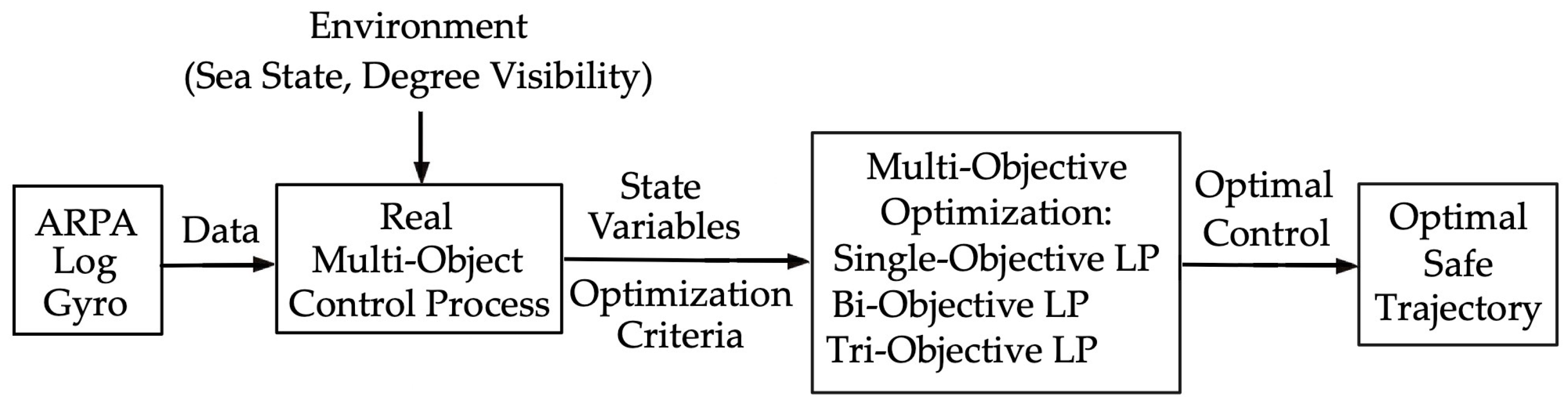
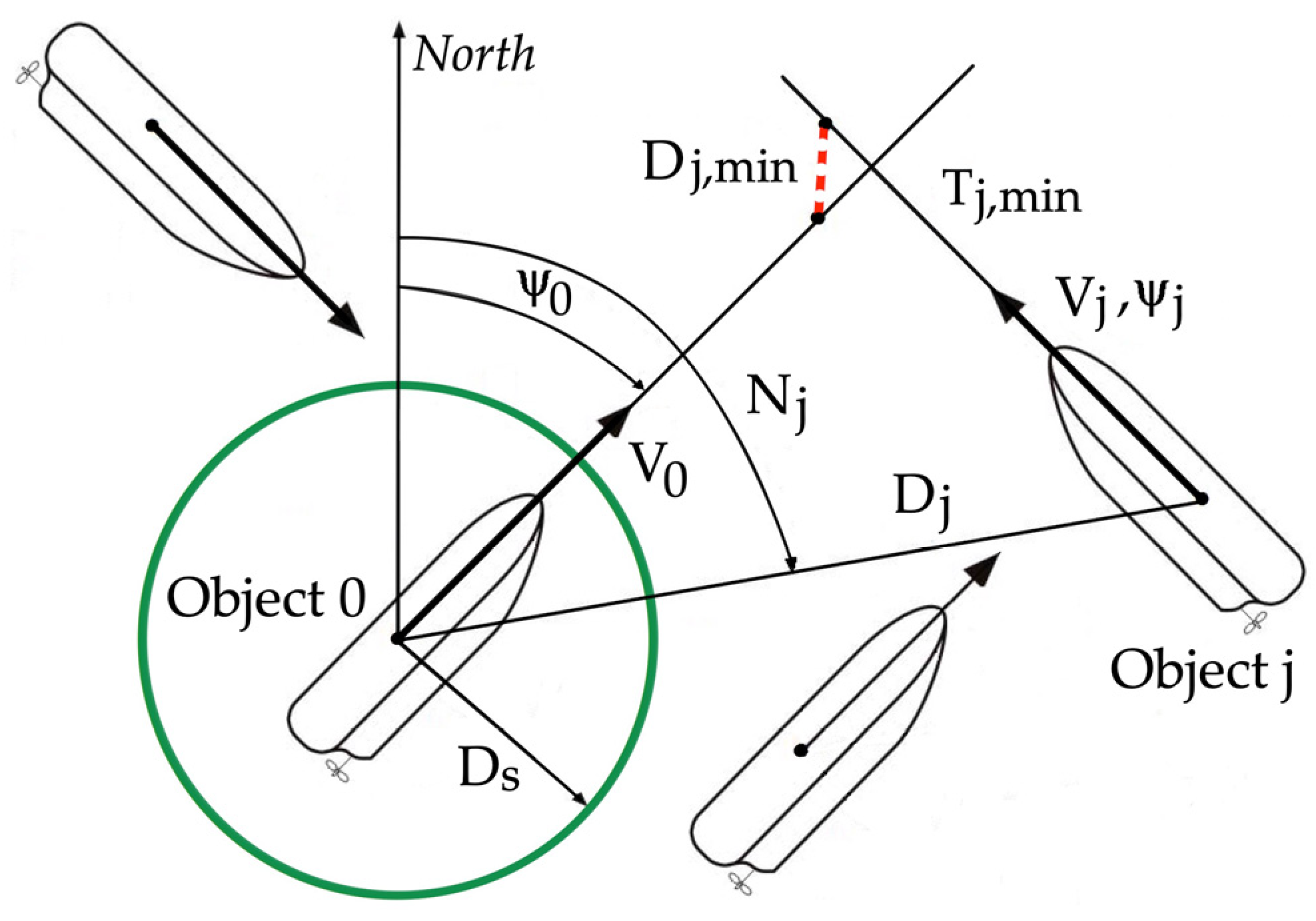
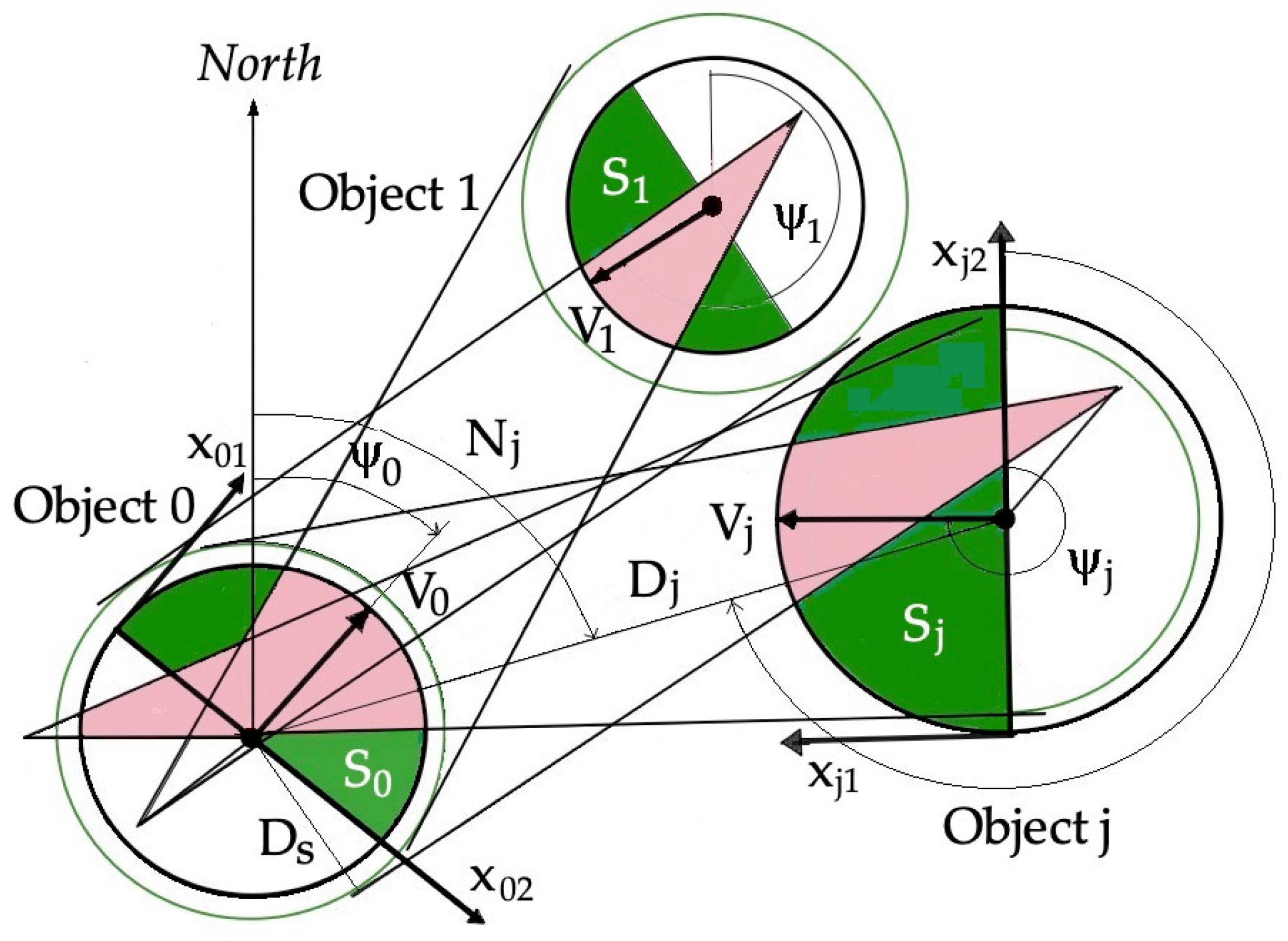
2. Model of a Multi-Object Control Process
- For Object 0:
- For Object j:
3. Multi-Objective Optimization Methods
3.1. Single-Objective Linear Programming
3.2. Bi-Objective Linear Programming
3.3. Tri-Objective Linear Programming
4. Multi-Objective Optimization Algorithms
- Single-objective linear programming algorithm s-oLP;
- Bi-objective linear programming non-cooperative algorithm b-oLP_nc;
- Bi-objective linear programming cooperative algorithm b-oLP_c;
- Tri-objective linear programming non-cooperative algorithm s-oLP_nc;
- Tri-objective linear programming cooperative algorithm s-oLP_c.
4.1. Single-Objective Linear Programming Algorithm S-oLP
4.2. Bi-Objective Linear Programming Non-Cooperative Algorithm B-oLP_nc
4.3. Bi-Objective Linear Programming Cooperative Algorithm B-oLP_c
4.4. Tri-Objective Linear Programming Non-Cooperative Algorithm T-oLP_nc
4.5. Tri-Objective Linear Programming Cooperative Algorithm T-oLP_c
5. Simulation Studies of Algorithms
5.1. Example of a Multi-Object Situation
5.2. Safe Object 0 Trajectories
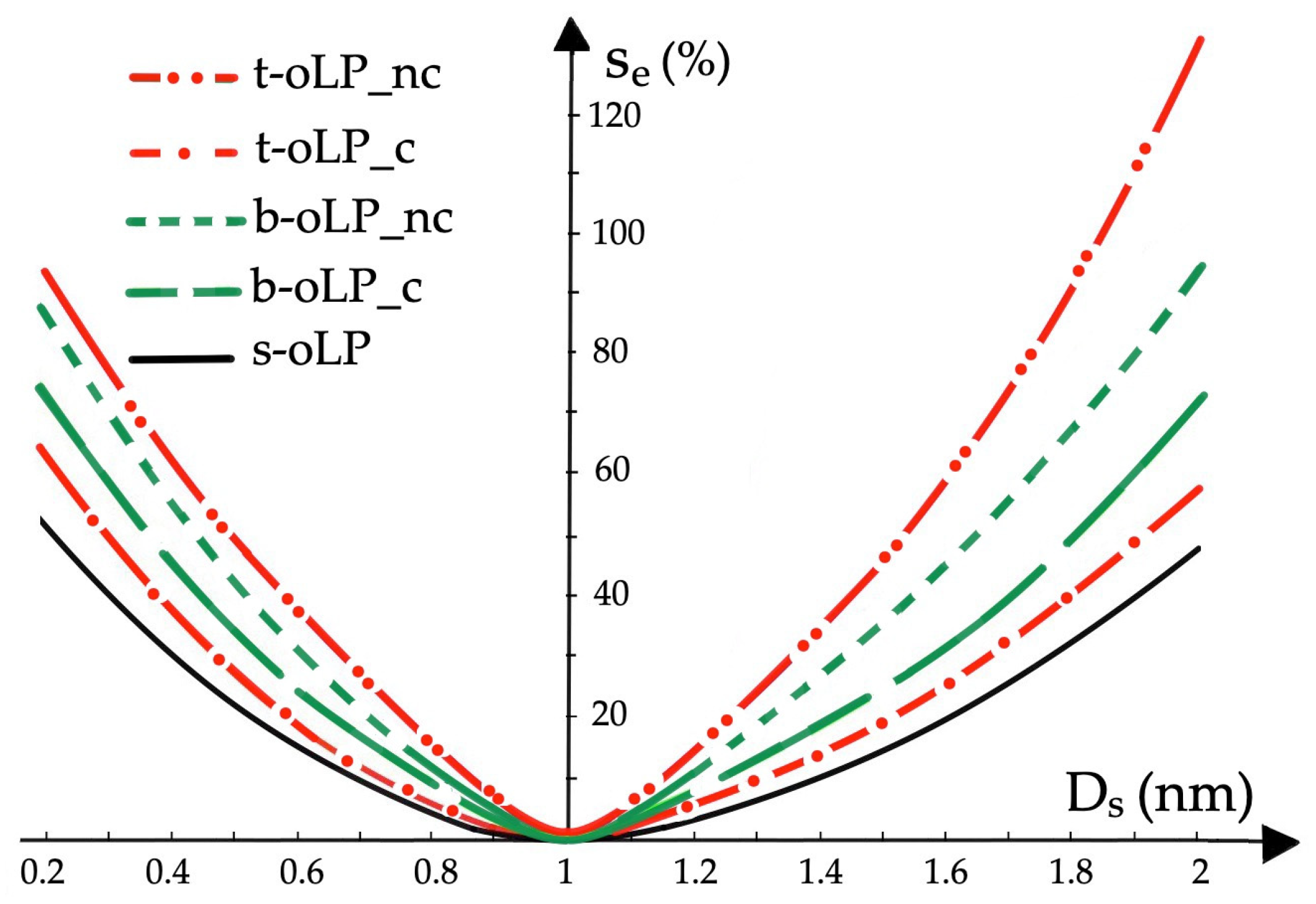
5.3. Sensitivity Characteristics of Multi-Objective Optimization
- It is further characterized by the sensitivity function sa of the first sk,a for the kth order of the object model a’s parameters:
- The sensitivity function sx of the first sk,x for the kth order of the optimal object control is as follows:
6. Conclusions
- The multi-object optimization model enables the mapping of various properties in the actual control process, such as the risk of object collisions, deviation from the object’s trajectory and its course, and the degree of maneuvering cooperation between objects;
- A comparison of optimization results allows the appropriate multi-objective method to be adapted to the conditions of the actual control process;
- Characterizing the sensitivity of individual optimization algorithms allows their resistance to changes in environmental conditions to be assessed that characterize sea states and the degree of visibility at sea.
- An analysis of the multi-objective optimization’s sensitivity to the risk of collisions due to inaccuracies in the measured state variables for multi-object control processes;
- Taking into account disturbances in the control process;
- Synthesizing methods for the multi-objective optimization of control processes in the nature of a game.
Funding
Data Availability Statement
Conflicts of Interest
References
- Pardalos, P.; Hearn, D.W. Multi-Objective Linear Programming. In Multi-Criteria Decision Analysis via Ratio and Difference Judgement; Lootsma, F.A., Ed.; Springer: Boston, MA, USA, 1999; Applied Optimization; Volume 3, pp. 229–257. [Google Scholar] [CrossRef]
- Khodadadi, N.; Abualigah, L.; Al-Tashi, Q.; Mirjalili, S. Multi-objective chaos game optimization. Neural Comput. Appl. 2023, 35, 14973–15004. [Google Scholar] [CrossRef]
- Chen, F.; Huang, G.; Fan, Y. A linearization and parameterization approach to tri-objective linear programming problems for power generation expansion planning. Energy 2015, 87, 240–250. [Google Scholar] [CrossRef]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Yilmaz, S.; Sen, S. Metaheuristic approaches for solving multiobjective optimization problems. In Comprehensive Metaheuristics; Mirjalili, S., Gandomi, A.G., Eds.; Academic Press: Cambridge, MA, USA, 2023; Chapter 2; pp. 21–48. [Google Scholar] [CrossRef]
- Sharifi, M.R.; Akbarifard, S.; Qaderi, K.; Madadi, M.R. A new optimization algorithm to solve multi-objective problems. Sci. Rep. 2021, 11, 20326. [Google Scholar] [CrossRef]
- Snasel, V.; Rizk-Allah, R.M.; Hassanien, A.E. Guided golden jackal optimization using elite-opposition strategy for efficient design of multi-objective engineering problems. Neural Comput. Appl. 2023, 35, 20771–20802. [Google Scholar] [CrossRef]
- Rudloff, B.; Ulus, F.; Vanderbei, R. A parametric simplex algorithm for linear vector optimization problems. Math. Program. 2016, 163, 213–242. [Google Scholar] [CrossRef]
- Löhne, A.; Weißing, B. Equivalence between polyhedral projection, multiple objective linear programming and vector linear programming. Math. Methods Oper. Res. 2016, 84, 411–426. [Google Scholar] [CrossRef]
- Yap, E. A Literature Review of Multi-Objective Programming; Australian Mathematical Sciences Institute: Melborne, Australia, 2010; Volume 6, Available online: https://api.semanticscholar.org/CorpusID:18514208 (accessed on 2 October 2023).
- Halffmann, P.; Schafer, L.E.; Dachert, K.; Klamroth, K.; Ruzika, S. Exact algorithms for multiobjective linear optimization problems with integer variables: A state of the art survey. J. Multi-Criteria Decis. Anal. 2022, 29, 325–445. [Google Scholar] [CrossRef]
- Stidsen, T.; Andersen, K.A.; Dammann, B. A Branch and Bound Algorithm for a Class of Biobjective Mixed Integer Programs. Manag. Sci. 2014, 60, 4. [Google Scholar] [CrossRef]
- Mobus, R. Multi-Object Adaptive Cruise Control. Ph.D. Thesis, Swiss Federal Institute of Technology Zurich, Zurich, Switzerland, 2008. [Google Scholar]
- Rosa, A.; Khajavirad, A. Efficient Joint Object Matching via Linear Programming. Mathematics 2023, 2023, 1–46. [Google Scholar] [CrossRef]
- Jiang, H.; Fels, S.; Little, J.J. A Linear Programming Approach for Multiple Object Tracking. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, X.; Han, W.; Lu, S.; Chen, J.; Tang, T. Overlapping Coalition Formation Game via Multi-Objective Optimization for Crowdsensing Task Allocation. Electronics 2023, 12, 3454. [Google Scholar] [CrossRef]
- Caramia, M. “Multi-Objective and Multi-Level Optimization: Algorithms and Applications”: Foreword by the Guest Editor. Algorithms 2023, 16, 425. [Google Scholar] [CrossRef]
- Barichard, V.; Ehrgott, M.; Gandibleux, X.; T’Kindt, V. Multiobjective Programming and Goal Programming; Springer: Basel, Switzerland, 2009; ISBN 978-3-540-85645-0. [Google Scholar]
- Antunes, C.H.; Alves, M.J.; Climaco, J. Multiobjective Linear and Integer Programming; Springer: Basel, Switzerland, 2016. [Google Scholar] [CrossRef]
- Luc, D.T. Multiobjective Linear Programming: An Introduction; Springer: Basel, Switzerland, 2016. [Google Scholar] [CrossRef]
- Eslami, M. Theory of Sensitivity in Dynamic Systems; Springer: Berlin/Heidelberg, Germany, 1994; ISBN 978-3-662-01632-9. [Google Scholar]
- Rosenwasser, E.; Yusupov, R. Sensitivity of Automatic Control Systems; CRC Press: Boca Raton, FL, USA, 2000; ISBN 978-0-849-3229293-8. [Google Scholar]
- Nise, N.S. Control Systems Engineering, 8th ed.; John Wiley & Sons Inc.: San Luis Obispo, CA, USA, 2019; ISBN 978-1-119-47422-7. [Google Scholar]

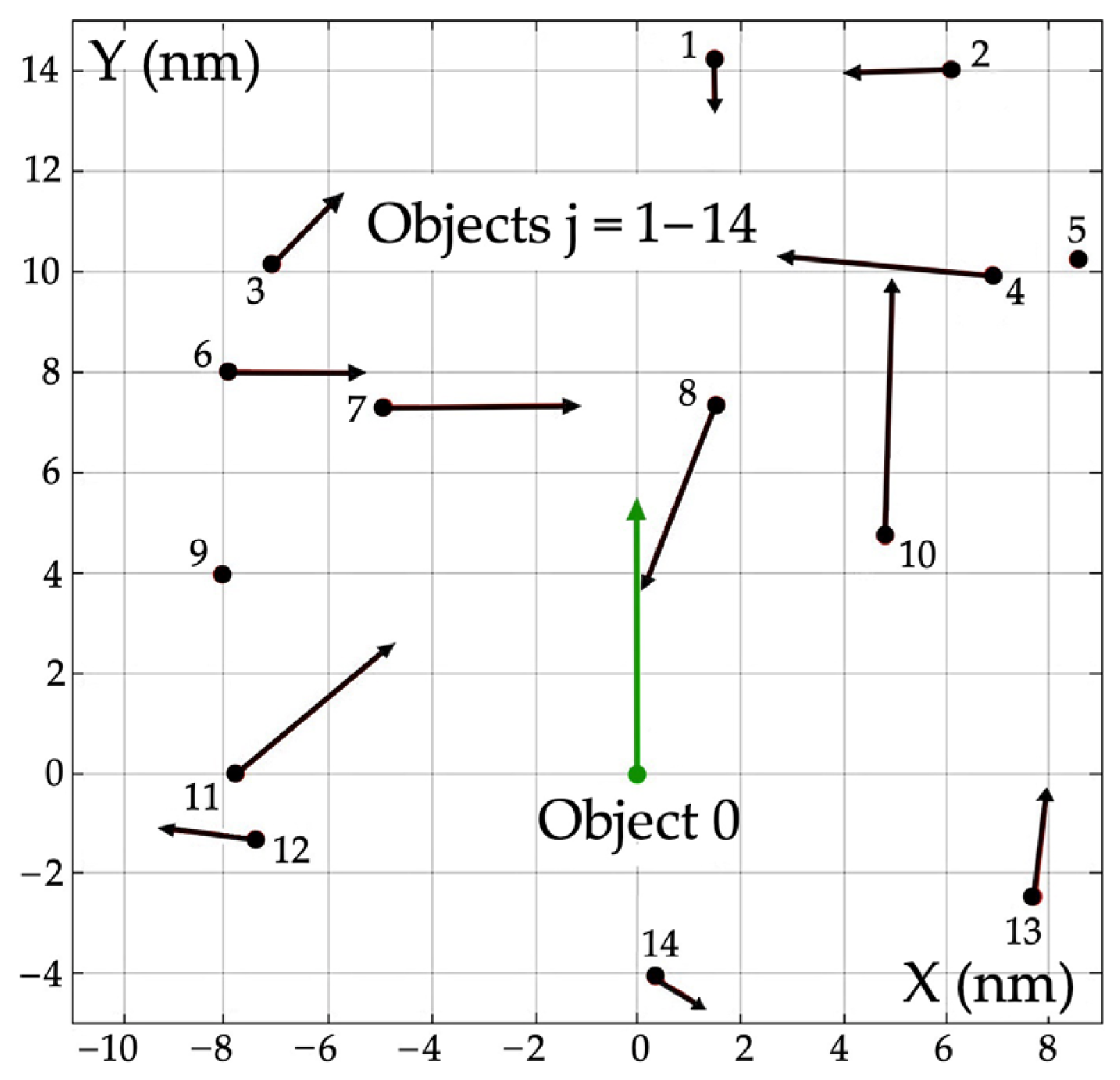
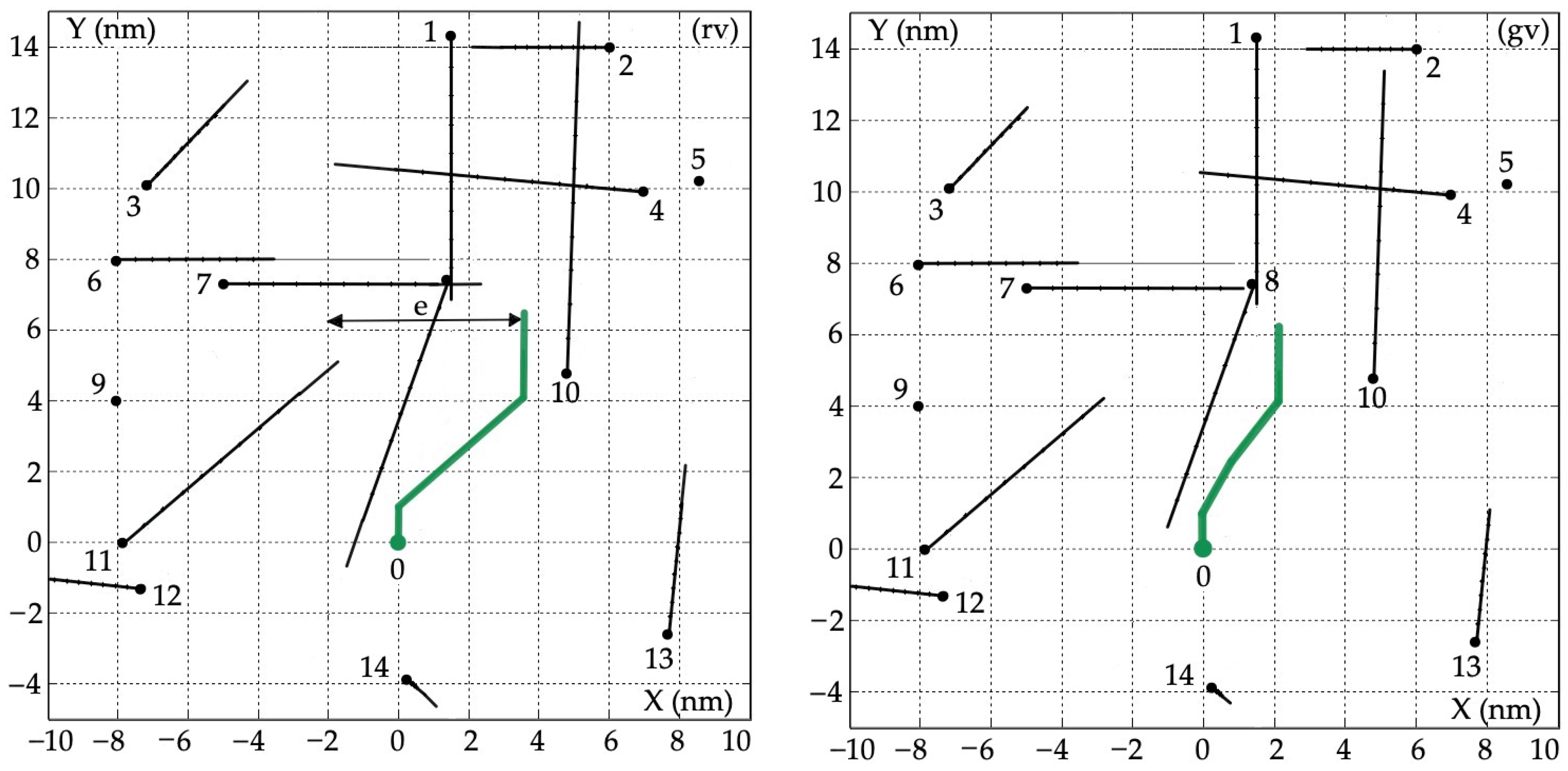
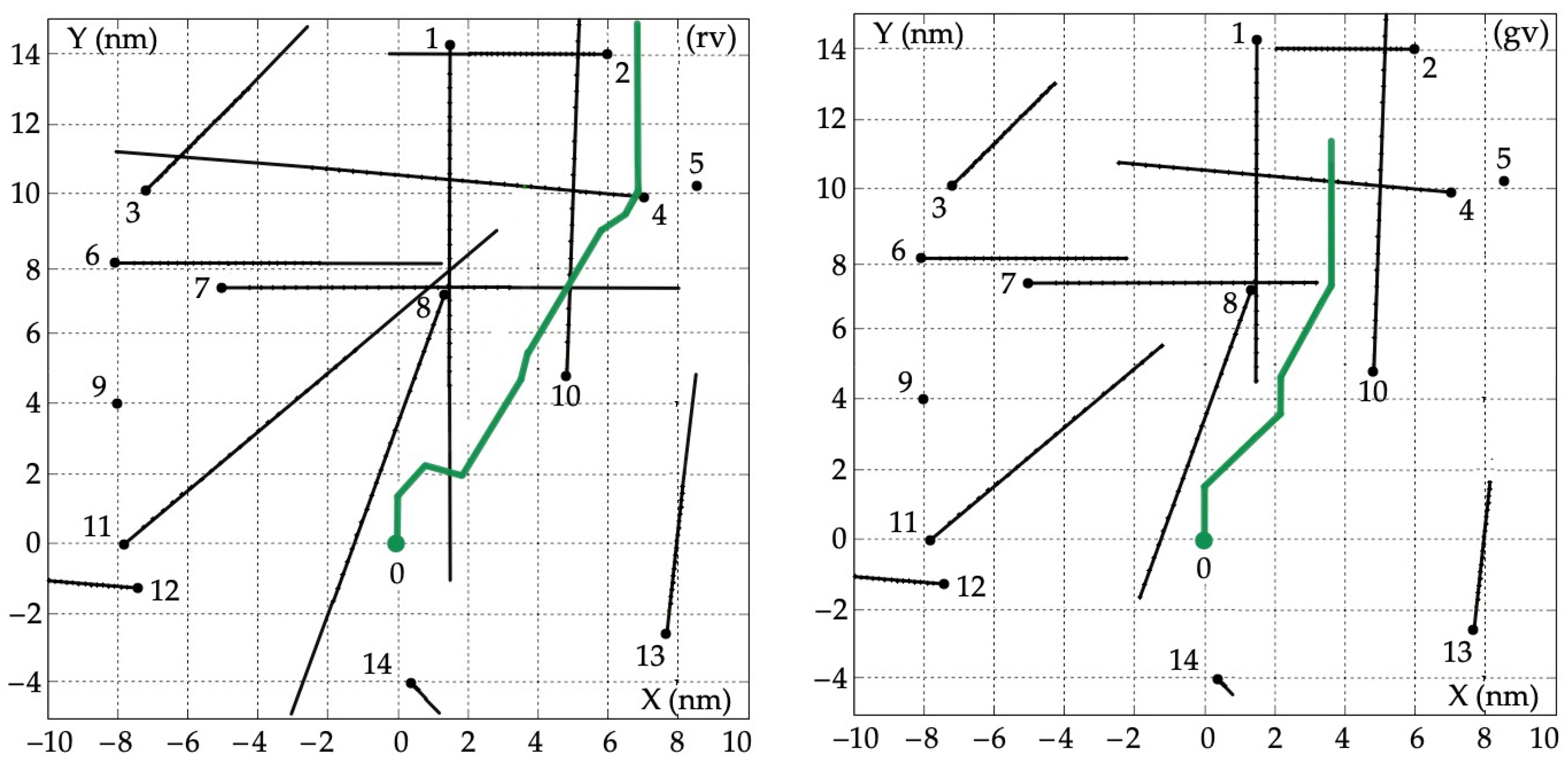
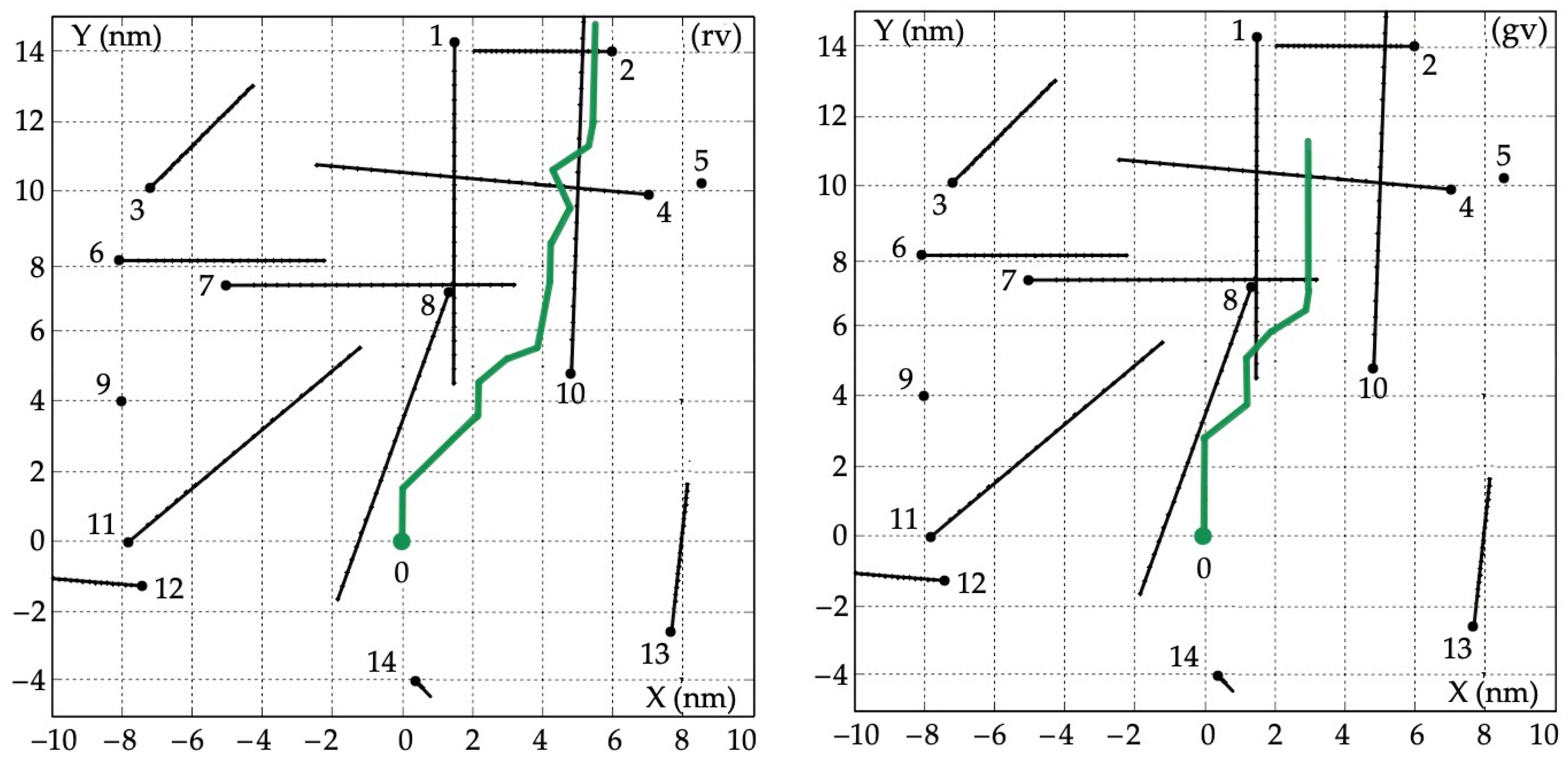
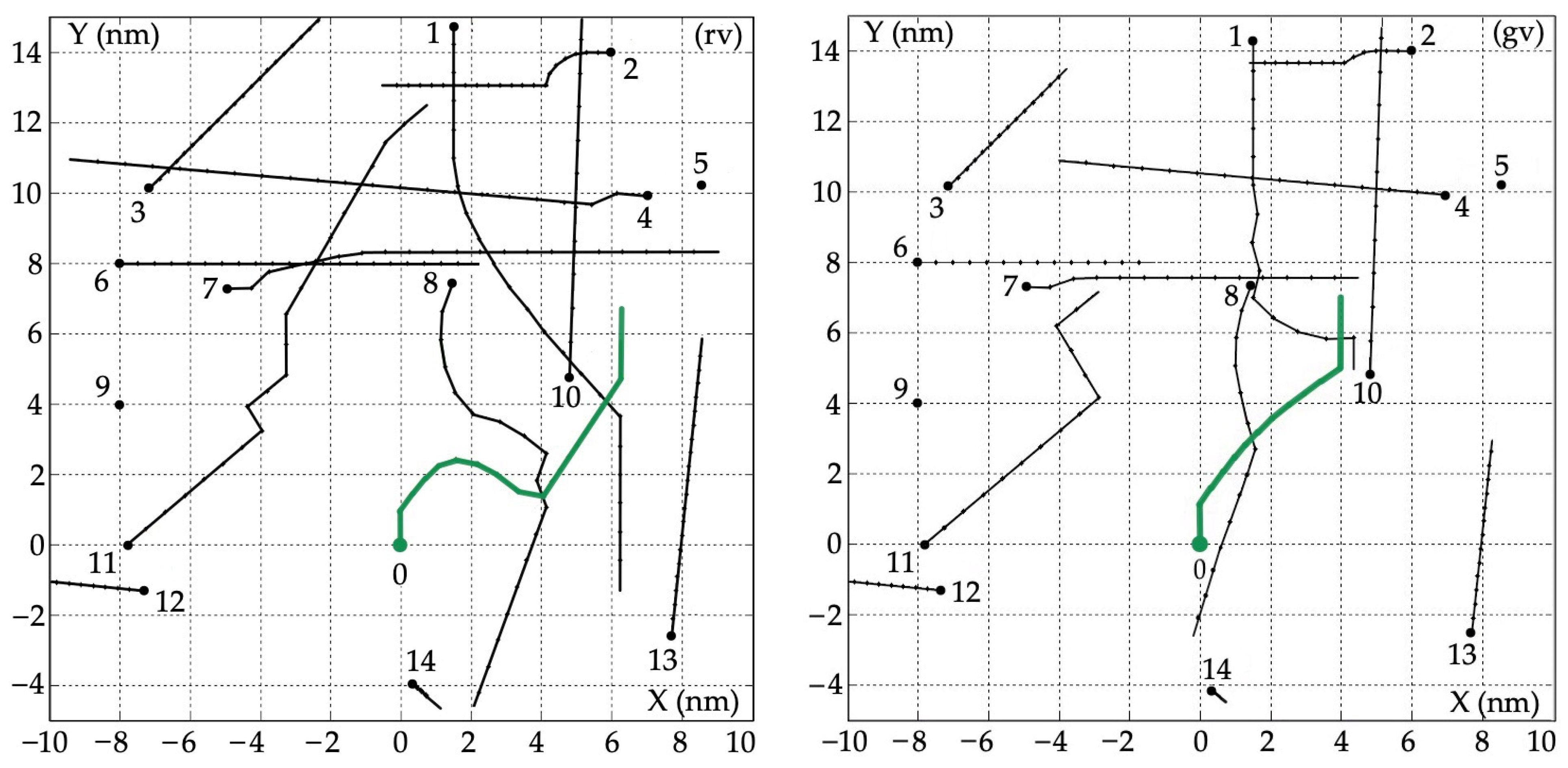
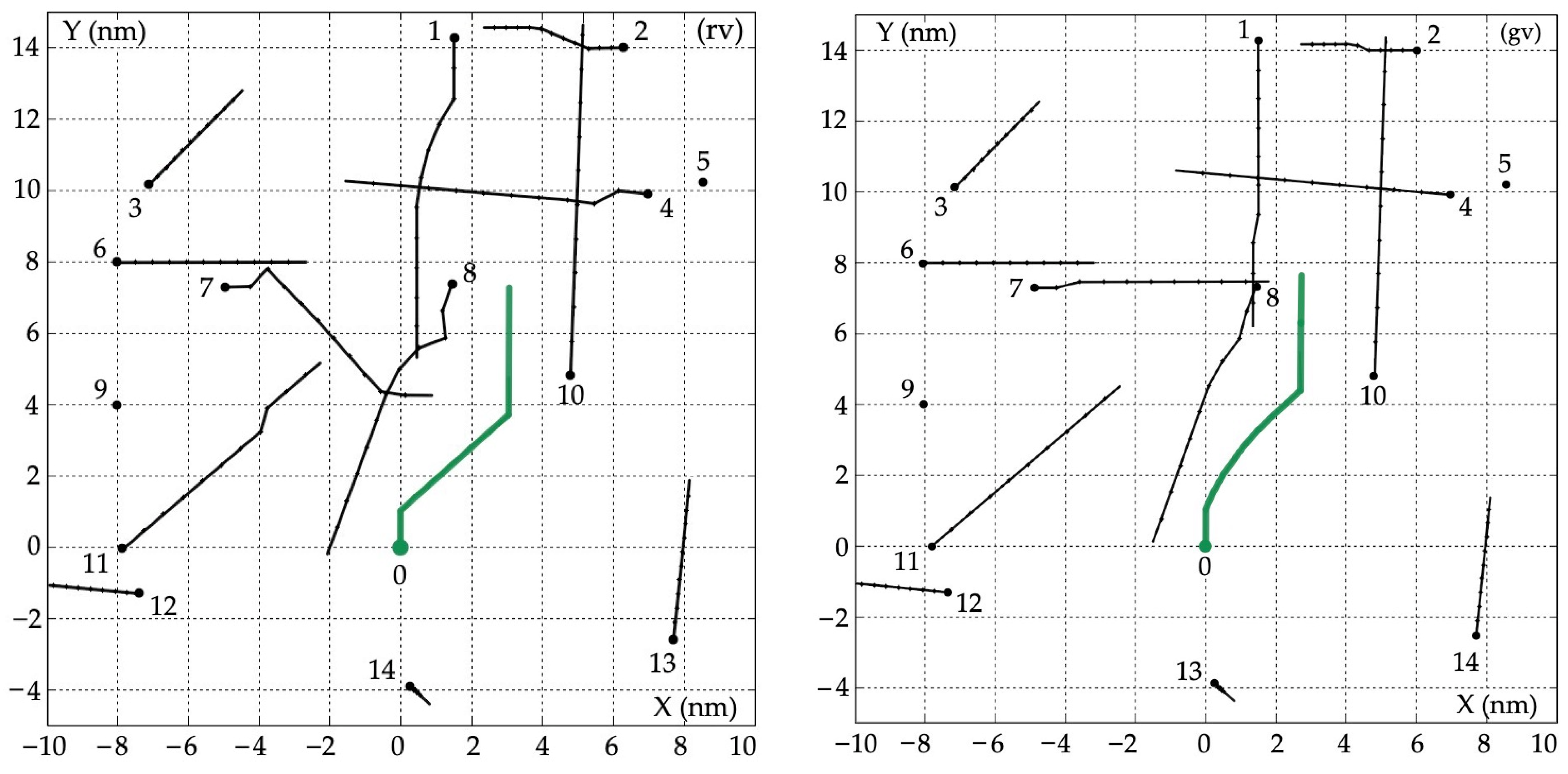
| Object j | Bearing Nj (deg) | Distance Dj (nm) | Speed Vj (kn) | Course ψj (deg) |
|---|---|---|---|---|
| 0 | - | - | 19.8 | 0 |
| 1 | 7 | 14.4 | 16.1 | 179 |
| 2 | 22 | 15.1 | 6.6 | 271 |
| 3 | 324 | 12.3 | 6.9 | 46 |
| 4 | 36 | 12.2 | 15.4 | 275 |
| 5 | 41 | 13.2 | 0 | 0 |
| 6 | 325 | 8.9 | 13.4 | 89 |
| 7 | 316 | 11.4 | 9.5 | 91 |
| 8 | 12 | 7.7 | 15.9 | 199 |
| 9 | 290 | 9.0 | 0 | 0 |
| 10 | 46 | 6.7 | 19.2 | 3 |
| 11 | 271 | 7.7 | 14.2 | 49 |
| 12 | 261 | 7.6 | 6.8 | 274 |
| 13 | 109 | 8.3 | 8.0 | 7 |
| 14 | 176 | 4.1 | 0.8 | 129 |
| Algorithm | s-oLP | b-oLP_nc | b-oLP_c | t-oLP_nc | t-oLP_c | |
|---|---|---|---|---|---|---|
| Deviation e (nm) | Restricted Visibility | 3.8 | 6.7 | 5.5 | 6.2 | 3.0 |
| Good Visibility | 2.0 | 3.6 | 3.0 | 4.0 | 2.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisowski, J. Comparison of Multi-Object Control Methods Using Multi-Objective Optimization. Electronics 2023, 12, 4198. https://doi.org/10.3390/electronics12204198
Lisowski J. Comparison of Multi-Object Control Methods Using Multi-Objective Optimization. Electronics. 2023; 12(20):4198. https://doi.org/10.3390/electronics12204198
Chicago/Turabian StyleLisowski, Józef. 2023. "Comparison of Multi-Object Control Methods Using Multi-Objective Optimization" Electronics 12, no. 20: 4198. https://doi.org/10.3390/electronics12204198
APA StyleLisowski, J. (2023). Comparison of Multi-Object Control Methods Using Multi-Objective Optimization. Electronics, 12(20), 4198. https://doi.org/10.3390/electronics12204198









