Impact of Age Violation Probability on Neighbor Election-Based Distributed Slot Access in Wireless Ad Hoc Networks

Abstract

In this paper, we propose an analytical model of neighbor election-based distributed slot access by considering the relationship between the age of information (AoI) and the slot access process of nodes in wireless ad hoc networks. A node first maintains the information updates from its neighbors by relaying and receiving messages and determines message transmission slots by holding elections with its relevant competing neighbors. We first find out and analyze the interaction relationship between the transmission probability of nodes, the competing probability of neighbor nodes, and the violation probability that AoI exceeds the timeliness threshold of the neighbor election. Next, we obtain the approximated expression of the competing probability and the age violation probability based on the comprehensive analysis of the neighbor election process. Numerical and simulation results show that our approximation is tighter than the one in the literature and also provides insights into enhancing the design of network-aware distributed multiple access schemes.

1. Introduction

A neighbor election is a distributed algorithm for the nodes to coordinate with their competing neighbors for slot access in wireless ad hoc networks. It was first proposed as neighborhood-aware contention resolution (NCR) [1] and then adopted as a multiple access scheme in WiMAX mesh mode for transmitting control messages [2,3]. In recent years, there has been an increasing demand for developing next-generation multiple access schemes for the evolving fifth-generation (5G) and sixth-generation (6G) wireless networks, Internet of Things (IoT) [4,5,6] and wireless sensor networks (WSN) [7,8], where the nodes are expected to schedule themselves in a distributed manner with the knowledge of their neighbors. With the characteristics of neighborhood awareness, the neighbor election has then attracted recent research interest again [9,10,11]. Different from the well-known contention-based slotted aloha (SA) and Carrier-Sense Multiple Access (CSMA), where the nodes randomly initiate transmissions without any prior knowledge about their neighboring network, neighbor election performs contention resolution by getting acquainted with their neighbors. To avoid collisions, a node using neighbor election needs to maintain the information updates from its one-hop and two-hop neighbors to ensure whether they will compete for a specific slot. This lightweight information maintenance will not require the successful two-way handshake processes between transmitters and receivers in reservation-based distributed coordination function (DCF) and other scheduling mechanisms, which may reduce the required control message overhead. If the information of a neighbor node cannot be timely updated, it will also be considered as a potential competitor, leading to an increasing number of competing neighbors. As a result, the insufficient timeliness of neighbor maintenance will decrease the probability of a node winning an election and starting its transmission [9]. Meanwhile, the maintenance of frequent neighbor updates is fundamentally supported by the communication among nodes, which implies an interaction relationship between the transmission probability of nodes and the timeliness of information maintenance.

The timeliness of information maintained in a neighbor election is first modeled in [9] as a function of the number of relaying nodes and the packet loss rate of wireless links. In contrast, the impact of a message transmission on the maintenance process is ignored. In the recent decade, the concept of age of information (AoI) [12] has been introduced as a novel metric to evaluate the information freshness in communication networks. As we are discussing the neighbor election-based slot access, throughout this paper, the AoI is determined as the age of maintained information updates from the neighbors of a receiver node [13]. For time-restricted applications, the timeliness of information maintenance can also be evaluated by the probability that AoI exceeds a given age threshold, which is termed as the age violation probability [14,15] or outage probability of AoI [16]. In [12], the real-time status updating by multiple information sources is comprehensively discussed. In [14], the age violation probability is derived based on the probability-generating function (pgf) of peak age at a steady state. The upper bound of age violation probability is given and tightened in [16]. While in [15], Hu et al. derive the mean age violation probability by analyzing the different cases that the AoI that may exceed an arbitrary age constraint and provide statistical results. This work makes it easy to analyze age violation probability by intuitively mapping the violation period within the evolution path of AoI.

Besides evaluating the AoI metric and its variations, some literature also try to build the connection between AoI and the concerned indicators in CSMA networks to bring more insights. The relation between beacon interval and AoI is given in [17], and the relation of AoI and the stability in control loops over non-beacon CSMA network is presented in [18]. However, the transmission timing in CSMA networks does not depend on AoI, as nodes using CSMA-based schemes only rely on direct channel sensing to initiate transmissions. Hence the change of AoI cannot affect the transmission process of nodes, and these analyses cannot be directly applied to the analysis of neighbor election process where interaction relationship between AoI and transmissions of nodes exists.

The main contributions of this paper are given as follows:

• We propose an approximated analytical model of the transmission probability of nodes in a wireless ad hoc network concerning its interaction relationship with the age violation probability of neighbor election-based distributed slot access. To our best knowledge, it is the first work that analyzes such interaction relationships in distributed multiple access schemes, which provides theoretical guidance for enhancing the design of distributed multiple access schemes with network-aware algorithms from the information freshness perspective.
• We define the concept of timely maintained neighbors in which information can be updated by a typical node on time. We then consider the competing probability of these neighbor nodes by analyzing the intersection of election intervals
• We verify the proposed approximation model by performing numerical simulations under different parameters, including the number of neighbors, the ratio of relaying nodes, and the packet loss rate. According to the simulation results, the proposed approximation model can enhance the accuracy of evaluating the transmission probability of nodes, which shows that the consideration of age violation probability of neighbor information is necessary.

The rest of the paper is organized as follows. We first introduce the system model of a wireless ad hoc network where the nodes use neighbor election-based slotted access in Section 2. Also, we first derive the interaction relationship between the transmission probability of nodes, the age violation probability of neighbor information, and the competing probability of timely maintained neighbors. Next, we discuss the election process of two neighboring nodes in Section 3 and linearly approximate their competing probability to simplify the derivations. Section 4 focuses on the information maintenance from the two-hop neighborhood, and the age violation probability is derived as the mean violation duration divided by the average maintenance interval. Numerical simulation results are illustrated in Section 5. The conclusions of this paper and future research aspects are summarized in Section 6.

2. Neighbor Election Based Distributed Slot Access

2.1. System Model

We consider a slotted wireless ad hoc network where the nodes attempt to access slots for transmitting their messages using a distributed neighbor election algorithm. The principle of neighbor election-based slot access is to control nodes’ transmission reasonably. As the literature describes [9,11], the nodes have to maintain neighbors’ information and avoid collisions in some future slots. A node should therefore announce to its neighbors the range of future slots it may compete for. The neighbors that receive this announcement will check the intersection of slots which they may compete together and avoid collision with the distributed neighbor election algorithm. As for broadcasting crucial control messages in WiMAX mesh mode, a node should ensure that the one-hop neighbors are ready to receive its message. A two-way reservation handshake is unsuitable for such transmission as it is complicated for a node to make handshakes with all its one-hop neighbors. However, election-based slot access helps the nodes initiate collision-free transmissions in a much more efficient way with the prior knowledge of neighbors. This makes it a promising candidate for designing next-generation multiple access schemes.

We start the analysis of the neighbor election by considering a typical node i. From the perspective of node i, the slots are partitioned into two types of intervals: the valid election interval and the hold-off interval. Node i first participates in the elections within its valid election interval of V slots and competes with its neighbors. After winning the chance of transmitting in a slot of index $Q\in \left\{1,\cdots ,V\right\}$, it suspends the participation in elections and steps into a hold-off interval of H slots. When the hold-off interval ends, node i will enter the next valid election interval and rejoin the election. The duration between the start of two consecutive valid election intervals is termed as an election cycle [9] of $\tau =H+Q$ slots, which is illustrated in Figure 1.

Algorithm 1 shows a simplified version of the neighbor election algorithm adopted in the WiMAX standard [2], where ${\mathcal{N}}_1$ and ${\mathcal{N}}_2$ denote the one-hop and two-hop neighbor set of i respectively; $C_t$ denotes the competing neighbor list for slot t and $Hash(i,t)$ is a two-input hash-based pseudo random number generating function which has a unique output when the input variables are given. where node i should maintain the election information from several N neighbors within its two-hop coverage. To realize the required two-hop neighborhood maintenance, the node message should contain a list of the latest election information updates of itself and its one-hop neighbors. The update of a neighbor node j has three fields: the identity of j, the range of its next valid election interval, and the earliest subsequent transmitting slot, i.e., the start of the second next valid election interval. This information helps node i to determine whether node j belongs to the competing neighbor list $C_t$. The information of node j itself will be updated right before its message transmission, which means there will be no queuing time for the update before being embedded into the message.

Algorithm 1: Distributed Neighbor Election Algorithm.

for slot $t=1,\cdots ,V$ in valid election interval do     for one-hop and two-hop neighbors $j\in {\mathcal{N}}_1\cup$${\mathcal{N}}_2$ do         if the valid election intervals of i and j overlap at slot t then            include j into $C_t$;         end if     end for     for competing neighbor $j\in C_t$ do         if pseudo-random value $Hash(i,t)>Hash(j,t)$ then            node i wins the election with j. continue;         else            node i loses the election. break;         end if     end for     if node i wins the election for slot t then         $Q\leftarrow t$, node i transmits in slot Q. break;     end if end for

2.2. Interaction Relationship among Parameters

For simplicity of analysis, we assume that each node is equal to the typical node i and operates with the same value of N in each slot. Let $p_{\mathrm{t}}$ denote the transmission probability of node i in an arbitrary slot after it wins an election. Let $p_{\mathrm{v}}$ denote the age violation probability that node i cannot timely maintain the updates from one of its neighbors. Let $p_{\mathrm{c}}$ denote the competing probability that a timely maintained neighbor node will compete with node i in a specific election. Let $N_{\mathrm{v}}$ denote the number of untimely maintained neighbors, which is binomial distributed with parameters N and $p_{\mathrm{v}}$. The number of timely maintained competing neighbors is denoted as $N_{\mathrm{c}}=\left(N-N_{\mathrm{v}}\right)p_{\mathrm{c}}$. Therefore, $p_{\mathrm{t}}$ can be expressed as the reciprocal of the mean number of nodes participating in an election:

$$p_{\mathrm{t}}=\frac{1}{E\left[N_{\mathrm{c}}+N_{\mathrm{v}}+1\right]}=\frac{1}{\left(p_{\mathrm{c}}-p_{\mathrm{c}}{p}_{\mathrm{v}}+p_{\mathrm{v}}\right)N+1}$$

(1)

Equation (1) shows that $p_{\mathrm{t}}$ is a function of N, $p_{\mathrm{c}}$ and $p_{\mathrm{v}}$. While the competing probability of maintained neighbors $p_{\mathrm{c}}$ is related to $p_{\mathrm{t}}$ as it is determined by the intersections of valid election intervals of competing neighbors, which is derived in Section 3. The age violation probability $p_{\mathrm{v}}$ also relates to $p_{\mathrm{t}}$ since it is determined by the information maintenance process, which will be analyzed in the Section 4.

3. Competing Probability of Timely Maintained Neighbors

We concentrate on the election process of typical node i and a timely maintained neighbor node j within two-hop distance. These two nodes will not win the same election and thus have different transmitting slots. To analyze the competing probability $p_{\mathrm{c}}$ of j, we suppose that node i and j enter their new election cycles at slot $t_1$ and $t_2>t_1$ respectively. Let $R=t_2-t_1$ denote the residual slot number of the previous election cycle of j when i has entered its new one. Node i will consider j as a competing node during the intersections of their valid election intervals, which can be divided into three cases as illustrated in Figure 2. Let $\xi$ denote the duration ratio of an intersection to node i’s related valid election interval. From the perspective of i, the competing probability of j can be written as the expectation of $\xi$:

$$p_{\mathrm{c}}:=E\left[\xi \right]={\sum }_{q=1}^V{f}_Q\left(q\right)·{\overline{\xi }}_q$$

(2)

where $f_Q\left(q\right)$ is the probability mass function (pmf) of Q, and ${\overline{\xi }}_q$ is the expectation of $\xi$ under the condition of $Q=q$.

Since Q is geometric distributed with parameter $p_{\mathrm{t}}$, the pmf of Q is written as:

$$f_Q\left(q\right):=Pr\left(Q=q\right)={{\widehat{p}}_{\mathrm{t}}}^{q-1}{p}_{\mathrm{t}},q=1,2,\dots ,V$$

(3)

where ${\widehat{p}}_{\mathrm{t}}=1-p_{\mathrm{t}}$ for simplifying notations.

In the first and second cases of Figure 2, which conditions are $1\le R<Q$ and $H<R<H+Q$ respectively, there should be $Q\ge 2$. Hence only the third case will happen when $Q=1$. The expectation of $\xi$ conditioned by $Q=q$ is then defined as:

$$\begin{array}{cc}\hfill {\overline{\xi }}_q:& =E\left[\xi \left|Q=q\right.\right]\hfill \\ \hfill & =\left\{\begin{array}{cc}\begin{array}{c}\hfill \sum _{r=H+1}^{H+V}{f}_R\left(r\right)\end{array}\hfill & ,q=1\hfill \\ \begin{array}{c}\hfill \sum _{r=1}^{q-1}\frac{\left(f_R\left(r\right)+f_R\left(r+H\right)\right)·r}{q}+\sum _{r=H+q}^{H+V}{f}_R\left(r\right)\end{array}\hfill & ,q>1\hfill \end{array}\right.\hfill \end{array}$$

(4)

where $f_R\left(r\right)$ is the pmf of residual slot number R of node j:

$$f_R\left(r\right):=Pr\left(R=r\right)=\sum _{k=max\left(r,H+1\right)}^{H+V}\frac{f_{\tau }\left(k\right)}{k},r=1,\cdots ,H+V$$

(5)

and $f_{\tau }\left(k\right)$ is the pmf of election cycle’s duration $\tau =H+Q$:

$$f_{\tau }\left(k\right):=Pr\left(\tau =k\right)=\left\{\begin{array}{cc}{f}_Q\left(k-H\right),\hfill & H<k\le H+V\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

The definition in Equation (5) is based on the fact that when $\tau$ is given, R is uniformly distributed in the range $\left\{1,\cdots ,\tau \right\}$.

To derive $p_{\mathrm{c}}$ as a function of $p_{\mathrm{t}}$, we start from the derivation of $f_R\left(r\right)$. When $r\le H+1$, Equation (5) can be simplified as:

$$f_R\left(r\left|r\le H+1\right.\right)=\sum _{k=H+1}^{H+V}\frac{f_{\tau }\left(k\right)}{k}=\sum _{q=1}^V\frac{f_Q\left(q\right)}{q+H}=\frac{1}{E\left[\tau \right]}$$

(7)

As for $r>H+1$, Equation (5) is truncated, and difficult to have a simple expression by reduction to a common denominator. According to [19], the limit distribution of the residual slot number R in a renewal process satisfies the following formula:

$$Pr\left(R\le r\right)\approx \frac{1}{E\left[\tau \right]}\sum _{i=1}^{r}Pr\left(\tau \ge i\right)$$

(8)

Thus when $r>H+1$ is given, Equation (5) can be approximated as:

$$\begin{array}{cc}\hfill f_R\left(r\left|r>H+1\right.\right)& =Pr\left(R\le r\right)-Pr\left(R\le r-1\right)\hfill \\ \hfill & \approx \frac{Pr\left(\tau \ge r\right)}{E\left[\tau \right]}=\frac{\sum _{k=r}^{H+V}{f}_{\tau }\left(k\right)}{E\left[\tau \right]}=\frac{{\widehat{p}}_{\mathrm{t}}^{r-H-1}-{\widehat{p}}_{\mathrm{t}}^V}{E\left[\tau \right]}\hfill \end{array}$$

(9)

With the expression in Equations (7) and (9), we obtain the mean of $\xi$ when $q=1$ and $q\ge 2$ respectively as follow:

$${\overline{\xi }}_1=\sum _{r=1}^V\frac{{\widehat{p}}_{\mathrm{t}}^{r-1}}{E\left[\tau \right]}-\frac{V{\widehat{p}}_{\mathrm{t}}^V}{E\left[\tau \right]}=\frac{p_{\mathrm{t}}^{-1}-{\widehat{p}}_{\mathrm{t}}^{V-1}-V{\widehat{p}}_{\mathrm{t}}^V}{E\left[\tau \right]}=\frac{E\left[Q\right]-2V{\widehat{p}}_{\mathrm{t}}^V}{E\left[\tau \right]}$$

(10)

$${\overline{\xi }}_{q\ge 2}=\frac{1-{\widehat{p}}_{\mathrm{t}}^V}{qE\left[\tau \right]}\sum _{r=1}^{q-1}r+\frac{1}{qE\left[\tau \right]}\sum _{r=1}^{q-1}r{\widehat{p}}_{\mathrm{t}}^{r-1}+\sum _{r=H+q}^{H+V}{f}_R\left(r\right)$$

(11)

where $E\left[Q\right]$ denotes the mean of Q and is written as:

$$E\left[Q\right]=\sum _{q=1}^{V}q·f_Q\left(q\right)=\frac{1}{p_{\mathrm{t}}}-\left(\frac{1}{p_{\mathrm{t}}}-V\right)·{\widehat{p}}_{\mathrm{t}}^V\approx \frac{1}{p_{\mathrm{t}}}$$

(12)

and the approximation in Equation (12) holds as ${\widehat{p}}_{\mathrm{t}}^V$ goes to zero when V is sufficiently large. For the same reason, $E\left[\tau \right]\approx H+p_{\mathrm{t}}^{-1}$, and the increment of ${\overline{\xi }}_q$ when $q\ge 2$ is approximated as:

$$\begin{array}{cc}\hfill {\overline{\xi }}_{q+1}-{\overline{\xi }}_q\approx & \frac{\left(1+{\widehat{p}}_{\mathrm{t}}^{q-1}\right)q}{\left(q+1\right)E\left[\tau \right]}-\frac{{\sum }_{r=1}^{q-1}r{\widehat{p}}_{\mathrm{t}}^{r-1}+{\sum }_{r=1}^{q-1}r}{q\left(q+1\right)E\left[\tau \right]}-\frac{{\widehat{p}}_{\mathrm{t}}^{q-1}}{E\left[\tau \right]}\hfill \\ \hfill =& \frac{1}{2E\left[\tau \right]}-\frac{{\widehat{p}}_{\mathrm{t}}^{q-1}}{\left(q+1\right)E\left[\tau \right]}-\frac{1-q{\widehat{p}}_{\mathrm{t}}^{q-1}+\left(q-1\right){\widehat{p}}_{\mathrm{t}}^q}{p_{\mathrm{t}}^{2}q\left(q+1\right)E\left[\tau \right]}\hfill \end{array}$$

(13)

As q grows, ${\widehat{p}}_{\mathrm{t}}^q$ goes to zero and so ${\overline{\xi }}_{q+1}-{\overline{\xi }}_q$ gradually tends to ${\left(2E\left[\tau \right]\right)}^{-1}$. Thus we consider to approximate ${\overline{\xi }}_q$ by a linear function defined as follow:

$${\overline{\xi }}_Q:={\overline{\xi }}_V-\frac{V-Q}{V-2}·\left({\overline{\xi }}_V-{\overline{\xi }}_2\right),Q>1$$

(14)

where the value of ${\overline{\xi }}_2$ and ${\overline{\xi }}_V$ are approximated by substituting Equations (9) and (12) into Equation (11):

$$\begin{array}{cc}\hfill {\overline{\xi }}_2=& \frac{2-{\widehat{p}}_{\mathrm{t}}^V}{2E\left[\tau \right]}+\sum _{r=H+2}^{H+V}{f}_R\left(r\right)=\frac{2-{\widehat{p}}_{\mathrm{t}}^V}{2E\left[\tau \right]}+\sum _{y=2}^V\frac{{\widehat{p}}_{\mathrm{t}}^{y-1}}{E\left[\tau \right]}-\frac{\left(V-1\right){\widehat{p}}_{\mathrm{t}}^V}{E\left[\tau \right]}\hfill \\ \hfill \approx & \sum _{y=1}^V\frac{{\widehat{p}}_{\mathrm{t}}^{y-1}}{E\left[\tau \right]}\approx \frac{\left(1-{\widehat{p}}_{\mathrm{t}}^V\right)/\phantom{\left(1-{\widehat{p}}_{\mathrm{t}}^V\right)p_{\mathrm{t}}}{p}_{\mathrm{t}}}{E\left[\tau \right]}\approx \frac{E\left[Q\right]}{E\left[\tau \right]}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\overline{\xi }}_V=& \sum _{r=1}^{V-1}\frac{\left(f_R\left(r\right)+f_R\left(r+H\right)\right)·r}{V}=\sum _{r=1}^{V-1}\frac{r{\widehat{p}}_{\mathrm{t}}^{r-1}}{VE\left[\tau \right]}+\frac{\left(V-1\right)\left(1-{\widehat{p}}_{\mathrm{t}}^V\right)}{2E\left[\tau \right]}\hfill \\ \hfill \approx & \frac{1}{V{p}_{\mathrm{t}}^{2}E\left[\tau \right]}+\frac{V-1}{2E\left[\tau \right]}\hfill \end{array}$$

(16)

Substitute Equations (15) and (16) into Equation (14), we have the expression of ${\overline{\xi }}_Q$ as follow:

$$\begin{array}{cc}\hfill {\overline{\xi }}_Q\approx & \left(\frac{1}{V^2{p}_{\mathrm{t}}^{2}E\left[\tau \right]}+\frac{1}{2E\left[\tau \right]}\right)\left(Q-2\right)+\frac{E\left[Q\right]\left(V-Q\right)}{\left(V-2\right)E\left[\tau \right]}\hfill \\ \hfill =& c_1\left(Q-2\right)-c_{2}Q+c_{2}V\hfill \\ \hfill =& \left(c_1-c_2\right)Q+\left(c_{2}V-2c_1\right)\hfill \end{array}$$

(17)

where $c_1={\left(V^2{p}_{\mathrm{t}}^{2}E\left[\tau \right]\right)}^{-1}+{\left(2E\left[\tau \right]\right)}^{-1}$ and $c_2=E\left[Q\right]/\phantom{E\left[Q\right]\left(\left(V-2\right)E\left[\tau \right]\right)}\left(\left(V-2\right)E\left[\tau \right]\right)$.

Finally, we obtain the approximated expression of $p_{\mathrm{c}}$ by some transformations and simplifications as follow:

$$\begin{array}{cc}\hfill p_{\mathrm{c}}\approx & \frac{1}{E\left[\tau \right]}+p_{\mathrm{t}}\left(c_1-c_2\right)\sum _{q=1}^{V}q{\widehat{p}}_{\mathrm{t}}^{q-1}+p_{\mathrm{t}}\left(V{c}_2-2c_1\right)·\sum _{q=1}^V{\widehat{p}}_{\mathrm{t}}^{q-1}\hfill \\ \hfill \approx & \frac{\left(c_1-c_2\right)}{p_{\mathrm{t}}}+c_1{p}_{\mathrm{t}}+V{c}_2-\frac{2}{V^2{p}_{\mathrm{t}}^{2}E\left[\tau \right]}-\frac{1}{E\left[\tau \right]}\hfill \\ \hfill \approx & \left(c_1-c_2\right)p_{\mathrm{t}}^{-1}+V{c}_2-{\left(E\left[\tau \right]\right)}^{-1}\hfill \\ \hfill \approx & \frac{-p_{\mathrm{t}}^{-2}+\left(1.5V-1\right)p_{\mathrm{t}}^{-1}+2-V}{\left(V-2\right)\left(H+p_{\mathrm{t}}^{-1}\right)}\hfill \end{array}$$

(18)

4. Age Violation Probability of Neighborhood Maintenance

We focus on analyzing the age violation probability $p_{\mathrm{v}}$ of the neighborhood maintenance process in this section. Consider that node i successfully receives a message $m_k$ from its neighbor node j for the k-th time. Let $t_k$ and $t_k^{\prime }$ denote the slot indices that node j transmits $m_k$ and node i successfully receives $m_k$. Let $u\left(t\right)$ denote the transmitting slot index of the last maintained update at slot t. The age of this update is denoted as $\mathsf{\Delta }\left(t\right)=t-u\left(t\right)$.

An illustration of the AoI process of node j observed at node i is presented in Figure 3, where $T_k=t_k^{\prime }-t_k$ denotes the consumed time of k-th successful maintenance, $X_k=t_{k+1}-t_k$ denotes the interval between two consecutive and successfully maintained updates, $Y_k=t_{k+1}^{\prime }-t_k^{\prime }$ denotes the duration of k-th maintenance interval. Let $\omega =2H$ denote the age threshold that a neighbor cannot be timely updated as referred to in Section 2, and let $Z_k$ denote the violation duration that AoI exceeds the threshold $\omega$ in k-th maintenance interval.

According to the derivation of Equation (25) in [15], the age violation probability of an update is defined as

$$p_{\mathrm{v}}:=Pr\left(\mathsf{\Delta }\left(t\right)>\omega \right)=\frac{E\left[Z_k\right]}{E\left[Y_k\right]}$$

(19)

where the mean of $Y_k$ and $Z_k$ will be derived in the following two subsections.

4.1. Mean Duration of Maintenance Interval

We first analyze the mean of $Y_k$. Since the updates happen along with the generation of messages, there is no queuing time, and so $t_k^{\prime }<t_{k+1}$. Therefore, the mean of $Y_k$ should be

$$E\left[Y_k\right]=E\left[X_k+T_{k+1}-T_k\right]=E\left[X_k\right]+E\left[T_{k+1}\right]-E\left[T_k\right]=E\left[X_k\right]$$

(20)

since the expectations of $T_k$ and $T_{k+1}$ are statistically equal. Equation (20) shows that $Y_k$ has the same mean of $X_k$. Consider that during the k-th maintenance interval, node i fails to maintain the updates from j for M times. Let $p_{\mathrm{m}}$ denote the successful maintenance probability of an update. As M is geometric distributed of parameter $p_{\mathrm{m}}$, the mean of M is $E\left[M\right]=p_{\mathrm{m}}^{-1}$, and the mean of $X_k$ is written as:

$$E\left[X_k\right]=E\left[M·\tau \right]=E\left[M\right]E\left[\tau \right]\approx H{p}_{\mathrm{m}}^{-1}+{\left(p_{\mathrm{t}}{p}_{\mathrm{m}}\right)}^{-1}$$

(21)

The analysis of $p_{\mathrm{m}}$ is given as follow. Note that the nodes should forward the updates of their one-hop neighbors to realize two-hop neighbor maintenance in a distributed neighbor election. Thus, node i can capture the updates of a one-hop neighbor by receiving messages from either the direct link or the forwarding links from their common one-hop neighbors. For the simplicity of analysis, we assume that a node’s two-hop coverage area is four times as large as its one-hop coverage, and each node has the same number of one-hop and two-hop neighbors. Hence we can have the number of one-hop and two-hop neighbors as $N_1=∥{\mathcal{N}}_1∥=\frac{N}{4}$ and $N_2=∥{\mathcal{N}}_2∥=N-N_1$ respectively. Suppose there are several $n\le N_1$ common one-hop neighbors between node i and j. They will transmit at least one time in the hold-off interval of j after its transmission. The probability that i can capture the update of j in an arbitrary slot via forwarding links can be considered as the service rate:

$$\mu =\frac{n}{H}·{\left(1-p_{\mathrm{out}}\right)}^2$$

(22)

where $p_{\mathrm{out}}$ is the identical outage rate of all the wireless links.

If i receives from j via direct link, there is no need to wait for the forwarded messages, and the time is only consumed in the forwarding process, and the pmf of $T_k$ can be written as:

$$\begin{array}{c}\hfill f_{T_k}\left(s\right):=Pr\left(T_k=s\right)=\left\{\begin{array}{cc}1-p_{\mathrm{out}},\hfill & j\in {\mathcal{N}}_1,s=0\hfill \\ p_{\mathrm{out}}{\left(1-\mu \right)}^{s-1}\mu ,\hfill & j\in {\mathcal{N}}_1,s=1,\dots ,H\hfill \\ 0,\hfill & j\in {\mathcal{N}}_2,s=0\hfill \\ {\left(1-\mu \right)}^{s-1}\mu ,\hfill & j\in {\mathcal{N}}_2,s=1,\dots ,H\hfill \end{array}\right.\end{array}$$

(23)

Finally, according to the definition of $p_{\mathrm{m}}$, it can be given as the cumulative probability of $T_k$, i.e., $p_{\mathrm{m}}={\sum }_{s=0}^H{f}_{T_k}\left(s\right)$.

4.2. Mean Violation Duration within a Maintenance Interval

Next, we analyze the mean of $Z_k$. Since the AoI at the start of k-th maintaining interval is $T_k\le H$ and always smaller than $\omega$, $Z_k$ can be obtained as given in [15]:

$$Z_k=max\left(X_k+T_{k+1}-\omega ,0\right)$$

(24)

The mean of $Z_k$ can be written as follow:

$$\begin{array}{cc}\hfill E\left[Z_k\right]=& \sum _{Z=\omega }^{\infty }\left(Z-\omega \right)·Pr\left(X_k+T_{k+1}=Z\right)\hfill \\ \hfill =& E\left[X_k+T_{k+1}-\omega \right]-\sum _{Z=H+1}^{\omega -1}\left(Z-\omega \right)·Pr\left(X_k+T_{k+1}=Z\right)\hfill \end{array}$$

(25)

where $E\left[X_k+T_{k+1}-\omega \right]=E\left[X_k\right]+E\left[T_{k+1}\right]-\omega$. In the second term of the rhs where $X_k$ and $T_{k+1}$ are independently distributed, there is $H+1\le X_k=M·\tau \le Z\le \omega -1$. So M can only be 1 and $X_k=\tau$. The pmf of $X_k+T_{k+1}$ can then be written as:

$$Pr\left(X_k+T_{k+1}=Z\right)=\sum _{s=max\left(Z-H-V,0\right)}^{Z-H-1}{f}_{\tau }\left(Z-s\right)f_{T_k}\left(s\right)$$

(26)

where $Z\in \left[H+1,\cdots ,2H-1\right]$.

5. Numerical and Simulation Analysis

According to the IEEE 802.16/WiMAX standard [2], the value of V and H are determined by the related duration exponents, i.e., $V=2^{Exp{}_{\mathrm{a}}}$ and $H=2^{Exp{}_{\mathrm{b}}}$. The duration exponents are usually set to ${Exp}_{\mathrm{a}}=4$ and ${Exp}_{\mathrm{b}}={Exp}_{\mathrm{a}}+x$, where x is an non-negative integer [9]. Here we set $x=2$ and so $V=16$, $H=64$.

To verify the accuracy of our approximations, we first take the age violation probability $p_{\mathrm{v}}$ as an independent variable to analyze its impact on the transmission probability $p_{\mathrm{t}}$. We substitute Equation (18) into Equation (1) and obtain the approximated value of $p_{\mathrm{t}}$ as the positive root of a quadratic equation, which is given as follow:

$$p_{\mathrm{t}}\approx \frac{-b_{\mathrm{t}}-\sqrt{b_{\mathrm{t}}^2-4a_{\mathrm{t}}{c}_{\mathrm{t}}}}{2a_{\mathrm{t}}}$$

(27)

where the coefficients are adjusted as $a_{\mathrm{t}}=\left(p_{\mathrm{v}}-H{p}_{\mathrm{v}}-1\right)VN$, $b_{\mathrm{t}}=\left(0.5N{p}_{\mathrm{v}}+H-1.5N\right)V$, and $c_{\mathrm{t}}=\left(1-p_{\mathrm{v}}\right)N+V$.

To intuitively present the impact of $p_{\mathrm{v}}$ on $p_{\mathrm{t}}$, we compare the numerical results of the approximated and exact value of $p_{\mathrm{t}}$ under different $p_{\mathrm{v}}$ in Figure 4. The exact value of $p_{\mathrm{t}}$ is obtained by directly calculating the result of Equation (4) without approximation. We can observe that as $p_{\mathrm{v}}$ increases, the neighbors are more likely to be competing nodes, which leads to a decreasing value of $p_{\mathrm{t}}$. We also find that the linear approximation of Equation (14) is tight when N is between 16 to 32, while for $N=8$ or $N=64$, the value of $p_{\mathrm{t}}$ is slightly overestimated due to the imperfection of linear approximation.

Next we consider that $p_{\mathrm{v}}$ is also related to $p_{\mathrm{t}}$ by summarizing the derivations in Section 4:

$$p_{\mathrm{v}}=\frac{N_{1}E\left[Z_k\left|j\in {\mathcal{N}}_1\right.\right]+N_{2}E\left[Z_k\left|j\in {\mathcal{N}}_2\right.\right]}{N_{1}E\left[Y_k\left|j\in {\mathcal{N}}_1\right.\right]+N_{2}E\left[Y_k\left|j\in {\mathcal{N}}_2\right.\right]}$$

(28)

To obtain the approximation results, we search the value of $p_{\mathrm{t}}$ which can satisfy both Equations (27) and (28) simultaneously under different parameters including the number of neighbors N, the ratio of relaying nodes $\frac{n}{N_1}$ and the packet loss rate $p_{\mathrm{out}}$.

As the interaction between $p_{\mathrm{v}}$ and $p_{\mathrm{t}}$ is now concerned, a C++-based virtual simulation platform is implemented to provide high-fidelity simulation results of the neighbor election based distributed slot access. This platform consists of virtual network nodes and wireless channels, where the synchronization procedures among nodes are predetermined to let them have the same timing of slot numbers and the start of slots. In each simulation slot, the transmitting nodes disseminate their messages to the relevant receiving nodes via virtual channels configured with different packet loss rates. The platform monitors the action of nodes and calculates the transmission probability and age violation probability from statistics. The simulation and approximation results are compared in Figure 5, where the analytical results in [9] are also plotted by black lines. We can first observe that for a greater packet loss rate, it is harder for the nodes to maintain the information updates, leading to a greater value of $p_{\mathrm{v}}$ and hence the transmission probability decreases. For $p_{\mathrm{out}}=0.1$, the result from [9] is underestimated when $N<40$, while it is slightly tighter than our approximations when $N>40$. For greater packet loss rate, saying $p_{\mathrm{out}}=0.6$, our approximation is tighter than the one in [9] when $N>20$, which shows that our approximation method is valid for greater $p_{\mathrm{out}}$.

After verifying the accuracy of our approximation models, we also want to investigate the impact of the outage rate $p_{\mathrm{out}}$ of wireless links onto the age violation probability $p_{\mathrm{v}}$, which is shown in Figure 6.

We can see that as $p_{\mathrm{out}}$ rises, $p_{\mathrm{v}}$ also monotonically increases. For $N=64$, the value of $p_{\mathrm{v}}$ is lower than 0.1 when $p_{\mathrm{out}}\le 0.3$, while it increases rapidly when $p_{\mathrm{out}}\ge 0.4$ compared to other cases with a smaller number of neighbors. This is because when $p_{\mathrm{out}}$ reaches a given level, the nodes cannot timely maintain the information from the two-hop and even one-hop neighbors, leading to higher age violation probability.

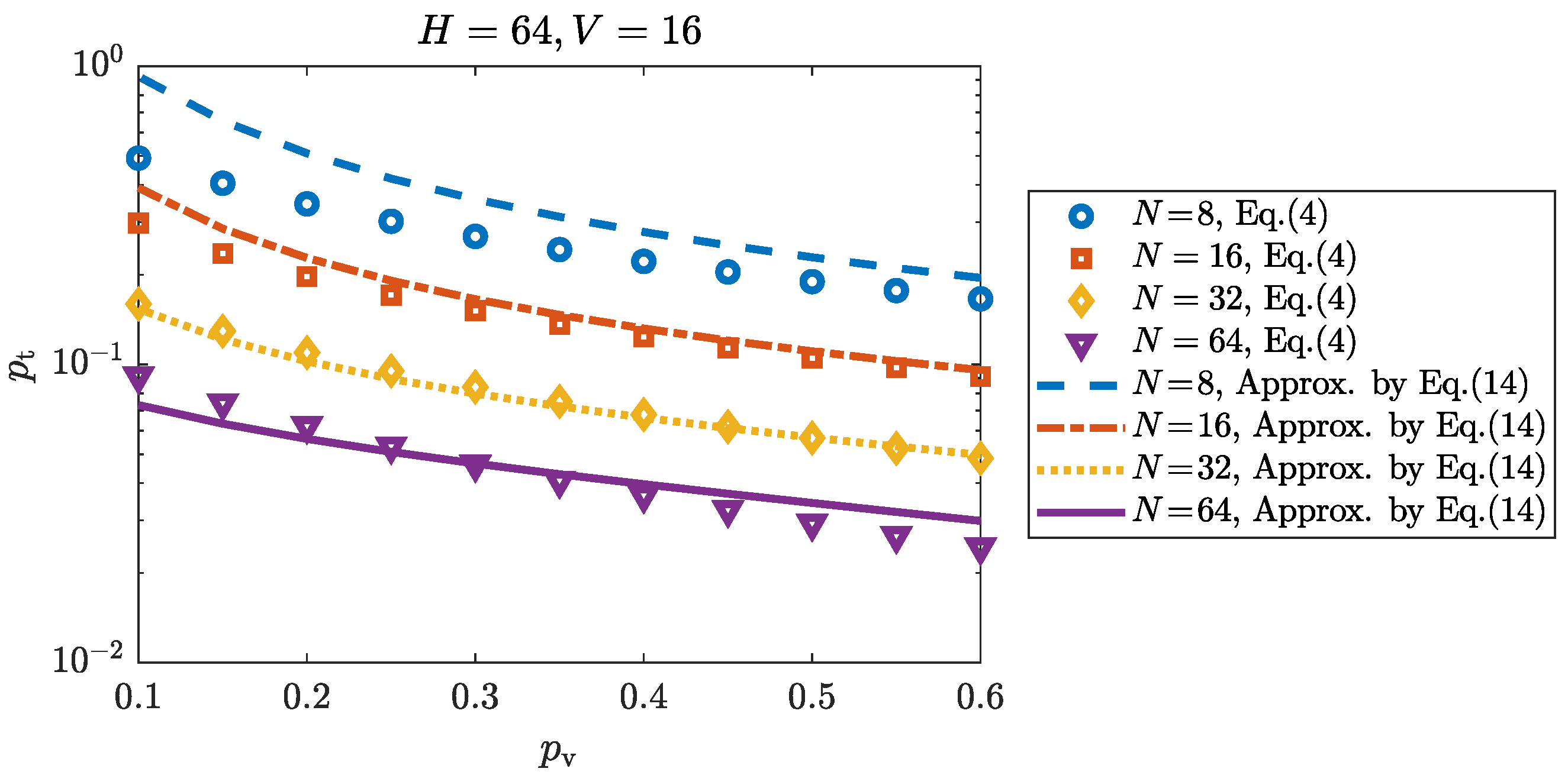
In Figure 7, the approximation and simulation results of $p_{\mathrm{t}}$ are illustrated against the ratio of relaying nodes, which reflects the connectivity of network topology. It shows that a growing ratio of relaying nodes is beneficial to the value of $p_{\mathrm{t}}$ as the information updates from neighbors can be timely maintained with higher probability. Meanwhile our approximation is tight when $n=0.025N_1$ and $n=0.05N_1$, and quite underestimated when $n=0.05N_1$ and $N>24$ due to imperfection linear approximation and should be improved.

6. Conclusions

In this paper, we develop an approximated analytical model of the interaction relationship between the transmission probability of nodes and the age violation probability of information update maintenance in neighbor election-based distributed slot access of wireless ad hoc networks. By introducing the novel AoI metric, we can understand the timeliness of neighbor information maintenance and its impact on communication performance in a new way. Numerical and simulation results also show that with the aid of analyzing the age violation probability metric, our approximation is much tighter than the one in the literature when a greater packet loss rate is configured. The interaction analysis also helps to extend the future research of next-generation network-aware distributed multiple access schemes, such as optimizing the timeliness threshold and improving the strategy of dealing with the untimely maintained neighbors and their information updates.