Abstract
An improved segment reduction-based space vector pulse width modulation (SVPWM) for an F-type three-level inverter (FT2LI) is presented in this article. The proposed SVPWM algorithm decreases the additional switching state transition of each triangle with the application of an improved nine- and three-segment reduction switching strategy. The main feature of the segment reduction technique is that it eliminates second-order harmonics in the inverter output side with good total harmonic distortion (THD), low switching losses, and minimum filter requirements when compared with carrier-based PWM (CBPWM) techniques such as multi-carrier sine PWM (MC-SPWM), sixty-degree PWM (60° PWM), and switching frequency optimal PWM (SFO PWM). The proposed modulation algorithm for FT2LI is implemented on the MATLAB/Simulink platform. The performance of the proposed segment reduction-based SVPWM algorithm is tested experimentally on an FT2LI at various amplitude and frequency modulation indices, and the experimental results are verified with the simulation results. Additionally, a comparative analysis carried out to study the relationship between the segment reduction-based SVPWM and CBPWM techniques inferred that the suggested segment reduction-based SVPWM algorithms can optimize high-order harmonic distributions and have a minimum computational burden.
1. Introduction
Power electronic drives are used in a wide range of applications in industry, including manufacturing sectors, process infrastructure, oil and gas plant sectors, as well as electric and hybrid vehicle transportation systems. Multilevel inverters (MLIs) have become the preferred power electronic converters to supply variable speed drives with a variable voltage and variable supply frequency. MLIs are often employed in applications involving high power owing to the superior performance that they offer in comparison to two-level converters. MLIs lower their output voltage stress on power switching devices in addition to decreasing the THD and the rate of change in voltage (dv/dt) [1]. The three-level converter was used first in [2], and the MLI topologies such as diode-clamped [3], capacitor-clamped, and cascaded H-bridge [4] have played a major role in power electronic applications. Traditional two-level inverters, multilevel inverters, and numerous PWM techniques to control MLIs are explored in abundance in much of the literature. As investigated in much of the literature, PWM methods play a significant role in all inverter circuits, which allow for optimal harmonic performance, as well as reduced switching losses and stress. Several PWM techniques have been devised for recently developed MLI topologies. These modulation techniques can be classified into three types: (1) carrier-based PWM (CBPWM) [5], phase-shifted (PSPWM) [6], and phase disposition (PDPWM) [7]; (2) space vector PWM (SVPWM) [8]; and (3) nearest-level modulation techniques [9] etc. In that sense, carrier-based PWM (CBPWM) and space vector PWM (SVPWM) are two PWM algorithms that have been extensively used. When compared to CBPWM, the SVPWM has many advantages, including the ability to produce the maximum attainable fundamental output voltage, the minimum THD in the inverter output terminal, and the capability of being digitally implemented. Paper [10] summarizes the SVPWM techniques for MLIs such as the α-β frame, g-h frame, K-L frame, α’-β’ frame, and SVPWM based on an imaginary coordinate system. In the above-said SVPWM techniques, G-H frames and K-L frames depend on 60° and 120° coordinate systems, respectively. A comparison of five SVPWM techniques infers that SVPWM-based imaginary coordinate systems provide a simple method to calculate duty ratios. On the other hand, SVPWM can conveniently provide additional flexibility to the switching sequence of sub-sectors and switching state transitions, depending on two simple and general mapping processes. This flexibility includes redundant switching method regions and configurable duty cycles, irrespective of the inverter levels [11]. Paper [12] illustrates the SVPWM implementation of a seven-phase voltage source inverter (VSI); it depicts the complexities of developing the sectors and their dwell times. The problem with the implementation of SVPWM on MLI is that the higher number of levels are the switching states and switching patterns. Additionally, this study compares carrier-based and SVPWM for seven-phase VSI.
Manuscript [13] proposes an optimized configuration of a three-phase, T-structured, three-level inverter for drive applications with sixteen power semiconductor devices and fewer filter requirements. The component count in the above inverter is significantly higher than the normal three-level inverters. Multilevel SVPWM is learned in detail, and its fundamental distinction between SVPWM and CBPWM is outlined in [14]. Four discontinuous SSVM (DSSVM) techniques for three-level inverters were implemented in [15] to lower the switching losses and common mode voltage in the low modulation indices. Improving the linear modulation index to 1.15 is proposed in the paper [16]. Additionally, this paper analyzes the need of maximizing the modulation index with simple PWM techniques for an NPC three-level inverter that has unbalanced capacitor voltages. Article [17] introduces discontinuous synchronized modulation into multimode synchronized modulation methods for a high-power medium-voltage three-level inverter. In article [18], hybrid discontinuous modulation for three-level inverter-fed two-phase loads is covered. For CBPWM applied to a three-level NPC inverter, Article [19] suggests a new simple approach for correlating all three reference voltage signals and two dc-link capacitor voltages, respectively, to identify the injected zero-sequence voltage signal. To obtain fixed switching frequency (FSF) with low current harmonics, an improved model predictive control (MPC) approach is proposed in [20], which makes use of optimized voltage vectors and switching sequences to achieve FSF. Paper [21] analyzes pulse pattern performance and proposes a harmonic-reduced pulse pattern selection technique that accounts for a modulation index. In this study, the operation of MLI in the over-modulation region is evaluated and compared to its effectiveness in a typical modulation region [22,23]. In [24], the author undertakes an extensive study regarding the association among the SVPWM and CBPWM using an offset voltage injection. The paper [25] presents an easier, and less computational SVM technique for four-leg, three-level NPC converters. The paper [26] suggests and examines new switching sequences for a three-level inverter that remains equated to the switching patterns 1012, 2721, 0121, and 7212 for a two-level converter. The implementation of fault detection, localization, and diagnosis of Z-source inverters for vehicle applications is described in [27]. Paper [28] shows an asymmetric five-segment switching scheme for conventional two-level voltage source inverter-fed AC motor drives with FPGA-based current control logics. A carrier-based PWM template for a five-level switch-clamped cascaded H-bridge inverter is investigated in [29]. The research paper [30] proposes a hysteresis SVPWM reconfigurable fault-tolerant control technique for single-phase voltage source multilevel inverters with current tracking. The idea of employing the selective torque component elimination method is presented in article [31] in order to minimize a specific frequency of mechanical pulsations while achieving a full range of speed control. Paper [32] aims to investigate the electrical losses noted in a five-phase synchronous reluctance motor drive system and also attempts to study the electrical losses observed in this motor.
From the above literature, it is understood that the implementation of SVPWM for higher-level MLI is a difficult task owing to the complexity that lies in the determination of switching states and redundant switches. Because of the above-mentioned challenges of SVPWM methods, segment reduction-based SVPWM is attracting much attention, particularly for MLIs. Segment reduction-based SVPWM reduces the switching state transition, which in turn decreases switch losses.
This article analyzes the performance of SVPWM-based FT2LI [33] to optimize the efficacy of high-order harmonics and output waveform quality. The following are the main findings of this paper:
- (a)
- Nine- and three-segment SVPWM algorithms different from conventional CBPWM are developed for an FT2LI.
- (b)
- The array of switching state transitions and profiles is broadly studied in detail for various SVPWM algorithms and compared with CBPWM.
- (c)
- An analysis and comparison of the magnitude of harmonic concentration around the switching frequency in CBPWM and segment reduction-based SVPWM in FT2LI are discussed.
A generalized switching scheme for FT2LI based on segment reduction SVPWM is presented. By comparing carrier-based PWM techniques such as sine PWM, 60° PWM, and switching frequency optimal PWM, this technique offers reduced THD in output voltage and current with an increased fundamental output voltage that maintains the availability of a high RMS voltage at the output. Compared to CBPWM FT2LI, the maximum boosted voltage is attained in SVPWM FT2LI for the same modulation index with the minimum switching frequency, reduced switching loss, and inverter size. The segment reduction-based SVPWM technique is able to act under a minimum switching frequency with fewer switching losses, which improves the inverter efficiency. The structure of the manuscript is as follows: Section 2 discusses the analysis used to formulate the SVPWM technique for FT2LI. The primary element of the suggested approach consists of an initiative to analyze and sector identification of SVPWM-based FT2LI with segment reduction presented in this section. The implementation of SVPWM with segment reduction algorithms for four sub-sectors of sector I is outlined in Section 3. The simulation and experimental results are discussed in Section 4 to validate the SVPWM-based FT2LI algorithms. Detailed performance comparisons of various PWM techniques can be found in this section. The core conclusions are presented in Section 5.
2. Implementation of SVPWM for FT2LI
2.1. Diode-Free FT2LI Topology
T-type and neutral point configurations are the two most common three-level inverter topologies described in the literature. For low-voltage applications, the T-NPC inverter is more cost-effective and efficient than the NPC inverter [34]. Figure 1 depicts the fundamental layout of the diode-free FT2LI, which consists of three levels of output for each phase (A, B, and C) and 12 switching devices (four in each leg) with no clamping diodes. In phase A, the labels for the semiconductor devices are SAUU, SAUL, SALU, and SALL. Similarly, phase B and phase C can be identified.
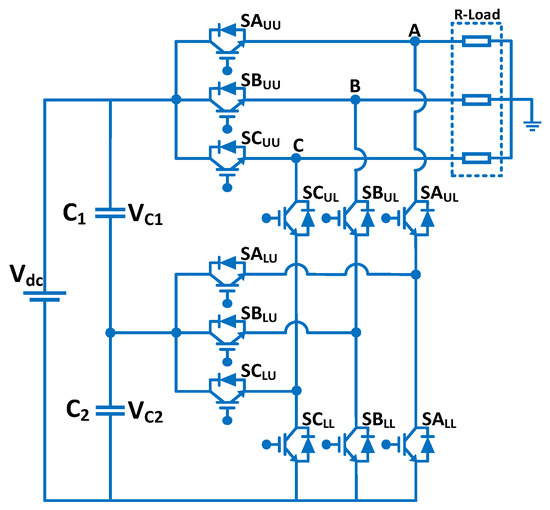
Figure 1.
Structure of FT2LI.
The DC link, which consists of two capacitors (C1 = C2), is used to couple the FT2LI with the input dc supply. Vc1 and Vc2 denote the voltages of two dc link capacitors, while their values are both set to Vdc/2. The zero-voltage junction is defined as the point where two dc input sources are connected to the FT2LI’s neutral point. The FT2LI incorporates the three operational modes in each phase, and their output voltages are listed in Table 1. Each phase arm’s operation is designated by three switching states: H, 0, and L. The switching state “H” indicates that two upper arm switches (SAUU, SALU) in the phase arm A are switched on; the switching state “L” indicates that two lower arm switches (SAUL, SALL) in the phase arm A are switched on; and the switching state “0” indicates that two internal switches (SAUL, SALU) in the phase arm A are switched on.

Table 1.
Switching states of phase A.
2.2. Development of the SVPWM Algorithm
Space vector PWM (SVPWM) uses sine wave as a fixed amplitude vector revolving at a fixed frequency along with a reference voltage vector (Vref) that revolves at the angular frequency of 2ff (fundamental frequency, ff = 50 Hz) which is around the origin of the space vector diagram. Figure 2 depicts a space vector diagram of FT2LI with three phases and three levels. This article examines SVPWM approaches for FT2LI. It is made up of 24 active voltage vectors (6 large, 6 medium, and 12 small) and triple null vectors (HHH, 000, and LLL). The space vector diagram has been divided into six sectors (I to VI), with each sector subdivided by four triangles (1 to 4), for a total of 24 triangles. In this illustration, sector I comprises of triangles 1, 2, 3, and 4. Table 2, Refs. [30,31,32], present a comparative study of several three-level inverters, including PN-NPC (positive-negative NPC), T-type MLI, and 3L-ANPC ZCT (zero current transition), based on the number of components (including switches, diodes, inductors, and capacitors).
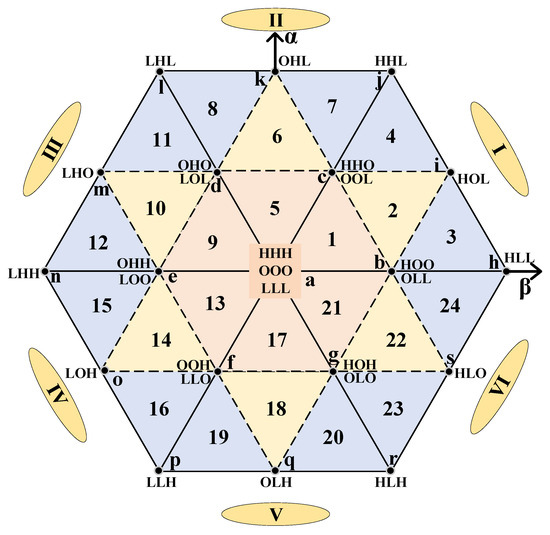
Figure 2.
Space vector diagram of three-level inverter(”I–VI”—Sectors, “1–24”—Subsectors).

Table 2.
Conventional three-level inverter comparison with FT2LI.
Table 3 lists the possible switching sequences for all sub-sectors of FT2LI. Space vector PWM involves identifying the sector of the reference voltage vector, detecting the three nearest switching vectors, deciding on a suitable switching sequence, and calculating the on-time of the switches for that sequence. Each major sector corresponds to of the fundamental cycle.

Table 3.
Switching sequence of sub-sectors.
In any SVPWM based on a voltage-second balance equation, the set of voltage vectors representing the switching states of the inverter are applied to average a reference value in one sampling period. There are 27 transition states when three phases of the inverter are considered. Each of these transitioning states can be expressed as a vector by (1):
where, Va, Vb, and Vc are reference three-phase voltages of the nearest switching vectors, and Vcα and Vcβ are reference vector components in the coordinate system.
2.2.1. Sector Identification
Using the Clark transformation, as shown in Expression (2), the a-b-c three-phase coordinate system is converted into a 2-dimensional frame that facilitates sector identification. As shown in Figure 2, the voltage vectors are positioned at various locations on the two hexagons that are interleaved based on their switching patterns. The large voltage vectors of the three-level space vector diagram have an amplitude of 2Vdc/3 and are situated on the edges of the outside hexagon. The median voltage vector is the voltage vector with the amplitude Vdc/√3 positioned at the outer hexagon’s one-half. The corners of the inner hexagon contain small vectors with amplitudes of Vdc/3.
When the rotating voltage vector enters a particular sector in a proposed inverter, nearby voltage vectors are picked to create the required rotating voltage vector based on the principle of vector synthesis, which results in three-phase PWM signals. When evaluating the phase angle and the magnitude of a rotating reference voltage vector Vref, it is possible to ascertain the sector where the inverter output voltage (Vo*) resides.
The duty values of all four switches corresponding to each phase can be determined based on the status of the two switches that are part of each limb in the applied switching states, as shown in Table 4.This table depicts corresponding line voltages and phase voltages in each phase with respect to their voltage vectors for sub-sector 1 (Δabc).

Table 4.
Voltage vectors of sub-sector 1.
2.2.2. Determination of Adjacent Vectors for Vref
As indicated previously, the switching states of redundant vectors result in a similar voltage vectors at the output. The location in the reference vector must be determined before calculating the three nearest voltage vectors and their duty cycles. Where (Vcα, Vcβ) is the coordinate values of Vref in α_β coordinates, (Va, Vb, Vc) is the coordinate values of Vref in a three-phase coordinate system. A Vref could be identified within any sub-sector (1–4) in one of the sectors (I–VI), as depicted in Figure 3a.
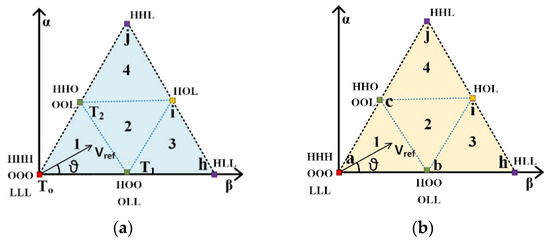
Figure 3.
(a) Switching time representation of sub-sector 1. (b) Voltage vectors of sub-sector 1.
When considering the reference vector, Vref is located in sub-sector 1 of sector I.
The three nearest switching vectors of sub-sector 1 can be decided by the following:
Volt-sec balance equation for sector I, sub-sector 1,
where
Ts—one switching period;
To—vector ‘a’ switching time;
T1—vector ‘b’ switching time;
T2—vector ‘c’ switching time.
a, b, and c are the nearest voltage vectors expressed for the inner triangle of sector I, sub-sector 1, shown in Figure 3b. Voltage vector ‘a’ can be calculated as follows: where V01, V02, and V03 are the redundant voltage vectors of this node.
Voltage vector ‘a’ is equal to
where VO1 = LLL, VO2 = OOO, VO3 = HHH,
Apply the Equation (1),
Similarly,
V21, and V22 are the redundant voltage vectors expressed for the node ‘b’ of sector I, sub-asector 1, and their expressions are
where V21 = OLL, V22 = HOO,
V11, and V12 are the redundant voltage vectors expressed for the node ‘c’ of sector I, sub-sector 1, and their expressions are,
where V11 = OOL, V12 = HHO,
2.2.3. Dwell Time Calculation of Each Vector
Following the identification of the three nearest vectors, the volt-sec balance strategy can be used to compute the turn on times of the relevant vectors [38], Ref. [39], where Ts is the sampling time and To, T1, and T2 are the on times for the voltage vectors V0, V1, and V2, respectively. Equation (3) can be written as follows:
where a = Vo, b = V1, c = V2.
The dwell time of the related vectors can be calculated by solving Equations (3) and (4).
The dwell time of all sub-sectors in sector I is represented in Table 5.

Table 5.
Dwell time of sector I.
Where . Similar to the method shown in this table, it is possible to calculate the on times for all the connected vectors in all other sectors.
2.2.4. Selection of Redundant Vector Arrangement for a Suitable Pattern
Next in the SVPWM implementation process is the selection of a suitable transition sequence for redundant states. This assists in balancing the DC link capacitor voltages, tolerance in fault, and decreasing the switching frequency. Table 6 displays all the possibilities of the switching pattern configurations for every sub-sector of sector I, and Figure 4a–c depicts a graphical illustration of sub-sector 1. It displays the switching times of each switch in phase A, B, and C.

Table 6.
Redundant states of sector I.
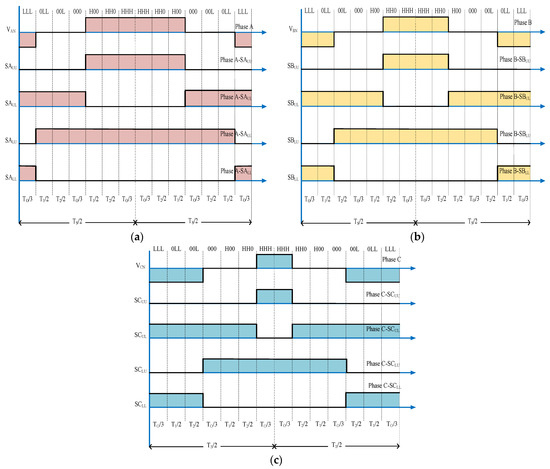
Figure 4.
Switching time representation of sub-sector 1; (a) phase A; (b) phase B; (c) phase C.
3. Segment Reduction in SVPWM
The segment reductions in the switching sequence have been chosen for their low switching loss, their simple method for the handling of states, and the online implementation of switching sequence. In this article, three-segment- and nine-segment-based switching sequences are analyzed for sector I.
The number of voltage vectors in one switching period is used in this article to differentiate amongst the SVPWM algorithms. The following are the detailed design procedures for various SVPWMs. Figure 5 depicts a three-level inverter’s typical modulation index, which has been utilized to locate the sub-sector containing the reference voltage vector. This SVPWM technique is classified into three classes based on the segment reduction count: class 1, class 2, and class 3.
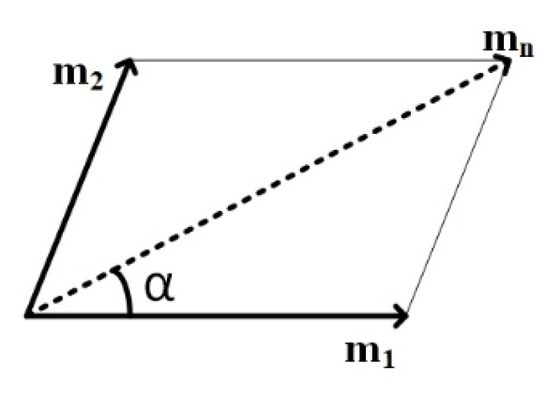
Figure 5.
Modulation index of three-level SVPWM.
3.1. Segment Reduction in Sub-Sector 1 (Class 1)
For triangles like triangle Δabc in Figure 3b, where m1 and m2 are each less than 0.5 and m1 + m2 is less than 0.5, the triangle can be classified as a class 1 triangle. The dwell times in sub-sector 1 may be estimated by applying the inverse matrix derived from the voltage-sec balance Equations (3) and (4).
When the reference vector lies in sub sector -1 the dwell time T0, T1, T2 is valid for the linear modulation of mn = 0.5. This triangle is represented as sub-sector 1, and it shows the tip of the reference vector. By eliminating the redundant voltage vectors HH0-HHH-HHH-HH0-H00 from the middle of the vector sequence, the nine-segment SVPWM method enhances switching frequency utilization. This segment reduction was carried out for sub-sector 1, which is represented as a class 1 triangle. Figure 6a, b depict the fourteen segment and reduced nine segment switching patterns for sub-sector 1.
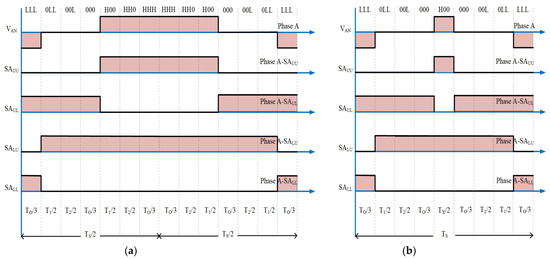
Figure 6.
Phase A switching period of Δabc in sub-sector 1. (a) Actual fourteen segment sequence. (b) Reduced nine segment sequence.
3.2. Segment Reduction in Sub-Sector 2 (Class 2)
When the reference voltage (Vr) lies in sub-sector 2, in which the value of m1 + m2 > 0.5, the corresponding triangle Δbci can be called a class 2 triangle, and these m1 and m2 values could be less than 0.5. Figure 7a,b depicts a segment reduction technique for class 2 triangles in which the switching sequence is counted as 10 segments. For phase voltage VAN, segment reduction can be implemented and reduced to a three-segment format.
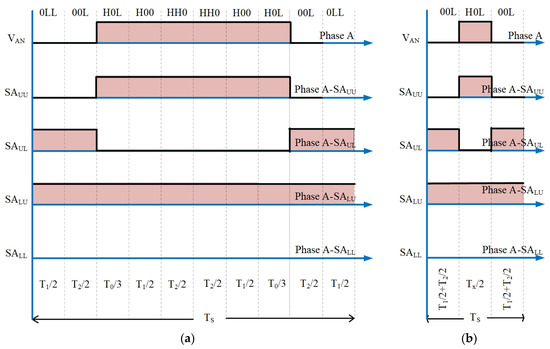
Figure 7.
A switching period of Δbci in sub-sector 2. (a) Actual ten-segment sequence. (b) Reduced three-segment sequence.
3.3. Segment Reduction in Sub-Sector 3 (Class 3)
If the reference voltage (Vr) lies in sub-sector 3, in this case, the value of m1 ≥ m2 and the corresponding triangle Δbhi can be called class 3 triangles, and these m1 and m2 values could be greater than 0.5. The actual eight-segment switching sequence for phase voltage (VAN) of sub-sector 3 is depicted in Figure 8a. This segment can be reduced to a three-segment format, known as a class 3 triangle, using segment reduction. A concise SVPWM sequence with three segments is designed as shown in Figure 8b.
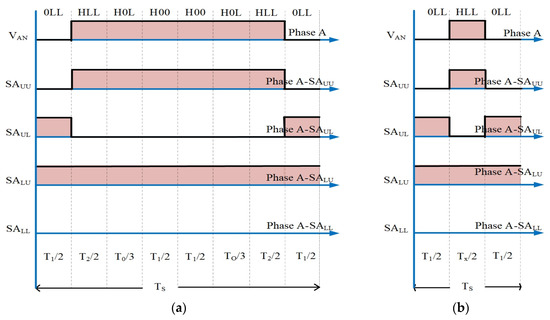
Figure 8.
A switching period of Δbhi in sub-sector 3. (a) Actual eight-segment sequence. (b) Reduced three-segment sequence.
3.4. Segment Reduction in Sub-Sector 4 (Class 3)
When sub-sector 4 is the location of the reference voltage vector (Vr), the values of m1 and m2 may both be greater than 0.5, but m1 must be smaller than m2 for the triangle Δcij to fall into the class 3 mode. Figure 9 illustrates a segment reduction technique for class 3 triangles, where the actual switching sequence for sub-sector 4 is counted as eight segments and is depicted in Figure 9a. Segment reduction can be implemented for phase voltage VAN and reduced to a three-segment format. Figure 9b depicts the development of a simplified three-segment SVPWM sequence for sub-sector 4.
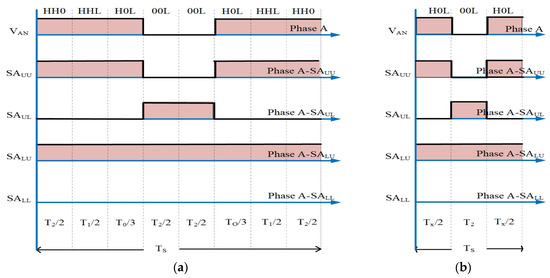
Figure 9.
A switching period of Δcij in sub-sector 4. (a) Actual eight-segment sequence. (b) Reduced three-segment sequence.
4. Result Analysis and Discussion
4.1. Simulation Results
To evaluate the efficacy of FT2LI, extensive simulations were conducted with the help of the proposed nine-segment and three-segment switching schemes. The SVPWM-based FT2LI is simulated in MATLAB for different frequencies and amplitude modulation indices. The information thus obtained about line voltage and %THD is outlined in Table 7. In Table 8, the inference thus obtained with the application of SVPWM is compared with the outputs of carrier-based PWM methods designed for FT2LI. In comparison to carrier-based PWM techniques, the SVPWM technique provides superior performance at all modulation ranges. This study examines the significance between triangle carrier-based PWM and SVPWM for FT2LI. The simulation was performed with two 100 µF capacitors at a DC link voltage of Vdc = 400 V. The proposed class 2, three-segment reduction switching scheme was evaluated using FT2LI with switching frequencies of odd and triplen, odd and not triplen, even and triplen, and even and not triplen. Figure 10a–d depicts the output voltage simulation results for FT2LI at various frequency modulation indices (mf = 63, 100, 120, and 145).

Table 7.
Performance parameters of SVPWM-based FT2LI.

Table 8.
Comparison of carrier-based and space vector PWM used for FT2LI.
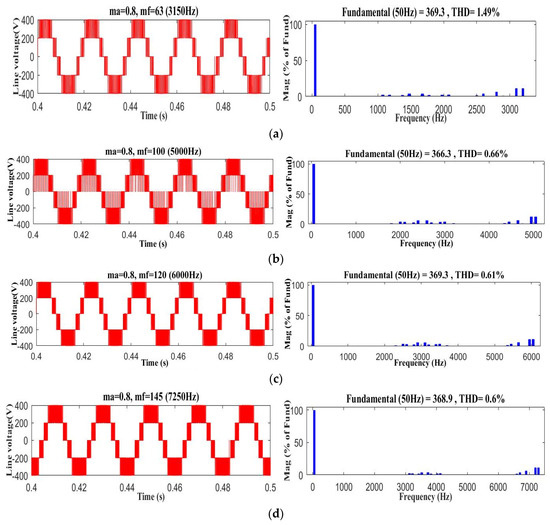
Figure 10.
Simulation results of SVPWM based FT2LI fr ma = 0.8 with different frequency modulation indices (mf): (a) 63, (b) 100, (c) 120, and (d) 145.
The simulation is performed for amplitude modulation indices of 0.7, 0.8, and 0.9 with frequency modulation indices of 63, 100, 120, and 145. The harmonic characteristics of conventional and proposed SVPWM-based FT2LI are demonstrated in Table 7 for different amplitude modulation indices with various switching frequencies. It is inferred from Table 7 that the performance of FT2LI with segment reduction SVPWM showcases better THD and output voltage. To highlight the features further, segment reduction-based SVPWM is compared with carrier-based PWMs such as SPWM, 60° PWM, and SFO PWM, as shown in Table 8. In addition, the outcomes are contrasted based on their THD performance and inverter output voltage. Table 8 presents a summary of the comparative study. Figure 11 depicts the maximum and minimal THD magnitudes in carrier-based PWM and SVPWM for four distinct switching frequencies. This analysis provides the highest output voltage and RMS voltage.
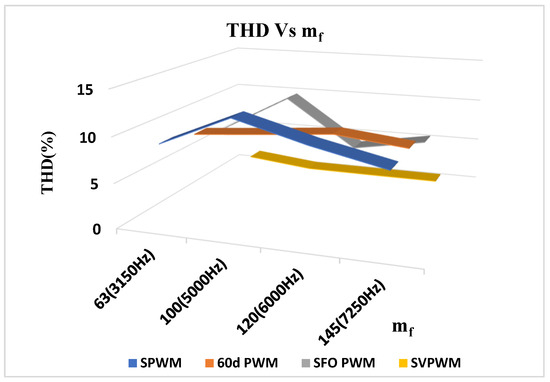
Figure 11.
Comparison of THD with different PWM techniques.
4.2. Experimental Results
To validate the simulation results of a three-phase FT2LI system, a 500 W prototype model was developed and tested. The test bench of the proposed system shown in Figure 12 has various components, which include two dc-link capacitors of 100 µF, 12-IGBT power switches, a SPARTAN-6 FPGA controller, and three-phase loads. A dc voltage from the programmable power supply is fed as an input to the inverter. The inverter delivers the output current to the load. Two switches from the upper arm of a phase and two switches from the lower arm of a different phase generate three-level ±Vdc, ±Vdc/2, and 0. The segment reduction-based SVPWM algorithm is implemented in the SPARTAN-6 FPGA controller. Using the FLUKE meter, the harmonic components of the line voltage (VAB) corresponding to the segment reduction-based SVPWM algorithm have been measured up to the 146th harmonic component. It can be observed that the experimental waveforms of the line voltage VAB, phase voltage VAN, and harmonic spectra corresponding to a modulation index (ma) of 0.8 are shown in Figure 13 and Figure 14.

Figure 12.
Experimental setup of FT2LI.
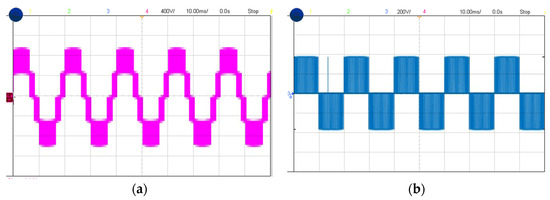
Figure 13.
Prototype results using SVPWM at “ma = 0.8” and “mf = 145”. (a) Line voltage (VAB); (b) phase voltage (VAN).
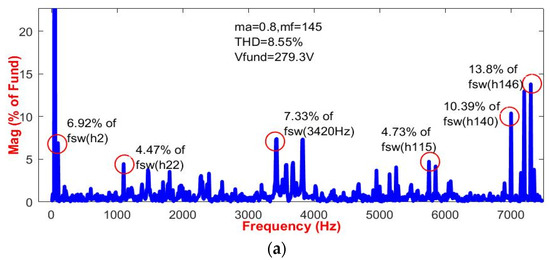
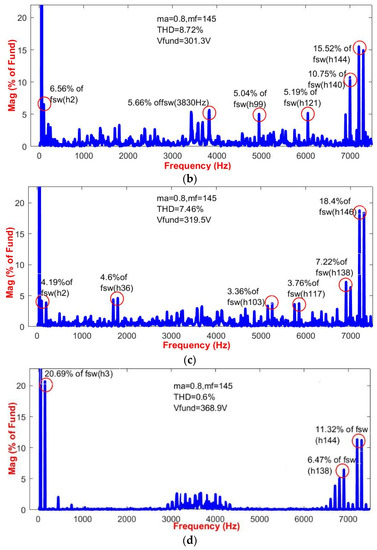
Figure 14.
Harmonic spectrums comparison of the voltage Vab (ma = 0.8, mf = 145). (a) SPWM. (b) 60° PWM. (c) SFO PWM. (d) Proposed SVPWM.
The experimental results show that the higher-order harmonics are distributed randomly between the fundamental frequency (ff) and the switching frequency (fsw). The dominant high-order harmonics of the SPWM can be observed in the cluster of harmonics distributed around h2, h22, h115, h140, and h146, respectively. Likewise, 60° PWM harmonics are distributed around h2, h99, h121, h140, and h144. The spectrum in SFO PWM is behind h2, h36, h103, h117, h138, and h146. In the vicinity of fsw, the magnitude of the harmonic of SVPWM is considerably less than that of the other carrier-based PWM methods, and the cluster of the harmonic spectrum is distributed around fsw. Figure 14a–d depicts that THD is greater in the three PWM techniques described above than in SVPWM. The prevalent high-order harmonics in SVPWM-based FT2LI are observed to be primarily distributed around the switching frequency. When compared to the other three PWM techniques, second-order harmonics are eliminated in SVPWM, which produces good THD performance. However, because high-frequency harmonics are more readily filtered by the inductor, the THD of the line voltage in the proposed SVPWM-based FT2LI is significantly lower than in conventional ones. Based on this comparison, the modulation scheme of the converter can be designed flexibly by modifying weight coefficients to meet actual performance requirements. The comparison between the conventional SVPWM MLIs and segment reduction-based SVPWM FT2LIs is shown in Table 9. It is evident that the suggested converter with segment reduction-based SVPWM offers low-voltage stress across the switches, low switching loss, and eliminates the presence of even harmonics.

Table 9.
Comparative study of SVPWM-based MLI’s with FT2LI.
5. Conclusions
A new SVPWM technique based on segment reduction for an F-type multilevel inverter has been proposed and validated using the FT2LI prototype fabricated in the laboratory. One of the significant features of the segment reduction-based SVPWM algorithm is the reduction of switching state transitions, which in turn reduces switching stress and losses. The total harmonic distortions with various switching frequencies at the output of segment reduction-based SVPWM-fed FT2LI are less than those of conventional SVPWM-based FT2LI. As compared to the existing CBPWM techniques of FT2LI, the proposed segment reduction-based SVPWM technique offers less THD, fewer switching losses, fewer filter requirements, and reduced switching transition counts. The implementation complexity of SVPWM techniques based on the segment reduction algorithm is lower compared to the existing SVPWM approach. In addition to the above-mentioned features, the proposed segment reduction-based SVPWM for FT2LI has a lower harmonic concentration, which shifts toward the switching frequency. Simulation and experimental results substantiate the effectiveness of segment reduction-based SVPWM algorithms for FT2LI.
Author Contributions
M.M.; analysis of inverter, investigation with PWM techniques, and preparing the original draft of this paper, C.N.; supervision, validation, M.J.H.; review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FT2LI | F-type three-level inverter |
| SVPWM | space vector pulse width modulation |
| CBPWM | carrier-based PWM |
| MC-SPWM | multi-carrier sine PWM |
| 60° PWM | sixty-degree PWM |
| SFO PWM | switching frequency optimal PWM |
| MLIs | multilevel inverters |
References
- Rodríguez, J.; Lai, J. Multilevel Inverters: A Survey of Topologies, Controls, and Applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Yuan, X.; Barbi, I. Fundamentals of a New Diode Clamping Multilevel. IEEE Trans. Power Electron. 2000, 15, 711–718. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A Survey on Neutral-Point-Clamped Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Cho, Y.; Labella, T.; Lai, J.; Senesky, M.K. A Carrier-Based Neutral Voltage Modulation Strategy for Multilevel Cascaded Inverters Under Unbalanced DC Sources. IEEE Trans. Ind. Electron. 2014, 61, 625–636. [Google Scholar] [CrossRef]
- Lee, T.; Li, B.; Yang, M.; Tsai, Y. A Carrier-Based PWM for Three-Level T-Type Inverter to Tolerate Open-Circuit Fault. IEEE Trans. Power Electron. 2018, 33, 8787–8796. [Google Scholar] [CrossRef]
- Pwm, C.P.; Lim, Z.; Maswood, A.I.; Ooi, G.H.P. Modular-Cell Inverter Employing Reduced Flying Capacitors with Hybrid Phase-Shifted. IEEE Trans. Ind. Electron. 2015, 62, 4086–4095. [Google Scholar] [CrossRef]
- Ghias, A.M.Y.M.; Pou, J.; Capella, G.J.; Agelidis, V.G.; Aguilera, R.P.; Meynard, T. Single-Carrier Phase-Disposition PWM Implementation for Multilevel Flying Capacitor Converters. IEEE Trans. Power Electron. 2015, 30, 5376–5380. [Google Scholar] [CrossRef]
- Li, C.; Yang, T.; Kulsangcharoen, P.; Calzo, G.L.; Bozhko, S.; Gerada, C.; Wheeler, P. A Modified Neutral-Point Balancing Space Vector Modulation for Three-Level Neutral Point Clamped Converters in High Speed Drives. IEEE Trans. Ind. Electron. 2018, 66, 910–921. [Google Scholar] [CrossRef]
- Orfanoudakis, G.I.; Yuratich, M.A.; Sharkh, S.M. Nearest-Vector Modulation Strategies with Minimum Amplitude of Low-Frequency Neutral-Point Voltage Oscillations for the Neutral-Point-Clamped Converter. IEEE Trans. Power Electron. 2013, 28, 4485–4499. [Google Scholar] [CrossRef]
- Attique, Q.M.; Li, Y.; Wang, K. A Survey on Space-Vector Pulse Width Modulation for Multilevel Inverters. CPSS Trans. Power Electron. Appl. 2017, 2, 226–236. [Google Scholar] [CrossRef]
- Deng, Y.; Teo, K.H.; Duan, C.; Habetler, T.G.; Harley, R.G. A Fast and Generalized Space Vector Modulation Scheme for Multilevel Inverters. IEEE Trans. Power Electron. 2014, 29, 5204–5217. [Google Scholar] [CrossRef]
- Al-hitmi, M.A.; Moinoddin, S.; Iqbal, A.; Rahman, K.; Meraj, M. Space Vector vs. Sinusoidal Carrier-Based Pulse Width Modulation for a Seven-Phase Voltage Source Inverter. CPSS Trans. Power Electron. Appl. 2019, 4, 230–243. [Google Scholar] [CrossRef]
- Hota, A.; Jain, S.; Agarwal, V. A Modified T-Structured Three-Level Inverter Configuration Optimized with Respect to PWM Strategy Used for Common-Mode. IEEE Trans. Ind. Appl. 2017, 53, 4779–4787. [Google Scholar] [CrossRef]
- Yao, W.; Hu, H.; Lu, Z. Comparisons of Space-Vector Modulation and Carrier-Based Modulation of Multilevel Inverter. IEEE Trans. Power Electron. 2008, 23, 45–51. [Google Scholar] [CrossRef]
- Das, S.; Narayanan, G.; Pandey, M. Space-Vector-Based Hybrid Pulsewidth Modulation Techniques for a Three-Level Inverter. IEEE Trans. Power Electron. 2014, 29, 4580–4591. [Google Scholar] [CrossRef]
- Ye, Z.; Xu, Y.; Wu, X.; Tan, G.; Deng, X.; Wang, Z. A Simplified PWM Strategy for a Converter with Unbalanced DC Links. IEEE Trans. Power Electron. 2016, 31, 3227–3238. [Google Scholar] [CrossRef]
- Inverter, M.T. An Improved Multimode Synchronized Space Vector Modulation Strategy for High-Power. IEEE Trans. Power Electron. 2021, 36, 4686–4696. [Google Scholar] [CrossRef]
- Zhang, G.; Peng, S.; Geng, Q.; Shi, T.; Xia, C. Hybrid Discontinuous Space Vector PWM Strategy. IEEE Trans. Power Electron. 2022, 37, 1711–1721. [Google Scholar] [CrossRef]
- Inverter, T.N.P.C.; Chen, F.; Qiao, W.; Wang, H.; Qu, L. A Simple Zero-Sequence Voltage Injection Method for Carrier-Based Pulsewidth Modulation of the Three-Level NPC Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4687–4699. [Google Scholar] [CrossRef]
- Liu, C.; Xing, X.; Du, C.; Zhang, B.; Zhang, C.; Blaabjerg, F. An Improved Model Predictive Control Method Using Optimized Voltage Vectors for Vienna Rectifier with Fixed Switching Frequency. IEEE Trans. Power Electron. 2023, 38, 358–371. [Google Scholar] [CrossRef]
- Xiao, L.; Li, J.; Xiong, Y.; Chen, J.; Gao, H. Strategy and Implementation of Harmonic-Reduced Synchronized SVPWM for High-Power Traction Machine Drives. IEEE Trans. Power Electron. 2020, 35, 12457–12471. [Google Scholar] [CrossRef]
- Chen, Y.T.; Lin, H.T. Analysis and Implementation of a Novel Space Vector Modulation Strategy for Multilevel Inverter about the Operations in the Overmodulation Region. In Proceedings of the 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010; pp. 417–422. [Google Scholar] [CrossRef]
- Prieto, J.; Barrero, F.; Durán, M.J.; Marín, S.T.; Perales, M.A. SVM Procedure for n -Phase VSI With Low Harmonic Distortion in the Overmodulation Region. IEEE Trans. Ind. Electron. 2014, 61, 92–97. [Google Scholar] [CrossRef]
- Song, W.; Wang, S.; Xiong, C.; Ge, X.; Feng, X. Single-phase three-level space vector pulse width modulation algorithm for grid-side railway traction converter and its relationship of carrier-based pulse width modulation. IET Electr. Syst. Transp. 2014, 4, 78–87. [Google Scholar] [CrossRef]
- Roberto, C.; Kennel, R.; Clare, J.C. A Simplified Space-Vector Modulation Algorithm for Four-Leg NPC Converters. IEEE Trans. Power Electron. 2017, 32, 8371–8380. [Google Scholar] [CrossRef]
- Inverter, S.T. Novel Switching Sequences for a Space-Vector-Modulated Three-Level Inverter. IEEE Trans. Ind. Electron. 2012, 59, 1477–1487. [Google Scholar]
- Sharma, V.; Hossain, M.J.; Mukhopadhyay, S. Fault-Tolerant Operation of Bidirectional-Fed Induction Motor Drive for Vehicular Applications. Energies 2022, 15, 6976. [Google Scholar] [CrossRef]
- Tsai, M.-F.; Tseng, C.-S.; Cheng, P.-J. Implementation of an FPGA-Based Current Control and SVPWM ASIC with Asymmetric Five-segment Switch Scheme for AC Motor Drives. Energies 2021, 14, 1462. [Google Scholar] [CrossRef]
- Odeh, C.I.; Kondratenko, D.; Lewicki, A.; Morawiec, M.; Jąderko, A.; Baran, J. Pulse-Width Modulation Template for Five-Level Switch-Clamped H-Bridge-Based Cascaded Multilevel Inverter. Energies 2021, 14, 7726. [Google Scholar] [CrossRef]
- Li, G.; Wang, L.; Li, F. Single-Phase Voltage Source Multi-Level Inverter Hysteresis SVPWM Reconfigurable Fault-Tolerant Control Method. Energies 2022, 15, 2557. [Google Scholar] [CrossRef]
- Chudzik, P.; Steczek, M.; Tatar, K. Reduction in selected Torque Harmonics in a Three level NPC Inverter fed Induction Motor Drive. Energies 2022, 15, 4078. [Google Scholar] [CrossRef]
- Tawfiq, K.B.; Ibrahim, M.N.; Sergeant, P. Power loss analysis of a Five-phase Drive system using a synchronous reluctance motor and an indirect matrix converter with reduced switching losses. Machines 2022, 10, 738. [Google Scholar] [CrossRef]
- Odeh, C.; Lewicki, A.; Morawiec, M.; Kondratenko, D. Three-Level F-Type Inverter. IEEE Trans. Power Electron. 2021, 36, 11265–11275. [Google Scholar] [CrossRef]
- Schweizer, M.; Kolar, J.W. Design and implementation of a highly efficient three-level T-type converter for low-voltage applications. IEEE Trans. Power Electron. 2013, 28, 899–907. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; Feng, L.; Wu, H.; Xing, Y. A family of neutral point clamped full-bridge topologies for transformerless photovoltaic grid-tied inverters. IEEE Trans. Power Electron. 2013, 28, 730–739. [Google Scholar] [CrossRef]
- Madasamy, P.; Kumar, V.S.; Sanjeevikumar, P.; Holm-Nielsen, J.B.; Hosain, E.; Bharatiraja, C. A three-phase transformerless T-Type-NPC-MLI for grid connected PV systems with common-mode leakage current mitigation. Energies 2019, 12, 2434. [Google Scholar] [CrossRef]
- Li, J.J.; Liu, J.; Boroyevich, D.; Mattavelli, P.; Xue, Y. Three-level active neutral-point-clamped zero-current-transition converter for sustainable energy systems. IEEE Trans. Power Electron. 2011, 26, 3680–3693. [Google Scholar] [CrossRef]
- Celanovic, N.; Boroyevich, D. A fast space-vector modulation algorithm for multilevel three-phase converters. IEEE Trans. Ind. Appl. 2001, 37, 637–641. [Google Scholar] [CrossRef]
- Kaarthik, R.S.; Gopakumar, K.; Cecati, C.; Nagy, I. Timing Calculations for a General N-Level Dodecagonal Space Vector Structure Using only Reference Phase Voltages. IEEE Trans. Ind. Electron. 2016, 63, 1395–1403. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).