Abstract
Medical three-dimensional (3D) positioning technology amalgamates traditional medical instrumentation with computational technology and medical imaging to facilitate the real-time visualization of anatomical lesions, surgical implements, and other relevant objects, thereby augmenting the physician’s diagnostic and therapeutic capabilities. Predominantly, optical positioning technologies are employed; however, they inherently suffer from limitations such as optical occlusion, precluding precise positioning. To surmount these challenges, the present manuscript introduces a phase-based 3D electromagnetic positioning technique predicated on spectral interpolation. Initially, four spectral lines exhibiting maximal signal amplitude are designated for the computation of a correction factor. Subsequently, the functional relationship between this correction factor and frequency offset is modeled via polynomial fitting, from which signal frequency and phase correction equations are derived. Experimental analyses executed within the ANSYS software (2021R2) environment substantiate the utility of the phase correction formula in calculating the phase disparity between the signals of the transmitting and receiving electromagnetic coils. This, in turn, enables the acquisition of the linear distance between these coils, which is instrumental in determining their spatial coordinates. The introduced 3D electromagnetic positioning methodology based on spectral interpolation effectively circumvents the issue of multiple solutions engendered by solving nonlinear equations inherent in traditional electromagnetic positioning systems. Simulation analyses corroborate that the proposed technique enhances phase detection accuracy by 1–2 orders of magnitude over conventional methods, achieving a positional accuracy within the effective measurement space of 3 mm—an improvement of at least 70% in comparison with established positioning paradigms.
1. Introduction
As advancements in medical imaging technology unfold, an increasing number of medical institutions and physicians are adopting image-based surgical navigation systems as clinical intervention apparatuses. These systems substantially mitigate the necessity for repetitive X-ray evaluations to ascertain lesion localizations, consequently attenuating deleterious radiation-induced effects on healthcare personnel [1]. Comparative analyses have empirically substantiated that the utilization of surgical positioning systems notably enhances multiple surgical metrics—namely, precision, duration, inflicted trauma, and postoperative convalescence [2]. Throughout surgical operation, these positioning platforms facilitate the integration of the real-time visualization of surgical instruments with the patient’s corporeal coordinates in physical space, thereby refining surgical precision and minimizing iatrogenic risk [3].
Several modalities of positioning techniques have been delineated in the extant literature, including but not limited to ultrasound positioning [4], optical positioning [5], and electromagnetic positioning [6]. Predominantly, optical positioning systems—manufactured by industry leaders such as the Canadian NDI Company and American Medtronic—are ubiquitously deployed, with the Polaris system by the NDI Company acknowledged as the global benchmark for positioning systems, boasting a positional accuracy of up to 0.1 mm [7]. Despite its commendable accuracy, optical positioning technology is beleaguered by an intrinsic limitation within the clinical environment: the linear propagation of light, which inhibits the positioning capability in certain surgical loci.
In contradistinction, electromagnetic fields exhibit robust penetration capacities and minimal physiological detriments. Pertinently, the morphological attributes of magnetic fields remain negligibly altered post-penetration through human tissues [8]. This renders electromagnetic positioning as a viable alternative for the computation of both the spatial coordinates and orientation angles of the targeted locus, characterized by multi-dimensionality and elevated positioning accuracy.
The primary objective of the phased three-dimensional electromagnetic positioning methodology predicated on spectral line interpolation delineated herein is to facilitate congruency between medical imaging and actual anatomical positioning during clinical examinations. This serves to assist physicians in the precise localization of pathological lesions, thereby furnishing them with enhanced diagnostic acumen and actionable insights for efficacious medical intervention. Underpinned by the magnetic dipole model and leveraging Ferrari’s law of electromagnetic induction, this work employs difference frequency phase analysis coupled with quadrilinear spectral line interpolation algorithms to surmount the challenges associated with multi-solution spaces and the intricate computational procedures inherent in conventional electromagnetic positioning paradigms. The utilization of electromagnetic fields offers the advantage of bio-permeability with negligible physiological detriment, thus obviating the issues related to optical occlusion prevalent in traditional optical positioning technologies.
2. Theoretical Analysis
2.1. Theoretical Foundation
2.1.1. Magnetic Dipole Model
The electromagnetic field engendered by a constant electric current is computable through Biot-Savart’s Law, predicated upon the current flux within the conductor and its geometric morphology. A magnetic dipole can be characterized as a planar loop of conductive material with a diminutive surface area and an arbitrary geometrical configuration. Circular current loops serve as the most efficacious method for electromagnetic field generation, and the spatial flux distribution of such a magnetic dipole is delineated in Figure 1.
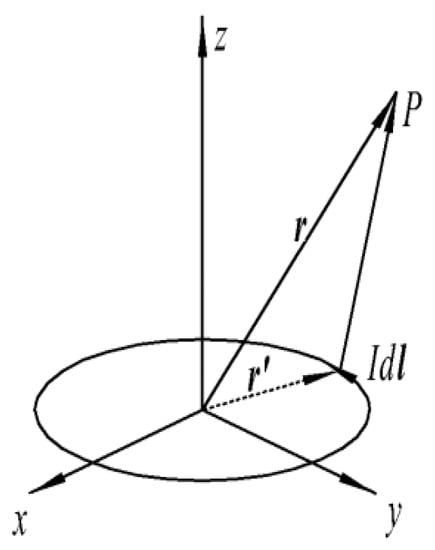
Figure 1.
Model of magnetic dipole at the origin.
Within the context of Figure 1, the coordinate origin serves as the magnetic dipole’s epicenter. The electric current traversing the loop is designated as I, with a counterclockwise orientation deemed as positive. The loop encompasses an area S, and point P (x, y, z) signifies an arbitrary spatial coordinate, distanced r from the dipole’s center. A differential current element dI is selected along the loop, situated at distance r from the center.
Derived from Biot–Savart’s Law, the axiom of electromagnetic induction is thus mathematically formalized as follows:
where and S are oriented according to the right-hand rule.
When magnetic flux undergoes alteration within a conductive loop, it gives rise to an induced electromotive force within the loop, manifesting in direct proportionality to the rate of flux variation. This phenomenon is formalized by the governing equations of electromagnetic induction, denoted as follows:
Among them, n is the number of coil turns, is the magnetic flux passing through the surface S, and E is the induced electromotive force generated.
2.1.2. Phase-Based Three-Dimensional Electromagnetic Positioning Principle
Phase Ranging Principle
Contemporary three-dimensional electromagnetic positioning systems predominantly employ algorithms, such as Gauss–Newton and Levenberg-Marquardt, for the solution of nonlinear equations. The Gauss–Newton algorithm exhibits a pronounced sensitivity to initial value approximations. If substantial discrepancies exist between these initial approximations and the true parameter values, it becomes imperative that the matrix corresponding to the function model retains full rank at every iterative stage; failing to meet this condition leads to flawed solutions and highlights the algorithm’s proclivity for local convergence [9,10].
Conversely, the Levenberg-Marquardt algorithm is critically dependent on the radius of the so-called trust region. An excessively expansive radius diminishes computational efficacy, rendering the algorithm behaviorally analogous to gradient descent methodologies and consequentially decelerating the iterative progression. This results in reduced algorithmic efficiency [9,10]. A minuscule trust region radius, on the other hand, imbues the algorithm with characteristics akin to Gauss–Newton methods, compromising stability and necessitating a full-rank Jacobian matrix throughout the computational operations.
Considering the inherent complexities and computational intricacies involved in deriving three-dimensional coordinates via nonlinear equations, the present study proposes a phase-based three-dimensional electromagnetic positioning paradigm, predicated upon spectral line interpolation. The core principles of phase ranging are illustrated in Figure 2 [11,12].
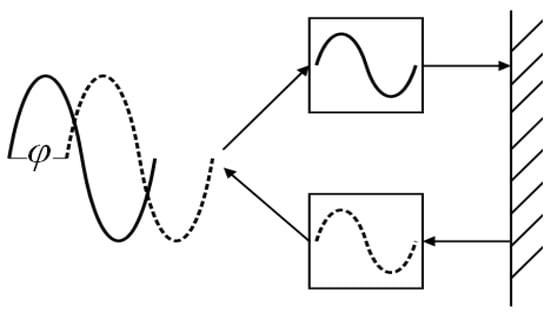
Figure 2.
Schematic of phase ranging principle.
Let the transmitted electromagnetic coil’s amplitude-modulated sinusoidal signal be represented by:
In the formula, E is the signal amplitude and f0 is the modulation frequency. Consonant with Biot–Savart’s Law and the principles of electromagnetic induction, the received signal by the receiving coil is described by:
Presume that the transmitted signal serves as the reference, designating its zero-crossing moment as t0, while the zero-crossing moment of the received signal is t1. That is, when u0(t) = 0 and u1(t) = 0, the phase difference between the two signals is:
The target distance is given by:
In the formula, is the wavelength of the signal, is the number of external integers, [ ] means rounding, and means the phase less than . In this context, the wavelength of the modulated electromagnetic wave serves as an “electromagnetic gauge” instrumental to phase ranging procedures.
Phase measurement can only detect phase which is less than ; that is, only can be determined, but K cannot be determined. Consequently, the evaluated distance R is circumscribed by the wavelength of the modulated electromagnetic wave, referred to as the electromagnetic gauge. When the distance is sub-wavelength (K = 0), the distance can be unequivocally ascertained: . It can be seen from this that if the measured distance is longer, the modulation frequency can be lowered so that , and the distance R can be determined. It should be noted, however, that the amplification of the wavelength inadvertently escalates the standard uncertainty associated with ranging due to inherent phase measurement deviations within the system.
The Determination of the Measurement Frequency for the Ruler
Within the specialized realm of cranial neurosurgery, the positioning system is tasked with transmuting cranial and facial anatomical data into a three-dimensional lattice model, parameterized by spatial coordinates. This model serves as an auxiliary tool by enabling clinicians to localize pathological sites within the cranial cavity with augmented precision, thereby enhancing operative efficiency. The extant positioning range mandated by these clinical applications spans approximately 0.3–0.5 m, as illustrated in the medical application diagram in Figure 3.
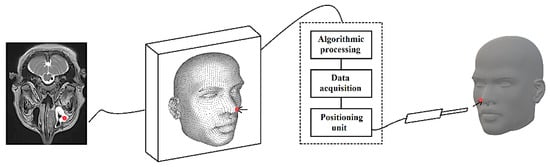
Figure 3.
Conceptual illustration of medical application. The red dot in the figure indicates the target location that needs to be identified.
Regarding the selection of appropriate measuring scales, a unidimensional gauge is deployed, characterized by a radiation range spanning 0.3–0.5 m. It is imperative that the operational range of this gauge is congruent with the upper limit of 0.5 m. The frequency modulation prerequisites for achieving this range are delineated in references [13,14].
Positioning Principle
In a reference coordinate system engendered by three sets of energized solenoids, designated as 01, 02, and 03, the distances L1, L2, and L3 from these solenoids to the designated point P can be calculated utilizing Equation (6). Refer to Figure 4 for the positioning schematic and Figure 5 for the corresponding ANSYS-based finite element analysis model.
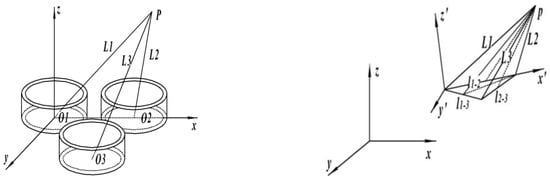
Figure 4.
Positioning schematic.
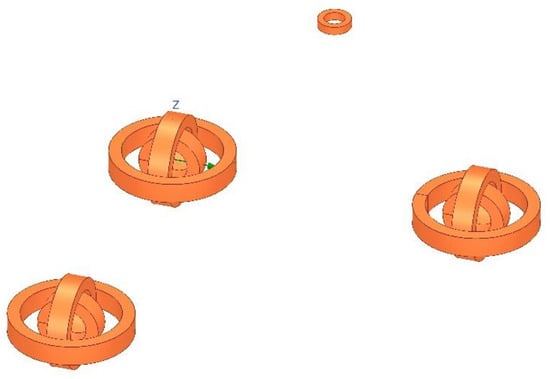
Figure 5.
ANSYS location model.
In the aforementioned reference coordinate system, the spatial coordinates of the target point P are (x, y, z), the coordinates of solenoid 01 are (a1, b1, c1), those of solenoid 02 are (a2, b2, c2), and those of solenoid 03 are (a3, b3, c3). In conjunction with Figure 4 and Figure 5, as well as Equations (5) and (6), and adhering to the principles of phase-based ranging, the distances L1, L2, and L3 between the energized solenoids 01, 02, and 03 and the point P can be ascertained. Subsequently, a system of equations articulated by Equation (8) can be algebraically manipulated to solve the three unknown variables, thus yielding the spatial coordinates of the designated point P. Nevertheless, it is pertinent to note that due to inherent geometric symmetries, multiple solutions are plausible. Therefore, constraints are applied such that only solutions within the first octant of the coordinate system are considered valid.
2.2. Key Technology Research
2.2.1. Differential Frequency Phase Detection Technique
The inaccuracy engendered during phase measurement constitutes the primary source of the system’s positional error. Consequently, augmenting phase measurement precision emerges as a pivotal factor in the overall system optimization. Differential frequency technology serves to extend the phase-carrying signal cycle by factors ranging from tens to tens of thousands, thereby significantly enhancing the accuracy of the phase difference measurement.
When the modulation frequency of the electromagnetic signal is elevated, the direct utilization of this frequency for phase measurement imposes stringent demands on the signal acquisition apparatus. Parameters such as the sampling rate, signal-to-noise ratio, and sampling fidelity inexorably influence the precision of phase measurements, thereby compromising positional accuracy. To ameliorate this, a differential frequency phase detection approach is employed. This technique involves mixing the transmitted and received signals with a local oscillator signal, culminating in the superposition of signal components at two distinct frequencies. Subsequent low-pass filtering yields a low-frequency signal, the phase measurement of which alleviates hardware constraints and improves both ranging and positioning accuracies. The underlying principle of differential frequency phase measurement is illustrated in Figure 6 [13].
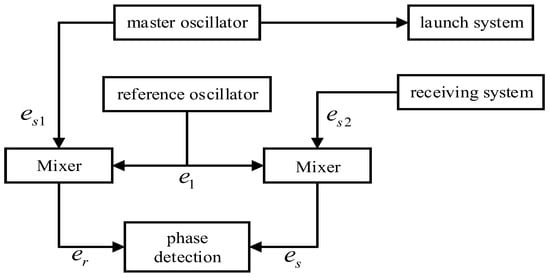
Figure 6.
Principle diagram of frequency difference phase measurement.
The signal of the master control oscillator is:
The signal returned to the receiving system after distance R is:
represents the phase variation.
The reference oscillator signal is:
Mix with and , respectively, and obtain the difference frequency signal and the ranging signal at the output of the mixer, which can be expressed as:
The phase difference of the two mixed frequency signals measured after phase detection is . The phase difference of the two low-frequency signals obtained after frequency difference is the same as the phase difference of the direct measurement of the high-frequency modulation signal.
In alignment with the criteria for the frequency selection of the measuring ruler [9], the system is designed to adhere to positioning standards with a primary signal oscillation frequency of 600 MHz, a local oscillator signal frequency of 600.02 MHz, and a differential frequency signal frequency of 20 KHz.
Table 1 delineates the comparative hardware requirements for high-frequency and differential frequency techniques.

Table 1.
Comparison of hardware equipment requirements.
An examination of hardware specifications reveals that a signal without frequency differentiation necessitates ultra-high-frequency sampling that satisfies both sampling accuracy and multi-channel capabilities—requirements that are unattainable with current mainstream acquisition devices. Conversely, the utilization of differential frequency significantly relaxes equipment prerequisites, enabling compliance with mainstream acquisition devices and reducing hardware expenditures by a minimum of 500%.
2.2.2. Phase Difference Calculation Algorithm
The quantification of phase disparities between two sinusoidal signals of identical frequency holds considerable import in engineering disciplines. Existing methodologies for such quantification bifurcate into analog [15] and digital modalities [16]. Analog approaches entail intricate measurement systems that necessitate specialized hardware, thereby escalating costs. Digital methods encompass automatic digital phase detection, digital synchronous demodulation [17], and spectral analysis techniques [18]. The deployment of automatic digital identification is prone to substantive errors attributable to discrepancies in the positional coordinates of the phase methodology. While both digital synchronous demodulation and Fast Fourier Transform (FFT) techniques are computationally parsimonious and possess capabilities to mitigate Gaussian white noise, their arc cosine operations inherently circumscribe the scope of phase detection. Moreover, FFT demonstrates limited efficacy in the suppression of spectral leakage, thereby compromising the system’s positional accuracy.
To surmount these limitations, the present study adopts a phase calculation algorithm premised on tetra spectral interpolation within a Hanning window framework [19,20]. This algorithm enhances traditional Hanning window FFT through the implementation of a four-line spectral interpolation correction, thereby ameliorating both amplitude and phase calculation accuracy between the transmitted and received signals.
Window function selection exerts a profound impact on the outcomes of spectral line interpolation. It is imperative that the chosen window function should not only exhibit superior sidelobe characteristics, but also maintain an optimized mainlobe width to prevent the substantial degradation of frequency resolution. Figure 7 elucidates that both the Kaiser and Nuttall windows manifest more pronounced sidelobe characteristics compared to the Hanning window, albeit at the expense of a broader mainlobe. Consequently, this study opts for the Hanning window, articulated in the frequency domain, as delineated in Equation (17).
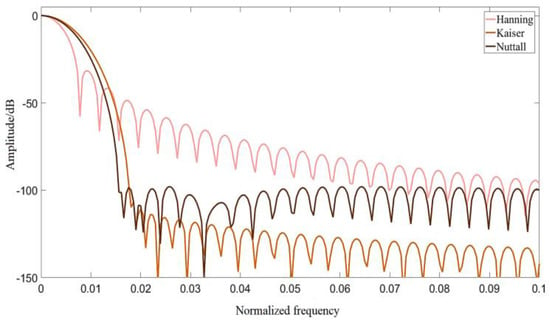
Figure 7.
Normalized spectrum.
A Hanning window of known width M is expressed as follows:
Taking its Fourier Transform yields:
In the formula, .
In Formula (15), , k is the number of discrete spectral lines and k = 0, 1, 2, …, N − 1, and its DFT transformation is:
Sampling a single-frequency complex exponential sequence x(n) at the sampling rate fs, the obtained discrete signal expression is:
In the formula, are the amplitude, frequency, and phase of the signal, respectively. After performing FFT on it, it is transformed into:
In the equation, represents the frequency resolution, and k = 0, 1, …, N − 1.
As depicted in Figure 8, asynchronous or aperiodic signal sampling engenders spectral peak deviations due to the barrier effect, rendering the precise localization of harmonic frequencies on discrete spectra problematic. To ameliorate this issue, spectral interpolation correction is commonly employed, embracing double, triple, and quadruple spectral interpolations [19,20].
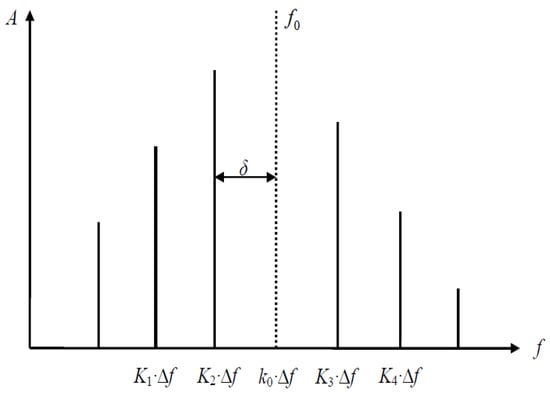
Figure 8.
Spectrum of asynchronously sampled signals.
In the context of this manuscript, a tetra-spectral interpolation method serves as the cornerstone for spectral error correction. The authentic spectral line under examination is symbolically represented as k0, and a selection criterion is employed to identify four spectral lines k1, k2, k3, and k4 with the maximum amplitudes to the left and right of k0. The relationships are as follows: k1 ≤ k2 ≤ k0 ≤ k3 ≤ k4, where k2 = k1 + 1, k3 = k2 + 1, and k4 = k3 + 1. The amplitude corresponding to the spectral line k0 is y0, and the amplitudes of the four spectral lines k1, k2, k3, and k4 are y1, y2, y3, and y4, respectively, where y1 = | W(k1) |, y2 = | W(k2) |, y3 = | W(k3) |, and y4 = | W(k4) |. Since 0 ≤ k0 − k1 ≤ 1, we introduce a frequency offset:
Definition of Correction Factor Calculation , as derived from Equation (18):
When N is large, the above formula can be simplified to , that is, there is a functional relationship between the frequency offset and the correction factor, and its inverse function is . After obtaining the peak values of the four spectral lines, this frequency offset is determined via inverse computational methods. This culminates in the derivation of an empirically substantiated frequency correction formula.
The phase correction is:
Taking into consideration that k2 and k3 are the two nearest lines to the real spectral line, we enhance their weights, resulting in the amplitude correction formula:
The normalized magnitude function of the Hanning window is:
The amplitudes y1, y2, y3, and y4 of the four spectral lines required for calculation can be obtained as:
In the quest for enhanced phase accuracy, the algorithmic framework in this study utilizes a specialized approach where the initial phase is determined based on the medial two spectral lines that exhibit a higher weightage. The resultant values derived from these weighted spectral lines are then subjected to an averaging process, culminating in an elevated level of accuracy that surpasses conventional computational methodologies.
3. Experiment and Experimental Result Analysis
3.1. Comparison of Phase Calculation Errors
The classical signal is:
In the formula ; ; ; ; ; ; .
The error comparison results of various parameters in the horizontal calculation are shown in Table 2.

Table 2.
Comparison of Parameter Errors in Horizontal Calculation.
In juxtaposition with conventional phase detection algorithms, the methodological framework employing spectral line interpolation in this study manifests a discernible enhancement in precision, exhibiting an improvement on the order of 1–2 magnitudes. Quantitative delineation of the associated error metrics is provided in Table 3 for scholarly scrutiny.

Table 3.
Comparison of Vertical Phase Detection Errors.
As discerned from the extant literature [21,22], the zero-crossing methodology demonstrates aptitude primarily for low-frequency signal environments. However, when the signals are confounded with direct current (DC) or harmonic elements, the magnitude of measurement error tends to escalate. Conversely, the correlation function approach, while efficacious in rapid computational throughput and noise suppression, exhibits periodic fluctuations in estimation errors as a function of variations in the actual phase difference values, and the phase difference with in 359° to 360°, 0° to 1°, 179° to 181° rarely occurs, resulting in larger measurement error.
Integrating data from Table 2 and Table 3, it is evident that, in a non-periodic sampling regime, the phase detection algorithm delineated in the current manuscript surpasses traditional methodologies by an order of magnitude range of 1–2, and possesses the capability to scrutinize harmonic signals. In contrast to window function-based spectral line interpolation techniques, the proposed algorithm affords more precise analysis of both harmonic signal frequencies and their corresponding phases. Whether evaluated on a horizontal or vertical comparative scale, the computational accuracy of the present algorithm elevates by 1–2 orders of magnitude.
3.2. Spatial Localization Simulation
Initially, the phase disparity between the transmitted and received signals is ascertained via the frequency-differential phase detection modality. Subsequent to this, phase rectification is executed by employing a Hanning window tetra-spectral line interpolation algorithm. Upon securing the rectified phase difference, the spatial coordinates are extrapolated in accordance with established principles of spatial localization. The schematic representation of this experimental workflow is elucidated in Figure 9.
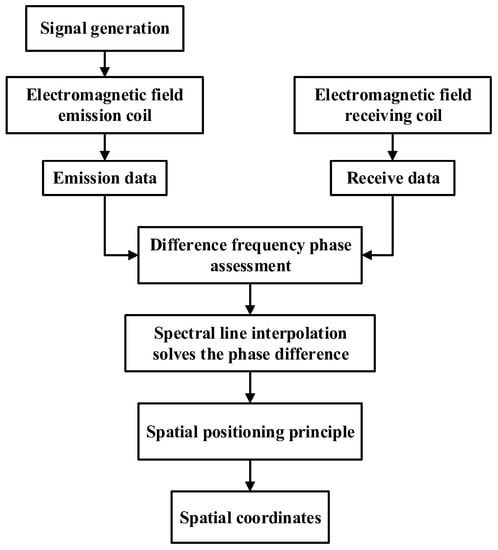
Figure 9.
Experiment flowchart.
3.3. Finite Element Simulation Experiment
In the ANSYS framework, a triad of magnetic field generators is modulated to emit temporally distinct electromagnetic radiations into the spatial domain. As governed by the principles of electromagnetic induction, the receiving coil registers three correlative sets of induced electromotive forces. The finite element simulation outcomes are graphically represented in Figure 10.
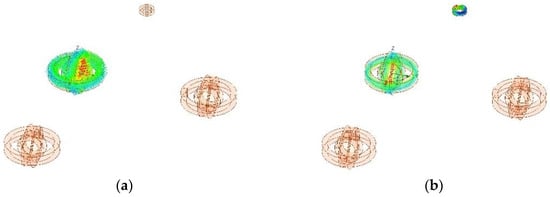
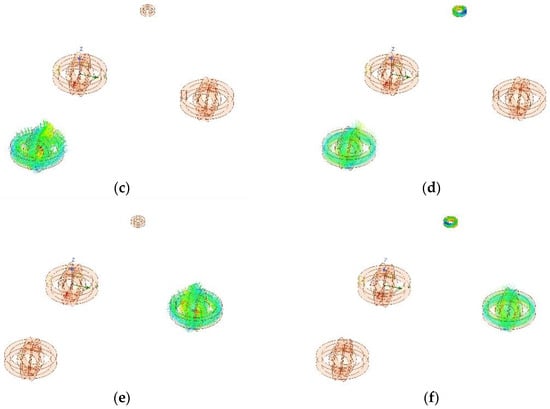
Figure 10.
Finite element analysis results: delineates two primary components: Subfigure (a,c,e) elucidates a schematic representation of magnetic induction lines dispersed into the spatial domain by the inaugural set of magnetic field generators. Subfigure (b,d,f), in contrast, illustrates the energy captured by the receiving coil subsequent to activation by this inaugural set.
In the ANSYS computational environment, spatial coordinates are allocated to three distinct sets of solenoids—01, 02, and 03—as [0, 0, 0], [500 mm, 0, 0], and [0, 500 mm, 0], respectively. Let it be postulated that upon energization, solenoid 01 disseminates electromagnetic radiation into the spatial continuum at a certain moment:
The electromagnetic signal received by the point P to be measured is:
Herein, the amplitude relationships between the transmitted and received signals E1, E2 are in concordance with Equations (1) and (2). The beat signal frequency f is fixed at 20 kHz. Phase values at t1 and t2 are quantified as 0.8 rad and 1.06 rad, respectively, with the reference phase being designated as 0 rad. The application of the spectral interpolation phase difference algorithm yields Δϕ1 as 0.7997 rad and Δϕ2 as 1.0602 rad, culminating in a resultant phase difference of 0.2605 rad. Upon substitution into Equation (6), L1 is deduced to approximate 621.9 mm, where C symbolizes the velocity of light. Figure 11 shows the schematic diagram of phase difference calculation, with the reference signal phase set at 0°.
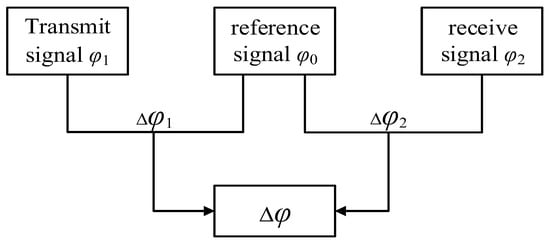
Figure 11.
Illustration of phase difference calculation.
Following the ascertainment of L1, the energized solenoid 02 projects electromagnetic radiations into the spatial domain. The measured phase angles are 3.8 rad and 3.54 rad, respectively, yielding a phase difference of 0.26 rad. Employing spectral line interpolation for a phase difference calculation produces phase angles of 3.7997 rad and 3.5392 rad, yielding a terminal phase difference of 0.2605 rad. Accordingly, L2 approximates 621.9 mm. The energization of solenoid 03 results in measured phase angles for the emitted electromagnetic signals as 4.23 rad and 4.45 rad, respectively. The computed phase difference is 0.22 rad, and the spectral line interpolation algorithm yields phase angles of 4.2297 rad and 4.4492 rad, culminating in a final phase difference of 0.2195 rad. Consequently, L3 is approximated as 524.0 mm.
3.4. Analysis of Experimental Results
By substituting L1, L2, and L3 into Equation (8)
the following solutions are found: x1 = x2 = 362.2, y1 = y2 = 250, z1 = 439.4, and z2 = −439.4. The spatial coordinates are illustrated in Figure 12.
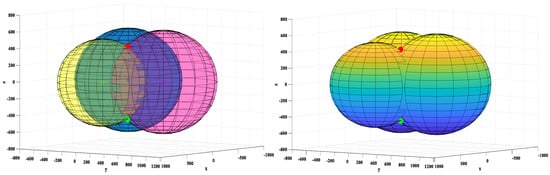
Figure 12.
Spatial location of the testing point.
Owing to the inherent symmetry of the positioning coordinates, only the spatial coordinates of the initial octant’s limit point—denoted visually by a red dot—are retained for practical applications. Based on the triad of phase sets, theoretical phase differences are ascertained to be 0.26 rad, 0.26 rad, and 0.22 rad. Correspondingly, the distances deduced theoretically are 620.7 mm, 620.7 mm, and 525.2 mm. Subsequent computational analysis yields the solutions x1 = x2 = 360, y1 = y2 = 250, z1 = 440, and z2 = −440. The associated error metrics are delineated in Figure 13.
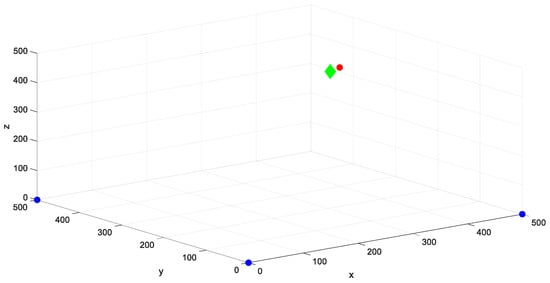
Figure 13.
Spatial position error map of the point to be measured. The green diamond indicates the theoretical phase difference coordinates, the red dots represent the coordinates obtained by spectral line interpolation, and the blue dots indicate the position of the transmitting coil.
The linear distance discrepancy, engendered by comparing the coordinates derived from theoretical phase errors to those extracted from spectral line interpolation phase errors, is quantified to be 2.3 mm. Within a circumscribed range, Table 4 exhibits a comparative analysis of positioning accuracy relative to the conventional electromagnetic positioning methodology reliant on the resolution of nonlinear equations.

Table 4.
Comparison of parameter errors in horizontal calculation.
In the extant literature, the rotation matrix approach, as elucidated in [23], is encumbered with the limitations of a constrained positioning range and elevated error rates. Alternatively, the quaternion technique, expounded in [24], augments the positioning range but suffers from escalating positioning accuracy as the distance to the positioning point increases. These variances in methodology introduce complexities pertaining to system stability. Nevertheless, the theoretical positioning error delineated in this manuscript remains inferior to 3 mm. This metric manifests a marked superiority over traditional methodologies employed for the resolution of nonlinear equations. It is pertinent to note, however, that current algorithmic capabilities are limited to the computation of spatial coordinates of positioning points; the spatial attitude angle remains unquantifiable.
4. Conclusions
In the present manuscript, we introduce a phase-centric tri-dimensional electromagnetic positioning algorithm predicated on spectral line interpolation techniques. Employing a structured analysis of correction factors and polynomial fitting, we delineate the functional interplay between correction factors and frequency offsets, while concurrently establishing a rectification formula for signal frequency and phase. Through rigorous finite element analysis via ANSYS, the theoretical underpinnings of the spectral line interpolation approach for three-dimensional electromagnetic positioning have been empirically corroborated. Our findings reveal that the algorithm enhances positioning accuracy to within 3 mm in the effective spatial domain, yielding an improvement of at least 70% relative to traditional electromagnetic positioning paradigms. This methodology furnishes a novel conceptual framework for electromagnetic positioning, ameliorating the vexing issue of the multiple solutions inherent in nonlinear equation systems, as prevalent in established electromagnetic positioning techniques. The algorithm’s precision in the context of signal frequency and phase resolution exceeds that of the extant Hamming and triangular window methods by 1–2 orders of magnitude.
Nonetheless, despite the notable advancements in positioning accuracy, reduced error rates, and streamlined computational processes, several limitations persist. As of the time of this publication, the prototype design remains incomplete, and the extant positioning algorithm is confined to a mere three degrees of freedom. Future work is slated to focus on the incremental design of a functioning prototype and the enhancement of theoretical methodology.
Author Contributions
Conceptualization: Y.G. (Corresponding Author) and H.C.; Writing—Original Draft: Z.J. (First Author); Software: H.T.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, S.-Y.; Sha, K.; Lu, C.-L. Application progress of computer navigation in trauma orthopedic surgery. J. Guangxi Med. Univ. 2022, 39, 849–855. [Google Scholar] [CrossRef]
- Song, M.; Chen, T.; Chen, C.; Chen, J. Analysis of Rectification Measures for Radiation Emission of Medical Optical Positioning System. J. Saf. Electromagn. Compat. 2022, 4, 67–70. [Google Scholar]
- Pei, D.; Huang, D.; Chen, J.; Zhang, J. Research status and development trend of surgical navigation system. Clin. Med. Eng. 2017, 24, 1326–1328. [Google Scholar]
- Hassfeld, S.; Mühling, J. Computer assisted oral and maxillofacial surgery—A review and an assessment of technology. Int. J. Oral Maxillofac. Surg. 2001, 30, 2–13. [Google Scholar] [CrossRef] [PubMed]
- Decker, R.S.; Shademan, A.; Opfermann, J.D.; Leonard, S.; Kim, P.C.; Krieger, A. Biocompatible near-infrared three-dimensional tracking system. IEEE Trans. Biomed. Eng. 2017, 64, 549–556. [Google Scholar] [PubMed]
- Bale, R.; Widmann, G. Navigated CT-guided interventions. Minim. Invasive Ther. Allied Technol. 2007, 16, 196–204. [Google Scholar] [CrossRef] [PubMed]
- Wang, S. Research on Three-Dimensional Positioning System in Surgical Navigation. Ph.D. Thesis, Central South University for Nationalities, Wuhan, China, 2012. [Google Scholar]
- Zhao, X. Research on Medical 3D Electromagnetic Positioning System. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar] [CrossRef]
- Li, G.; Su, M.; Zhu, D. An improved LM algorithm in bundle adjustment. J. Xi’an Univ. Sci. Technol. 2022, 42, 152–159. [Google Scholar]
- Zhang, H.; Wu, T. Application of genetic algorithm in solving nonlinear equations. J. Zhaoqing Univ. 2002, 4, 16–19. [Google Scholar]
- Chen, S.; Xu, L.; Zhuang, H.; Zhu, W. A Laser Radar System for Measurement of Separation Processes in Spacecrafts. Missiles Space Launch Technol. 2019, 5, 122–126. [Google Scholar]
- Dong, C.; Zhao, Y.; Zhang, C.; Li, M. Phase-based laser ranging system based on FPGA. Foreign Electron. Meas. Technol. 2021, 40, 5. [Google Scholar]
- Xi, J. Design of Phase Laser Ranging Instrument and Analysis of Influencing Factors on Its Performance. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2022. [Google Scholar] [CrossRef]
- Chen, H. Research on Phase Laser Ranging System. Master’s Thesis, China Jiliang University, Hangzhou, China, 2019. [Google Scholar] [CrossRef]
- Nejad, S.M.; Fasihi, K.; Olyaee, S. Modified Phase-Shift Measurement Technique to Improve Laser-Range Finder Performance. J. Appl. Sci. 2008, 8, 316–321. [Google Scholar]
- Xu, S.; Chen, Y.; Zhao, Q. Research on implementation method of small size high-precision laser ranging system. Infrared Laser Eng. 2008, s3, 243–246. [Google Scholar]
- Poujouly, S.; Journet, B.; Miller, D. Laser range finder based on fully digital phase-shift measurement. In Proceedings of the 16th IEEE Instrumentation and Measurement Technology Conference, Venice, Italy, 24–26 May 1999; IMTC/99. IEEE: Piscataway, NJ, USA, 1999; Volume 3, pp. 1773–1776. [Google Scholar]
- Jia, F.; Ding, Z.; Yuan, F.; Ge, D. Laser dynamic target real-time ranging system based on all-phase fast Fourier transform spectral analysis. Acta Opt. Sin. 2010, 30, 2928–2934. [Google Scholar]
- Chen, Z.; Wang, L.; Wang, C.; Shen, P.; Li, Z. Power harmonic analysis method based on combined cosine optimization window four-spectrum line interpolation FFT. Power Syst. Technol. 2020, 44, 1105–1113. [Google Scholar] [CrossRef]
- Hao, Z.; Gu, W.; Chu, J.; Ma, C. A power network harmonic detection method based on the four-spectrum-line interpolation FFT. Power Syst. Prot. Control 2014, 42, 107–113. (In Chinese) [Google Scholar]
- Liu, Y. Key Technology Research on Phase Measurement Distance Based on RF Electro-Optic Modulation. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2015. [Google Scholar]
- Li, Z. Research on Phase Discrimination Method for Phase-Based Laser Ranging. Master’s Thesis, Xidian University, Xi’an, China, 2014. [Google Scholar]
- Bai, Y. Research on Six Degrees of Freedom Electromagnetic Positioning Vector Signal Transceiver Technology. Master’s Thesis, Jilin University, Changchun, China, 2015. [Google Scholar]
- Chen, M. Research on Six Degrees of Freedom Electromagnetic Positioning Algorithm and Device Design. Master’s Thesis, Jilin University, Changchun, China, 2015. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).