Cooperative Decisions of a Multi-Agent System for the Target-Pursuit Problem in Manned–Unmanned Environment

Abstract

With the development of intelligent technology, multi-agent systems have been widely applied in military and civilian fields. Compared to a single platform, multi-agent systems can complete more dangerous, difficult, and heavy tasks. However, due to the limited autonomy of unmanned platforms and the regulatory needs of personnel, multi-agent systems cooperating with manned platforms to perform tasks have been more widely promoted at this stage of development. This paper addresses a differential game method for cooperative decision-making of a multi-agent system cooperating with the manned platform for the target-pursuit problem. The manned platform pursues the target according to a certain trajectory, and its state can be obtained by the multi-agent system. Firstly, for the case that the target moves with a fixed trajectory, the target-pursuit problem in a manned–unmanned environment is viewed in the form of game based on a communication graph among agents. Secondly, strategies of all agents are proposed while maintaining their group cohesion. A set of coupled differential equations is solved to implement strategy calculation. Compared to purely unmanned systems, the strategies combine the advantages of the manned platform and add a reference item, which can achieve team cohesion relatively quickly. Furthermore, a brief analysis is made on the scenarios where the target is in another case or adopts other strategies. Finally, comparative simulations have verified the effectiveness and synergy of the strategy.

1. Introduction

The multi-agent system is widely concerned with the development of the unmanned system and intelligent technology [1,2]. Due to its advantages such as autonomy, loose coupling, high fault tolerance, and scalability, multi-agent systems are widely used in fields such as formation control [3], intelligent logistics [4], and collaborative search [5], among others. The cooperative decision-making of multi-agent systems focuses on the interactive behaviors among agents as well as the information exchanging between agents and the environment. Agents ultimately cooperate or compete with each other to accomplish tasks. In recent years, game theory has become a hot topic of research because of its ability to establish models for strategic interactions among agents, which can involve both cooperation and competition [6,7,8].

Due to the limitations in autonomy and intelligence of current unmanned systems, in many complex real-world scenarios, tasks are often executed through the collaboration of manned platforms and multiple unmanned platforms [9,10]. This collaborative approach allows for the full utilization of the strengths of both manned and unmanned platforms, addressing challenges that unmanned systems alone may struggle to tackle. Moreover, the participation of manned platforms can enhance task execution efficiency, success rate, and safety, thereby reducing people’s concerns about responsibility, decision-making, safety, and other regulatory aspects in multi-agent systems to some extent [11]. Therefore, as an emerging area of study, manned–unmanned collaboration is rapidly developing and being applied.

As a typical topic of the collaborative field, target-pursuit problems have received significant attention in recent decades due to their widespread application, such as drone planning [12], territorial defense [13], and search and rescue [14]. In [15], the pursuit problem was proposed first, where the agents move in a grid to capture randomly moving targets. A cooperative algorithm for the multi-agent system to pursue static targets was proposed in [16]. In [17], a real-time approach for the target-pursuit problem of the multi-agent system was studied, wherein two coordination strategies, blocking escape directions (BES), and using alternative proposals (UAL) were adopted. For the moving targets, an opportunistic framework was proposed for multi-robot pursuit of targets in a dynamic environment with partial observability [18]. The consensus pursuit problem was discussed in [19] for multi-agent systems; the authors designed a distributed multi-flocking approach based on the local information. Agents could choose the target adaptively by combining information with the circle formation control law proposed. Inspired by the division of roles in wolf hunting, new strategies for multi-robot collaborative tracking of targets was proposed in [20], which improved the convergence performance of the algorithm and shortened the hunting time significantly.

Furthermore, dynamic game theory is often used for target-pursuit problems because of its advantage in dynamic interaction and decision-making, and because the decision-making process of the game players is the process of cooperation or competition within the team [21]. The game theory approach in [22] attempted to address the target-tracking problem by using cost functions in an obstacle-free environment, and a PD-like fuzzy controller was used to tune the cost function weights. In [23], the pursuit of invisible targets was discussed within the framework of a game, and some results on how the minor closed properties are related to pathwidth are concluded. In the case of multiple pursuers, three kinds of pursuit strategies, cooperative, non-cooperative, and greedy, are proposed in [24], and the sufficient conditions for achieving uniform exponential stability are given. Furthermore, the multiple pursuers strategy in the presence of the parameter of uncertainty was given in [25], and the acquisition probability was determined using the Monte Carlo method. The distributed strategy designed by combining differential game theory with collaborative control theory can handle target-pursuit situations in system communication topology switching [26]. In [27], evolutionary game theory was introduced to solve the pursuit problem of multiple targets, an innovative three-level decomposition method was used to decompose the previously complex multiplayer game into multiple small-scale games, and a multi-agent Q-learning method based on evolutionary game models was proposed.

The studies mentioned above only consider the situations of target-pursuit problems by unmanned platforms or multi-agent systems. However, in practice, it is almost impossible that unmanned platforms perform complex tasks independently until now. The multi-agent system often needs to cooperate with manned platforms or accept commands from manned platforms. There are some results considering manned–unmanned cooperation, mostly qualitative decision-making on manned platforms and quantitative decision-making on unmanned platforms [28,29]. Cooperative operations of Manned/Unmanned Aerial Vehicle hybrid formation in antisubmarine warfare were analyzed in [30]. In order to compensate for the lack of intelligence in unmanned systems, the composition and key challenges of the MAV-UAV collaborative combat system were explored in [31]. These studies mostly focused on top-level planning from a global perspective, without considering coordination issues from the perspective of unmanned platforms. And note that none of the above literature focuses on target-pursuit problems.

In response to the above discussion, this paper proposes a cooperative decision-making method for the multi-agent system cooperating with a manned platform using differential game theory. The key idea of this method is to model the target-pursuit problem in the form of a game, where each agent is seen as a player, and each player can interact with their neighbors for state and strategies. The agents make decisions in the process of the dynamic game continuously, then cooperate with a manned platform to complete the target-pursuit task. More specifically, the contributions of this paper include the following:

• A novel formulation of the differential game as a target-pursuit strategy in a manned–unmanned environment that can be applied in various manned–unmanned cooperative systems.
• We propose a hierarchical decision-making approach for target-pursuit scenarios. The proposed method can enable the multi-agent system to cooperate with the manned platforms in a reasonable manner, ultimately achieving team cohesion while capturing the target. Furthermore, we discuss scenarios where the target is in different forms of motion. The method proposed in this paper can be applied to the static target, the target moving along fixed trajectories, and it can be extended to situations where the target adopts escape strategies.
• Simulations prove that the proposed method can pursue the target in a manned–unmanned environment successfully. And the effects of each parameter are analyzed through comparative simulations.

The rest of this paper is organized as follows: Section 2 presents the required preliminaries and the formulation of the target-pursuit problem. In Section 3, the strategies for agents are designed using linear quadratic differential game theory, and simulations are presented to verify the effectiveness of the proposed approach. The discussion and outlook on the results are presented in Section 4. Section 5 concludes the paper.

Notation 1.

The notation used in the paper is fairly standard except where otherwise stated. $\mathbb{R}$ denotes the field of real numbers, ${\mathbb{R}}^n$ denotes the set of n-dimensional real-valued column vectors and ${\mathbb{R}}^{n\times m}$ denotes the set of all $n\times m$ real matrices. I denotes the identity matrix of the compatible dimension and $0_{m\times n}$ denotes the n-by-m dimensional zero matrix. $A^T$ represents the transpose of the matrix A; $A^{-1}$ represents the inverse of the matrix A. For a matrix $Q\in {\mathbb{R}}^n$, the notation $Q\succ 0$ means that Q is positive definite and $Q\succcurlyeq 0$ means positive semidefinite. In symmetric block matrices, ★ is used to denote a term induced by symmetry. The notation $\mathit{blkdiag}\{A_1,\cdots ,A_n\}$ represents a block diagonal matrix whose main diagonal consists of square matrices $A_1,\cdots ,A_n$. The norm $\parallel x\parallel$ denotes the Euclidean norm of vector x, $\parallel x\parallel ={\left(x^{T}x\right)}^{1/2}$, $x\in {\mathbb{R}}^n$. $A\otimes B$ is the Kronecker product of matrix A and matrix B.

2. Problem Formulation

We consider the target-pursuit problem of the multi-agent system in this paper. The multi-agent system cooperates with an manned platform to pursue a target while maintaining its cohesive state. We describe the target-pursuit problem in the form of a game, which terminates when the target is successfully captured. Without loss of generality, agents are represented as nodes in the network, and the communication relationships among agents are represented by the edges of the network. Then, we introduce some basic knowledge of graph theory to describe the multi-agent system and the internal relationships.

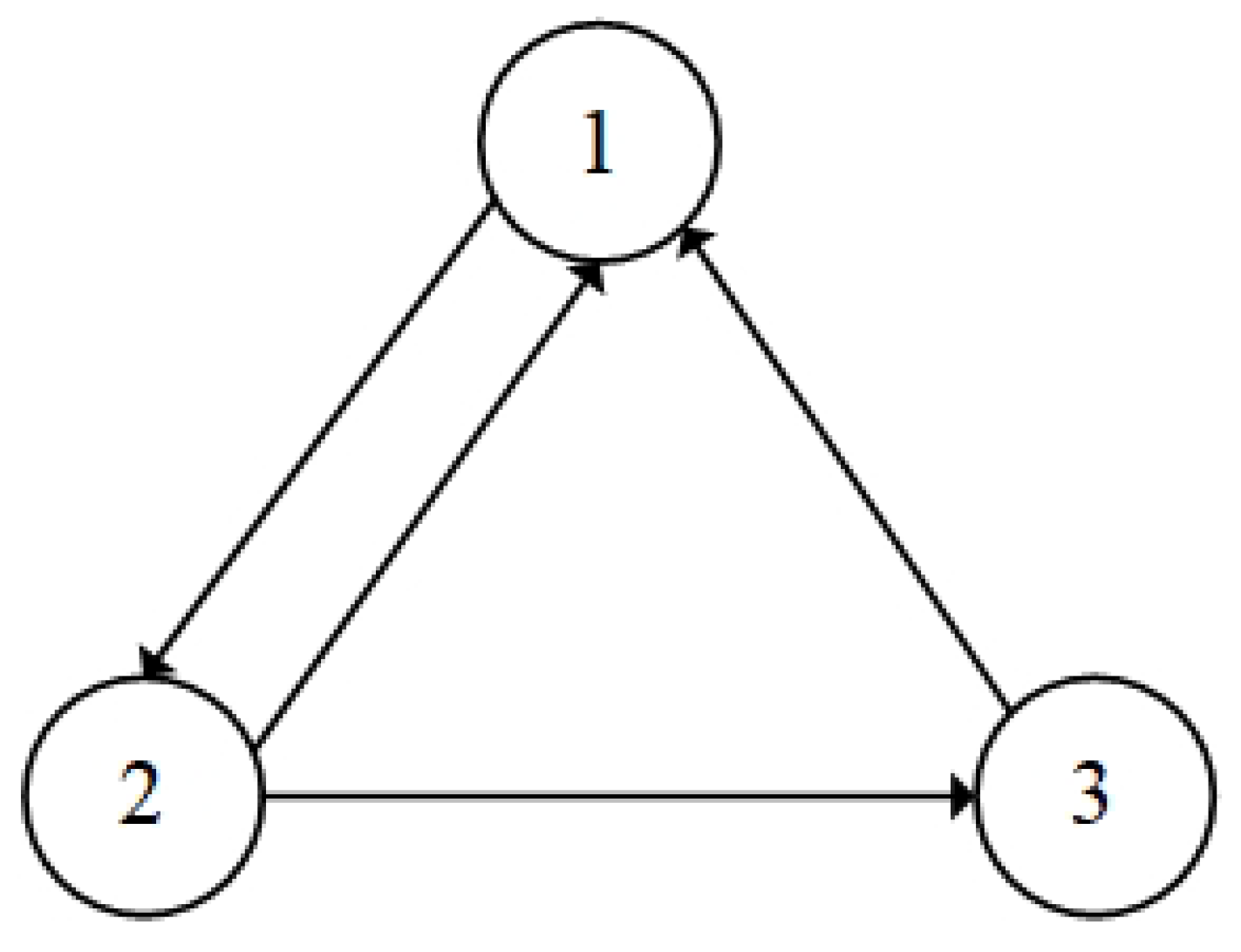
2.1. Communication Graph

The internal relationships of the multi-agent system and communication among agents can be represented by a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where $\mathcal{V}=\{1,2,...,l\}$ is the finite nonempty vertices set and $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ is the set of edges. The set of vertices corresponds to the agents and the edges represent the interconnection between two agents. The edge of the graph $(i,j)$ denotes that agent i can obtain information from agent j with weight ${\omega }_{ij}\ge 0$. The set of all neighbors of agent i in the graph $\mathcal{G}$ is represented by $\mathbb{N}\left(i\right)$. If there is a path from vertex i to vertex j in graph $\mathcal{G}$, then i and j are said to be connected. If every pair of vertices is connected, then the graph $\mathcal{G}$ is said to be connected.

For the directed graph $\mathcal{G}$, the incidence matrix D describes the relationship between vertices and edges. D is the $0,\pm 1$ matrix, where its $uv$th element is equal to 1 if node u is the head of the edge v, $-1$ if node u is the tail of the edge v, and 0 if u is not the vertex of v. For the weighted graph, each edge has its own weight coefficient. The weight matrix is represented by $W=diag\left({\omega }_{ij}\right)$, which is a diagonal matrix. For agent i, its weight matrix $W_i$ is related to its neighbors. The Laplacian matrix L of the directed graph $\mathcal{G}$ can be defined as $L=DW{D}^T$, which contains important properties of the graph.

Assumption 1.

The graph $\mathcal{G}$ does not have self-loops and only contains ordered pairs of distinct vertices. Graph $\mathcal{G}$ is a connected graph.

Assumption 2.

The manned platform can observe the state information of the target. All nodes of the multi-agent system can observe the state information of the manned platform, and some nodes can observe the state information of the target.

2.2. Game Model of Target-Pursuit Problem

Consider a scenario where a manned platform and a group of l agents cooperate to pursue a target. The manned platform pursues the target along a certain trajectory, and the multi-agent system makes decisions based on observing the states of the manned platform. The cooperative decision of the multi-agent system can be modeled as a class of a linear quadratic differential game with l players.

The cooperative decision-making process between the manned platform and multi-agent system can be seen as the form of hierarchical game. For a target, the manned platform takes the initiative in making decisions due to its superior capabilities, the multi-agent system observes the state of the manned platform and makes decisions accordingly to collaborate with the manned platform in completing the task.

Each agent acts as a player in the game, and its state equation is as follows:

$$\begin{array}{c}\hfill {\dot{x}}_i=A_i{x}_i+b_i{u}_i,i=1,2,...,l,\end{array}$$

(1)

where i represents the number of the players, $x_i\left(t\right)\in {\mathbf{R}}^{2n}$ is the state vector, and $u_i\left(t\right)\in {\mathbf{R}}^n$ is the control vector for player i. $A_i=\left[\begin{array}{cc}{0}_{n\times n}& I_n\\ 0_{n\times n}& 0_{n\times n}\end{array}\right],b_i=\left[\begin{array}{c}{0}_{n\times n}\\ I_n\end{array}\right]$.

Consider the vector $z={[x_1^T,x_2^T,...,x_l^T]}^T\in {\mathbb{R}}^{2nl},$ according to (1), the system dynamics is given as follows:

$$\begin{array}{c}\hfill \dot{z}=Az+\sum _{i=1}^l{B}_i{u}_i,\end{array}$$

(2)

where $A=blkdiag\left\{A_1,A_2,...,A_l\right\},$$B_i={[0_{1\times (i-1)},1,0_{1\times (l-i)}]}^T\otimes b_i\in {\mathbb{R}}^{2nl\times n}.$

Suppose that the target moves along a fixed trajectory, and its state equation is

$$\begin{array}{c}\hfill {\dot{x}}_t=A_t{x}_t,\end{array}$$

(3)

where $x_t\left(t\right)\in {\mathbf{R}}^{2n}$ is the state vector of the target. Suppose that the manned platform moves along a certain trajectory to pursue the target, and its state equation is

$$\begin{array}{c}\hfill {\dot{x}}_m=A_m{x}_m,\end{array}$$

(4)

where $x_m\left(t\right)\in {\mathbf{R}}^{2n}$ is the state vector of the manned platform.

Consider the vector $\overline{z}={[x_1^T,x_2^T,...,x_l^T,x_m^T,x_t^T]}^T\in {\mathbb{R}}^{2n(l+2)},$ the augmented system dynamics is given as follows:

$$\begin{array}{c}\hfill \dot{\overline{z}}=\overline{A}\overline{z}+\sum _{i=1}^l{\overline{B}}_i{u}_i,\end{array}$$

(5)

where $\overline{A}=\left[\begin{array}{ccc}A& 0_{2nl\times 2n}& 0_{2nl\times 2n}\\ 0_{2n\times 2nl}& A_m& 0_{2n\times 2n}\\ 0_{2n\times 2nl}& 0_{2n\times 2n}& A_t\end{array}\right],{\overline{B}}_i=\left[\begin{array}{c}{B}_i\\ 0_{2n\times n}\\ 0_{2n\times n}\end{array}\right].$

Then, we are intended to design individual cost functions for each agent according to its role in the system. Define the set of agents that can obtain the target’s state information as $\mathbb{P}$, and the other agents as set $\mathbb{F}$. For agent $i\in \mathbb{P}$, the goal is to maintain a cohesive state with their neighbors $\mathbb{N}\left(i\right)$ while cooperating with the manned platform to pursue the target as efficiently as possible. Hence, the weighted distance that agent i needs to optimize is

$$\begin{array}{c}\hfill \sum _{p\in \mathbb{N}\left(i\right)}{\omega }_{ip}\parallel x_i-x_p{\parallel }^2+\parallel x_i-x_m{\parallel }^2+{\parallel x_i-x_t\parallel }^2,\end{array}$$

(6)

where the first term is the weighted sum of the distance between agent i and its neighbors $\mathbb{N}\left(i\right)$, which is the term that denotes system cohesion; the second term is the distance between between agent i and the manned platform; the third term is the distance between agent i and the target.

The weighted distance (6) can be transformed into the following form:

$$\begin{array}{c}\hfill {\overline{z}}^T{\overline{L}}_i\overline{z}+{\overline{z}}^T{\overline{K}}_{i2}\overline{z}+{\overline{z}}^T{\overline{K}}_{i3}\overline{z},\end{array}$$

(7)

where ${\overline{L}}_i=\left[\begin{array}{ccc}{L}_i\otimes I_{2n}& 0_{2nl\times 2n}& 0_{2nl\times 2n}\\ 0_{2n\times 2nl}& 0_{2n\times 2n}& 0_{2n\times 2n}\\ 0_{2n\times 2nl}& 0_{2n\times 2n}& 0_{2n\times 2n}\end{array}\right]$, $L_i=D{W}_i{D}^T$, $W_i$ is the weight matrix of agent i; ${\overline{K}}_{i2}={\tilde{K}}_{i2}\otimes I_{2n}$, ${\tilde{K}}_{i2}\in {\mathbb{R}}^{(l+2)\times (l+2)}$, ${\tilde{K}}_{i2}(i,i)=1$, ${\tilde{K}}_{i2}(i,l+1)=-1$, ${\tilde{K}}_{i2}(l+1,i)=-1$, ${\tilde{K}}_{i2}(l+1,l+1)=1$, and the remaining elements are 0; ${\overline{K}}_{i3}={\tilde{K}}_{i3}\otimes I_{2n}$, ${\tilde{K}}_{i3}\in {\mathbb{R}}^{(l+2)\times (l+2)}$, ${\tilde{K}}_{i3}(i,i)=1$, ${\tilde{K}}_{i3}(i,l+2)=-1$, ${\tilde{K}}_{i3}(l+2,i)=-1$, ${\tilde{K}}_{i3}(l+2,l+2)=1$, and the remaining elements are 0.

The agent minimizes their own cost function during the game process. Using $u_{-i}$ represents the weighted sum of strategies of all neighbors of agent i, which attempts to minimize the cost function of i; its form is as follows:

$$\begin{array}{c}\hfill u_{-i}={\alpha }_i\sum _{j\in \mathbb{N}\left(i\right)}{u}_j.\end{array}$$

(8)

Design ${\overline{B}}_{-i}={\alpha }_i{\sum }_{j\in \mathbb{N}\left(i\right)}{\overline{B}}_j$, ${\overline{Q}}_i={\overline{\tau }}_{i1}{\overline{L}}_i+{\overline{\tau }}_{i2}{\overline{K}}_{i2}+{\overline{\tau }}_{i3}{\overline{K}}_{i3}$, where ${\overline{\tau }}_{i1}$, ${\overline{\tau }}_{i2}$, and ${\overline{\tau }}_{i3}$ are weight coefficients. ${\overline{\tau }}_{i1}$ represents the importance that the agent i places on achieving cohesive states, ${\overline{\tau }}_{i2}$ indicates the importance that the agent i places on collaborating with human platforms to accomplish the task, and ${\overline{\tau }}_{i3}$ indicates the importance that the agent i places on pursuing the target.

Remark 1.

For agents that cannot observe the target’s information (the set $\mathbb{F}$), the weighted distance does not include the third term, hence, we set ${\overline{\tau }}_{i3}=0$. The strategy of this type of agent is to maintain the cohesive state with its neighbors and the manned platform as much as possible. In practical scenarios, this type of agent is often a lower-level platform.

The cost function for agent i to be minimized can be expressed as follows:

$$\begin{array}{c}\hfill {\overline{J}}_i={\int }_0^{t_f}({\overline{z}}^T{\overline{Q}}_i\overline{z}+u_i^T{\overline{R}}_i{u}_i+u_{-i}^T{\overline{R}}_{-i}{u}_{-i})dt+{\overline{z}}^T\left(t_f\right){\overline{Q}}_{if}\overline{z}\left(t_f\right),i=1,2,...,l,\end{array}$$

(9)

where $t_f$ is is the terminal moment, ${\overline{Q}}_i={\overline{Q}}_i^T$, ${\overline{Q}}_{if}={\overline{Q}}_{if}^T$, $R_i\succ 0$ and $R_{-i}\succ 0$. The purpose of this article is to solve strategy $u_i^{*}$ so that it satisfies the following condition:

$$\begin{array}{c}\hfill {\overline{J}}_i(u_i^{*},u_{-i}^{*})\preccurlyeq {\overline{J}}_i(u_i,u_{-i}^{*}),\end{array}$$

(10)

where $i\in \mathcal{V}=\{1,2,...,l\}$.

3. Results

3.1. Solution to the Target-Pursuit Problem

In this subsection, we give strategies for the multi-agent system which cooperate with a manned platform to execute the target-pursuit task when the target moves along a fixed trajectory. We address a linear quadratic differential game method for the target-pursuit problem. According to the game model of Equations (5) and (9), the following theorem provides the pursuit strategies of agents while maintaining a cohesive state with the manned platform and neighbors.

Theorem 1.

Consider the system (5), the state Equations (1) of agents, and (9) of cost functions, then, the strategy of agent i

$$\begin{array}{c}\hfill u_i^{*}=-R_i^{-1}{B}_i^T{\overline{P}}_{i11}z-R_i^{-1}{B}_i^T{b}_i-R_i^{-1}{B}_i^T{c}_i,\end{array}$$

(11)

satisfies the inequality (10).

In Equation (11), ${\overline{P}}_{i11}={\overline{P}}_{i11}^T\succ 0$ and ${bc}_i$, $c_i$ are solutions of the following coupled differential equation in $[0,t_f]$:

$$\begin{array}{ccc}\hfill -{\dot{\overline{P}}}_{i11}& = & Q_i+{\overline{P}}_{i11}\left(A-\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)+{\left(A-\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)}^{\mathrm{T}}{\overline{P}}_{i11}\hfill \end{array}$$

$$\begin{array}{cc}-& {\overline{P}}_{i11}{S}_i{\overline{P}}_{i11}-{\overline{P}}_{i11}{S}_{-i}{\overline{P}}_i,\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\overline{P}}_{i11}\left(t_f\right)& = & Q_{if},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\dot{b}}_i& = & \left(-A^{\mathrm{T}}+{\overline{P}}_{i11}{S}_i+{\overline{P}}_{i11}{S}_{-i}+\sum _{p=1,p\ne i}^l{\overline{P}}_{p11}{S}_p\right)b_i-{\overline{Q}}_{i12}{x}_m+{\overline{P}}_{i11}\sum _{p=1,p\ne i}^l{S}_p{b}_p,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill b_i\left(t_f\right)& = & {\overline{Q}}_{i12f}{x}_m\left(t_f\right),\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\dot{c}}_i& = & \left(-A^{\mathrm{T}}+{\overline{P}}_{i11}{S}_i+{\overline{P}}_{i11}{S}_{-i}+\sum _{p=1,p\ne i}^l{\overline{P}}_{p11}{S}_p\right)c_i-{\overline{Q}}_{i13}{x}_t+{\overline{P}}_{i11}\sum _{p=1,p\ne i}^l{S}_p{c}_p,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill c_i\left(t_f\right)& = & {\overline{Q}}_{i13f}{x}_t\left(t_f\right),\hfill \end{array}$$

(17)

where $S_i=B_i{R}_i^{-1}{B}_i^{\mathrm{T}}$, $S_{-i}=B_{-i}{R}_{-i}^{-1}{B}_{-i}^{\mathrm{T}}$.

Proof of Theorem 1.

Define the function $V_i(t,\overline{z})={\overline{J}}_i^{*}$; according to [32], we can obtain

$$\begin{array}{c}\hfill -{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial t}}=\underset{u_i{u}_{-i}}{min}\left\{{\left({\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}\right)}^{\mathrm{T}}(\dot{\overline{z}}+{\overline{B}}_{-i}{u}_{-i})+{\overline{z}}^{\mathrm{T}}{\overline{Q}}_i\overline{z}+u_i^{\mathrm{T}}{\overline{R}}_i{u}_i-u_{-i}^{\mathrm{T}}{\overline{R}}_{-i}{u}_{-i}\right\},\end{array}$$

(18)

$$\begin{array}{c}\hfill V_i(t_f,\overline{z})={\overline{z}}^{\mathrm{T}}\left(t_f\right){\overline{Q}}_{if}\overline{z}\left(t_f\right).\end{array}$$

(19)

Minimizing Equation (18), we have

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}\right)}^{\mathrm{T}}{\overline{B}}_i+2{\overline{R}}_i{u}_i^{*}=0,\end{array}$$

(20)

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}\right)}^{\mathrm{T}}{\overline{B}}_{-i}+2{\overline{R}}_{-i}{u}_{-i}^{*}=0,\end{array}$$

(21)

then, the following equations hold

$$\begin{array}{c}\hfill u_i^{*}=-{\displaystyle \frac{1}{2}}{\overline{R}}_i^{-1}{\overline{B}}_i^{\mathrm{T}}{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}};\end{array}$$

(22)

$$\begin{array}{c}\hfill u_{-i}^{*}=-{\displaystyle \frac{1}{2}}{\overline{R}}_{-i}^{-1}{\overline{B}}_{-i}^{\mathrm{T}}{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}.\end{array}$$

(23)

Define ${\overline{S}}_i={\overline{B}}_i{\overline{R}}_i^{-1}{\overline{B}}_i^{\mathrm{T}}$, ${\overline{S}}_{-i}={\overline{B}}_{-i}{\overline{R}}_{-i}^{-1}{\overline{B}}_{-i}^{\mathrm{T}}$, by applying Equations (22) and (23) to (18), so we easily obtain

$$\begin{array}{ccc}\hfill -{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial t}}& =& {\left({\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}\right)}^{\mathrm{T}}\left[\overline{A}\overline{z}-{\displaystyle \frac{1}{2}}{\overline{S}}_i{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}-{\displaystyle \frac{1}{2}}{\overline{S}}_{-i}{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}+\sum _{p=1,p\ne i}^l{\overline{B}}_p{u}_p\right]\hfill \\ & +& {\overline{z}}^{\mathrm{T}}{\overline{Q}}_i\overline{z}+{\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}\right)}^{\mathrm{T}}{\overline{S}}_i{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}+{\displaystyle \frac{1}{4}}{\left({\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}\right)}^{\mathrm{T}}{\overline{S}}_{-i}{\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}.\hfill \end{array}$$

(24)

In order to solve the above partial differential equation, define $V_i(t,\overline{z})={\overline{z}}^{\mathrm{T}}{\overline{P}}_i\overline{z}$, then we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial \overline{z}}}& =& 2{\overline{P}}_i\overline{z},\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial V_i(t,\overline{z})}{\partial t}}& =& {\overline{z}}^{\mathrm{T}}{\dot{\overline{P}}}_i\overline{z}.\hfill \end{array}$$

(26)

By applying Equation (25) to (20), we obtain $u_i^{*}=-{\overline{R}}_i^{-1}{\overline{B}}_i^{\mathrm{T}}{\overline{P}}_i\overline{z}$. Similarly, it can be obtained that $u_{-i}^{*}=-R_{-i}^{-1}{\overline{B}}_{-i}^{\mathrm{T}}{\overline{P}}_i\overline{z}$. $u_i^{*}$, $u_{-i}^{*}$ and Equations (24)–(26) lead to the conclusion that

$$\begin{array}{ccc}\hfill -{\overline{z}}^{\mathrm{T}}{\dot{\overline{P}}}_i\overline{z}& & =2{\overline{z}}^{\mathrm{T}}{\overline{P}}_i\left(\overline{A}\overline{z}-{\overline{S}}_i{\overline{P}}_i\overline{z}-{\overline{S}}_{-i}{\overline{P}}_i\overline{z}-\sum _{p=1,p\ne i}^l{\overline{S}}_p{\overline{P}}_p\overline{z}\right)+{\overline{z}}^{\mathrm{T}}{\overline{Q}}_{di}\overline{z}\hfill \\ & & +{\overline{z}}^{\mathrm{T}}{\overline{P}}_i{\overline{S}}_i{\overline{P}}_i\overline{z}+{\overline{z}}^{\mathrm{T}}{\overline{P}}_i{\overline{S}}_{-i}{\overline{P}}_i\overline{z}.\hfill \end{array}$$

(27)

Then, it is straightforward to see that

$$\begin{array}{ccc}\hfill 0& & ={\overline{z}}^{\mathrm{T}}[{\dot{\overline{P}}}_i+{\overline{Q}}_i-{\overline{P}}_i{\overline{S}}_i{\overline{P}}_i-{\overline{P}}_i{\overline{S}}_{-i}{\overline{P}}_i+{\overline{P}}_i\left(\overline{A}-\sum _{p=1,p\ne i}^l{\overline{S}}_p{\overline{P}}_p\right)\hfill \\ & & +{\left(\overline{A}-\sum _{p=1,p\ne i}^l{\overline{S}}_p{\overline{P}}_p\right)}^{\mathrm{T}}{\overline{P}}_i]\overline{z},\hfill \end{array}$$

(28)

hence, the following equation holds

$$\begin{array}{ccc}\hfill -{\dot{\overline{P}}}_i& = & {\overline{Q}}_i+{\overline{P}}_i\left(\overline{A}-\sum _{p=1,p\ne i}^l{\overline{S}}_p{\overline{P}}_p\right)+{\left(\overline{A}-\sum _{p=1,p\ne i}^l{\overline{S}}_p{\overline{P}}_p\right)}^{\mathrm{T}}{\overline{P}}_i\hfill \end{array}$$

$$\begin{array}{ccc}& - & {\overline{P}}_i{\overline{S}}_i{\overline{P}}_i-{\overline{P}}_i{\overline{S}}_{-i}{\overline{P}}_i,\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill {\overline{P}}_i\left(t_f\right)& = & {\overline{Q}}_{if}.\hfill \end{array}$$

(30)

The time derivative of $V_i(t,\overline{z})$ is given by

$$\begin{array}{ccc}\hfill {\dot{V}}_i& =& -{\overline{z}}^{\mathrm{T}}{\overline{Q}}_i\overline{z}-u_i^{\mathrm{T}}{\overline{R}}_i{u}_i+{(u_i-u_i^{*})}^{\mathrm{T}}{\overline{R}}_i(u_i-u_i^{*})-u_{-i}^{\mathrm{T}}{\overline{R}}_{-i}{u}_{-i}\hfill \\ & +& {(u_{-i}-u_{-i}^{*})}^{\mathrm{T}}{\overline{R}}_{-i}(u_{-i}-u_{-i}^{*}).\hfill \end{array}$$

(31)

We integrate both sides of Equation (27) in $[0,t_f]$ and then have

$$\begin{array}{ccc}\hfill {\overline{J}}_i& =& {\int }_0^{t_f}({(u_i-u_i^{*})}^{\mathrm{T}}{\overline{R}}_i(u_i-u_i^{*})+\hfill \\ & & {(u_{-i}-u_{-i}^{*})}^{\mathrm{T}}{\overline{R}}_{-i}(u_{-i}-u_{-i}^{*}))\mathrm{d}t+V_i\left(\overline{z}\left(0\right)\right).\hfill \end{array}$$

(32)

The above equation shows that the control strategy $u_i^{*}$ can minimize the cost function of the agent i.

Partitioning the matrix ${\overline{P}}_i\in {\mathbb{R}}^{2n(l+2)\times 2n(l+2)}$ yields

$$\begin{array}{c}\hfill {\overline{P}}_i=\left[\begin{array}{ccc}{\overline{P}}_{i11}& {\overline{P}}_{i12}& {\overline{P}}_{i13}\\ ★& {\overline{P}}_{i22}& {\overline{P}}_{i23}\\ ★& ★& {\overline{P}}_{i33}\end{array}\right],\end{array}$$

(33)

where ${\overline{P}}_{i11}\in {\mathbf{R}}^{2nl\times 2n)}$, ${\overline{P}}_{i12}\in {\mathbf{R}}^{2nl\times 2n}$, ${\overline{P}}_{i22}\in {\mathbf{R}}^{2nl\times 2n}$.

Similarly, matrices ${\overline{Q}}_i$, ${\overline{S}}_i$, ${\overline{S}}_{-i}$, and $\overline{A}$ can also be partitioned according to this rule. Let $Q_i={\tau }_{i1}{\widehat{L}}_i+{\tau }_{i2}{\widehat{K}}_{i2}+{\tau }_{i3}{\widehat{K}}_{i3}$, where ${\tau }_{i1}$, ${\tau }_{i2}$, and ${\tau }_{i3}$ are weight coefficients, ${\widehat{L}}_i=L_i\otimes I_{2n}$, ${\widehat{K}}_{i2}=K_{i2}\otimes I_{2n}$ and ${\widehat{K}}_{i3}=K_{i3}\otimes I_{2n}$, $K_{i2}$ and $K_{i3}$ are $l\times l$ matrices, $K_{i2}(i,i)=1$, $K_{i3}(i,i)=1$, and the remaining elements are 0. Therefore,

$$\begin{array}{ccc}\hfill {\overline{Q}}_{i11}& =& Q_i,{\overline{A}}_{11}=A,{\overline{A}}_{22}=A_m,{\overline{A}}_{33}=A_t,\hfill \\ \hfill {\overline{S}}_{i11}& =& S_i=B_i{R}_i^{-1}{B}_i^{\mathrm{T}},{\overline{S}}_{-i11}=S_{-i}=B_i{R}_{-i}^{-1}{B}_i^{\mathrm{T}}\hfill \\ \hfill {\overline{Q}}_{i12}& =& {\{0_{1\times (i-1)},-1,0_{1\times (l-i)}\}}^T\otimes I_{2n},{\overline{Q}}_{i13}={\{0_{1\times (i-1)},-1,0_{1\times (l-i)}\}}^T\otimes I_{2n}.\hfill \end{array}$$

According to the above definition of block matrices, Riccati differential Equations (29) and (30) can be decomposed; specifically, we obtain

$$\begin{array}{ccc}\hfill -{\dot{\overline{P}}}_{i11}& = & Q_i+{\overline{P}}_{i11}\left(A-\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)+{\left(A-\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)}^{\mathrm{T}}{\overline{P}}_{i11}\hfill \end{array}$$

$$\begin{array}{ccc}& - & {\overline{P}}_{i11}{S}_i{\overline{P}}_{i11}-{\overline{P}}_{i11}{S}_{-i}{\overline{P}}_i,\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\overline{P}}_{i11}\left(t_f\right)& = & Q_{if},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill -{\dot{\overline{P}}}_{i12}& = & {\overline{P}}_{i12}{A}_m-{\overline{P}}_{i11}\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p12}-{\left(\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)}^{\mathrm{T}}{\overline{P}}_{i12}\hfill \end{array}$$

$$\begin{array}{ccc}& + & A^{\mathrm{T}}{\overline{P}}_{i12}-{\overline{P}}_{i11}{S}_{-i}{\overline{P}}_{i12}-{\overline{P}}_{i11}{S}_i{\overline{P}}_{i12}+{\overline{Q}}_{i12},\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill {\overline{P}}_{i12}\left(t_f\right)& = & {\overline{Q}}_{i12f},\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill - {\dot{\overline{P}}}_{i13}& = & {\overline{P}}_{i13}{A}_t-{\overline{P}}_{i11}\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p13}-{\left(\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)}^{\mathrm{T}}{\overline{P}}_{i13}\hfill \end{array}$$

$$\begin{array}{ccc}& + & A^{\mathrm{T}}{\overline{P}}_{i13}-{\overline{P}}_{i11}{S}_{-i}{\overline{P}}_{i13}-{\overline{P}}_{i11}{S}_i{\overline{P}}_{i13}+{\overline{Q}}_{i13},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {\overline{P}}_{i13}\left(t_f\right)& = & {\overline{Q}}_{i13f}.\hfill \end{array}$$

(39)

Obviously, Equation (34) and (35) are coupled differential Equations (12) and (13) of Theorem 1.

Due to $\overline{z}={[z^{\mathrm{T}},x_m^{\mathrm{T}},x_t^{\mathrm{T}}]}^{\mathrm{T}}$, control strategy $u_i^{*}=-{\overline{R}}_i^{-1}{\overline{B}}_i^{\mathrm{T}}{\overline{P}}_i\overline{z}$ can be expressed as

$$\begin{array}{c}\hfill u_i^{*} = -R_i^{-1}{B}_i^{\mathrm{T}}{\overline{P}}_{i11}z-R_i^{-1}{B}_i^{\mathrm{T}}{\overline{P}}_{i12}{x}_m-R_i^{-1}{B}_i^{\mathrm{T}}{\overline{P}}_{i13}{x}_t,\end{array}$$

(40)

where the first term $-R_i^{-1}{B}_i^{\mathrm{T}}{\overline{P}}_{i11}z$ on the right-hand side is dependent on the state of neighboring agents, the second term $-R_i^{-1}{B}_i^{\mathrm{T}}{\overline{P}}_{i12}{x}_m$ is related to the state of the manned platform, and the third term $-R_i^{-1}{B}_i^{\mathrm{T}}{\overline{P}}_{i13}{x}_t$ is related to the state of the target.

Let $b_i={\overline{P}}_{i12}{x}_m$, $i=1,2,...m$, taking the derivative of $b_i$, we have

$$\begin{array}{ccc}\hfill {\dot{b}}_i& = & {\dot{\overline{P}}}_{i12}{x}_m+{\overline{P}}_{i12}{\dot{x}}_m\hfill \\ \hfill & = & {\overline{P}}_{i12}{A}_m{x}_m-({\overline{Q}}_{i12}-{\overline{P}}_{i11}{S}_i{\overline{P}}_{i12}-{\overline{P}}_{i11}{S}_{-i}{\overline{P}}_{i12}+{\overline{P}}_{i12}{A}_m+A^{\mathrm{T}}{\overline{P}}_{i12})x_m\hfill \\ & + & {\left(\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)}^{\mathrm{T}}{\overline{P}}_{i12}{x}_m+{\overline{P}}_{i11}\left(\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p12}\right)x_m\hfill \\ \hfill & = & \left(-A^{\mathrm{T}}+{\overline{P}}_{i11}{S}_i+{\overline{P}}_{i11}{S}_{-i}+\sum _{p=1,p\ne i}^l{\overline{P}}_{p11}{S}_p\right)b_i-{\overline{Q}}_{i12}{x}_m+{\overline{P}}_{i11}\sum _{p=1,p\ne i}^l{S}_p{b}_p,\hfill \end{array}$$

(41)

and $b_i\left(t_f\right)={\overline{P}}_{i12}\left(t_f\right)x_m\left(t_f\right)={\overline{Q}}_{i12f}{x}_m\left(t_f\right)$, namely, coupled differential Equations (14) and (15) are valid.

Let $c_i={\overline{P}}_{i13}{x}_t$, $i=1,2,...m$, taking the derivative of $c_i$, we have

$$\begin{array}{ccc}\hfill {\dot{c}}_i& = & {\dot{\overline{P}}}_{i13}{x}_t+{\overline{P}}_{i13}{\dot{x}}_t\hfill \\ \hfill & = & {\overline{P}}_{i13}{A}_t{x}_t-({\overline{Q}}_{i13}-{\overline{P}}_{i11}{S}_i{\overline{P}}_{i13}-{\overline{P}}_{i11}{S}_{-i}{\overline{P}}_{i13}+{\overline{P}}_{i13}{A}_m+A^{\mathrm{T}}{\overline{P}}_{i13})x_m\hfill \\ & + & {\left(\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p11}\right)}^{\mathrm{T}}{\overline{P}}_{i13}{x}_t+{\overline{P}}_{i11}\left(\sum _{p=1,p\ne i}^l{S}_p{\overline{P}}_{p13}\right)x_m\hfill \\ \hfill & = & \left(-A^{\mathrm{T}}+{\overline{P}}_{i11}{S}_i+{\overline{P}}_{i11}{S}_{-i}+\sum _{p=1,p\ne i}^l{\overline{P}}_{p11}{S}_p\right)c_i-{\overline{Q}}_{i13}{x}_t+{\overline{P}}_{i11}\sum _{p=1,p\ne i}^l{S}_p{c}_p,\hfill \end{array}$$

(42)

and $c_i\left(t_f\right)={\overline{P}}_{i13}\left(t_f\right)x_t\left(t_f\right)={\overline{Q}}_{i13f}{x}_t\left(t_f\right)$, therefore, coupled differential Equations (16) and (17) hold. □

Remark 2.

Once given the initial state of each agent, communication topology, and weight coefficients, we can calculate ${\overline{P}}_{i11}$, $b_i$, $c_i$ at different times by performing backward iterations on the terminal values of the coupled differential equations. The strategy $u_i^{*}$ can be obtained by applying the equations’ solutions to (11). Furthermore, we can solve the trajectory of each agent through the state Equation (1).

Remark 3.

The theorem in this paper can also be extended to the case where the target is stationary. Without loss of generality, supposed that the target $x_t$ is at the origin, namely, $x_t={[0,...,0]}^T\in {\mathbb{R}}^{2n}$, then, the last term $-R_i^{-1}{B}_i^{\mathrm{T}}{\overline{P}}_{i13}{x}_t$ in the control input (11) is equal to 0. Therefore, strategy $u_i^{*}$ only includes the the first two items. On the other hand, $x_t$ is a constant value if the target $x_t$ is not at the origin, so we can solve strategically similarly.

Remark 4.

It can be seen from Theorem 1 that solving the strategy of each agent does not need the specific form of state equation of the manned platform and the target. We provided $A_m$ and $A_t$ in the previous section only for the convenience of the system’s expression. In fact, models of the manned platform and the target often cannot be obtained in practical scenarios, we can only observe its states through sensors. Therefore, the strategic solving method only relies on the states $x_m$ and $x_t$ in this paper. This assumption also corresponds to the situation where the multi-agent system cooperates with the manned platform to perform tasks in the actual manned–unmanned environment.

3.2. Simulation

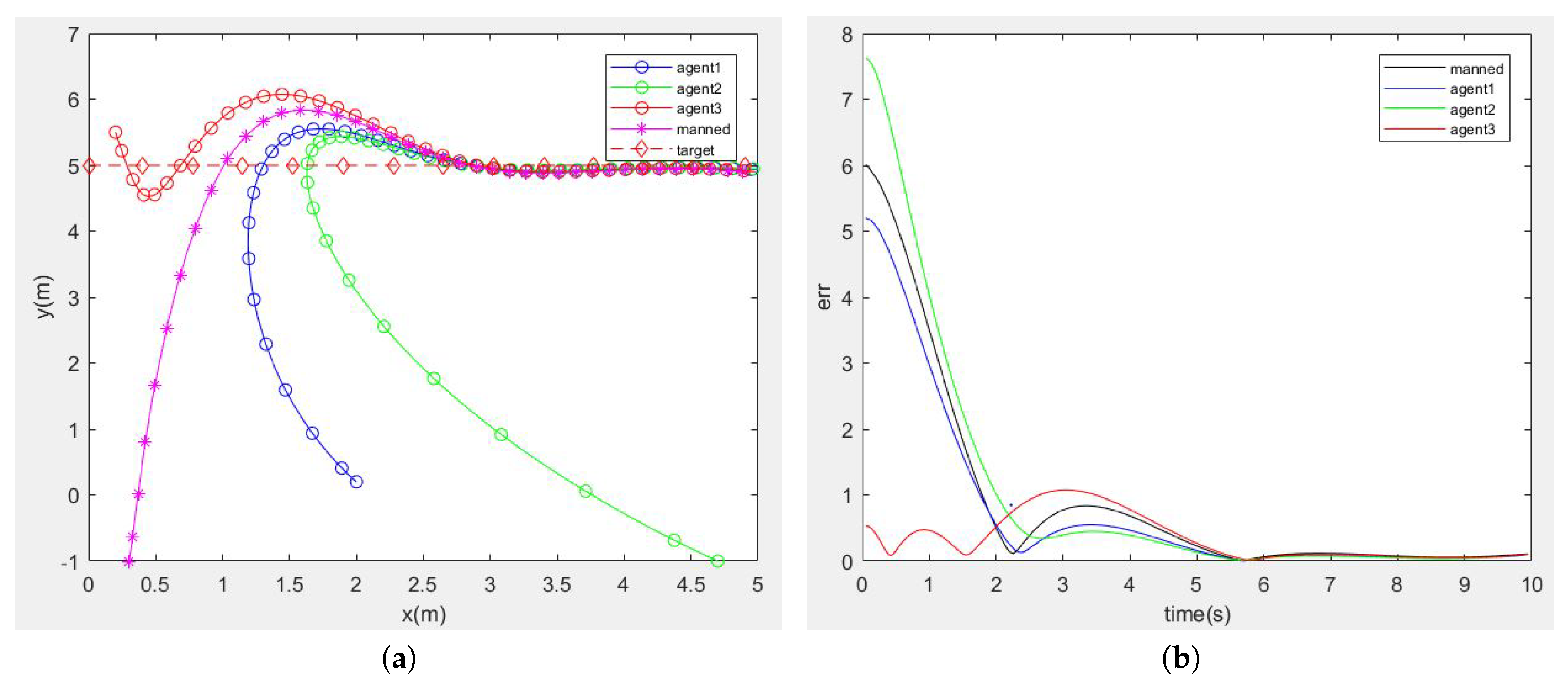
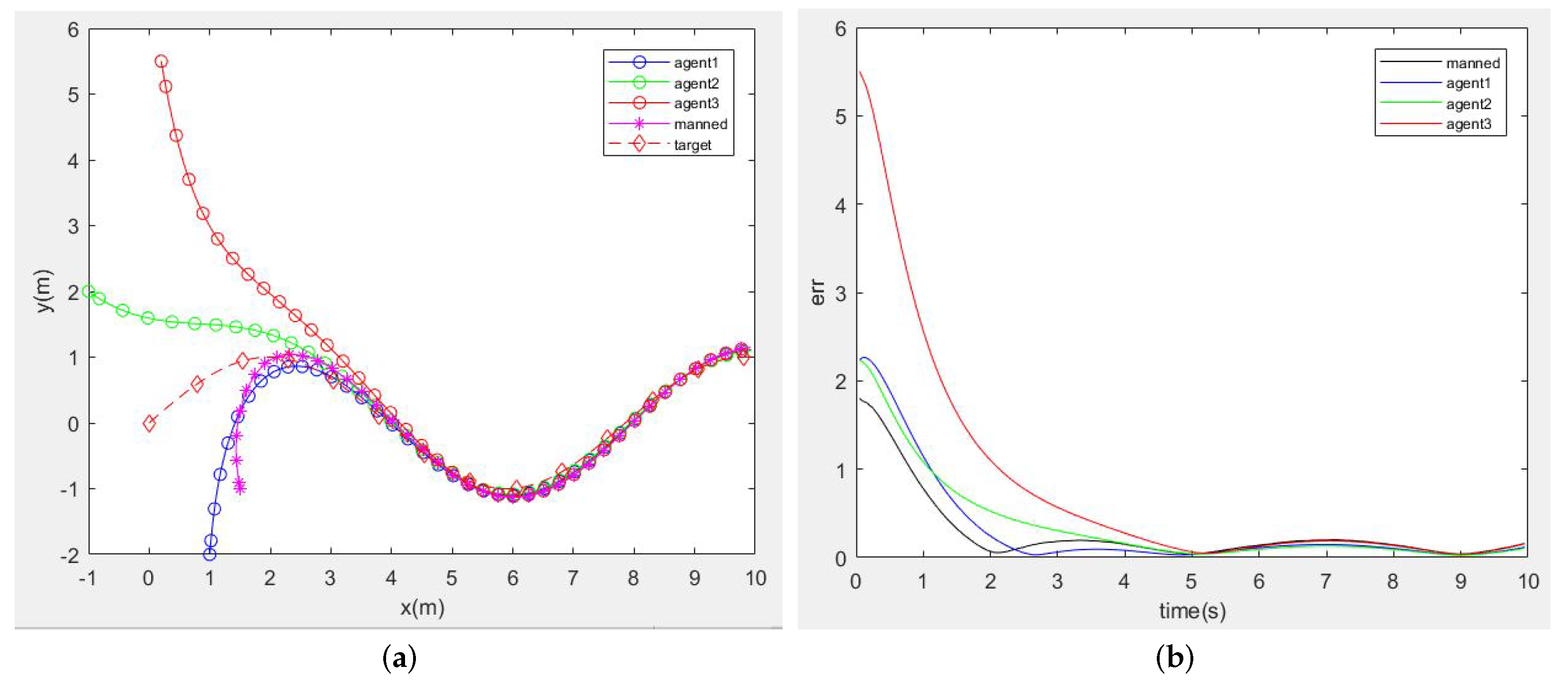
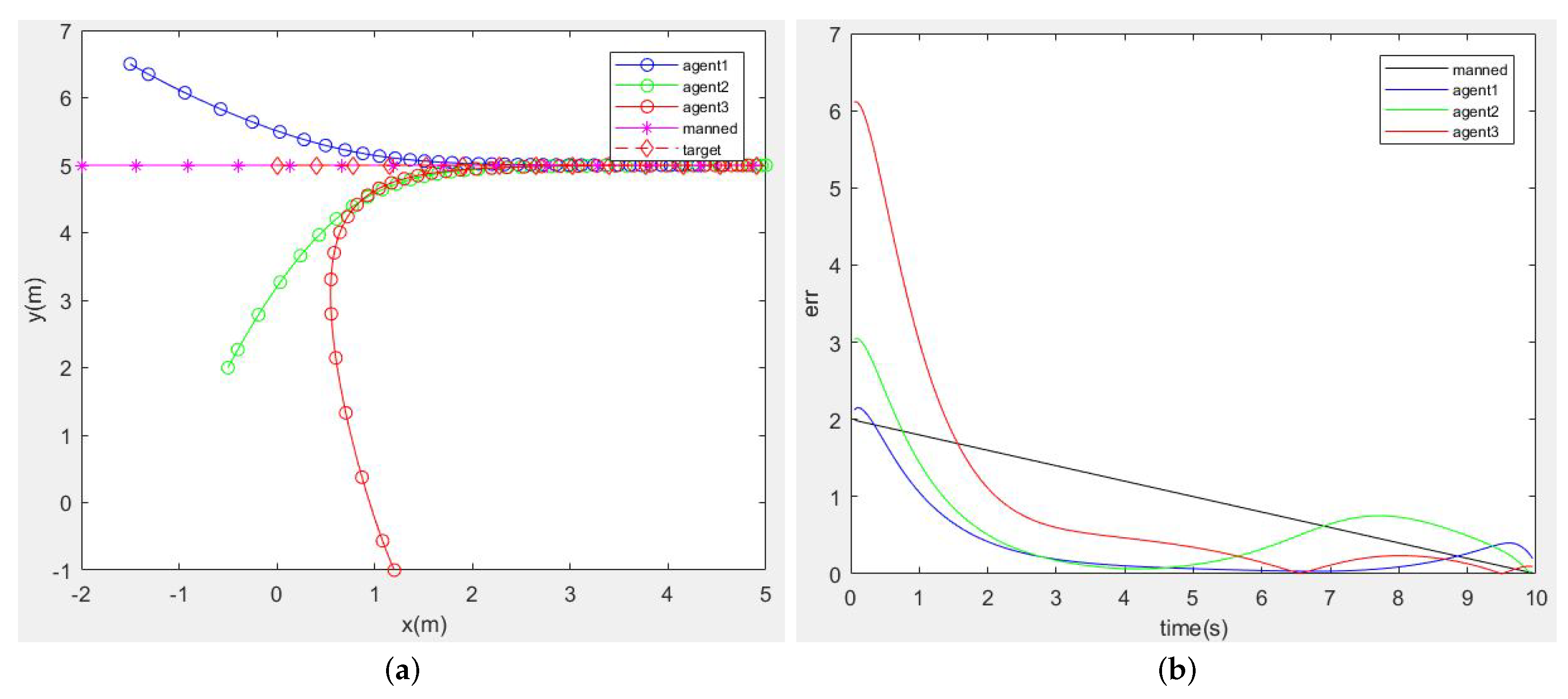
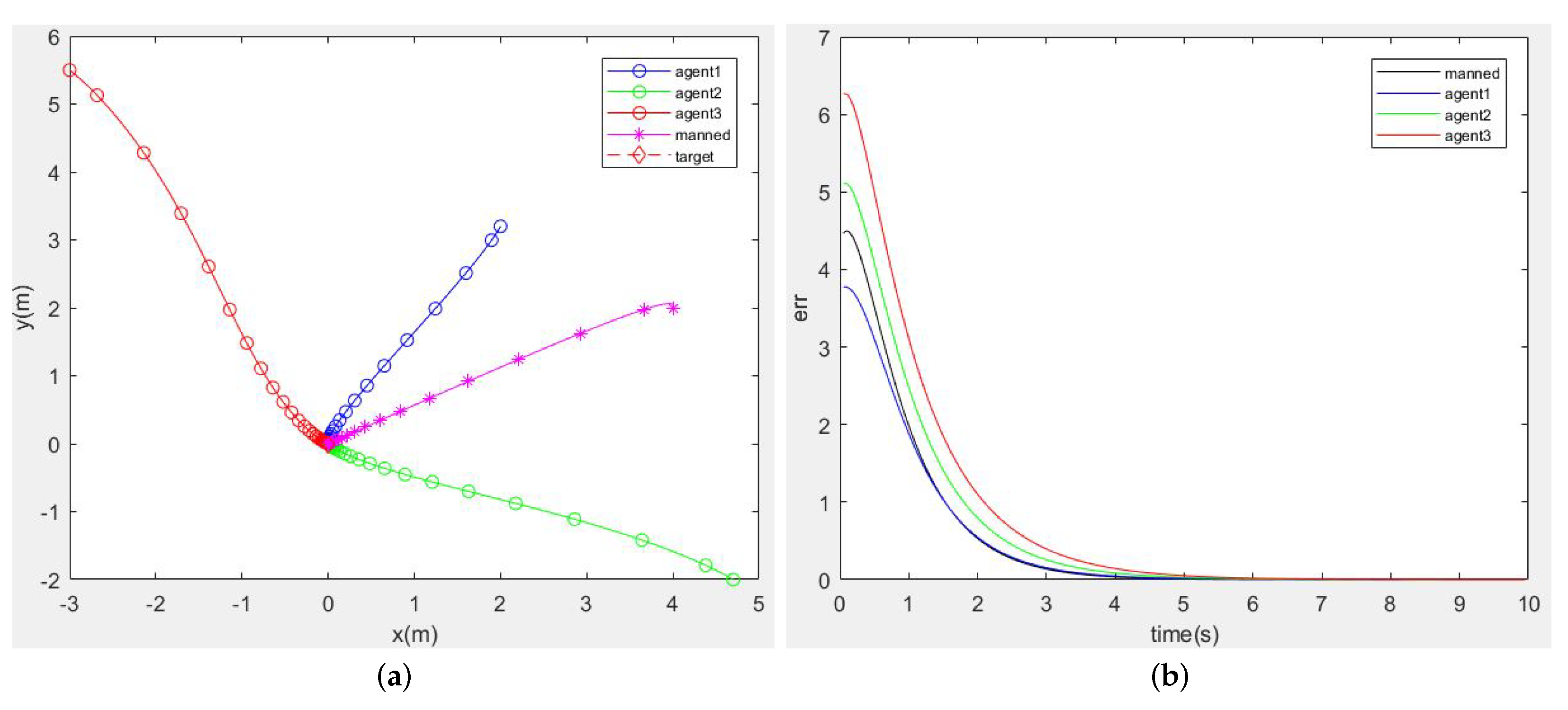
3.2.1. Simulations under Different Target Trajectories

This subsection shows the results of the simulation examples. Assume there is a team of three agents ($l=3$) and the dimension of the state vectors for all agents is 2 (e.g., $n=2$). Each agent adopts a double integral dynamic model. In order to facilitate computation, $R_i$, $R_{-i}$ in cost functions are both taken as identity matrices corresponding to their respective dimensions. Consider the target $x_t$ and the manned platform $x_m$, assume that agent 1 and agent 2 can obtain the target’s information while agent 3 cannot observe the target. The communication graph among agents is shown in Figure 1. The corresponding incidence matrix is

$$\begin{array}{c}\hfill D=\left[\begin{array}{cccc}-1& 1& 0& 1\\ 1& -1& -1& 0\\ 0& 0& 1& -1\end{array}\right].\end{array}$$

(1)

A Target Moving along a Fixed Trajectory

Firstly, assume that the target moves in a straight line, and the state of the target is $x_t={[0.5t,5,1,0]}^T$. Assume that the manned platform pursues the target with the certain strategy by itself. The agents make decisions based on the state of the target and the manned platform. Let the capture radius to be 0.2 m, sample time to be 0.05 s, and the terminal time $t_f$ = 10 s. The weight coefficients are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_i& =1,\hfill \\ \hfill {\overline{\tau }}_{11}& =1,{\overline{\tau }}_{12}=10,{\overline{\tau }}_{13}=5,{\overline{\tau }}_{11f}=1,{\overline{\tau }}_{12f}=10,{\overline{\tau }}_{13f}=5,\hfill \\ \hfill {\overline{\tau }}_{21}& =2,{\overline{\tau }}_{22}=9,{\overline{\tau }}_{23}=6,{\overline{\tau }}_{21f}=2,{\overline{\tau }}_{22f}=9,{\overline{\tau }}_{23f}=6,\hfill \\ \hfill {\overline{\tau }}_{31}& =3,{\overline{\tau }}_{32}=12,{\overline{\tau }}_{33}=0,{\overline{\tau }}_{31f}=3,{\overline{\tau }}_{32f}=12,{\overline{\tau }}_{33f}=0.\hfill \end{array}\end{array}$$

Notice that agent 3 cannot observe the target, therefore ${\overline{\tau }}_{33}=0$ and ${\overline{\tau }}_{33f}=0$. Set the initial state of each agent $x_1\left(0\right)={[2,0.2,0,0]}^T$, $x_2\left(0\right)={[4.7,-1,0,0]}^T$, $x_3\left(0\right)={[0.2,5.5,0,0]}^T$. According to the strategies $u_i^{*}$ in Theorem 1, the motion trajectories of each agent can be obtained (as shown in the Figure 2a). It can be seen that the manned platform and agents have captured the target successfully. Figure 2b shows the relative distance between the target and each agent. At the terminal time $t_f$, the distances between each agent and the target are 0.0995 m, 0.1077 m, and 0.1012 m, which are all smaller than the capture radius.

Secondly, assume that the target moves along a sine trajectory, and the state of the target is $x_t={[t,sin\left(0.8t\right),1,0.8cos\left(0.8t\right)]}^T$. Assume that the manned platform pursues the target with the certain strategy. The weight coefficients are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_i& =1,\hfill \\ \hfill {\overline{\tau }}_{11}& =1,{\overline{\tau }}_{12}=10,{\overline{\tau }}_{13}=5,{\overline{\tau }}_{11f}=1,{\overline{\tau }}_{12f}=10,{\overline{\tau }}_{13f}=5,\hfill \\ \hfill {\overline{\tau }}_{21}& =0.1,{\overline{\tau }}_{22}=9,{\overline{\tau }}_{23}=6,{\overline{\tau }}_{21f}=1,{\overline{\tau }}_{22f}=9,{\overline{\tau }}_{23f}=6,\hfill \\ \hfill {\overline{\tau }}_{31}& =3,{\overline{\tau }}_{32}=12,{\overline{\tau }}_{33}=0,{\overline{\tau }}_{31f}=3,{\overline{\tau }}_{32f}=12,{\overline{\tau }}_{33f}=0.\hfill \end{array}\end{array}$$

Set the initial state of each agent $x_1\left(0\right)={[1,-2,0,0]}^T$, $x_2\left(0\right)={[-1,2,0,0]}^T$, $x_3\left(0\right)={[0.2,5.5,0,0]}^T$. The simulation results are shown in Figure 3a,b. The distances between each agent and the target are 0.1174 m, 0.1058 m, and 0.1556 m, and the target was captured successfully.

Thirdly, assume that the target moves along a straight line, and the state of the target is $x_t={[0.5t,5,0,0]}^T$. Assume that the manned platform pursues the target at a faster speed on the same straight line. The weight coefficients are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_1& =0.99,{\alpha }_2=1.11,{\alpha }_3=0.005\hfill \\ \hfill {\overline{\tau }}_{11}& =1,{\overline{\tau }}_{12}=0.99,{\overline{\tau }}_{13}=21,{\overline{\tau }}_{11f}=1,{\overline{\tau }}_{12f}=0.99,{\overline{\tau }}_{13f}=21,\hfill \\ \hfill {\overline{\tau }}_{21}& =0.5,{\overline{\tau }}_{22}=0,{\overline{\tau }}_{23}=22,{\overline{\tau }}_{21f}=0.5,{\overline{\tau }}_{22f}=0,{\overline{\tau }}_{23f}=22,\hfill \\ \hfill {\overline{\tau }}_{31}& =10,{\overline{\tau }}_{32}=7.35,{\overline{\tau }}_{33}=0,{\overline{\tau }}_{31f}=10,{\overline{\tau }}_{32f}=7.35,{\overline{\tau }}_{33f}=0.\hfill \end{array}\end{array}$$

Set the initial state of each agent $x_1\left(0\right)={[-1.5,6.5,0,0]}^T$, $x_2\left(0\right)={[-0.5,2,0,0]}^T$, $x_3\left(0\right)={[1.2,-1,0,0]}^T$. The simulation results are shown in Figure 4a,b. The distances between each agent and the target are 0.1993 m, 0.0251 m, and 0.0965 m, and the target was captured successfully.

(2)

Stationary Target

Assume that the target is stationary ($x_t={[0,0,0,0]}^T$). The manned platform pursues the target with the certain strategy. The weight coefficients are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\alpha }_i& =1,\hfill \\ \hfill {\overline{\tau }}_{11}& =1,{\overline{\tau }}_{12}=10,{\overline{\tau }}_{13}=5,{\overline{\tau }}_{11f}=1,{\overline{\tau }}_{12f}=10,{\overline{\tau }}_{13f}=5,\hfill \\ \hfill {\overline{\tau }}_{21}& =0.1,{\overline{\tau }}_{22}=9,{\overline{\tau }}_{23}=6,{\overline{\tau }}_{21f}=1,{\overline{\tau }}_{22f}=9,{\overline{\tau }}_{23f}=6,\hfill \\ \hfill {\overline{\tau }}_{31}& =3,{\overline{\tau }}_{32}=12,{\overline{\tau }}_{33}=0,{\overline{\tau }}_{31f}=3,{\overline{\tau }}_{32f}=12,{\overline{\tau }}_{33f}=0.\hfill \end{array}\end{array}$$

Set the initial state of each agent $x_1\left(0\right)={[2,3.2,0,0]}^T$, $x_2\left(0\right)={[4.7,-2,0,0]}^T$, $x_3\left(0\right)={[-3,5.5,0,0]}^T$. The simulation results are shown in Figure 5a,b. The distances between each agent and the target are $0.0682\times {10}^{-3}$ m, $0.1479\times {10}^{-3}$ m, and $0.2865\times {10}^{-3}$ m, and the target was captured successfully.

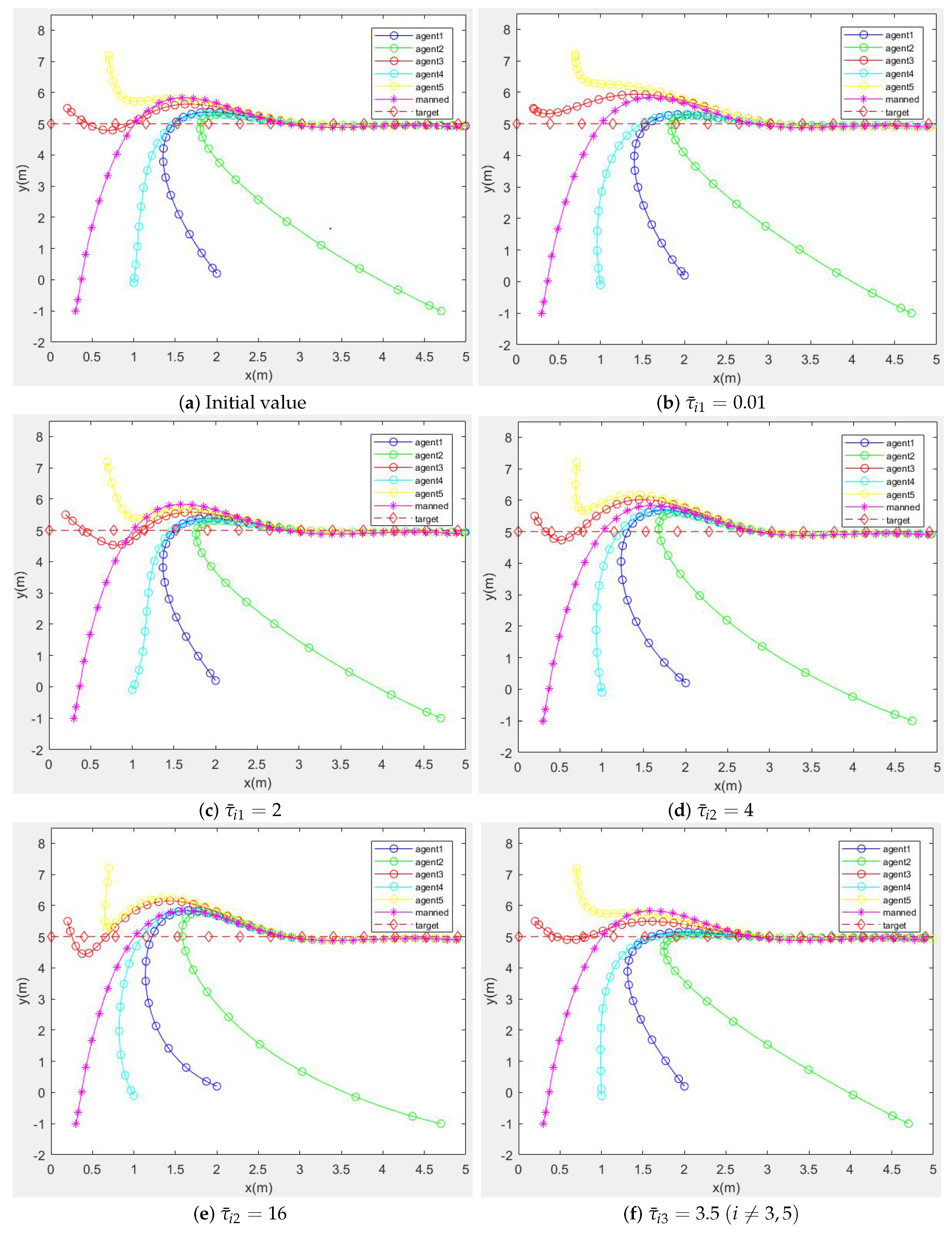
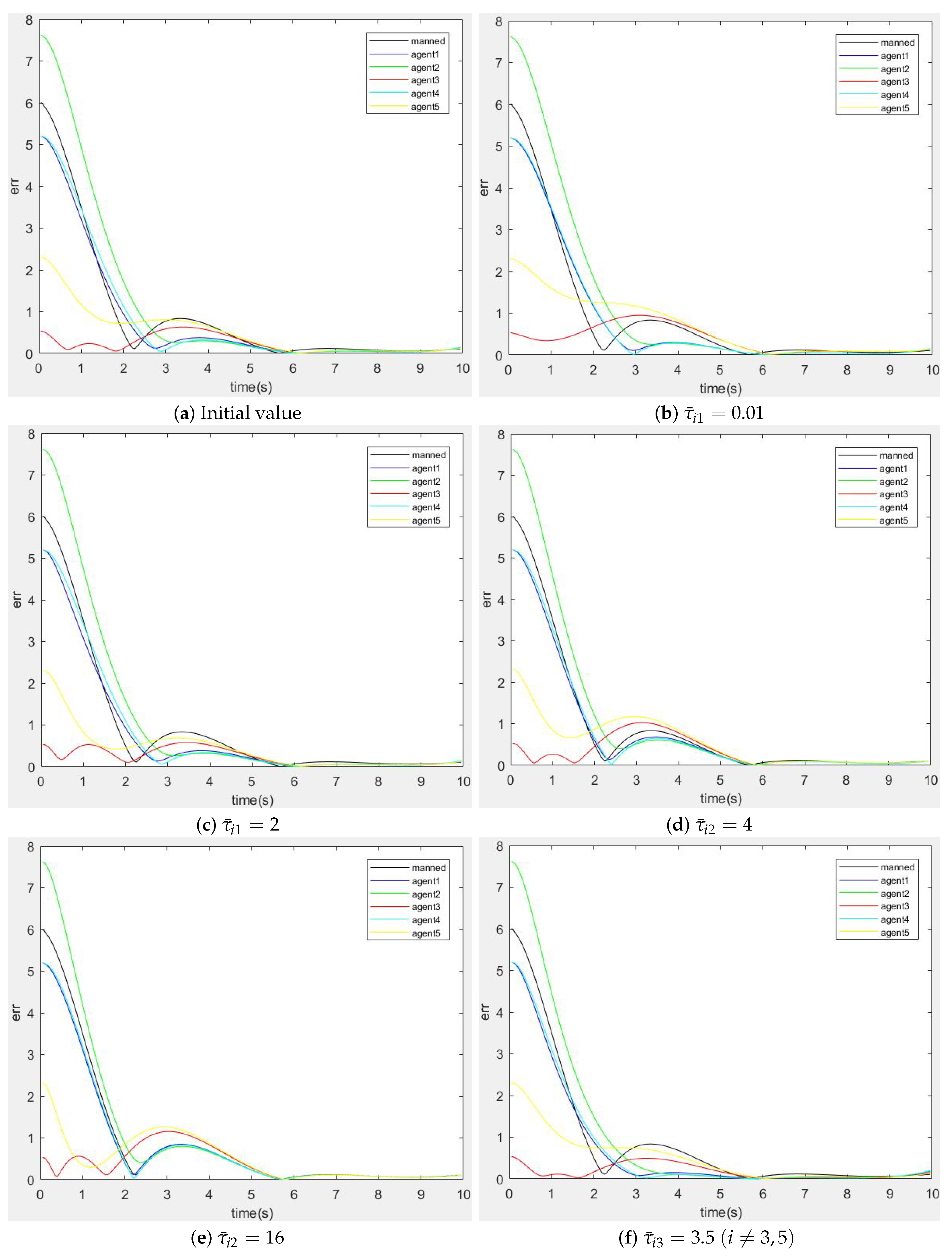
3.2.2. The Influence of Different Weight Coefficients on Strategies

Furthermore, consider the case of 5 agents ($l=5$), where the corresponding incidence matrix is as follows, assuming that agent 3 and agent 5 cannot observe the target (${\overline{\tau }}_{33}=0$, ${\overline{\tau }}_{53}=0$). In the initial state, set the weights ${\overline{\tau }}_{i1}=1$, ${\overline{\tau }}_{i2}=1$, ${\overline{\tau }}_{i3}=1(i\ne 3,5)$. We adjust the weight coefficients ${\overline{\tau }}_{i1}$, ${\overline{\tau }}_{i2}$, ${\overline{\tau }}_{i13}$ separately to study the impact of different weights on simulation results, then obtain the trajectory (Figure 6a–f) of each agent and distance (Figure 7a–f) between each agent and the target.

$$\begin{array}{c}\hfill D=\left[\begin{array}{cccccccccc}-1& -1& 0& 0& 1& 0& 0& 0& 0& 1\\ 1& 0& -1& -1& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& -1& -1& -1& 1& 0& 0\\ 0& 0& 0& 1& 0& 1& 0& -1& -1& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 1& -1\end{array}\right].\end{array}$$

From the Figure 6a–c and Figure 7a–c, it can be seen that the larger the weight coefficient ${\overline{\tau }}_{i1}$, the higher the degree of cohesiveness of agents, and agents tend to shorten their distance from their neighbors. From the Figure 6a,d,e and Figure 7a,d,e, it can be seen that increasing the weight coefficient ${\overline{\tau }}_{i2}$ means that each agent places more emphasis on cooperating with the manned platform, leading to a tendency for agents to narrow their distance from the manned platform in the decision-making process. The entire manned–unmanned system reaches the cohesive state in a shorter time. From the Figure 6a,f and Figure 7a,f, it can be seen that increasing the weight coefficient ${\overline{\tau }}_{i3}$ makes each agent more inclined to pursue the target and reduces the degree of cohesiveness of the team. Due to the inability of agents 3 and 5 to observe the target, their trajectories’ changes are relatively small, while agents 1, 2, and 4 clearly maintained a close distance from the target at an earlier time.

3.2.3. Comparison with the Target-Pursuit Problem in the Multi-Agent System

In the known studies on target-pursuit problems, most of them only consider the case of multi-agent systems, without considering the coordination of the manned platform. Therefore, we compare such a simulation with this paper; the simulation results of the multi-agent system pursuing the target are shown in the Figure 8. By comparing with the Figure 6 and Figure 7, it can be seen that each agent tends to maintain team cohesion while pursuing the target without the trajectory of a manned platform. In manned–unmanned scenarios, the trajectory of the manned platform is equivalent to the reference trajectory of various agents. Agents that cannot observe the target also have motion references, so the manned–unmanned team tends to converge faster. Relatively speaking, in scenarios without a manned platform, it takes longer for the team to reach the cohesive state. Similarly, agents also need to spend more time reaching the target’s capture distance.

4. Discussion

In practical scenarios, the manned platform makes driving decisions using drivers. The strategies of drivers are complex and variable, and the numerical examples in this paper adopt different simulated trajectories. However, the multi-agent system makes decisions by observing the state of the manned platform $x_t$, so the simulation is effective in verifying Theorem 1.

The theorem in this paper can also be extended to the case where the target adopts an escape strategy. The actual scenario corresponding to this case is that the target can also observe our action states, as the strategy such as $u_t=-R_{ti}^{-1}{B}_t^{\mathrm{T}}{\overline{P}}_{t}z$ is taken away from our platform. Therefore, the problem transforms into a standard pursuit–evasion game. The strategies are $u_i^{*}=-R_i^{-1}{B}_i^T{\tilde{P}}_{i11}\tilde{z}-R_i^{-1}{B}_i^T{\tilde{b}}_i$ according to [24] ($\tilde{z}={[x_1^T,x_2^T,...,x_l^T,x_t^T]}^T$). At this point, iterative calculation of ${\tilde{P}}_{i11}$ requires information from $A_t$. If we cannot obtain the target’s model, we can use the reinforcement learning method to approximate the solution [33]. For these situations where adversarial strategies are adopted towards the target, it is more feasible to use reinforcement learning or other approximate approaches since it is difficult to obtain the target’s model. This is one of our future research directions. For future work, we will consider the following in more detail:

• The environment in this paper is relatively ideal; we will consider the target-pursuit problem when obstacles exist. At the same time, we will consider the situation of multiple targets, so that the strategy can adapt to more practical scenarios.
• For the situation where the target adopts an escape strategy, we will conduct further analysis, introduce reinforcement learning methods in cases where the model is difficult to obtain, and balance the relationship between computational cost and algorithm performance.
• The cooperation between multi-agent systems and the manned platform is passive in this paper. In the future, we will introduce trajectory prediction methods for the manned platform, so that agents can make active decisions based on a certain degree of predictive information, thereby improving the efficiency of team task execution.

5. Conclusions

In this paper, we consider a manned–unmanned cooperative decision-making problem in a target-pursuit case. For the target, the manned platform and the multi-agent adopt a hierarchical decision-making approach. The manned platform makes decisions first, followed by agents observing the state of the manned platform and making decisions with interacting information with neighbors. The target-pursuit problem is formulated as a linear quadratic differential game through the directed communication graph. The strategies that be given by solving a system of coupled differential equations iteratively. To make decisions in different pursuit scenarios, we have explored the feasibility of strategies that can adapt to multiple types of targets. We have demonstrated the feasibility of the proposed method through simulation experiments. From the simulation results, the following can be seen: (1) The strategies can enable agents to cooperate with the manned platform to capture a target successfully. (2) The strategies can achieve the pursuit of both the static target and the dynamic target. (3) Different weight coefficients have impacts on algorithm convergence speed, team cohesiveness degree, and target-pursuit time. (4) Compared to the pure unmanned system performing target-pursuit tasks, the manned platform trajectory provides a certain reference for agents, enabling the manned–unmanned collaborative system to complete tasks more efficiently.

However, this approach is proposed in a relatively ideal environment. Additionally, the simulations did not consider more complex platform kinematics models and dynamics models. Therefore, the proposed approach needs to be further experimentally validated in different manned–unmanned collaborative systems, while gradually increasing the complexity of the scenario to ensure the robustness of these strategies.