Time and Energy Benefits of Using Automatic Optimization Compilers for NPDP Tasks

Abstract

In this article, we analyze the program codes generated automatically using three advanced optimizers: Pluto, Traco, and Dapt, which are specifically tailored for the NPDP benchmark set. This benchmark set comprises ten program loops, predominantly from the field of bioinformatics. The codes exemplify dynamic programming, a challenging task for well-known tools used in program loop optimization. Given the intricacy involved, we opted for three automatic compilers based on the polyhedral model and various loop-tiling strategies. During our evaluation of the code’s performance, we meticulously considered locality and concurrency to accurately estimate time and energy efficiency. Notably, we dedicated significant attention to the latest Dapt compiler, which applies space–time loop tiling to generate highly efficient code for the NPDP benchmark suite loops. By employing the aforementioned optimizers and conducting an in-depth analysis, we aim to demonstrate the effectiveness and potential of automatic transformation techniques in enhancing the performance and energy efficiency of dynamic programming codes.

1. Introduction

Non-serial polyadic dynamic programming (NPDP) kernels are used to assess the performance of tiled code generated by means of state-of-the-art optimizing compilers [1,2,3,4]. The NPDP dependence pattern represents the most complex category of Dynamic Programming (DP) due to its non-uniform dependences, which are characterized by irregularities and are represented using affine expressions. The idea of DP is to start from the simplest instance of a problem, find an optimal solution for it, and extend the optimal solution to bigger instances. This solution is used in classical bioinformatics approaches, such as the Needleman and Wunsch algorithm [5]. These base algorithms encompass intricate NPDP dependence patterns that pose limitations to achieving high-performance and energy-efficient code through automatic optimizers. These tools not only facilitate multi-threading of the code but also enhance its locality by employing techniques like loop tiling.

Loop tiling, also known as loop blocking or partitioning, is a compiler optimization technique that boosts cache utilization and enhances loop-based computation performance [6]. It achieves this by dividing loops into smaller, cache-fitting sub-loops, leveraging spatial locality for accessing closely located data elements in memory. This approach reduces cache misses and optimizes memory access patterns. While parallelization for NPDP codes often involves classical techniques like loop skewing, achieving effective tiling poses a greater challenge for compilers [7].

In this paper, we employ three automatic compilers, namely Pluto [8], Traco [9], and Dapt [10], to generate optimized codes for the NPDP benchmark [11]. This benchmark collection consists of eight bioinformatics kernels and two classical computer science algorithms. All three compilers are based on the polyhedral model but employ different approaches to loop tiling. Pluto utilizes the affine transformation framework (ATF), TRACO implements the transitive closure of the dependence relation graph, and Dapt applies space–time tiling with the dependence uniformization approach. To evaluate the results, we selected three AMD machines (two EPYC models and one Ryzen Threadripper), which have gained popularity in the realm of cluster computing, and analyzed the performance of generated codes in terms of execution time and energy efficiency using AMD RAPL [12].

The remaining sections of this paper are structured as follows: Section 2 provides a detailed description of the mentioned compilers, benchmarks, and relevant prior work. Section 3 compares the tiled codes generated by these compilers. Section 4 presents the experimental methodology and results. Finally, the paper concludes in the last section, which highlights future directions for research.

2. NPDP Code Optimization

Efficient comparison of biological sequences requires considering gaps and mismatches. Dynamic programming is a commonly used approach to tackle this task. In the NPDP kernels, a significant portion of the computation involves constructing matrices that represent the similarity between two sequences using appropriate scoring functions. Unfortunately, even simple NPDP loop kernels involve a lot of non-uniform loop dependences.

Let us consider the Knuth algorithm represented by the following program loop [4]:

for(i=n-1; i>=1; i--)

 for(j=i+1; j<=n; j++)

  for(k=i+1; k<j; k++)

   c[i][j] = MIN(c[i][j], w[i][j]+c[i][k]+c[k][j]);

The dependence analyzer Petit [13] extracts the following dependences:

anti    c(i,j) -> c(i,j)          (0,0,+)    non-uniform, only positive

flow    c(i,j) -> c(i,j)          (0,0,1)    uniform

flow    c(i,j) -> c(i,k)          (0,+,1)    non-uniform, only positive

flow    c(i,j) -> c(k,j)          (+,*,*)    non-uniform

flow    c(i,j) -> c(i,j)          (0,0,+)    non-uniform, only positive

flow    c(i,j) -> c(i,k)          (0,+,*)    non-uniform

flow    c(i,j) -> c(k,j)          (+,0,*)    non-uniform

output   c(i,j) -> c(i,j)          (0,0,+)    non-uniform, only positive

The first column indicates the type of dependence (anti: read–write, flow: write–read, output: write–write), while the next two columns represent the memory references denoting the source and destination of the dependence, respectively. The fourth column displays the dependence vectors. A value of 0 indicates no loop-carried dependence, a “+” symbol signifies that the destination is later than the source, and a “*” symbol indicates that the destination could be either later or earlier than the source at a specific element vector.

Vectors represent the distance between the source and destination in an iteration loop space and for uniform dependences contain only constants. Anti and output dependences, uniform dependences, and non-uniform ones with only zeros and + in the vector are generally easier to handle when applying loop transformations to generate rectangular tiles [14]. On the other hand, flow dependences with non-uniform vectors such as (+, *, *) pose significant challenges for automatic optimizers. It is important to note that the domain of dependences is parameterized with unknown values during compile-time. These types of irregular dependence patterns are commonly encountered in the NPDP benchmark suite [11].

The NPDP benchmark contains 10 kernels. Eight of them are classical and well-known bioinformatics tasks.

• The Nussinov algorithm [15] (RNA folding)
• The Zuker algorithm [16] (RNA folding)
• The Smith–Waterman algorithm [17] (aligning sequences)
• The Needleman–Wunsch algorithm [5] (aligning sequences)
• The Smith–Waterman algorithm for three sequences [17] (aligning sequences)
• The counting algorithm [18] (RNA folding)
• The McCaskill’s kernel [19] (RNA folding)
• MEA [20] (RNA folding)

The suite contains additionally two classical computer science NPDP kernels: the Knuth algorithm (optimal binary search tree) [21] and the optimal (polygon) triangulation problem [22]. The NPDP benchmark suite was presented in [11] in detail.

There are many related benchmarks suites like PolyBench [23], Livermoore [24], NASA Parallel Benchmark [25], SPEC [26], LORE [27], and others [28,29] dedicated for optimizers. However, they are not focused mainly on the challenging NPDP problems.

Although the NPDP loops contain complex dependence patterns, they can be presented within the polyhedral model. It means that array references, loop bounds, and constraints are represented by affine expressions, and loops do not contain break or continue statements. The polyhedral model is applied in modern optimizers and represents dependence patterns in mathematical forms like matrices or unions of relations. This powerful theoretical framework allows us to implement many loop transformations, such as tiling, and handle complex parameterized non-uniform and arbitrary nested program loops.

Numerous manual and semi-automatic strategies are available in papers [2,3,30,31,32,33,34] to improve the locality of the NPDP tasks. However, they are limited to the serial code, limited to only one considered NPDP problem, or no-implemented and maintained. Hence, we focused on the well-documented automatic, source-to-source optimizers that realize multi-threading using OpenMP [35].

Polyhedral optimizers employ parallelization and loop-tiling techniques to enhance the performance of serial code. Loop tiling, a widely recognized transformation, is utilized for optimizing both sequential and parallel programs. This technique enables the generation of parallel high-performance code by increasing the code granularity and improving data locality. These optimizations are especially beneficial for executing programs on modern multi-core architectures, as they enable efficient utilization of parallel processing capabilities and enhance overall program performance.

The state-of-the-art source-to-source PLuTo compiler [8] enables automatic tiling and parallelization of program loop nests. It utilizes the affine transformation framework (ATF) to generate parallel tiled code for the target platform. This approach involves a series of execution-reordering loop transformations that facilitate multi-threading and improve locality.

The compiler employs a powerful and versatile cost function embedded in an Integer Linear Programming (ILP) formulation to create effective tiling hyperplanes. These hyperplanes help extract coarse-grained parallelism while minimizing communication and enhancing code locality. In the processor space, PLuTo reduces inter-tile communication volume and optimizes reuse distances for local execution on each node. It supports both one-dimensional and multi-dimensional time schedules for loop nest statement instances, treating schedules using the same algorithm. The Pluto algorithms are implemented in some academic tools like Apollo [36] and PTile [37].

PLuTo offers synchronization-free parallelism, pipelining, and fully permutable loops at various levels. However, the tile dimensionality provided by PLuTo is constrained by the number of linearly independent solutions to the space/time partition constraints [10].

To form valid target tiles, TRACO [9] utilizes the transitive closure of dependence relation graphs, which capture all the dependencies present in the loop nest. The process begins by partitioning the iteration space of the loop nest into smaller rectangular subspaces, known as original tiles.

The tile correction strategy involves removing the dependence destinations whose sources belong to the tiles in the subspace that includes tiles with identifiers greater than the given tile. To accomplish this, the transitive closure of the dependence graph is applied to the iteration subspace. It finds statements that are dependence destinations directly or transitively connected with the sources. This ensures the removal of invalid dependence destinations from the set representing the statement instances of the given tile.

Finally, each invalid dependence target that has been removed from a tile is added to exactly one tile with a lexicographically greater identifier than the tile it was originally a part of. To parallelize NPDP tiled codes, loop skewing is used. The TRACO compiler does not implement any of the ATF techniques or affine function calculating.

When dealing with non-uniform dependencies, the associated time-tiling constraints are inherently nonlinear and are prone to escalate the size and computational complexity once they transition into a linear model. To circumnavigate this issue, DAPT [10] has introduced an approach to approximate these non-uniform dependencies to uniform counterparts, an innovation proven to be simpler than the methods used by Pluto.

Indeed, DAPT has succeeded in normalizing non-uniform dependencies to uniform ones. Unlike Pluto, which only generates code that supports two-dimensional tiling, DAPT and Traco are capable of generating codes that cater to three-dimensional tiling as well nussinov, nw, sw benchmarks. This illustrates the importance and advantage of DAPT’s uniformization process.

In order to generate regular code and enhance the tile dimension, the DAPT compiler [10,38] incorporates space–time tiling that utilizes the intersection operation on sets representing sub-spaces and time slices to generate target tiles. This approach divides the computation into time partitions, where each partition consists of independent iterations that can be executed in parallel. It is important to note that the time partitions need to be enumerated in lexicographical order.

Each space tile is then divided into multiple time slices. The number of time partitions within each time slice is determined using the ISL scheduler [14], with the flexibility for the user to define the desired number of time partitions. Consequently, the tile dimension is increased by one.

Smaller tiles are enumerated within each space tile in the resulting target code. This approach improves code locality by increasing the likelihood of efficiently utilizing the cache and capturing all the data associated with each smaller tile. The proper selection of the number of time partitions forming the time slice is crucial for optimizing cache utilization and achieving improved code locality. Space–time tiling has been demonstrated as having promising potential in the development of new polyhedral-optimizing compilers in paper [4].

However, the crux of the matter is the emphasis on the usage of the uniformization method within the DAPT space–time tiling, serving as a crucial reminder of the importance of uniformization. Despite this, it is worth noting that the field of uniformization has seen a dearth of research in recent times. Consequently, this scarcity of research has given rise to solutions that lack optimal uniformization techniques, highlighting the need for a renewed focus and further investigation into this field [39].

3. Results

To evaluate the performance of the tiled codes generated by the aforementioned compilers, we assessed the time reduction and energy efficiency of the code execution. As the target machines, we chose three AMD Zen 2 computers released in late 2019 and characterized in

Table 1. Technical data for the tested AMD machines.

Processor	Base Clock (GHz)	Turbo Clock (GHz)	Number of Cores	Number of Threads	Cache (MB)	RAM (GB)
EPYC 7542	2.9	3.4	32	64	128	256
EPYC 7H12	2.6	3.3	64	128	256	64
Ryzen Threadripper 3970X	3.7	4.5	32	64	144	128

:

All machines work under Ubuntu Linux 22.04 “jammy” equipped with the compiler g++ 9.3.0. Generated codes were compiled with the flags “-O3 -lgomp -fopenmp”. Source codes of the benchmarks, including optimized codes by compilers, are available at the repository https://github.com/markpal/NPDP_Bench (accessed on 1 August 2023).

To measure energy consumption on the AMD machine, we employed the “amd_energy” approach, which was developed by Naveen Krishna Chatradhi [40]. The kernel driver amd_energy supports AMD 17th family and 19th family processors. Specifically, it is supported by the Zen 3 architecture, which includes processors such as the AMD Ryzen 5000-series and AMD EPYC 7003-series server processors. The energy driver provides access to the energy counters reported through the model-specific registers (MSRs) of the running average power limit (RAPL) model. These energy counters can be accessed through the hardware monitor (HWMON) sysfs interface. These registers are updated every 1 ms.

Energy information, measured in joules, is derived from a multiplier represented by $1/2^{ESU}$, where ESU is an unsigned integer obtained from the MSR_RAPL_POWER_UNIT register. The default value for ESU is 10,000 b, indicating that the energy status unit is incremented by 15.3 micro-joules.

The reported energy values are scaled using the following formula:

$$scaledvalue=((1/2^{ESU})\ast \left(Rawvalue\right)\ast 1,000,000UL)$$

in micro-joules. To calculate power for a specific domain, users can determine the change in energy ($dEnergy$) over a given time period ($dTime$) and divide the result by that time: $Power=dEnergy/dTime$. By calculating the derivative of energy with respect to time, users can estimate the power consumption for a particular domain.

Unfortunately, we were not able to measure energy for the EPYC 7H12 because the host was only available to us under a VMWare environment, which does not support RAPL events.

Table 2. Execution times for the original and optimized codes in seconds for the AMD EPYC 7542.

Benchmark	Size	Original	Pluto	Traco	Dapt
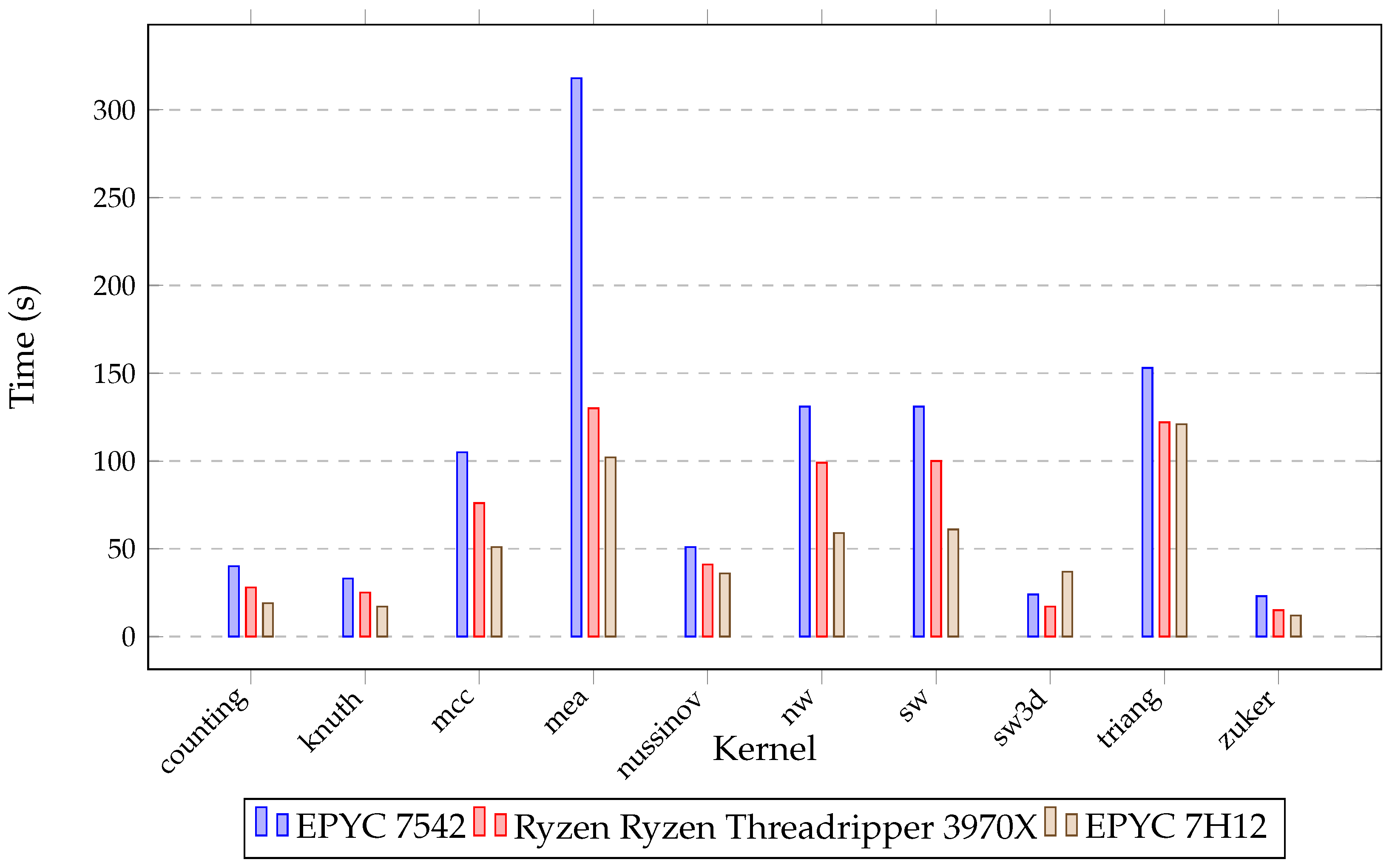
counting	10,000	1282.01	57.1	49.9	40.01
knuth	10,000	855.42	34.29	40.3	33.84
mcc	10,000	2632.3	1021.43	149.02	105.85
mea	2500	6397.83	352.42	481.98	318.77
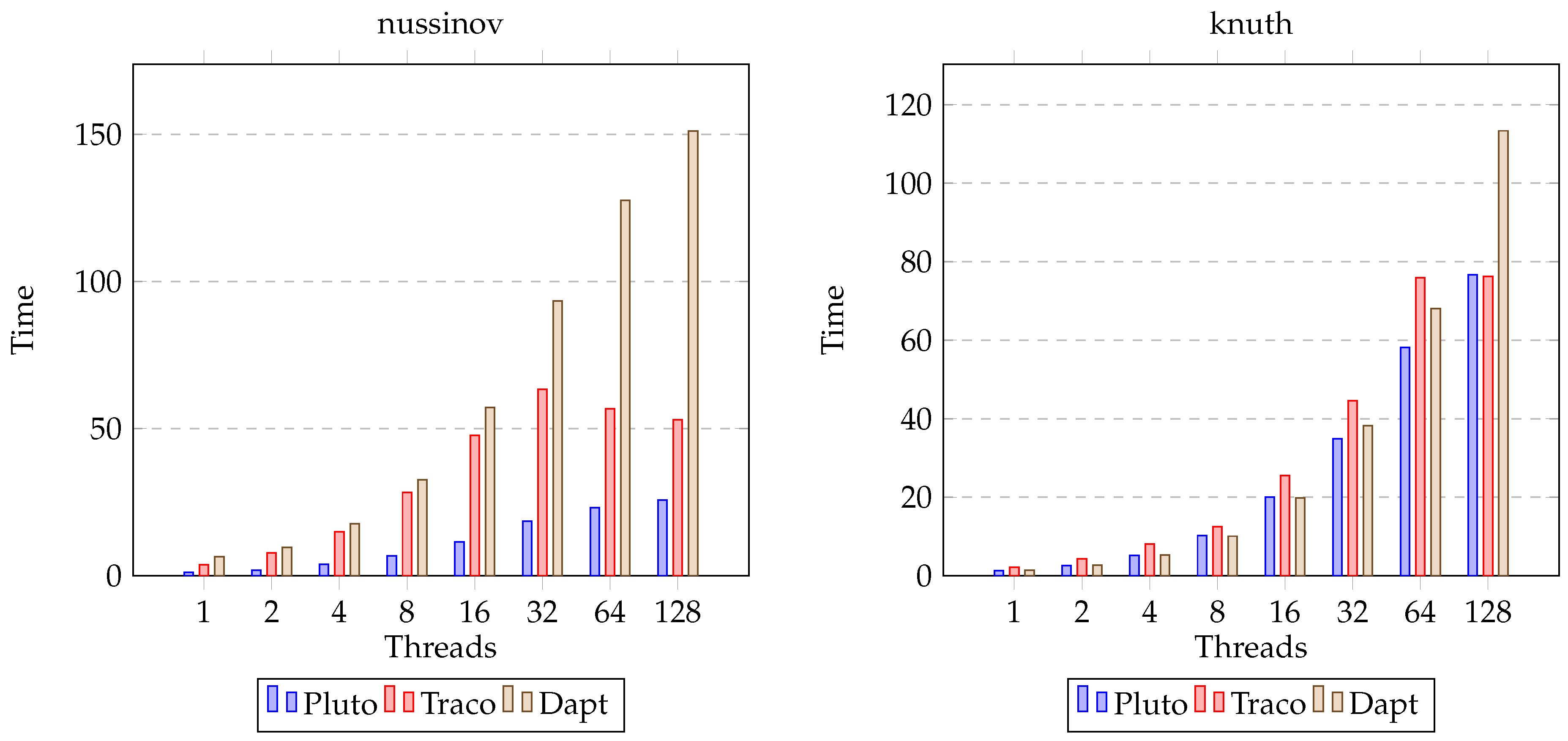
nussinov	10,000	3880.43	205.33	78.74	51.03
nw	10,000	4567.33	182.56	131.33	177.32
sw	10,000	4483.13	183.96	132.46	178.33
sw3d	500	309.87	25.01	29.07	24.02
triang	10,000	3574.98	177.32	223.32	153.76
zuker	2000	415.55	29.98	60.02	23.3

showcases a comprehensive comparison of benchmarks, study sizes, and execution times for both the original and generated codes, measured in seconds for 64 threads of the AMD EPYC 7542. The speed-up is depicted in Figure 1.

Table 3. Energy consumption for the original and optimized codes in joules for the AMD EPYC 7542.

Benchmark	Size	Original	Pluto	Traco	Dapt
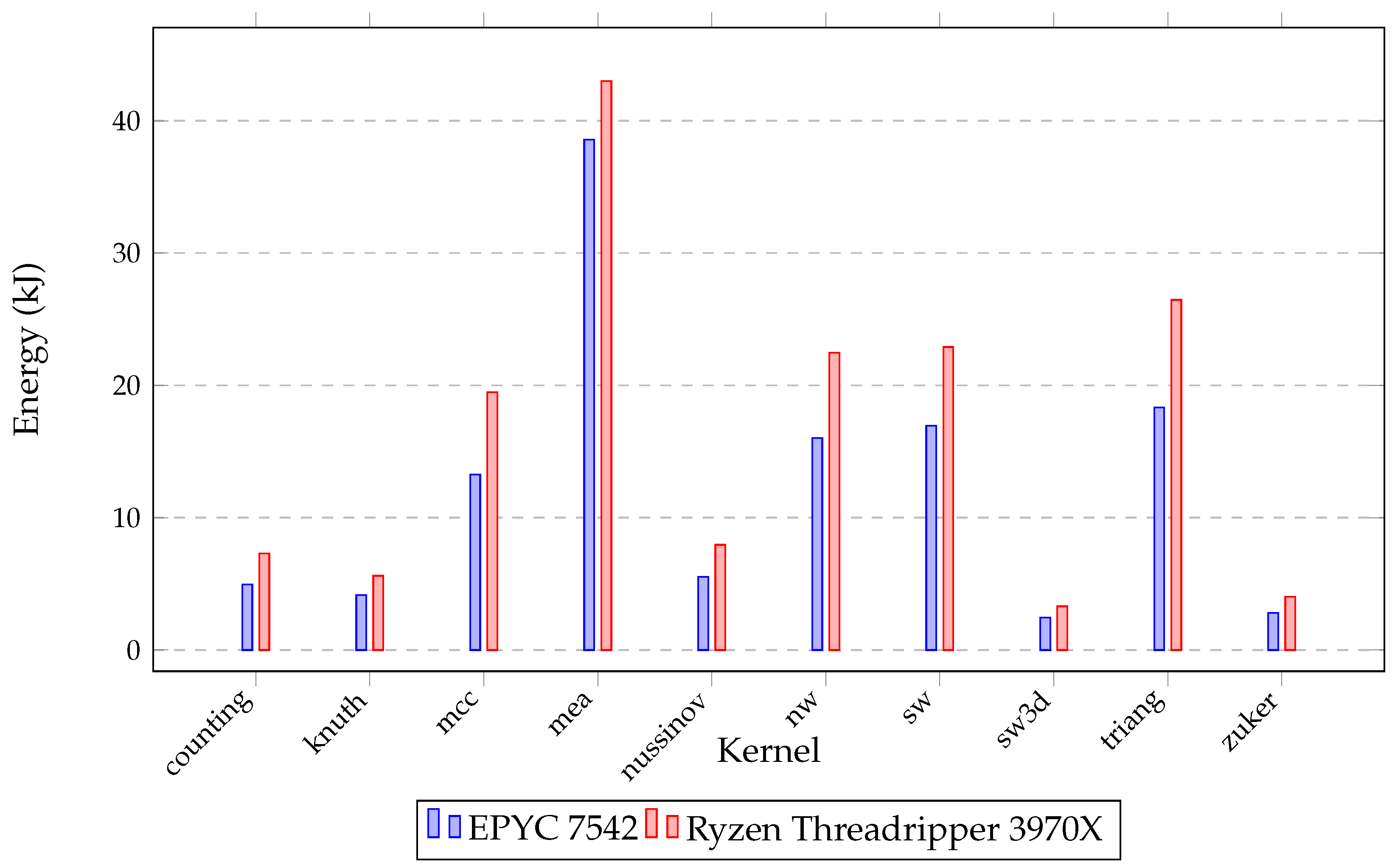
counting	10,000	63,781	6212	5942	4946
knuth	10,000	41,317	4238	4873	4153
mcc	10,000	127,733	49,207	19,089	13,265
mea	2500	343,617	42,311	57,750	38,564
nussinov	10,000	184,569	24,189	8854	5519
nw	10,000	220,543	20,236	16,023	19,995
sw	10,000	215,963	20,541	16,960	20,349
sw3d	500	15,253	2478	2577	2450
triang	10,000	175,934	20,889	27,236	18,321
zuker	2000	20,124	3244	5394	2796

provides a detailed analysis of the energy advantages, measured in joules, when contrasting the original code with the generated counterparts. Notably, the codes generated using the DAPT compiler exhibit the shortest length and consume the least amount of energy. For similar codes in the nw and sw benchmarks, the tiled code with the tile correction strategy (Traco) delivers the best performance. Conversely, employing the technique based on affine transformations (Pluto) resulted in inferior performance or yielded results comparable to other benchmarks (mea, sw3d, zuker). This issue can be attributed to the challenge of tiling all loop nests effectively or the absence of parallelism in the mcc benchmark.

Table 4. Execution times for the original and optimized codes in seconds for the AMD EPYC 7H12.

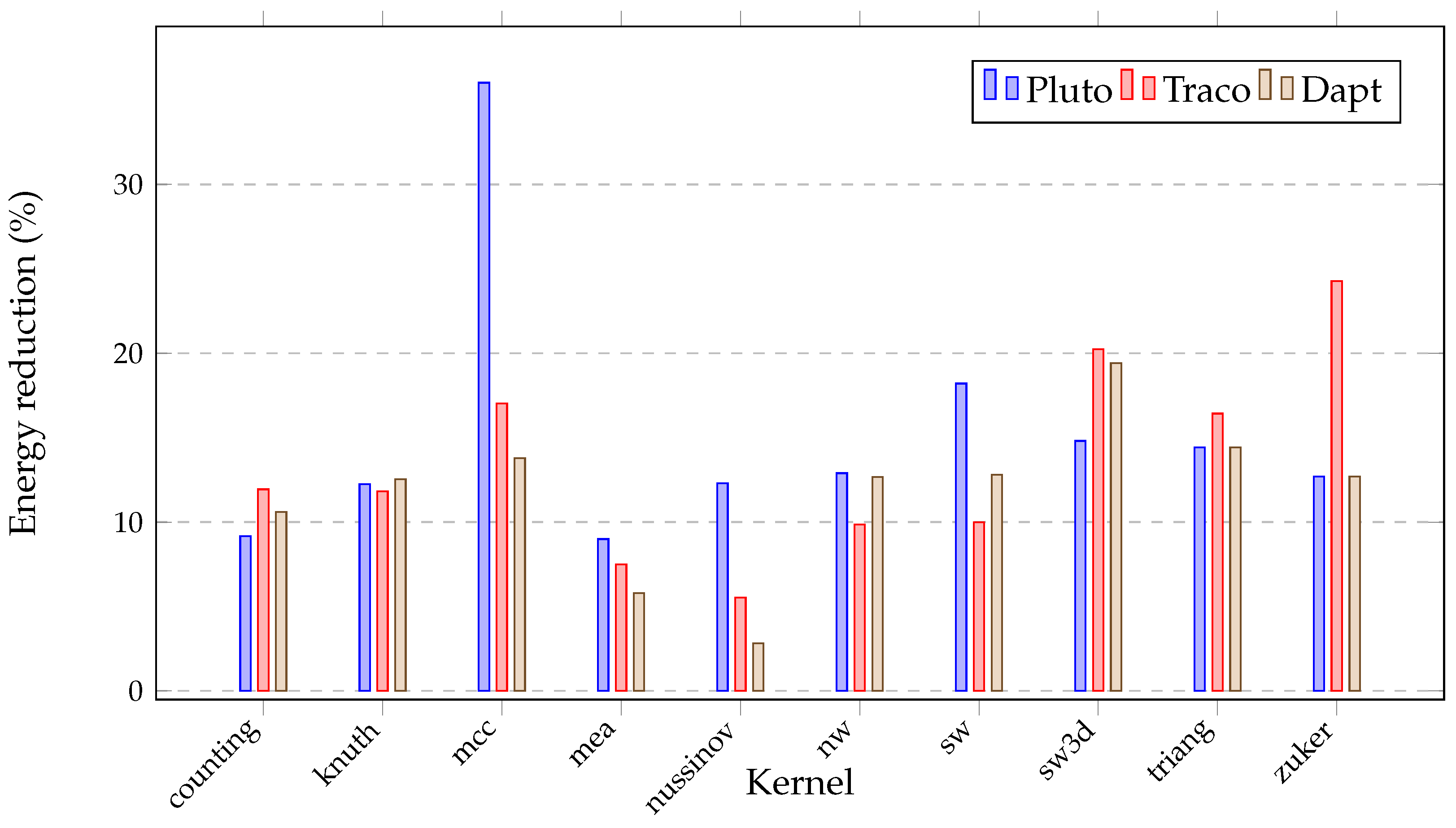
Benchmark	Size	Original	Pluto	Traco	Dapt
counting	10,000	1531.82	23.62	27.26	19.01
knuth	10,000	1939.06	25.3	25.42	17.11
mcc	10,000	3274.18	1033.98	194.6	51.84
mea	2500	4578.58	156.56	102.52	117.02
nussinov	10,000	5583.45	217.04	106.7	36.94
nw	10,000	5643.59	209.38	59.13	116.58
sw	10,000	5726.92	103.55	61.3	92.54
sw3d	500	363.64	41.05	37.18	54.92
triang	10,000	4207.33	212.6	148.7	121.37
zuker	2000	628.89	32.93	55.59	12.59

presents the time execution of optimized codes in seconds for the AMD EPYC 7H12 and 128 hardware threads. We observed that the Dapt compiler is able to generate the fastest code for six benchmarks. In the other cases, the tile correction strategy gives us the best times. Times for the Pluto code executions are much worse for five kernels (mcc, mea, nussinov, nw, triang). Speed-ups are depicted in Figure 2.

We analyzed the AMD EPYC 7H12 scalability due to the number of threads for the four chosen benchmarks (depicted in Figure 3). The DAPT codes are scalable; however, for the sw kernel, better results are achieved with the Traco compiler. A growing number of threads does not reduce the time for the TRACO codes of the Nussinov and Zuker benchmarks. This is caused by the irregular shapes of tiles. The times for the Pluto code executions are inferior to the rest of the results, particularly for 2d-tiled nussinov [41].

For the AMD Ryzen Threadripper 3970, we evaluated both time and energy performance. The numbers of instructions and cache misses were also considered to examine the locality of the optimized codes, as shown in

Table 5. Experimental study of time, energy, and locality for NPDP kernels on Threadripper 3970X.

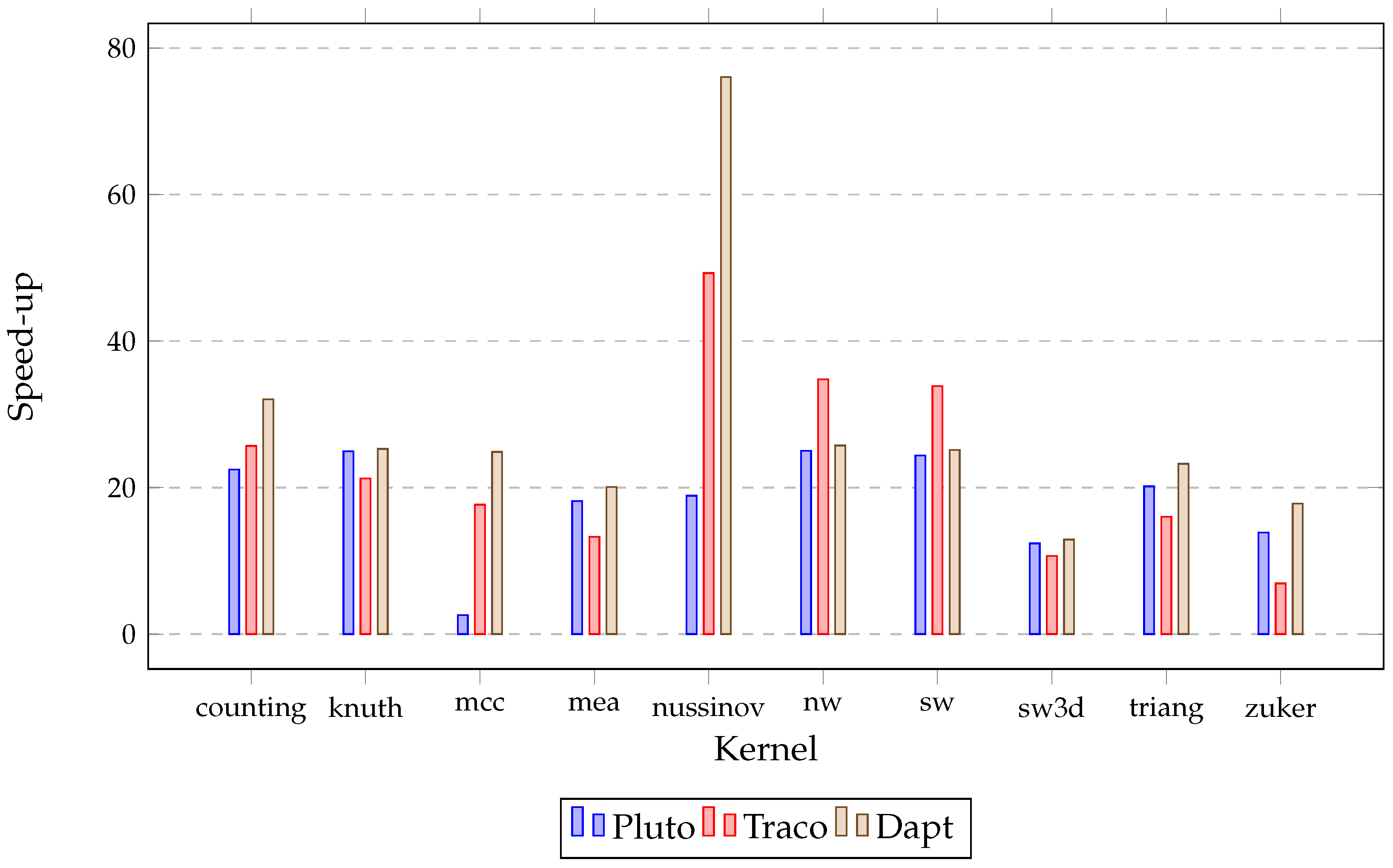
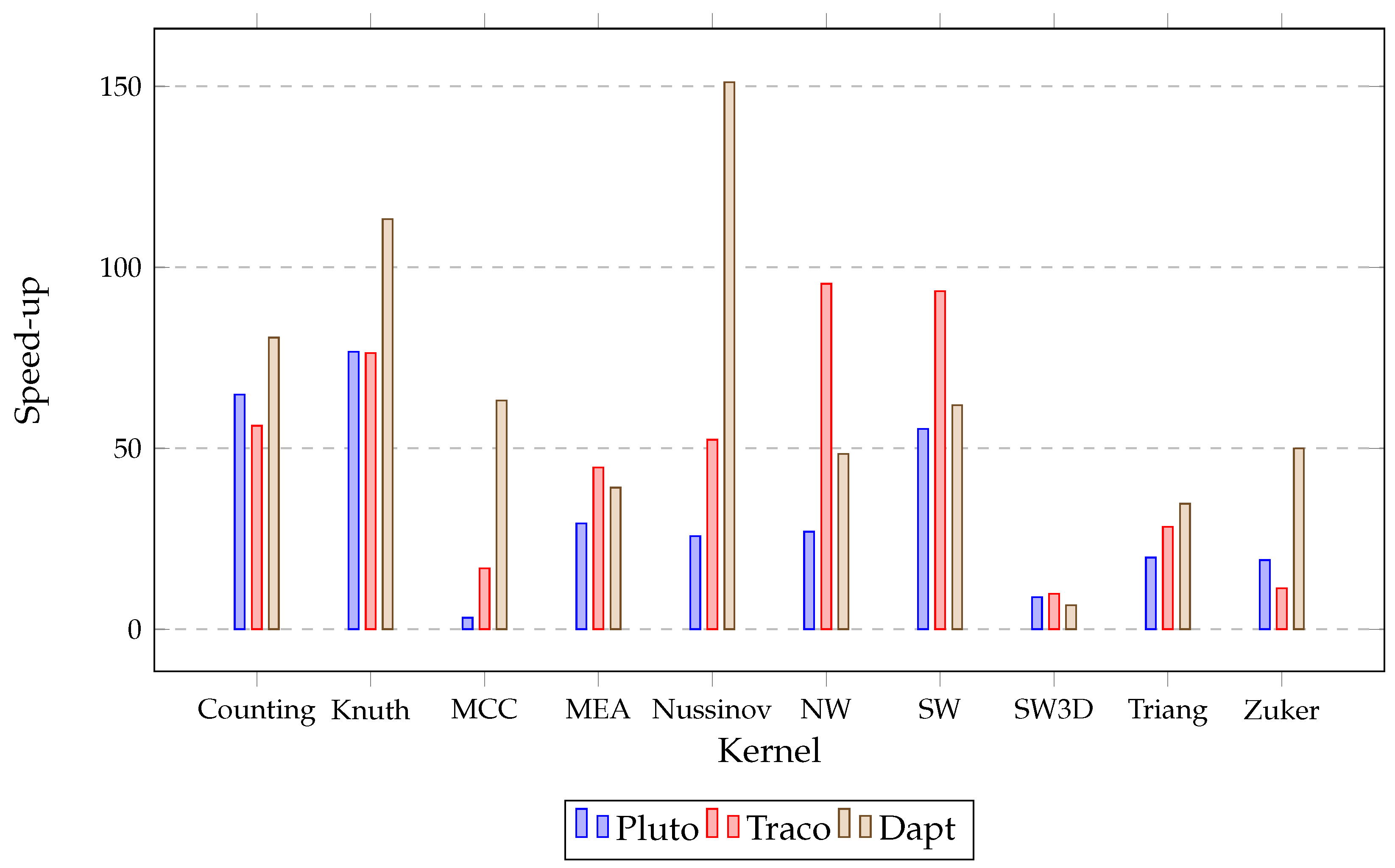
Benchmark	Compiler	Serial Time (s)	Time (s)	Speed-Up	Energy (kJ)	Instr. per Cycle	Cache Misses (%)
	Pluto		30.68	32.71	6.31	0.76	35.94
counting	Traco	1003.51	34.93	28.73	8.22	0.72	22.51
	Dapt		28.77	34.88	7.30	0.77	22.37
	Pluto		25.94	25.26	5.54	0.29	25.68
knuth	Traco	655.36	25.07	26.14	5.35	0.26	21.81
	Dapt		25.48	25.72	5.68	0.29	25.15
	Pluto		755.70	2.66	50.93	1.86	49.68
mcc	Traco	2007.32	110.66	18.14	24.08	0.27	47.63
	Dapt		76.89	26.11	19.49	0.35	34.12
	Pluto		151.87	22.56	36.83	3.17	17.86
mea	Traco	3426.01	148.96	23.00	65.66	3.11	15.23
	Dapt		130.53	26.25	52.99	2.98	14.02
	Pluto		215.39	20.05	47.58	0.05	54.43
nussinov	Traco	4319.22	81.38	53.07	15.61	0.19	19.98
	Dapt		41.51	104.05	7.94	0.57	7.22
	Pluto		142.39	24.22	28.03	0.44	33.94
nw	Traco	3448.38	99.77	34.56	22.47	0.39	30.85
	Dapt		144.45	23.87	28.91	0.37	33.64
	Pluto		152.33	22.72	29.55	0.37	31.73
sw	Traco	3461.01	100.52	34.43	22.90	0.39	31.54
	Dapt		146.33	23.65	29.34	0.37	34.57
	Pluto		17.66	13.93	3.09	1.91	4.54
sw3d	Traco	245.98	22.22	11.07	3.43	1.57	5.42
	Dapt		17.51	14.05	3.29	1.71	4.41
	Pluto		132.28	20.40	27.37	0.96	22.58
triang	Traco	2698.32	140.29	19.23	30.35	0.68	38.45
	Dapt		122.93	21.95	26.64	0.91	22.55
	Pluto		22.69	20.07	4.56	1.91	8.47
zuker	Traco	455.37	49.08	9.28	7.66	1.71	7.17
	Dapt		15.91	28.62	4.01	1.71	8.21

. These metrics were also gauged using RAPL events.

Remarkable DAPT results are evident for the Nussinov kernel, which reduces the RAM memory calls to 7.22% compared to the Traco compiler’s 19.98% and the Pluto optimizer’s 54.43%. It also increases the number of instructions per cycle to 0.57 in contrast to Traco’s 0.19 and Pluto’s 0.05. In a manner similar to the AMD 7542, the Traco compiler enables us to achieve the best execution times for the benchmark suite, with the exception of the nw and sw kernels. These kernels are well-optimized through the tile correction strategy. Figure 4 illustrates energy reduction in percentages, represented as the ratio of energy consumed by the optimized code to the energy used by the original code.

4. Discussion

We selected the AMD EPYC platform for our experimental study due to several reasons. Firstly, the latest release of the Top 500 list underscores AMD’s remarkable achievements in super-computing [42]. The exascale-class Frontier system, powered by AMD, remains the fastest globally—an exceptional feat. AMD’s dominance is clear, as they now occupy four of the top ten positions and a commendable 12 out of the top 20 spots on the list. Secondly, to assess energy efficiency, we utilized the recently introduced AMD RAPL kernel module [40]. The amd_energy module greatly aided our research.

In terms of peak performance, AMD offers two multi-threaded models: the Ryzen Threadripper (and its Pro variant) and the EPYC processor. The EPYC platform excels in scalability/core count, RAM density/channels, energy efficiency, and EEC support. (Error-correcting code (EEC) memory can detect and correct data corruption. It is vital in applications where data integrity is paramount, such as scientific computing or server operations.) The Ryzen Threadripper, marketed as a workstation platform, boasts a higher boost (turbo) frequency—contributing to a significant leap in single-threaded performance—and demonstrates better availability and compatibility.

Table 6. AMD features of EPYC and Ryzen Threadripper.

Features/Machine	EPYC	Ryzen Threadripper
Target:	Server/datacenter platform	Efficient workstation platform
Characteristics:	Dual CPU configuration supports - up to 2 TB RAM in 8 channels - doubling number of cores (up to 128) and threads (up to 256)	Single socket supports - up to 256 GB RAM in 4 channels - 64 total processing cores (and 128 threads)
Frequency:	Boost/Turbo around 3.2 GHz,	Boost speed of 4.3–4.5 GH
Software:	Machine learning; scientific simulations like CFD	VFX, video, and rendering; CAD; media and entertainment
Strong points:	Higher core count, scalability, better efficiency/performance per watt, easier cooling	Availability, more compatible motherboards, Windows 11 support with drivers, lower price
EEC support:	Yes	Only PRO version

details the characteristics of both the AMD EPYC and Ryzen Threadripper platforms. When comparing time results for kernels on each machine, the Ryzen Threadripper 3970X is observed to surpass the EPYC 7542 using the same number of threads (64). The most significant time reduction for kernels is achieved using the EPYC 7H12 with 128 threads, indicating the scalability of the generated codes, as shown in Figure 5. In a comparison of energy consumption for NPDP kernel execution, the Threadripper demands more watts during parallel code execution, as seen in Figure 6. This increased consumption can be attributed to the Threadripper’s superior base and turbo clock speeds.

The NPDP benchmark suite kernels offer a useful approach for comparing various types of parallel machines. In this paper, we aim to present a technical report comparing compilers, pinpointing which one most effectively improves performance for the NPDP benchmark suite. Our analysis encompasses metrics such as execution times, speed-ups, energy efficiency, locality (represented by cache misses), and scalability; all are evaluated using the RAPL methodology. Exceptional results were recorded for the Nussinov kernel, where superlinear speed-up was observed due to the time–space tiling strategy. The Dapt compiler also showcased excellent performance for the counting, mcc, and triang benchmarks.

Overall, the most favorable results stemmed from the Dapt compiler, which registered the shortest execution times in 6 out of 10 benchmarks for the 7H12, 8 out of 10 for the 7542, and 7 out of 10 for the ThreadRipper 3970X. Dapt-compiled codes are scalable, energy-efficient, and cache-friendly and achieve superlinear speed-ups; this is particularly evident in the nussinov benchmark.

The TRACO compiler’s limitation lies in its handling of the transitive closure relation within the dependency relations graph. This can impact the irregular tiling shapes. However, tile correction proves advantageous when the majority of tiles retain their rectangular form. For instance, our research observed optimal time results for the nw and sw benchmarks across all three tested machines.

Conversely, codes compiled using the Pluto compiler occasionally underperform, especially when the generated codes are either non-parallel (mcc) or when most of the nested loops remain untiled (nussinov, nw, sw). Yet the ATF strategy is adept at handling benchmarks with intricate structures featuring quadruple-nested loop nests (mea, sw3d, zuker), primarily because it aims to uphold load-balanced and uniform tile shapes.

In summation, the polyhedral model remains the sole identified method for automatic optimization aimed at bolstering performance for the discussed NPDP tasks. The findings from Dapt emphasize that innovative strategies can still surpass established state-of-the-art approaches for NPDP kernels. Future research should extend to diverse parallel machines, with design motivations ranging from scalability and core count to boost clock rates and sustainable computing.

5. Conclusions

The discussed research in this paper contributes to advancing the field, particularly in bioinformatics tasks like RNA folding, where optimized code execution plays a pivotal role in achieving efficient computational solutions. The Dapt compiler integrates the time–space strategy with the dependence uniformization method, producing notably efficient code for NPDP tasks. Our evaluations highlighted superior efficiency concerning execution time, cache utilization, and energy consumption. Moreover, these codes exhibit scalability in relation to both problem dimensions and thread count. A distinctive merit of this technique is its independence from the need to solve affine functions or to compute the transitive closure of the dependence graph. The research findings are based on assessments conducted on three distinct AMD machines and consider a range of parallel code quality metrics.

Looking ahead, our intent is to scrutinize compilers for problems outside the NPDP scope, with a focus on traditional benchmark implementations, giving special emphasis to the time–space paradigm. We are also keen on verifying our experimental outcomes using upcoming generations of both AMD Zen and Intel processors. Furthermore, our curiosity extends to understanding the efficacy of these codes in a cluster computing environment, specifically within distributed memory architectures and the message-passing model.