A Novel NLMS Algorithm for System Identification
Abstract
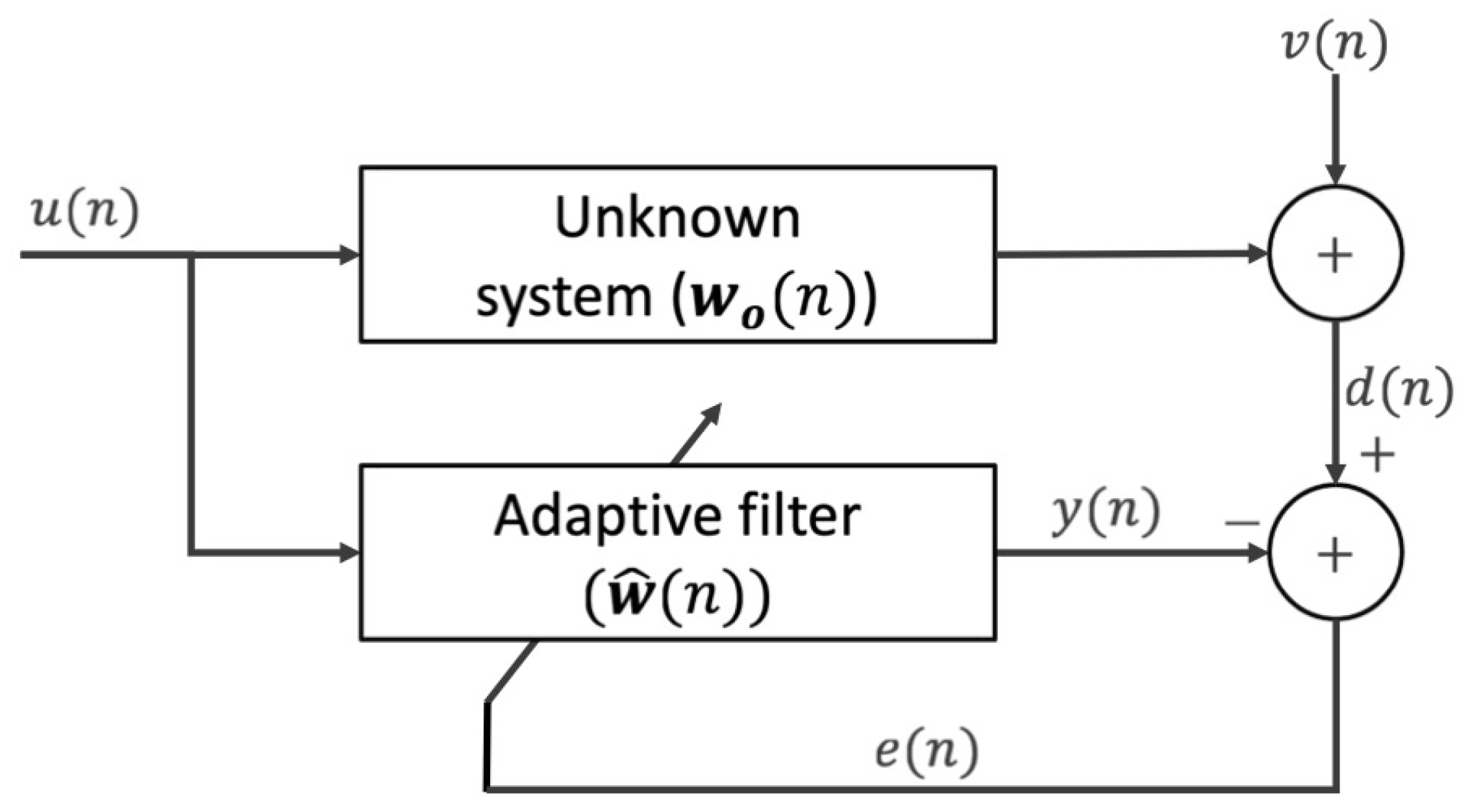
1. Introduction
2. Review of the Conventional NLMS Algorithm
3. MSD Analysis of the NLMS Algorithm Using the Random Walk Model
4. Proposed NLMS Algorithm
4.1. Steady-State Value of the Proposed NLMS Algorithms
4.2. Practical Consideration
| Algorithm 1 Proposesd NLMS algorithm summary. |
| Initialization: |
| Parameters: |
| , known or estimated |
| , (for white inputs) or (for colored inputs) |
| For each index n: |
5. Simulation Results
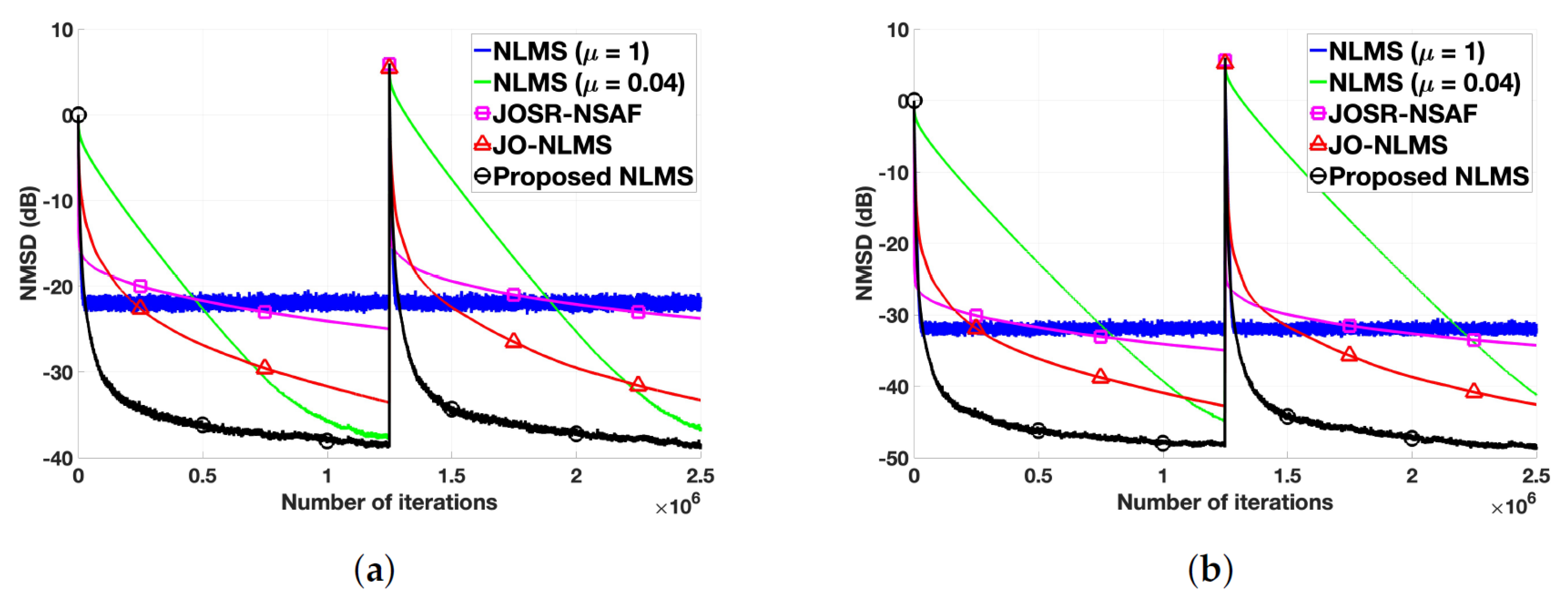
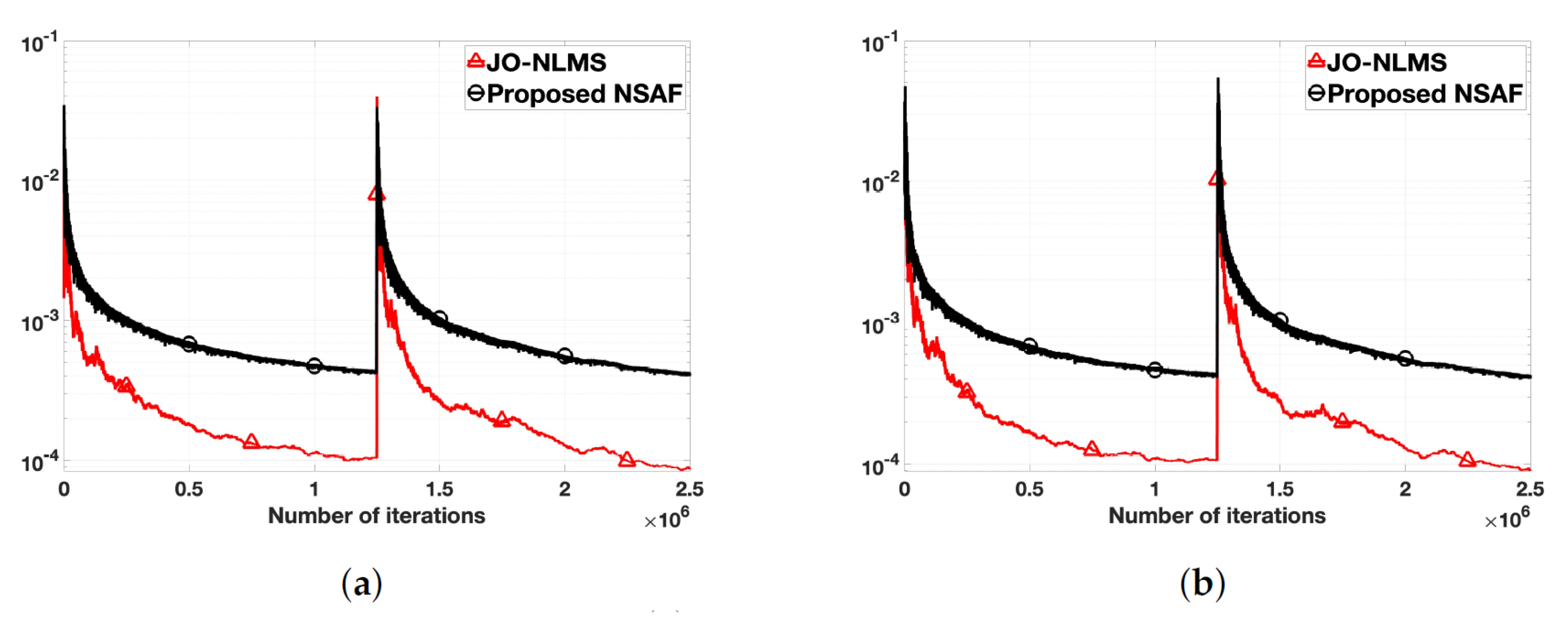
5.1. Performance Comparison with White and Colored Input Signals
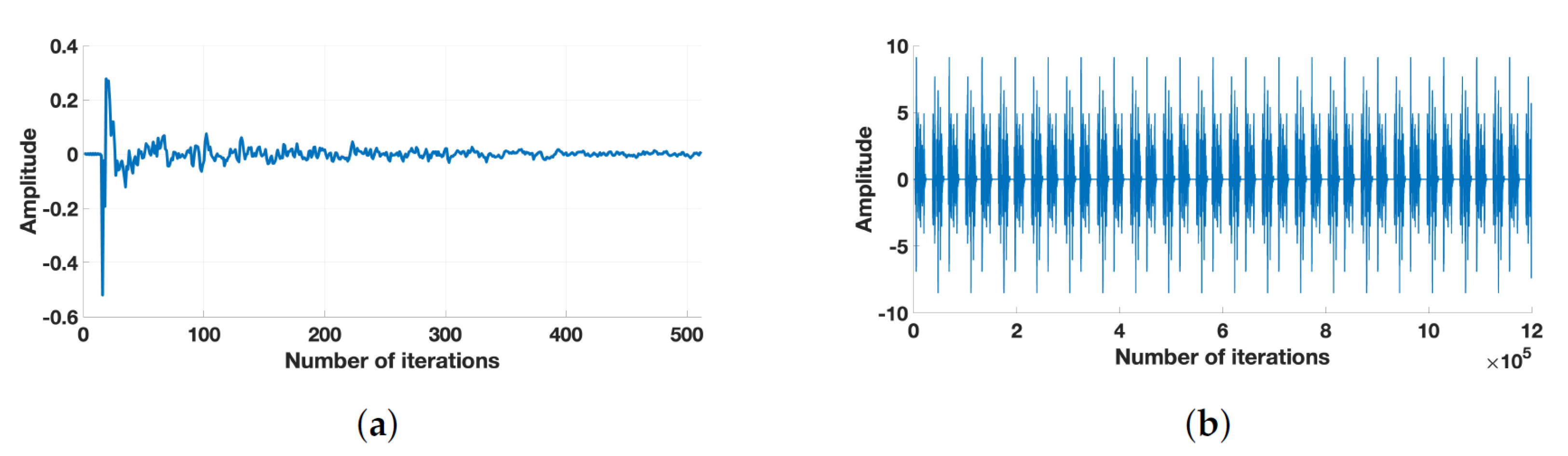
5.2. Performance Comparison with Speech Input Signals
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, G.; Zhang, P.; Ma, G.; Xiao, W. System identification of the nonlinear residual errors of an industrial robot using massive measurements. Robot. Comput.-Integr. Manuf. 2019, 59, 104–114. [Google Scholar] [CrossRef]
- Akanyeti, O.; Nehmzow, U.; Billings, S.A. Robot training using system identification. Robot. Auton. Syst. 2008, 56, 1027–1041. [Google Scholar] [CrossRef]
- Bähnemann, R.; Burri, M.; Galceran, E.; Siegwart, R.; Nieto, J. Sampling-based motion planning for active multirotor system identification. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3931–3938. [Google Scholar]
- Worley, R.; Yu, Y.; Anderson, S. Acoustic echo-localization for pipe inspection robots. In Proceedings of the 2020 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Karlsruhe, Germany, 14–16 September 2020; pp. 160–165. [Google Scholar]
- Haykin, S. Adaptive Filter Theory, 4th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley: New York, NJ, USA, 2003. [Google Scholar]
- Paleologu, C.; Ciochina, S.; Benesty, J. Variable step-size NLMS algorithm for under-modeling acoustic echo cancellation. IEEE Signal Process. Lett. 2008, 15, 5–8. [Google Scholar] [CrossRef]
- Huang, H.C.; Lee, J. A new variable step-size NLMS algorithm and its performance analysis. IEEE Trans. Signal Process. 2011, 60, 2055–2060. [Google Scholar] [CrossRef]
- Benesty, J.; Rey, H.; Vega, L.R.; Tressens, S. A nonparametric vss nlms algorithm. IEEE Signal Process. Lett. 2006, 13, 581–584. [Google Scholar] [CrossRef]
- Song, I.; Park, P. A normalized least-mean-square algorithm based on variable-step-size recursion with innovative input data. IEEE Signal Process. Lett. 2012, 19, 817–820. [Google Scholar] [CrossRef]
- Lee, M.; Park, T.; Park, P. Variable Step-Size ℓ0-Norm Constraint NLMS Algorithms Based on Novel Mean Square Deviation Analyses. IEEE Trans. Signal Process. 2022, 70, 5926–5939. [Google Scholar] [CrossRef]
- Park, P.; Chang, M.; Kong, N. Scheduled-stepsize NLMS algorithm. IEEE Signal Process. Lett. 2009, 16, 1055–1058. [Google Scholar] [CrossRef]
- Rey, H.; Vega, L.R.; Tressens, S.; Benesty, J. Variable explicit regularization in affine projection algorithm: Robustness issues and optimal choice. IEEE Trans. Signal Process. 2007, 55, 2096–2109. [Google Scholar] [CrossRef]
- Choi, Y.S.; Shin, H.C.; Song, W.J. Robust regularization for normalized LMS algorithms. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 627–631. [Google Scholar] [CrossRef]
- Ciochină, S.; Paleologu, C.; Benesty, J. An optimized NLMS algorithm for system identification. Signal Process. 2016, 118, 115–121. [Google Scholar] [CrossRef]
- Lee, C.H.; Park, P. Scheduled-step-size affine projection algorithm. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2034–2043. [Google Scholar] [CrossRef]
- Shin, J.; Park, B.Y.; Lee, W.I.; Yoo, J.; Cho, J. A novel normalized subband adaptive filter algorithm based on the joint-optimization scheme. IEEE Access 2022, 10, 9868–9876. [Google Scholar] [CrossRef]
- Park, P.; Lee, C.H.; Ko, J.W. Mean-square deviation analysis of affine projection algorithm. IEEE Trans. Signal Process. 2011, 59, 5789–5799. [Google Scholar] [CrossRef]
- Shin, J.; Yoo, J.; Park, P. Adaptive regularisation for normalised subband adaptive filter: Mean-square performance analysis approach. IET Signal Process. 2018, 12, 1146–1153. [Google Scholar] [CrossRef]
- Yin, W.; Mehr, A.S. Stochastic analysis of the normalized subband adaptive filter algorithm. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 58, 1020–1033. [Google Scholar] [CrossRef]
- Slock, D.T. On the convergence behavior of the LMS and the normalized LMS algorithms. IEEE Trans. Signal Process. 1993, 41, 2811–2825. [Google Scholar] [CrossRef]
- Sankaran, S.G.; Beex, A.L. Convergence behavior of affine projection algorithms. IEEE Trans. Signal Process. 2000, 48, 1086–1096. [Google Scholar] [CrossRef]
- Zhi, Y.; Yang, Y.; Zheng, X.; Zhang, J.; Wang, Z. Statistical tracking behavior of affine projection algorithm for unity step size. Appl. Math. Comput. 2016, 283, 22–28. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, H. A joint-optimization NSAF algorithm based on the first-order Markov model. Signal Image Video Process. 2017, 11, 509–516. [Google Scholar] [CrossRef]
- Ni, J.; Li, F. A variable step-size matrix normalized subband adaptive filter. IEEE Trans. Audio Speech Lang. Process. 2009, 18, 1290–1299. [Google Scholar]
- Iqbal, M.A.; Grant, S.L. Novel variable step size NLMS algorithms for echo cancellation. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 241–244. [Google Scholar]



| Algorithm | Multiplications | Divisions |
|---|---|---|
| JO-NLMS | 3 | |
| JOSR-NSAF | 2 | |
| Proposed NLMS algorithm | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, J.; Park, B.Y.; Lee, W.I.; Shin, J. A Novel NLMS Algorithm for System Identification. Electronics 2023, 12, 3159. https://doi.org/10.3390/electronics12143159
Yoo J, Park BY, Lee WI, Shin J. A Novel NLMS Algorithm for System Identification. Electronics. 2023; 12(14):3159. https://doi.org/10.3390/electronics12143159
Chicago/Turabian StyleYoo, Jinwoo, Bum Yong Park, Won Il Lee, and JaeWook Shin. 2023. "A Novel NLMS Algorithm for System Identification" Electronics 12, no. 14: 3159. https://doi.org/10.3390/electronics12143159
APA StyleYoo, J., Park, B. Y., Lee, W. I., & Shin, J. (2023). A Novel NLMS Algorithm for System Identification. Electronics, 12(14), 3159. https://doi.org/10.3390/electronics12143159







