RAdam-DA-NLSTM: A Nested LSTM-Based Time Series Prediction Method for Human–Computer Intelligent Systems

Abstract

At present, time series prediction methods are widely applied for Human–Computer Intelligent Systems in various fields such as Finance, Meteorology, and Medicine. To enhance the accuracy and stability of the prediction model, this paper proposes a time series prediction method called RAdam-Dual stage Attention mechanism-Nested Long Short-Term Memory (RAdam-DA-NLSTM). First, we design a Nested LSTM (NLSTM), which adopts a new internal LSTM unit structure as the memory cell of LSTM to guide memory forgetting and memory selection. Then, we design a self-encoder network based on the Dual stage Attention mechanism (DA-NLSTM), which uses the NLSTM encoder based on the input attention mechanism, and uses the NLSTM decoder based on the time attention mechanism. Additionally, we adopt the RAdam optimizer to solve the objective function, which dynamically selects Adam and SGD optimizers according to the variance dispersion and constructs the rectifier term to fully express the adaptive momentum. Finally, we use multiple datasets, such as PM2.5 data set, stock data set, traffic data set, and biological signals, to analyze and test this method, and the experimental results show that RAdam-DA-NLSTM has higher prediction accuracy and stability compared with other traditional methods.

1. Introduction

As a crucial component of the data-driven economy, the vast amount of data generated by Human–Computer Intelligent Systems is playing a critical role in the current social and economic landscape [1,2]. Most of them belong to time series. Therefore, the time series prediction method is a research hotspot in Human–Computer Intelligent Systems.

At present, the application of time series prediction methods led by RNNs (Recurrent Neural Networks) is extremely extensive in the fields of Finance [3,4], Meteorology [5,6], Medicine [7], etc. RNNs have a certain memory ability by introducing local or global feedback connections into the forward structure. However, the gradient disappearance and gradient explosion of an RNN will make its prediction accuracy low in practical applications [8]. On the contrary, LSTM (Long Short-Term Memory) [9] uses memory units to replace hidden layer neurons, which can deal with problems related to time series more effectively. When there are enough training samples, LSTM can fully mine the information contained in massive data and has the ability of deep learning [10,11]. Therefore, some scholars began to study LSTM to solve the problems of RNNs. Karevan et al. [12] established a data-driven forecast model based on LSTM to predict the weather. Xie et al. [13] used LSTM to predict blood glucose levels in patients with type 1 diabetes. Pathan et al. [14] used a prediction model based on LSTM to predict the future mutation rate of the COVID-19 virus.

In recent years, scholars have focused on exploring more possibilities of LSTM and making it more effective in processing high-dimensional complex big data, and began to study its optimization methods, especially feature aggregation, network structure improvement, and objective function optimization.

In feature aggregation, some scholars study autoencoder networks, which are widely popular for their successful application in the direction of machine translation [15,16,17]. Its core idea is to transform the input sequence into a fixed-length vector through encoding, and then transform the previously generated fixed vector into the output sequence through decoding. However, the performance of the autoencoder network deteriorates rapidly with the increase in input sequence length [18,19]. Therefore, inspired by human attention theory, some scholars studied the automatic coding network based on the attention mechanism, which can adaptively select the input (or feature) subset to improve its ability to analyze long sequences. Hra [20] proposed a momentum LSTM autoencoder network based on an attention mechanism to realize behavior recognition, which has better simulation results than traditional methods. Baddar [21] proposed an LSTM autoencoder network with attention mode variation to realize face recognition, which improved the accuracy of face recognition. Pandey [22] adopted LSTM as an encoder to achieve machine translation, which improved the effectiveness of machine translation. However, the autoencoder network based on the attention mechanism has only been proven effective in machine translation, face recognition, and image processing, and there are few studies on time series prediction [23,24,25].

In network structure improvement, Cho et al. [26] proposed the Gated Recurrent Unit (GRU), which has simplified the LSTM structure while ensuring the original classification results. Inspired by LSTM and GRU, Sun et al. [27] proposed the Gated Memory Unit (GMU) and evaluated it from the aspects of parameter volume, convergence, and accuracy. The results showed that GMU is a potential choice for handwriting recognition tasks. Lei et al. [28] proposed the Simple Recurrent Unit (SRU), which improved the training speed of the LSTM for recognition tasks. The above models ignore their performance to improve the model training speed and simplify the network structure. However, the nonlinear mapping ability of the model is particularly important in time series prediction. Scholars often take stacked network structure [29,30] to improve the model’s ability, but the model training speed is often not ideal. How to improve the network structure of LSTM to improve its nonlinear mapping ability and ensure the training speed is the focus of scholars.

In objective function optimization, common optimizers include the Stochastic Gradient Descent (SGD) optimizer, Adaptive Gradient (Adagrad) optimizer, Root Mean Square Prop (RMSProp) optimizer, Adaptive Moment Estimation (Adam) optimizer, etc. [31,32,33]. The convergence effect of the SGD optimizer is excellent, but the convergence speed is not ideal. The Adagrad optimizer relies on global learning rates and tends to become stuck at local extremum points when training time is too long. The RMSProp optimizer adaptively adjusts the magnitude of the gradient in each direction but is prone to gradient explosions. The Adam optimizer combines the advantages of AdaGrad and RMSProp and can calculate the updated step size by considering the first and second-moment estimation of the gradient, and the convergence speed is faster. However, the adaptive learning rate of the Adam optimizer can produce large variance fluctuation and easily fall into the local optimal solution. Therefore, Liu et al. [34] proposed a modified Adam optimizer—Rectified Adam optimizer (RAdam), which can dynamically select Adam and SGD optimizer according to variance dispersion, and construct a rectifier term. The adaptive momentum as a potential variance function is allowed to be fully expressed slowly but steadily, it can enhance the stability of model training. Therefore, RAdam has the advantages of both Adam and SGD, which can ensure fast convergence speed and it is difficult to fall into the local optimal solution.

In this paper, we propose a novel time series prediction method called RAdam-Dual Stage Attention Mechanism-Nested Long Short-Term Memory (RAdam-DA-NLSTM) through the exploration and research of the above-related work. Our approach involves several key contributions as follows:

• We introduce Nested LSTM (NLSTM), an internal LSTM unit structure designed to guide memory forgetting and memory selection. By incorporating NLSTM as the memory cell of LSTM, we enhance prediction accuracy.
• We develop an autoencoder network based on the Dual Stage Attention Mechanism (DA-NLSTM). This network utilizes an NLSTM encoder with an input attention mechanism and an NLSTM decoder with a time attention mechanism. This design addresses the attention dispersion issue present in traditional LSTM architectures. It effectively captures long-term time dependencies in time series data and enhances feature aggregation within the network.
• We employ the RAdam optimizer to optimize the objective function. RAdam dynamically selects between the Adam and SGD optimizers based on variance dispersion. Additionally, we introduce a rectifier term to bolster the model’s stability.

In summary, our proposed RAdam-DA-NLSTM method represents an innovative approach to time series prediction. It encompasses advancements in model enhancement, feature aggregation optimization, and objective function optimization. These contributions have significantly contributed to the field of time series forecasting and paved the way for further research and practical applications.

2. RAdam-DA-NLSTM

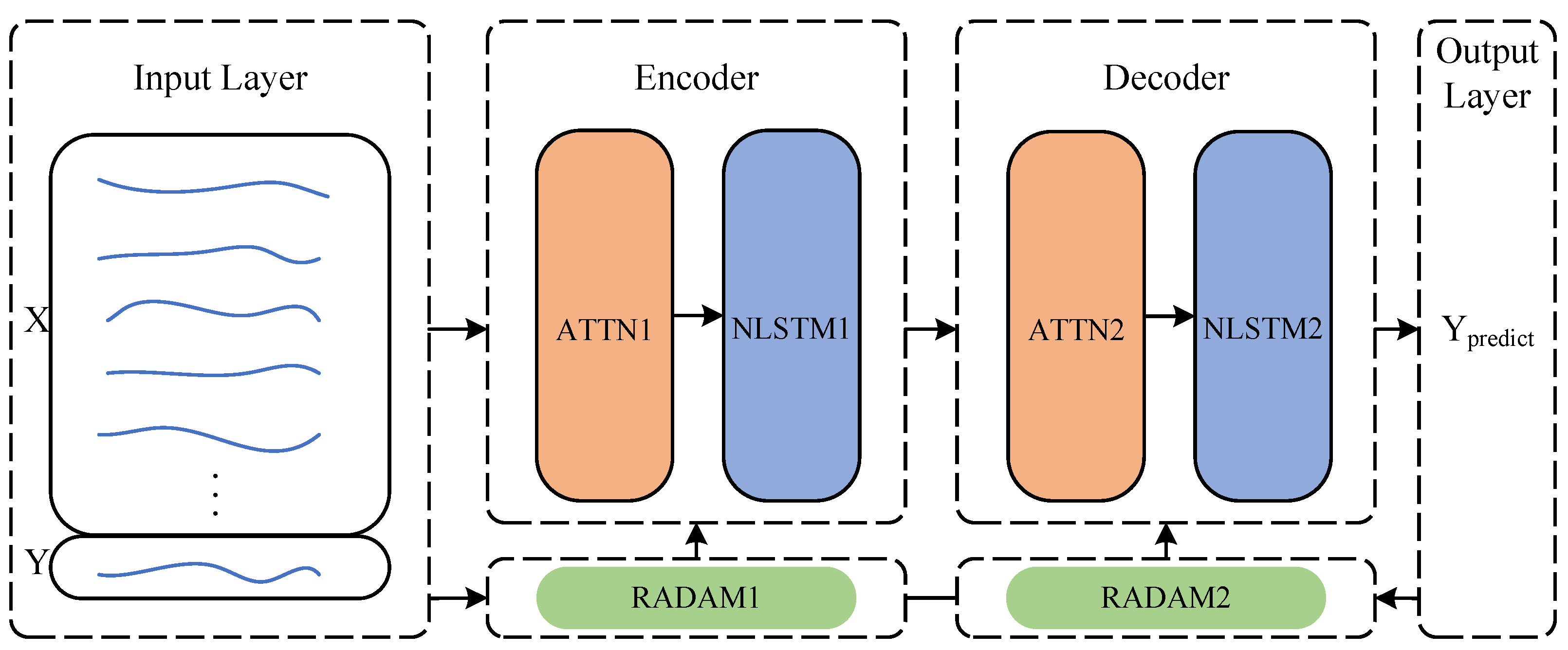
Radam-DA-NLSTM adopts the self-encoder network model structure and has four layers, including the input layer, encoder, decoder, and output layer. It adopts two Nested LSTMs as encoder and decoder, respectively, which use the input attention mechanism to optimize the NLSTM1 encoder and uses the time attention mechanism to optimize the NLSTM2 decoder. And they use the Radam optimizer to update the DA-NLSTM network objective function during encoding and decoding. Figure 1 is the block diagram of the model construction.

Input layer input matrix is $X=\left[\begin{array}{c}{x}_1^1,\dots ,x_t^1,\dots ,x_T^1\hfill \\ ⋮\hfill \\ x_1^n,\dots ,x_t^n,\dots ,x_T^n\hfill \\ ⋮\hfill \\ x_1^N,\dots ,x_t^N,\dots ,x_T^N\hfill \end{array}\right]$ and target sequence is $Y_{}=(y_1^{},\dots ,y_{t-1}^{},\dots ,y_{T-1}^{})$. Through learning the time series prediction model of Radam-DA-NLSTM, obtain a mapping function F to predict the unknown values $y_T^{}$.

$$\widehat{Y}=F(y_1^{},\dots ,y_t^{},\dots ,y_{T-1}^{},X)$$

(1)

where $x_t^n$ denotes the information of n sequences in the t-th time step.

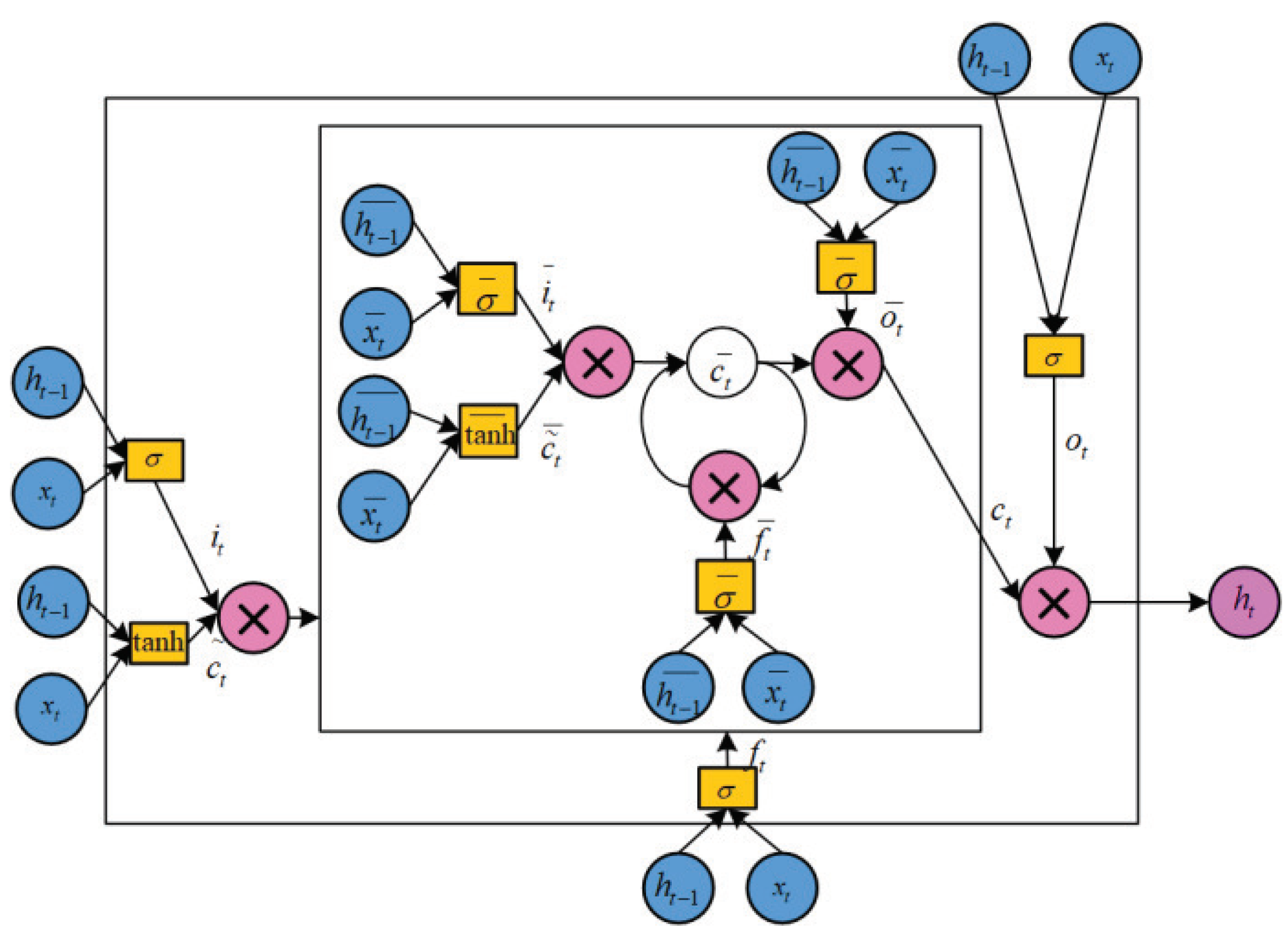
2.1. Nested LSTM

Nested LSTM uses a new internal LSTM structure to replace the memory cells of the traditional LSTM. When accessing the internal memory, it is gated in the same way. Therefore, the Nested LSTM can access the internal memory more pertinently [11], it makes the Nested LSTM prediction model have stronger processing ability and higher prediction accuracy. Figure 2 shows the Nested LSTM unit model structure.

Nested LSTM is divided into internal LSTM and external LSTM. Their gating systems are consistent with the traditional LSTM. Nested LSTM has four gating systems, namely forget gate, input gate, candidate memory cell, and output gate. The calculation formulas for each gate are as follows:

Forget gate:

$$f_t=\sigma (W_{fx}{x}_t+W_{fh}{h}_{t-1}+b_f)$$

(2)

Input gate:

$$i_t=\sigma (W_{ix}{x}_t+W_{ih}{h}_{t-1}+b_i)$$

(3)

Candidate memory cell:

$$\widetilde{c_t}=tanh(W_{cx}{x}_t+W_{ch}{h}_{t-1}+b_c)$$

(4)

Memory cell: The input and hidden states of the internal LSTM are:

$${\overline{h}}_{t-1}=f_t·c_{t-1}$$

(5)

$${\overline{x}}_t=i_t·\widetilde{c_t}$$

(6)

$${\overline{f}}_t=\sigma ({\overline{W}}_{fx}\overline{x_t}+{\overline{W}}_{fh}{\overline{h}}_{t-1}+{\overline{b}}_f)$$

(7)

$${\overline{i}}_t=\sigma ({\overline{W}}_{ix}\overline{x_t}+{\overline{W}}_{ih}{\overline{h}}_{t-1}+{\overline{b}}_i)$$

(8)

$${\tilde{\overline{c}}}_t=tanh({\overline{W}}_{cx}\overline{x_t}+{\overline{W}}_{ch}{\overline{h}}_{t-1}+{\overline{b}}_c)$$

(9)

$${\overline{o}}_t=\sigma ({\overline{W}}_{ox}\overline{x_t}+{\overline{W}}_{oh}{\overline{h}}_{t-1}+{\overline{b}}_o)$$

(10)

$${\overline{c}}_t={\overline{f}}_t·{\overline{c}}_{t-1}+{\overline{i}}_t·{\tilde{\overline{c}}}_t$$

(11)

$${\overline{h}}_t={\overline{o}}_t·tanh\left({\overline{c}}_t\right)$$

(12)

The update method of external LSTM memory cell is:

$$c_t={\overline{h}}_t$$

(13)

Output gate:

$$o_t=\sigma (W_{ox}{x}_t+W_{oh}{h}_{t-1}+b_o)$$

(14)

A new round of hidden state:

$$h_t=o_t·tanh\left(c_t\right)$$

(15)

where $\sigma$ denotes the sigmoid function. In the external LSTM, $W_{fx}$ and $W_{fh}$ denote the weight matrix of the forget gate; $W_{ix}$ and $W_{ih}$ denote the weight matrix of the input gate; $W_{cx}$ and $W_{ch}$ denote the weight matrix of the candidate memory cell; $W_{ox}$ and $W_{oh}$ denote the weight matrix of the output gate; $b_f$, $b_i$, $b_c$ and $b_o$ denote the bias of the forget gate, input gate, candidate memory cell, and output gate, respectively. In the internal LSTM, ${\overline{x}}_t$, ${\overline{h}}_{t-1}$ and ${\overline{c}}_{t-1}$ denote the current input, the hidden state and memory cell of the previous round, respectively. ${\overline{W}}_{fx}$ and ${\overline{W}}_{fh}$ denote the weight matrix of the forget gate; ${\overline{W}}_{ix}$ and ${\overline{W}}_{ih}$ denote the weight matrix of the input gate; ${\overline{W}}_{cx}$ and ${\overline{W}}_{ch}$ denote the weight matrix of the candidate memory cell; ${\overline{W}}_{ox}$ and ${\overline{W}}_{oh}$ denote the weight matrix of the output gate; ${\overline{b}}_f$, ${\overline{b}}_i$, ${\overline{b}}_c$ and ${\overline{b}}_o$ denote the bias of the forget gate, input gate, candidate memory cell, and output gate, respectively; ${\overline{x}}_t$, ${\overline{h}}_{t-1}$ and ${\overline{c}}_{t-1}$ denote the current input, the hidden state and memory cell of the previous round, respectively.

The output of the output layer is:

$$y_t=\sigma \left(W_{yh}{h}_t\right)$$

(16)

where $W_{yh}$ denotes the weight matrix of the output layer.

2.2. DA-NLSTM

DA-NLSTM includes the NLSTM encoder based on the input attention mechanism and the NLSTM decoder based on the time attention mechanism.

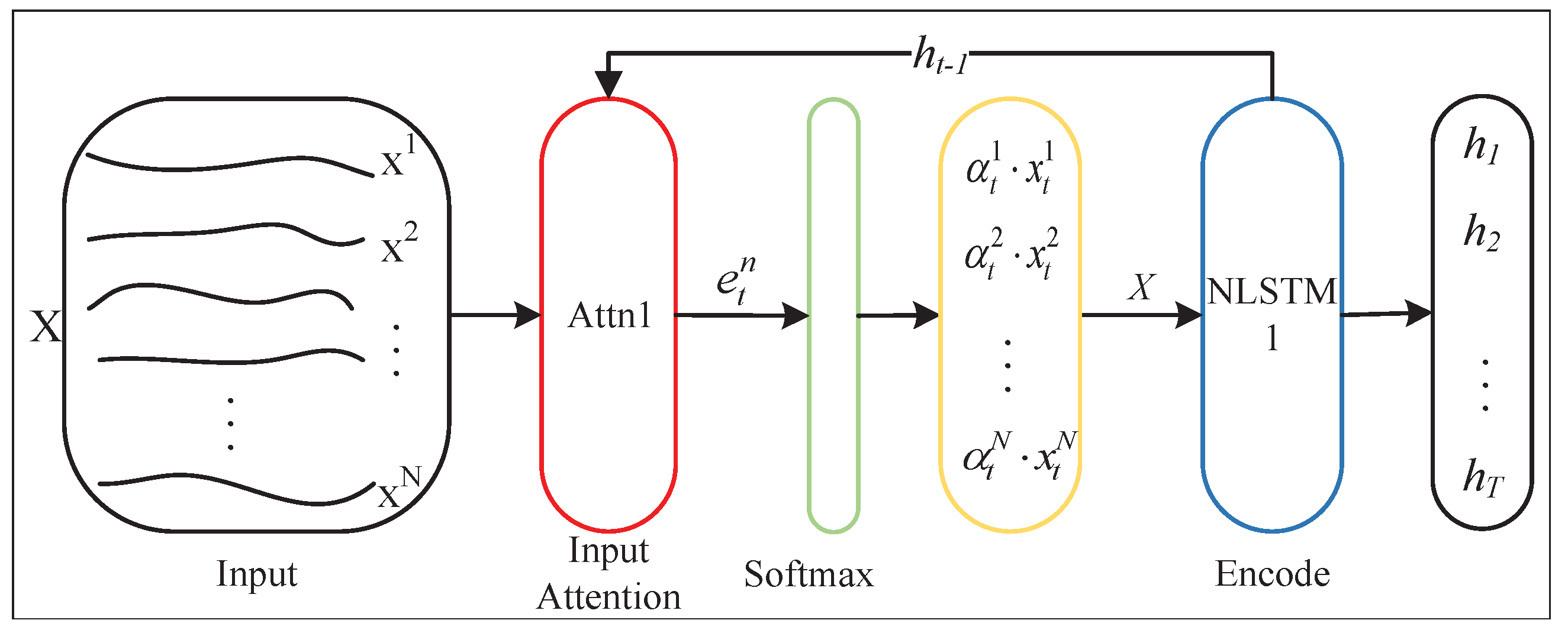
2.2.1. The NLSTM Encoder Based on Input Attention Mechanism

The NLSTM encoder based on the input attention mechanism is composed of the input attention mechanism and NLSTM1. Figure 3 shows its structure.

RAdam-DA-NLSTM uses the input attention on the NLSTM encoder to preprocess X. The query, key, and value corresponding to the input attention are as follows: query is the splicing of the last hidden state $h_{t-1}$ and cell state $c_{t-1}$ of NLSTM1, key is the whole sequence information, value is the same as the key. We can calculate the attention score $e_t^n$ by query and key, and normalize it by softmax to obtain the weight ${\alpha }_t^n$ of each sequence:

$$e_t^n=V_e^{T}tanh(W_e[h_{t-1};s_{t-1}]+U_e{x}^n)$$

(17)

$${\alpha }_t^n=\frac{exp\left(e_t^n\right)}{{\displaystyle \sum _{i=1}^N}exp\left(e_t^i\right)}$$

(18)

where $V_e^T$, $W_e$ and $u_e$ denote the training parameters, $[h_{t-1};s_{t-1}]$ denotes the query of the input attention; $x^n$ denotes the n-th training sequence, i.e., the key of the input attention, tan denotes the function tan. Then, we can obtain the preprocessed data from each sequence weight and sequence information:

$$\tilde{X}=\sum _{n=1}^N{\alpha }_t^n{x}_t^n$$

(19)

Then we input $\tilde{X}$ to NLSTM1, and finally, we can obtain the hidden state of the coding layer corresponding to each time point t:

$$h_t=f_1(h_{t-1},\tilde{X})$$

(20)

where $f_1$ denotes the calculation method of unit NLSTM1.

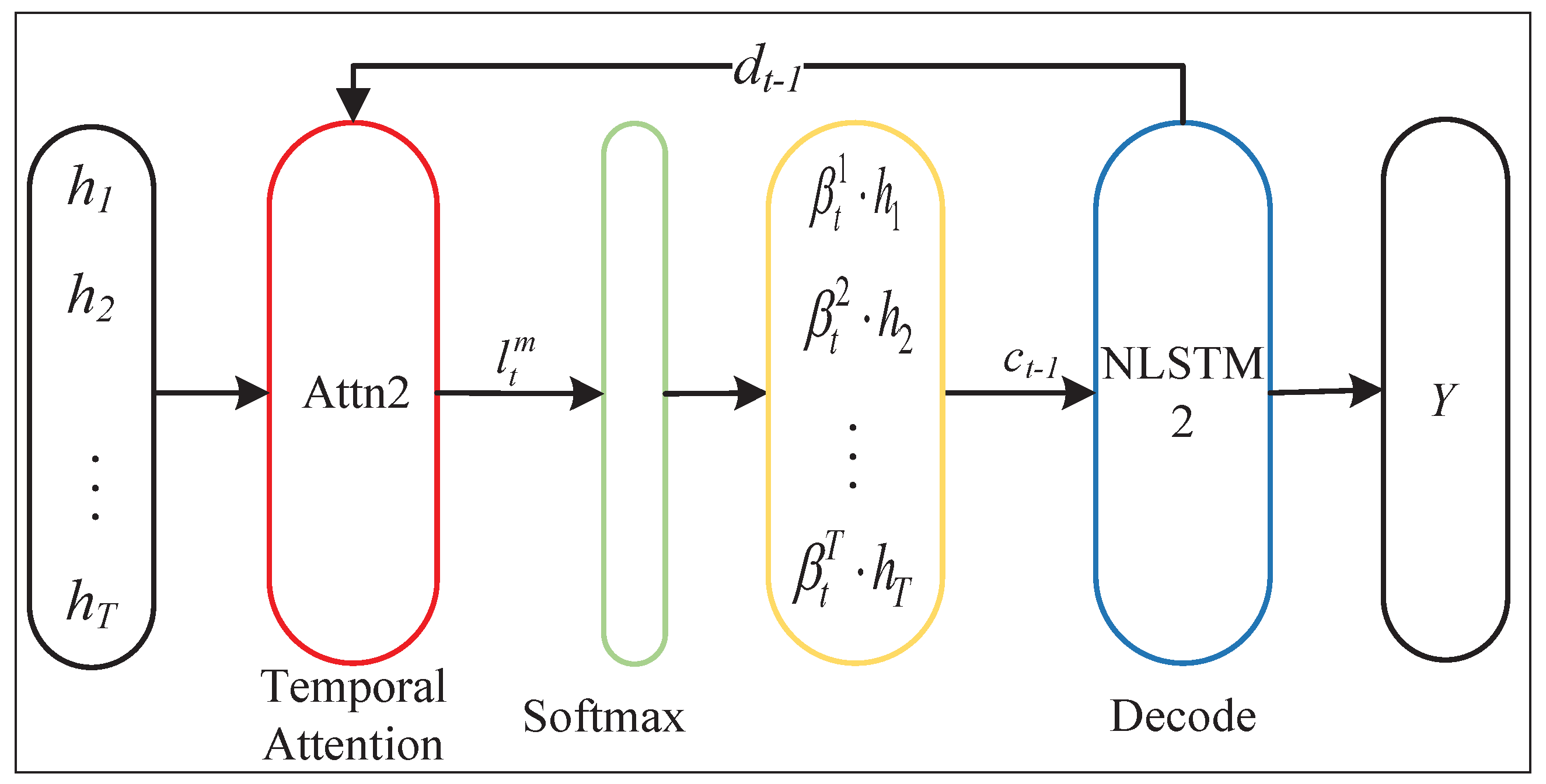
2.2.2. The NLSTM Decoder Based on Time Attention Mechanism

The NLSTM decoder based on the time attention mechanism is composed of the time attention mechanism and NLSTM2. Figure 4 shows its structure.

RAdam-DA-NLSTM uses the time attention on the decoder to preprocess $h_t$. The query, key, and value corresponding to the time attention are as follows: query is the splicing of the last hidden state $h_{t-1}$ and cell state $s{}_{t-1}^{\prime }$ of NLSTM2, the key is the hidden state $h_t$ of NLSTM1 at each time point, and value is the same as the key. We can calculate the attention score $l_t^m$ by query and key, and normalize the attention score by softmax to obtain the weight ${\beta }_t^m$ of the hidden state corresponding to each time point.

$$l_t^m=V_d^{T}tanh(W_d[d_{t-1};s{}_{t-1}^{\prime }]+U_d{h}_m),1\le m\le T$$

(21)

$${\beta }_t^m=\frac{exp\left(l_t^m\right)}{{\displaystyle \sum _{j=1}^T}exp\left(l_t^j\right)}$$

(22)

where $V_d^T$, $W_d$, $U_d$ denote the training parameters, $[d_{t-1};s{}_{t-1}^{\prime }]$ denotes the query of the time attention, $h_m$ denotes the hidden state of NLSTM1, i.e., the key of the time attention. Through each sequence weight ${\beta }_t^m$ and sequence information of the hidden state, we can obtain the updated hidden layer state with all time points:

$$c_t=\sum _{m=1}^T{\beta }_t^m{h}_m$$

(23)

Then, we can obtain $\tilde{Y}=(\widetilde{y_1^{}},\dots \widetilde{y_{t-1}^{}},\dots ,\widetilde{y_{T-1}^{}})$ by the combination $[y_{t-1}^{};c_{t-1}]$ of the updated hidden layer state and the known target sequence $Y_{}=(y_1^{},\dots ,y_{t-1}^{},\dots ,y_{T-1}^{})$:

$$\widetilde{y_{t-1}^{}}=w^T[y_{t-1}^{};c_{t-1}]+b$$

(24)

where $[y_{t-1}^{};c_{t-1}]$ denotes the combination of the decoder input and the updated hidden layer state, $w^T$ and b denote the size parameters of the combination mapped to the decoder. Then, we input $\widetilde{y_{t-1}^{}}$ to NLSTM2 to obtain the hidden layer state $d_t$ corresponding for each time point t.

$$d_t=f_2[d_{t-1}^{};\widetilde{y_{t-1}}]$$

(25)

where $f_2$ denotes the calculation method of unit NLSTM2. The final output $\widehat{Y}$ is:

$$\begin{array}{c}\widehat{Y}=F(y_1^{},\dots ,y_t^{},\dots ,y_{T-1}^{},X)\hfill \\ =V_y^T(W_y[d_T;c_T]+b_w)+b_v\hfill \end{array}$$

(26)

where $[d_T;c_T]$ denotes the combination of the hidden layer state of NLSTM2 and the updated hidden layer state, $W_y$ and $b_w$ denote the size parameters of the combination mapped to the decoder, $V_y$ and $b_v$ denote the weight and bias of the final result obtained for the linear function.

2.3. RAdam Optimizer

We use the RAdam optimizer to optimize the objective function, i.e., we use the SGD momentum optimizer at the initial stage of training, then switch to the improved Adam optimizer at a certain time according to the potential divergence of variance. And it builds a rectifier term, which allows the adaptive momentum to be fully expressed slowly but stably as a function of potential square difference, which can improve the stability of model training. Therefore, RAdam has the advantages of both Adam and SGD, which not only ensure fast convergence but also make it difficult to fall into the local optimal solution at the beginning of training.

In this paper, we use the square loss as the objective function, and the formula is as follows:

$$J(Y,\widehat{Y})=\frac{1}{N}\sum _{i=1}^N{(Y^i-{\widehat{Y}}^i)}^2$$

(27)

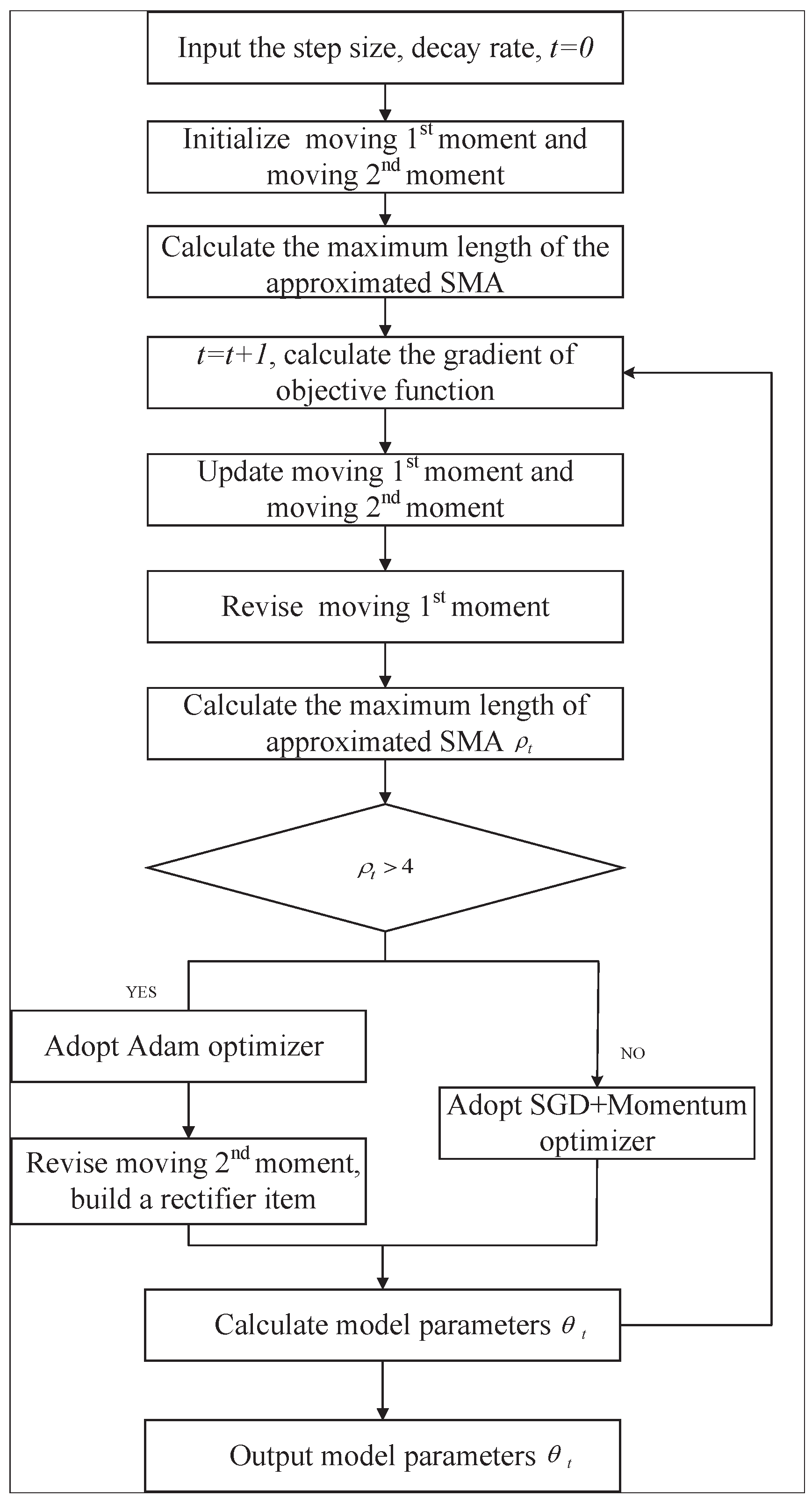
where N denotes the number of training samples. $Y^i$ denotes the target sequence value of the training sample and ${\widehat{Y}}^i$ denotes the predicted sequence value of the training sample. Figure 5 is the flow chart of the RAdam optimizer solving the objective function, and the steps are as follows.

Step 1.

Input the step size ${\alpha }_t$, decay rate $\left\{{\beta }_1,{\beta }_2\right\}$, $t=0$.

Step 2.

Initialize moving 1st moment and moving 2nd moment, calculate the maximum length ${\rho }^{\infty }$ of the approximated SMA.

$${\rho }^{\infty }=2/\phantom{2(1-{\beta }_2)}(1-{\beta }_2)-1$$

(28)

Step 3.

$t=t+1$, calculate the gradient $g_t$ of objective function, update moving 1st moment $m_t$ and moving 2nd moment $v_t$, revise moving 1st moment $\widehat{m_t}$, and calculate the maximum length ${\rho }_t$ of approximated SMA.

$$g_t={\nabla }_{\theta }{J}_t\left({\theta }_{t-1}\right)$$

(29)

$$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$$

(30)

$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t^{}$$

(31)

$$\widehat{m_t}=m_t/\phantom{m_t(1-{\beta }_1^t)}(1-{\beta }_1^t)$$

(32)

$${\rho }_t={\rho }_{\infty }-2t{\beta }_2^t/\phantom{2t{\beta }_2^t(1-{\beta }_2^t)}(1-{\beta }_2^t)$$

(33)

where ${\nabla }_{\theta }$ denotes gradient solution, $J_t\left({\theta }_{t-1}\right)$ denotes objective function, ${\theta }_{t-1}$ denotes the model parameters when $t-1$.

Step 4.

Calculate ${\theta }_t$ according to ${\rho }_t$. If ${\rho }_t>4$, adopt Adam optimizer, revise moving 2nd moment, and build a rectifier item $r_t$, then obtain the revised moving 2nd moment value $\widehat{v_t}$ and the model parameters ${\theta }_t$.

$$\widehat{v_t}=\sqrt{v_t/\phantom{v_t(1-{\beta }_2^t)}(1-{\beta }_2^t)}$$

(34)

$$r_t=\sqrt{\frac{({\rho }_t-4)({\rho }_t-2){\rho }_{\infty }}{({\rho }_{\infty }-4)({\rho }_{\infty }-2){\rho }_t}}$$

(35)

$${\theta }_t={\theta }_{t-1}-{\alpha }_t{r}_t\widehat{m_t}/\phantom{{\alpha }_t{r}_t\widehat{m_t}\widehat{v_t}}\widehat{v_t}$$

(36)

If ${\rho }_t\le 4$, adopt SGD+Momentum optimizer, then obtain the training parameters ${\theta }_t$.

$${\theta }_t={\theta }_{t-1}-{\alpha }_t\widehat{m_t}$$

(37)

Step 5.

Output the model parameters ${\theta }_t$.

3. Experiment and Simulation

3.1. Data Sources

To prove the effectiveness of RAdam-DA-NLSTM, we apply the model to PM2.5 prediction, stock prediction, traffic prediction, and biological signal prediction, respectively.

PM2.5 prediction: We use the Beijing PM2.5 dataset for prediction. This dataset is a series of 43,824 time steps collected by the U.S. Embassy in Beijing from 1 January 2010, to 31 December 2014, including the current time, PM2.5 concentration, dew point, temperature, pressure, wind direction, wind speed, hours, rainfall hours, etc. at Beijing Capital International Airport.

Stock prediction: We use the Nasdaq 100 stock data set (Nasdaq 100) for prediction. The data set covers a series of 40,560-time steps from 26 July 2016 to 22 December 2016, including the stock price data of 81 major companies under the Nasdaq 100 index.

Traffic prediction: We use the California traffic volume data set of 24 sections in the California transportation performance measurement system (PEMs) for traffic volume prediction and use the Seattle traffic speed data set for traffic speed prediction. The sampling time interval of California traffic flow data is 5 min, and the data time range is 61 days from 1 May 2014 00:00:00 to 30 June 2014 23:59:00. Seattle speed data are the vehicle speed data set from Seattle in 2015 collected by 323 detectors, and the sampling interval is also 5 min.

Biological signal prediction: We use two types of biological signals: ECG signal and BCG signal. The ECG signal was obtained from the dynamic ECG database of sudden cardiac death, available on PhysioNet. This dataset includes ECG signals from patients who experienced actual cardiac arrest. The signal was collected using two leads, and the sampling frequency was set to 250 Hz. To ensure accuracy, the ECG signal was meticulously annotated by medical experts, identifying the starting point of the sudden cardiac death beat. The BCG signal was obtained from a large-scale and complex dataset provided by a medical device company. The dataset contains recordings of cardio ballistics from over 100 patients with abnormal cardio ballistics, spanning from 2016 to 2020. This dataset belongs to a million-level time series, making it a valuable resource for predictive analysis in the field of bio-signal-assisted prediction. By analyzing these diverse and comprehensive datasets, we aimed to derive meaningful insights and improve the accuracy of predictions in the context of biological signal analysis.

The above data conforms to the high-dimensional complex characteristics and is suitable for testing the effectiveness of RAdam-DA-NLSTM.

3.2. Parameter Setting

RAdam-DA-NLSTM needs to set four important parameters, namely time steps L, encoder hidden units number $m1$, decoder hidden units number $m2$, and batch size b. These parameters were obtained through iterative experiments.

Table 1. Parameter setting results.

Datasets	L	$\mathit{m}1$	$\mathit{m}2$	b
Beijing PM2.5	10	64	64	64
NASDAQ 100	15	128	128	64
California traffic volume	15	64	64	64
Seattle traffic speed	20	64	64	64
ECG signal	15	128	128	64
BCG signal	20	128	128	64

shows the model parameter setting results of the above data.

3.3. Comparative Analysis

We use 70% of the data sets as the training set, 10% of the data sets as the validation set and 20% of the data sets as the test set. To further reflect the advantages of the RAdam-DA-NLSTM, we use SVM, RNN, GRU, LSTM, attention LSTM, and DA-LSTM prediction models to conduct 20 experiments on the data set, and use four evaluation indexes: mean absolute error ($MAE$), mean absolute percentage error ($MAPE$), root mean square error ($RMSE$) and coefficient of determination ($R^2$) to evaluate and analyze the prediction accuracy.

$$MAE=\frac{1}{N}\sum _{i=1}^N\left|Y^i-\widehat{Y^i}\right|$$

(38)

$$MAPE=\frac{100\%}{N}\sum _{i=1}^N\left|\frac{Y^i-\widehat{Y^i}}{Y^i}\right|$$

(39)

$$RMSE=\sqrt{\frac{1}{N}{\sum _{i=1}^N(Y^i-\widehat{Y^i})}^2}$$

(40)

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^N}|\widehat{Y^i}-Y^i|}{{\displaystyle \sum _{i=1}^N}|\widehat{Y^i}-\overline{Y^i}|}$$

(41)

where N denotes the number of samples, $Y^i$ denotes the target sequence value of samples, $\widehat{Y^i}$ denotes the predicted sequence value of samples and $\overline{Y^i}$ denotes the target sequence average value of samples.

3.3.1. PM2.5 Prediction

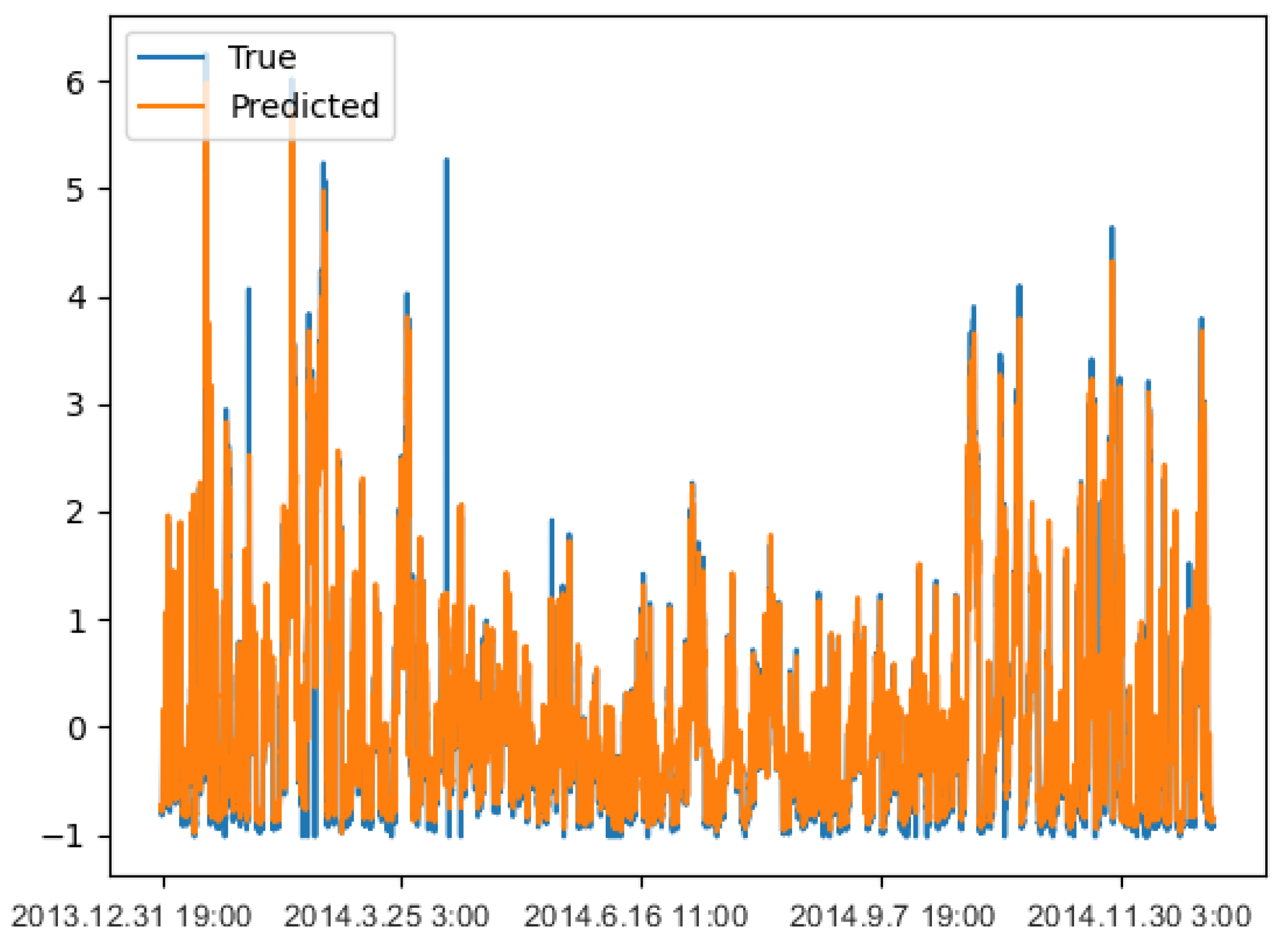
In recent years, air pollution has become extremely serious, and the problem of air quality has attracted more and more attention. Judging the air quality according to the concentration of pollutants in the air reflects the degree of air pollution. PM2.5 refers to particles with a diameter less than or equal to 2.5 microns in the atmosphere, also known as particles that can enter the lung. Although the content of PM2.5 in the earth’s atmosphere is relatively small, it contains a large number of toxic and harmful substances and has a long residence time and long transportation distance in the atmosphere, which greatly affects the air quality and has a direct or indirect impact on human health and plant growth. Therefore, it is very necessary to monitor and predict PM2.5 concentration in real time. 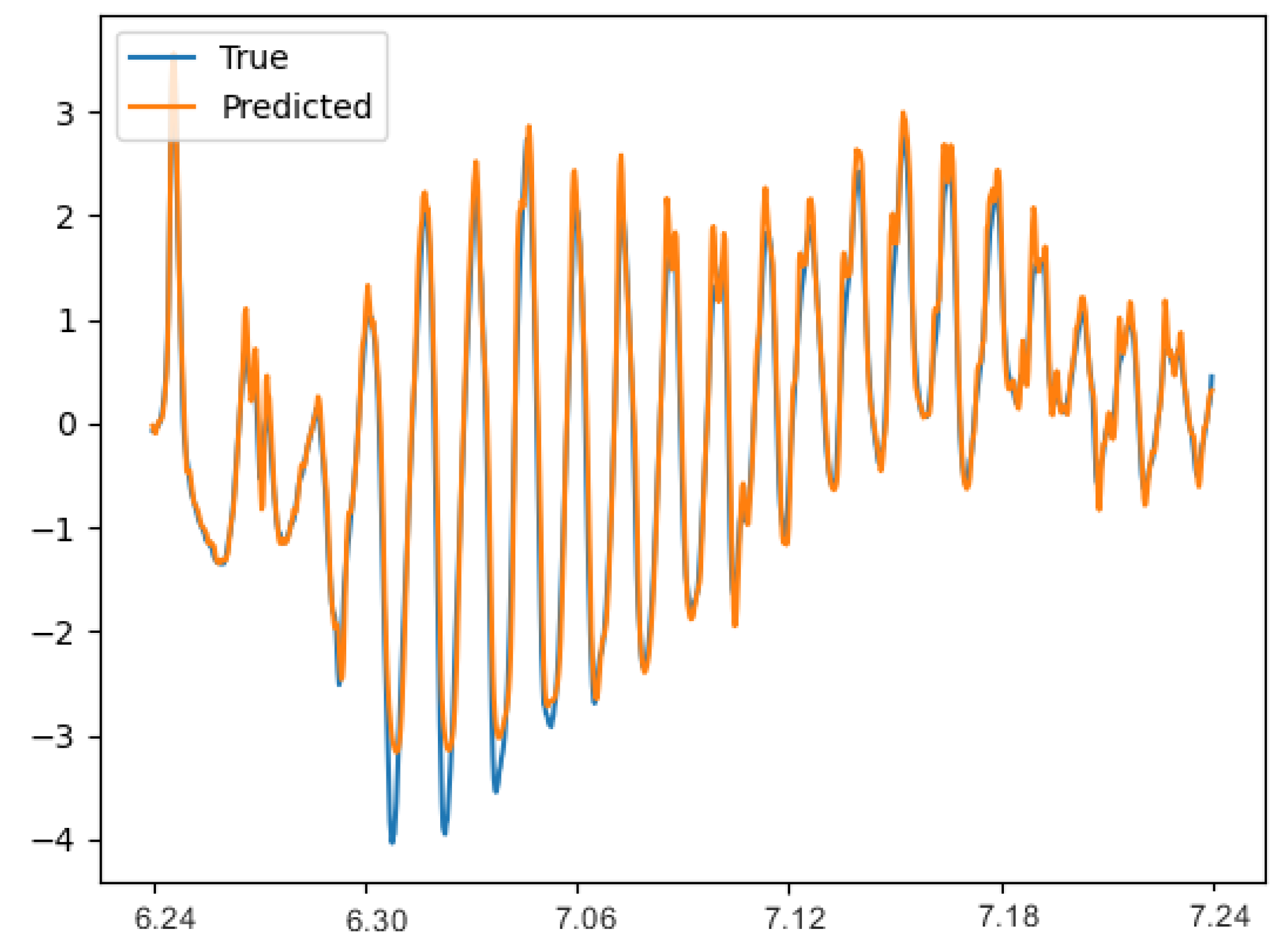The following are the prediction results of this model on the Beijing PM2.5 test data set, and Figure 6 shows the prediction fitting diagram.

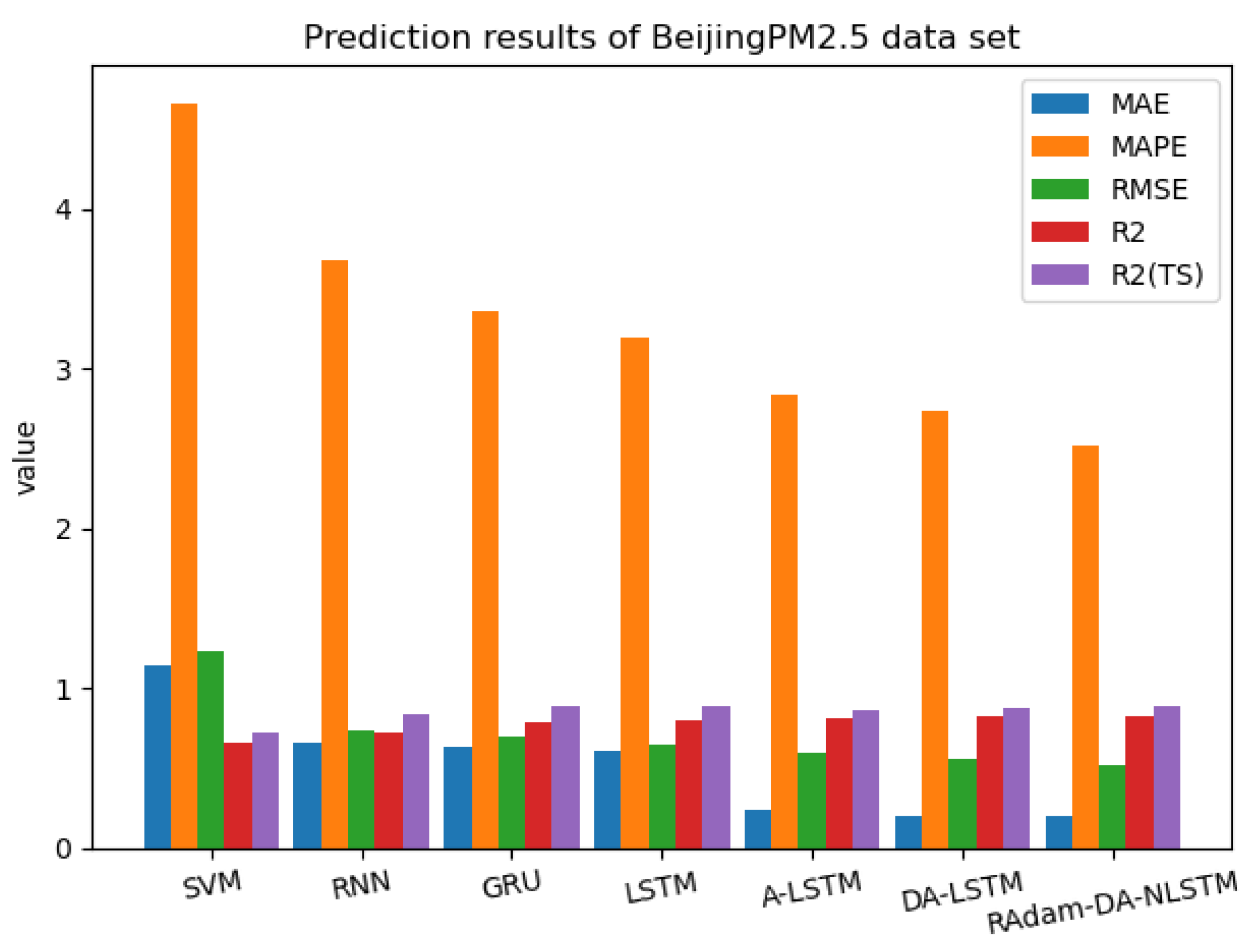
Figure 6 shows that the trend of the predicted value and the real value curve of the RAdam-DA-NLSTM on the Beijing PM2.5 test data set is roughly consistent, indicating that the fitting result is ideal. Further, we compare the evaluation results of the Beijing PM2.5 test data set predicted by the above seven models. The evaluation results take the average value of 20 experiments.

Table 2. Evaluation results (Beijing PM2.5).

Models	MAE	MAPE	RMSE	${\mathit{R}}^2$	${\mathit{R}}^2$ (TS)
SVM	1.1451	4.6632	1.2365	0.6532	0.7217
RNN	0.6621	3.6754	0.7321	0.7229	0.8323
GRU	0.6323	3.3632	0.6941	0.7892	0.8814
LSTM	0.6098	3.1946	0.6380	0.7921	0.8920
A-LSTM	0.2324	2.8312	0.5919	0.8126	0.8620
DA-LSTM	0.2032	2.7328	0.5521	0.8181	0.8705
RAdam-DA-NLSTM	0.1921	2.5217	0.5117	0.8213	0.8831

and Figure 7 show the results.

Table 2 and Figure 7 present the prediction results of $MAE$, $MAPE$, $RMSE$, and $R^2$ for the Beijing PM2.5 test dataset, comparing RAdam-DA-NLSTM with other models. It is evident that RAdam-DA-NLSTM outperforms the other models in terms of smaller $MAE$, $MAPE$, and $RMSE$, values, as well as having a higher $R^2$ score. These results highlight the enhanced prediction accuracy of RAdam-DA-NLSTM for the Beijing PM2.5 dataset and its advantages over other models in PM2.5 prediction. Notably, the $R^2$(TS) metric reflects the prediction performance on the training set. By observing the $R^2$(TS) values, we can notice that LSTM achieves better training results. However, when it comes to the test results, LSTM performs significantly worse compared to A-LSTM, DA-LSTM, and RAdam-DA-NLSTM. This discrepancy indicates that LSTM tends to overfit the PM2.5 prediction.

3.3.2. Stock Prediction

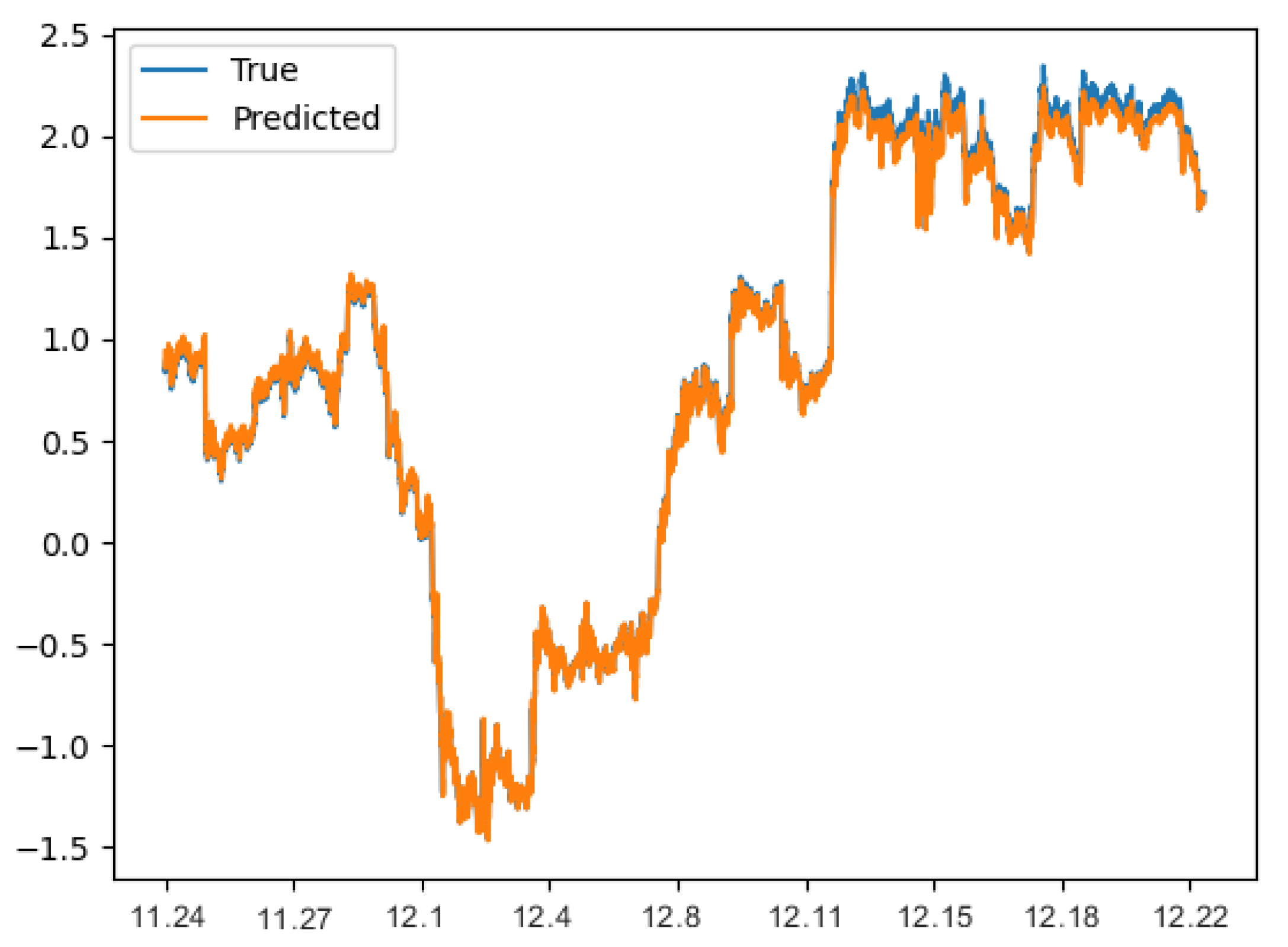
Stock prediction in the financial field has always been a hot topic in time series prediction. Stock forecasting refers to the behavior of predicting the future development direction of the stock market or the rise and fall range of stocks according to the development of the stock market. Short-term stock prediction is of great significance for stock investors to analyze the market rhythm and manage the investment risk of holding shares. 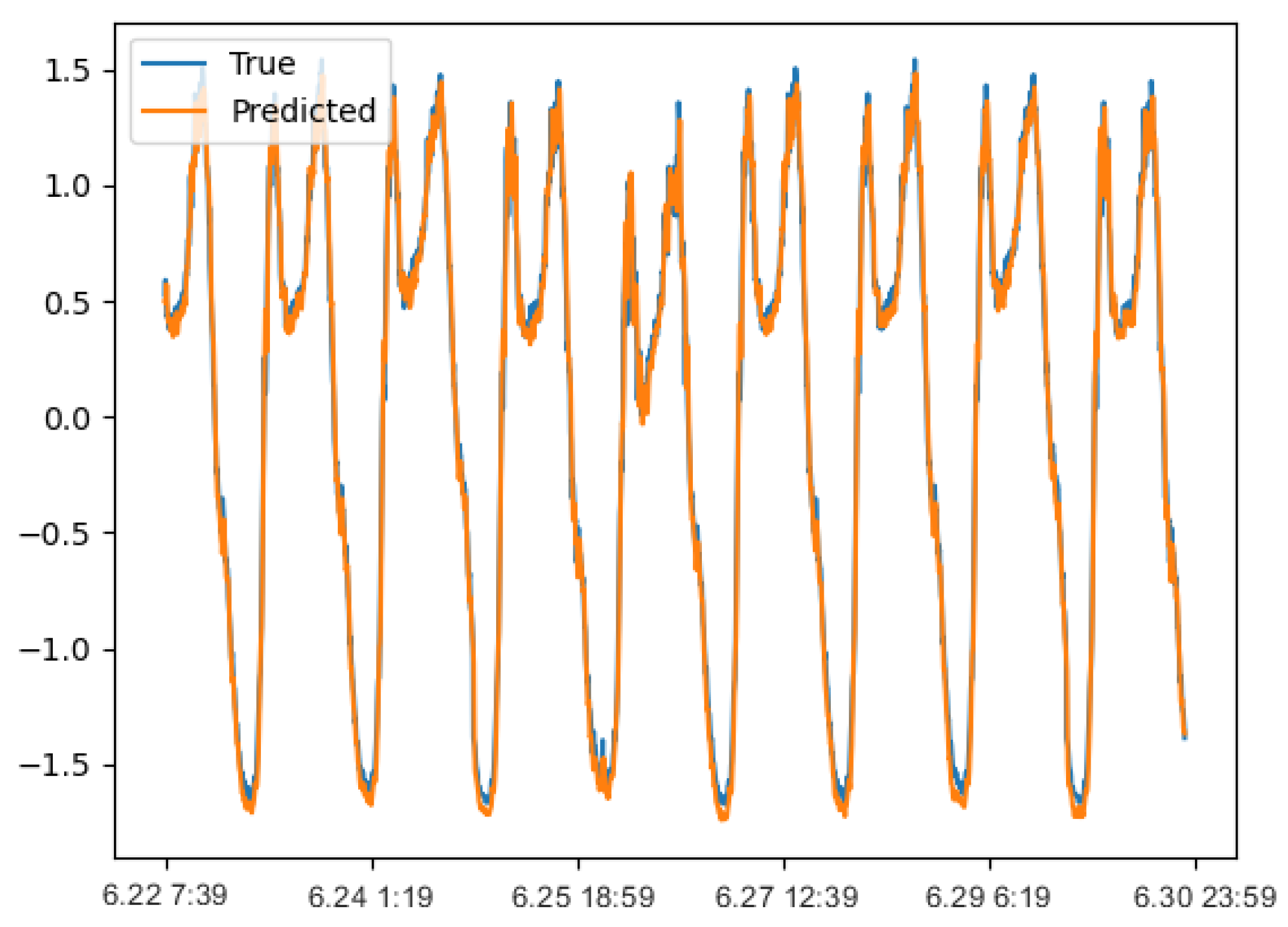We use the Nasdaq 100 index stock test data set for prediction in this paper, and Figure 8 shows the fitting diagram for Nasdaq 100 index stock test data.

Figure 8 shows that the trend of the predicted value and real value curve of the RAdam-DA-NLSTM on the Nasdaq 100 index stock test data set is also roughly consistent, and the fitting result is quite well. In addition, it is necessary to compare the evaluation results of the above seven models in predicting the Nasdaq 100 index stock test data set. The evaluation results take the average value of 20 experiments.

Table 3. Evaluation results (NASDAQ 100).

Models	MAE	MAPE	RMSE	${\mathit{R}}^2$	${\mathit{R}}^2$ (TS)
SVM	0.3901	0.5013	0.5211	0.7172	0.8272
RNN	0.2163	0.2586	0.2681	0.7621	0.9031
GRU	0.2031	0.2512	0.2761	0.7663	0.9226
LSTM	0.1821	0.1931	0.2317	0.7874	0.9306
A-LSTM	0.0923	0.1034	0.1522	0.8021	0.9155
DA-LSTM	0.0478	0.0526	0.0632	0.8302	0.9207
RAdam-DA-NLSTM	0.0301	0.0516	0.0531	0.8825	0.9361

and Figure 9 show the results.

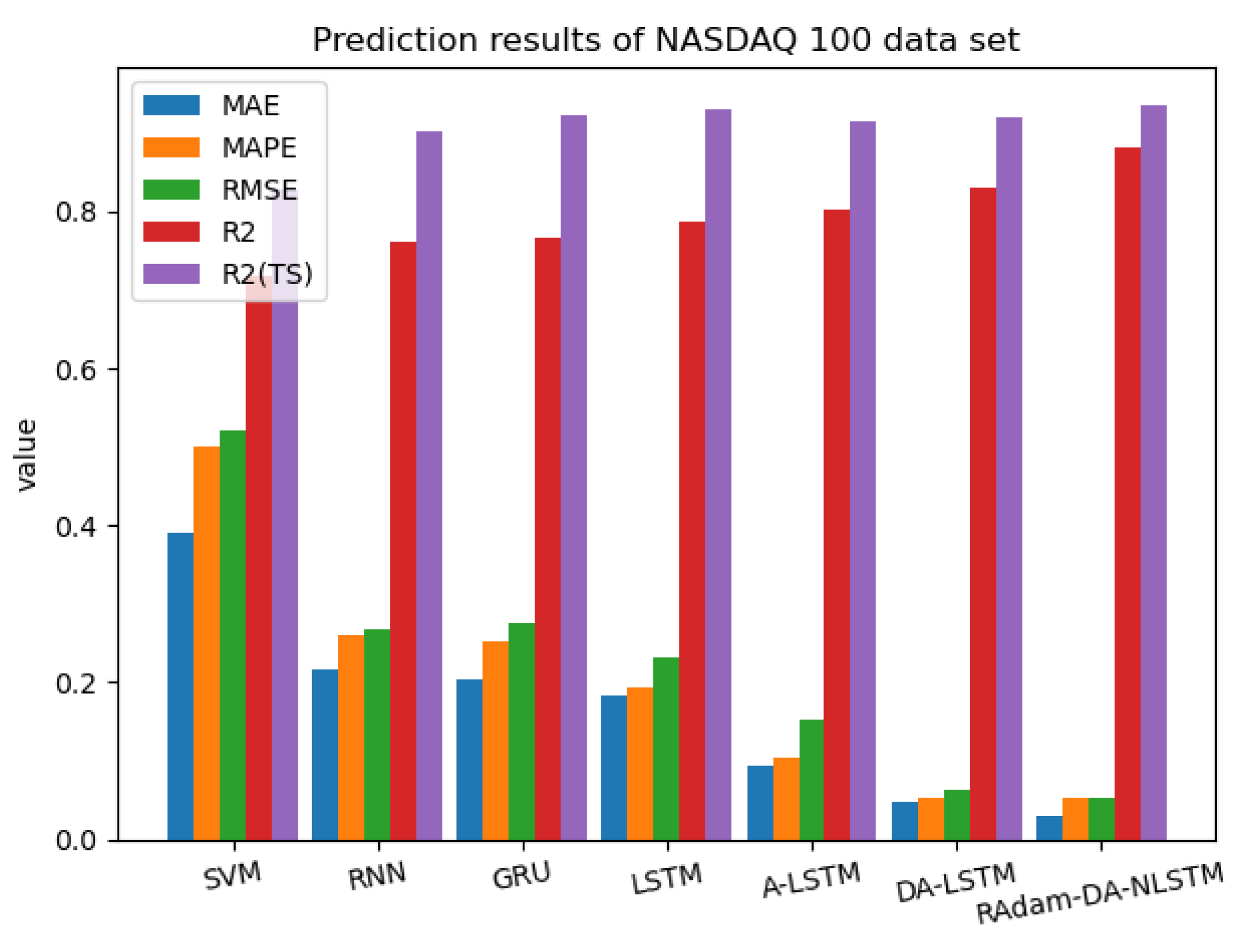
Table 3 and Figure 9 provide compelling evidence that RAdam-DA-NLSTM achieves superior results on the Nasdaq-100 stock test dataset compared to other models. Specifically, RAdam-DA-NLSTM demonstrates smaller $MAE$, $MAPE$, and $RMSE$ values, indicating its enhanced forecasting accuracy. Furthermore, the $R^2$ value of RAdam-DA-NLSTM outperforms other models, underscoring its robust analytical capability when applied to complex stock datasets. These findings highlight the effectiveness of RAdam-DA-NLSTM in predicting stock market behavior and its potential for generating valuable insights in the domain of financial analysis.

3.3.3. Traffic Prediction

The traffic information system provides fast traffic guidance for cities. Traffic volume prediction and traffic speed prediction are the key points in the traffic information system. However, urban traffic has its characteristics, the traffic flow and traffic speed data are hard to estimate. Therefore, traffic information prediction is highly significant but not easy. We adopt the RAdam-DA-NLSTM to predict the California vehicle volume data set and Seattle vehicle speed data set, and Figure 10 and Figure 11 show the fitting diagrams.

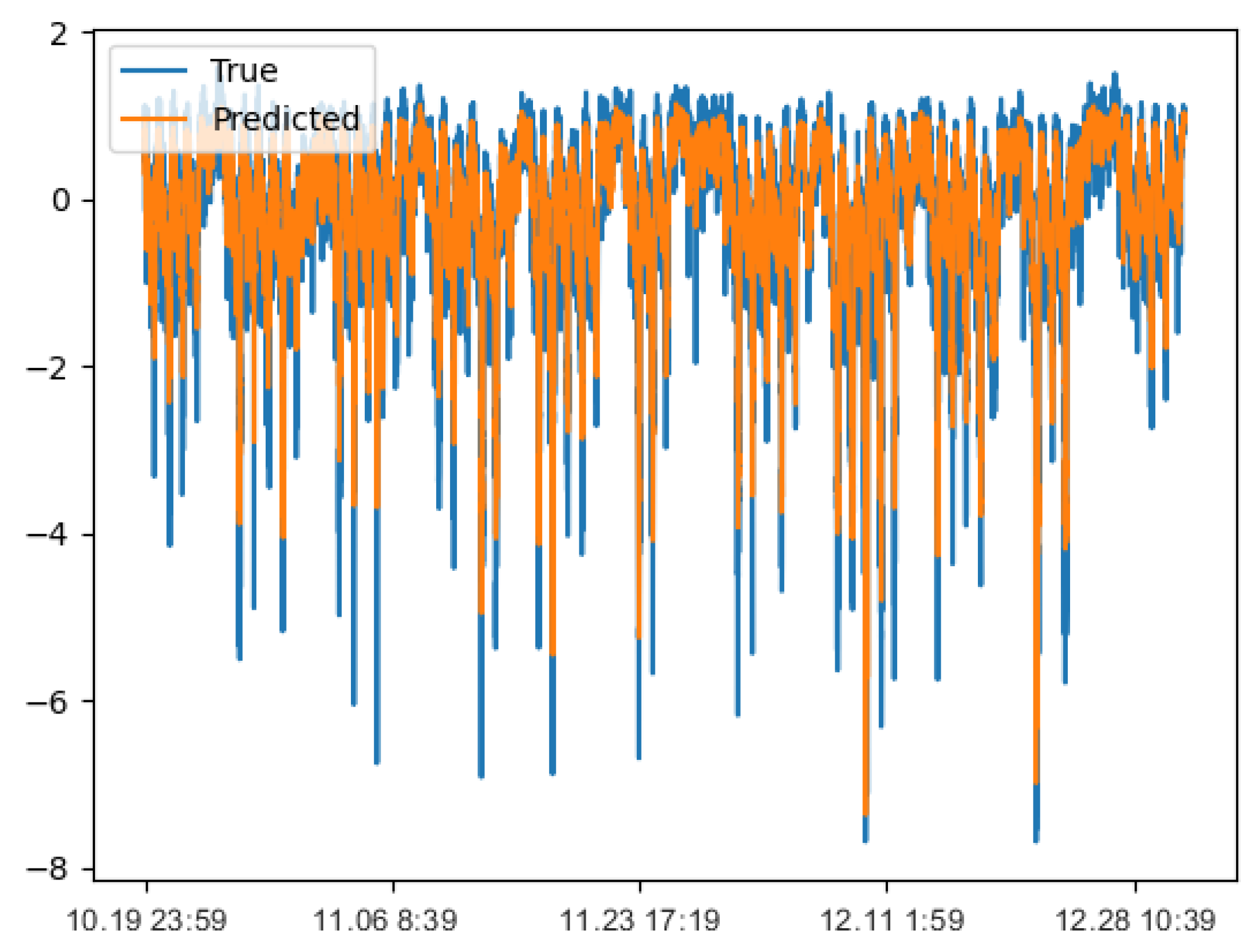
Figure 10 and Figure 11 show that the RAdam-DA-NLSTM has good fitting results for the California traffic volume data set and Seattle speed data set. Especially in the fitting of the California vehicle volume data set, it greatly highlights the advantages of the model. Then, we further compare the evaluation results of the traffic data set predicted by the above seven models.

Table 4. Evaluation results (California traffic volume).

Models	MAE	MAPE	RMSE	${\mathit{R}}^2$	${\mathit{R}}^2$ (TS)
SVM	0.2903	0.9233	0.3218	0.7621	0.8562
RNN	0.1642	0.5215	0.2811	0.8054	0.9172
GRU	0.1327	0.3291	0.2316	0.8298	0.9238
LSTM	0.1244	0.2282	0.1843	0.8536	0.9423
A-LSTM	0.0836	0.2132	0.1641	0.8721	0.9321
DA-LSTM	0.0624	0.1801	0.0912	0.8863	0.9626
RAdam-DA-NLSTM	0.0598	0.1721	0.0825	0.9136	0.9645

and

Table 5. Evaluation results (Seattle traffic speed).

Models	MAE	MAPE	RMSE	${\mathit{R}}^2$	${\mathit{R}}^2$ (TS)
SVM	0.8931	4.6548	1.2031	0.6518	0.7931
RNN	0.4362	3.9325	0.9121	0.7029	0.8216
GRU	0.4210	3.8978	0.8945	0.7112	0.8344
LSTM	0.3834	3.6427	0.8649	0.7235	0.8367
A-LSTM	0.3756	3.5471	0.7921	0.7616	0.8721
DA-LSTM	0.2921	2.9221	0.4382	0.7915	0.8925
RAdam-DA-NLSTM	0.2651	2.6945	0.4213	0.8120	0.9024

and Figure 12 and Figure 13 show the results.

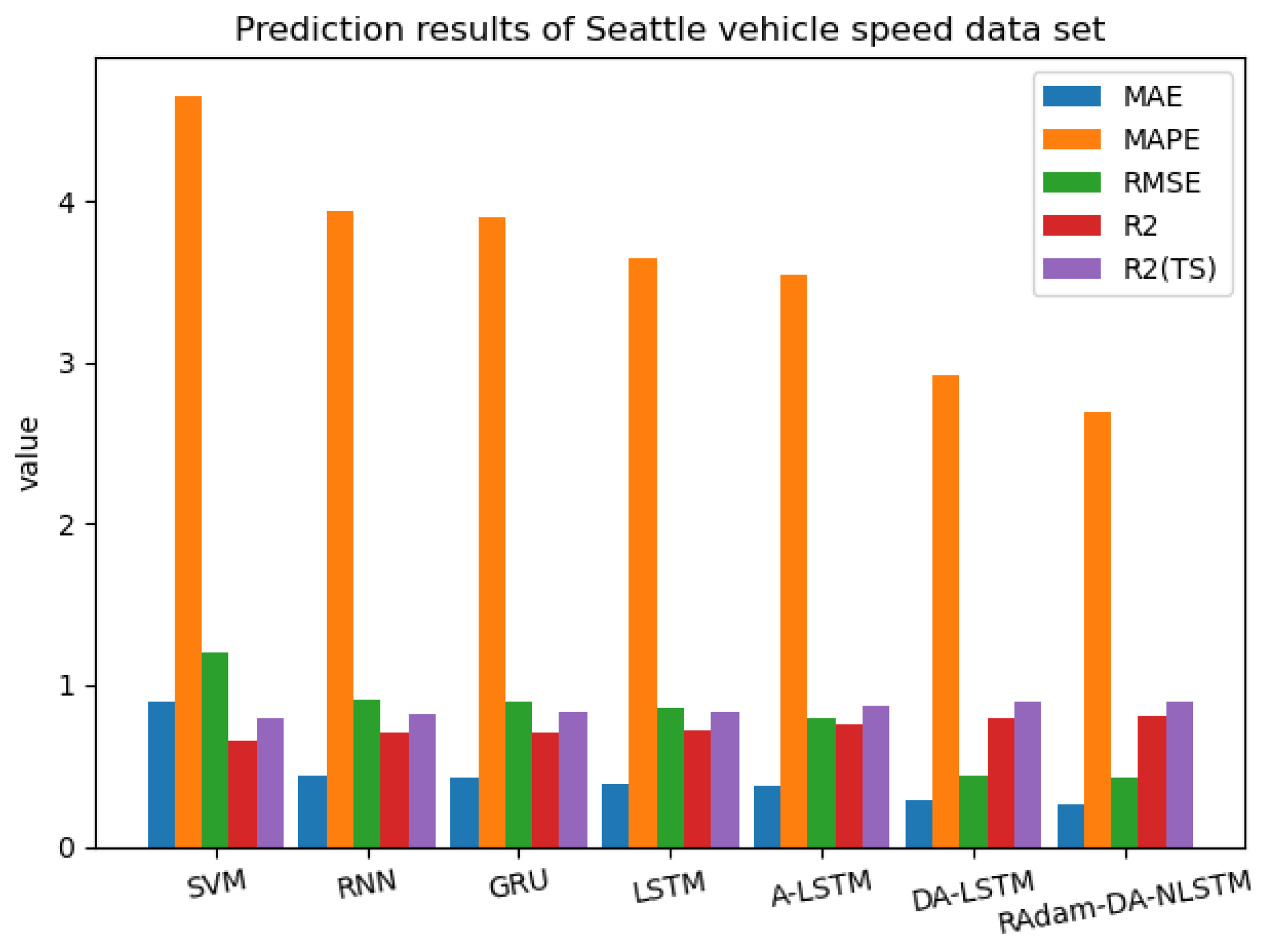
Table 4 and Table 5 and Figure 12 and Figure 13 illustrate that the prediction errors for the California volume dataset and the Seattle speed dataset are lower for RAdam-DA-NLSTM compared to other models. Additionally, the obtained $R^2$ values are relatively large, indicating the robust prediction capabilities of RAdam-DA-NLSTM for the aforementioned datasets. The findings from this study demonstrate the model’s strong prediction abilities for traffic information, emphasizing its significant practical significance in the field of traffic prediction.

3.3.4. Biological Signal Prediction

ECG (Electrocardiogram) signal has strong nonlinearity, non-stationary nature, and randomness, making it both precise and challenging to analyze. It is important for patients with potential Sinus rhythm, coronary heart disease, hypertension, and other diseases to predict ECG signals in advance and identify sudden cardiac death, which can save lives through timely intervention during sudden cardiac events. 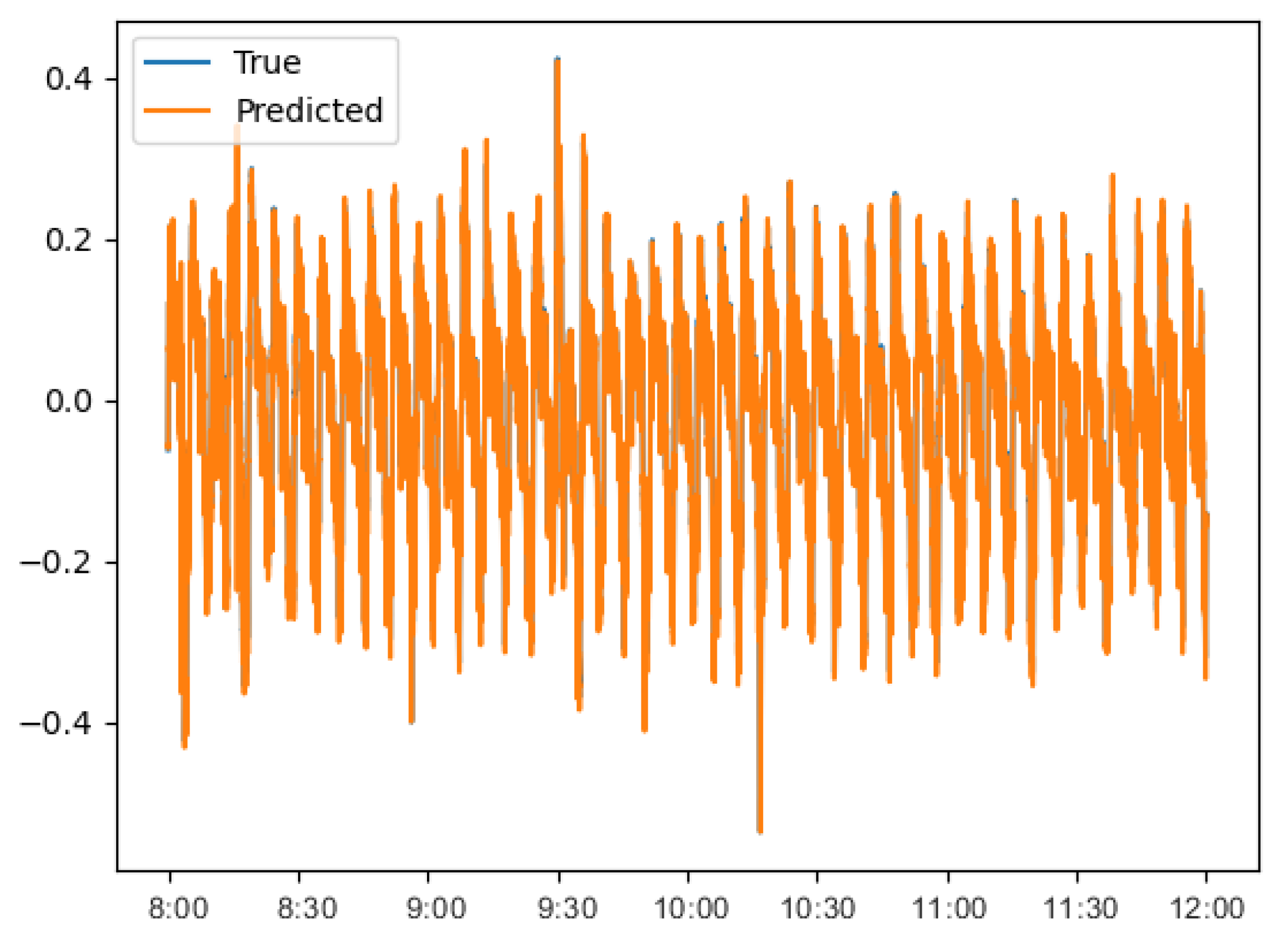Figure 14 illustrates the fitting diagram depicting RAdam-DA-NLSTM’s performance in predicting ECG signal datasets. BCG (Ballistocardiogram) is a graphical representation of the cardiac shock signal generated by the movement of the heart in response to blood ejection. It carries valuable information about cardiac function and condition, and can provide early indications of potential cardiac abnormalities. Extracting heart-related information from cardiac shocks using BCG signals and detecting abnormal cardiac shocks to diagnose heart disease can significantly assist in remote patient monitoring. Figure 15 showcases the fitting diagram of RAdam-DA-NLSTM for BCG signal dataset prediction.

Figure 14 and Figure 15 show that the RAdam-DA-NLSTM has a strong nonlinear mapping ability for ECG signal prediction and BCG signal prediction. Then, we compare the evaluation results of the ECG signal data set predicted by the above seven models.

Table 6. Evaluation results (ECG signal).

Models	MAE	MAPE	RMSE	${\mathit{R}}^2$	${\mathit{R}}^2$ (TS)
SVM	0.2991	3.0238	0.4832	0.7232	0.8136
RNN	0.2834	2.7622	0.4025	0.7621	0.8648
GRU	0.2802	2.3254	0.3819	0.7796	0.8432
LSTM	0.2725	2.2435	0.3021	0.7728	0.8560
A-LSTM	0.2531	1.8432	0.2563	0.8126	0.8922
DA-LSTM	0.2289	1.2003	0.2016	0.8345	0.8837
RAdam-DA-NLSTM	0.2232	1.2189	0.1782	0.8426	0.8856

and

Table 7. Evaluation results (BCG signal).

Models	MAE	MAPE	RMSE	${\mathit{R}}^2$	${\mathit{R}}^2$ (TS)
SVM	0.5326	3.2431	0.6238	0.6532	0.6865
RNN	0.3211	3.0121	0.3442	0.7254	0.7773
GRU	0.2967	2.8320	0.3002	0.7422	0.7932
LSTM	0.2332	2.9233	0.3126	0.7527	0.7942
A-LSTM	0.2017	2.5321	0.2812	0.7632	0.8329
DA-LSTM	0.1822	2.3208	0.2636	0.7921	0.8232
RAdam-DA-NLSTM	0.1675	2.3026	0.2431	0.8053	0.8321

and Figure 16 and Figure 17 show the results.

Table 6 and Table 7 and Figure 16 and Figure 17 show that RAdam-DA-NLSTM exhibits strong predictive ability on biological signal datasets, with smaller $MAE$, $MAPE$, and $RMSE$, and larger $R^2$ compared to other models. This highlights the model’s ability to effectively predict biological signal data. Similar to the previous experiments, RAdam-DA-NLSTM may not achieve the best results on the training set, but it delivers relatively good results on the test set. This once again validates the model’s superior capacity to address underfitting and overfitting issues, ensuring accurate predictions.

4. Discussion

Time series prediction methods are extensively utilized across various domains, including Finance, Healthcare, Environment, and Transportation. For instance, it has become possible to predict future trends and fluctuations in stock prices by analyzing historical stock market data. This is crucial for investors, traders, and fund managers as they can make informed investment decisions, manage portfolios, and develop effective trading strategies based on forecasted outcomes. Similarly, in the realm of atmospheric pollution, analyzing and modeling historical air quality data allows for predicting future PM2.5 levels. This information proves valuable for environmental departments, city planners, and public health organizations, as they can take appropriate measures to combat air pollution and safeguard public health.

Time series prediction also plays a vital role in transportation planning and management. By analyzing historical traffic data, including road traffic flow, congestion level, and public transportation demand, future traffic volume and congestion can be predicted. Consequently, urban transportation planners and traffic management organizations can utilize these predictions to formulate transportation plans, optimize traffic signal control, and provide effective traffic management solutions.

Furthermore, time series prediction holds significant importance in the medical field, particularly in analyzing biometric signals such as Electrocardiogram (ECG) and Ballistocardiogram (BCG). By modeling and analyzing these signals, it is possible to predict the progression of patients’ conditions, assess disease risks, and identify changes in physiological states. This empowers doctors, researchers, and healthcare providers to implement crucial medical interventions, devise personalized treatment strategies, and deliver improved healthcare based on projected outcomes, thereby enabling timely intervention and potentially saving lives.

In this paper, a novel time series prediction method called RAdam-DA-NLSTM is proposed, focusing on feature aggregation optimization, model enhancement, and objective function optimization. Experimental evaluations are conducted across four domains with six datasets, including stock data, PM2.5 data, traffic speed data, traffic volume data, ECG, and BCG. RAdam-DA-NLSTM exhibits superior fitting capabilities when compared to six comparative algorithms (SVM, RNN, GRU, LSTM, A-LSTM, and DA-LSTM) using four evaluation indicators ($MAE$, $MAPE$, $RMSE$, and $R^2$). By addressing underfitting and overfitting issues prevalent in most models, this paper demonstrates the robust nonlinear mapping abilities of RAdam-DA-NLSTM in processing high-dimensional, complex, and nonlinear data.

However, it is important to acknowledge the limitations of the proposed time series prediction method in this paper. The experiments were limited to one-step predictions in order to facilitate better comparisons across different domains. While this approach is meaningful for forecasting PM2.5 levels and stock prices, it is essential to conduct multi-step prediction experiments for time series data with compact time frequencies and urgent demands, such as BCG signals. These experiments would further validate the long-term prediction capabilities of RAdam-DA-NLSTM. Additionally, it is crucial to note that demonstrating the generalization performance of RAdam-DA-NLSTM based solely on four domains may be an exaggeration. Future research and experiments must encompass a wider range of domains, taking into account the unique characteristics of each domain. This will contribute to the field of time series forecasting through more effective and specialized studies.

5. Conclusions

In the field of Human–Computer Intelligent Systems, our study proposes a powerful time series prediction model called RAdam-DA-NLSTM, which employs a self-encoder architecture. This model improves the memory ability of the system using Nested LSTM as encoder and decoder. Additionally, it includes both input and time attention mechanisms to enhance the feature cohesion ability of the model. We integrate the RAdam optimizer to solve the objective function, which results in a more stable prediction system. In our simulation experiment, we used different datasets such as Beijing PM2.5, Nasdaq 100, California traffic flow, Seattle traffic speed, ECG signals, and BCG signals. The results demonstrate that RAdam-DA-NLSTM has higher prediction accuracy and stability.

For future work, our team will explore multi-step prediction of time series, integrate our prediction method in more applications, and contribute to the time series prediction of the Internet of Things (IoT) world. Our goal is to improve the efficiency and accuracy of predictions in the field of Human–Computer Intelligent Systems.