Abstract
Meta-learning is attracting attention as a crucial tool for few-show learning tasks. Meta-learning involves the establishment and acquisition of “meta-knowledge”, enabling the ability to adapt to a novel field using only limited data. Transductive meta-learning has garnered increasing attention as a solution to the sample bias problem arising from meta-learning’s reliance on a limited support set for adaptation. This approach surpasses the traditional inductive learning perspective, aiming to address this issue effectively. Transductive meta-learning infers the class of each instance in time by considering the relation of instances in the test set. In order to enhance the effectiveness of transductive meta-learning, this paper introduces a novel technique called task-specific pseudo labelling. The main idea is to produce synthetic labels for unannotated query sets by propagating labels from annotated support sets. This approach allows the utilization of the supervised setting as is, while incorporating the unannotated query set into the adjustment procedure. Consequently, our approach enables handling a larger number of examples during adaptation compared to inductive approaches, leading to improved classification performance of the model. Notably, this approach represents the first instance of employing task adaptation within the context of pseudo labelling. Based on the experimental outcomes in the evaluation configurations of few-shot learning, specifically in the 5-way 1-shot setup, the proposed method demonstrates noteworthy enhancements over two existing meta-learning algorithms, with improvements of 6.75% and 5.03%, respectively. Consequently, the proposed method establishes a new state-of-the-art performance in the realm of transductive meta-learning.
1. Introduction
One significant distinction between computers and humans in the learning stage lies in the utilization of prior knowledge, while machines struggle to apply previously acquired knowledge to a new task seamlessly, humans possess the ability to quickly leverage their existing knowledge with minimal effort. As a result, numerous researchers have actively engaged in the study of few-shot learning, aiming to bridge this gap between machine and human learning capabilities [1,2,3]. In other words, they aimed to learn with limited information. Few-shot learning aims to train a model capable of achieving effective generalization and accurate predictions, even when presented with a limited number of labelled examples for each class or task. The term “few-shot” refers to the limited number of examples available for training. There are various approaches to few-shot learning, but one common approach is to use meta-learning or learning to learn. Meta-learning involves training a model on a distribution of tasks or classes, where each task or class has only a small number of labelled examples. The model learns to extract useful information from the limited labelled data and generalize that knowledge to new, unseen tasks or classes. Another approach is to leverage techniques such as transfer learning or feature extraction from pre-trained models. The pre-trained models are normally trained on large-scale datasets, which capture a wide range of visual or semantic information. By using the pre-trained models as a starting point, few-shot learning algorithms can fine-tune them on the limited labelled data to adapt them to specific tasks or classes. In particular, meta-learning has garnered significant attention as it acquires meta-knowledge [4] from task distributions and subsequently transfers this knowledge to new target tasks.
Model-agnostic meta-learning (MAML) [5] stands out as one of the most renowned meta-learning approaches. MAML focuses on learning the initialization of model parameters using meta-knowledge for effective transfer learning. Notably, this initialization encompasses task-generic knowledge, enabling efficient adaptation to new tasks within a reduced number of steps.
In few-shot learning (FSL), a mini-batch is composed of tasks [6,7], instead of individual samples. Typically, FSL-based classification task usually considers N classes, and it consists of a support set and a query set: The former for adaptation and the latter for evaluation. Commonly, these tasks adhere to either the 1-shot or 5-shot settings. To elaborate further, in the support set, each class is represented by only 1 or 5 images, resulting in adapting to a target task with a minimal amount of data. However, the limited data in the support set may not adequately capture the characteristics of the respective classes. This discrepancy between the small amount of data and the class representation is commonly known as the sample bias problem [8]. In order to address the sample bias problem, transductive learning has been employed in few-shot learning by [9,10,11]. Figure 1 illustrates the conceptual visualization of transductive learning in the context of few-shot learning.
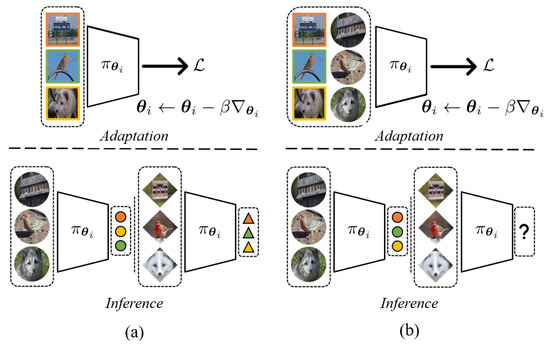
Figure 1.
Comparison of (a) inductive meta-learning (b) transductive meta-learning. The former focuses on adapting the task without utilizing the unlabelled query set, whereas the latter incorporates the unlabelled query set (without edge colour) during the adaptation stage. Since the support set contains a limited number of samples, inductive meta-learning is prone to encountering sample bias issues during adjustment.
Transductive learning operates under the premise of directly accessing test samples. However, inductive learning trains a generalized model so that it performs well on random samples. In the context of meta-learning, transductive learning incorporates the unannotated query set and offers the advantage of adjustment through a greater volume of data. However, the labels of the query set are seldom employed for training. Thus, this paper tackles this issue.
We propose a novel task-specific pseudo labelling (TSPL). TSPL is the first task-adaptation approach for synthesizing labels in the context of transductive meta-learning. TSPL incorporates adaptive assignment of pseudo labels (PL) to unannotated query sets based on the target task. To accomplish this, we employ the transductive propagation network (TPN) [9], which utilizes a graph neural network (GNN) to propagate labels from the support sets to the unannotated query sets during the inference process. TSPL leverages this approach to propagate PLs from the support sets to the unannotated query sets, thus facilitating label dissemination. Subsequently, the support sets and query sets through synthetic labelling are jointly adjusted in a supervised manner, following a similar approach to MAML. Since synthetic labels are sort of hard labels, specifically one-hot vectors, fine-tuning the label propagation process for the target task becomes infeasible. To overcome this limitation, we introduce a compact sub-network responsible for generating layer-wise parameters in the graph construction network (GCN) of TPN. These task-specific labels are then propagated using this modified network. By incorporating a representation vector of the present task, the parameters of GCN become task-conditioned, allowing for effective adaptation.
The key contributions of TSPL can be itemized as follows:
- TSPL addresses the sample bias issue in transductive meta-learning, which has received relatively less attention in the field of meta-learning.
- TSPL demonstrates either state-of-the-art (SOTA) or comparable performance on two widely recognized datasets used for few-shot classification tasks.
2. Related Work
The primary objective of meta-learning is to transfer meta-knowledge, which refers to shared information across tasks [12]. Notable meta-learning strategies are divided into several categories, e.g., metric-based [13,14], optimization-based [5,15,16], and model-based ones [17,18,19]. Metric-based algorithms map and adapt each input into an embedding space via an embedding function. Here, the embedding function clusters samples in class units through the training set and makes other classes more distant from each other. Optimization-based algorithms literally optimize the adaptation process. They do not use hand-crafted update rules, but rather make decisions through learning to better adapt to few-shot data. Meanwhile, in model-based meta-learning, sub-networks are employed for the adjustment stage. For example, one approach is to encode the training set using this sub-network model [20]. They encode the training set to parameterize a given task or utilize a separate buffer. The proposed TSPL encodes a task and performs label propagation based on it. Hence, TSPL is classified as a model-based approach.
MAML [5] is a well-known meta-learning scheme, whose goal is to improve the learning process itself rather than optimizing a specific task. MAML is a sort of model-agnostic approach because it can be applied to a wide range of machine learning models, including neural networks, without requiring any modifications to their architecture. The key idea behind MAML is to train a model in such a way that it can quickly adapt to new tasks with minimal fine-tuning. The MAML algorithm consists of two main steps:
- Inner Loop: In this step, the model is trained on a small amount of data from a specific task, typically called the support set. The parameters of the model are updated using gradient descent to minimize the loss on the support set.
- Outer Loop: In this step, the model’s updated parameters from the inner loop are evaluated on a separate set of data, called the query set. The loss on the query set is used to compute the gradients with respect to the initial parameters of the model. These gradients are then used to update the initial parameters to improve the model’s generalization across tasks.
By iteratively repeating the above-mentioned two steps on multiple tasks, MAML aims to find a set of initial parameters that allow the model to quickly adapt to new tasks by performing only a few gradient steps. This way, the model can effectively generalize to new tasks with limited labelled data.
Transductive meta-learning refers to a type of meta-learning framework that aims to leverage unannotated or partially labelled data during the meta-learning process, while traditional meta-learning approaches typically rely on labelled data from the training tasks to learn a model that can generalize to new tasks, the transductive meta-learning framework extends beyond the use of labelled data and takes advantage of unannotated or partially labelled data available during both the meta-training and meta-testing stages. This additional data is used to improve the meta-learning process and enhance the model’s ability to generalize to new tasks. Note that the transductive meta-learning framework typically consists of two main steps, i.e, meta-training and meta-testing. Transductive meta-learning aims to overcome limitations associated with traditional meta-learning approaches, which rely solely on labelled data. By utilizing unannotated or partially labelled data, transductive meta-learning can potentially improve the model’s performance and adaptability to new tasks, especially when labelled data is scarce or expensive to acquire.
While transductive meta-learning offers advantages in utilizing unannotated or partially labelled data, it also has some limitations that should be considered. One of them can be dependency on unannotated data quality. The performance of transductive meta-learning heavily relies on the quality and relevance of the available unannotated data. If the unannotated data is noisy, irrelevant, or not representative of the tasks, it can lead to poor generalization and hinder the effectiveness of the meta-learning process. Another one we consider is the limited availability of unannotated data, while transductive meta-learning aims to make use of unannotated or partially labelled data, the availability of such data may be limited in certain domains or scenarios. Acquiring large amounts of high-quality unannotated data can be challenging and expensive, which restricts the practicality and applicability of transductive meta-learning approaches in some real-world settings. Thus, while transductive meta-learning offers promising opportunities for leveraging unannotated data, it is essential to carefully consider these limitations and evaluate its feasibility and effectiveness in specific contexts before applying it to real-world problems.
From the perspective of transductive meta-learning, TPN [9] introduced the propagation of labels from the support set. It was designed to enhance inference on the query, while TPN enables supervised learning on unannotated query sets, it lacks task-adaptivity in the label propagation stage. On the other hand, MeTAL [11] presented a task-oriented loss. However, MeTAL should carefully consider various factors (e.g., architecture, input type) when designing the loss function. In contrast, the proposed TSPL employs task adaptation within the label propagation process through the graph structure. Unlike MeTAL, which relies on ALFA [21], the proposed method offers the advantage of being applicable to the backbone meta-learning framework.
Meanwhile, previous works such as [22,23,24] have taken into account the distribution discrepancy between datasets and its impact on the generalization performance of metric learning. They have also explored the benefits of optimizing the initial representation. To address these concerns, they introduced a model-independent meta-learning algorithm and developed a multi-scale meta-relational network. Furthermore, they extended this concept to incorporate visual reasoning tasks.
3. Proposed Method
To incorporate the data from unannotated query sets (QS) into the adjustment stage, a bypass strategy that never relies on ground truth (GT) labels is required. As a result, conventional transductive meta-learning approaches [10,11] have introduced label-free loss functions implemented through neural networks. Our inspiration for this study came from TPN [9], which propagates labels from the support set to the query set. TPN accomplishes this by generating a graph that encompasses samples from both the support set (SS) and the unannotated QS (UQS). By applying an explicit solution, TPN obtains predictions for UQS. Based on this concept, we conceived the idea of obtaining PLs for UQS through label propagation. Thus, we effectively make use of UQS in a supervised fashion for adaptation.
However, we never directly employ TPN for pseudo labelling due to its inability to task-adaptively propagate labels. More specifically, since PLs are trained as hard labels and the argmax operation used to extract these labels is non-differentiable, it becomes challenging to achieve end-to-end adaptation to the target task.
To achieve successful pseudo-labelling, we apply a task-specific property to label propagation. At this time, in order to leverage the benefits of end-to-end learning, we can ask whether it is advantageous to use PLs as soft labels. However, we have to consider that the bi-level optimization of MAML may incur noticeable memory cost. Thus, if PLs are used as soft labels for label propagation, it would increase memory as well as computational costs.
On the contrary, utilizing PLs as hard labels is highly connected to minimizing entropy [21]. Thus, we decide to employ PLs as hard labels for adaptation. In addition, we introduce a step to produce the parameters of GCN conditional on the present task.
Task-Specific Pseudo Labelling
This section describes the details of the proposed method. Figure 2 illustrates its overview. Task adaptation and label propagation constitute the inner loop. Similar to prior works such as [10,11], the parameters and logits of a neural network denoted as represent a task. is optimized for a target dataset, enabling to capture the data distribution and extract relevant features. , on the other hand, instinctively depicts the label space of the target task. Similarly, a task-represented vector is defined. The parameters and logits are individually averaged and combined into a unified feature vector. The dimension of is , assuming that the few-shot classification adopts an N-way K-shot setup and the backbone network comprises M layers.
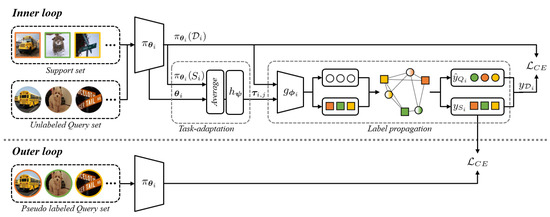
Figure 2.
The overall view of our method. Pseudo labels for the unannotated query set are generated through label propagation from the support set. The support set examples are represented by squares, while the query set examples are represented by circles. Each colour corresponds to a specific class in the current task.
Next, we leverage to introduce task-adaptivity into the label propagation process. To train UQS, we propagate the labels from SS to QS using , i.e., the graph construction network. In this step, by incorporating , we adjust each parameter of . Then, a task-adaptation parameter is generated by a small multi-layer perceptron (MLP) that takes as the input. Thus, task-adaptation using is represented by
where L represents the quantity of layers in . By incorporating the task-adaptation parameter into , we enable to be conditional on the current task, enhancing the effectiveness of the label propagation process for that specific task. Let C denote the complexity of . Then, the complexity increase in TSPL with respect to TPN amounts to . However, the rise in complexity is insignificant as is implemented by a small-size MLP, which is further examined in our experiments.
In the process of label propagation, the task-specific GCN constructs a graph by incorporating the logits from both SS and QS. Then, PLs are transformed into by argmax. This allows us to leverage UQS for task adaptation via a full supervision. Subsequently, by concatenating the hard labels with the SS label , we generate the label for the combined set , which includes samples from both the support set and the query set. Utilizing , we perform adaptation for the target task within the inner loop, optimizing the parameters of .
Using the pseudo-labelled QS, all trainable parameters, namely , , and , are optimized in the outer loop. However, using as an one-hot vector makes non-trainable because of non-differentiable argmax, so we take a different approach. Before applying argmax, we compute the cross-entropy (CE) loss. The CE loss is computed between the output of and the GT label of QS. We achieve a more precise propagation of PLs, by enabling the outer loop to learn the parameters in regards to .
Consequently, by optimizing the model with a larger number of samples, the proposed method mitigates the occurrence of sample bias in the inner loop. This implies that the proposed approach serves as a viable solution to address the limitations of transductive meta-learning discussed earlier. The summarized procedure of the proposed method can be found in Algorithm 1.
| Algorithm 1 Task-specific pseudo labelling |
Definition 1: : Learning rates Definition 2: J: The number of inner-loop updates
|
4. Experiments
In all experiments, we employed a configuration based on four convolutional blocks sourced from [6]. Each convolutional block encompasses a single convolution layer with a kernel size of 3 × 3, a batch normalization layer [25], and a ReLU activation function. A max-pooling layer with a 2 × 2 kernel and stride 2 is positioned between the convolutional blocks. For the optimization in the outer loop, we utilized the Adam optimizer [26]. The sub-network follows a simple MLP architecture with two layers. ReLU is applied, and the final stage employs a sigmoid function.
We utilized two well-known datasets commonly used for few-shot classification tasks. The first dataset is miniImageNet [27], which is derived from the ImageNet dataset [28]. It consists of 100 classes and a total of 60,000 images. A total of 600 images with dimensions of 84 × 84 constitute a class. These 100 classes are divided into three sets: 64 classes for meta-training, 16 classes for meta-validation, and 20 classes for meta-testing. Importantly, there is no overlap between the classes in each set. The second dataset we employed is tieredImageNet [29], which is larger in scale compared to miniImageNet. TieredImageNet contains 608 classes with a total of 779,165 images of 84 × 84 pixels, which are extracted from ImageNet, similar to miniImageNet. Unlike miniImageNet, the tieredImageNet are classified into 34 higher-level categories. Specifically, 20 categories are used for meta-training, 6 categories for meta-validation, and 8 categories for meta-testing. Just like in miniImageNet, the classes in tieredImageNet do not overlap between different phases. The phase-wise mutual exclusivity of classes makes both datasets appropriate for assessing the generalization ability.
Data augmentation was not applied during the learning process. For the 1-shot setting, the batch size was set to 4, while for the 5-shot setting, it was set to 2. The inner loop optimization followed the configuration of CxGrad, which involved using a stochastic gradient descent (SGD) optimizer. , , and were 0.01, 1.0, and 0.001, respectively, and the models were trained for five iterations. As for the outer loop optimization, Adam was used as the optimizer with a learning rate of 0.001. The miniImageNet dataset was trained for 50,000 iterations, while tieredImageNet was trained for 125,000 iterations. All reported numbers are averages obtained from three different random seeds to ensure robustness and generalizability of the results. The proposed method was implemented using the PyTorch framework, and the iteration times were measured on a Quadro RTX 8000 GPU.
Note that TSPL and conventional gradient-based meta-learning techniques are independent of each other, allowing TSPL to be seamlessly integrated. As a result, we employed a combined model of TSPL and CxGrad [30] for all the experiments in this paper. This combined model facilitated representation change by enhancing backbone learning, leading to significant improvements in the performance of MAML.
4.1. Few-Shot Classification
We conducted an experiment for five-way few-shot classification as in Table 1. This experiment is composed of 1-shot and 5-shot classifications for the validation set. Each value of the table corresponds to the ensemble of top five results in terms of accuracy. In the 1-shot classification, our method demonstrates the best performance for both datasets. While TSPL demonstrated an exceptional performance improvement of approximately 2% over the third-ranked method in miniImageNet, the enhancement in tieredImageNet was relatively minimal. We found that the inherent characteristics of the backbone framework, namely TPN, cause the variation in performance improvement between the two different shot scenarios. That is, TPN employs a simple GCN with small receptive fields to propagate labels. Consequently, it struggles to grasp relevant information from five to shot data. Hence, achieving higher performance with many-shot data necessitates the use of an improved GCN.

Table 1.
Accuracy in five-way few-shot classification.
4.2. Visualization
In this section, the visualization in the embedding space investigates the association between UQS and QS. We employ UMAP [35], a popular non-linear dimension reduction technique commonly used to visualize the embeddings of examples. UMAP makes us identify the relationship between the pseudo-labelled UQS and the SS of the same class. The UMAP for miniImageNet is visualized in Figure 3. This is for five-way 5-shot classification. With each colour indicating the class indicated by the PL, the geometric figures represent distinct GT classes. The support set (SS) is represented by figures that are larger in size and have a darker colour, while the query set (QS) is represented by smaller figures with a lighter colour. For instance, a sample in the QS can be depicted in blue (representing C1) and circle shape (representing C0), if it has a GT label of C0 and a PL of C1. Figure 3 reveals that majority of samples in the UQS are located near the SS of each ground truth label. Additionally, it is observed that the PLs align with the corresponding GT labels. This indicates that by constructing task-specific graphs, TSPL achieves effective pseudo labelling, thereby yielding positive outcomes for adaptation.
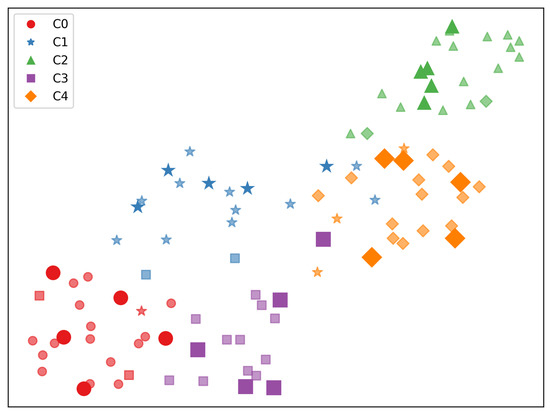
Figure 3.
The visualization demonstrates the procedure that synthetic labels are assigned to unannotated QSs. Multiple samples from the unannotated QS are assigned the same label as the corresponding GT. Additionally, samples with the equivalent synthetic label exhibit close proximity to one another in the embedding space.
4.3. Ablation Study
This subsection provides an analysis on how to construct task-adaptive graphs and then examines responsible for regulating the extent of propagated information. Additionally, it investigates the impact of the sub-network for task adaptation on computational complexity. The iteration time in training is measured on Quadro RTX 8000.
From Table 2, we can find that the use of task-specific graph construction increases approximately 1.1%. On the other hand, the iteration time of TSPL in training is 0.72 s, representing a mere 1.4% increase compared to TPN. Importantly, it should be noted that the inference time of the trained model remains unchanged, as the additional cost incurred by the proposed method is limited to the learning process alone. Consequently, we assert that TSPL entails a highly reasonable cost, considering its benefits and impact on performance.

Table 2.
The adaptability to tasks and the ability to learn of .
5. Discussion
Table 1 provides evidence of the superior performance of the proposed method over other meta-learning approaches in typical few-shot classification tasks. Moreover, Table 2 demonstrates that significant performance improvements can be achieved with only a minimal increase in inference time. These two experimental results substantiate the main contributions of the proposed method. Furthermore, Figure 3 visually showcases the effective adaptive graph construction of the proposed pseudo-labelling technique, indirectly confirming the technical superiority of the approach. However, it is acknowledged that the proposed method still possesses certain structural limitations. For instance, the accuracy in the 5-shot scenario remains unsatisfactory. Future research endeavours will focus on exploring structural approaches to address this limitation and further improve the method’s performance.
6. Conclusions
To address the sample bias issue encountered in conventional meta-learning, transductive meta-learning leverages an unannotated QS in the adaptation stage. This paper introduces a novel transductive meta-learning approach that incorporates task-specific pseudo labelling. Specifically, synthetic labels are propagated into the unannotated QSs. Consequently, learning can occur within the framework of the established supervised setting. Through extensive experimentation, it was demonstrated that the proposed method effectively achieves adaptation and notably achieves state-of-the-art (SOTA) performance in 1-shot classification.
In the future, the proposed method holds potential for application in other computer vision tasks with similar objectives. However, it is worth noting that the current implementation exhibits a structural limitation, resulting in unacceptable 5-shot accuracy. This challenge remains an area for future exploration and improvement.
Author Contributions
Methodology, S.L. (Seunghyun Lee); Writing—original draft, S.L. (Sanghyuk Lee); Supervision, B.C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was fully supported by the INHA UNIVERSITY Research Grant.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, W.; Huang, K.; Geng, J.; Deng, X. Multi-scale metric learning for few-shot learning. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 1091–1102. [Google Scholar] [CrossRef]
- Shao, S.; Xing, L.; Xu, R.; Liu, W.; Wang, Y.J.; Liu, B.D. MDFM: Multi-decision fusing model for few-shot learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 5151–5162. [Google Scholar] [CrossRef]
- Zhou, D.W.; Wang, F.Y.; Ye, H.J.; Ma, L.; Pu, S.; Zhan, D.C. Forward compatible few-shot class-incremental learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9046–9056. [Google Scholar]
- Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5149–5169. [Google Scholar] [CrossRef] [PubMed]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching networks for one shot learning. arXiv 2016, arXiv:1606.04080. [Google Scholar] [CrossRef]
- Zhang, L.; Zuo, L.; Du, Y.; Zhen, X. Learning to adapt with memory for probabilistic few-shot learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4283–4292. [Google Scholar] [CrossRef]
- Cui, W.; Guo, Y. Parameterless transductive feature re-representation for few-shot learning. In Proceedings of the International Conference on Machine Learning, Virtual Event, 18–24 July 2021; pp. 2212–2221. [Google Scholar]
- Liu, Y.; Lee, J.; Park, M.; Kim, S.; Yang, E.; Hwang, S.J.; Yang, Y. Learning to propagate labels: Transductive propagation network for few-shot learning. arXiv 2018, arXiv:1805.10002. [Google Scholar]
- Antoniou, A.; Storkey, A.J. Learning to learn by self-critique. arXiv 2019, arXiv:1905.10295. [Google Scholar] [CrossRef]
- Baik, S.; Choi, J.; Kim, H.; Cho, D.; Min, J.; Lee, K.M. Meta-Learning with Task-Adaptive Loss Function for Few-Shot Learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 17 October 2021; pp. 9465–9474. [Google Scholar]
- Thrun, S.; Pratt, L. Learning to learn: Introduction and overview. In Learning to Learn; Springer: Berlin/Heidelberg, Germany, 1998; pp. 3–17. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 6–11 July 2015; Volume 2. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. arXiv 2017, arXiv:1703.05175. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Denil, M.; Gomez, S.; Hoffman, M.W.; Pfau, D.; Schaul, T.; Shillingford, B.; De Freitas, N. Learning to learn by gradient descent by gradient descent. arXiv 2016, arXiv:1606.04474. [Google Scholar] [CrossRef]
- Zhu, H.; Li, L.; Wu, J.; Zhao, S.; Ding, G.; Shi, G. Personalized image aesthetics assessment via meta-learning with bilevel gradient optimization. IEEE Trans. Cybern. 2020, 52, 1798–1811. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yuan, Y.; Zheng, G.; Krikidis, I.; Wong, K.K. Embedding model-based fast meta learning for downlink beamforming adaptation. IEEE Trans. Wirel. Commun. 2021, 21, 149–162. [Google Scholar] [CrossRef]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T. Meta-learning with memory-augmented neural networks. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1842–1850. [Google Scholar]
- Lai, N.; Kan, M.; Han, C.; Song, X.; Shan, S. Learning to Learn Adaptive Classifier-Predictor for Few-Shot Learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3458–3470. [Google Scholar] [CrossRef] [PubMed]
- Munkhdalai, T.; Yu, H. Meta networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2554–2563. [Google Scholar]
- Grandvalet, Y.; Bengio, Y. Semi-supervised learning by entropy minimization. Adv. Neural Inf. Process. Syst. 2004, 17. [Google Scholar]
- Zheng, W.; Liu, X.; Ying, L. Research on image classification method based on improved multi-scale relational network. PeerJ Comput. Sci. 2021, 7, e613. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Ying, L. Characterization inference based on joint-optimization of multi-layer semantics and deep fusion matching network. PeerJ Comput. Sci. 2022, 8, e908. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Liu, X.L.; Ni, X.; Yin, L.Y.; Yang, B. Improving Visual Reasoning Through Semantic Representation. IEEE Access 2021, 9, 91476–91486. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the ICLR (Poster), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ravi, S.; Larochelle, H. Optimization as a Model for Few-Shot Learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Ren, M.; Ravi, S.; Triantafillou, E.; Snell, J.; Swersky, K.; Tenenbaum, J.B.; Larochelle, H.; Zemel, R.S. Meta-Learning for Semi-Supervised Few-Shot Classification. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lee, S.; Lee, S.; Song, B.C. Contextual Gradient Scaling for Few-Shot Learning. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 July 2022; pp. 834–843. [Google Scholar]
- Oh, J.; Yoo, H.; Kim, C.; Yun, S.Y. BOIL: Towards representation change for few-shot learning. arXiv 2020, arXiv:2008.08882. [Google Scholar]
- Antoniou, A.; Edwards, H.; Storkey, A. How to train your MAML. In Proceedings of the Seventh International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Baik, S.; Choi, M.; Choi, J.; Kim, H.; Lee, K.M. Meta-learning with adaptive hyperparameters. Adv. Neural Inf. Process. Syst. 2020, 33, 20755–20765. [Google Scholar]
- Baik, S.; Hong, S.; Lee, K.M. Learning to forget for meta-learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 19 June 2020; pp. 2379–2387. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).