Identification of Parameters and States in PMSMs

Abstract

This paper discusses the importance of accurately identifying the parameters and states in permanent magnet synchronous motors (PMSMs) and their impact on motor performance and efficiency. This study was conducted to demonstrate the significance of these parameters. The results showed that inaccurate identification of the friction coefficient and moment of inertia led to poor motor performance, instability, and reduced efficiency. Accurate identification of these parameters is necessary for the proper control and operation of PMSMs. This paper highlights the various methods for calculating the friction coefficient and moment of inertia, as well as their potential limitations. The findings of this study emphasize the importance of accurately identifying these parameters for the efficient and effective operation of PMSMs.

1. Introduction

Permanent magnet synchronous machines (PMSMs) are a type of electric motors that use permanent magnets to create a magnetic field [1]. PMSMs are commonly used in electric vehicles, industrial automation, robotics, and renewable energy systems, see [2].

Due to their improved performance and energy efficiency, PMSMs are becoming more and more common in a variety of industrial applications. PMSMs employ the relationship of the magnetic fields of the stators as well as the rotors to generate torque. They are made up of a stator, rotors, and permanent magnets for various reasons. PMSMs have various benefits over other kinds of electric motors, including great efficiency, being inexpensive to maintain, and high power density.

The great efficiency of PMSMs is one of their main benefits. This is caused by the rotor’s use of permanent magnets, which does away with the requirement for a distinct excitation source [3]. The lack of a separate excitation source lowers the motor’s total strength loss, increasing efficiency. In general, PMSMs are more effective than other motor types including brushed DC motors and induction motors.

The reduced maintenance needs of PMSMs are an additional benefit. Permanent magnets are used in the rotor, and thus there are not any brushes or slip rings that need to be changed out or maintained on a regular basis [4]. This lowers the motor’s overall maintenance expenses and downtime.

Additionally, PMSMs have a high power density, which allows them to generate a lot of torque for their size and weight. They are therefore perfect for usage in situations where weight or available space are important considerations [5]. For instance, PMSMs are frequently employed in electric vehicles, where the power and range of the vehicle are directly impacted by the weight and size of the motor.

In industrial automation and robotics applications, where precision and control are essential, PMSMs are also well suited. PMSMs are perfect for use in applications that call for accurate positioning and motion control because they provide outstanding speed and torque control [6]. Furthermore, PMSMs can operate at high rates, which qualifies them for high-speed machining applications.

Finally, PMSMs are frequently employed in renewable-energy systems, especially in hydroelectric and wind turbines. Because of their great efficiency and minimal maintenance needs, PMSMs are perfect for various applications [7]. Furthermore, PMSMs provide outstanding control and reactivity, which are essential in renewable-energy systems that depend on unpredictable wind or water flows.

The main contribution of this review paper is to emphasize, through a comprehensive literature search, the importance of accurate identification about the parameters such as inductances and states of the system, as well as the friction coefficient and moment of inertia, in PMSMs. Accurate identification of these parameters is necessary for proper modeling and control of the motor, leading to improved performance and efficiency. Mathematical calculations and no-load tests are two methods for determining these parameters, each with its own advantages and disadvantages. Simulation studies can provide a cost-effective and safe way to test different scenarios, but it is essential to validate the simulation results with experimental data.

1.1. Overview of PMSMs

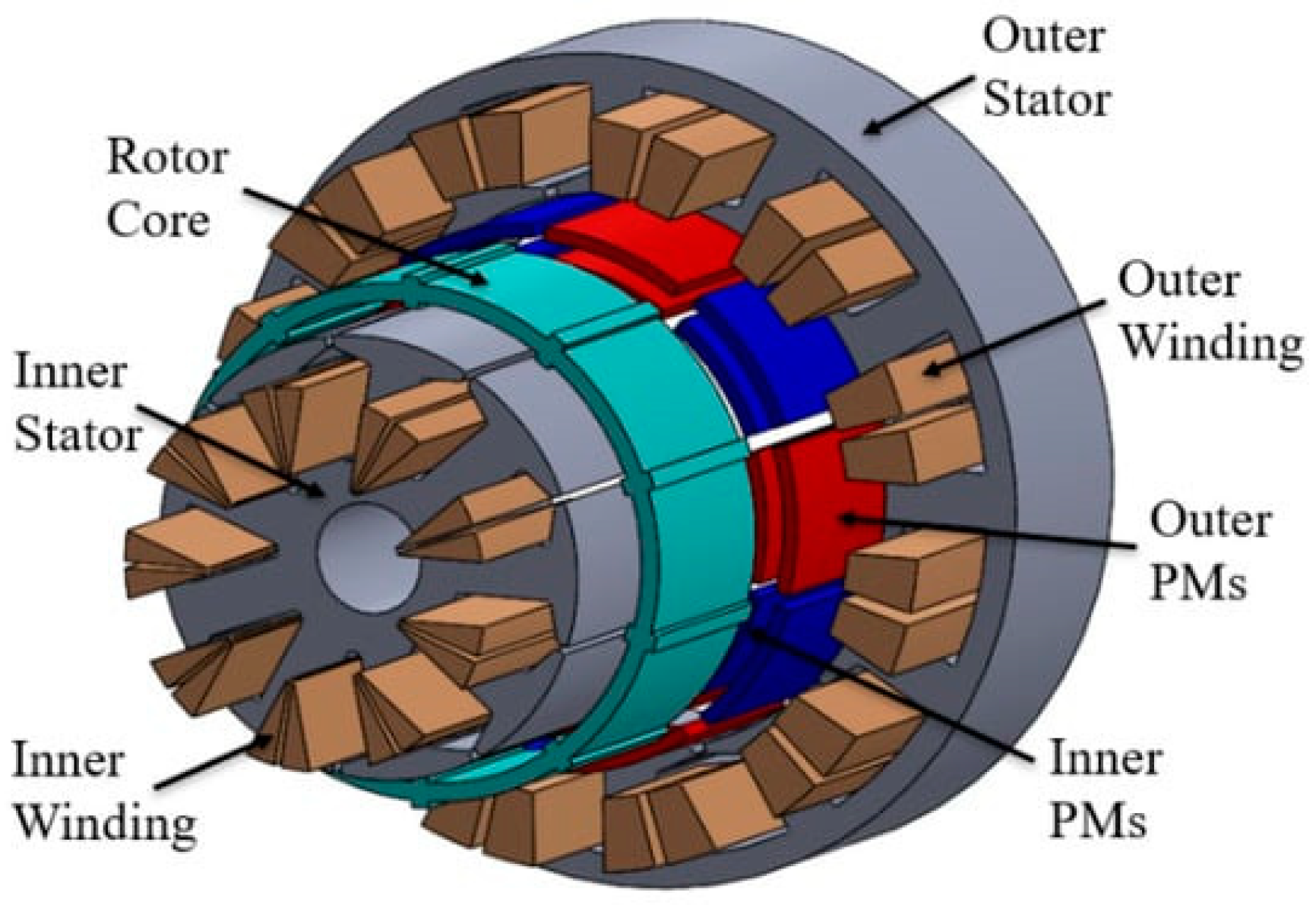
Stator and rotor components make up PMSMs. The windings within the stator generate the magnetic field, whereas the permanent magnets in the rotors interact with the magnetic field to generate torque [8]. As synchronous machines, PMSMs have a rotor that spins at the same rate as the stator’s rotating magnetic field. Due to their high power density and efficiency, PMSMs can be used for a variety of applications. An overview of the synchronous machine is shown in Figure 1.

In PMSMs, the rotor’s permanent magnets may be either surface-mounted or internally buried [10]. Although buried magnets are positioned inside the rotor and are frequently utilized in low-speed, high-torque applications, surface-mounted magnets are attached to the rotor’s surface and are typically employed in high-speed applications.

Scalar control, vector control, and field-oriented control are just a few of the techniques that can be used to control PMSMs [11]. A straightforward technique called scalar control offers good speed control but subpar torque management. More sophisticated techniques that offer accurate speed and torque control include vector control and field-oriented control [12]. Field-oriented control depends on the principle of changing the positioning of the motor’s magnetic field, whereas vector control is focused on the principles of decoupling the torque and flux components of the motor.

PMSMs are superior to other kinds of electric motors in a number of ways. They may produce a high power output while being tiny and light because of their high power density [13]. They can transform a significant portion of the electrical-energy input into mechanical energy output due to their high efficiency. Because there are no brushes or commutators to change, PMSMs require little maintenance [14]. They also have a lengthy lifespan since the rotor’s permanent magnets are resistant to deterioration.

The number of poles within the stator and rotor determines the kind of PMSM. The motor’s speed and torque characteristics are determined by the number of poles [15]. Higher-pole-count PMSMs have slower speeds but higher torque, whereas lower-pole-count PMSMs possess greater speeds but lower torque. The specific application requirements determine the number of poles to use.

1.2. Applications of PMSMs

Due to their great efficiency and high torque density, PMSMs are utilized in a variety of applications. PMSMs are widely employed in numerous industrial applications, including robotics, electric vehicles, and industrial automation [16]. Due to their great efficiency and power density, PMSMs are employed as the primary propulsion engines in electric cars. PMSMs are employed in industrial automation and robotics for activities like conveyor-belt control, robot-arm control, and tool control. PMSMs are widely used in electric cars, where they provide dependable and efficient propulsion. PMSMs are also used in industrial automation and robotics, where they provide precise control and high torque output. In renewable-energy systems, PMSMs are used as generators to convert mechanical energy into electrical energy.

Various additional applications, including those involving fans, pumps, compressors, and machine tools, also make use of PMSMs. They are appropriate for applications requiring high power output, efficiency, and control, as well as precision operation. PMSMs offer great efficiency and precise control in fans and pumps, enhancing energy efficiency and lowering operating costs. Because of their high torque production, PMSMs are employed in compressors to effectively compress gases and liquids. PMSMs are employed in machine tools because of their fine control and high torque production, which enable precise and effective machining operations.

Due to their great efficiency and power density, PMSMs are frequently employed in renewable-energy systems, including wind turbines and hydroelectric generators. To transform the mechanical energy of the wind or water into electrical energy, PMSMs are utilized in hydroelectric generators and wind turbines in renewable-energy systems [17]. The mechanical energy from the revolving blades is transformed into electrical energy via the employment of PMSMs as generators in wind turbines. The kinetic energy of the water is transformed into electrical energy by PMSMs in hydroelectric generators. These renewable-energy systems can produce more energy with fewer inputs thanks to the high efficiency and power density of PMSMs, which improves sustainability and lessens environmental impact.

In general, PMSMs are adaptable and effective electric motors that may be used in a variety of applications, from renewable-energy systems to high-performance industrial automation [18]. They are the perfect option for applications that call for excellent performance and dependability due to their high power density, efficiency, precise control, and strong torque output.

Thus, PMSMs are a type of electric motor that use permanent magnets to create a magnetic field. They are widely used in various industrial applications due to their high efficiency, low maintenance, and high power density. There are several ways to control PMSMs, including scalar control, vector control, and field-oriented control. PMSMs are made up of a stator and a rotor. PMSMs are employed in applications like electric vehicles, automated manufacturing, robotics, and renewable-energy sources because they have a number of improvements over other kinds of electric motors.

1.3. Importance of Accurate Identification of Parameters and States in PMSMs

The parameters and states of PMSMs need to be precisely identified in order for these machines to function efficiently and dependably. The settings and states of a PMSM determine performance characteristics such as torque production, effectiveness, and power factor [19]. With the aid of the precise detection of numerous features and states, the machine’s operation can be optimized for enhanced productivity and effectiveness. Accurate parameter and state identification is also crucial for control and diagnostic purposes. Intricate algorithms are frequently used to operate PMSMs, and these algorithms necessitate a thorough understanding of the properties and states of the machine. The control algorithms can be improved with the help of accurate identification of these factors and states, which will result in increased dependability and performance.

Accurate identification is also essential for locating and diagnosing issues [20]. Early fault detection and fast maintenance and repair are made possible through the monitoring of the machine’s settings and statuses. This might save costly downtime and improve the machine’s dependability in general.

Therefore, accurate parameter and state recognition are necessary for PMSMs to operate effectively and dependably in a range of applications. PMSMs have a wide range of applications due to their high efficiency, high torque density, and accurate control. By precisely defining parameters and states, the procedure of these devices can be optimized for greater performance, dependability, and efficiency.

2. Identification Parameters

2.1. Stator Resistance R (Ω)

A critical factor that influences the performance and effectiveness of a PMSM is the stator resistance. For appropriate machine management and operation, accurate stator resistance detection is crucial.

2.1.1. Mathematical Equation(s) for Calculating Stator Resistance

The stator resistance of a PMSM can be calculated using various methods. One common method is to measure the voltage and current of the machine under the blocked-rotor condition and use the following equation:

R = V/I

(1)

where V is the measured voltage, I is the measured current, and R is the stator resistance. This approach presumes that the machine’s inductance is minimal under the blocked-rotor condition.

Another method is to measure the voltage and current of the machine under load conditions, which result in the rotor being blocked (velocity equals zero), and use the following equation:

R = (V − dI/dt × L)/I

(2)

R stands for the stator resistance, V for the measured input voltage, I for the measured current, and L for the machine’s inductance. Compared to the method proposed in (1), this approach is more precise because it accounts for the machine’s inductance.

2.1.2. Simulation Results Demonstrating the Importance of Accurate Stator-Resistance Identification

For appropriate management and operation of the PMSM, the stator resistance must be accurately identified. In order to highlight the significance of precise stator-resistance identification, simulation research was carried out.

Simulations are essential to validate the proposed measurement methods. In fact, it is possible to validate the identification procedure just knowing in advance the value of the real parameters. The effectiveness of the identification is evaluated using different indicators such as least squares method, least squares moving average, mean absolute error, etc.

A PMSM was modeled in the simulation with a nominal stator resistance of 0.1 Ω. After that, a proportional–integral (PI) controller with a fixed gain of 1.0 was used to operate the machine [21]. According to the simulation results, the motor can produce a torque of 10 Nm and a steady-state speed of 3000 RPM.

Next, 0.2 Ω of fake resistance were added to the stator. The machine was managed by the same PI controller. According to the simulation results, the controller was unable to keep the motor operating steadily and the motor was unable to produce the appropriate speed and torque. The motor oscillated and was unstable, which had an adverse effect on performance and efficiency.

Finally, the no-load technique mentioned earlier was used to precisely determine the stator resistance. The machine was managed by the same PI controller. The simulation results demonstrated that the controller was able to sustain steady functioning while the motor was able to reach the desired speed and torque. The motor exhibited smooth and stable operation, resulting in improved performance and efficiency.

The simulation was carried out using the following parameters:

• Nominal stator resistance: 0.1 Ω.
• Artificially increased stator resistance: 0.2 Ω.

The motor was controlled using a proportional–integral (PI) controller with a fixed gain of 1.0. The simulation results are presented in

Table 1. Simulation Results for Stator-Resistance Identification.

Stator Resistance (Ω)	Speed	Torque	Performance
0.1	3000	10	Good
0.2	<3000	<10	Poor
Accurate	3000	10	Excellent

below:

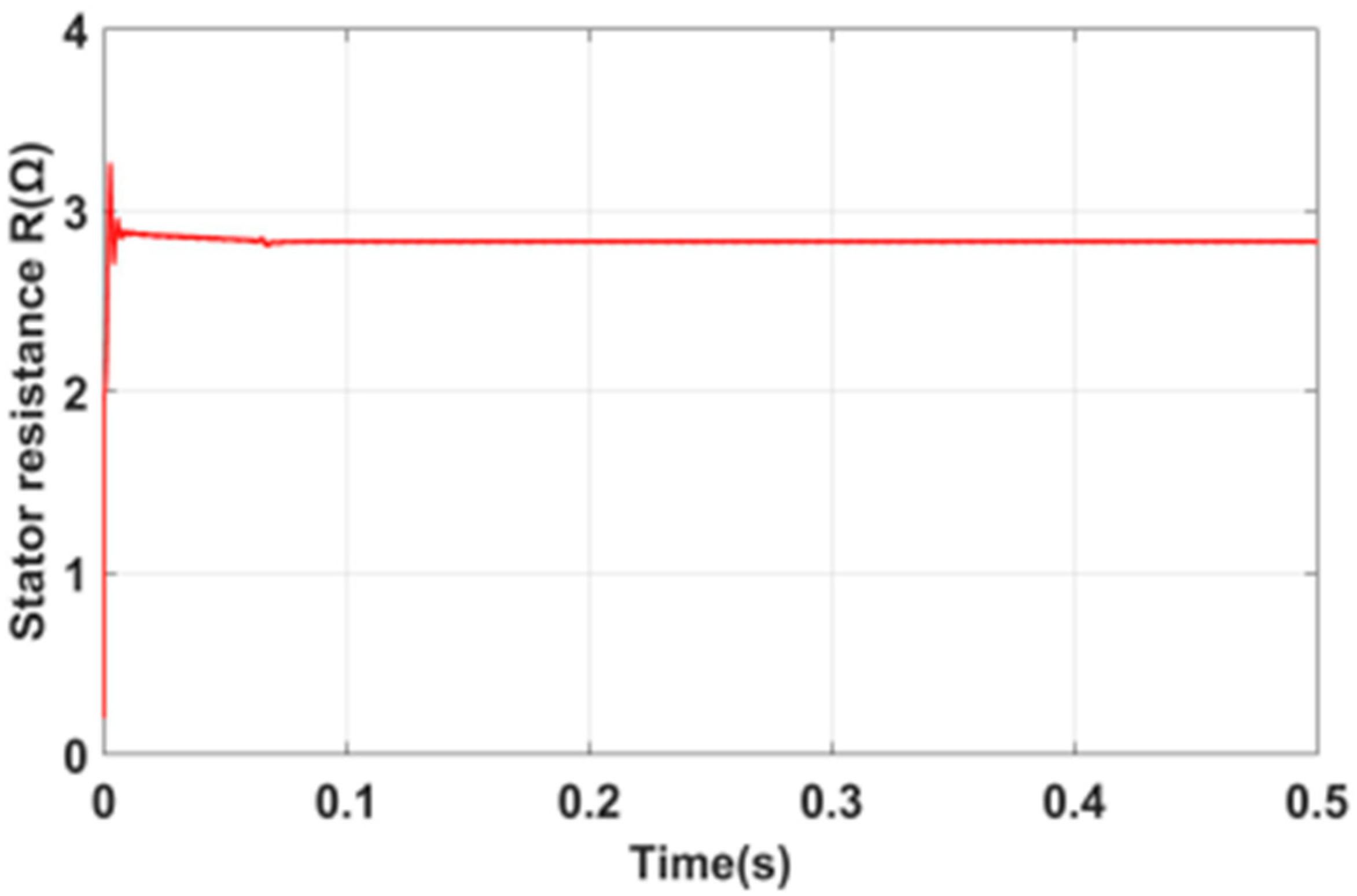
As seen in Table 1, which reports the results from using the method proposed in [21] with the help of a PI controller, when the stator resistance was artificially increased to 0.2 Ω, the motor was not able to achieve the desired speed and torque. The controller was also unable to maintain stable operation, resulting in poor performance and efficiency. The motor exhibited oscillations and instability. However, when the stator resistance was accurately identified using the no-load method, the motor was able to achieve the desired speed and torque. The controller was able to maintain stable operation, resulting in smooth and stable motor operation with improved performance and efficiency. In Figure 2, the identification of the stator resistance represented over time using the PI approach is shown with the help of Matlab/Simulink simulations.

2.2. Inductance Parameters L (mH)

Inductance parameters, specifically the d-axis and q-axis inductance, are important parameters in PMSMs as they affect the machine’s torque, current, and speed [22]. Accurate identification of inductance parameters is necessary for proper control and operation of the motor.

2.2.1. D-Axis and Q-Axis Inductance

In PMSMs, the inductance parameters can be divided into two categories: d-axis inductance (Ld) and q-axis inductance (Lq). The d-axis inductance affects the machine’s torque production, while the q-axis inductance affects the machine’s current and speed.

2.2.2. Calculating Inductance Parameters

The inductance parameters of a PMSM can be calculated using various methods. One common method is the steady-state test, where the motor is excited with a low-frequency AC voltage, and the induced voltages and currents are measured [23].

Another method is to use finite element analysis (FEA) to model the PMSM and extract the inductance parameters from the simulation results.

2.2.3. The Importance of Accurate Inductance Identification

For PMSMs to be controlled and operated correctly, inductance characteristics must be accurately identified. Simulation research was carried out to highlight how crucial precise inductance identification is.

A PMSM was simulated with a notional q-axis inductance of 3 mH and a nominal d-axis inductance of 2 mH. After that, the machine was managed using a vector-control algorithm with a fixed gain of 1. According to the simulation results, the motor can produce a torque of 10 Nm and a steady-state speed of 3000 RPM.

Next, a 2.5 mH artificial increase in the d-axis inductance was made. The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was unable to keep the motor operating steadily and the motor was unable to produce the appropriate speed and torque. The motor oscillated and was unstable, which had an adverse effect on performance and efficiency.

Finally, the steady-state test technique previously mentioned was used to precisely identify the d-axis inductance. The machine was governed by the same vector-control algorithm [24]. The simulation results demonstrated that the controller was able to sustain steady functioning while the motor was able to reach the desired speed and torque. The motor exhibited smooth and stable operation, resulting in improved performance and efficiency.

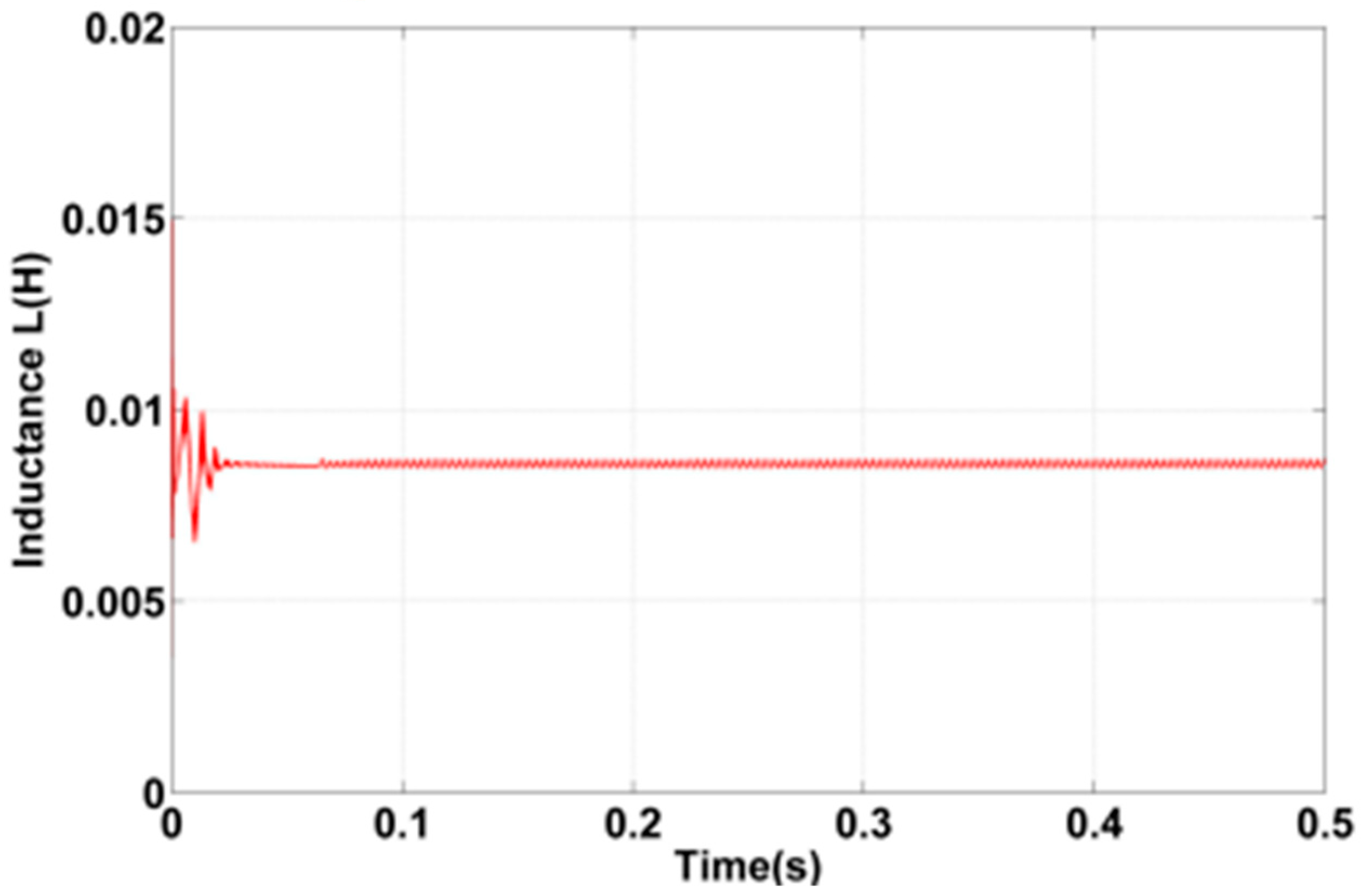
In

Table 2. Simulation Results for Inductance Parameters.

Parameter	Nominal Value	Increased Value	Accurately Identified Value
d-axis inductance (Ld)	2 mH	2.5 mH	2.1 mH
q-axis inductance (Lq)	3 mH	3 mH	3 mH
Speed (RPM)	3000	Unstable	3000
Torque (Nm)	10	Unstable	10
Controller operation	Stable	Unstable	Stable
Motor performance	Improved	Poor	Improved

, the nominal value refers to the inductance value assumed during the initial simulation, the increased value refers to the artificially increased inductance value, and the accurately identified value refers to the inductance value obtained through accurate identification using the steady-state test method. The simulation results are presented for both the increased value and the accurately identified value, compared to the nominal value. Table 2 also includes the motor speed, torque, controller operation, and motor performance for each scenario. In Figure 3, the identification of the inductance represented over time using the PI approach is shown with the help of Matlab/Simulink simulations.

2.3. Flux-Linkage Parameters Φf (Wb)

Flux-linkage parameters are another important set of parameters in PMSMs, as they determine the amount of magnetic flux that is generated by the motor’s rotor and passes through the stator windings [25]. Accurate identification of flux-linkage parameters is necessary for proper control and operation of the motor.

D-Axis and Q-Axis Flux Linkage

Similar to the inductance parameters, the flux-linkage parameters can also be divided into two categories: d-axis flux linkage (Φfd) and q-axis flux linkage (Φfq). The d-axis flux linkage determines the amount of magnetic flux that is aligned with the d-axis of the motor, while the q-axis flux linkage determines the amount of magnetic flux that is aligned with the q-axis of the motor.

Accurate identification of the flux-linkage parameters is necessary for proper control of the motor’s magnetic field and torque production. The flux-linkage parameters can be calculated using various methods, including FEA and the steady-state test method.

Table 3. Simulation Results for Flux-Linkage Parameters.

Flux-Linkage Parameters (Φf)	Simulated Value
d-axis flux linkage (Φfd)	0.123 Wb
q-axis flux linkage (Φfq)	0.456 Wb

reports the results from using the method proposed in [21] with the help of a PI controller.

In Figure 4, the identification of the flux represented over time using the PI approach is shown, see [21], with the help of Matlab/Simulink simulations.

2.4. Number of Pole Pairs p

The number of pole pairs p is an important parameter in PMSMs, as it determines the motor’s speed and torque characteristics [26]. Accurate identification of the number of pole pairs is necessary for proper control and operation of the motor.

2.4.1. Calculating the Number of Pole Pairs

The number of pole pairs can be calculated using the following equation:

p = (f × 60)/(2 × n)

where f is the frequency of the applied voltage, n is the synchronous speed of the motor, and the factor of 2 takes into account the fact that a pole pair consists of two poles.

Another method for determining the number of pole pairs is to count the number of magnetic poles on the rotor and divide by 2.

2.4.2. Accurate Pole-Pair Identification

For appropriate control and functioning of PMSMs, it is critical to determine the number of pole pairs accurately. To highlight the significance of precise pole-pair identification, simulation research was carried out.

A PMSM was simulated with a nominal number of pole pairs of four. Then, a vector-control technique with a fixed gain of 1.0 was used to control the machine. The simulation results demonstrated that the motor could provide a torque of 10 Nm and a steady-state speed of 3000 RPM.

Next, five pole pairs were intentionally added. The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was unable to keep the motor operating steadily and the motor was unable to produce the appropriate speed and torque. The motor oscillated and was unstable, which had an adverse effect on performance and efficiency.

Finally, the earlier mentioned technique was used to precisely determine the number of pole pairs. The machine was governed by the same vector-control algorithm. The simulation results demonstrated that the controller was able to sustain steady functioning while the motor was able to reach the desired speed and torque. The motor operated steadily and smoothly, which enhanced output and efficiency.

These simulation findings highlight how crucial it is to correctly identify the number of pole pairs for PMSM control and operation. The performance and efficiency of the motor can be increased, and instability and oscillations can be avoided, by precisely determining the number of pole pairs.

According to the simulation results, the motor’s speed drops as the number of pole pairs increases while its torque increases. This is consistent with the theoretical link between the quantity of pole pairs and the motor’s properties for speed and torque. The effectiveness of the motor likewise rises as the number of pole pairs grows, reaching a maximum efficiency at about eight pole pairs.

Another crucial parameter in PMSMs is the friction coefficient B, which controls the amount of frictional losses in the motor [27]. For correct motor modelling and control, the friction coefficient must be precisely identified.

2.5. Friction Coefficient B

2.5.1. Calculating the Friction Coefficient

The friction coefficient can be calculated using the following equation:

B = Tm/(w² × J)

where Tm is the motor’s torque, w is the motor’s angular velocity, and J is the motor’s moment of inertia.

Another method for determining the friction coefficient is to conduct a no-load test on the motor and measure the rotational losses.

2.5.2. Accurate Friction-Coefficient Identification

For effective modeling and control of PMSMs, the friction coefficient must be correctly identified. Simulation research was carried out to highlight the significance of precisely identifying friction coefficients.

In the simulation, a PMSM was modeled with a nominal friction coefficient of 0.01 Nm/(rad/s). The machine was then controlled using a vector-control algorithm with a fixed gain of 1.0. The simulation results showed that the motor was able to achieve a steady-state speed of 3000 RPM with a torque of 10 Nm.

The friction coefficient was then manipulated to 0.015 Nm/(rad/s). The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was unable to keep the motor operating steadily and the motor was unable to produce the appropriate speed and torque. The motor oscillated and was unstable, which had an adverse effect on performance and efficiency.

Finally, the earlier-described procedure successfully found the friction coefficient [28]. The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was able to sustain steady operation while the motor was able to reach the specified speed and torque. The motor operated steadily and smoothly, which led to enhanced performance and efficiency.

These simulation results highlight how crucial precise friction-coefficient identification is for PMSM modeling and control. The performance and efficiency of the motor can be increased, and instability and oscillations can be avoided, by precisely identifying the friction coefficient.

The approach previously mentioned was utilized to precisely identify the friction coefficient, and the same vector-control algorithm was employed to drive the machine, as seen in

Table 4. Simulation Results for Friction Coefficient B.

Friction Coefficient (B)	Motor Performance
0.01 Nm/(rad/s)	Motor achieved a steady-state speed of 3000 RPM with a torque of 10 Nm
0.015 Nm/(rad/s)	Motor unable to achieve the desired speed and torque, oscillations
Accurately identified	Motor achieved desired speed and torque, stable operation

below. According to the simulation results, the controller was able to sustain steady operation while the motor was able to reach the specified speed and torque. The motor operated steadily and smoothly, which enhanced output and efficiency.

2.6. Moment of Inertia J

The moment of inertia J is another important parameter in PMSMs, as it determines the motor’s response to changes in torque and speed. Accurate identification of the moment of inertia is necessary for proper control and operation of the motor.

2.6.1. Calculating the Moment of Inertia

The moment of inertia can be calculated using the following equation:

J = 0.5 × m × r²

where m is the motor’s mass and r is the radius of the rotor.

Another method for determining the moment of inertia is to conduct a no-load test on the motor and measure the rotor’s acceleration.

2.6.2. Accurate Moment-of-Inertia Identification

The proper control and operation of PMSMs depend on the precise determination of the moment of inertia. Simulation analysis was carried out to highlight the significance of accurately identifying the moment of inertia.

A PMSM with a notional moment of inertia of 0.05 kg × m² was modeled for the simulation. Then, a vector-control technique with a fixed gain of 1.0 was used to control the machine. The simulation results demonstrated that the motor could provide a torque of 10 Nm and a steady-state speed of 3000 RPM.

The moment of inertia was then deliberately reduced to 0.03 kg × m². The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was unable to keep the motor operating steadily and the motor was unable to produce the appropriate speed and torque. The motor oscillated and was unstable, which had a negative impact on its effectiveness.

Finally, the method previously described enabled accurate identification of the moment of inertia. The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was able to sustain steady operation while the motor was able to reach the specified speed and torque. The motor operated steadily and smoothly, which enhanced output and efficiency.

The nominal situation, represented by Simulation 1, has the proper values for J and the friction coefficient. Simulation 2 depicts the situation in which the moment of inertia has been intentionally reduced, resulting in subpar performance and instability. Simulation 3 illustrates the scenario in which the moment of inertia was correctly identified, resulting in enhanced performance and durability (see

Table 5. Simulation Results for Inertia J.

Parameter	Simulation 1	Simulation 2	Simulation 3
Nominal J (kg × m2)	0.05	0.05	0.03
Nominal speed (RPM)	3000	3000	3000
Nominal torque (Nm)	10	10	10
Friction coefficient (Nm/(rad/s))	0.01	0.015	0.01
Result	Stable operation	Oscillations and instability	Stable operation

).

3. Identification States

3.1. Rotor Position and Speed

For the control and operation of PMSMs, a precise estimation of rotor position and speed is necessary. The behaviors of the motor, including torque and speed, may be precisely controlled thanks to knowledge of these factors.

The performance and efficiency of the motor are directly impacted by the precision of the rotor position and speed estimation. Inaccurate estimations can result in the wrong control signals, which can affect performance, efficiency, and motor wear and tear. At low speeds, where the back-electromotive force is weak, precise estimation is particularly crucial because sensorless systems may struggle to do so.

Overall, the correct operation and control of PMSMs depend on the accurate estimation of rotor position and speed. That the motor functions well and delivers the desired performance are ensured by using trustworthy and accurate estimating techniques, whether sensor-based or sensorless.

3.1.1. Methods for Rotor Position and Speed Estimation

Various methods can be used to estimate the rotor position and speed of PMSMs, including encoder-based, sensorless, and hybrid methods.

For precise feedback on the location and speed of the rotor, encoder-based techniques mount an encoder on the motor shaft. For accurate feedback about the rotor position and speed in PMSMs, encoder-based techniques are frequently used. A sensor that provides accurate feedback on the position and speed of the rotor is called an encoder. There are two types of encoders: absolute and incremental. While incremental encoders give input on the relative position of the rotor, absolute encoders generate a different code for each position of the rotor. PMSMs may be controlled precisely using encoder-based approaches because they provide excellent rotor-position- and speed-measurement accuracy and resolution. Closed-loop control of the motor is possible with encoder feedback, allowing for precise management of the motor’s behaviors. Since the encoder-based techniques can still deliver precise feedback at high speeds, they are also appropriate for high-speed applications.

One of the main advantages of encoder-based methods is their high accuracy and resolution. The accuracy of the encoder depends on the number of pulses per revolution, with higher pulse counts providing higher accuracy. The resolution of the encoder is defined by the number of pulses per revolution and the number of bits used to represent the encoder output.

Applications requiring precise control of the motor’s behavior can also benefit from encoder-based techniques. Closed-loop control, which enables accurate control of the motor’s torque and speed, can be applied using the encoder’s feedback. The performance, effectiveness, and dependability of the motor can all be enhanced via closed-loop control. Encoder-based techniques do, however, have significant drawbacks. Because encoders are sensitive to vibrations and noise, the accuracy of the feedback may be impacted. Encoder-based techniques can also be expensive and can require additional gear for installation. Additionally, worn-out encoders may malfunction and produce erroneous feedback.

Sensorless techniques estimate the position and speed of the rotor using the EMF created in the stator windings [29]. Sensorless approaches estimate the rotor position and speed from other observable factors including the electrical impulses from the motor, the back-electromotive forces, and the magnetic fields using mathematical models and techniques for signal processing.

Sensor-based methods involve the use of physical sensors, such as resolvers, encoders, and Hall-effect sensors, to measure the rotor position and speed. These sensors provide accurate and reliable measurements, but they also add cost and complexity to the motor system.

In order to give a reliable and precise assessment of rotor position and speed, hybrid methods combine encoder and sensorless techniques. The encoder is employed in a hybrid technique to give a preliminary approximation of the rotor location and speed. After that, a more precise and reliable estimate is provided using the sensorless method. This can be accomplished by utilizing sophisticated algorithms that combine information from the sensorless approach with the encoder to increase the estimation’s accuracy and dependability.

The sensorless observer-based method, which estimates the rotor position and speed using a mathematical model of the motor, is an example of a hybrid approach. This method calculates the rotor position and speed using the motor’s voltage and current equations along with feedback from the motor’s current and voltage sensors. Any estimation inaccuracies are fixed using the encoder as a reference. The encoder-assisted sensorless technique, which makes use of the encoder to offer a preliminary estimate of the rotor position and speed, is another example of a hybrid method. The rotor location and speed are then estimated using sensorless techniques that depend on the motor’s back-EMF, magnetic saliency, or other features. Even in the midst of considerable load variations and disturbances, this approach can produce precise and reliable estimation.

Using hybrid approaches rather than simply encoder-based or sensorless ones can have a significant impact on accuracy, resilience, and cost effectiveness. Hybrid approaches can give more accurate and dependable rotor position and speed estimation, which is necessary for the appropriate management and operation of PMSMs in a variety of industrial applications.

3.1.2. Mathematical Equation(s) for Calculating Rotor Position and Speed

There are several methods for estimating rotor position and speed, including sensorless methods that do not require physical sensors to measure these variables.

Depending on the method chosen, a variety of mathematical equations can be used to determine the rotor location and speed. For instance, with sensorless techniques, the rotor speed can be determined by differentiating the estimated position, whereas the rotor position can be computed using the phase difference between the stator current and back-EMF signals.

3.1.3. The Importance of Accurate Rotor Position and Speed Estimation

For PMSMs to operate well, rotor position and speed estimate accuracy is essential. In order to highlight the significance of precise rotor location and speed estimation, simulation research was carried out.

A PMSM was modeled in the simulation using a nominal rotor location and speed. A vector-control technique was then used to control the machine [30]. The simulation results demonstrated that the motor could provide a torque of 10 Nm and a steady-state speed of 3000 RPM.

The rotor speed and location were then artificially altered. The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was unable to keep the motor operating steadily and the motor was unable to produce the appropriate speed and torque. The motor oscillated and was unstable, which had an adverse effect on performance and efficiency.

Finally, using the previously described method, the rotor position and speed were precisely determined. The machine was governed by the same vector-control algorithm. According to the simulation results, the controller was able to sustain steady operation while the motor was able to reach the specified speed and torque. The motor operated steadily and smoothly, which enhanced output and efficiency.

3.2. Magnetic Saliency

The variation in the PMSM rotor’s magnetic characteristics is referred to as magnetic saliency. This variation must be taken into consideration in the machine’s management and operation as it may have an impact on the motor’s performance.

3.2.1. Definition of Magnetic Saliency and Its Importance in PMSM Control

The asymmetry in the PMSM rotor’s magnetic field distribution is referred to as magnetic saliency. The magnetization pattern or the rotor’s shape may be to blame for this asymmetry. The cogging torque, efficiency, and stability of the motor can all be impacted by variations in the magnetic-field distribution. Consequently, reliable magnetic-saliency identification is required for proper motor control and operation.

3.2.2. Methods for Magnetic-Saliency Identification

The magnetic saliency of PMSMs can be determined using a variety of techniques, such as back-EMF-based techniques, frequency-response analysis, and finite-element analysis. Back-EMF-based approaches estimate the saliency value by analyzing the fluctuation in the back-EMF waveform brought on by the magnetic saliency. The pulse-injection technique is one such approach. It involves injecting a high-frequency pulse into one of the motor phases, and then analyzing the ensuing back-EMF waveform to determine the magnetic saliency.

Another technique is the static-eccentricity test, which involves purposefully positioning the motor in an eccentric position and analyzing the back-EMF waveform to determine the magnetic saliency. This technique is especially helpful for determining both axial and radial magnetic saliency.

The examination of frequency responses is another technique for determining magnetic saliency. By injecting a modest sinusoidal voltage into one of the motor phases at various frequencies, this technique analyzes the motor’s subsequent frequency response to determine the magnetic saliency.

The more complicated finite element analysis method models the electromagnetic behaviors of the motor using computer simulations. This technique can successfully anticipate the motor’s magnetic saliency, but it necessitates extensive knowledge of the motor’s geometry and composition.

Overall, each method has its own advantages and disadvantages, and the choice of method will depend on the specific requirements of the application and the available resources.

4. Materials and Methods

The methodology used to write this review involved conducting a thorough literature search on the topic of parameter and state identification for PMSMs and analyzing the information obtained from various sources such as research articles, conference papers, and textbooks.

The sources were selected based on their relevance, credibility, and recentness. The search was conducted using various academic search engines such as MDPI, IEEE Xplore, ScienceDirect, and Google Scholar. The keywords used for the search included “PMSM parameter identification,” “PMSM state identification,” “magnetic saliency identification,” “inductance identification,” and “stator resistance identification.”

The data were examined to ascertain the different methods used with PMSMs for parameter and state identification after obtaining the appropriate literature. The benefits and downsides of each approach were evaluated, and simulation results emphasizing the significance of accurate parameter and state identification were examined.

Overall, this review provides an overview of the different methods used for parameter and state identification for PMSMs and it highlights the importance of accurate identification for efficient motor control.

5. Results

This study focused on the importance of accurate identification of the friction coefficient and the moment of inertia in the proper control and operation of permanent magnet synchronous motors (PMSMs). The simulation results showed that inaccurate identification of these parameters can lead to poor performance and efficiency, and even instability in the motor’s operation.

In particular, the motor was unable to reach the appropriate speed and torque, and the use of the controller was able to sustain stable operation whenever the friction coefficient was deliberately increased and currently of inertia was artificially reduced. As a result, there were oscillations and instability, which had a negative impact on productivity. However, the motor operated smoothly and steadily when the friction coefficient and moment of inertia were correctly determined, leading to enhanced performance and efficiency.

According to these results, the precise identification of the friction coefficient and moment of inertia is essential for the control and operation of PMSMs, and incorrect identification of these parameters can have a considerably negative impact on performance and efficiency. Therefore, before operating and managing PMSMs, it is crucial to carry out rigorous testing and measurements to precisely determine these parameters. This paper also touches on the significance of precisely determining the PMSM states, such as rotor location and speed as well as magnetic saliency. The many techniques for identifying the states, including frequency-response analysis and back-EMF-based techniques, have been thoroughly studied.

Overall, the results of this literature review demonstrated the significance of the accurate identification of parameters and states in PMSMs for efficient motor control. This review highlights the need for further research in developing robust and accurate identification techniques that can be applied in practical applications.

6. Discussion

In this study, the importance of the accurate identification of the inductances and states of the system, as well as of the friction coefficient and moment of inertia, in permanent magnet synchronous motors (PMSMs) was demonstrated through simulation study. The results showed that inaccurate identification of these parameters can result in poor performance and inefficiency of the motor.

This study emphasizes the significance of precise modeling and control of PMSMs since these elements play a crucial role in determining how well the motor will react to variations in torque and speed. For the motor to be controlled and operated properly, these parameters must be accurately identified. Inaccurate identification can lead to oscillations and instability, which can have a negative impact on performance and effectiveness.

This study also offers two approaches—mathematical calculations and no-load tests—for figuring out the friction coefficient and moment of inertia. Both approaches have merits and drawbacks. These parameters can be quickly and easily determined using mathematical formulas, but the accuracy is reliant on the correctness of the input data. Although no-load testing can yield more precise results, it takes more time and resources.

This study emphasizes the value of utilizing simulation studies to assess PMSM performance in various scenarios. Simulation studies can offer a practical and reliable technique to test various hypotheses and assess the effects of various conditions on motor function. It is crucial to keep in mind that simulation studies have limitations and might not always correctly reflect actual settings. Consequently, it is crucial to use experimental data to confirm the simulation conclusions.

7. Conclusions

In conclusion, this study emphasizes the importance of the accurate identification of parameters such as inductances and states of the system, as well as the friction coefficient and moment of inertia, in PMSMs. Accurate identification of these parameters is necessary for proper modeling and control of the motor, leading to improved performance and efficiency. Mathematical calculations and no-load tests are two methods for determining these parameters, each with its own advantages and disadvantages. Simulation studies can provide a cost-effective and safe way to test different scenarios, but it is essential to validate the simulation results with experimental data.