Rate-Compatible Protograph LDPC Codes for Source Coding in Joint Source—Channel Coded Modulation Systems
Abstract
:1. Introduction
- In contrast to the design of source code parameters for a specific source probability, a searching algorithm for the source code parameters is proposed to obtain high shaping gains across the whole considered range of source probabilities for a given source coding rate.
- Combining the achievable system rate analysis and the source decoding thresholds, some design principles for source codes are proposed to simultaneously improve the error-floor quality and guarantee the PAS performance of JSCCM systems for a range of source probabilities.
- A family of source codes with rates ranging from 1/3 to 3/4 is proposed for a JSCCM system by code lengthening; these codes have good source decoding thresholds and obtain shaping gains for different source probabilities, which are attractive for adaptive coding in systems with changing source statistics.
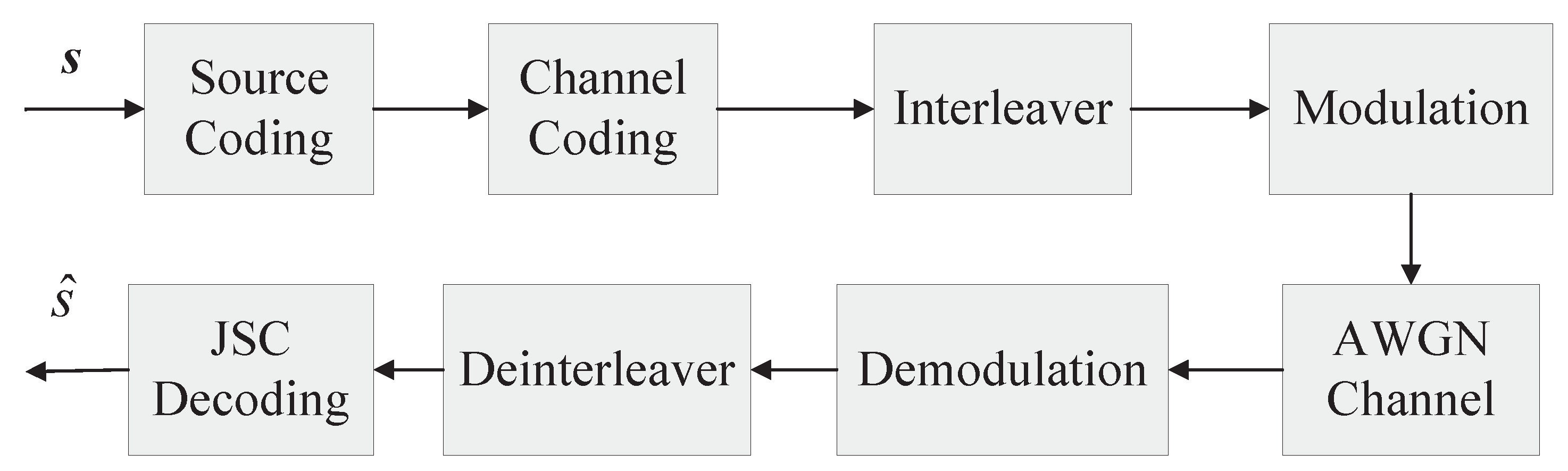
2. System Model
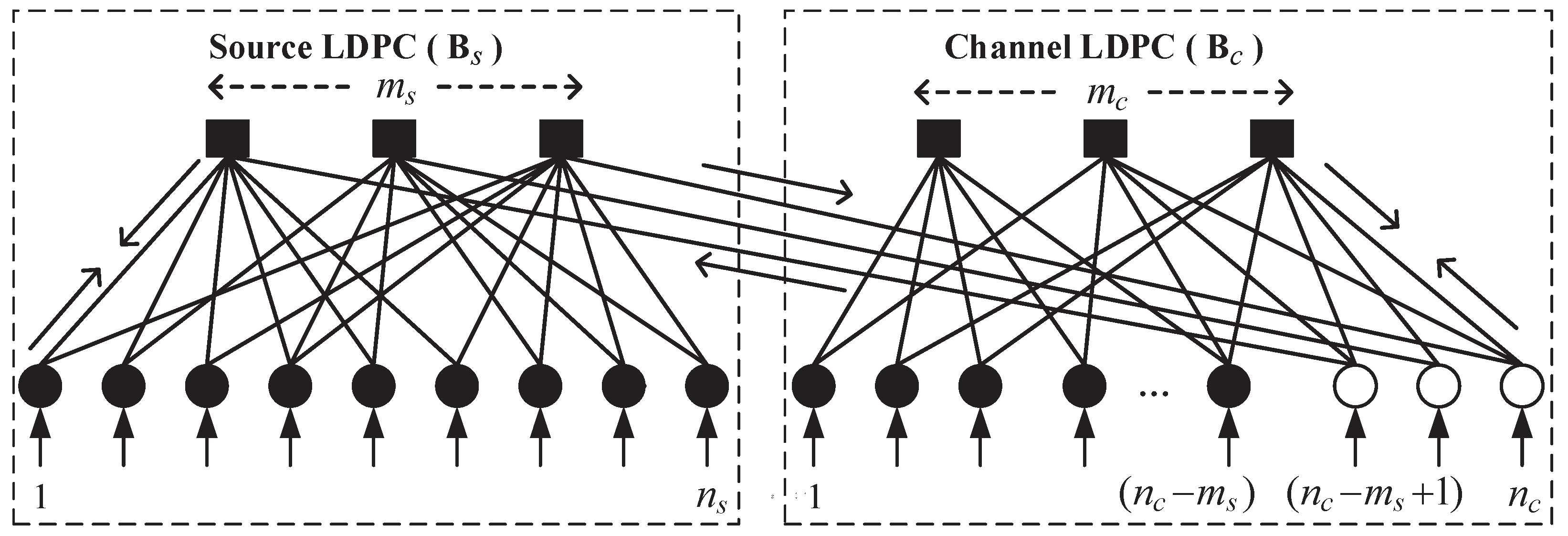
3. Design of Source Codes
3.1. Achievable System Rate Analysis
- The choice of influences the system design. On the one hand, a small value of , which means a small gap to the Shannon limit, leads to a small number of candidates and hence limits the search for a source code with good source decoding thresholds. On the other hand, increasing can enlarge the search space for source codes with a good error-floor performance at the expense of the PAS performance. As a consequence, the proposed Algorithm 1 can strike a balance between the PAS performance and the error-floor performance by adjusting the value of .
- The value of is related to the step size of p in Algorithm 1. We use in our search process based on trial and error.
| Algorithm 1 Search for the row weight distribution of the source code |
Require:
|
3.2. Source PEXIT Chart Analysis
- denotes the AMI from to ;
- denotes the EMI from to ;
- denotes the AMI from to ;
- denotes the EMI from to ;
- denotes the APM for .
| Algorithm 2 Source decoding threshold |
Require: |
3.3. Design of Rate-Compatible Source Codes for JSCCM systems
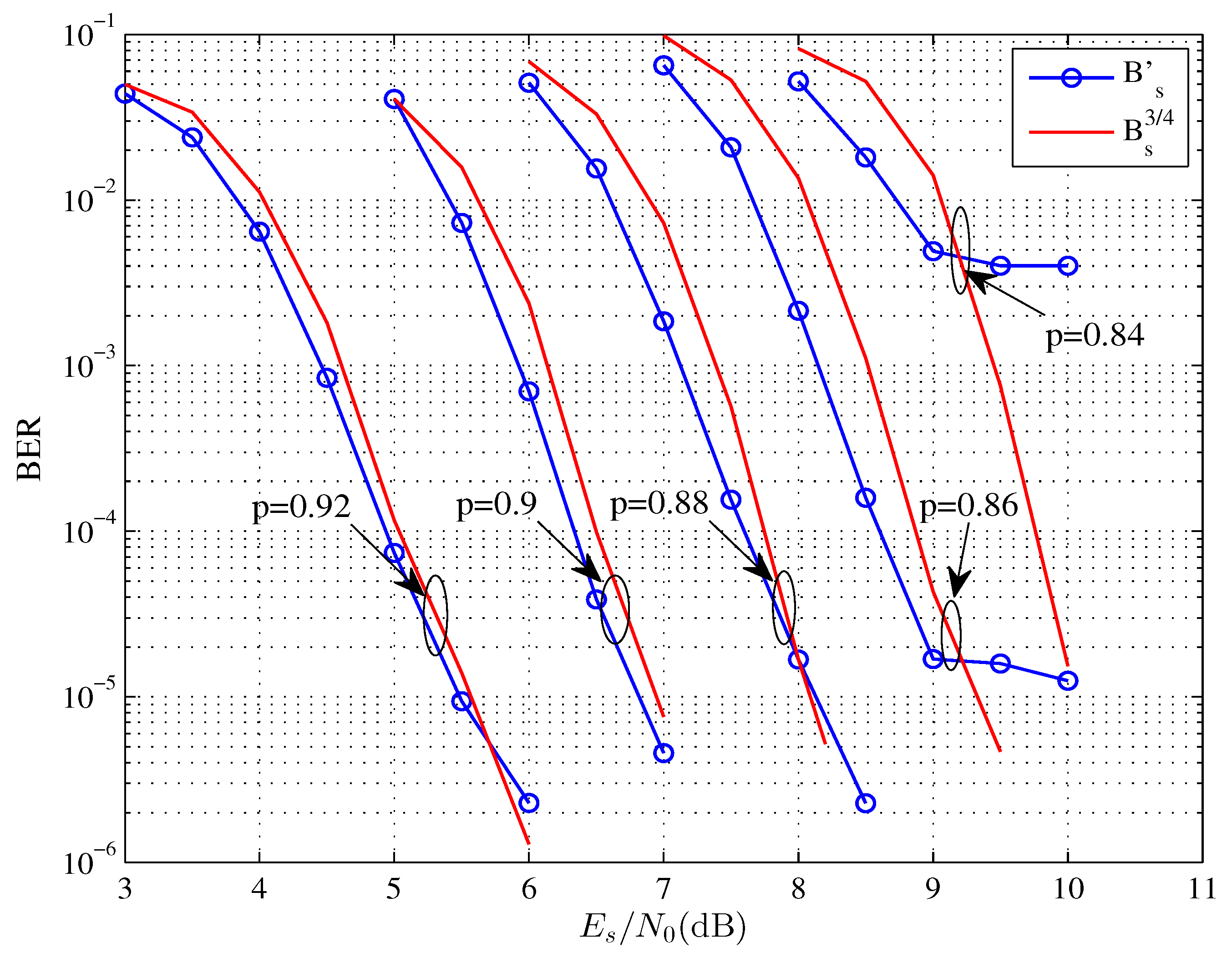
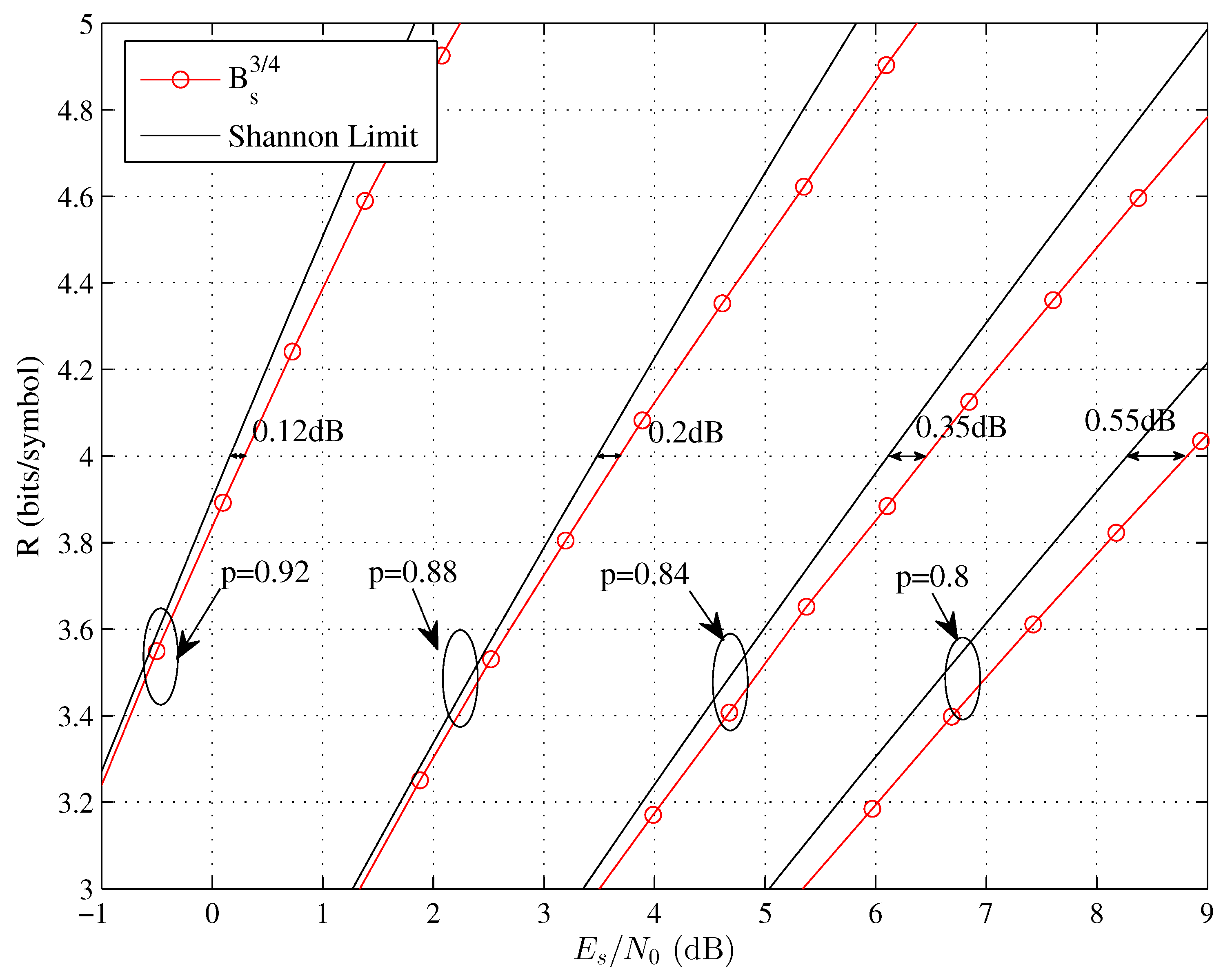
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASK | amplitude-shift keying |
| AMI | a priori mutual information |
| APM | a posteriori mutual information |
| AWGN | additive white Gaussian noise |
| BER | bit-error rate |
| BICM | bit-interleaved coded modulation |
| BSC | binary symmetric channel |
| CN | check nodes |
| DM | distribution matcher |
| EMI | extrinsic mutual information |
| GS | geometric shaping |
| JSCC | joint source–channel coding |
| JSCCM | joint source–channel coded modulation |
| LDPC | low-density parity-check |
| MI | mutual information |
| PAS | probabilistic amplitude shaping |
| PS | probabilistic shaping |
| PEXIT | protograph extrinsic information transfer |
| PEG | progressive edge growth |
| QAM | quadrature amplitude modulation |
| SNR | signal-to-noise ratio |
| VN | variable node |
References
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Forney, G.D.; Gallager, R.G.; Lang, G.; Longstaff, F.; Qureshi, S. Efficient modulation for band-limited channels. IEEE J. Sel. Areas Commun. 1984, 5, 632–647. [Google Scholar] [CrossRef] [Green Version]
- R1-1700679. Non-Uniform Constellations in NR. Sony, 3GPP TSG RAN1 NR Ad Hoc Meeting. 2017, pp. 16–20. Available online: https://www.google.com.hk/url?sa=i&rct=j&q=&esrc=s&source=web&cd=&ved=0CAIQw7AJahcKEwiYwKGP5LL_AhUAAAAAHQAAAAAQBQ&url=https%3A%2F%2Fwww.3gpp.org%2Fftp%2Ftsg_ran%2FWG1_RL1%2FTSGR1_AH%2FNR_AH_1701%2FDocs%2FTDoc_List_Meeting_RAN1-NR%25231.xlsx&psig=AOvVaw1Pxfv9KqWmRZ-3oXRKIcTA&ust=1686283064829716 (accessed on 5 June 2023).
- Zoellner, J.; Loghin, N. Optimization of high-order nonuniform QAM constellations. In Proceedings of the International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB) 2013, London, UK, 5–7 June 2013. [Google Scholar]
- Barsoum, M.F.; Jones, C.; Fitz, M. Constellation design via capacity maximization. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007. [Google Scholar]
- A/322:2017; NATSC Proposed Standard: Physical Layer Protocol (A/322). Advanced Television Systems Committee: Washington, DC, USA, 2016.
- Digital Video Broadcasting (DVB), Next Generation Broadcasting System to Handheld, Physical Layer Specification (DVB NGH) Tech. Rep. A160, November 2013. Available online: https://dvb.org/wp-content/uploads/2019/12/A160_DVB-NGH_Spec.pdf (accessed on 5 June 2023).
- Böcherer, G.; Steiner, F.; Schulte, P. Bandwidth efficient and rate-matched low-density parity-check coded modulation. IEEE Trans. Commun. 2015, 12, 4651–4665. [Google Scholar] [CrossRef] [Green Version]
- Pikus, M.; Xu, W. Bit-Level Probabilistically Shaped Coded Modulation. IEEE Commun. Lett. 2017, 21, 1929–1932. [Google Scholar] [CrossRef]
- Corlay, V.; Gresset, N. A simple sign-bit probabilistic shaping scheme. IEEE Commun. Lett. 2022, 4, 763–767. [Google Scholar] [CrossRef]
- Steiner, F.; Böcherer, G.; Liva, G. Protograph-based LDPC code design for shaped bit-metric decoding. IEEE J. Sel. Areas Commun. 2016, 2, 397–407. [Google Scholar] [CrossRef] [Green Version]
- Steiner, F.; Böcherer, G.; Liva, G. Bit-metric decoding of non-binary LDPC codes with probabilistic amplitude shaping. IEEE Commun. Lett. 2018, 11, 2210–2213. [Google Scholar] [CrossRef] [Green Version]
- Caire, G.; Taricco, G.; Biglieri, E. Bit-interleaved coded modulation. IEEE Trans. Inf. Theory 1998, 3, 927–946. [Google Scholar] [CrossRef] [Green Version]
- Schulte, P.; Böcherer, G. Constant composition distribution matching. IEEE Trans. Inf. Theory 2016, 62, 430–434. [Google Scholar] [CrossRef] [Green Version]
- Takahara, G.; Alajaji, F.; Beaulieu, N.C.; Kuai, H. Constellation Mappings for Two-Dimensional Signaling of Nonuniform Sources. IEEE Trans. Commun. 2003, 51, 400–408. [Google Scholar] [CrossRef]
- Chen, Q.; He, Y.; Chen, C.; Zhou, L. Optimization of protograph LDPC codes via surrogate channel for unequal power allocation. IEEE Trans. Commun. 2023, 71, 1284–1295. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Wang, L.; He, Y.-C.; Chen, Y. Probabilistic shaping for protograph LDPC-coded modulation by residual source redundancy. IEEE Trans. Commun. 2021, 7, 4267–4281. [Google Scholar] [CrossRef]
- Chen, C.; Wang, L.; Xiong, Z.X. Matching criterion between source statistics and source coding rate. IEEE Commun. Lett. 2015, 19, 1504–1507. [Google Scholar] [CrossRef]
- Chen, C.; Wang, L.; Liu, S. The design of protograph LDPC codes as source codes in a JSCC system. IEEE Commun. Lett. 2018, 22, 672–675. [Google Scholar] [CrossRef]
- Chen, Q.; Lau, F.C.M.; Wu, H.; Chen, C. Analysis and Improvement of Error-Floor Performance for JSCC Scheme Based on Double Protograph LDPC Codes. IEEE Trans. Veh. Technol. 2020, 69, 14316–14329. [Google Scholar] [CrossRef]
- Nguyen, V. Design of Capacity-Approaching Protograph-Based LDPC Coding Systems. Ph.D. Thesis, University of Texas at Dallas, Dallas, TX, USA, December 2012. [Google Scholar]
- Fresia, M.; Perez-Cruz, F.; Poor, H.V.; Verdú, S. Joint source and channel coding. IEEE Signal Process. Mag. 2010, 27, 104–113. [Google Scholar] [CrossRef]
- Uchikawa, H. Design of non-precoded protograph-based LDPC codes. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2779–2783. [Google Scholar]
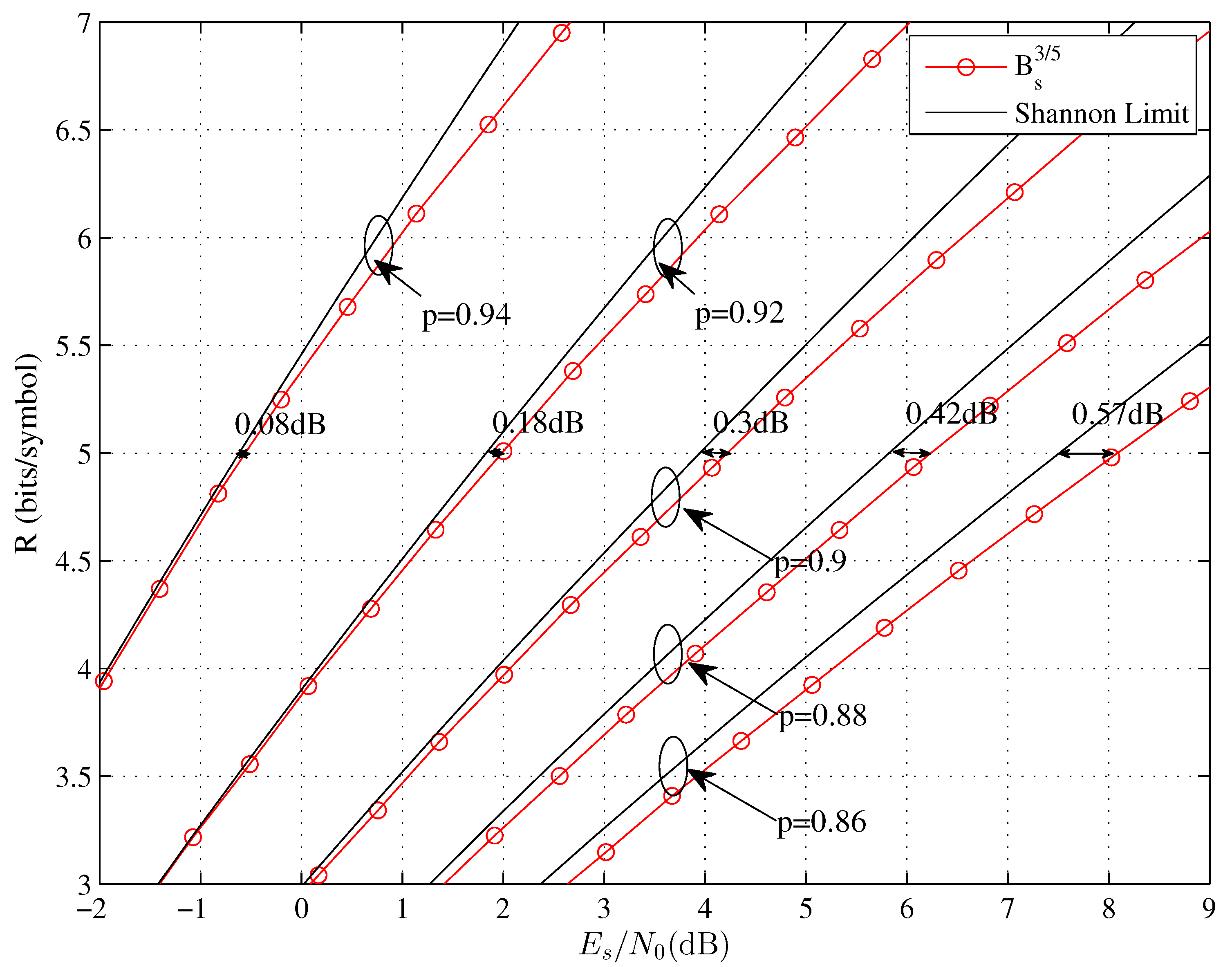
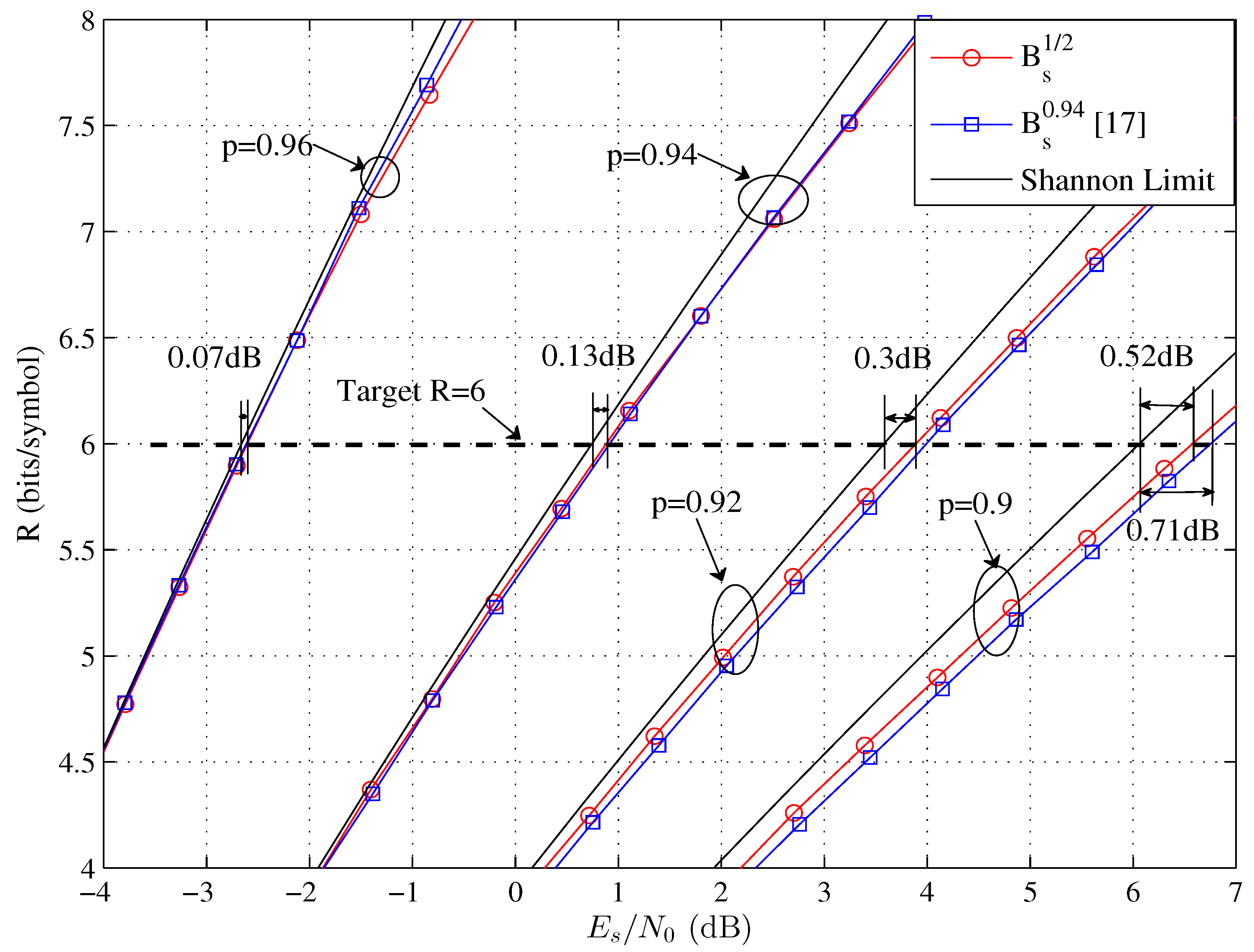

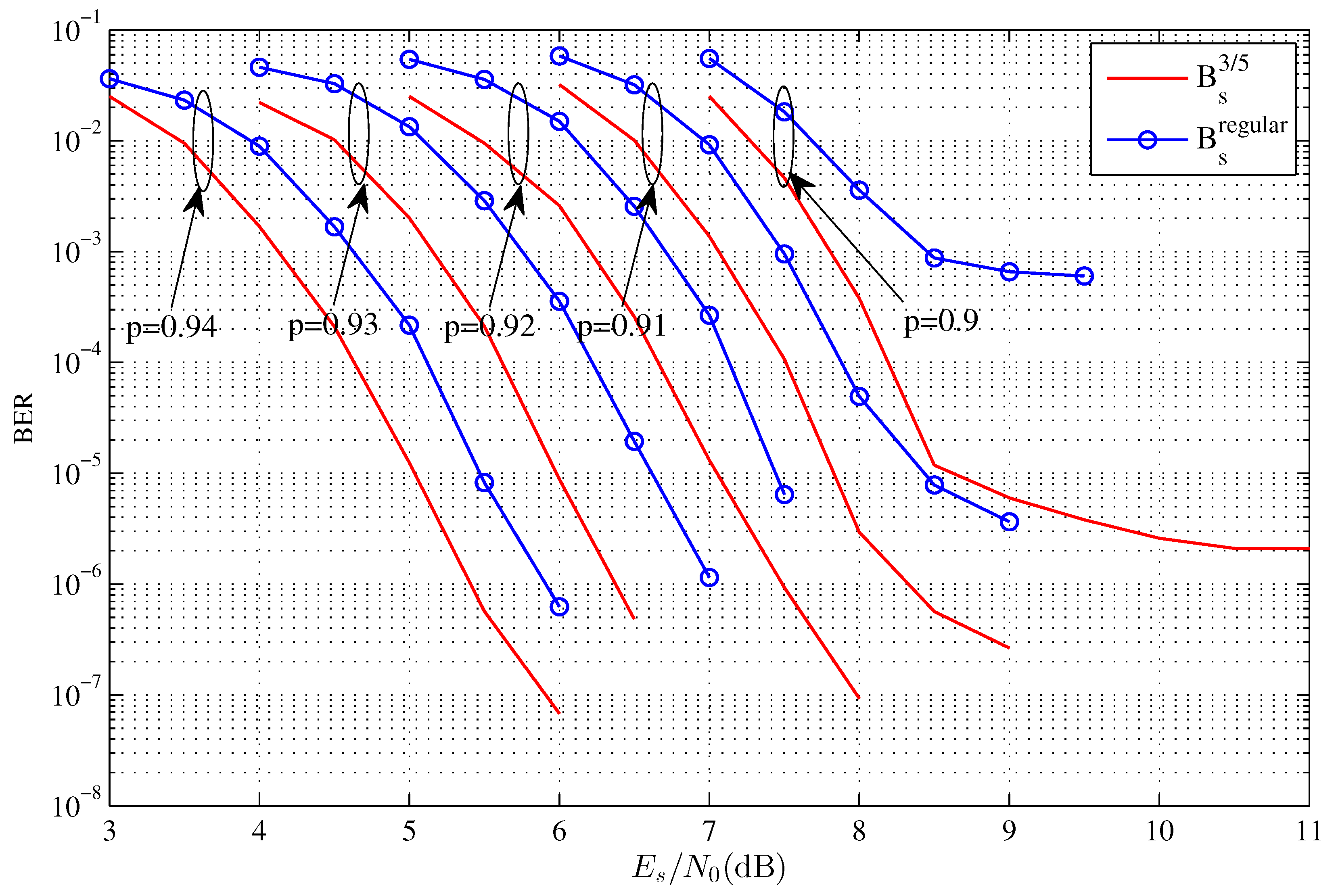
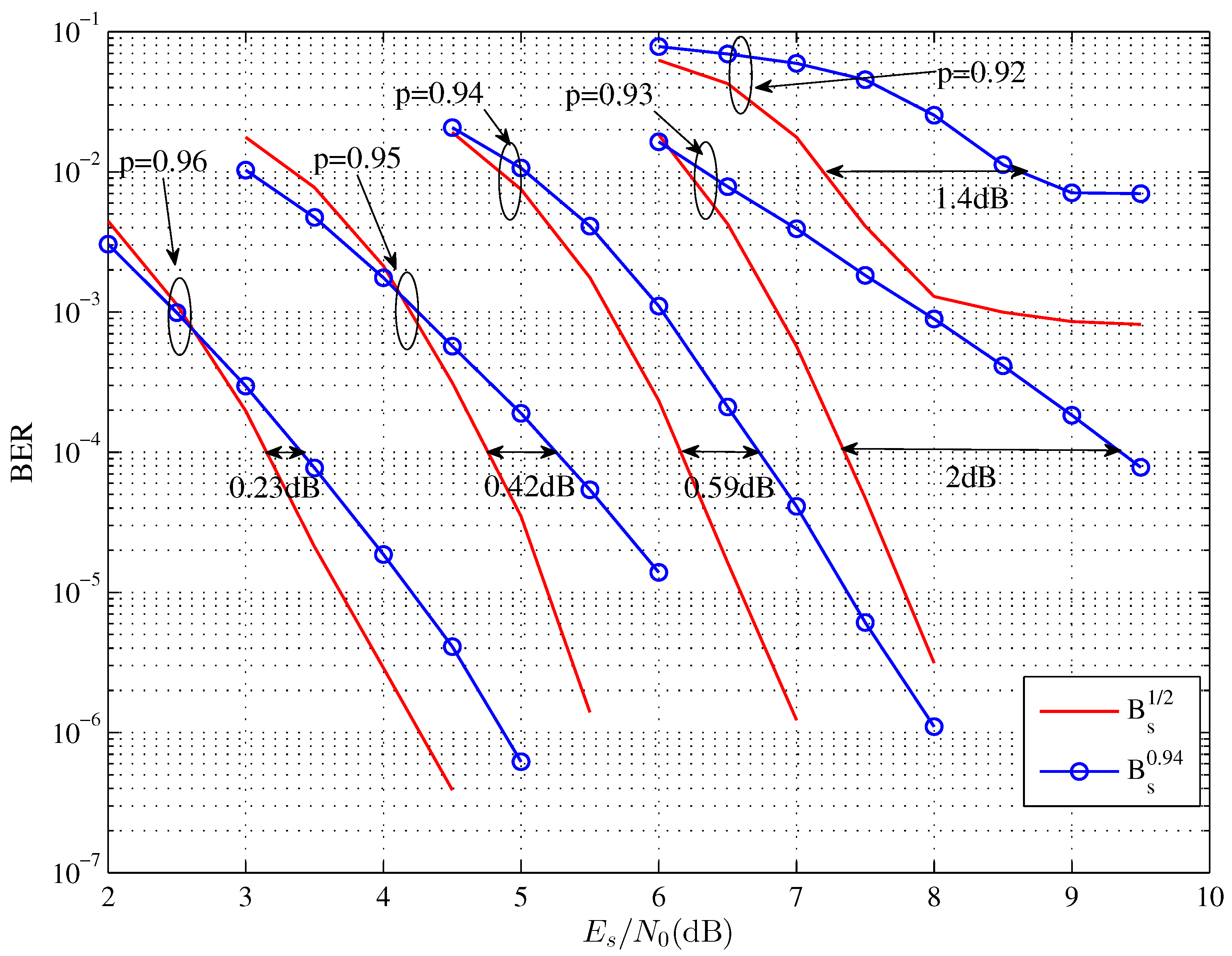

| Source Coding Rate | Target System Rate (Bits/Symbol) | Size of | |
|---|---|---|---|
| , for |
| Source Codes | W | Source Decoding Threshold | Gap |
|---|---|---|---|
| , | 0.0527 | ||
| , | 0.0621 | ||
| , | 0.0702 | ||
| , | 0.0512 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Liu, S.; Chen, Q.; Xu, Z. Rate-Compatible Protograph LDPC Codes for Source Coding in Joint Source—Channel Coded Modulation Systems. Electronics 2023, 12, 2610. https://doi.org/10.3390/electronics12122610
Chen C, Liu S, Chen Q, Xu Z. Rate-Compatible Protograph LDPC Codes for Source Coding in Joint Source—Channel Coded Modulation Systems. Electronics. 2023; 12(12):2610. https://doi.org/10.3390/electronics12122610
Chicago/Turabian StyleChen, Chen, Sanya Liu, Qiwang Chen, and Zhiping Xu. 2023. "Rate-Compatible Protograph LDPC Codes for Source Coding in Joint Source—Channel Coded Modulation Systems" Electronics 12, no. 12: 2610. https://doi.org/10.3390/electronics12122610
APA StyleChen, C., Liu, S., Chen, Q., & Xu, Z. (2023). Rate-Compatible Protograph LDPC Codes for Source Coding in Joint Source—Channel Coded Modulation Systems. Electronics, 12(12), 2610. https://doi.org/10.3390/electronics12122610







