Phase-Shifted Energy Balance Control for Multilevel Inverters in Grid-Connected PV Systems
Abstract
:1. Introduction
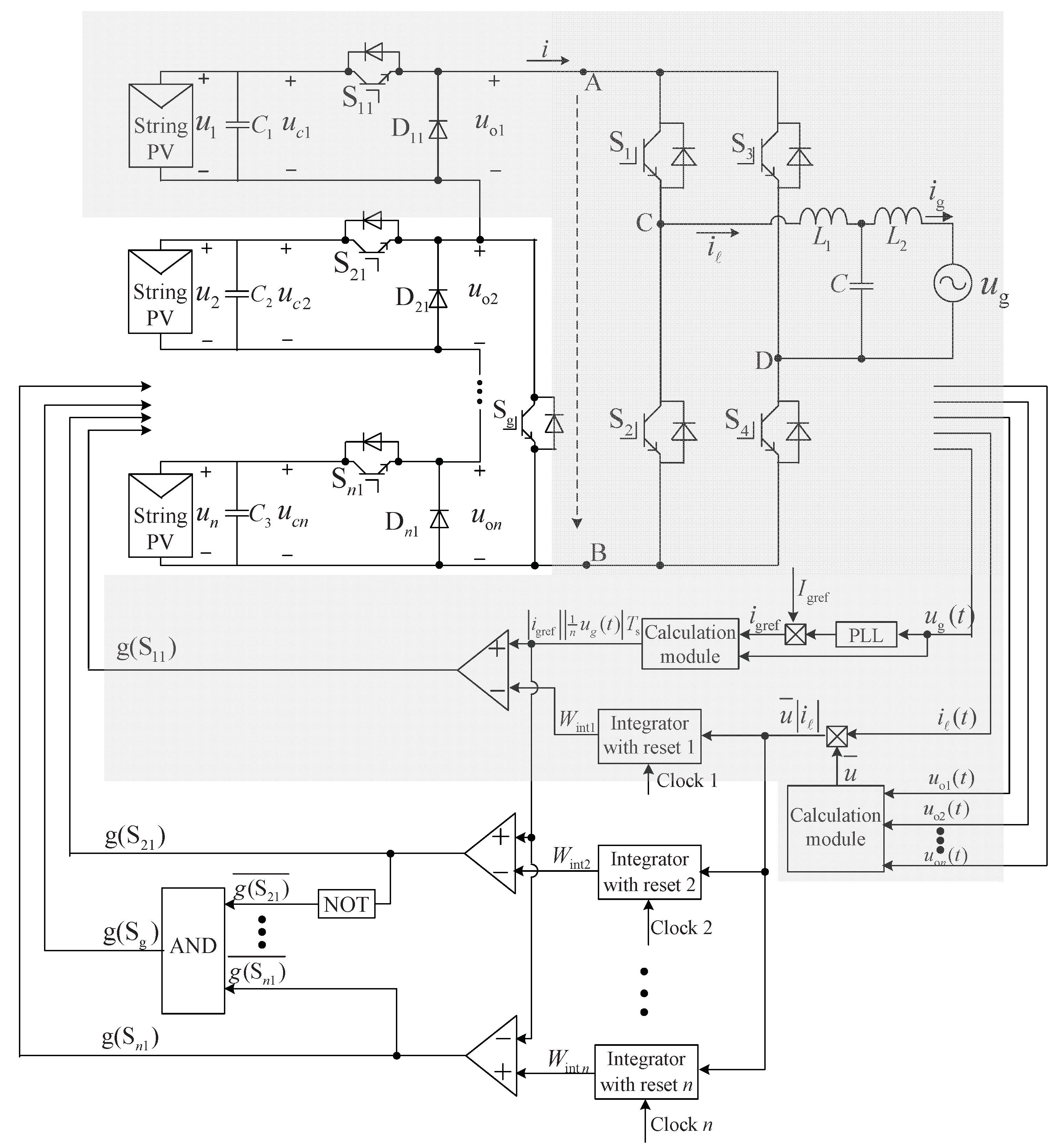
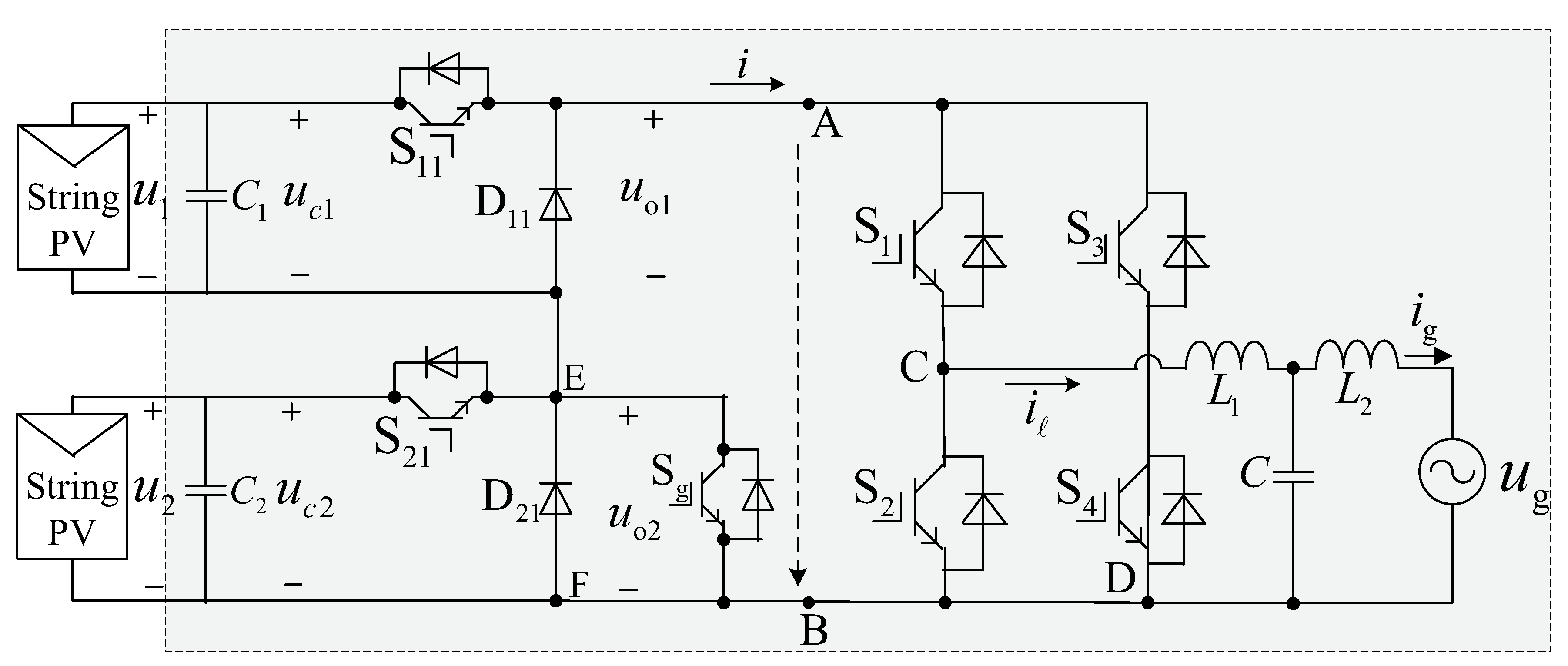
2. Deriving the Control Equation Based on the CSD Multilevel Topology
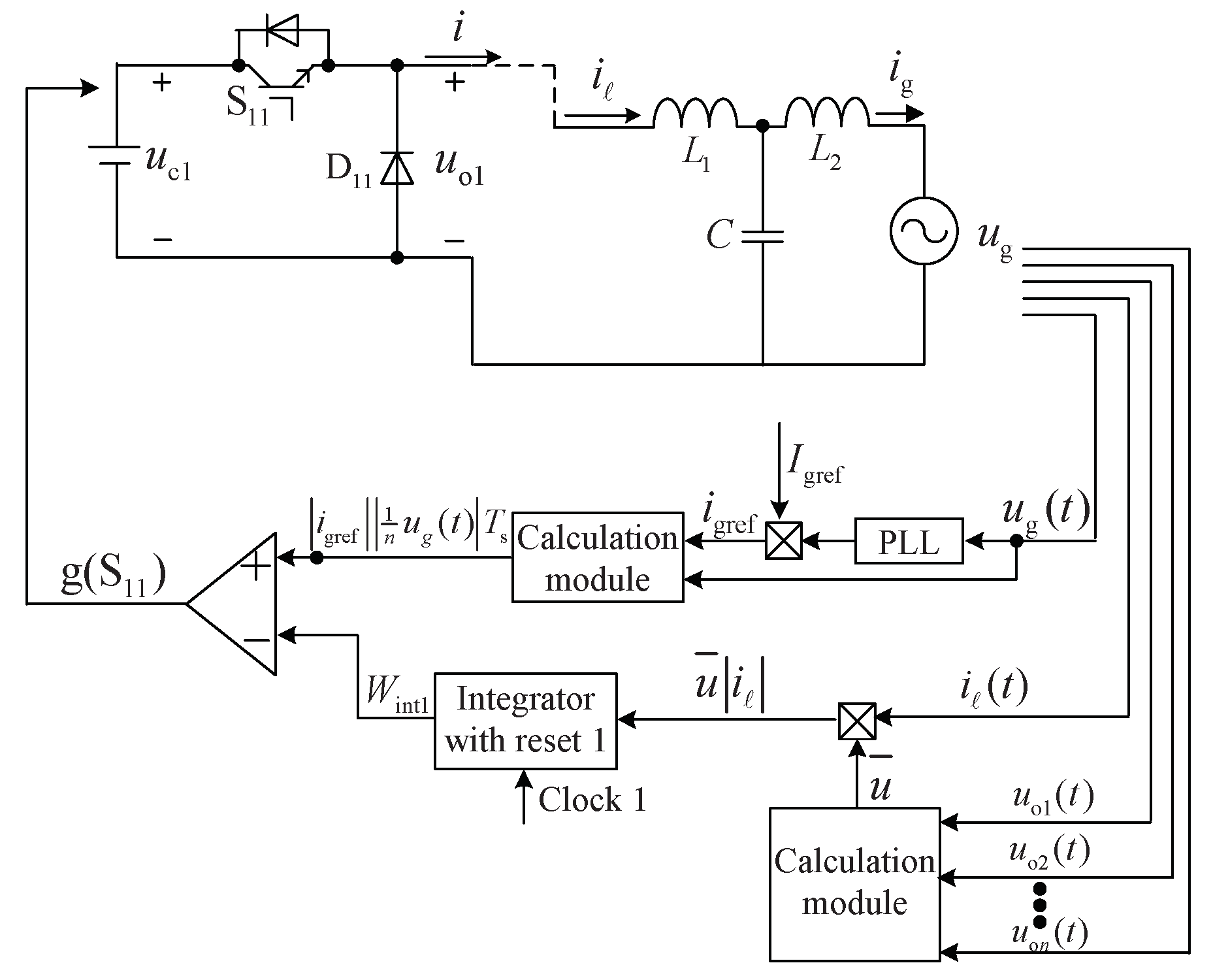
3. The Design and Implementation of the Proposed CPS Energy Balance Control Method
4. Simulation Results
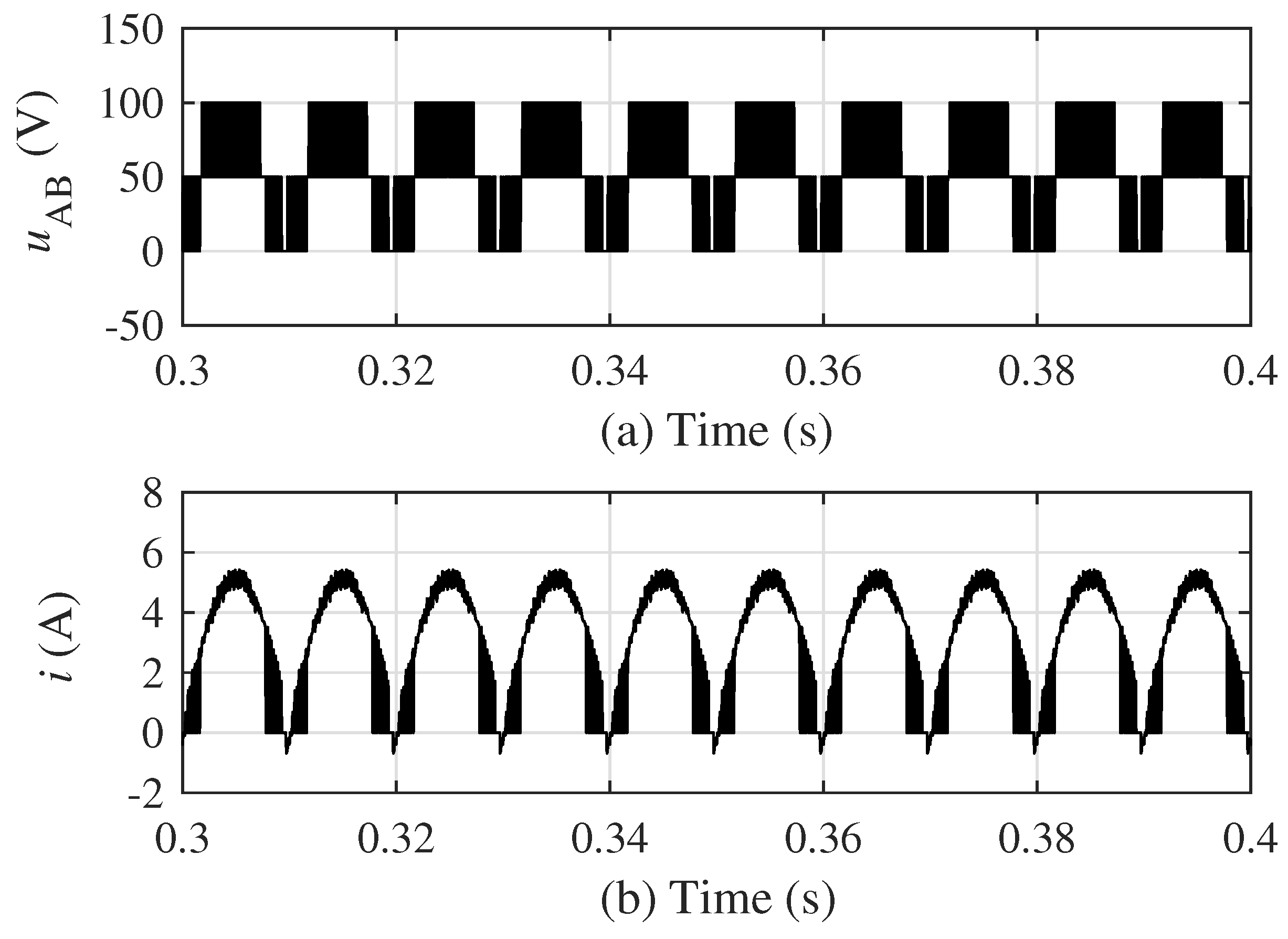
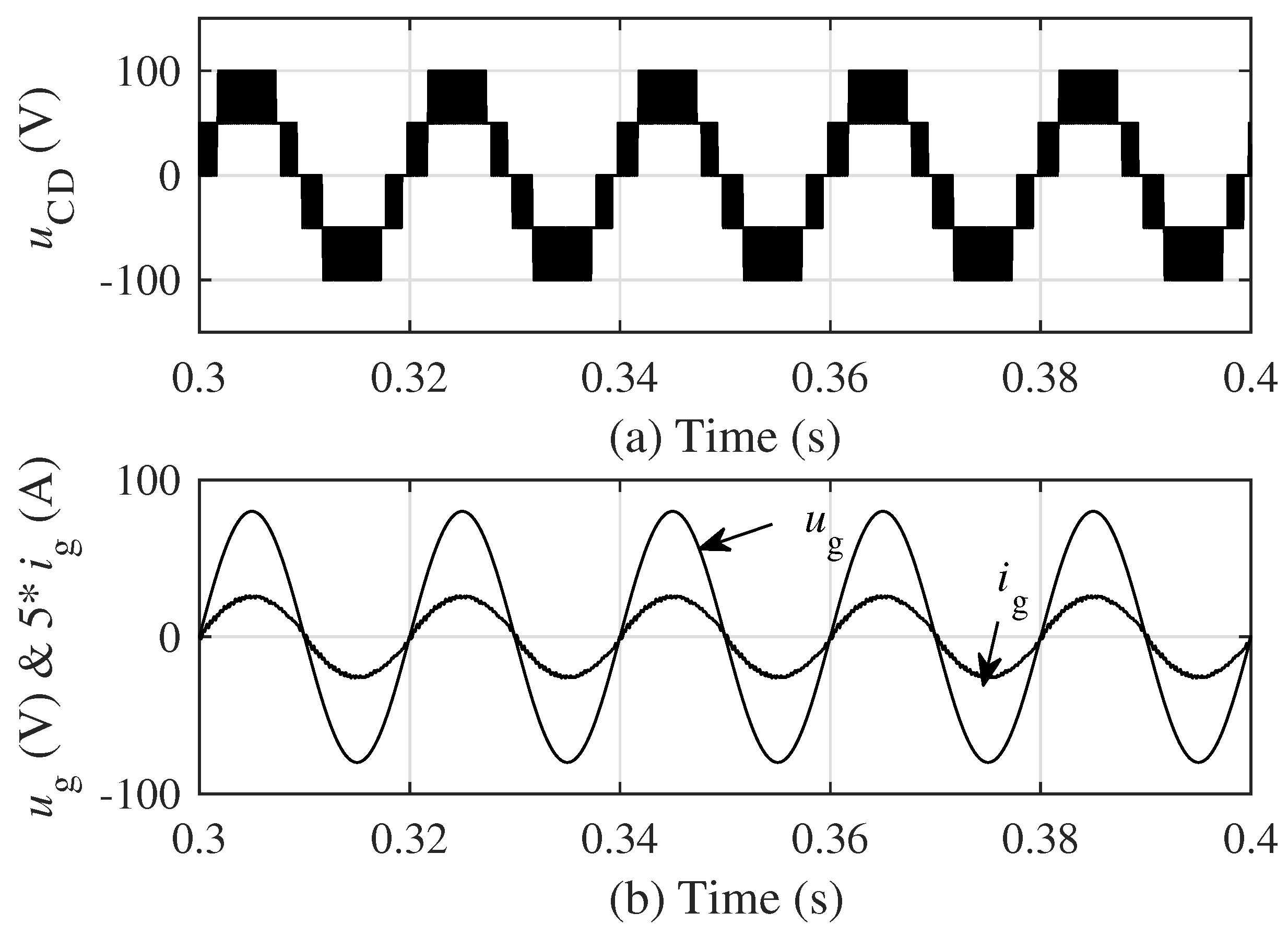
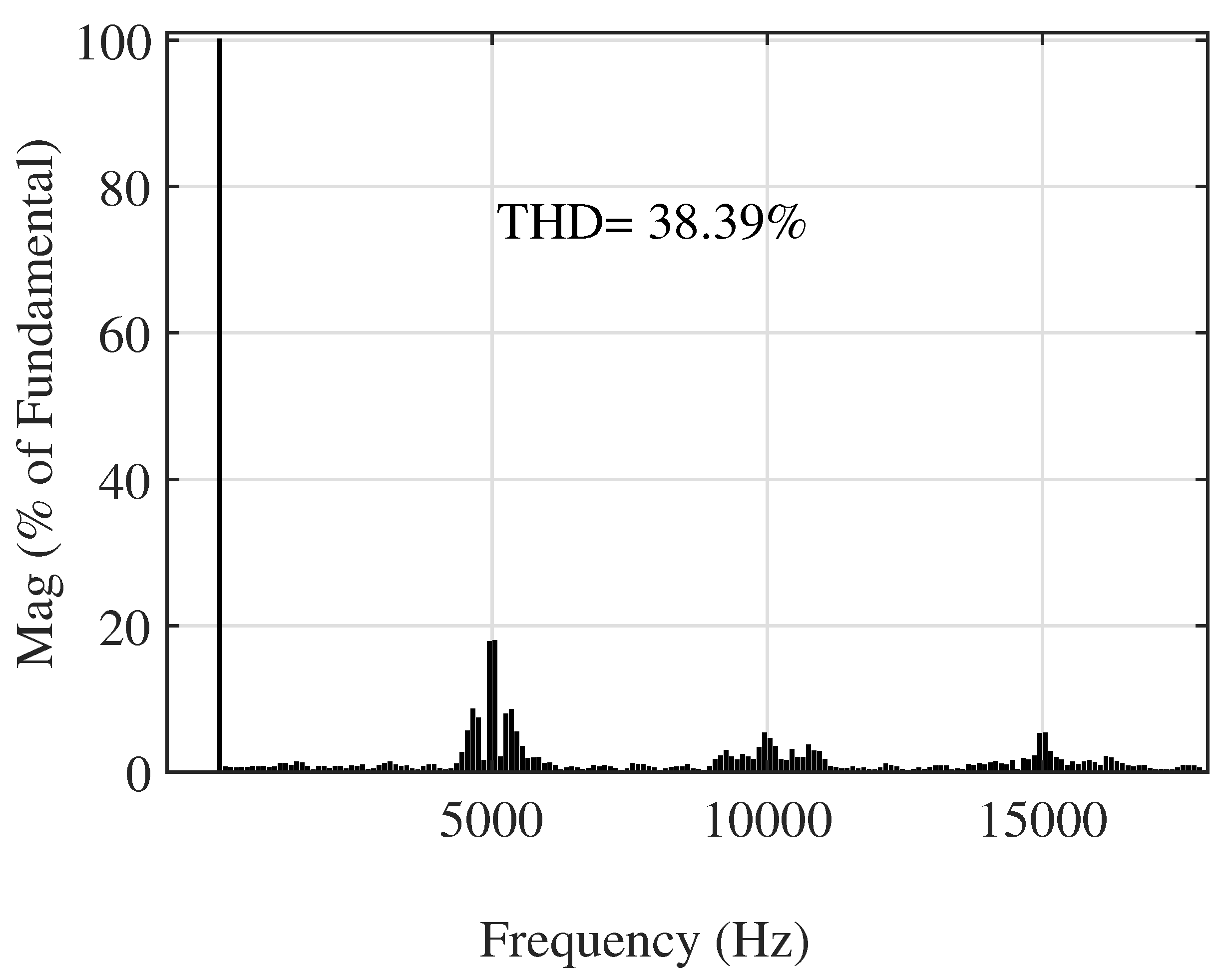
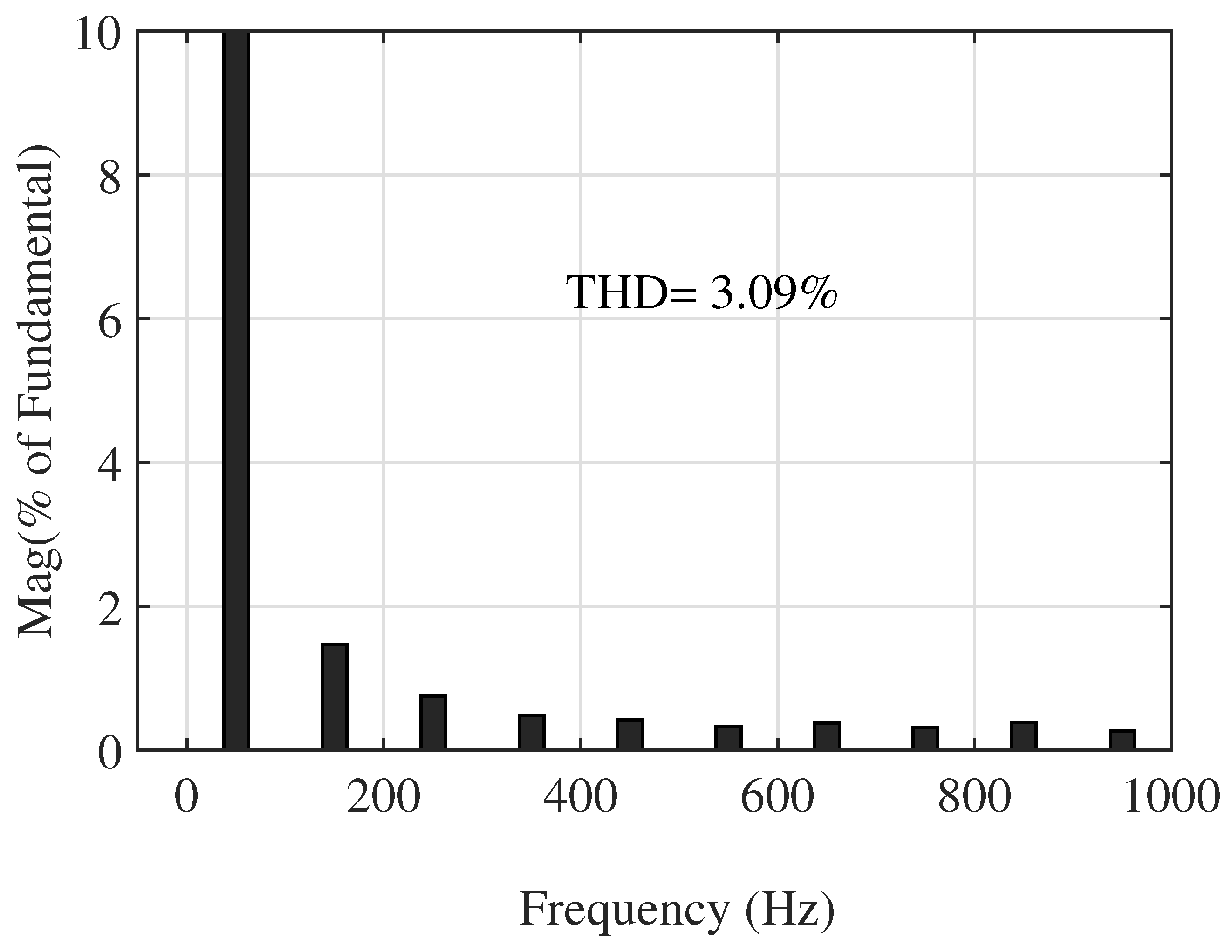
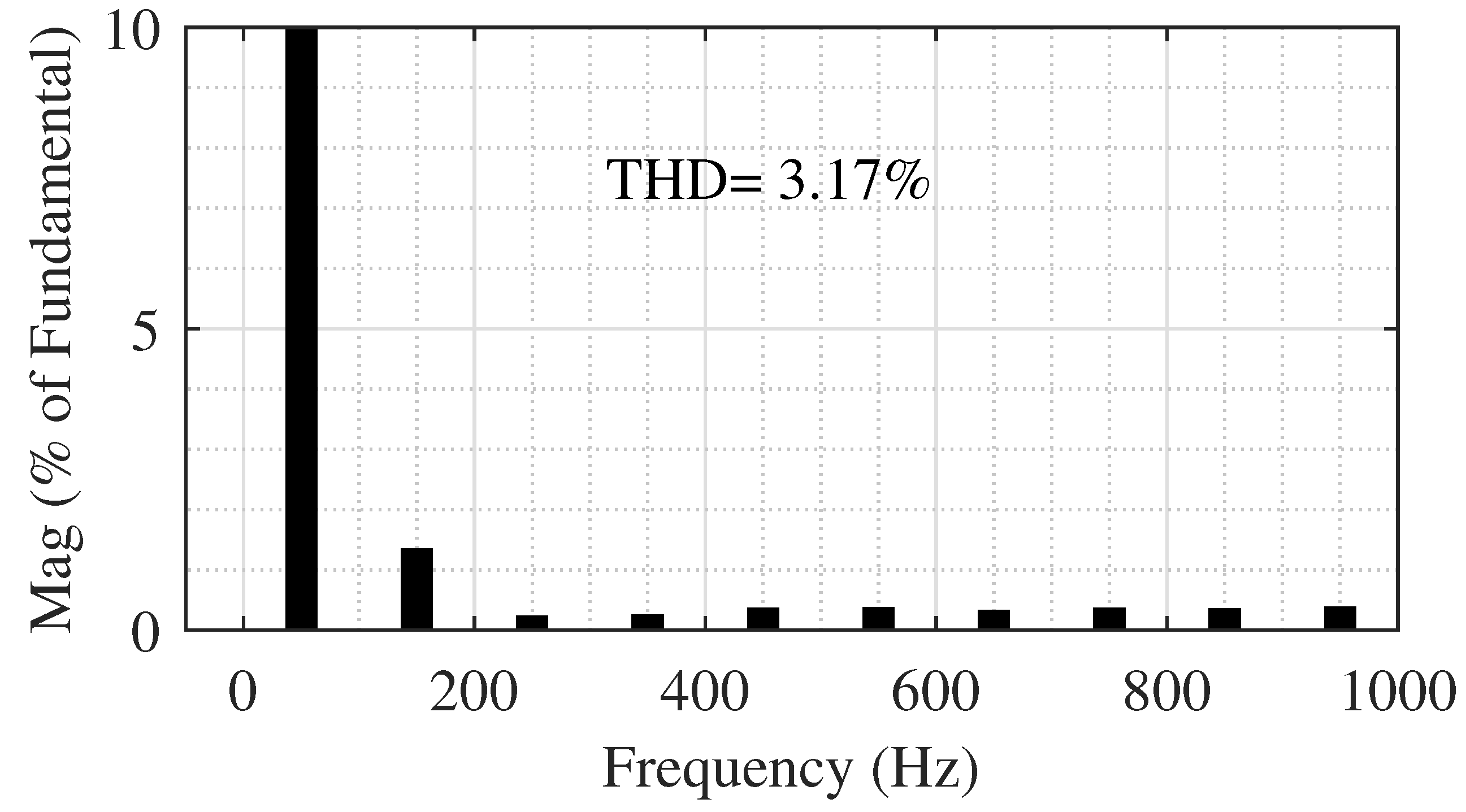
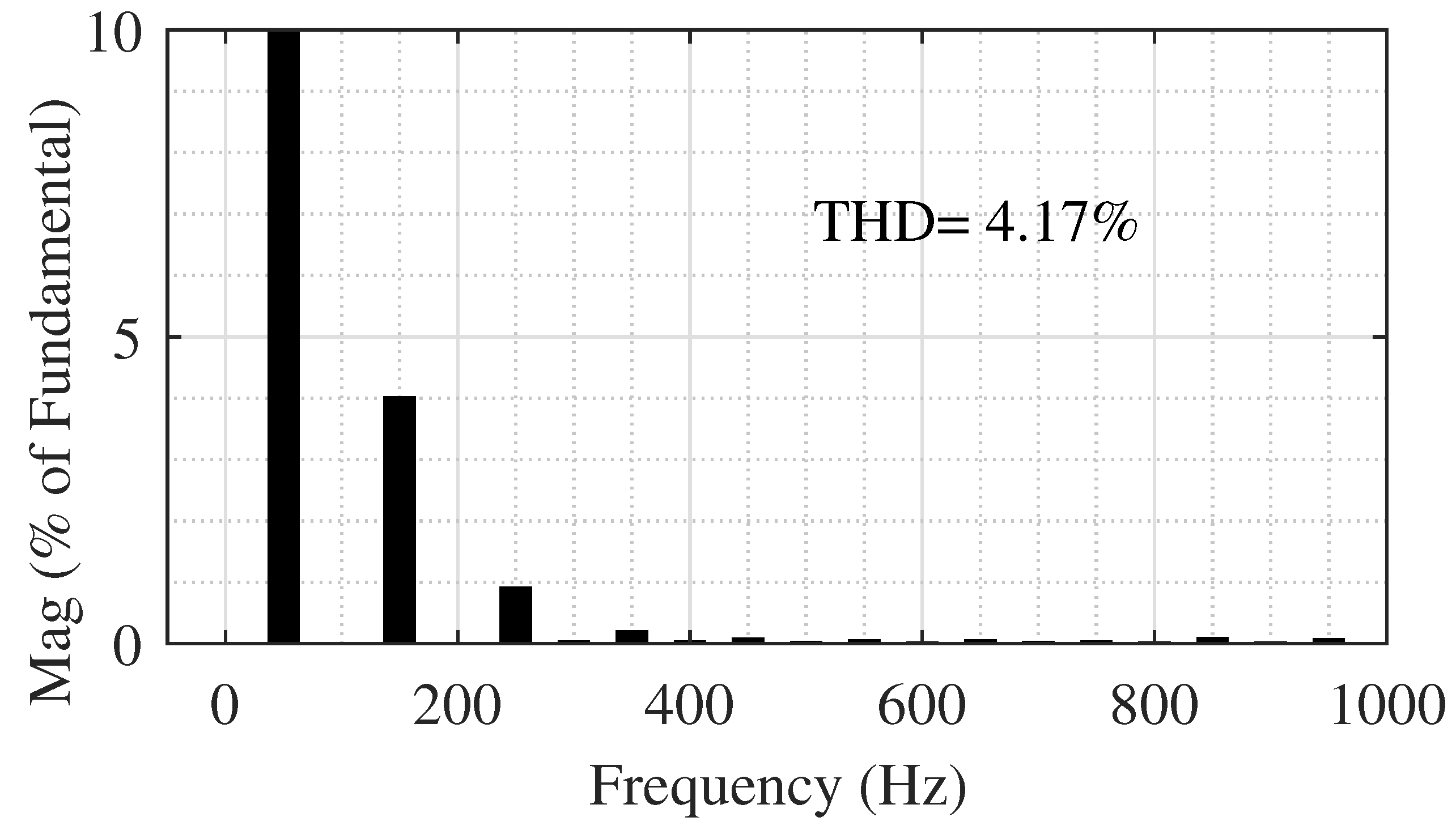
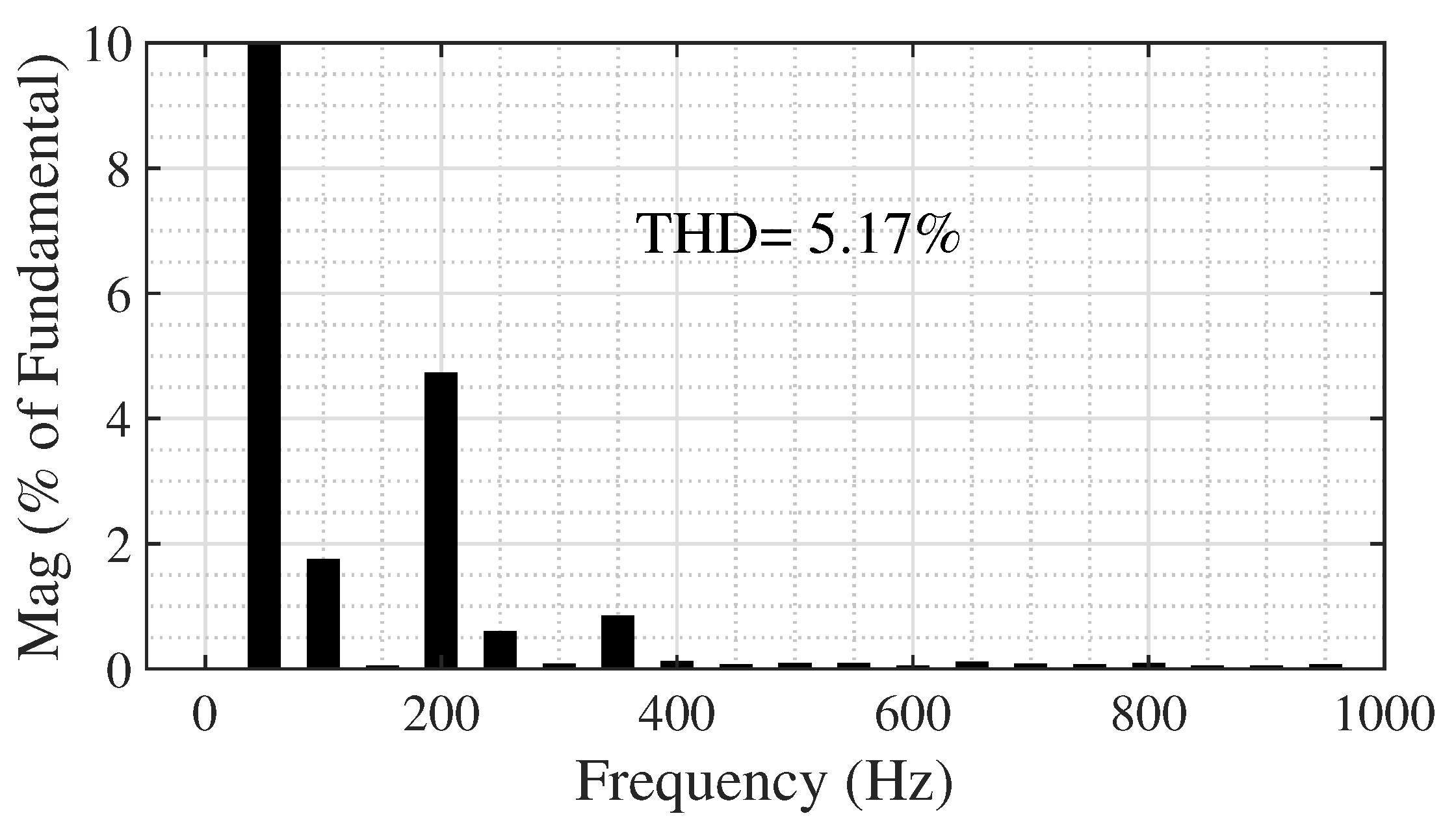
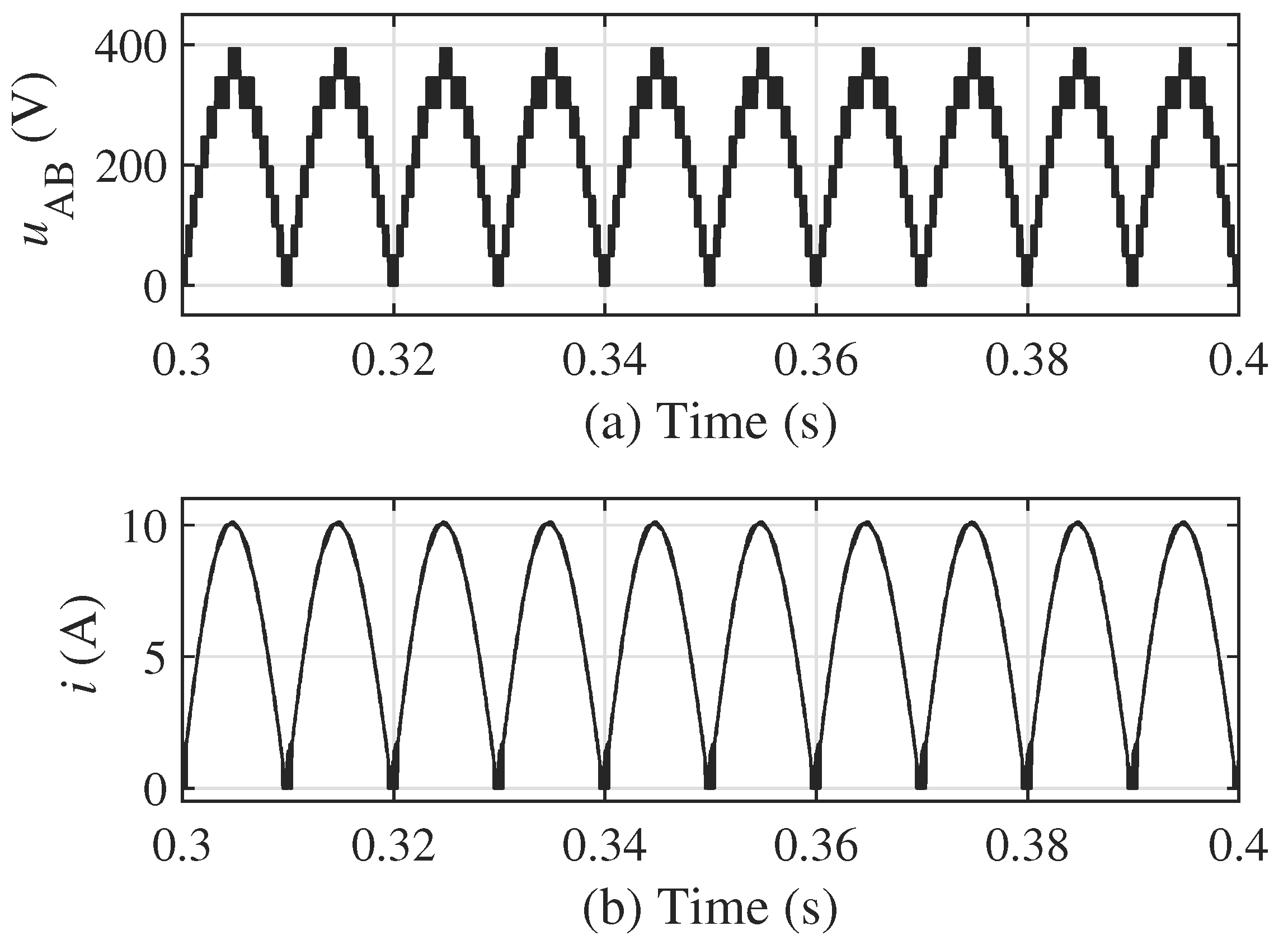
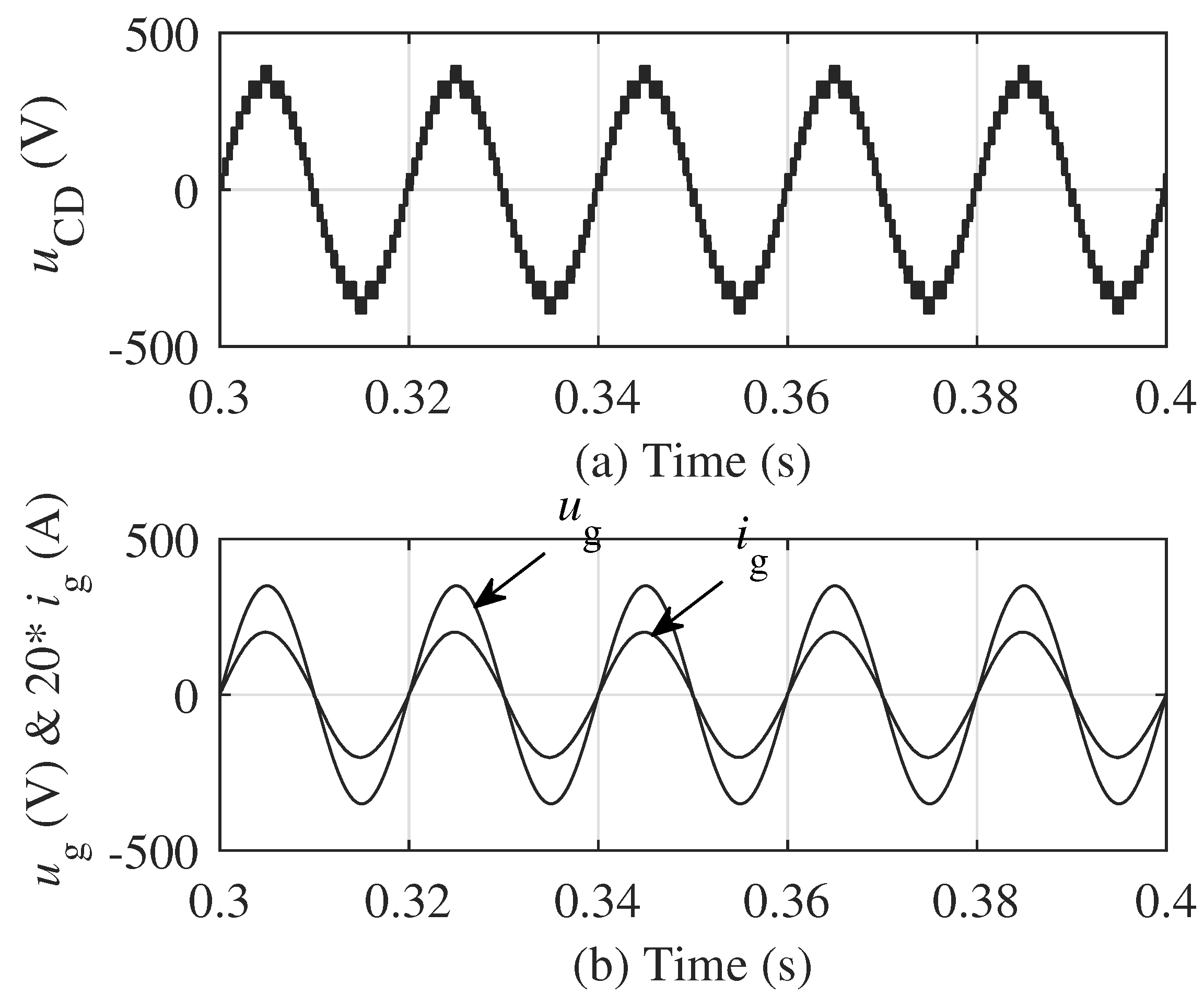
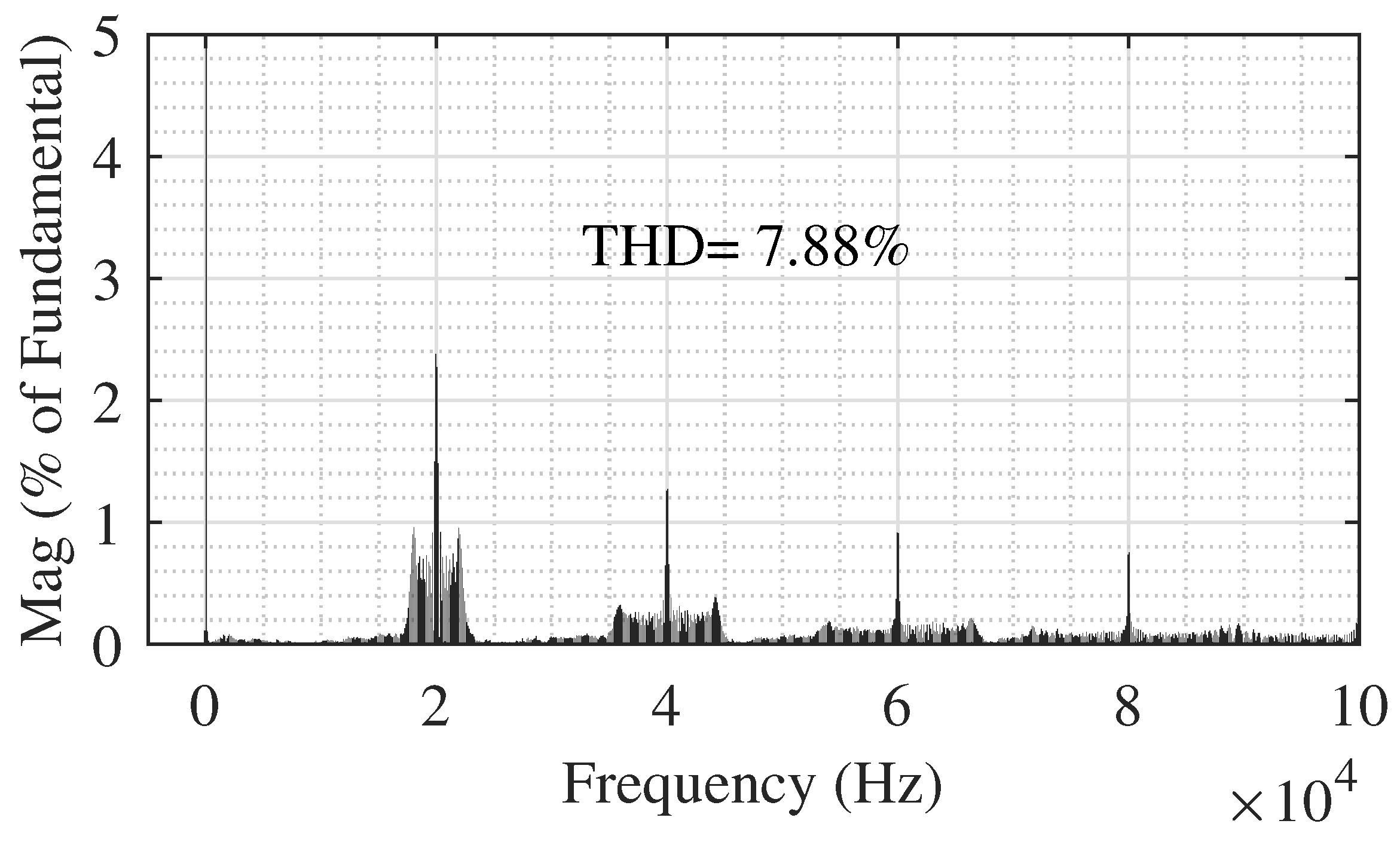
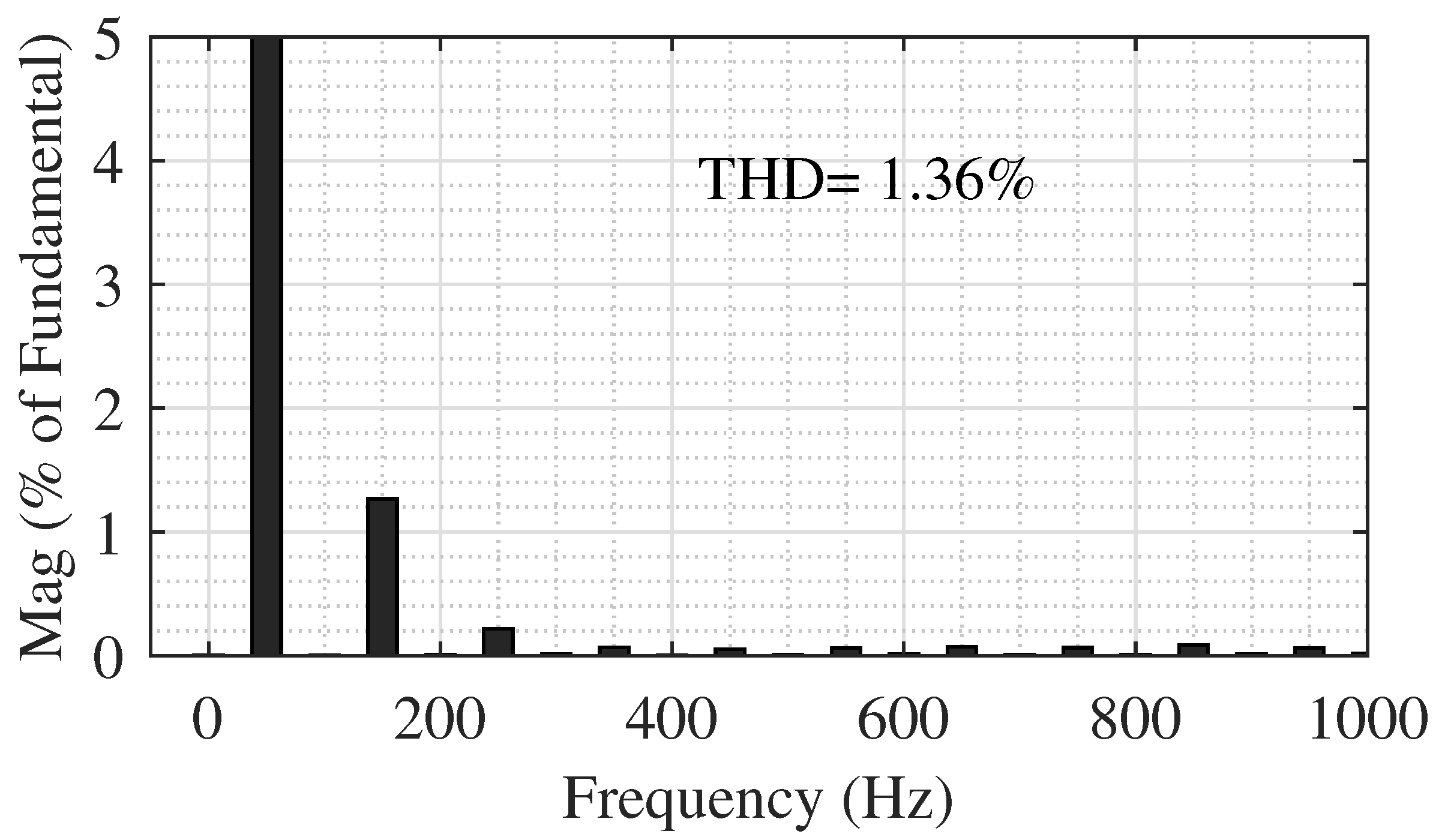
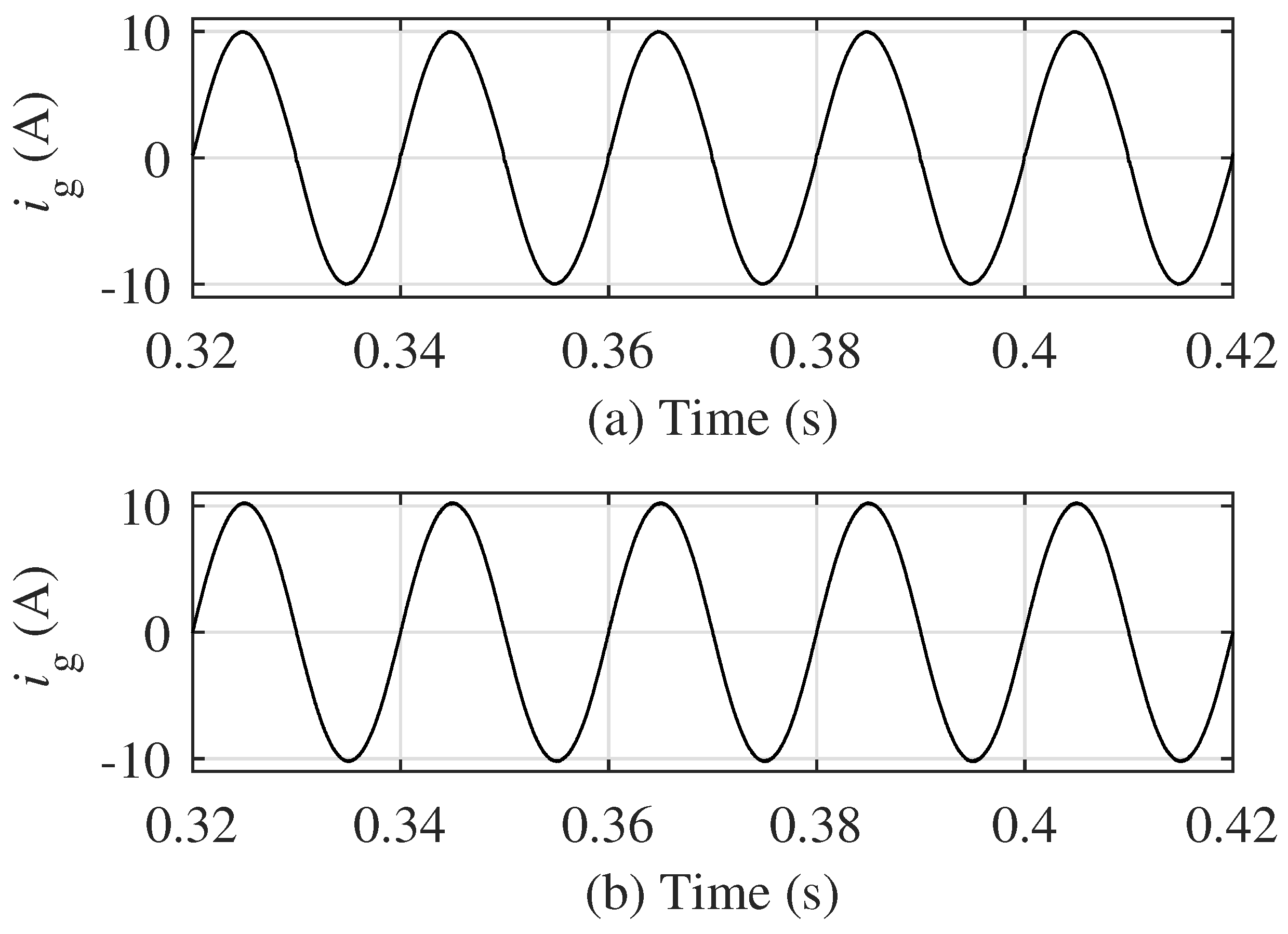
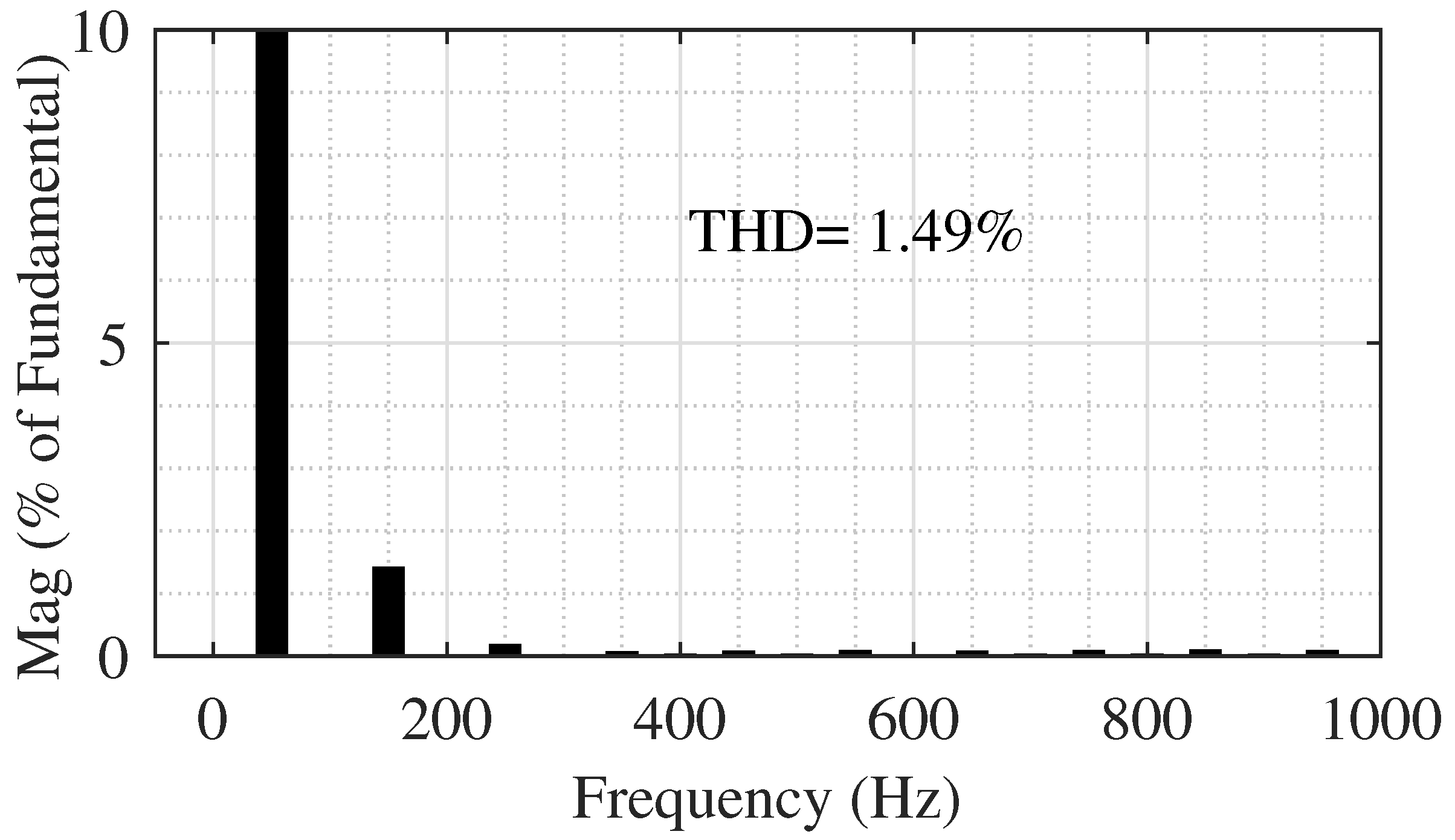
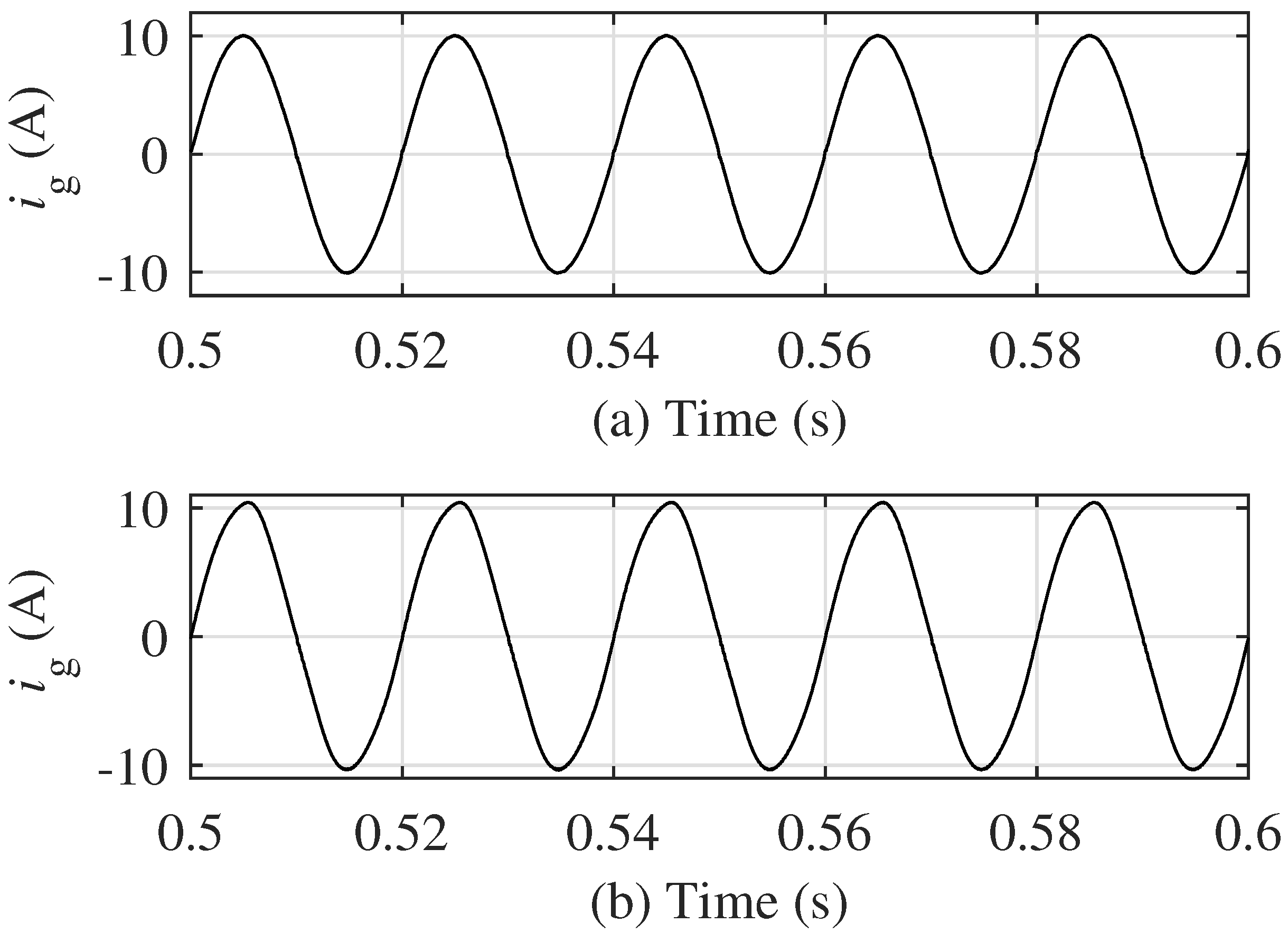
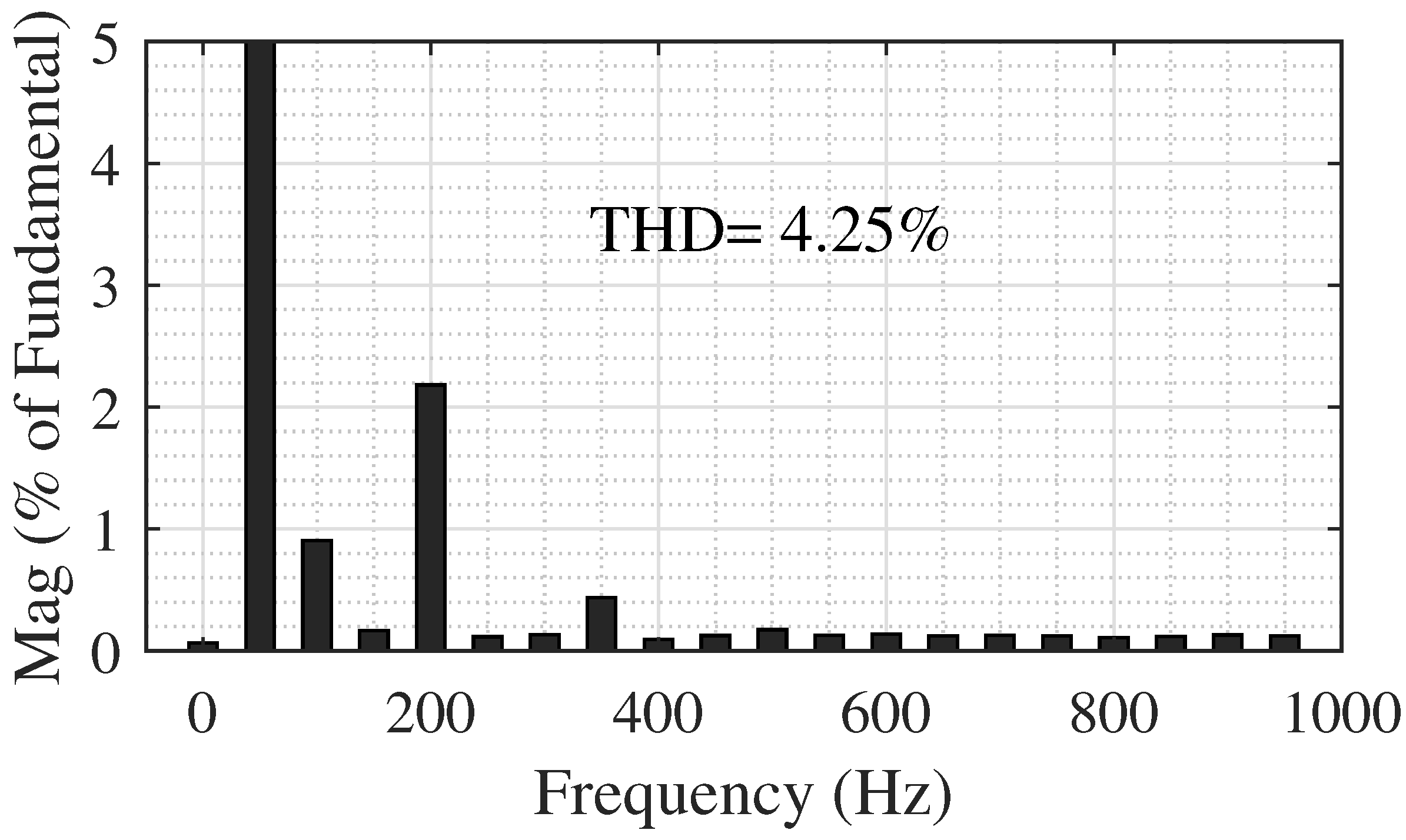
4.1. Simulation Results of the 5-Level Topology
4.2. Simulation Results of the 17-Level Topology
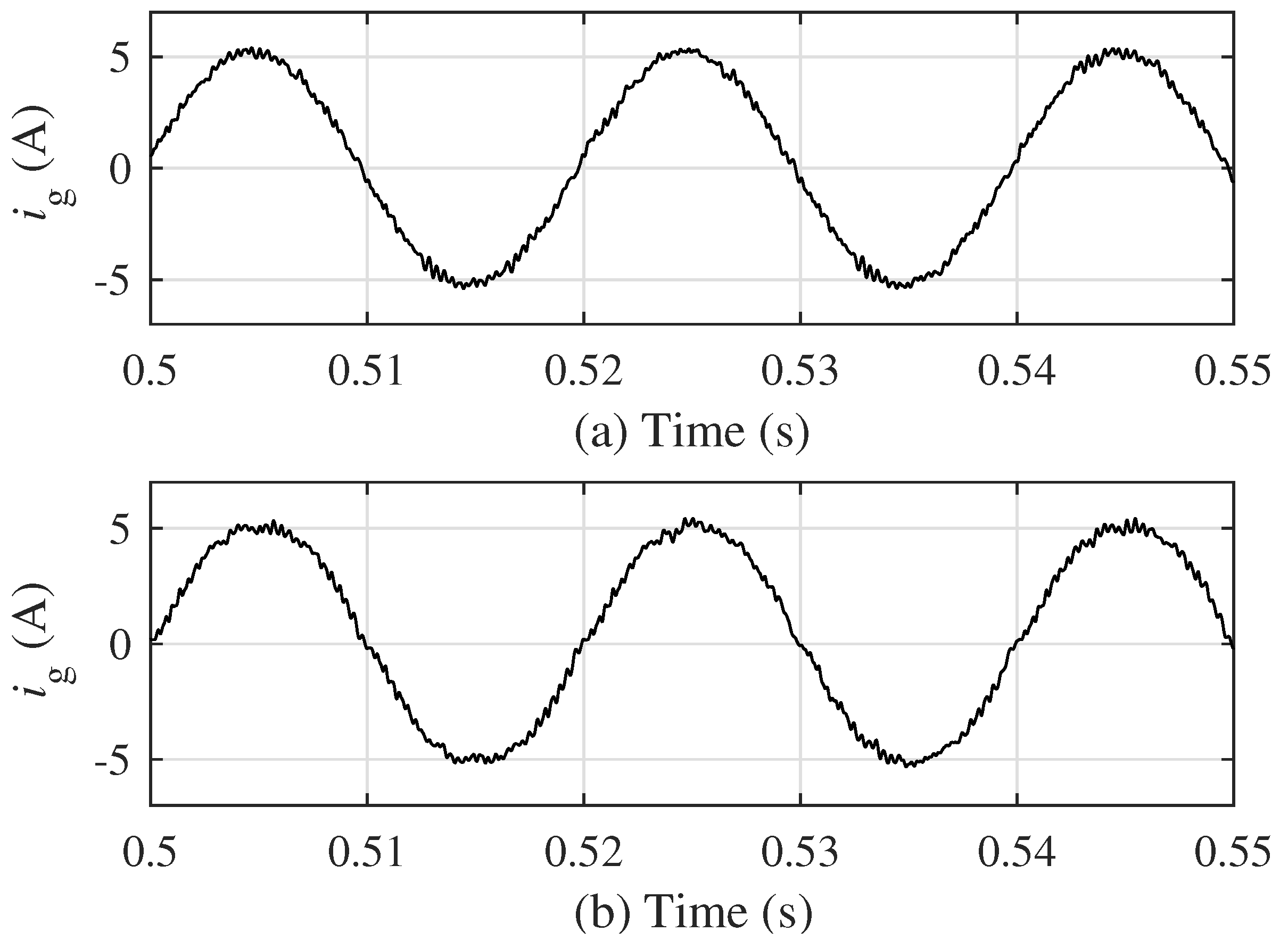
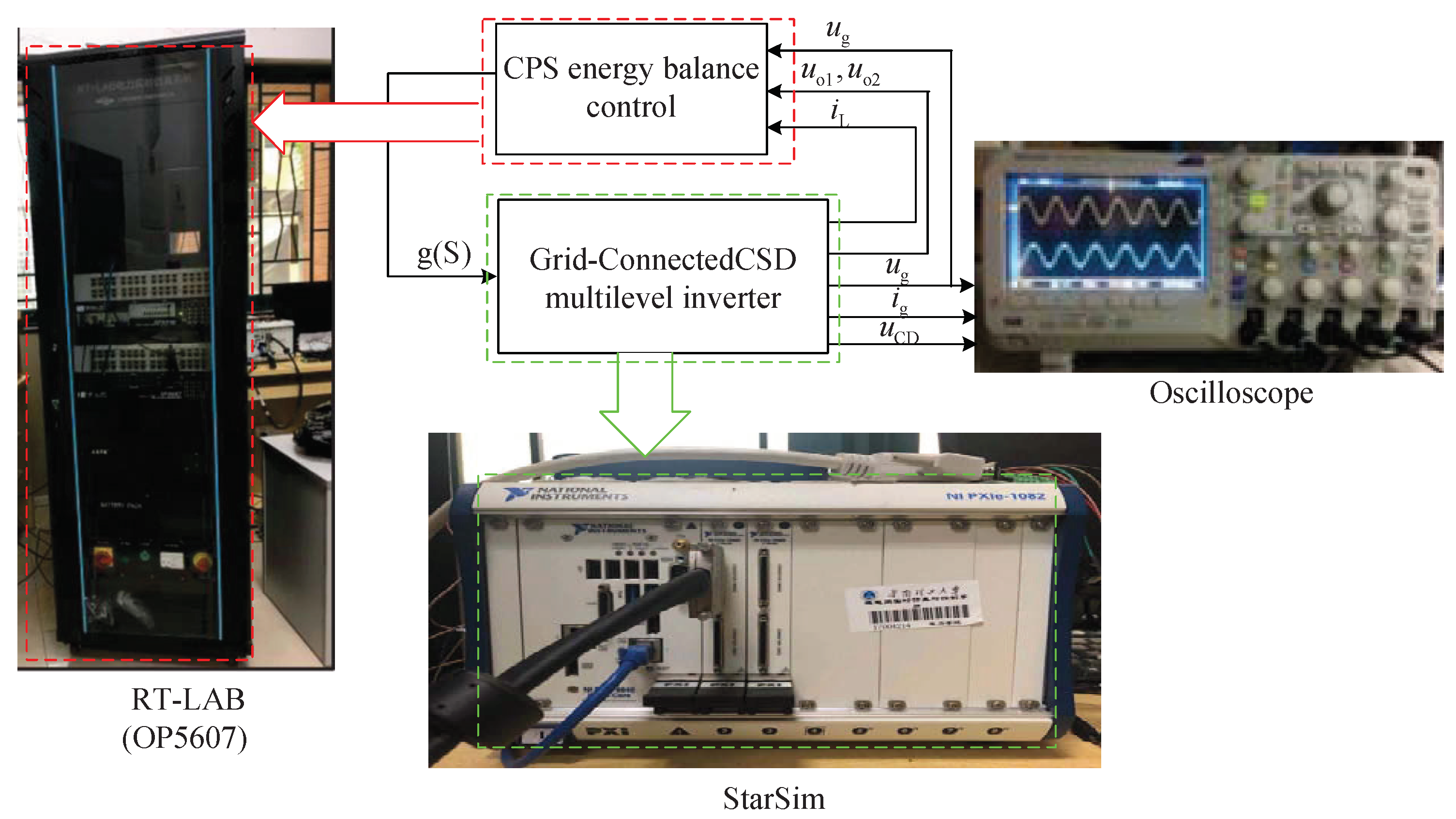
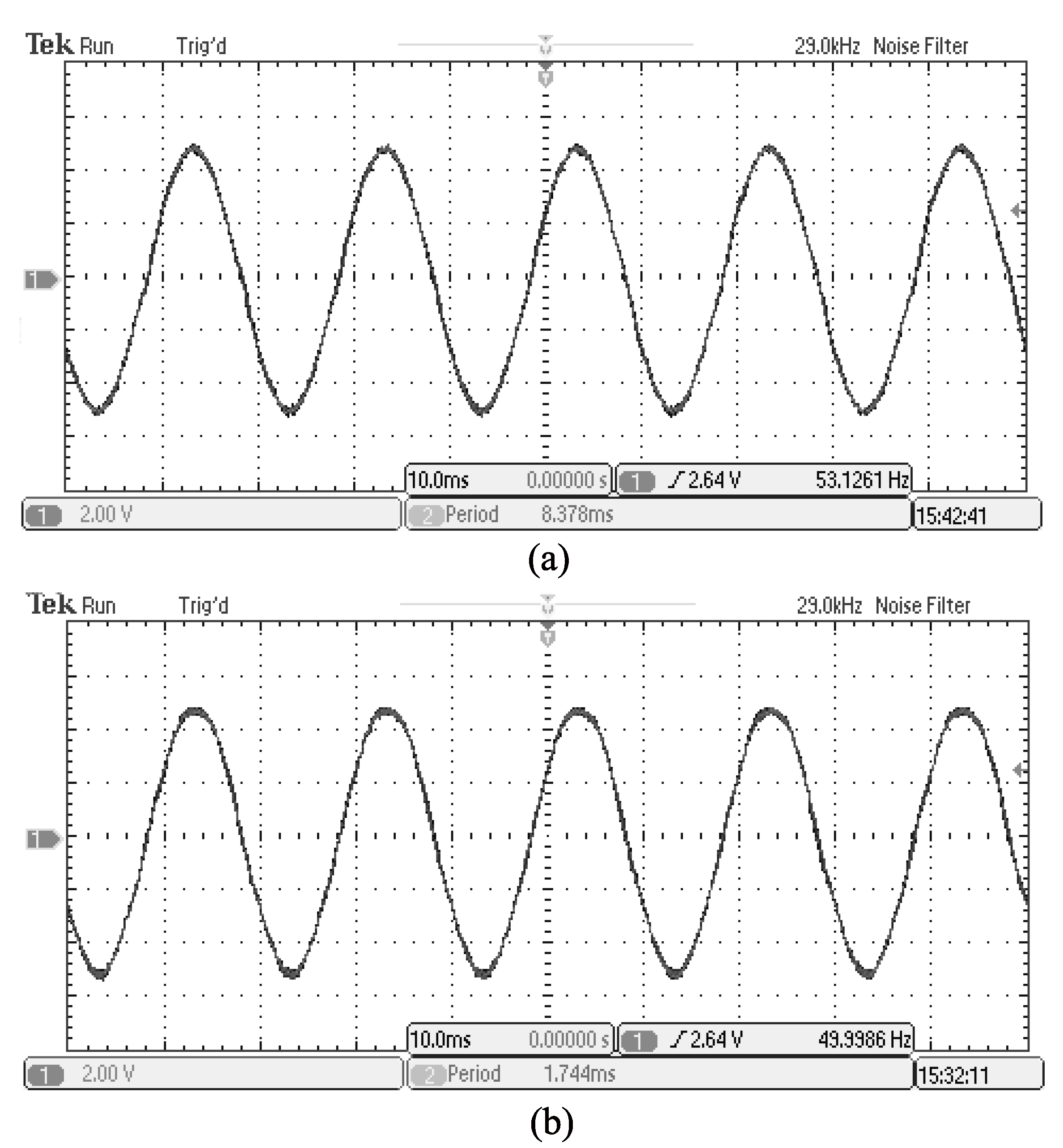
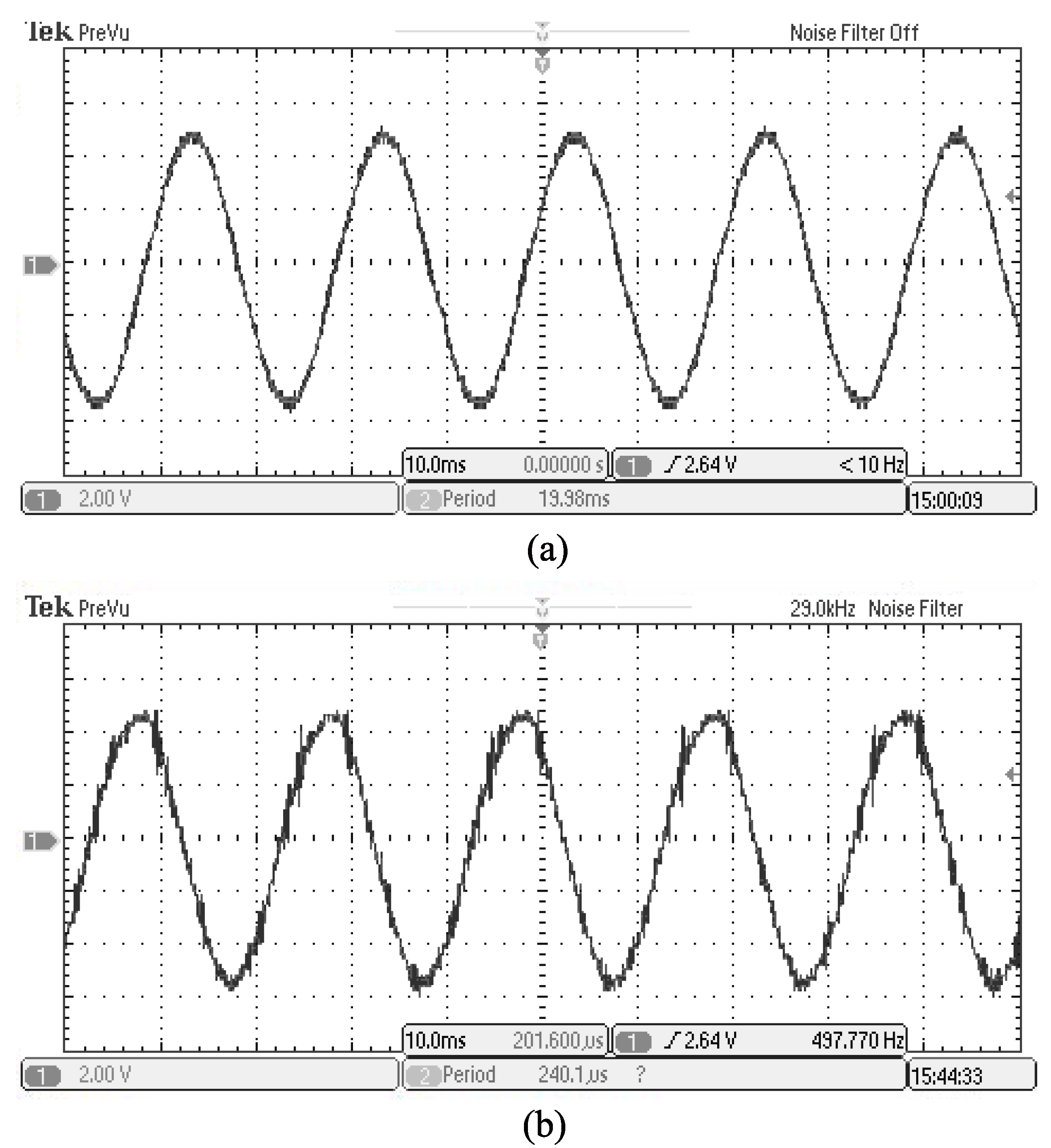
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CPS | clock phase-shifted |
| PV | photovoltaic |
| DG | distributed generation |
| CSD | cascaded switched-diode |
| THD | total harmonic distortion |
| PS-PWM | phase-shifted pulse width modulation |
| MPPT | maximum power point tracking |
References
- Wang, T.; O’Neill, D.; Kamath, H. Dynamic control and optimization of distributed energy resources in a microgrid. IEEE Trans. Smart Grid 2015, 6, 2884–2894. [Google Scholar] [CrossRef] [Green Version]
- Hussain, M.M.; Javed, W.; Akram, R.; Javed, T.; Razaq, A.; Siddique, M. Distributed energy management analysis for microgrids. In Proceedings of the 2021 56th International Universities Power Engineering Conference (UPEC), Middlesbrough, UK, 31 August–3 September 2021; pp. 1–6. [Google Scholar]
- Xiao, B.; Hang, L.; Mei, J.; Riley, C.; Tolbert, L.M.; Ozpineci, B. Modular cascaded H-bridge multilevel PV inverter with distributed MPPT for grid-connected applications. IEEE Trans. Ind. Appl. 2015, 51, 1722–1731. [Google Scholar] [CrossRef]
- Mittal, N.; Singh, B.; Singh, S.P.; Dixit, R.; Kumar, D. Multilevel inverters: A literature survey on topologies and control strategies. In Proceedings of the 2012 2nd International Conference on Power, Control and Embedded Systems, Allahabad, India, 17–19 December 2012; pp. 1–11. [Google Scholar]
- Wang, L.; Wu, Q.H.; Tang, W.H. Novel cascaded switched- diode multilevel inverter for renewable energy integration. IEEE Trans. Energy Convers. 2017, 32, 1574–1582. [Google Scholar] [CrossRef]
- Alishah, D.N.R.S.; Hosseini, S.H. Novel topologies for symmet- ric, asymmetric, and cascade switched-diode mutilevel converter with minimum number of power electronic components. IEEE Trans. Ind. Electron. 2014, 61, 5300–5310. [Google Scholar] [CrossRef]
- Babaei, E.; Hosseini, S.H. New cascaded multilevel inverter topology with minimum of switches. Energy Convers. Manag. 2009, 50, 2761–2767. [Google Scholar] [CrossRef]
- Alishah, R.S.; Nazarpour, D. New hybrid structure for multilevel inverter with fewer number of components for high-voltage levels. IET Power Electron. 2013, 7, 96–104. [Google Scholar] [CrossRef]
- Devi, V.S.K.; Srivani, S.G. Modified phase shifted PWM for cascaded H bridge multilevel inverter. In Proceedings of the 2017 Third International Conference on Advances in Electrical, Electronics, Information, Communication and Bio-Informatics (AEEICB), Chennai, India, 27–28 February 2014; Volume 29, pp. 347–355. [Google Scholar]
- Garg, V.; Sinha, S.K.; Dave, M.P. Phase shifted PWM cascaded multilevel inverter for solar PV grid integration. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–5. [Google Scholar]
- Schenck, M.E.; Lai, J.S.; Stanton, K. Fuel cell and power conditioning system interactions. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 6–10 March 2005; pp. 114–120. [Google Scholar]
- Michail, V.; Alfred, R.; Antoine, B. Modular converter architecture for medium voltage ultra fast ev charging stations: Global system considerations. In Proceedings of the IEEE International Electric Vehicle Conference (IEVC), Greenville, SC, USA, 4–8 March 2012; pp. 1–7. [Google Scholar]
- Cai, W.; Liu, B.; Duan, S.; Jiang, L. An active low-frequency ripple control method based on virtual capacitor concept for BIPV sytems. IEEE Trans. Power Electron. 2014, 29, 1733–1745. [Google Scholar] [CrossRef]
- JItoh, I.; Hayashi, F. Ripple current reduction of a fuel cell for a single-phase isolated converter using a DC active filter with a center tap. IEEE Trans. Power Electron. 2010, 25, 550–556. [Google Scholar]
- Shi, Y.J.; Liu, B.Y.; Duan, S.X. Low-frequency input current ripple reduction based on load current feedforward in a two-stage single-phase inverter. IEEE Trans. Power Electron. 2016, 31, 7972–7985. [Google Scholar] [CrossRef]
- Zhu, G.; Ruan, X.; Zhang, L.; Wang, X. On the reduction of second harmonic current and improvement of dynamic response for two stage single-phase inverter. IEEE Trans. Power Electron. 2015, 30, 1028–1041. [Google Scholar] [CrossRef]
- He, L.; Zhang, K.; Xiong, J.; Fan, S.; Xue, Y. Low-Frequency Ripple 48 Suppression for Medium-Voltage Drives Using Modular Multilevel Converter with Full-Bridge Submodules. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 657–667. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Xiong, Y.; Ma, R. Low-frequency suppression strategy based on predictive control model for modular multilevel converters. J. Power Electron. 2021, 21, 1407–1415. [Google Scholar] [CrossRef]
- Wang, K.; Kong, D.; Zhong, Z.; Gao, N.; Jiang, F.; Wu, W.; Liserre, M. Suppression of Low-frequency Voltage Ripple in 56 Cascaded H-bridge Multilevel Converters-based Large-scale PV Systems. In Proceedings of the 2022 IEEE 13th 57 International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; pp. 1–5. [Google Scholar]
- Wang, L.; Xiahou, K.S.; Wu, Q.H.; Tang, W.H.; Ma, W. Direct Grid Current Regulation for Grid-Connected PV Systems with Cascaded Multilevel Inverter. In Proceedings of the 2022 5th International Conference on Power and Energy Applications (ICPEA), Guangzhou, China, 18–20 November 2022; pp. 86–91. [Google Scholar]





| State | Switches States | |||||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | ||||||
| C | |||||
|---|---|---|---|---|---|
| C | |||||
|---|---|---|---|---|---|
| 1.1 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Chen, L.; Ye, W.; Ma, W. Phase-Shifted Energy Balance Control for Multilevel Inverters in Grid-Connected PV Systems. Electronics 2023, 12, 2582. https://doi.org/10.3390/electronics12122582
Wang L, Chen L, Ye W, Ma W. Phase-Shifted Energy Balance Control for Multilevel Inverters in Grid-Connected PV Systems. Electronics. 2023; 12(12):2582. https://doi.org/10.3390/electronics12122582
Chicago/Turabian StyleWang, Lei, Lidan Chen, Weiqiang Ye, and Wei Ma. 2023. "Phase-Shifted Energy Balance Control for Multilevel Inverters in Grid-Connected PV Systems" Electronics 12, no. 12: 2582. https://doi.org/10.3390/electronics12122582
APA StyleWang, L., Chen, L., Ye, W., & Ma, W. (2023). Phase-Shifted Energy Balance Control for Multilevel Inverters in Grid-Connected PV Systems. Electronics, 12(12), 2582. https://doi.org/10.3390/electronics12122582







