Ship Trajectory Prediction Based on the TTCN-Attention-GRU Model

Abstract

As shipping continues to play an increasingly important role in world trade, there are consequently a large number of ships at sea at any given time, posing a risk to maritime traffic safety. Therefore, the tracking and monitoring of ships at sea has gradually attracted the attention of scholars. Ship trajectory prediction comprises an important aspect of ship tracking and monitoring. Trajectory prediction describes the forecasting of a ship’s future trajectory over a period of time through use of historical trajectory information of the ship, so as to predict the sailing dynamics of the ship in advance. Accurate trajectory prediction can help maritime regulatory authorities improve supervision efficiency and reduce collisions between ships. Temporal Convolutional Network (TCN) offers good time memory ability and has shown better performance in time series prediction in recent years. Ship trajectory sequence belongs to the category of time series. Thus, in this paper, we introduce TCN into the field of ship trajectory prediction and improve on it, and propose Tiered-TCN (TTCN). The attention mechanism is a way to help neural networks learn data features by highlighting features that have a greater impact on predicted values. Gate Recurrent Unit (GRU) is an important variant of Recurrent Neural Networks (RNN), which bears a strong nonlinear fitting ability. In this paper, TTCN, attention mechanism and GRU network are integrated to construct a hybrid model for trajectory prediction, which is referred to as TTCN-Attention-GRU (TTAG). By optimizing the advantages of each module, the prediction effect is achieved with high precision. The experimental results show that the TTAG model is superior to all the baseline models presented in this paper.

1. Introduction

An Automatic Identification System [1] (AIS) is a system that records, sends and receives ship navigation data. A ship in a certain sea area will send relevant information to nearby AIS receivers. Shipborne AIS can receive information about surrounding ships to provide decision support for the ship operators. Maritime authorities can supervise various areas of sea in a timely and effective manner based on the AIS information received by satellites or shore-based base stations.

At present, the research on maritime traffic mainly focuses on the following four areas: abnormality detection [2,3,4], path planning [5,6,7], collision prevention [8,9] and trajectory prediction [10,11,12]. The sequence of tracks can be expressed as a sequence consisting of multiple tuples, as follows:

$$S=((la{t}_0,lo{n}_0,t_0),\dots ,(la{t}_k,lo{n}_k,t_k),(la{t}_{k+1},lo{n}_{k+1},t_{k+1}))$$

(1)

where, $t_i$ (i = 0, 1, …, k, $k+1$) represents the time stamp, $la{t}_i$ represents the latitude at time $t_i$, and $lo{n}_i$ represents the longitude at time $t_i$. Trajectory prediction details obtaining the trajectory after $t_i$ moment by using the trajectory before $t_i$ moment, for example, according to the orbit characteristics of $t_0$ to $t_k$ period, we can obtain the predicted value of $t_{k+1}$ moment (${\widehat{lat}}_{k+1}$, ${\widehat{lon}}_{k+1}$). One of the purposes of trajectory prediction is to allow ships to sail at sea more safely and avoid collisions. In this respect, researchers have carried out many studies on land vehicles, pedestrians and robots, which are of reference significance [13,14,15,16]. The future trajectory of a ship is closely related to its historical navigation characteristics. The greater the amount of historical data, the higher the accuracy of extracting these features. Traditional trajectory prediction algorithms cannot fully learn ship historical navigation characteristics from massive AIS data, but the emergence of deep learning model solves this problem. Scholars at home and abroad have realized the prediction of future trajectory based on deep neural networks and achieved good results. On this basis, research efforts have recently been directed toward constructing a hybrid model to further improve prediction accuracy [17,18]. The hybrid model refers to the combination of different models and a higher prediction accuracy is achieved by optimizing and implementing the advantages of different modules.

Deep learning was proposed in 2006 and has shown good performance in many tasks [19,20,21]. Due to the strong learning ability of neural networks, an increasing number of scholars have applied them to the field of maritime traffic. The researchers in [22] proposed an architecture for ship monitoring. The authors of [23] proposed a classification algorithm based on convolutional neural network, and Ref. [24] forecasted the flow of ships in ports based on a ConvLSTM model.

For trajectory prediction, traditional prediction methods mostly use the Kalman filter, the Markov chain models, etc. For example, Jiang [25] et al. made improvements on the basis of Kalman filtering algorithm to solve the problem of missing track data to a certain extent and realize ship position prediction; however, their model showed a low utilization rate of historical track information, and thus the prediction accuracy was not high. Guo [26] et al. adopted the classical algorithm to grid the designated sea area, calculated the grid state with the position, speed and direction of the ship as the key elements, and established the state transition matrix with K-order Markov chain for prediction. However, there is also the problem of low utilization rate of historical track information.

A growing body of research has shown that the performance of the neural networks is better. Hu [27] et al. preprocessed data based on the Gauss–Kruger projection and an improved linear interpolation method, then made a trajectory prediction through the GRU models. The disadvantage is that they did not make much improvement to the models. Quan [28] et al. combined AIS data and Long Short-Term Memory (LSTM) model, and used longitude, latitude, speed, heading and time interval as input to predict the future trajectory, breaking the limitation of using fixed time interval so that the model could predict the trajectory at any time interval; however, the method is still an application of LSTM, and not an improvement. Ding [29] designed a PSO-LSTM model for ship tracking prediction. PSO algorithm improves the prediction accuracy of LSTM network, but the calculation efficiency of the model is greatly reduced after the introduction of PSO algorithm. It is a worthwhile effort to design a Seq2Seq model to realize trajectory prediction [30], but the environment at sea differs vastly from that of inland rivers. Some researchers [31] built a bilinear autoencoder model based on a generative model to predict ship trajectories. They adopt a joint prediction approach that predicts full trajectories rather than predicting future states iteratively, while the method depends on the ability to cluster trajectories to some extent. Zhao [32] et al. combined an RNN network with a Bi-LSTM network creatively, but it takes more time to train a two-way network.

To sum up, traditional prediction methods bear certain limitations, such as the need to establish the ship motion equation of state, or the trajectory being required to meet a certain distribution. At the same time, due to the complexity of ship movement, traditional methods only demonstrate good prediction performance within brief time windows. The performance of recurrent neural networks and their variants has been verified in many trajectory prediction scenarios. However, this approach also has some shortcomings. TCN is a relatively new class of network model, which shows better performance in time series problems [33,34,35,36]. The research works of some scholars show that the prediction accuracy of TCN in certain time-series scenarios is greater than that of common network models, and ship trajectory sequence belonging to the category of time series. Therefore, it is feasible to introduce the TCN network into the field of ship trajectory prediction. In addition, compared with RNN and LSTM networks, the TCN network offers the following advantages:

• TCN can process data in parallel;
• The gradient of TCN is more stable;
• The receptive field size of TCN can be flexibly controlled according to different tasks;
• The TCN network does not require a large memory footprint.

We improved on the traditional TCN network, creatively proposed tiered-TCN network, which we named TTCN, on the basis of which, we constructed the ship trajectory prediction model. The main contributions of this paper are as follows:

• A TCN network is introduced into the field of ship trajectory prediction. On this basis, we improve the traditional TCN residuals and construct the TTCN network in this paper;
• By combining the TTCN network with the attention mechanism and GRU network, we construct the trajectory prediction model, known as the TTAG model, playing the role of different modules and achieving high prediction accuracy. By comparing with the baseline model, we verify the validity of the proposed model;
• We open source part of the code for the reference of scholars in related fields. The address is as follows: https://github.com/linzuOne/TrajectoryPrediction, accessed on 11 May 2023.

The remainder of this paper is structured as follows: The first chapter gives an introduction; In Section 2, AIS equipment, trajectory prediction model, experimental environment and data sources are introduced. In Section 3, several experiments are carried out, including a comparison experiment between the TTAG model and baseline models, a parameter determination experiment of the TTAG model, ablation experiment, etc. Section 4 summarizes the content of this paper and gives future research directions.

2. Materials and Methods

2.1. AIS System

The AIS system includes shipborne AIS equipment, satellite-based AIS and shore-based AIS. In this paper, we refer to shipborne AIS equipment, which is mainly divided into three major parts; the data-processing and transmission part, the external part, and the sensors. Among them, the role of the sensors part is crucial. Key dynamic information in AIS data is mostly obtained through sensors. Nowadays, with the development of information technology, sensor networks have become more intelligent and energy efficient, meanwhile, building collaborative networks is one direction in the future [37,38,39,40,41].

As shown in Figure 1, there are several sensor types in the AIS system, including a GPS positioning sensor, speed-measuring sensor, direction sensor and rotation direction sensor. The sensors acquire data related to the ship’s navigation and broadcast on very high frequency. After the broadcast data are obtained, they need to be further decoded.

2.2. TTCN-Attention-GRU Architecture

Dilated causal convolution is used in the TCN network. Causal convolution, as the name suggests, is a model with strict time constraints. Dilated convolution, using fewer parameters than ordinary with the same receptive field. The receptive field refers to the range of information seen by convolutional kernel. The larger the receptive field is, the more contextual relationships there are. Dilated causal convolution, combining the advantages of causal convolution and dilated convolution. The structures of dilated causal convolution is shown in Figure 2. Residual connection is used in TCN network. As shown in Figure 3, in the TCN residual unit, assuming that the input is x and the expected output is h(x), it is difficult for the network to directly learn the identity mapping function $h\left(x\right)=x$. However, if the network is designed as $h\left(x\right)=f\left(x\right)+x$, the learning of the identity mapping function can be converted to the learning of the residual function $f\left(x\right)=h\left(x\right)-x$. As long as $f\left(x\right)=0$, the identity mapping $h\left(x\right)=x$ is formed. During parameter initialization, the weight parameters are generally small, which is very suitable for learning $f\left(x\right)=0$. Therefore, fitting the residual will be easier.

Parameters such as expansion coefficient and convolution kernel size jointly determine the range of receptive field of TCN network. The size of the receptive field must be larger than the time step of the input data, otherwise the training effect of the model is not good. The calculation formula is shown as follows:

$$R_{field}=1+2\ast (N_{kernel}-1)\ast N_{stack}\ast \sum d$$

(2)

where $R_{field}$ represents the receptive field, $N_{kernel}$ represents the convolution kernel size, which is set as 3 in this paper, $N_{stack}$ represents the number of residual blocks, which is set as 1 in this paper, and d represents the expansion coefficient.

To make the model work better and avoid over fitting, this paper proposes a Tiered-TCN (TTCN) network structure creatively. We replace one dilated causal convolution layer in the original TCN network with multiple parallel dilated causal convolution layers corresponding to different expansion coefficients, and then pass the output of the parallel dilated causal convolution layers through a fully connected network. In order to avoid over-complicating the model, only three parallel causal convolution layers are set in this paper. Figure 4 shows the improved TCN residual cell structure. $D_1$, $D_2$ and $D_3$, respectively, represent dilated causal convolution layers corresponding to different expansion coefficients.

The TTAG model proposed in this paper based on TTCN consists of six layers, which are the input layer, Tiered-TCN layer, Attention layer, Reshape layer, GRU layer, and Dense layer. The Attention layer gives different weights to the vectors of the output of the Tiered-TCN layer. After the dimension transformation on features in the Reshape layer, the GRU layer further extracted data features and then carried out feature integration through the Dense layer to realize the final prediction. The structure of TTAG model is shown in Figure 5.

1.

Input layer

The preprocessed data are normalized and then passed into the input layer. On the one hand, data normalization can eliminate the influence of dimension, on the other hand, it also speeds up the operation speed of gradient descent algorithm. In this paper, MinMaxScaler function is used for normalization. The calculation formula is shown as (3).

$$x_{scaled}=\frac{x-x_{min}}{x_{max}-x_{min}}$$

(3)

where, x is the true value, $x_{min}$ is the minimum value in the data, $x_{max}$ is the maximum value in the data, and $x_{scaled}$ is the normalized value. The input data format of the model is [Batch size, 20, 2], where Batch size represents the number of samples, 20 indicates the historical data with 20 time steps, and 2 represents the dimensions of each time step, namely longitude and latitude.

2.

TTCN layer

In the previous section, we introduced dilated causal convolution and residual units. TCN network can accurately learn the dependence of time series and achieve good results in many time-series prediction problems. In this paper, based on the traditional TCN network, we integrate the improved TTCN network with attention mechanism and GRU network and introduce it into the field of ship trajectory prediction for the first time. In the residual element, the formula for calculating one-dimensional dilated causal convolution is as follows:

$$F\left(s\right)=\sum _{i=0}^{k-1}f\left(i\right)\ast x_{s-di}$$

(4)

where x is the input data, f is the filter, d is the expansion factor, k is the size of the convolution kernel, and $s-di$ ensures that only past input can be convolved. In the TTCN network, for the three-layer dilated causal convolution layer, the corresponding maximum expansion coefficients are set as 2, 8 and 32, respectively.

3.

Attention layer

When we observe a ship at sea, we do not pay attention to the vast ocean. On the contrary, our attention is focused on the ship and our eyes move with the movement of the ship, which is the simple explanation of the attention mechanism [42]. At present, many scholars have integrated an attention mechanism with neural network and achieved good results [43,44,45]. The attention mechanism can be divided into two categories: one being the spatial attention mechanism and the other being a temporal attention mechanism, which, respectively, correspond to weight allocation in spatial dimension and weight allocation in time step. This paper focuses on weight distribution on time steps.

Let $X=[x_1,\dots ,x_N]$, $x_n\in R^M$, $n\in [1,N]$. X represents input data. In order to extract the key information related to the task from the existing information, a query vector Q is introduced, which can be generated by learning. Under the premise of given query vector Q and X, we choose the following method to determine the weight:

$$a_n=\frac{exp\left(s(x_n,Q)\right)}{{\sum }_{j=1}^{N}exp\left(s(x_n,Q)\right)}$$

(5)

where $a_n$ is the weight of the data, which satisfies the normalization condition, and $s(x_n,Q)$ represents the attention scoring function. Different scoring functions have different attention aggregation operations. In the model of this paper, we adopt the dot product mapping mode for $s(x_n,Q)$. After determining the weights of each element, we perform a weighted sum over the input information.

Taking the output of the TTCN layer further through the Attention layer can help the model to highlight important information. The weight is the importance of trajectory information at different time steps. The operation flow of Attention layer is shown in Figure 6.

4.

Reshape layer

The Reshape layer changes the dimensions of the data without changing the data itself. After the weight distribution of features in the Attention layer, the feature dimension changes from 3D to 2D. In order to match the input format of the GRU layer, a Reshape layer is set for dimension expansion.

5.

GRU layer

Compared with LSTM network, the GRU network has a short training time and similar performance, and can even realize higher accuracy in some cases, so the GRU network is selected for further feature extraction on the information after the Reshape layer [46,47]. Figure 7 shows a structural diagram of the GRU network, where $x_t$ is the input sequence, $h_{t-1}$ is the implicit state vector of the previous moment, and $h_t$ is the state of the current moment.

6.

Dense layer

The Dense layer refers to the fully connected layer. After the GRU layer, we set up a fully connected layer. The essence of the fully connected layer is to transform from one feature space to another. Therefore, the purpose of the fully connected layer is to extract the correlation between the features extracted from the previous layers after linear and nonlinear changes, and finally map them to the output space.

After passing through the above layers, we obtain the final predicted value. In the TTAG model, the number of filters in the TTCN module is set to 64, and then the temporal attention mechanism in this paper is used to extract important information. The GRU layer adopts a single-layer structure, and the number of neurons in the hidden layer is set to 32. The number of neurons in the Dense layer is set to 2. The maximum number of training rounds in this paper is 500, and we set up an early stop mechanism. When the model is trained for a long time, the loss function of the training set and the verification set will not decrease basically. At this time, continuing to train the model will reduce training efficiency, and may lead to the phenomenon of overfitting on the test set. In the early stop mechanism, we set a loss function threshold $\gamma$ and end the training if the loss function of the validation is set less than $\gamma$. The value of $\gamma$ in this experiment is ${10}^{-8}$.

2.3. Evaluation Index

When training the model, the neural network makes the model better fit the label value by learning the mapping relationship between the given feature and label. Given an x as input, the output value $\widehat{y}$ is deviated from the real value y. According to this deviation, the back propagation algorithm or similar algorithm is adopted to update the model parameters so that the error value becomes smaller and smaller, that is, the predicted value is closer and closer to the real value. Loss function is used to represent the difference between the predicted value and the real value. The smaller the loss value is, the better the training effect of the model will be. Therefore, a loss function can be used as an indicator to evaluate the model performance. Commonly used loss functions include Mean Absolute Error Loss (MAE), Mean Squared Error Loss (MAE) and Root Mean Square Error (RMSE), etc. The evaluation indexes adopted in this paper are MSE and RMSE.

After dividing the data into training set, verification set and test set according to 8:1:1, this paper evaluates the performance of the model by calculating the loss value on the test set. The calculation formulas of evaluation indexes are shown as (6) and (7), respectively, where $y_i$ is the real track value and $\widehat{y_i}$ is the predicted track value.

$$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2$$

(6)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2}$$

(7)

2.4. Data and Environment

1.

Data source

The experimental data in this paper come from the publicly available ship trajectory data website [48], which provides free AIS data for ships transiting US waters from 2009 to 2022. In some research works, researchers collect and integrate the navigation data of multi-source, which can improve the quality of data to a certain extent. However, the use of multi-source data requires various problems to be considered such as data matching, which is relatively complicated, so only AIS data are used in this paper [49]. Figure 8 shows the UTM map of the United States and its surrounding areas, in which there are many ships in the 10th region, and thus AIS data are relatively rich. Therefore, this paper selects the AIS data covered by the 10th region of the UTM map in 2017, and generates a CSV table file with a data size of 16.3 GB.

AIS raw data need to be further cleaned.

Table 1. AIS sample data.

MMSI	BaseDateTime	LAT	LON	SOG	COG
209012000	2017-07-31T22:53:27	46.050	−122.880	8.1	355
209012000	2017-07-31T22:54:36	46.053	−122.88	8.5	355
209012000	2017-07-31T22:55:37	46.055	−122.88	8.7	348
209012000	2017-07-31T22:56:38	46.057	−122.882	8.9	346
209012000	2017-07-31T22:57:45	46.060	−122.883	9.1	346

shows AIS sample data after preliminary processing. MMSI stands for ship unique identifier, BaseDateTime is the data recording time, LAT indicates the latitude of the ship, LON indicates the longitude of the ship, SOG is the speed of the ship to the ground, COG is the Angle of the ship to the ground. We finally obtain 33,524 training sequences, 3849 validation sequences, and 3858 test sequences.

2.

Experimental environment (

Table 2. Experimental environment.

Hardware environment	CPU	Intel(R) Xeon(R) Silver 4210 CPU @ 2.20 GHz
	memory	251 GB
	number of cores	40
	Graphics Card	RTX3080
Software environment	Deep learning framework	keras2.4
	Programming software	pycharm
	Programming language	python3.7
	Operating system	Ubuntu20.4

)

The CPU model used in this paper is Intel(R) Xeon(R) Silver4210, the main frequency is 2.20 GHz, the memory is 251 GB, and the number of cores is 40. The GPU model is GeForce RTX 3080. The programming language used in the experiment is Python, and the deep learning framework used is keras.

3. Experimental Section

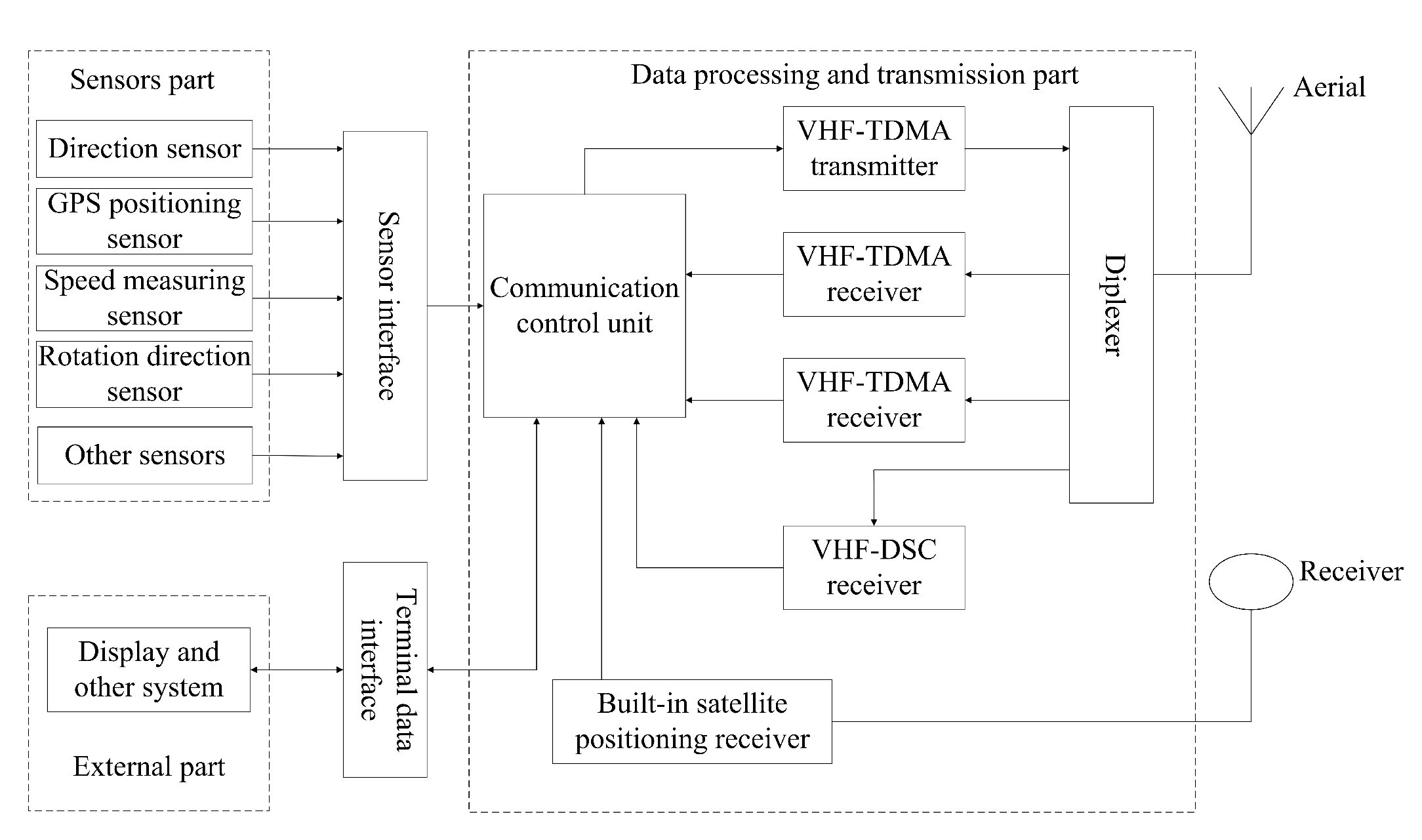
In this paper, we compare the performance of each model and four trajectories are randomly selected to measure the generalization ability of the model finally. Experimental results validate the effectiveness of the TTAG model.

Experimental Design and Analysis

1.

Comparison between the TTAG model and the baseline models

The processed AIS data were subjected to contrast experiments on the following seven models. The first 20-min sequence of historical tracks were entered to obtain the trajectory of future 1-min, 5-min, 10-min, as well as 15-min, respectively. We set the batch size to 2000, the maximum number of training rounds to 500, and the learning rate to 0.001. The experimental results are shown in

Table 3. Comparison of models (a).

Model	Predict the Trajectory of the Next 1 min				Predict the Trajectory of the Next 5 min
	MSE	RMSE	LAT_MSE	LON_MSE	MSE	RMSE	LAT_MSE	LON_MSE
GRU	$1.762\times {10}^{-4}$	$1.327\times {10}^{-2}$	$1.748\times {10}^{-4}$	$1.387\times {10}^{-6}$	$2.611\times {10}^{-4}$	$1.616\times {10}^{-2}$	$2.545\times {10}^{-4}$	$1.624\times {10}^{-5}$
LSTM	$1.751\times {10}^{-4}$	$1.323\times {10}^{-2}$	$1.747\times {10}^{-4}$	$1.845\times {10}^{-6}$	$3.509\times {10}^{-4}$	$1.873\times {10}^{-2}$	$2.642\times {10}^{-4}$	$9.951\times {10}^{-5}$
BiGRU	$1.730\times {10}^{-4}$	$1.315\times {10}^{-2}$	$1.701\times {10}^{-4}$	$3.116\times {10}^{-6}$	$2.068\times {10}^{-4}$	$1.438\times {10}^{-2}$	$1.211\times {10}^{-4}$	$2.287\times {10}^{-5}$
BiLSTM	$1.732\times {10}^{-4}$	$1.316\times {10}^{-2}$	$1.715\times {10}^{-4}$	$1.812\times {10}^{-6}$	$1.987\times {10}^{-4}$	$1.410\times {10}^{-2}$	$1.649\times {10}^{-4}$	$3.381\times {10}^{-5}$
TCN	$7.431\times {10}^{-5}$	$8.620\times {10}^{-3}$	$7.248\times {10}^{-5}$	$1.992\times {10}^{-6}$	$2.306\times {10}^{-4}$	$1.519\times {10}^{-2}$	$2.184\times {10}^{-4}$	$1.869\times {10}^{-5}$
TTCN	$6.331\times {10}^{-5}$	$7.957\times {10}^{-3}$	$6.207\times {10}^{-5}$	$1.729\times {10}^{-6}$	$1.915\times {10}^{-4}$	$1.384\times {10}^{-2}$	$1.873\times {10}^{-4}$	$1.297\times {10}^{-5}$
TTAG	$\mathbf{2}.\mathbf{743}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{5}.\mathbf{237}\times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{2}.\mathbf{718}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{3}.\mathbf{871}\times {\mathbf{10}}^{-\mathbf{7}}$	$\mathbf{5}.\mathbf{281}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{7}.\mathbf{267}\times {\mathbf{10}}^{-\mathbf{3}}$	$\mathbf{5}.\mathbf{153}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{3}.\mathbf{743}\times {\mathbf{10}}^{-\mathbf{6}}$

and

Table 4. Comparison of models (b).

Model	Predict the Trajectory of the Next 10 min				Predict the Trajectory of the Next 15 min
	MSE	RMSE	LAT_MSE	LON_MSE	MSE	RMSE	LAT_MSE	LON_MSE
GRU	$5.878\times {10}^{-4}$	$2.425\times {10}^{-2}$	$4.812\times {10}^{-4}$	$1.461\times {10}^{-4}$	$1.344\times {10}^{-3}$	$3.666\times {10}^{-2}$	$8.721\times {10}^{-4}$	$6.068\times {10}^{-4}$
LSTM	$1.651\times {10}^{-3}$	$4.063\times {10}^{-2}$	$6.887\times {10}^{-4}$	$1.062\times {10}^{-3}$	$5.864\times {10}^{-3}$	$7.658\times {10}^{-2}$	$1.622\times {10}^{-3}$	$4.808\times {10}^{-3}$
BiGRU	$2.761\times {10}^{-4}$	$1.662\times {10}^{-2}$	$2.296\times {10}^{-4}$	$4.028\times {10}^{-5}$	$4.144\times {10}^{-4}$	$2.036\times {10}^{-2}$	$3.188\times {10}^{-4}$	$1.076\times {10}^{-4}$
BiLSTM	$3.517\times {10}^{-4}$	$1.875\times {10}^{-2}$	$3.057\times {10}^{-4}$	$5.153\times {10}^{-5}$	$6.385\times {10}^{-4}$	$2.527\times {10}^{-2}$	$4.182\times {10}^{-4}$	$2.391\times {10}^{-4}$
TCN	$7.471\times {10}^{-4}$	$2.733\times {10}^{-2}$	$6.899\times {10}^{-4}$	$1.058\times {10}^{-4}$	$1.818\times {10}^{-3}$	$4.264\times {10}^{-2}$	$1.526\times {10}^{-3}$	$3.557\times {10}^{-4}$
TTCN	$5.352\times {10}^{-4}$	$2.313\times {10}^{-2}$	$4.487\times {10}^{-4}$	$1.025\times {10}^{-4}$	$1.208\times {10}^{-3}$	$3.476\times {10}^{-2}$	$9.635\times {10}^{-4}$	$3.296\times {10}^{-4}$
TTAG	$\mathbf{1}.\mathbf{125}\times {\mathbf{10}}^{-\mathbf{4}}$	$\mathbf{1}.\mathbf{060}\times {\mathbf{10}}^{-\mathbf{2}}$	$\mathbf{9}.\mathbf{964}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{2}.\mathbf{162}\times {\mathbf{10}}^{-\mathbf{5}}$	$\mathbf{2}.\mathbf{247}\times {\mathbf{10}}^{-\mathbf{4}}$	$\mathbf{1}.\mathbf{499}\times {\mathbf{10}}^{-\mathbf{2}}$	$\mathbf{1}.\mathbf{762}\times {\mathbf{10}}^{-\mathbf{4}}$	$\mathbf{7}.\mathbf{044}\times {\mathbf{10}}^{-\mathbf{5}}$

. We calculated not only the MSE values of the trajectory points, but also the respective MSE values for latitude and longitude. The experimental conclusions are as follows.

(1) For LSTM model and GRU model, it can be seen from the table that when predicting the trajectory of the future 1 min, the prediction accuracy of GRU model and LSTM model is similar, but compared with other models, the prediction accuracy of these two models is lower. In particular, the performance of the LSTM model decreases rapidly with the increase of the number of predicted points. The possible reason for this is that the LSTM model is not good at processing the data under the scenario presented in this paper.

(2) Both BiGRU and BiLSTM are two-way networks. Unlike the one-way network, which can only access past information, the two-way network can simultaneously access past and future information, thus making the prediction results more accurate. According to the experimental results of this paper, when BiGRU model and BiLSTM model predict the trajectory of the future 1 min, compared with GRU and LSTM model, the loss value decreases somewhat. With the increase in number of iterations, the loss value of bidirectional network increases more gently.

(3) Compared with recurrent neural networks, the accuracy of the TCN model in predicting the trajectory of the future 1 min is greatly improved. This is because the TCN network has a strong time memory ability, but with the increase of the number of iterations, the performance of the TCN network declines rapidly. We have conducted many experiments, and the results obtained are basically the same. For the problem of rapid deterioration of TCN network performance, the possible reason for this is that the extraction of data features by the TCN model in this experiment is still insufficient, and the TCN network may be more suitable for the prediction in a very short time.

(4) The TTCN model, namely the improved TCN model proposed in this paper, can be seen from the data in the table that its performance exceeds that of the traditional TCN model. When predicting the future trajectory, the accuracy of traditional TCN model decreases rapidly with the increase of prediction time, while the accuracy of TTCN model also decreases rapidly, but its MSE value is still smaller than that of BiGRU and BiLSTM bidirectional network when predicting the future trajectory of the next 5 min. The TTCN model outperformed both the TCN model and the GRU model in predicting the trajectory of the next 15 min. The experimental results show that our improvement on TCN is successful.

(5) The TTAG model is a model built in this paper that integrates the TTCN network. Based on the TTCN model, an attention mechanism and GRU network are added to further extract key data features, thus improving the accuracy of prediction. According to the experimental results, it can be seen that the loss value of TTAG model is the lowest among all models, regardless of whether predicting the trajectory of the next 1 min or the trajectory of the next 15 min. Figure 9 shows the relationship between the loss value of each model and the number of predicted points. Due to the poor performance of the LSTM model compared with other models in this section, we did not draw the loss curve of the LSTM model in order to see the comparison results of the other six models more clearly. It can be intuitively seen from the figure that the loss value of TTAG model is smaller than that of other models. With the increase in predicted points, although the loss value keeps rising, compared with the baseline model, the rise curve is more gentle. The experimental results in this section verify the validity of the TTAG model.

2.

Comparison experiment of TTCN-Attention-X models with different architectures

As can be seen from the results of Table 3 and Table 4, compared with the traditional recurrent neural network, the TTAG model exhibits obvious advantages in the experiment. Now we change the internal structure of the TTAG model and construct the TTCN-Attention-X model with different architectures for comparison, where X is other neural network, such as LSTM. We want to know whether models with TTA-X architecture all exhibit good performance in trajectory sequence prediction through comparative experiments. Due to the time-consuming training of the two-way network, only three models, i.e., TTCN-Attention-GRU, TTCN-Attention-LSTM (TTAL) and TTCN-Attention-RNN (TTAR) are compared in this experiment. Experimental results are shown in

Table 5. Comparison of TTCN-Attention-X architecture (a).

Model	Predict the Trajectory of the Next 1 min				Predict the Trajectory of the Next 5 min
	MSE	RMSE	LAT_MSE	LON_MSE	MSE	RMSE	LAT_MSE	LON_MSE
TTAG	$2.743\times {10}^{-5}$	$5.237\times {10}^{-3}$	$2.718\times {10}^{-5}$	$3.871\times {10}^{-7}$	$5.281\times {10}^{-5}$	$7.267\times {10}^{-3}$	$5.153\times {10}^{-5}$	$3.743\times {10}^{-6}$
TTAL	$2.850\times {10}^{-5}$	$5.339\times {10}^{-3}$	$2.821\times {10}^{-5}$	$4.112\times {10}^{-7}$	$5.452\times {10}^{-5}$	$6.723\times {10}^{-3}$	$5.207\times {10}^{-5}$	$3.994\times {10}^{-6}$
TTAR	$2.357\times {10}^{-4}$	$1.535\times {10}^{-2}$	$2.262\times {10}^{-4}$	$1.146\times {10}^{-5}$	/	/	/	/

and

Table 6. Comparison of TTCN-Attention-X architecture (b).

Model	Predict the Trajectory of the Next 10 min				Predict the Trajectory of the Next 15 min
	MSE	RMSE	LAT_MSE	LON_MSE	MSE	RMSE	LAT_MSE	LON_MSE
TTAG	$1.125\times {10}^{-4}$	$1.060\times {10}^{-2}$	$9.964\times {10}^{-5}$	$2.162\times {10}^{-5}$	$2.247\times {10}^{-4}$	$1.499\times {10}^{-2}$	$1.762\times {10}^{-4}$	$7.044\times {10}^{-5}$
TTAL	$1.547\times {10}^{-4}$	$1.244\times {10}^{-2}$	$1.107\times {10}^{-4}$	$4.570\times {10}^{-5}$	$3.549\times {10}^{-4}$	$1.884\times {10}^{-2}$	$2.912\times {10}^{-4}$	$8.773\times {10}^{-5}$

.

As can be seen in the following table, the loss value of TTAL model when predicting the trajectory of the future 1 min is not much different from that of the TTAG model. With the increase in prediction time, the performance of the TTAL model decreases significantly, while the accuracy of TTAR model is lower. The experimental results show that the performance of the TTA-X architecture depends on the performance of X network to some extent. The long-term memory capacity of RNN network is not good, so the performance of TTAR model is poor. The performance of TTAL model is weaker than that of TTAG model, possibly because GRU network is more suitable for the scenario in this paper.

3.

Effect of expansion coefficient and convolution kernel size on TTAG model

Compared with recurrent neural networks, receptive field is unique to convolutional neural networks. A larger receptive field means that convolutional neural networks can obtain more context information, but larger is not always better. Increasing the receptive field tends to increase the training time. In addition, the data fitting effect does not necessarily get better when the model becomes more complex. In this section, different receptive fields will be obtained by setting different expansion coefficients, and experimental comparison will be conducted for each group.

Table 7. The effect of different expansion coefficient on the model.

Different Expansion Coefficients	MSE	Receptive Field	Average Training Time per Round
Dilations = [1, 2, 4, 8]	$3.613\times {10}^{-5}$	61	179 s
Dilations = [1, 2, 4, 8, 16]	$3.402\times {10}^{-5}$	125	231 s
Dilations = [1, 2, 4, 8, 16, 32] (The expansion coefficient used by TTAG model in this paper)	$2.743\times {10}^{-5}$	253	317 s
Dilations = [1, 2, 4, 8, 16, 32, 64]	$1.140\times {10}^{-4}$	509	453 s
Dilations = [1, 2, 4, 8, 16, 32, 64, 128]	$7.663\times {10}^{-5}$	1021	709 s

is the experimental results. Due to the limited experimental environment, after fixing the two dilated causal convolution layers in the TTCN model with smaller expansion coefficient, we conduct experiments on the dilated causal convolution layer with the largest expansion coefficient, and only measure the MSE value in the next 1 min. As can be seen from the table, in the process of the expansion coefficient list from [1, 2, 4, 8] to [1, 2, 4, 8, 16, 32], the prediction accuracy of the model keeps rising, but after that, the model performance begins to decline. At the same time, it can be seen from the table that the average training time of the model increases significantly with the increase of receptive field. Under the premise of fixed expansion coefficient, we also carry out comparative experiments on the size of convolution kernel. It can be seen from

Table 8. The effect of different kernel size on the model.

	Different Convolution Kernel Sizes	MSE
When the expansion coefficient is fixed, different convolution kernel sizes are set for comparison experiments	kernel size = 2	$7.365\times {10}^{-5}$
	kernel size = 3 (Size of convolution kernel used by TTAG model in this paper)	$2.743\times {10}^{-5}$
	kernel size = 5	$1.039\times {10}^{-4}$
	kernel size = 7	$1.972\times {10}^{-4}$

that when the convolution kernel size is 3, the model achieves the best performance. With the increase of convolution kernel, the model becomes more complex, but the accuracy decreases.

4.

Ablation experiment

In the previous experiments, we have verified the validity of the TTAG model proposed in this paper. In order to observe the role of each module in the TTAG model, the ablation experiment is carried out in this section. For this purpose, different modules are removed, respectively, and the TTCN-Attention network, TTCN-GRU network and Attention-GRU network are constructed.

Table 9. Result of ablation experiment.

Architecture	MSE	Eliminated Module
TTCN-Attention	$5.450\times {10}^{-5}$	GRU module
TTCN-GRU	$9.351\times {10}^{-5}$	attention module
Attention-GRU	$1.713\times {10}^{-4}$	TTCN module
TTAG	$2.743\times {10}^{-5}$	/

is the experimental result, as above, here we only carried out the measurement experiment of trace MSE value in the next 1 min. As can be seen from the table, the accuracy of the model decreases when any module in the model is removed. When TTCN module is excluded, the performance of the model is only comparable to that of the baseline model, indicating that TTCN network can greatly improve the performance of the TTAG model. When the attention module and GRU module in this section are excluded, the performance of the model also decreases significantly. Meanwhile, according to the following table, the role of each module in improving the overall model performance is sorted as: TTCN module > attention module > GRU module. Ablation experiments show that any module in the TTAG model is indispensable, and each module does play a role in improving the accuracy of the overall model. It’s not necessarily better to build a complex model, only by giving full play to the role of each module and paying attention to the characteristic information that has a great influence on the predicted value can we achieve a better prediction effect.

5.

Model generalization

In order to verify the generalization ability of the TTAG model, four different trajectories are randomly selected for prediction at last. In addition to the first trajectory, the other three trajectories include curve segments. The track segments contain 100, 100, 274 and 588 track points, respectively.

Because the trajectory of the ship in the low-speed sailing stage is prone to clutter, the four trajectory segments selected are all trajectories of the medium- and high-speed sailing stages. We set an indicator $hit$ and an error threshold $\beta$. If the average distance between the predicted value and the real value of the track less than $\beta$, then we consider the prediction to be successful and the value of $hit$ is 1, otherwise, it is 0. We set $\beta$ = 250 m.

According to

Table 10. Model generalization.

Trajectory	MSE	LAT_MSE	LON_MSE	$\mathit{hit}$
trajectory1	$5.166\times {10}^{-6}$	$5.046\times {10}^{-6}$	$1.207\times {10}^{-7}$	1
trajectory2	$6.363\times {10}^{-6}$	$6.104\times {10}^{-6}$	$2.588\times {10}^{-7}$	1
trajectory3	$5.245\times {10}^{-6}$	$5.054\times {10}^{-6}$	$1.906\times {10}^{-7}$	1
trajectory4	$6.611\times {10}^{-6}$	$6.413\times {10}^{-6}$	$1.983\times {10}^{-7}$	1

, it can be seen that the hit of all four trajectories is 1, indicating that the deviation fall within a reasonable error range, and the MSE value of trajectory 1 is the least. Figure 10 shows the scatter plots of the predicted value and the real value of four trajectories, respectively. It can be intuitively seen from the figure that the predicted value and the real value have a high coincidence for both the first two shorter trajectories and the second two longer trajectories.

4. Conclusions

Since the TCN network shows excellent performance in time series prediction, and the ship trajectory sequence belongs to the category of time series, we introduce TCN network into the field of ship trajectory prediction. Meanwhile, on the basis of traditional TCN, this paper creatively proposes a layered TTCN network, in which one dilated causal convolution layer in the original TCN network is replaced by multiple parallel dilated causal convolution layers, corresponding to different expansion coefficients, respectively. Moreover, the results of multiple dilated causal convolution layers are output through a fully connected layer. When a larger expansion coefficient is set, the TCN network can capture more data features and generally improve the model effect. However, an excessively deep network may cause overfitting of the model, resulting in reduced generalization ability. When a small expansion coefficient is set, TCN network can obtain more original information in the input data, and the model cannot easily produce the overfitting phenomenon; however, the captured data feature scale is small. The TTCN network fuses features extracted from different dilated causal convolution layers, which makes it difficult for the model to overfit while capturing more features. We then combined the TTCN with an attention mechanism and GRU network, and built a TTAG ship trajectory prediction model by using the weight allocation of attention mechanism and the nonlinear fitting of GRU network. Compared with the traditional prediction model, the accuracy of neural networks has been verified in previous studies. Therefore, this paper did not build Kalman filter and other traditional models, but instead built LSTM, GRU, BiLSTM, BiGRU, traditional TCN and other neural network models as the baseline models to compare with the TTAG model in this paper. A series of experiments verify the validity of the TTAG model. Finally, we conducted generalization experiments on the four randomly selected trajectory segments, and the experimental results show that the errors between the real values and the predicted values of the four trajectory segments fall within a reasonable range.

Although the prediction accuracy of the TTAG model constructed in this paper is higher than that of the baseline models, the following problems still remain:

• There is still a certain deviation between the predicted value and the actual value;
• The network depth of the TTAG model proposed in this paper is relatively deep with more parameters;
• The factors that affect the accuracy of ship trajectory prediction are not only the longitude and latitude of the ship, but also other factors such as wind and waves.

In our next step, we will optimize the model to consider more influencing factors and build a prediction model with fewer parameters and higher accuracy. In addition, the purpose of this study is to apply the research content in practice and build a monitoring and display system for maritime regulatory authorities. In this process, secure communication, data storage, backup and other issues are involved, which requires us to carry out further research work [50,51].