Flatness-Based Backstepping Antisway Control of Underactuated Crane Systems under Wind Disturbance
Abstract
1. Introduction
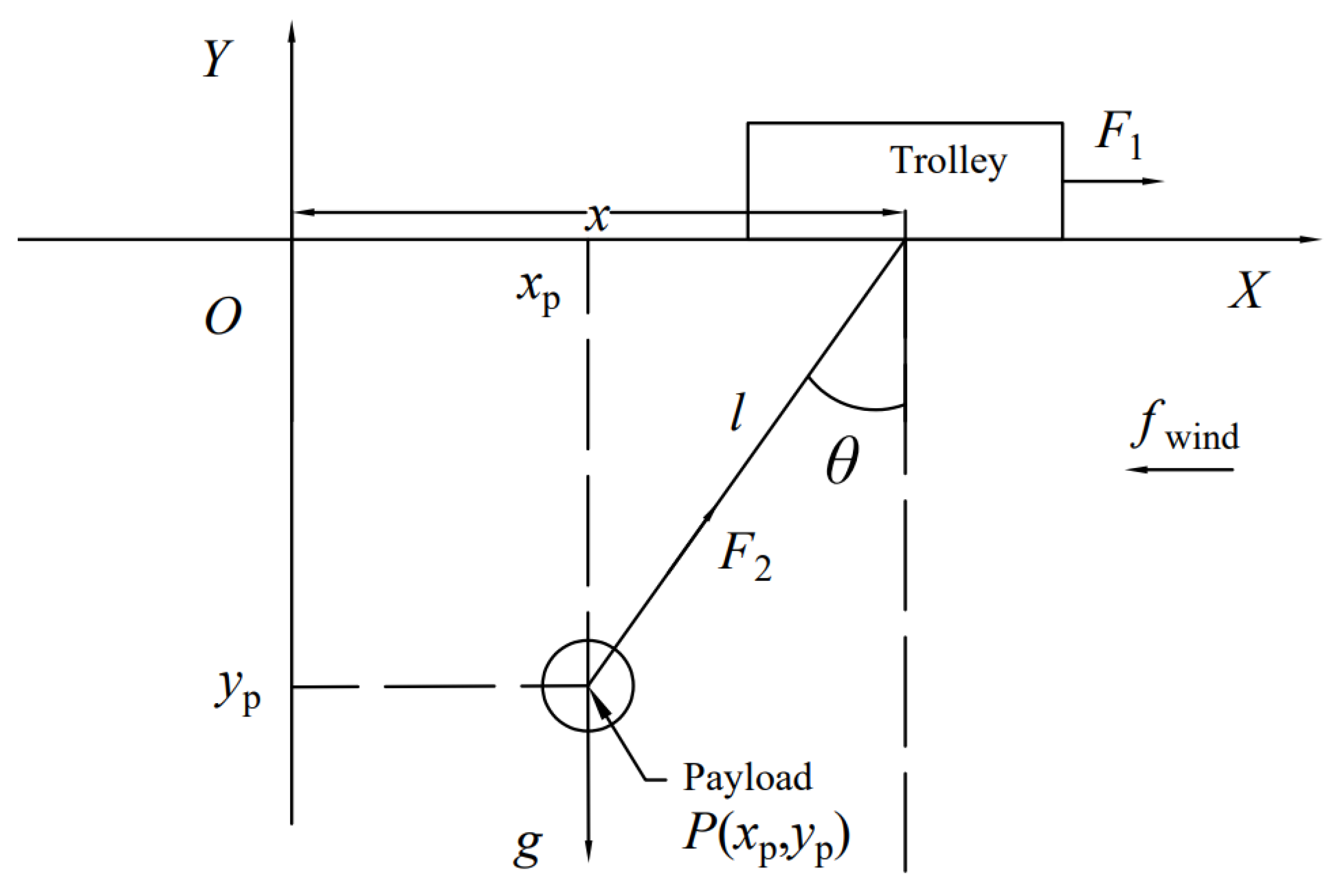
2. Mathematical Modelling
2.1. Dynamic Model
2.2. Differential Flat Output Construction
3. Feedforward Control Design
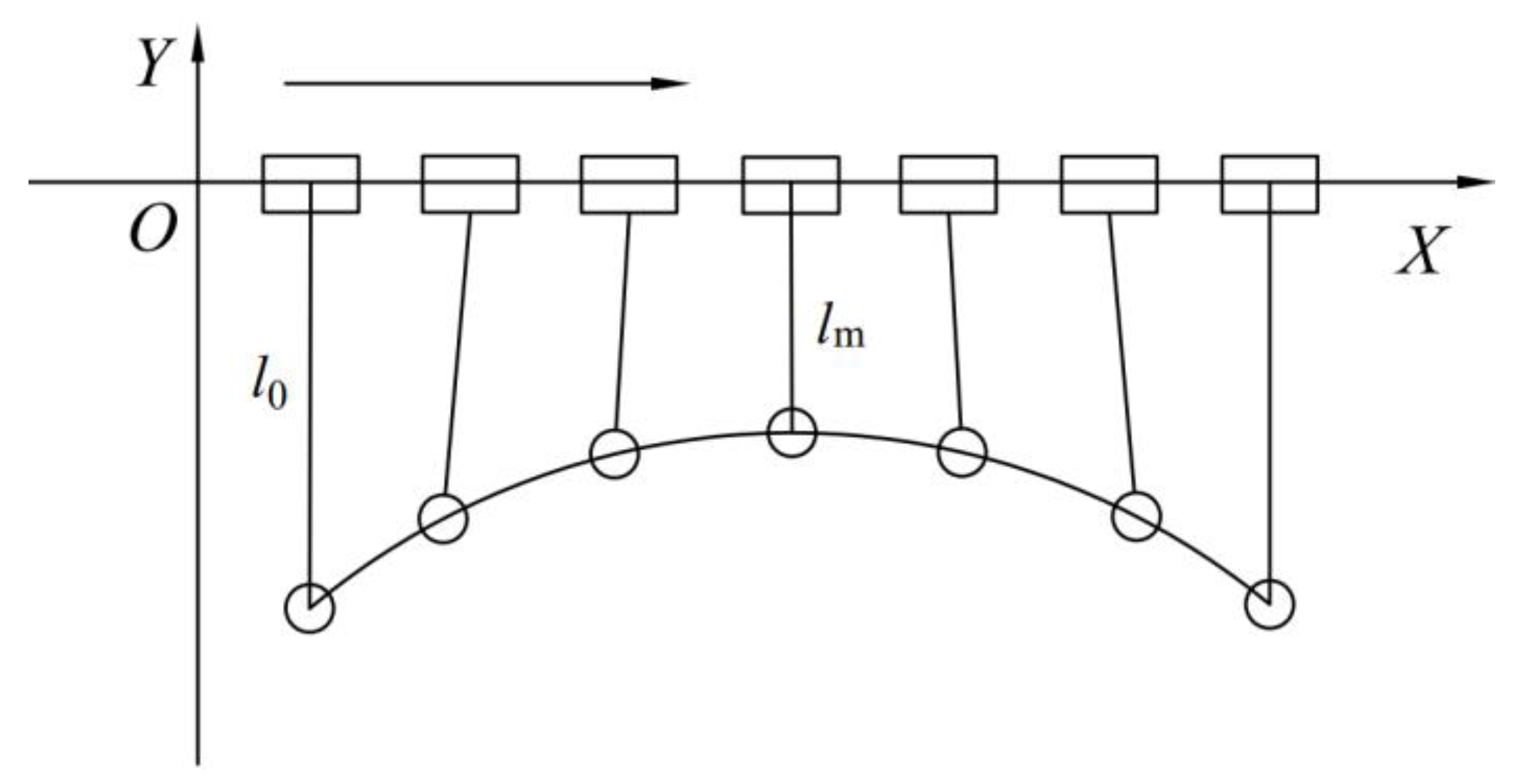
3.1. Constraint Consideration
3.2. Trajectory Planning
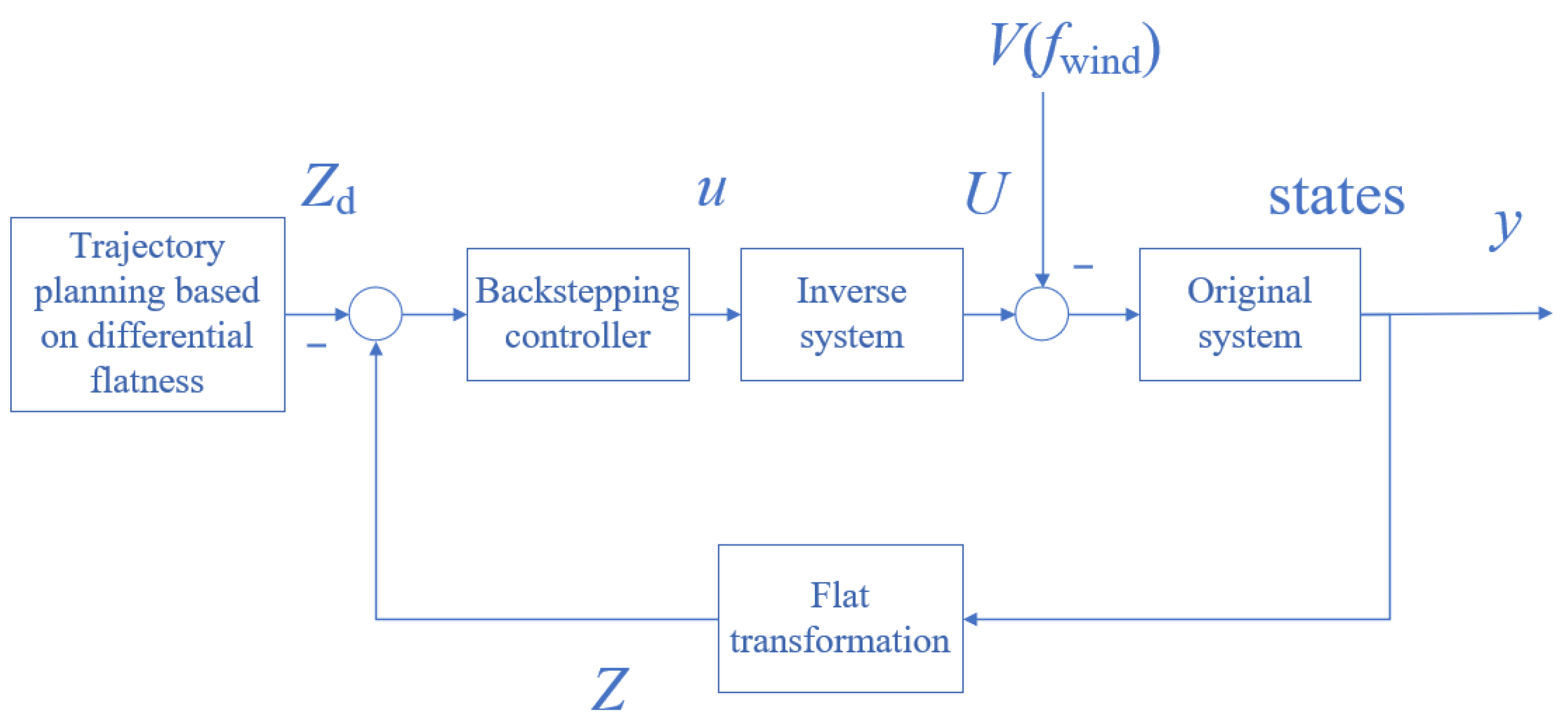
4. Trajectory Tracking Control
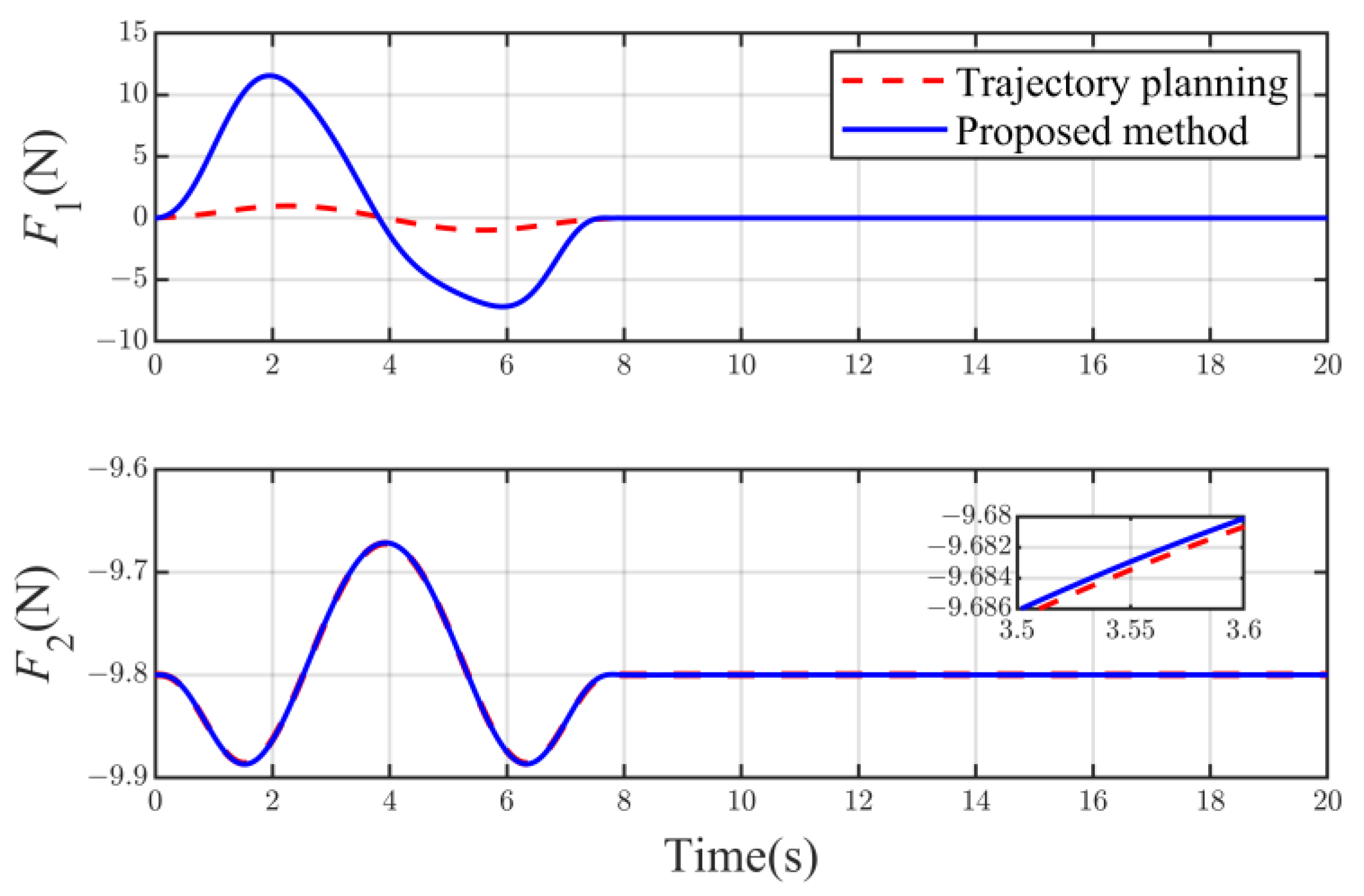
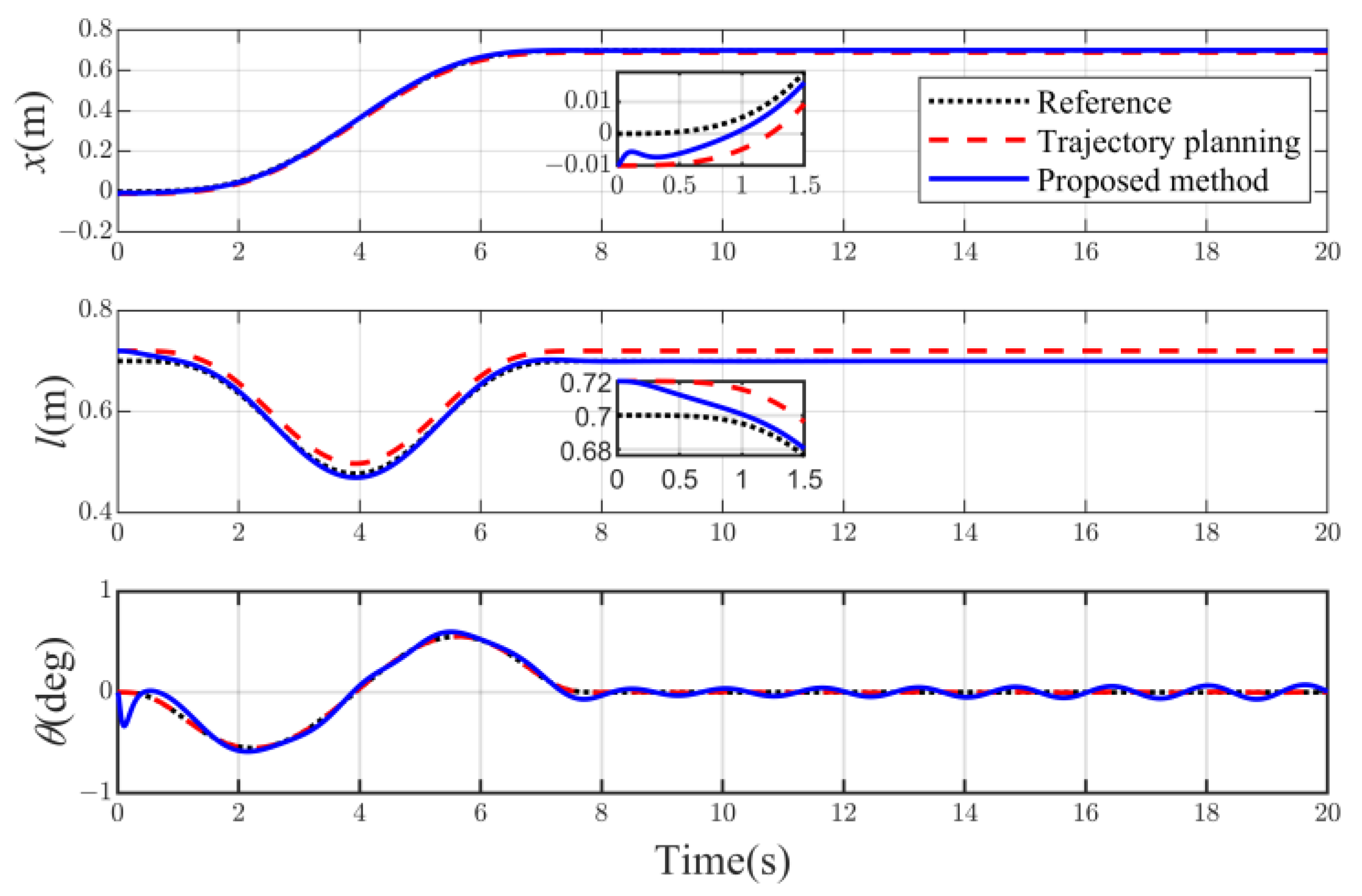
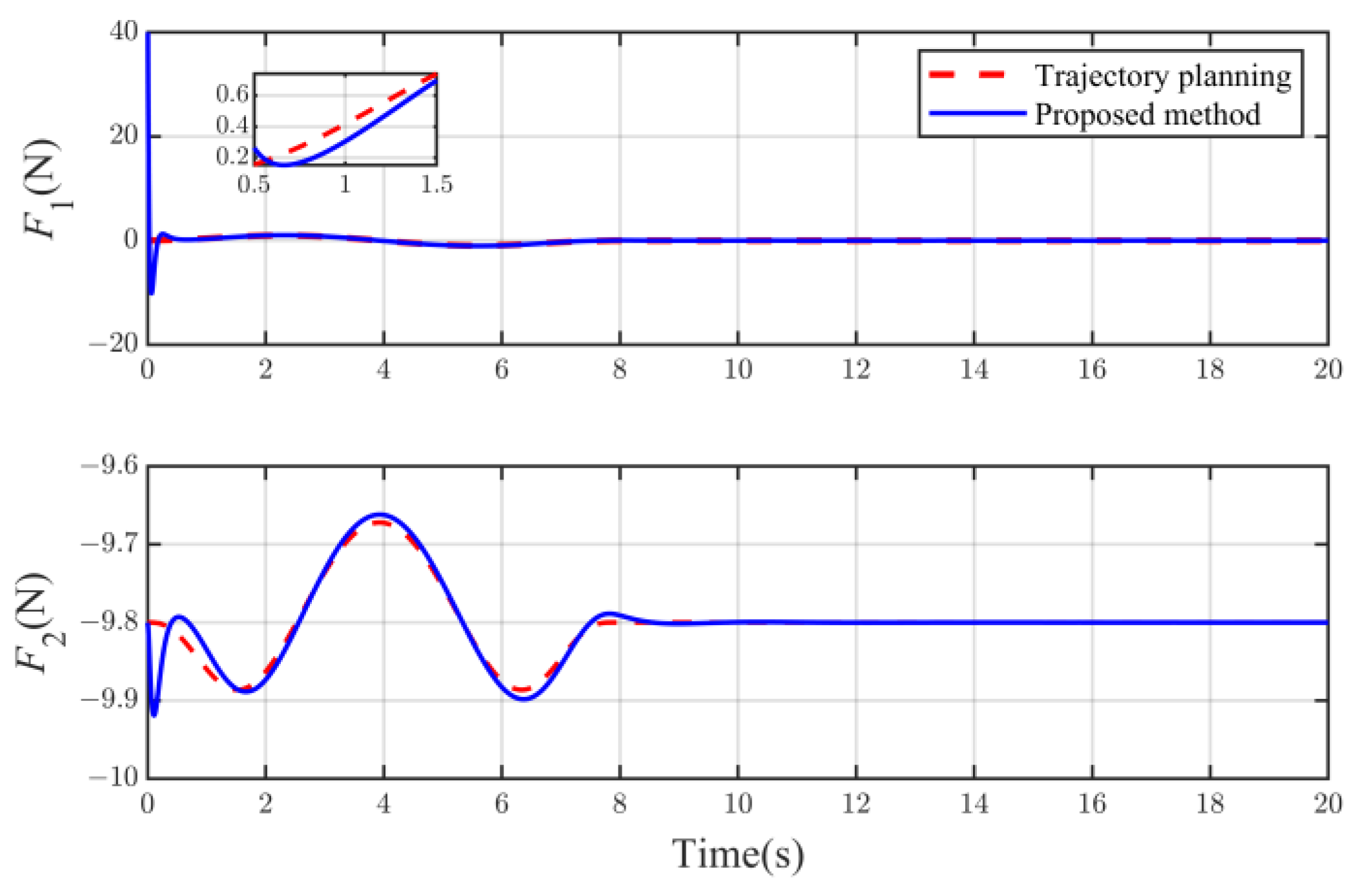
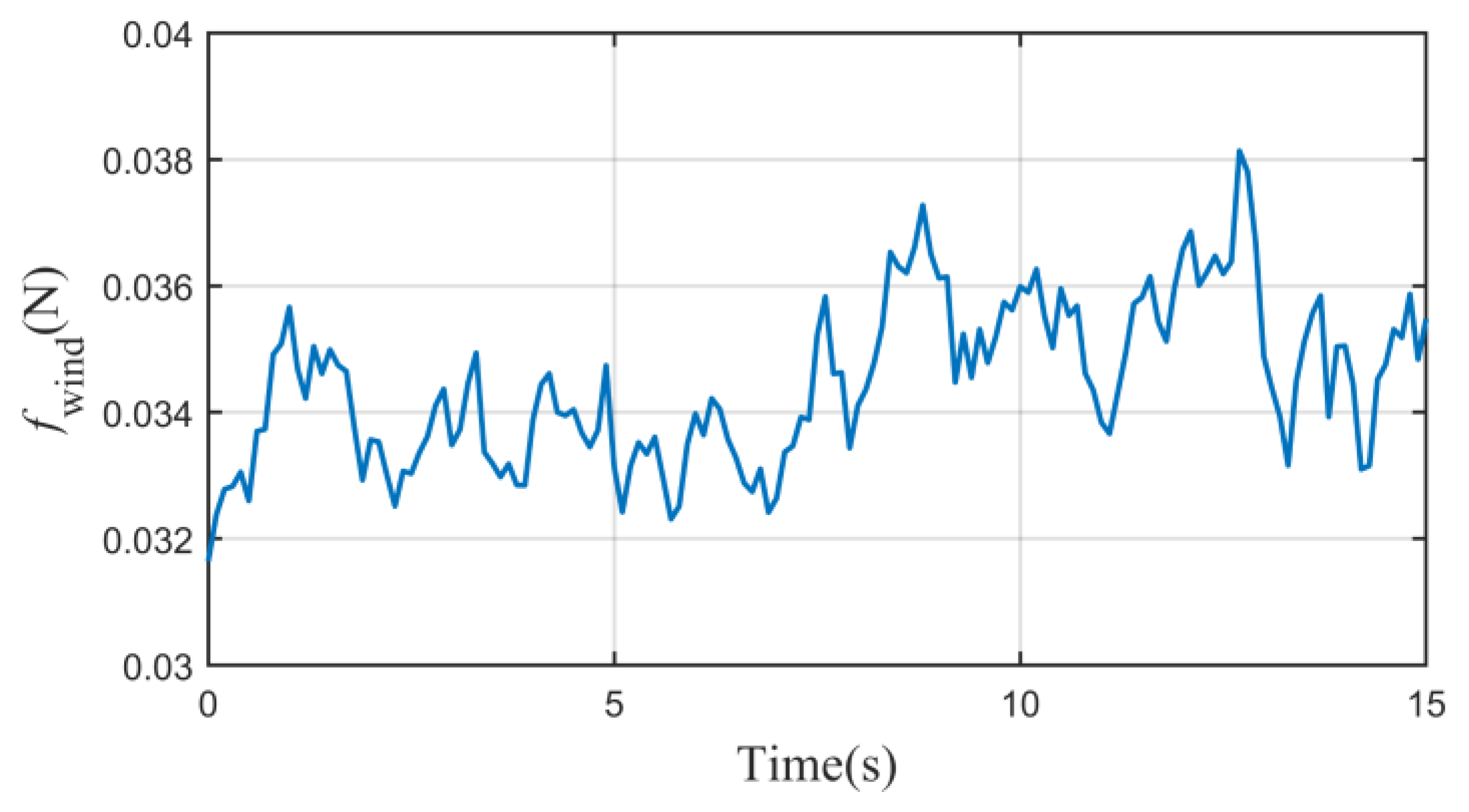
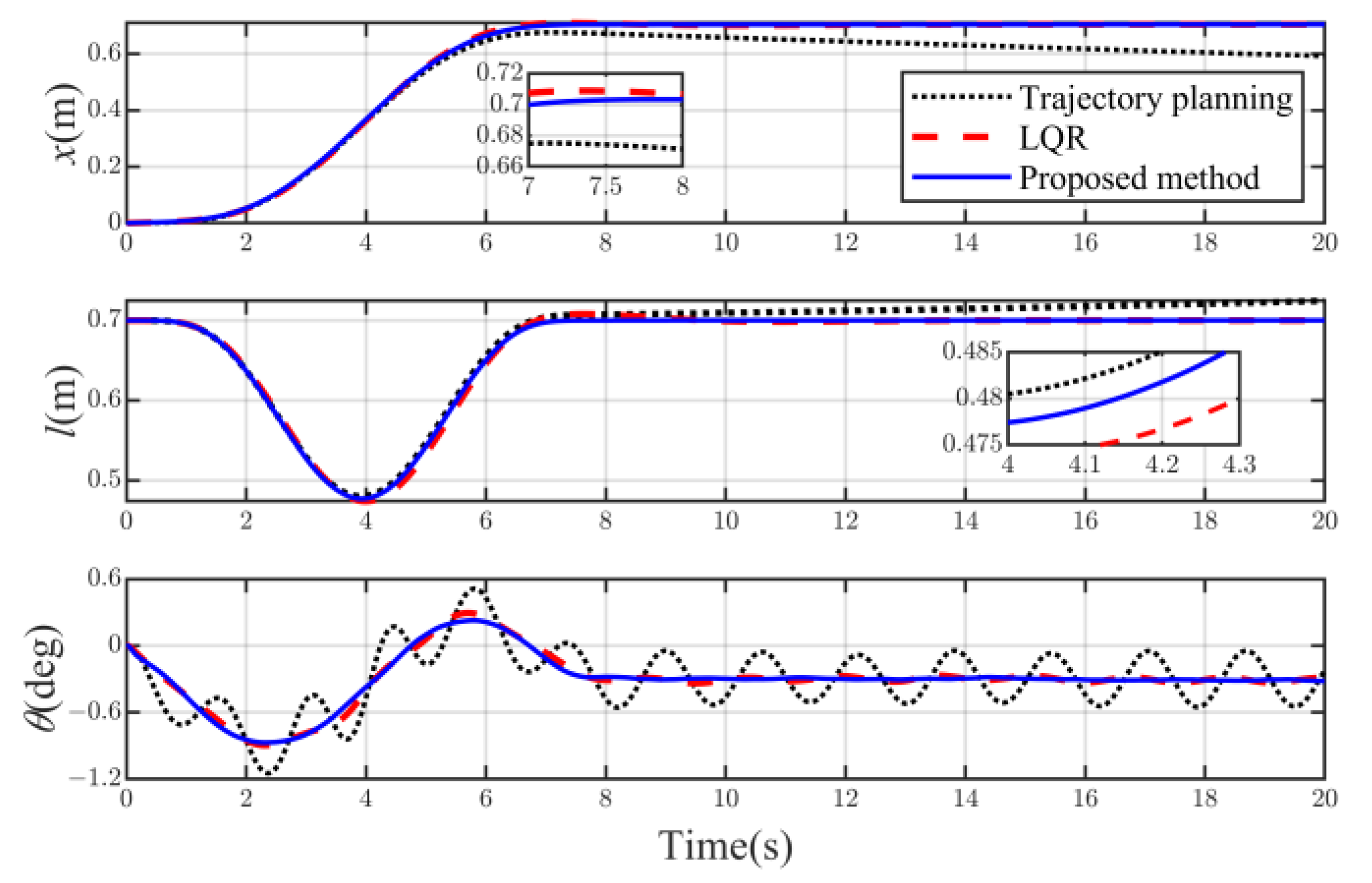
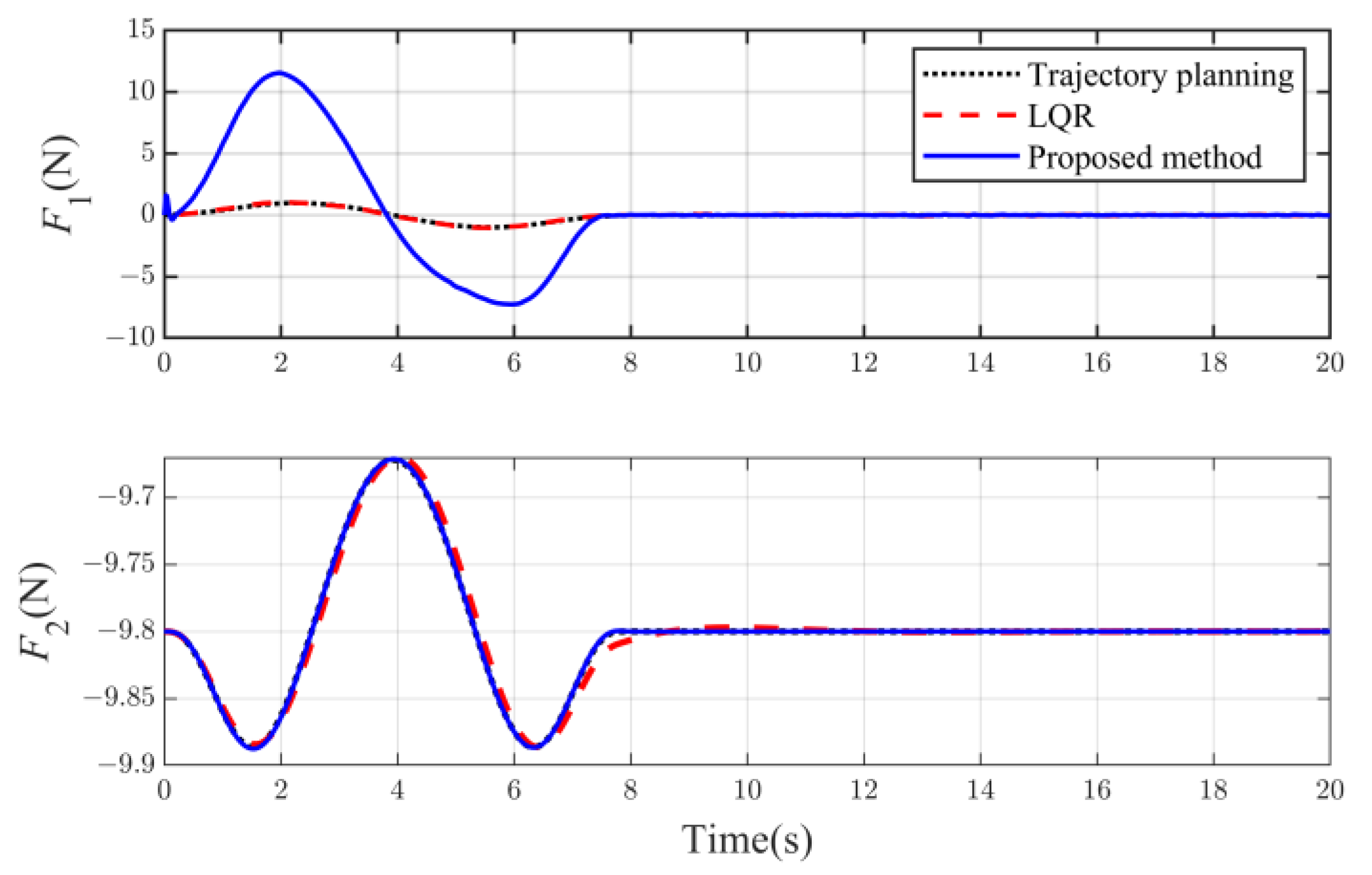
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Piedrafita, R.; Comín, D.; Beltrán, J.R. Simulink® implementation and industrial test of Input Shaping techniques. Control Eng. Pract. 2018, 79, 1–21. [Google Scholar] [CrossRef]
- La, V.D.; Nguyen, K.T. Combination of input shaping and radial spring-damper to reduce tridirectional vibration of crane payload. Mech. Syst. Signal Process. 2019, 116, 310–321. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Hua, L.; Xia, M. Dynamic analysis and time optimal anti-swing control of double pendulum bridge crane with distributed mass beams. Mech. Syst. Signal Process. 2020, 144, 106968. [Google Scholar] [CrossRef]
- Lee, H.H. A New Motion-Planning Scheme for Overhead Cranes with High-Speed Hoisting. J. Dyn. Syst. Meas. Control-Trans. Asme 2004, 126, 359–364. [Google Scholar] [CrossRef]
- Lee, H.H. Motion planning for three-dimensional overhead cranes with high-speed load hoisting. Int. J. Control 2005, 78, 875–886. [Google Scholar] [CrossRef]
- Almutairi, N.B.; Zribi, M. Sliding Mode Control of a Three-dimensional Overhead Crane. J. Vib. Control 2009, 15, 1679–1730. [Google Scholar] [CrossRef]
- Tuan, L.A.; Lee, S.G.; Nho, L.C.; Kim, D.H. Model Reference Adaptive Sliding Mode Control for Three Dimensional Overhead Cranes. Int. J. Precis. Eng. Manuf. 2013, 14, 1329–1338. [Google Scholar] [CrossRef]
- Wu, X.Q.; Xu, K.X.; Lei, M.Z.; He, X.X. Disturbance-Compensation-Based Continuous Sliding Mode Control for Overhead Cranes with Disturbances. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2182–2189. [Google Scholar] [CrossRef]
- Gutierrez, I.; Collado, J. An LQR controller in the obstacle avoidance of a two-wires hammerhead crane. Neurocomputing 2017, 233, 14–22. [Google Scholar] [CrossRef]
- Shao, X.J.; Zhang, J.G.; Zhang, X.L. Takagi-Sugeno Fuzzy Modeling and PSO-Based Robust LQR Anti-Swing Control for Overhead Crane. Math. Probl. Eng. 2019, 2019, 4596782. [Google Scholar] [CrossRef]
- Kumar, D.; Mija, S.J. Design and Performance Evaluation of LQR and Optimized Sliding Mode Controllers for a Class of Underactuated Nonlinear Systems. IFAC-Pap. 2022, 55, 579–585. [Google Scholar] [CrossRef]
- Jolevski, D.; Bego, O. Model predictive control of gantry/bridge crane with anti-sway algorithm. J. Mech. Sci. Technol. 2015, 29, 827–834. [Google Scholar] [CrossRef]
- Wu, Z.; Xia, X.H.; Zhu, B. Model predictive control for improving operational efficiency of overhead cranes. Nonlinear Dyn. 2015, 79, 2639–2657. [Google Scholar] [CrossRef]
- Iles, S.; Matusko, J.; Kolonic, F. Sequential distributed predictive control of a 3D tower crane. Control Eng. Pract. 2018, 79, 22–35. [Google Scholar] [CrossRef]
- Solihin, M.I.; Wahyudi; Legowo, A. Fuzzy-tuned PID Anti-swing Control of Automatic Gantry Crane. J. Vib. Control 2010, 16, 127–145. [Google Scholar] [CrossRef]
- Yu, W.; Li, X.O.; Panuncio, F. Stable Neural PID Anti-Swing Control for an Overhead Crane. Intell. Autom. Soft Comput. 2014, 20, 145–158. [Google Scholar] [CrossRef]
- Urbas, A.; Klosinski, J.; Augustynek, K. The influence of the PID controller settings on the motion of a truck-mounted crane with a flexible boom and friction in joints. Control Eng. Pract. 2020, 103, 104610. [Google Scholar] [CrossRef]
- Masoud, Z.N.; Daqaq, M.F. A graphical approach to input-shaping control design for container cranes with hoist. IEEE Trans. Control Syst. Technol. 2006, 14, 1070–1077. [Google Scholar] [CrossRef]
- Blajer, W.; Kolodziejczyk, K. Motion planning and control of gantry cranes in cluttered work environment. Iet Control Theory Appl. 2007, 1, 1370–1379. [Google Scholar] [CrossRef]
- Böck, M.; Stöger, A.; Kugi, A. Efficient Generation of Fast Trajectories for Gantry Cranes with Constraints. IFAC-Pap. 2017, 50, 1937–1943. [Google Scholar] [CrossRef]
- Tomczyk, J.; Cink, J.; Kosucki, A. Dynamics of an overhead crane under a wind disturbance condition. Autom. Constr. 2014, 42, 100–111. [Google Scholar] [CrossRef]
- Abdullahi, A.M.; Mohamed, Z.; Selamat, H.; Pota, H.R.; Zainal Abidin, M.S.; Ismail, F.S.; Haruna, A. Adaptive output-based command shaping for sway control of a 3D overhead crane with payload hoisting and wind disturbance. Mech. Syst. Signal Process. 2018, 98, 157–172. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y.; Huang, J. Differential-flatness-based finite-time anti-swing control of underactuated crane systems. Nonlinear Dyn. 2017, 87, 1749–1761. [Google Scholar] [CrossRef]
- Xiao, R.X.; Wang, Z.L.; Guo, N.Y.; Wu, Y.T.; Shen, J.W.; Chen, Z. Multi-Objective Motion Control Optimization for the Bridge Crane System. Appl. Sci. 2018, 8, 473. [Google Scholar] [CrossRef]
- Lobe, A.; Ettl, A.; Steinboeck, A.; Kugi, A. Flatness-based nonlinear control of a three-dimensional gantry crane. IFAC-PapersOnLine 2018, 51, 331–336. [Google Scholar] [CrossRef]
- Sun, X.; Xie, Z. Reinforcement Learning-Based Backstepping Control for Container Cranes. Math. Probl. Eng. 2020, 2020, 2548319. [Google Scholar] [CrossRef]
- Xing, X.; Liu, J. Vibration and position control of overhead crane with three-dimensional variable length cable subject to input amplitude and rate constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 4127–4138. [Google Scholar] [CrossRef]
- Huang, J.S.; Wang, W.; Zhou, J. Adaptive Control Design for Underactuated Cranes with Guaranteed Transient Performance: Theoretical Design and Experimental Verification. IEEE Trans. Ind. Electron. 2022, 69, 2822–2832. [Google Scholar] [CrossRef]
- Kang, J.H.; Lee, S.J. Experimental study of wind load on a container crane located in a uniform flow and atmospheric boundary layers. Eng. Struct. 2008, 30, 1913–1921. [Google Scholar] [CrossRef]
- Niu, W.; Chu, J.; Gu, W. Constant Tension Control of the Anchor Chain of the Windlass under Sea Wind. In Proceedings of the 2008 International Workshop on Education Technology and Training & 2008 International Workshop on Geoscience and Remote Sensing, Washington, DC, USA, 21–22 December 2008; pp. 622–626. [Google Scholar]
- Fliess, M.; LéVINE, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 2003, 61, 1327–1361. [Google Scholar] [CrossRef]
- Boor, C.D. A Practical Guide to Splines; Springer: New York, NY, USA, 1978; Volume 27. [Google Scholar]
- Piegl, L.A.; Tiller, W. The Nurbs Book; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Hartley, P.J.; Judd, C.J. Parametrization of Bézier-type B-spline curves and surfaces. Comput.-Aided Des. 1978, 10, 130–134. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| M | 10 (kg) |
| m | 1 (kg) |
| g | 9.8 (m/s2) |
| l0 | 0.7 (m) |
| xe | 0.7 (m) |
| vl,max | 1.5 (m/s) |
| al,max | 0.75 (m/s2) |
| vmax | 0.2 (m/s) |
| amax | 0.5 (m/s2) |
| v1 | 9.5 |
| v2 | 0.17 |
| Parameters | Values |
|---|---|
| k1 | diag {8, 5} |
| k2 | diag {10, 5} |
| k3 | diag {8, 5} |
| k4 | diag {8, 5} |
| β1 | [0.01, 0.01]T |
| β2 | [0.01, 0.01]T |
| β3 | [0.01, 0.01]T |
| Parameters | Values |
|---|---|
| η1 | [12.247, 10]T |
| η2 | [32.675, 25.086]T |
| η3 | [37.463, 26.466]T |
| η4 | [18.026, 12.367]T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Niu, W. Flatness-Based Backstepping Antisway Control of Underactuated Crane Systems under Wind Disturbance. Electronics 2023, 12, 244. https://doi.org/10.3390/electronics12010244
Yu Z, Niu W. Flatness-Based Backstepping Antisway Control of Underactuated Crane Systems under Wind Disturbance. Electronics. 2023; 12(1):244. https://doi.org/10.3390/electronics12010244
Chicago/Turabian StyleYu, Zian, and Wangqiang Niu. 2023. "Flatness-Based Backstepping Antisway Control of Underactuated Crane Systems under Wind Disturbance" Electronics 12, no. 1: 244. https://doi.org/10.3390/electronics12010244
APA StyleYu, Z., & Niu, W. (2023). Flatness-Based Backstepping Antisway Control of Underactuated Crane Systems under Wind Disturbance. Electronics, 12(1), 244. https://doi.org/10.3390/electronics12010244






