Fast Supraharmonic Estimation Algorithm Based on Simplified Compressed Sensing Model
Abstract
1. Introduction
2. Algorithm Theory
2.1. Compressed Sensing Models for Supraharmonic
2.2. Simplified Compressed Sensing Model and its Calculation
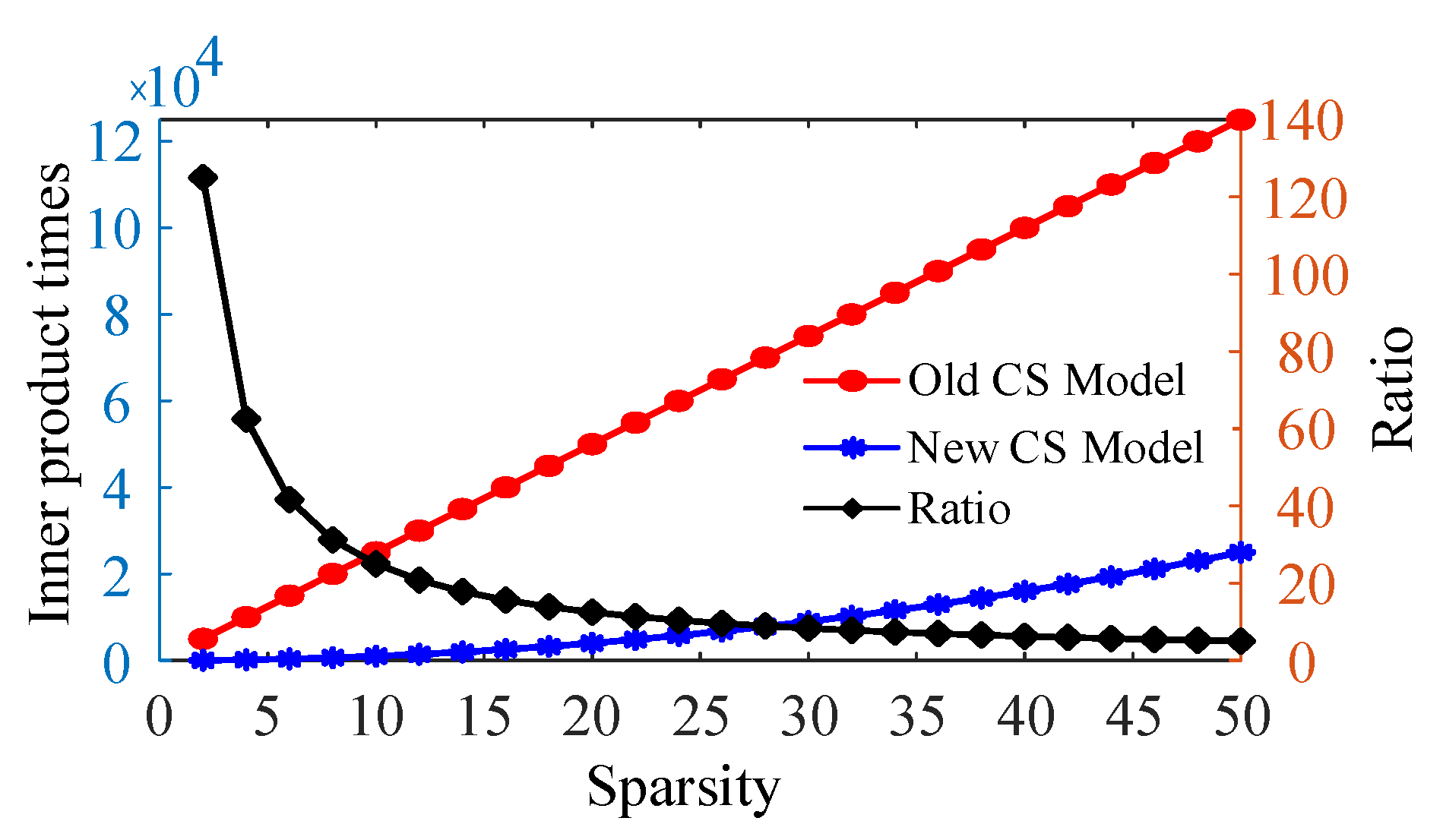
2.2.1. The Prediction of Sparsity S
2.2.2. Simplified Compressed Sensing Model
2.2.3. Compression Sensing Estimation of Spectrum
2.3. Discussion of Relevant Parameters
2.3.1. Original Spectral Array of Multi-measurement Vectors
2.3.2. The Relationship between the Interpolation Factor F and the Sparsity S
3. Algorithm Simulation Analysis
3.1. Simulation Model
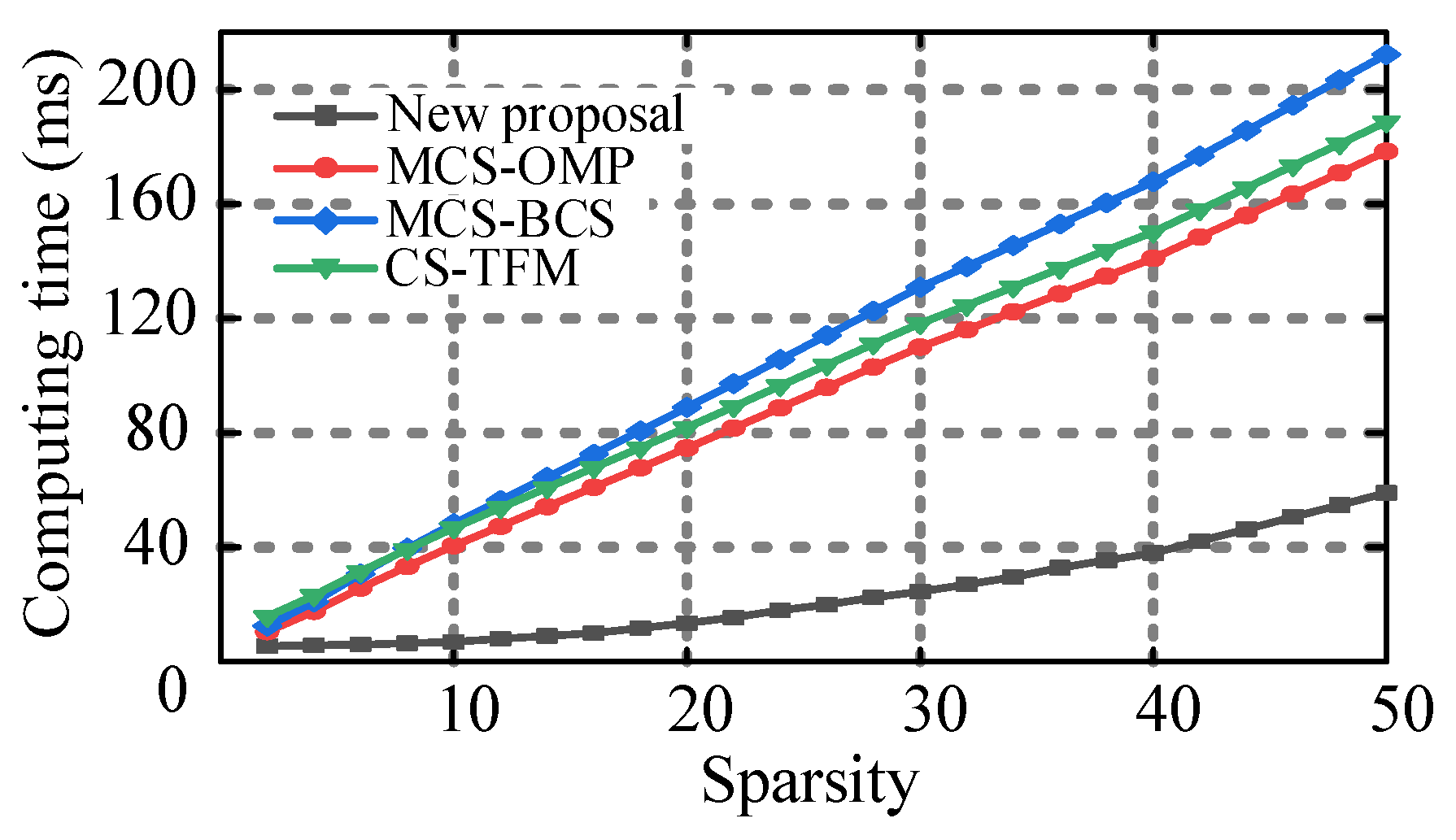
3.2. Algorithm Complexity and Computation Time
3.3. Calculation Accuracy
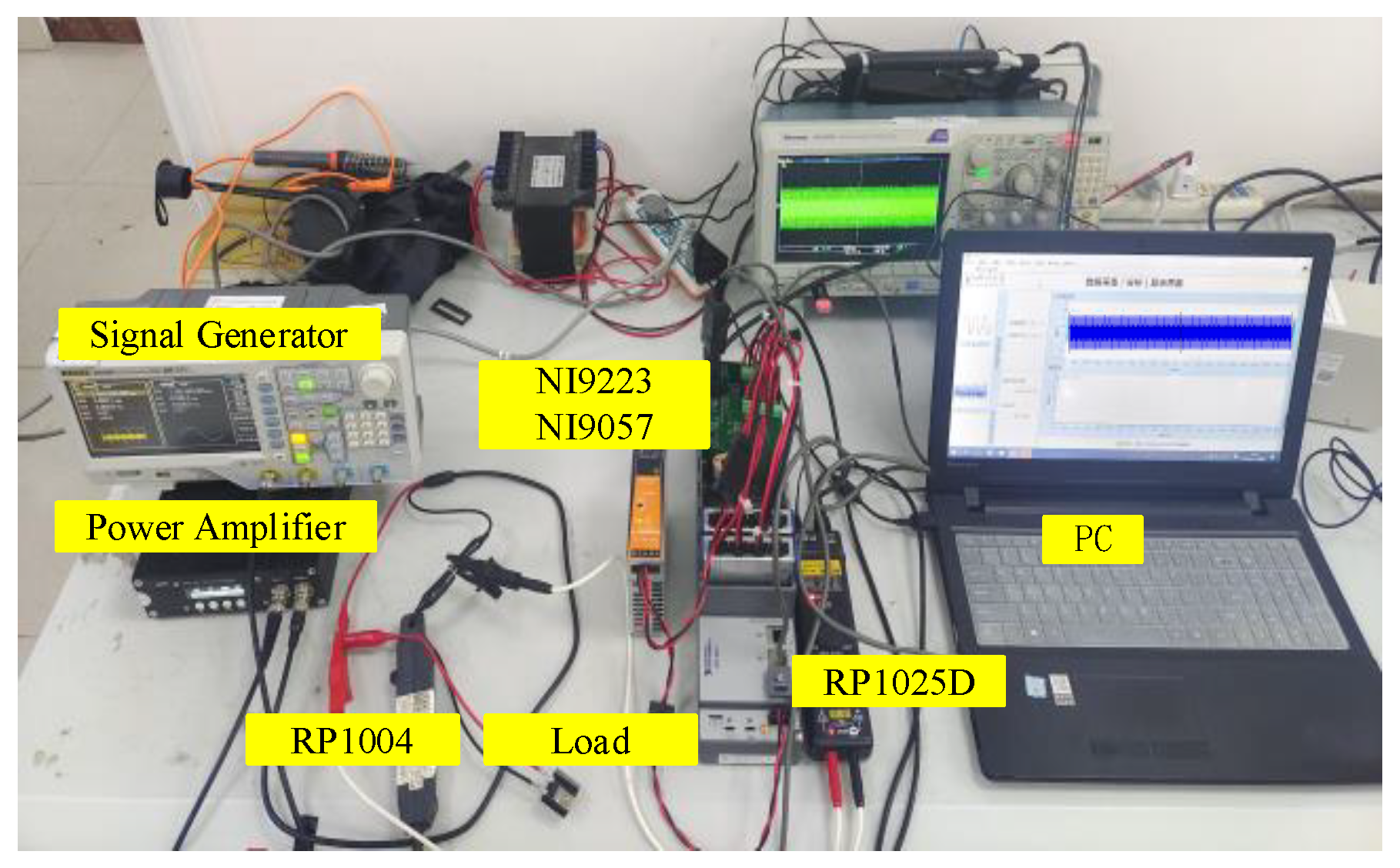
4. Experimental Test
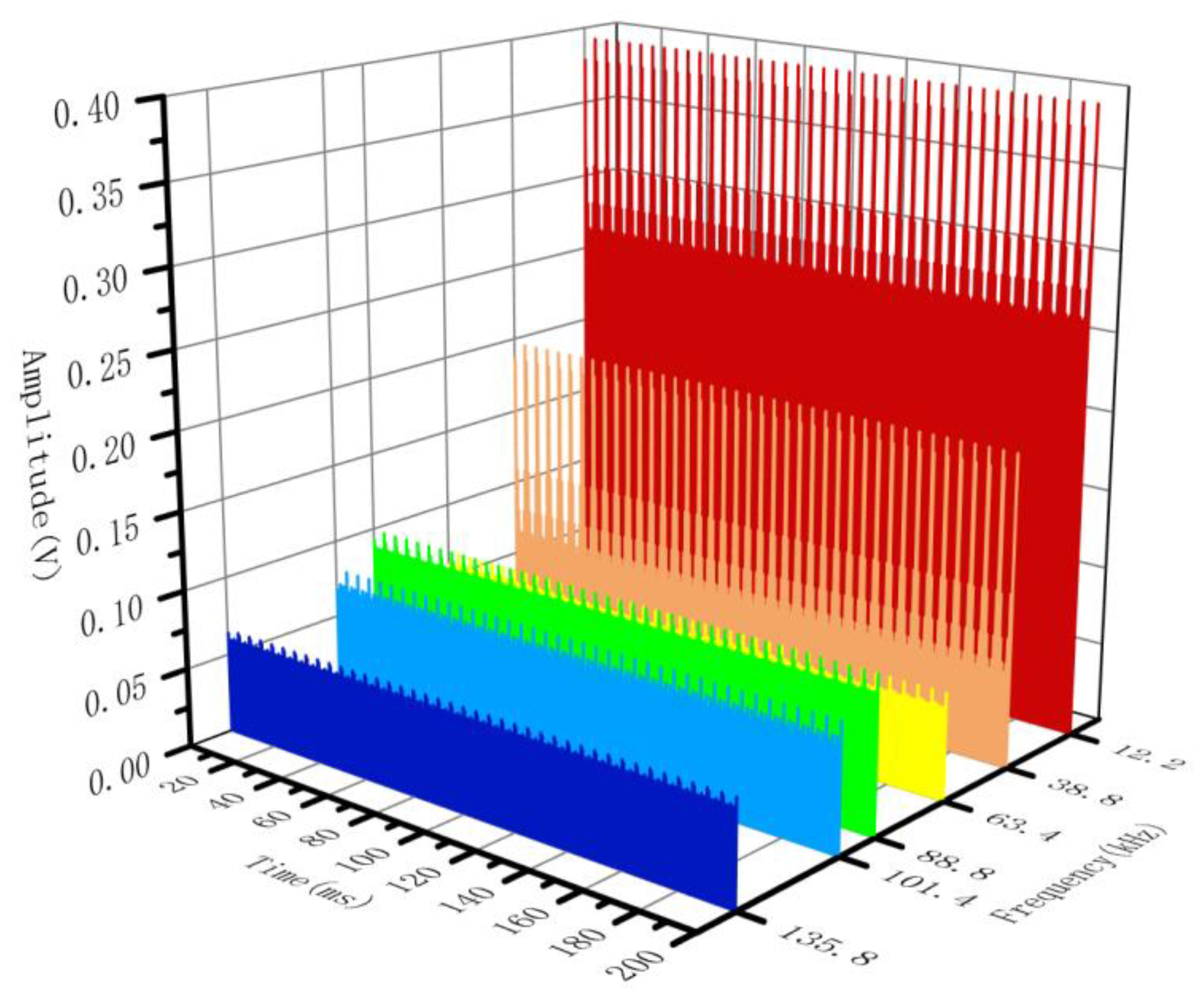
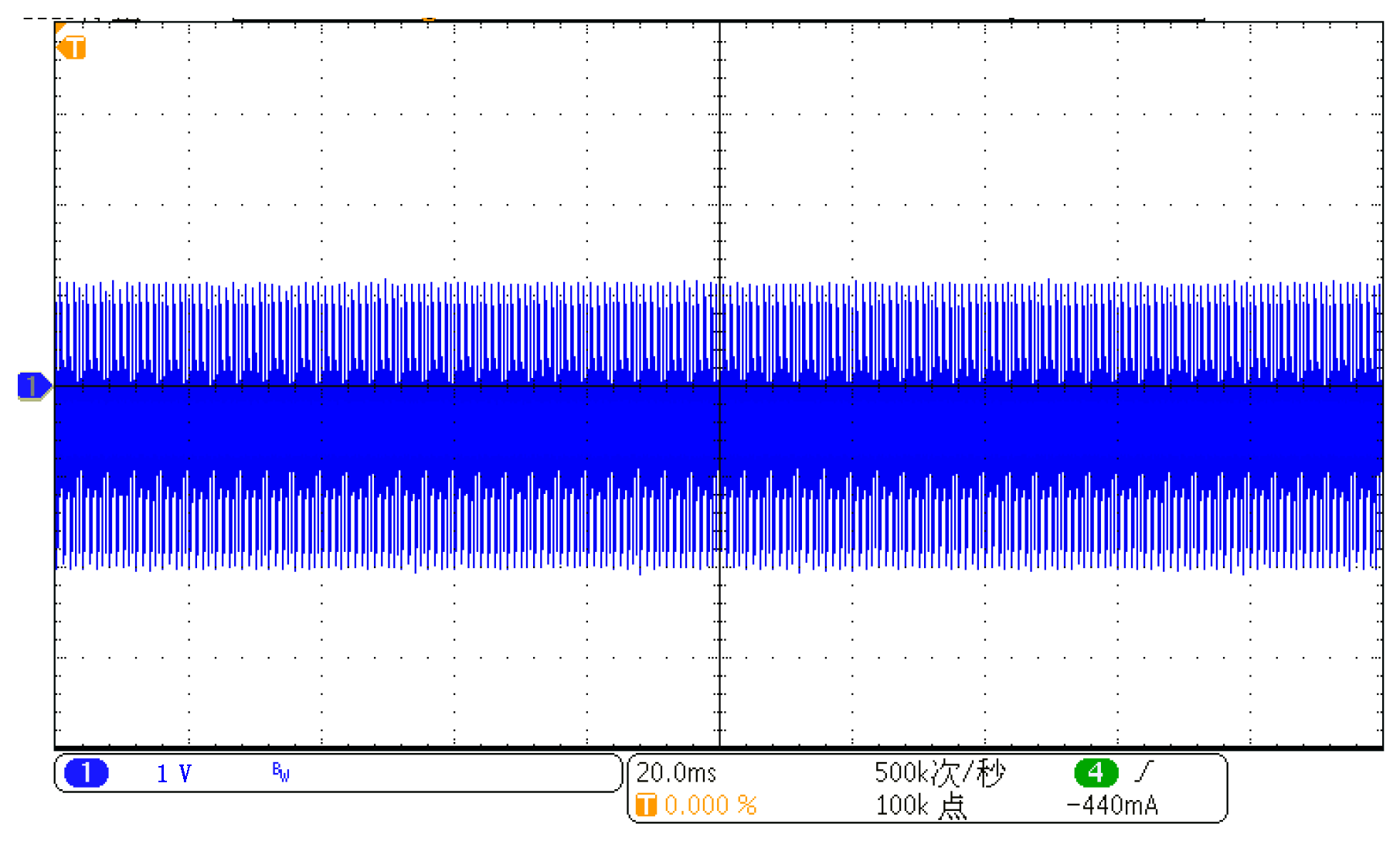
4.1. Class D Test Signal Experiment
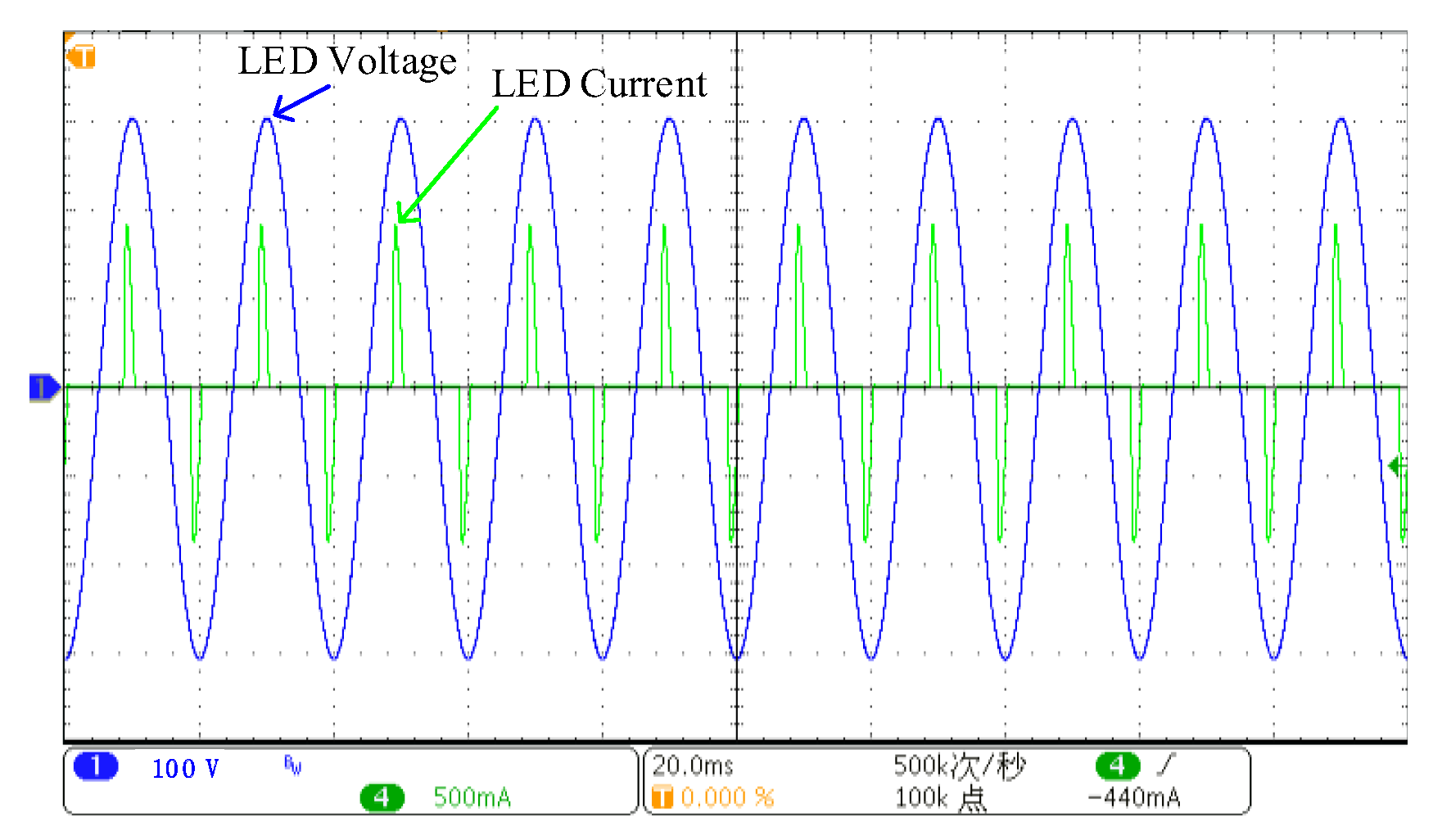
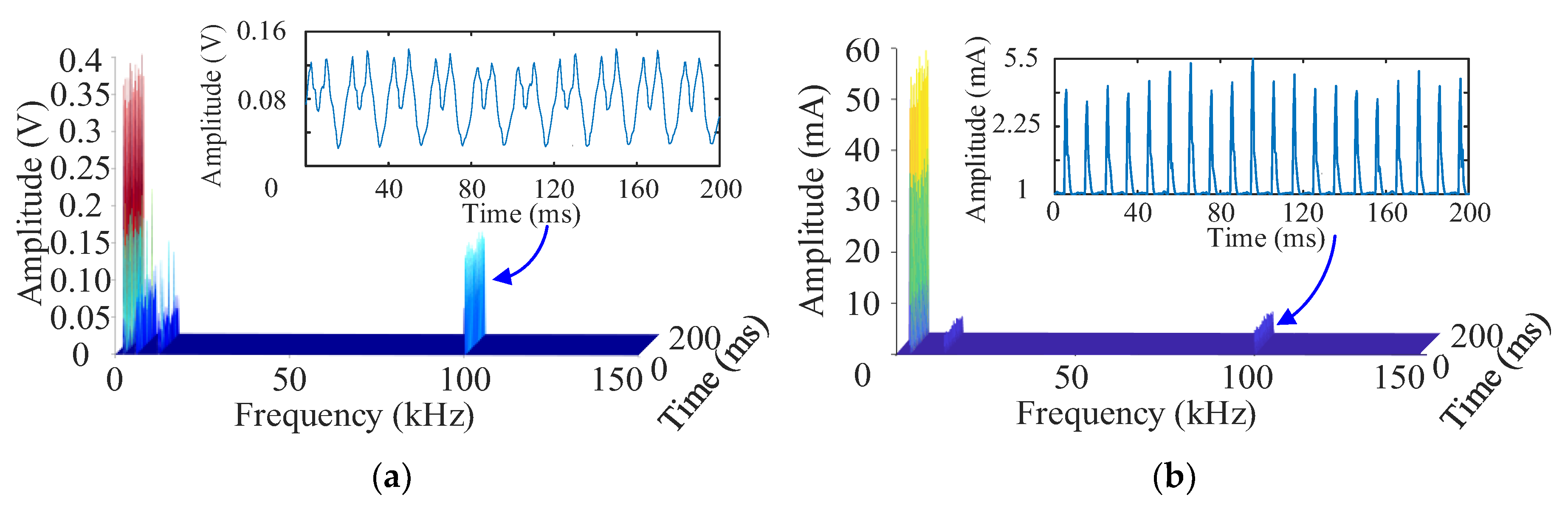
4.2. LED Supraharmonic Emission Test
4.3. Experimental Time Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guerrero, J.M.; Blaabjerg, F.; Zhelev, T.; Hemmes, K.; Monmasson, E.; Jemei, S.; Comech, M.P.; Granadino, R.; Frau, J.I. Distributed Generation: Toward a New Energy Paradigm. IEEE Ind. Electron. Mag. 2010, 4, 52–64. [Google Scholar] [CrossRef]
- Singh, M.; Khadkikar, V.; Chandra, A.; Varma, R.K. Grid Interconnection of Renewable Energy Sources at the Distribution Level With Power-Quality Improvement Features. IEEE Trans. Power Deliv. 2011, 26, 307–315. [Google Scholar] [CrossRef]
- Waniek, C.; Wohlfahrt, T.; Myrzik, J.M.A.; Meyer, J.; Klatt, M.; Schegner, P. Supraharmonics: Root Causes and Interactions between Multiple Devices and the Low Voltage Grid. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Meyer, J.; Bollen, M.; Amaris, H.; Blanco, A.M.; Gil de Castro, A.; Desmet, J.; Klatt, M.; Kocewiak, Ł.; Rönnberg, S.; Yang, K. Future Work on Harmonics—Some Expert Opinions Part II—Supraharmonics, Standards and Measurements. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 909–913. [Google Scholar] [CrossRef]
- Klatt, M.; Meyer, J.; Schegner, P.; Koch, A.; Myrzik, J.; Körner, C.; Darda, T.; Eberl, G. Emission Levels above 2 KHz—Laboratory Results and Survey Measurements in Public Low Voltage Grids. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Unger, C.; Krüger, K.; Sonnenschein, M.; Zurowski, R. Disturbances Due to Voltage Distortion in the KHz Range—Experiences and Mitigation Measures. In Proceedings of the CIRED 2005—18th International Conference and Exhibition on Electricity Distribution, Turin, Italy, 6–9 June 2005; pp. 1–4. [Google Scholar] [CrossRef]
- Meyer, J.; Haehle, S.; Schegner, P. Impact of Higher Frequency Emission above 2kHz on Electronic Mass-Market Equipment. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Ronnberg, S.K.; Bollen, M.H.J.; Wahlberg, M. Interaction Between Narrowband Power-Line Communication and End-User Equipment. IEEE Trans. Power Deliv. 2011, 26, 2034–2039. [Google Scholar] [CrossRef]
- Leferink, F.; Keyer, C.; Melentjev, A. Static Energy Meter Errors Caused by Conducted Electromagnetic Interference. IEEE Electromagn. Compat. Mag. 2016, 5, 49–55. [Google Scholar] [CrossRef]
- Chen, F.; Zhong, Q.; Zhang, H.; Zhu, M.; Müller, S.; Meyer, J.; Huang, W. Survey of harmonic and supraharmonic emission of fast charging stations for electric vehicles in china and germany. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Geneva, Switzerland, 20–23 September 2021; Volume 2021, pp. 1061–1065. [Google Scholar] [CrossRef]
- Slangen, T.; Ćuk, V.; Cobben, S.; De Jong, E. Characterization of Supraharmonic Emission from High-Power Electric Vehicle Chargers. In Proceedings of the CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems, Porto, Portugal, 2–3 June 2022; Volume 2022, pp. 133–137. [Google Scholar] [CrossRef]
- Espín-Delgado, Á.; Rönnberg, S. Assessment of grid impedance impact on supraharmonic propagation. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution, Geneva, Switzerland, 20–23 September 2021; Volume 2021, pp. 688–692. [Google Scholar] [CrossRef]
- Khokhlov, V.; Meyer, J.; Grevener, A.; Busatto, T.; Rönnberg, S. Comparison of Measurement Methods for the Frequency Range 2–150 KHz (Supraharmonics) Based on the Present Standards Framework. IEEE Access 2020, 8, 77618–77630. [Google Scholar] [CrossRef]
- IEC 61000-4-7; Electromagnetic Compatibility (EMC). Part 4: Testing and Measurement Techniques-General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto. International Electrotechnical Commission: Geneva, Switzerland, 2009; Volume 2, pp. 1–8.
- IEC 61000-4-30:2015; Electromagnetic Compatibility (EMC). Part 4-30: Testing and Measurement Techniques. Power Quality Measurement Methods. IEC: Geneva, Switzerland, 2015.
- *** CISPR 16-2-1; Specification for Radio Disturbance and Immunity Measuring Apparatus and Methods—Part 2-1: Methods of Measurement of Disturbances and Immunity-Conducted Disturbance Measurements. IEC: Geneva, Switzerland, 2014.
- Ritzmann, D.; Lodetti, S.; de la Vega, D.; Khokhlov, V.; Gallarreta, A.; Wright, P.; Meyer, J.; Fernández, I.; Klingbeil, D. Comparison of Measurement Methods for 2–150-KHz Conducted Emissions in Power Networks. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Mendes, T.M.; Ferreira, D.D.; Silva, L.R.M.; Ribeiro, P.F.; Meyer, J.; Duque, C.A. PLL Based Method for Supraharmonics Emission Assessment. IEEE Trans. Power Deliv. 2022, 37, 2610–2620. [Google Scholar] [CrossRef]
- Gallarreta, A.; Fernández, I.; Ritzmann, D.; Lodetti, S.; Khokhlov, V.; Wright, P.; Meyer, J.; de la Vega, D. A Light Measurement Method for 9–150 KHz Disturbances in Power Grids Comparable to CISPR Quasi-Peak. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar] [CrossRef]
- Zhuang, S.; Zhao, W.; Wang, R.; Wang, Q.; Huang, S. New Measurement Algorithm for Supraharmonics Based on Multiple Measurement Vectors Model and Orthogonal Matching Pursuit. IEEE Trans. Instrum. Meas. 2019, 68, 1671–1679. [Google Scholar] [CrossRef]
- Zhuang, S.; Zhao, W.; Wang, Q.; Huang, S. A New Measurement Method for Supraharmonics in 2–150 KHz. In Proceedings of the 2018 Conference on Precision Electromagnetic Measurements (CPEM 2018), Paris, France, 8–13 July 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Xingang, Y.; Aiqiang, P.; Guangzheng, Y.; Chenyang, L.; Yangxiu, Y. Supraharmonics Measurement Algorithm Based on CS-SAMP. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 160–164. [Google Scholar] [CrossRef]
- Zhuang, S.; Zhao, W.; Wang, Q.; Wang, Z.; Chen, L.; Huang, S. A High-Resolution Algorithm for Supraharmonic Analysis Based on Multiple Measurement Vectors and Bayesian Compressive Sensing. Energies 2019, 12, 2559. [Google Scholar] [CrossRef]
- Frigo, G.; Braun, J. Supraharmonic Dynamic Phasors: Estimation of Time-Varying Emissions. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Yap, B.W.; Sim, C.H. Comparisons of Various Types of Normality Tests. J. Stat. Comput. Simul. 2011, 81, 2141–2155. [Google Scholar] [CrossRef]
- Zhou, M.; Li, Y.; Tahir, M.J.; Geng, X.; Wang, Y.; He, W. Integrated Statistical Test of Signal Distributions and Access Point Contributions for Wi-Fi Indoor Localization. IEEE Trans. Veh. Technol. 2021, 70, 5057–5070. [Google Scholar] [CrossRef]
- Beygi, M.; Jalali, M. Background Levels of Some Trace Elements in Calcareous Soils of the Hamedan Province, Iran. Catena 2018, 162, 303–316. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P.; Garrett, R.G. Background and Threshold: Critical Comparison of Methods of Determination. Sci. Total Environ. 2005, 346, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Klatt, M.; Meyer, J.; Schegner, P.; Wolf, R.; Wittenberg, B. Filter for the Measurement of Supraharmonics in Public Low Voltage Networks. In Proceedings of the 2015 IEEE International Symposium on Electromagnetic Compatibility (EMC), Dresden, Germany, 16–22 August 2015; pp. 108–113. [Google Scholar] [CrossRef]
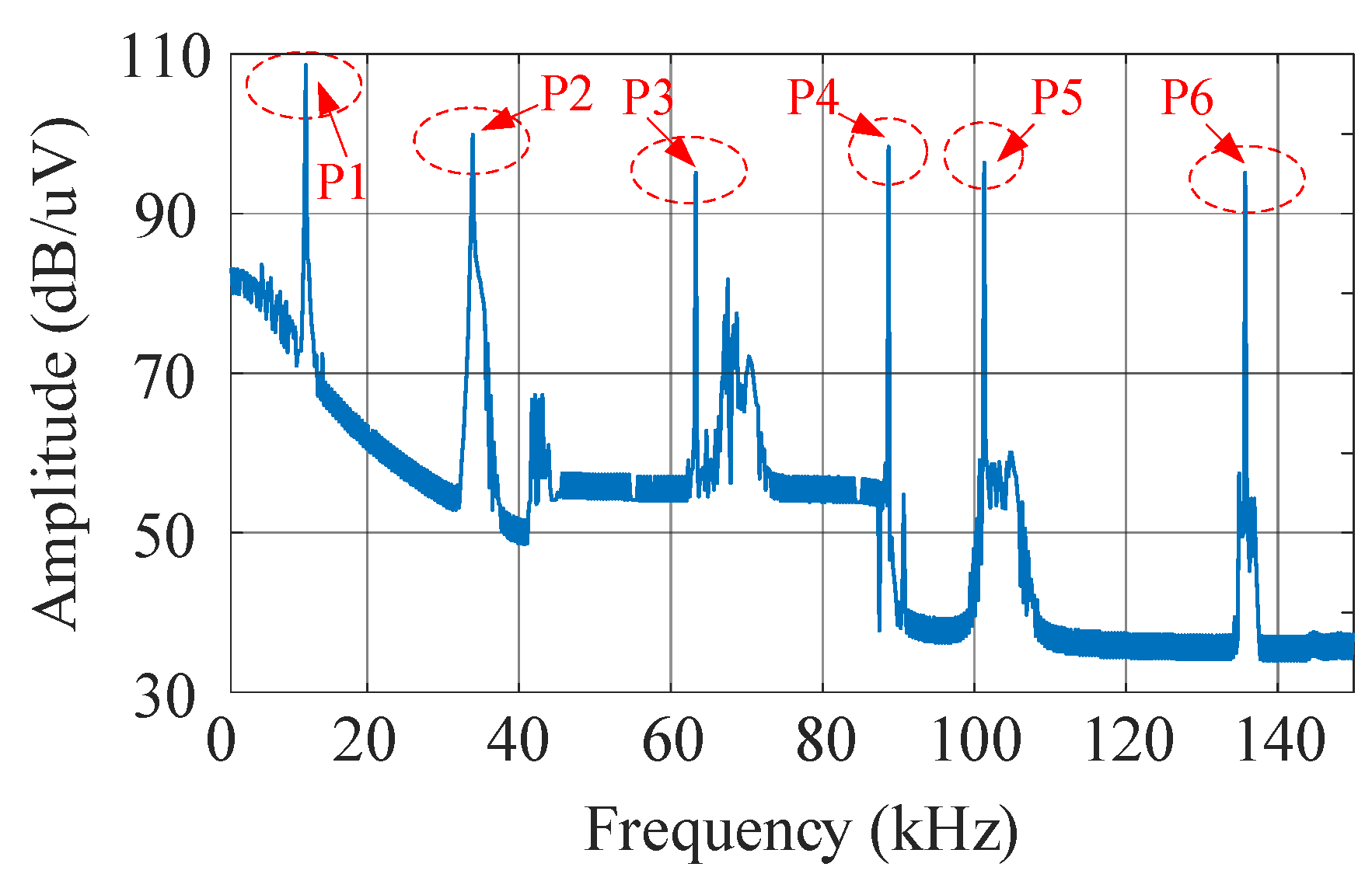


| No. | Frequency (kHz) | Amplitude (mV) |
|---|---|---|
| 1 | 49.8 | 500 |
| 2 | 50.2 | 750 |
| 3 | 99.8 | 800 |
| 4 | 100.2 | 1000 |
| No. | Frequency (kHz) | Amplitude (mV) |
|---|---|---|
| 1 | 12.2 | 271.09 |
| 2 | 38.8 | 97.83 |
| 3 | 63.4 | 57.33 |
| 4 | 88.8 | 83.09 |
| 5 | 101.4 | 66.82 |
| 6 | 135.8 | 57.09 |
| Algorithm | Time (ms) |
|---|---|
| new proposal | 5.7 |
| MCS-OMP | 13.4 |
| MCS-BCS | 14.2 |
| CS-TFM | 12.1 |
| No. | New Proposal | CS-OMP | CS-BCS | CS-TFM | ||||
|---|---|---|---|---|---|---|---|---|
| FE | ME | FE | ME | FE | ME | FE | ME | |
| 1 | 0 | 0.15 | 0 | 0.13 | 0 | 0.07 | 0 | 0.04 |
| 2 | 0 | 0.13 | 0 | 0.14 | 0 | 0.09 | 0 | 0.06 |
| 3 | 0 | 0.17 | 0 | 0.18 | 0 | 0.1 | 0 | 0.07 |
| 4 | 0 | 0.19 | 0 | 0.2 | 0 | 0.1 | 0 | 0.09 |
| 5 | 0 | 0.15 | 0 | 0.13 | 0 | 0.07 | 0 | 0.04 |
| 6 | 0 | 0.13 | 0 | 0.14 | 0 | 0.09 | 0 | 0.06 |
| No. | New Proposal | CS-OMP | CS-BCS | CS-TFM | ||||
|---|---|---|---|---|---|---|---|---|
| FE | ME | FE | ME | FE | ME | FE | ME | |
| 1 | 0 | 0.12 | 0 | 0.13 | 0 | 0.07 | 0 | 0.03 |
| 2 | 0 | 0.13 | 0 | 0.14 | 0 | 0.08 | 0 | 0.05 |
| 3 | 0 | 0.13 | 0 | 0.14 | 0 | 0.09 | 0 | 0.06 |
| 4 | 0 | 0.15 | 0 | 0.15 | 0 | 0.09 | 0 | 0.07 |
| 5 | 0 | 0.16 | 0 | 0.17 | 0 | 0.09 | 0 | 0.08 |
| 6 | 0 | 0.17 | 0 | 0.17 | 0 | 0.1 | 0 | 0.09 |
| Algorithm | Time(ms) | ||
|---|---|---|---|
| LED Voltage | LED Current | Class D | |
| New proposal | 35.7 | 34.2 | 106.3 |
| MCS-OMP | 155.1 | 132.3 | 387.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, Z.; Zhou, Q.; Zhou, H.; Liao, Z.; Wang, Z. Fast Supraharmonic Estimation Algorithm Based on Simplified Compressed Sensing Model. Electronics 2023, 12, 141. https://doi.org/10.3390/electronics12010141
Gui Z, Zhou Q, Zhou H, Liao Z, Wang Z. Fast Supraharmonic Estimation Algorithm Based on Simplified Compressed Sensing Model. Electronics. 2023; 12(1):141. https://doi.org/10.3390/electronics12010141
Chicago/Turabian StyleGui, Zesen, Qun Zhou, Hui Zhou, Zheng Liao, and Ziyi Wang. 2023. "Fast Supraharmonic Estimation Algorithm Based on Simplified Compressed Sensing Model" Electronics 12, no. 1: 141. https://doi.org/10.3390/electronics12010141
APA StyleGui, Z., Zhou, Q., Zhou, H., Liao, Z., & Wang, Z. (2023). Fast Supraharmonic Estimation Algorithm Based on Simplified Compressed Sensing Model. Electronics, 12(1), 141. https://doi.org/10.3390/electronics12010141







