Application of the Multiverse Optimization Method to Solve the Optimal Power Flow Problem in Alternating Current Networks

Abstract

In this paper, we solve the optimal power flow problem in alternating current networks to reduce power losses. For that purpose, we propose a master–slave methodology that combines the multiverse optimization algorithm (master stage) and the power flow method for alternating current networks based on successive approximation (slave stage). The master stage determines the level of active power to be injected by each distributed generator in the network, and the slave stage evaluates the impact of the proposed solution on each distributed generator in terms of the objective function and the constraints. For the simulations, we used the 10-, 33-, and 69-node radial test systems and the 10-node mesh test system with three levels of distributed generation penetration: 20%, 40%, and 60% of the power provided by the slack generator in a scenario without DGs. In order to validate the robustness and convergence of the proposed optimization algorithm, we compared it with four other optimization methods that have been reported in the specialized literature to solve the problem addressed here: Particle Swarm Optimization, the Continuous Genetic Algorithm, the Black Hole Optimization algorithm, and the Ant Lion Optimization algorithm. The results obtained demonstrate that the proposed master–slave methodology can find the best solution (in terms of power loss reduction, repeatability, and technical conditions) for networks of any size while offering excellent performance in terms of computation time.

1. Introduction

To understand the importance of this study, it is necessary to analyze the general context of distributed generation and its current importance for electrical networks, as well as the optimal power flow problem in AC grids. This section reviews the main contributions of other authors, presents the contributions of this study, and outlines the structure of this paper.

1.1. General Context

Electrical energy has become the backbone of society as we know it today because, when used properly and wisely, it contributes to improving the quality of life of people all around the world [1,2,3]. However, the comfort provided by electrical energy has also led to an increase in its consumption. As a result, power stations have been forced to meet the demand by producing electricity from fossil fuels and renewable energy sources and to implement large-scale electric power systems, which experience significant power losses and unfavorable operating conditions, such as voltage drops and current limit violations [4,5,6,7]. Thus, the ways in which electrical energy is generated and distributed should be expanded while keeping in mind critical aspects, e.g., reduction of greenhouse gas emissions, minimization of power losses associated with energy transport and distribution, and the provision of a reliable and high-quality service to end users. To satisfy these needs, both researchers and network operators have studied and proposed different power generation and distribution technologies and promoted the development and implementation of distributed energy resources such as distributed generators, batteries, and static reactive compensators [8,9,10]. In particular, Distributed Generators (GDs) are the distributed energy resource most widely studied and installed around the world; therefore, they are the focus of this paper.

DGs can be integrated into both Alternating (AC) and Direct Current (DC) networks. Nevertheless, the integration of these devices into AC networks has been more widely studied and applied because AC grids are more common around the world than their DC counterparts [10,11]. An adequate operation of DGs in an electrical system could improve its chargeability, reduce the power losses, and enhance the voltage profiles of the grid, among other aspects [12,13]. Considering these advantages and the widespread use of AC power distribution systems, this study focuses on optimal power flow applied to DGs in AC networks.

To ensure the correct operation of DGs in AC networks, first, we should identify the main components of these networks, which include the slack generator, distributed generators, energy distribution branches, and electrical loads [10]. Second, we need to establish the location of the DGs in the network and their technical constraints: number of generators and nodes, minimum and maximum distributed power levels, branch data, and voltage and current bounds, among others. Finally, we should devise operating strategies to control the power injected by the distributed energy resources into the network to obtain as many economic, technical-operating, and environmental benefits as possible [14]. This problem is referred to as the Optimal Power Flow (OPF) problem in the specialized literature. The OPF is a nonlinear nonconvex problem that must be solved using optimization techniques and numerical methods to find the power configuration of DGs that contributes to the improvement of technical, economical, and environmental indicators [15]. To solve this problem, a master–slave methodology is usually implemented. In this kind of methodology, the master stage is responsible for determining the power to be injected by each distributed energy resource in order to satisfy the objective function defined by the network operator. The slave stage is in charge of solving the load flow problem in order to establish the impact of each solution proposed in the master stage [16]. Multiple authors in the specialized literature have proposed different optimization techniques for the master and slave stages in order to improve the impact of DGs in an electrical grid, as can be observed in the following subsection.

1.2. State of the Art

In recent years, several authors interested in the energy sector have looked for and proposed solutions to the various problems that occur in AC networks, including power losses associated with energy distribution [17,18], optimal sizing and location of DGs in the network [19,20], proper energy storage using batteries [15], and reduction of CO₂ emissions [7]. Regarding the optimal power flow in AC networks that include DGs, different solution methodologies have been proposed in the literature. Some of them have used commercial software and solutions based on sequential programming implementing open-source software. These two types of solution methodologies help to find the optimal power levels to be injected by the DGs in a network.

Studies such as [21,22] employed commercial optimization software to solve the OPF problem, satisfying the limits and constraints associated with this problem. In [21], the authors proposed a discrete-continuous solution methodology, in which the Chu–Beasley genetic algorithm was implemented in the DigSILENT programming language. In that study, the tests were only conducted in 6-, 14-, and 39-node test systems, thus ignoring the performance of the proposed methodology in larger systems. Additionally, although the computation times and the voltage profiles were taken into account, the currents flowing through the lines and the standard deviation of the implemented methodology were not considered. As a result, the maximum current levels of the branches that compose the electrical system cannot be evaluated, which allows the method to propose infeasible solutions to the problem under analysis and eliminates the possibility of evaluating the repeatability of the solution each time the algorithm is executed. In [22], the authors presented a multi-objective optimization methodology based on the mixed-integer nonlinear programming model. The problem was modeled in GAMS language and later solved using the DICOPT solver. In that study, the OPF problem was tested in 14- and 30-node systems, thus ignoring its behavior in larger networks. However, it took into account computation times that the study (the same as the previous one) did not consider, the standard deviation of the solution methodologies, the currents flowing through the lines, or the nodal voltages.

Studies such as [23,24,25] employed algorithms based on sequential programming to solve the OPF problem in AC networks, thus avoiding the need for commercial software, which is costly and complex [12]. In [23], the authors proposed a biogeography-based optimization algorithm and used, as the objective function, the minimization of $P_{loss}$ in the IEEE 30- and 57-node test systems. In that study, both the computation times and the nodal voltages were taken into account; however, the standard deviation was not considered to evaluate the repeatability of the solution provided by the proposed methodology. In [24], an artificial bee colony optimization algorithm was employed, the objective function was the minimization of active power losses in AC networks, and the solution was tested in the IEEE 30- and 118-node systems. In the study mentioned, the authors considered the analysis of the nodal voltage constraints but not the computation times or the standard deviation of the techniques they used. In [25], a particle swarm optimization algorithm was proposed to solve the OPF problem in AC networks and tested using the IEEE 57- and 118-node systems. That study took into account the nodal voltages but not the computation times or the standard deviation of the implemented algorithms. Importantly, none of these studies considered the currents flowing through the lines, which does not ensure that the solution obtained with the implemented methodologies satisfies the technical-operating constraints of the test systems used in each paper. In [26], the authors proposed an efficient analytical (EA) method for solving the OPF in an electrical distribution system in order to minimize power losses. Their optimization method was tested in the 33- and 69-node systems, obtaining excellent results. They used multiple methods to make comparisons, but they did not consider the analysis of the processing times or the repeatability of the solutions obtained by the EA. In [27], the authors presented a methodology implementing the Biogeography-Based Optimization (BBO) method to solve the OPF problem in a power transmission system; their objective function was the reduction of power losses. All their simulations were carried out in Matlab using the 114-node test system. However, in that paper, they did not compare the their results with those reported in other studies in the literature. The authors of [28] proposed a master–slave methodology that combines the black hole (BH) optimization algorithm and the triangular-based power flow method to solve the OPF problem in an AC network; their objective function was the reduction of power losses. The numerical results they obtained in the 33- and the 69-node test systems demonstrated the effectiveness and robustness of the proposed approach compared to those of others in the literature. However, they did not analyze the repeatability of the algorithm or the processing times it required; furthermore, they neglected the current limits of the branches in their mathematical model. In [29], the authors used a particle swarm optimization algorithm to solve the optimal power flow problem by sizing a photovoltaic DG, wind DG, and a battery inside an electrical network. Their objective function was the reduction of the investment and management costs of these devices using a mono-nodal electrical network as the test system. Nevertheless, they did not compare their method to others and did not analyze the processing time it required or its repeatability. In [30], the authors addressed the OPF problem in radial distribution networks using a metaheuristic optimization technique known as the sine–cosine algorithm; their objective function was the reduction of power losses. They validated the effectiveness of the proposed solution in the 33- and 69-node test systems by comparing its results with those reported in other papers in the literature. Nevertheless, they did not consider the effects of the solution methods under analysis on processing times. Furthermore, they did not include the current limits of the branches in the constraints that compose the mathematical model.

It is important to highlight that none of the optimization algorithms employed in the studies above were tuned, making it impossible to guarantee the same conditions for the proposed solution techniques. Furthermore, all these methodologies proposed to solve the OPF were evaluated in AC networks with radial topologies, without analyzing their effect in mesh topologies, which are very common in conventional electrical systems.

After reviewing the state of the art, we identified the need for a new methodology based on sequential programming to solve the OPF problem in AC networks that also avoids the use of commercial software and can be replicated using open-source software. The methodology should consider different topologies and sizes of AC networks to obtain high quality solutions in short processing times. It should also analyze the operating constraints of AC network components that were not considered in the state of the art reviewed above, such as nodal voltage, current flowing through the transmission lines in the systems, and power generated by the DGs. To evaluate the repeatability of the solution method, the results should be assessed using a statistical approach that analyzes the standard deviation of each methodology. In order to satisfy this need, this article presents a master–slave methodology to solve the OPF problem that can be replicated using open-source software. The master stage uses the Multiverse Optimization (MVO) algorithm proposed by [31]. It was selected due to its high performance in solving research problems and the fact that it has been applied to issues associated with renewable energies, power generation, and distribution systems [32,33,34,35]. The slave stage uses the Successive Approximation (SA) method proposed in [36] because of its high performance in terms of convergence and processing time to solve the load flow problem, as reported by the authors. To validate this methodology, the 10-, 33-, and 69-node radial systems and a 10-node mesh system were used in this study. Each test system considers a maximum power injection allowed for the DGs of 20%, 40%, and 60% of the power provided by the slack generator in a scenario without distributed generation. Each scenario was tested 100 times to determine the repeatability of the proposed solution methodology.

1.3. Scope and Main Contributions

Considering the importance of minimizing power losses associated with energy transport in AC networks, as well as the need to develop new methodologies that help to find reliable and good quality solutions without using commercial software, this study proposes a master–slave methodology to solve the OPF problem in radial and mesh electrical topologies. In the master stage, the proposed methodology uses the MVO [31] to determine the power to be injected by each DG located in the network. In the slave stage, it applies the SA numerical method [36] to evaluate both the impact of the solution provided by the master stage and the set of constraints that compose the problem using the load flow. The following are the main contributions of this study to the state of the art:

• A new solution methodology based on sequential programming to solve the OPF problem in AC networks that considers radial and mesh topologies.
• A robust statistical method that can be used to identify the solution methodology with the best balance of solution quality, processing times, and repeatability.
• An optimization method selected because it yields the best results in terms of solution quality, repeatability, and processing time to solve the OPF problem in AC networks with radial and mesh topologies.

This study also makes the following contributions to the energy sector:

• A new methodology that can be used to determine the optimal power level to be injected by each DG in order to reduce power losses and thus better use existing energy resources.
• A methodology with short processing times to solve the problem of sizing DGs in electrical networks.

1.4. Structure of the Paper

This article is organized as follows: Section 2 presents the mathematical formulation of the OPF problem, as well as the constraints that compose it, where the objective function is the reduction of power losses associated with energy distribution. Section 3 describes the proposed solution methodology, which consists of a master stage that uses the MVO and a slave stage that employs the SA numerical method. Section 4 presents and describes the algorithms used here for comparison purposes. Section 5 details the radial and mesh test scenarios employed in this study to perform the simulations. Section 6 reports and analyzes the simulation results obtained by each optimization algorithm. Finally, Section 7 draws the conclusions and proposes future research directions.

2. Mathematical Formulation

A variety of objective functions can be used in AC networks: the minimization of the operating costs of the network, the optimal selection of power conductors in distribution networks, the reduction of CO₂ emissions, the minimization of power losses in the network, the optimal sizing and location of the DGs, and the improvement of voltage profiles. The selection of the objective function depends on the needs of the network operator. Due to its widespread use to evaluate the efficiency of the methodologies proposed to solve the OPF problem in AC networks [21,22,23,24,25], the objective function selected in this study is the minimization of the active power losses associated with energy distribution in AC networks [25].

2.1. Objective Function

The objective function is the variable to be optimized while respecting the constraints associated with the problem. The objective function selected for this study is represented by Equation (1) below:

$$min{P}_{loss}=Real\left\{v^T{Y}_{L}v\right\}$$

(1)

In this equation, $P_{loss}$ denotes the active power losses (i.e., the variable to be minimized in this study); v, a vector containing the complex voltages of the system calculated based on the load flow; $Y_L$, the admittance matrix associated with the distribution lines; and $v^T$, a transposed vector of v.

2.2. Set of Constraints

The set of constraints refers to the technical-operating limits of the equipment that composes the AC network. These limits, which are detailed below, are directly linked to the objective function selected in this study:

$$S_{CG}+S_{DG}-S_D=D\left(v\right)[Y_L+Y_N]v$$

(2)

$$S_{DG}^{min}\le S_{DG}\le S_{DG}^{max}$$

(3)

$$v^{min}\le v\le v^{max}$$

(4)

$$I_B<I_B^{max}$$

(5)

$$1^T{S}_{DG}\le \alpha 1^{T}Real\left\{S_D\right\}$$

(6)

Equations (2)–(6) represent the OPF problem. Equation (2) expresses the total (active and reactive) power balance in the network, where $S_{CG}$ is the complex power provided by the slack generator; $S_{DG}$, the complex power supplied by the DGs; $S_D$, the complex power demand; $D\left(v\right)$, a symmetrical matrix that contains the complex voltages of the system in its diagonal; and $Y_L$, a matrix of admittances associated with the nodal effects. Equation (3) presents the apparent power limits allowed for the DGs, where $S_{DG}^{min}$ and $S_{DG}^{max}$ are the minimum and maximum power that each DG can supply to the network, respectively. Importantly, the DGs only inject active power into the network. Equation (4) defines the nodal voltage limits of the system, where $v^{min}$ and $v^{max}$ are the minimum and maximum voltages allowed in each node of the system. Equation (5) represents the maximum current allowed inside the power distribution lines, where $I_B$ denotes the current flowing through the transmission lines; and $I_B^{max}$, the maximum current that can pass through the conductor. Equation (6) defines the maximum penetration percentage allowed for the DGs in the network, where $1^T$ is a row vector filled with ones; and $\alpha$, the penetration percentage allowed for each DG, which can be 20%, 40%, or 60% of the power provided by the slack generator. Finally, in this equation, $Real\left\{X\right\}$ corresponds to the real part of the complex vector (X) associated with the injection of active power by the DGs:

$$minz=\left(\begin{array}{c}{P}_{loss}+{\beta }_1{1}^{T}max\{0,v-v^{max}\}\\ +{\beta }_2{1}^{T}min\{0,v-v^{min}\}\\ +{\beta }_3{1}^{T}min\{0,S_{CG}-S_{CG}^{min}\}\\ +{\beta }_4{1}^{T}max\{0,S_{DG}-S_{DG}^{max}\}\\ +{\beta }_5{1}^{T}min\{0,S_{DG}-S_{DG}^{min}\}\\ +{\beta }_{6}max\{0,1^T{S}_{DG}-\alpha 1^{T}Real\left\{S_D\right\}\}\end{array}\right)$$

(7)

In addition to the equations that represent the set of constraints, we also present Equation (7), which guarantees that the constraints (Equations (2)–(6)) are respected at all times. This equation penalizes the algorithm if the limits presented above are violated. In this equation, ${\beta }_1$ to ${\beta }_6$ are the penalty factors, which, for this study, were heuristically calculated and are equal to 1000. When all the constraints are respected, all the penalty values are canceled out using the $min\{.\}$ and $max\{.\}$ functions, which causes z to be equal to $P_{loss}$.

To facilitate the comprehension of this article,

Table 1. Nomenclature.

Variable	Meaning
OPF	Optimal Power Flow
MVO	Multiverse Optimizer
SA	Successive Approximations
AC	Alternating Current
DC	Direct Current
DGs	Distributed Generators
DG	Distributed Generator
$P_{loss}$	Power losses
v	Vector containing all the nodal voltages of the system calculated based on the load flow
$G_L$	Conductance matrix of the energy distribution lines
$v^T$	Transposed vector of v
$S_g$	Power generated by the slack node
$S_{DG}$	Power supplied by the DGs installed in the system
$S_d$	Power demanded by the nodes in the system
$D\left(v\right)$	Symmetric positive matrix containing the nodal voltages of the system in its diagonal
$G_L$	Conductance of each transmission line
$G_N$	Resistive loads connected to the DC network
$S_{DG}^{min}$	Minimum power allowed for the DGs
$S_{DG}^{max}$	Maximum power allowed for the DGs
$v_{min}$	Minimum voltage allowed in each node of the system
$v_{max}$	Maximum voltage allowed in each node of the system
$I_{ij}$	Current that passes through the line that connects nodes i and j
$I_{ij}^{max}$	Current limit established by the conductor assigned to this line
$1^T$	Transposed vector composed of ones, which can be used to add up different penalties in the objective function
$\alpha$	Maximum power injection level allowed for each DG, which can be 20%, 40%, or 60% of the power supplied by the slack generator

presents the notation and nomenclature used for each variable in Equations (1)–(7), as well as the acronyms of the OPF problem.

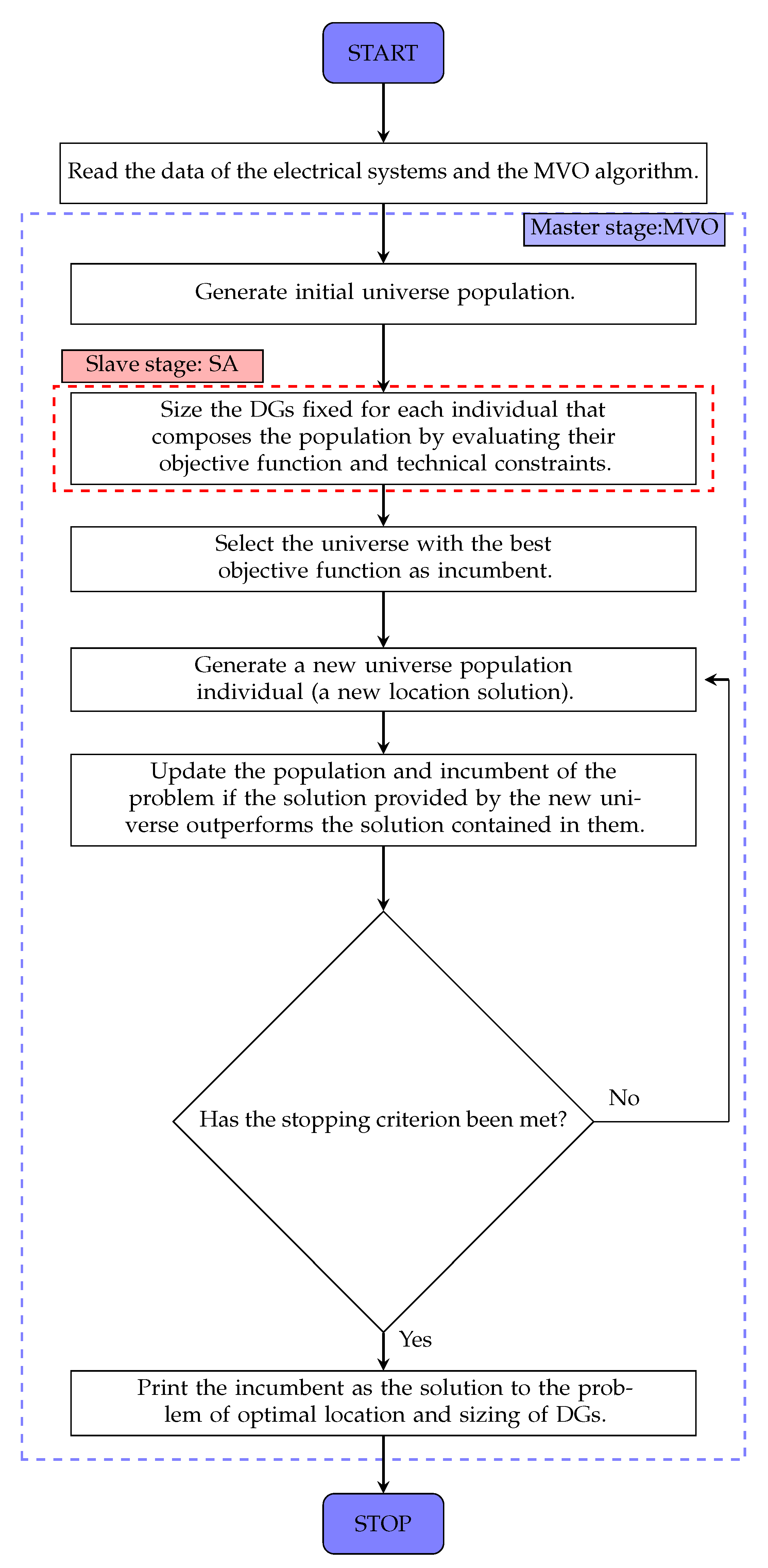
3. Proposed Solution Methodology

The equations presented in the previous section represent the OPF problem taking into account the operation of the DGs located in the AC network. Since this is a nonlinear nonconvex problem, it must be solved using optimization techniques and numerical methods. This study, therefore, proposes dividing the OPF problem into two stages: master and slave. In the first stage (master), the MVO [31] is used to determine the active power to be injected by each DG installed in the network. In the second stage (slave), the SA numerical method [36] is employed to solve the power flow problem and calculate the electrical variables provided by the master stage in order to determine their impact on the objective function we selected. The master–slave (MVO–SA) methodology proposed in this paper is described in the next subsections.

3.1. Master Stage: Multiverse Optimizer (MVO)

Although there are various theories about the origin of the universe, the Big Bang theory is one of the most well-known [37,38]. According to it, the Big Bang was an explosion that created the known universe [39,40]. Physicists have also proposed several theories suggesting the existence of universes other than the one we live in. One of them is known as the Multiverse theory, which claims that there are other universes and that each began as a result of an explosion (or Big Bang) [41,42,43,44]. The MVO is inspired by this theory, and it employs three of its main concepts: white holes, black holes, and wormholes [31]. Physicists regard the Big Bang as a white hole and the main component for the start of a new universe. White holes create and expel matter and energy [45,46,47,48]. Black holes, whose behavior is the complete opposite, absorb everything that comes near their event horizon, and nothing can escape them due to their colossal gravitational force [49,50,51,52,53]. Finally, wormholes connect two distant points in a universe, allowing objects to pass through them and creating instantaneous travel paths in the vastness of the universe [54,55,56,57].

The MVO mathematically models the behavior of white holes, black holes, and wormholes, and its search process consists of two stages. The first stage is exploration, in which white holes and black holes are used. In this stage, the algorithm explores the search space and suggests the most promising regions where the best local optima can be found. The second stage is exploitation, in which wormholes are employed. In this stage, a search is carried out in the regions where the best local optima have been found in order to find the global optimum.

The following subsections present the steps followed in this study for the computational development and to find a solution to the OPF problem using the MVO.

3.1.1. Generating the Initial Population

Equation (8) is used to generate the initial population of the universes, where each universe constitutes a solution to the problem addressed here (i.e., the power level to be injected by the DGs). In this equation, subscript i denotes the i-th universe, and subscript j represents the j-th object in universe i. In the OPF problem, each row represents a possible solution to the problem; and each column, the number of nodes (other than the slack node) that are allowed to inject power. Each universe ($U_{i,j}$) created with Equation (8) is located within the solution space, which is limited by the technical constraints of the OPF problem. In this equation, $ub$ and $lb$ are the maximum and minimum power that each DG can inject, respectively. In order for the algorithm to explore larger regions of the search space, the initial population of $U_{i,j}$ is generated randomly using the $rand$ command, which produces random values between 0 and 1 for each object j within universe i:

$$U_{i,j}=\left(\left(ub-lb\right)·rand\right)+lb$$

(8)

To generate the entire population of universes, this study proposes a population contained in a matrix of size $nxd$, where n is the number of universes, and d denotes the number of variables in the problem addressed here (see Equation (9)). In Equation (9), $U_n$ is the n-th universe in the $M_{Universes}$ matrix (which, in the case of the OPF problem, represents the possible solutions), and $U_d$ denotes the number of DGs located in the network:

$$M_{Universes}=\left[\begin{array}{c}{U}_1\\ U_2\\ ⋮\\ ⋮\\ U_n\end{array}\right]=\left[\begin{array}{ccccc}{U}_{1,1}& U_{1,2}& \cdots & \cdots & U_{1,d}\\ U_{2,1}& U_{2,2}& \cdots & \cdots & U_{2,d}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ U_{n,1}& U_{n,2}& \cdots & \cdots & U_{n,d}\end{array}\right]$$

(9)

3.1.2. Calculating the Objective Function

To assess the impact of every solution proposed in the $M_{Universes}$ matrix, the objective function of each $U_n$ is evaluated using the SA numerical method. This method evaluates the power levels injected by the DGs, which makes it possible to determine the power losses associated with each universe ($U_n$). The obtained values are stored in a matrix of size $n·1$ called $M{O}_{Universes}$, which is presented in Equation (10):

$$M{O}_{Universes}=\left[\begin{array}{ccccc}f\left(\right[U_{1,2}& U_{1,2}& \cdots & \cdots & U_{1,d}\left]\right)\\ f\left(\right[U_{2,1}& U_{2,2}& \cdots & \cdots & U_{2,d}\left]\right)\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ f\left(\right[U_{n,1}& U_{n,2}& \cdots & \cdots & U_{n,d}\left]\right)\end{array}\right]$$

(10)

Additionally, the $M{O}_{Universes}$ matrix is sorted in ascending order, where the first position represents the objective function with the best value, i.e., the lowest $P_{loss}$ for the system. This is selected as the incumbent solution to the OPF problem and stored in $Best\_Fob$ (Equation (11)). The variables that compose the best objective function are also stored in $Best\_U$ (Equation (12)), and this universe is selected as the one with the best solution found at the current iteration:

$$Best\_Fob=\left[f\left(U_{1,d}\right)\right]$$

(11)

$$Best\_U=\left[U_d\right]$$

(12)

3.1.3. Movement Strategy

The MVO technique is divided into two stages: exploration and exploitation. In the exploration stage, this technique uses black and white holes to explore the search space, and the algorithm tries to discover the most promising regions where the global optimum can be potentially found. In the exploitation stage, this technique uses wormholes to exploit the promising regions found in the exploration stage, and the algorithm converges toward the global optimum (moves forward toward the best solution). In the MVO method, each solution is assigned an inflation rate $\left(I{R}_i\right)$ that corresponds to the best $P_{loss}$ obtained so far by each universe. Such inflation rate is proportional to the fitness function provided by the slave stage after evaluating the objects j proposed by each one of the universes (i.e., the power levels to be injected by the DGs). In addition, the following rules are applied to the universes of the MVO:

• The higher the $IR$, the greater the probability of having a white hole.
• The lower the $IR$, the greater the probability of having a black hole.
• Universes with a high $IR$ tend to send objects through white holes.
• Universes with a low $IR$ tend to receive more objects through black holes.
• Any object in any universe can randomly move toward the best universe through wormholes, regardless of the $IR$.

Furthermore, black or white holes must change their behavior depending on the required solution approach (i.e., a maximization or minimization problem). In this case, it is a minimization problem.

In the MVO method, objects (search particles) move between universes through black/white holes, i.e., objects can be exchanged between universes. When a relationship is established between white/black holes in two universes, the universe with the higher $IR$ is considered to have a white hole, whereas that with the lower $IR$ is considered to have black holes. Thus, information is transferred from the white holes in the source universe to the black holes in the target universe. Moreover, regardless of their $IR$, all universes are assumed to have wormholes in order to randomly transport objects. Wormhole existence probability ($WEP$) and travel distance rate ($TDR$), which are denoted by Equations (13) and (14), respectively, are two fundamental coefficients for the optimal operation of the MVO. Equation (13) defines $WEP$ as the probability of existence of wormholes in the universes, which increases linearly over iterations to emphasize exploitation as progress made in the optimization process:

$$WEP=Min+l·\left(\frac{Max-Min}{L}\right)$$

(13)

This equation is able to generate a rate of change based on the sum of a minimum value $\left(Min\right)$ and a maximum value $\left(Max\right)$, both of which depend on the algorithm and the iterative process. In this equation, l is the current iteration, and L denotes the maximum number of iterations. This allows for changes at the exploration and exploitation levels of the optimization technique. Importantly, the $Min$ and $Max$ values were optimized to improve the quality of the solution to the problem addressed here.

Additionally, in Equation (14), $TDR$ defines the distance over which an object can be transported through a wormhole around the best universe obtained thus far. Unlike $WEP$, $TDR$ increases over iterations to provide a more precise local exploitation/search around the best universe found thus far:

$$TDR=1-\left(\frac{l^{1/P}}{L^{1/P}}\right)$$

(14)

In this equation, P denotes the level of precision of the exploitation of the algorithm, i.e., the higher its value, the faster and more precise the search exploitation of the algorithm. In this study, parameter P was optimized to find the best solution to the OPF problem in AC networks.

3.1.4. Evolution of the Universes in the Iterative Process

The relationship between white and black holes allows objects to be exchanged between universes through white/black tunnels. In addition, a universe can update the value of an object based on the information of an object from another universe. Their interaction occurs as a function of $IR$. Objects travel from a source white hole to a target black hole. Black holes make objects in a universe disappear, and they are replaced with others coming from white holes. Equation (15) shows how the normalized inflation rate of the i-th universe is obtained, where the $IR$ values calculated for each universe in the population are normalized. When this equation is applied to the set of universes, the vector of size $n·1$ (where n is the number of solutions or universes) is obtained with normalized values in the [0–1] range:

$$NI\left(I{R}_i\right)=\left(\frac{I{R}_i}{max\left(I{R}_i\right)}\right)$$

(15)

The white/black tunnel is generated by means of Equation (16), where each object j in universe i can be replaced with an object j from universe k, and the position of k is selected using a roulette wheel that offers the option of arbitrarily selecting any universe in the solution space. The exchange of objects between universes occurs for the same element, and this is achieved by comparing a random number $r1$ with the normalized inflation rate $\left(NI\left(I{R}_i\right)\right)$.

$$U_{i,j}=\left\{\begin{array}{cc}{U}_{k,j}\hfill & r1<NI\left(I{R}_i\right)\hfill \\ U_{i,j}\hfill & r1\ge NI\left(I{R}_i\right)\hfill \end{array}\right.{\forall }_i=1,2,\cdots ,n;{\forall }_j=1,2,\cdots ,d$$

(16)

In the equation above, $U_{k,j}$ is the object j of universe k selected by the roulette wheel and transported through the white/black tunnel to universe i. An object is transferred to universe i if and only if the random value $r1$ in the [0–1] range is below the $NI\left(I{R}_i\right)$. Otherwise, there is no exchange of objects through white/black tunnels, i.e., the object of universe $U_{i,j}$ will not be updated and will keep its current value. Equation (17) is used to determine the k-th universe to which object j will be transported. In this equation, k is chosen using the roulette wheel function [58], which selects a random integer in the [1–n] range, where n is the number of solutions proposed for the problem. Algorithm 1 presents the pseudocode to select universe k by means of Equation (17):

$$k=RouletteWheelSelection(-NI)$$

(17)

Importantly, since this is a minimization problem, the selection using the roulette wheel must be performed with $-NI$. If the problem to be solved is a maximization one, $-NI$ should be replaced with the positive $NI$.

Algorithm 1. Proposed pseudocode of the roulette wheel to select universe k to transport element j to universe i.

1: function $choice=RouletteWheelSelection\left(weights\right)$  2: $accumulation=cumsum\left(weights\right);$  3: $p=rand\left(\right)\ast accumulation\left(end\right);$  4: $chosen\_index=-1;$  5: for $index=1:length\left(accumulation\right)$ do  6:      if $\left(accumulation\right(index)>p)$ then  7:            $chosen\_index=index;$  8:            break  9:      end if  10:      $chose=chosen\_index;$  11:end for

3.1.5. Updating Universes Based on Wormholes

Wormholes allow for the instantaneous teleportation of objects j to the best universe found thus far, where $IR$ represents the evaluation of the objective function (in this case, the minimization of power losses in the system). As the algorithm advances, each universe experiences random teleportation of its objects to the best universe $(Best\_U(1,j\left)\right)$ through wormholes. This process is repeated until a stopping criterion is met.

To guarantee changes in each universe, there must be a high probability of improvement of the $IR$ through wormholes, assuming that the latter are always established between new universes randomly generated depending on parameter $r4$ and the best universe ($Bes{t}_U(1,j)$), which are represented in Equation (18):

$$U_{i,j}=\left\{\begin{array}{cc}\left\{\begin{array}{cc}\left[Best\_U_{(1,j)}+TDR·\left(\left(ub-lb\right)·r4+lb\right)\right]& r3<0.5\left(a\right)\\ \left[Best\_U_{(1,j)}-TDR·\left(\left(ub-lb\right)·r4+lb\right)\right]& r3\ge 0.5\left(b\right)\end{array}\right.& r2<WEP\\ U_{i,j}& r2\ge WEP\\ {\forall }_i=1,2,\cdots ,n;{\forall }_j=1,2,\cdots ,d\end{array}\right.$$

(18)

This equation can be used to generate new objects j for universe i$\left(U_{i,j}\right)$ at each iteration, which depends on $WEP$ and random parameter $r2$ in the [0–1] range. If $r2<WEP$, a new element j will be generated for universe i depending on the value that parameter $r3$ takes, which is a random number in the [0–1] range. As selection criteria, we have that, if $r3<0.5$, Equation (18) $\left(a\right)$ will be used, but, if $r3\ge 0.5$, Equation (18) $\left(b\right)$ will be employed. However, if $r2\ge WEP$, a new object j will not be generated in universe i; instead, the current value of object j will be kept until $r2<WEP$.

3.1.6. Stopping Criteria

The following two stopping criteria are employed for the master stage:

• Maximum number of iterations: The iterative process will finish when the algorithm reaches the maximum number of iterations (L), which are controlled by counter l.
• Number of non-improvement iterations: The algorithm will stop when the incumbent solution is not updated after n consecutive iterations.

3.2. Slave Stage

The slave stage allows us to determine the impact of each solution proposed in the master stage by evaluating the objective function associated with each solution ($U_{n,d}$). In other words, the slave stage assesses the electrical variables provided by the master stage, which are used to estimate the $P_{loss}$ in the system. Hence, a numerical method is necessary to solve the load flow problem in an iterative manner and ensure that the constraints of the problem are respected. Considering that, this paper proposes implementing the SA numerical method presented in [59], which was chosen due to its excellent performance in solving the power flow problem and because it is able to solve the load flow problem for radial as well as mesh networks. This method is based on Equation (19):

$$Y_{dd}·v_d=-D_d^{-1}\left(v_d^{*}\right)S_d^{*}-Y_{dg}·v_g$$

(19)

In this equation, $Y_{dd}$ and $Y_{dg}$ are the components of the nodal admittances matrix of the network that relate load nodes to generator nodes, respectively. The variables $v_d$ and $v_g$ represent the voltages in the demand and generator nodes, respectively. The nodal voltage profiles in the demand nodes can be calculated by means of a mathematical development applied to Equation (19):

$$v_d=-Y_{dd}^{-1}[D_d^{-1}\left(v_d^{*}\right)S_d^{*}-Y_{dg}·v_g]$$

(20)

In order to estimate the nodal voltages ($v_d$) of the system with an almost-null convergence error, an iterative process must be implemented. For this purpose, a counter (t) is included in Equation (20). As a result, the following equation can be used to calculate the nodal voltages of the system:

$$v_d^{t+1}=-Y_{dd}^{-1}[D_d^{-1}\left({\left(v_d^{*}\right)}^t\right)S_d^{*}-Y_{dg}·v_g]$$

(21)

Figure 1 shows a flowchart that describes the iterative process of the master–slave (MVO–SA) methodology used here to solve the OPF problem.

4. Methods Used for Comparison Purposes

To evaluate the capacity of the MVO to converge toward the best solution in terms of quality and computation times, it was compared with four other optimization techniques that have been reported in the specialized literature to solve the OPF problem: the Particle Swarm Optimization (PSO) algorithm, the Ant Lion Optimization (ALO) algorithm, the Black Hole (BH) optimization algorithm, and a Continuous Genetic Algorithm (CGA). The PSO algorithm is inspired by the behavior of schools of fish when exploring a region in search of food [60]. The ALO mimics the hunting mechanism of ant lions, which dig a cone-shaped hole in the ground to catch their prey [61]. The BH algorithm is based on the dynamic interaction between stars and black holes [62]. Finally, the CGA is inspired by the genetic crossover, selection, and mutation processes of living beings, through which parents pass on their DNA to their offspring [63]. These four optimization algorithms were selected because of their excellent performance in solving the OPF problem in AC networks [19,21,30,64]. Each one of them was implemented here in the master stage of the master–slave methodology. Thus, the master stage employed one of these optimization algorithms, and the slave stage always used the SA numerical method to solve the load flow problem [36].

In this study, we used the 10-, 33-, and 69-node radial test systems and the 10-node mesh test system (which are described in Section 5) to solve the OPF problem and assess the effectiveness of the proposed methodology in these types of electrical systems.

To ensure a fair comparison of all the optimization algorithms we employed, each one of them was tuned to guarantee the same conditions and that they could find the best solution to the problem addressed in this paper. To carry out such tuning, we used the PSO algorithm [60] with an initial population of 10 individuals and a maximum number of iterations of 300. The tuning parameters were a population size in the [1–100] range, a maximum number of iterations for each algorithm in the [1–1000] range, and a number of non-improvement iterations in the [1–1000] range. Moreover, for the MVO, parameters P, $Max$, and $Min$ were tuned using [1–10], [0.001–1], and [0.001–1] ranges, respectively.

Table 2. Parameters of the continuous methods employed here in the master stage.

Method	MVO	PSO	ALO	BH	CGA
Number of particles	80	58	62	83	57
Maximum iterations	432	723	992	667	551
Non-improvement iterations	300	252	725	340	551
P parameter	6	-	-	-	-
Max parameter	0.81	-	-	-	-
Min parameter	0.09	-	-	-	-

presents the turned parameters that allow each optimization algorithm to find the best solution to the OPF problem.

Importantly, the parameters reported in Table 2 can be used to replicate each optimization technique in networks of any size.

5. Test Scenarios and Considerations

To evaluate the robustness and quality of the solution provided by each method, we used the 10-, 33-, and 69-node radial test systems, but we also employed a 10-node mesh test system to assess the effectiveness of the proposed methodology in mesh topologies. These four test systems were selected in order to assess the ability of each optimization algorithm to find the best solution in networks of different sizes. In each test system, DGs were allowed to inject 20%, 40%, and 60% of the power provided by the slack generator. In addition, each system features a single slack generator in a scenario without DGs (i.e., the base case).

5.1. Radial Test Systems

This subsection presents the radial test systems used in this paper.

5.1.1. 10-Node Radial Test System

Figure 2 illustrates the 10-node system, which consists of 9 lines and 10 nodes. In a scenario without distributed generation, the slack generator produces 12,591.4181 kW, and the active power losses amount to $223.4181$ kW. In this system, the DGs were located at nodes 5, 9, and 10, considering three maximum penetration levels: 20%, 40%, and 60% of the active power provided by the slack generator in the base case. For all the DGs, the minimum injection power was 0 kW at each penetration level. Likewise, the maximum injection powers for the 20%, 40%, and 60% penetration levels were $2518.2836$ kW, $5036.5673$ kW, and $7554.8509$ kW, respectively. The maximum current for this system (i.e., $581.2757$ A) was calculated using the load flow. Considering this value, we used a 1250-kcmil conductor operating at 75 °C, which establishes a maximum line current of 590 A. Since this study investigates a non-telescopic electrical network, this current limit applies to all the lines in the system. For all the calculations related to this system, we employed a base power of 100 kVA and a base voltage of 23 kV.

Table 3. Electrical parameters of the 10-node radial test system.

Node i	Node j	Rij [Ω]	Xij [Ω]	P [kW]	Q [kVAr]
1	2	0.1233	0.4127	1840	460
2	3	0.2467	0.6051	980	340
2	4	0.7469	1.2050	1790	446
4	5	0.6984	0.6084	1598	1840
2	6	1.9837	1.7276	1610	600
6	7	0.9057	0.7886	780	110
7	8	2.0552	1.1640	1150	60
7	9	4.7953	2.7160	980	130
3	10	5.3434	3.0264	1640	200

reports the electrical parameters of the 10-node system. The first two columns specify the output and input nodes. The third column shows the resistance of the conducting lines. The fourth column details the reactances. Finally, the fifth and sixth columns present the active and reactive powers, respectively, which correspond to the powers demanded by each node in the system.

5.1.2. 33-Node Radial Test System

Figure 3 presents the 33-node system, which consists of 33 nodes and 32 lines. The base case of this system uses a base voltage of $12.66$ kV and a base apparent power of 100 kVA. In the base case, the slack generator injects an active power of $3925.9785$ kW, and the active power losses amount to $210.9785$ kW. The locations of the DGs in this system were defined as in [10], i.e., they were located at nodes 12, 15, and 31. As in the previous system, DGs are allowed to inject 20%, 40%, and 60% of the power supplied by the slack generator in the base case. For all the DGs, the minimum active power was 0 kW, and the maximum active powers were $785.1957$ kW, $1570.3914$ kW, and $2355.5871$ kW for the 20%, 40%, and 60% penetration levels, respectively. When the base case was evaluated, the maximum line current was $365.2518$ A. Based on this value, we used a 700-kcmil conductor operating at 60 °C in each segment of the system, which establishes a maximum line current of 385 A.

Table 4. Electrical parameters of the 33-node radial test system.

Node i	Node j	Rij [Ω]	Xij [Ω]	P [kW]	Q [kVAr]	Node i	Node j	Rij [Ω]	Xij [Ω]	P [kW]	Q [kVAr]
1	2	0.0922	0.0477	100	60	17	18	0.7320	0.5740	90	40
2	3	0.4930	0.2511	90	40	2	19	0.1640	0.1565	90	40
3	4	0.3660	0.1864	120	80	19	20	1.5042	1.3554	90	40
4	5	0.3811	0.1941	60	30	20	21	0.4095	0.4784	90	40
5	6	0.8190	0.7070	60	20	21	22	0.7089	0.9373	90	40
6	7	0.1872	0.6188	200	100	3	23	0.4512	0.3083	90	50
7	8	1.7114	1.2351	200	100	23	24	0.8980	0.7091	420	200
8	9	1.0300	0.7400	60	20	24	25	0.8900	0.7011	420	200
9	10	1.0400	0.7400	60	20	6	26	0.2030	0.1034	60	25
10	11	0.1966	0.0650	45	30	26	27	0.2842	0.1447	60	25
11	12	0.3744	0.1238	60	35	27	28	1.0590	0.9337	60	20
12	13	1.4680	1.1550	60	35	28	29	0.8042	0.7006	120	70
13	14	0.5416	0.7129	120	80	29	30	0.5075	0.2585	200	600
14	15	0.5910	0.5260	60	10	30	31	0.9744	0.9630	150	70
15	16	0.7463	0.5450	60	20	31	32	0.3105	0.3619	210	100
16	17	1.2890	1.7210	60	20	32	33	0.3410	0.5302	60	40

, which is organized in the same way as Table 3, reports the electrical parameters of the 33-node system.

5.1.3. 69-Node Radial Test System

Figure 4 shows the 69-node system, which consists of 69 nodes and 68 lines. The scenario without DGs in this system employs a base voltage of $12.66$ kV and a base apparent power of 100 kVA. In addition, the slack generator supplies an active power of $4132.8423$ kW, and the active power losses amount to $242.1523$ kW. As in the other two systems, DGs are allowed to inject 20%, 40%, and 60% of the power provided by the slack generator. The location of the DGs in this system was defined as in [10], i.e., they were located at nodes 26, 61, and 66. For all the DGs, the minimum active power was 0 kW, and the maximum active powers were $826.5685$ kW, $1653.1369$ kW, and $2479.7054$ kW for the 20%, 40%, and 60% penetration levels, respectively. When the load flow was simulated for this system, the maximum current was $394.4489$ A. Therefore, a 750-kcmil conductor operating at 60 °C was used in each segment of the system, with a maximum current of 400 A.

Table 5. Electrical parameters of the 69-node radial test system.

Node i	Node j	Rij [Ω]	Xij [Ω]	P [kW]	Q [kVAr]	Node i	Node j	Rij [Ω]	Xij [Ω]	P [kW]	Q [kVAr]
1	2	0.0005	0.0012	0	0	3	36	0.0044	0.0108	26	18.55
2	3	0.0005	0.0012	0	0	36	37	0.0640	0.1565	26	18.55
3	4	0.0015	0.0036	0	0	37	38	0.1053	0.1230	0	0
4	5	0.0215	0.0294	0	0	38	39	0.0304	0.0355	24	17
5	6	0.3660	0.1864	2.6	2.2	39	40	0.0018	0.0021	24	17
6	7	0.3810	0.1941	40.4	30	40	41	0.7283	0.8509	102	1
7	8	0.0922	0.0470	75	54	41	42	0.3100	0.3623	0	0
8	9	0.0493	0.0251	30	22	42	43	0.0410	0.0478	6	4.3
9	10	0.8190	0.2707	28	19	43	44	0.0092	0.0116	0	0
10	11	0.1872	0.0619	145	104	44	45	0.1089	0.1373	39.22	26.3
11	12	0.7114	0.2351	145	104	45	46	0.0009	0.0012	39.22	26.3
12	13	1.0300	0.3400	8	5	4	47	0.0034	0.0084	0	0
13	14	1.0440	0.3400	8	5	47	48	0.0851	0.2083	79	56.4
14	15	1.0580	0.3496	0	0	48	49	0.2898	0.7091	384.7	274.5
15	16	0.1966	0.0650	45	30	49	50	0.0822	0.2011	384.7	274.5
16	17	0.3744	0.1238	60	35	8	51	0.0928	0.0473	40.5	28.3
17	18	0.0047	0.0016	60	35	51	52	0.3319	0.1140	3.6	2.7
18	19	0.3276	0.1083	0	0	9	53	0.1740	0.0886	4.35	3.5
19	20	0.2106	0.0690	1	0.6	53	54	0.2030	0.1034	26.4	19
20	21	0.3416	0.1129	114	81	54	55	0.2842	0.1447	24	17.2
21	22	0.0140	0.0046	5	3.5	55	56	0.2813	0.1433	0	0
22	23	0.1591	0.0526	0	0	56	57	1.5900	0.5337	0	0
23	24	0.3463	0.1145	28	20	57	58	0.7837	0.2630	0	0
24	25	0.7488	0.2475	0	0	58	59	0.3042	0.1006	100	72
25	26	0.3089	0.1021	14	10	59	60	0.3861	0.1172	0	0
26	27	0.1732	0.0572	14	10	60	61	0.5075	0.2585	1244	888
3	28	0.0044	0.0108	26	18.6	61	62	0.0974	0.0496	32	23
28	29	0.0640	0.1565	26	18.6	62	63	0.1450	0.0738	0	0
29	30	0.3978	0.1315	0	0	63	64	0.7105	0.3619	227	162
30	31	0.0702	0.0232	0	0	64	65	1.0410	0.5302	59	42
31	32	0.3510	0.1160	0	0	65	66	0.2012	0.0611	18	13
32	33	0.8390	0.2816	10	10	66	67	0.0047	0.0014	18	13
33	34	1.7080	0.5646	14	14	67	68	0.7394	0.2444	28	20
34	35	1.4740	0.4873	4	4	68	69	0.0047	0.0016	28	20

, which is organized in the same way as Table 3 and Table 4, presents the parameters of the 69-node system.

5.2. Mesh Test System

This subsection describes the mesh test system used in this study.

10-Node Mesh Test System

Figure 5 presents the topology of the 10-node mesh network. This 10-node system is the same we used previously, but, in this case, it has 10 nodes and 11 lines. The same voltage and apparent power of the 10-node radial test system are used in the base case. In the case without distributed generation, the slack generator provides a power of 12,558.3237 kW, and the active power losses equal 190.3237 kW. As in its radial counterpart, the DGs are located at nodes 5, 9, and 10, and this feeder uses penetration percentages of 20%, 40%, and 60% of the power produced by the slack generator. This way, each DG can produce a minimum power of 0 kW and maximum powers of 2511.6647 kW, 5023.3295 kW, and 7534.9942 kW, respectively. The maximum voltage flowing through the lines is 579.7276 A. Thus, a 1250-kcmil conductor at 75 °C was selected according to NTC 2050 standard, and a maximum line power of 590 A was established for each section of the network. Using the same order as in Table 3, Table 4, Table 5,

Table 6. Electrical parameters of the 10-node mesh system.

Node i	Node j	Rij [Ω]	Xij [Ω]	P [kW]	Q [kVAr]
1	2	0.1233	0.4127	1840	460
2	3	0.2467	0.6051	980	340
2	4	0.7469	1.2050	1790	446
4	5	0.6984	0.6084	1598	1840
2	6	1.9837	1.7276	1610	600
6	7	0.9057	0.7886	780	110
7	8	2.0552	1.1640	1150	60
7	9	4.7953	2.7160	980	130
3	10	5.3434	3.0264	1640	200
5	10	0.1426	0.4522	-	-
8	10	0.2018	0.5214	-	-

,

Table 7. Results of the simulations in the 10-node radial test system.

10-Node Radial Test System
Method	Node/ Power [kW]	Power Losses				Vworst [p.u]/ Node	Imax [A]
		Minimum [kW]/ Reduction [%]	Average [kW]/ Reduction [%]	Time [s]	STD [%]
Without DGs	—	223.4181	—	—	—	0.9–1.1	590
20% penetration
MVO	5/0.05	116.9220/47.6667	116.9250/47.6654	3.75	0.005	0.9723/8	433.3324
	9/1589.82
	10/928.41
PSO	5/0	116.9218/47.6668	117.2119/47.5370	4.50	1.328	0.9723/8	433.3321
	9/1589.55
	10/928.73
ALO	5/0.51	116.9473/47.6554	117.9188/47.2206	6.66	0.721	0.9723/8	433.3827
	9/1586.68
	10/929.96
BH	5/96.28	117.9244/47.2181	121.5254/45.6063	3.35	1.746	0.9729/8	433.5938
	9/1696.06
	10/720.92
CGA	5/18.86	117.0415/47.6132	117.4801/47.4169	3.29	0.173	0.9725/8	433.4102
	9/1619.67
	10/878.08
40% penetration
MVO	5/1619.69	80.7608/63.8522	80.7619/63.8517	3.68	0.001	0.9752/8	322.2694
	9/1971.25
	10/1445.62
PSO	5/1620.68	80.7608/63.8522	80.9785/63.7547	4.25	0.910	0.9751/8	322.2693
	9/1970.20
	10/1445.69
ALO	5/1570.43	80.7922/63.8381	81.8538/63.3629	6.61	1.797	0.9752/8	322.2936
	9/1979.08
	10/1486.52
BH	5/1606.93	80.9765/63.7556	82.4371/63.1019	3.29	1.084	0.9751/8	323.3491
	9/1969.06
	10/1435.96
CGA	5/1642.03	80.7807/63.8433	81.0075/63.7417	3.30	0.179	0.9751/8	322.3464
	9/1959.77
	10/1433.01
60% penetration
MVO	5/2992.61	72.1260/67.7170	72.1260/67.7170	3.88	9.38 × 10−7	0.9771/8	235.1382
	9/2235.19
	10/1804.14
PSO	5/2992.59	72.1260/67.7170	72.1260/67.7170	2.39	1.22 × 10−10	0.9771/8	235.1409
	9/2235.17
	10/1804.13
ALO	5/2993.04	72.1308/67.7149	72.7952/67.4175	6.70	1.613	0.9770/8	236.2086
	9/2219.08
	10/1795.22
BH	5/2941.39	72.1498/67.7064	73.1556/67.2562	3.78	1.129	0.9773/8	236.3767
	9/2267.73
	10/1794.37
CGA	5/3020.79	72.1345/67.7132	72.1848/67.6907	3.46	0.061	0.9772/8	234.3459
	9/2245.92
	10/1783.47

,

Table 8. Simulation results in the 33-node radial test system.

33-Node Radial Test System
Method	Node/ Power [kW]	Power Losses				Vworst [p.u]/ Node	Imax [A]
		Minimum [kW]/ Reduction [%]	Average [kW]/ Reduction [%]	Time [s]	STD [%]
Without DGs	—	210.9785	—	—	—	0.9–1.1	380
20% penetration
MVO	12/44.88	127.4984/39.5680	127.4994/39.5676	11.18	0.001	0.9377/33	241.4931
	15/398.94
	31/341.37
PSO	12/45.68	127.4984/39.5681	127.8911/39.3819	11.97	0.524	0.9377/33	241.4931
	15/398.71
	31/340.81
ALO	12/55.13	127.5029/39.5659	127.6270/39.5071	17.44	0.091	0.9376/33	241.4970
	15/391.34
	31/338.68
BH	12/88.70	127.6257/39.5077	128.4504/39.1168	9.19	0.404	0.9358/18	241.5142
	15/333.88
	31/362.48
CGA	12/76.31	127.5192/39.5582	127.6041/39.5180	9.27	0.044	0.9376/33	241.4996
	15/370.19
	31/338.64
40% penetration
MVO	12/409.59	90.3771/57.1629	90.3777/57.1626	10.73	0.001	0.9594/33	176.5392
	15/397.41
	31/763.40
PSO	12/410.02	90.3771/57.1629	90.7890/56.9677	11.47	1.159	0.9594/33	176.5392
	15/397.60
	31/762.78
ALO	12/429.24	90.3861/57.1586	90.5850/57.0644	17.30	0.218	0.9591/33	176.5422
	15/388.74
	31/752.38
BH	12/348.19	90.5000/57.1047	91.7172/56.5277	9.04	0.777	0.9594/33	176.7536
	15/455.18
	31/764.43
CGA	12/432.88	90.4019/57.1511	90.4811/57.1136	9.48	0.053	0.9591/33	176.5933
	15/384.37
	31/752.48
60% penetration
MVO	12/596.31	85.7789/59.3423	85.7789/59.3423	10.68	6.11 × 10−7	0.9700/33	144.2656
	15/397.76
	31/980.31
PSO	12/596.32	85.7789/59.3423	85.7789/59.3423	6.63	8.00 × 10−6	0.9700/33	144.2657
	15/397.74
	31/980.32
ALO	12/604.99	85.7813/59.3412	86.0098/59.2329	18.03	0.347	0.9699/33	144.6453
	15/388.35
	31/976.24
BH	12/598.86	85.8045/59.3302	86.3709/59.0618	9.80	0.607	0.9694/33	146.3655
	15/380.11
	31/968.85
CGA	12/594.56	85.7803/59.3417	85.7999/59.3324	10.07	0.017	0.9699/33	144.7778
	15/395.17
	31/978.16

,

Table 9. Simulation results in the 69-node radial test system.

69-Node Radial Test System
Method	Node/ Power [kW]	Power Losses				Vworst [p.u]/ Node	Imax [A]
		Minimum [kW]/ Reduction [%]	Average [kW]/ Reduction [%]	Time [s]	STD [%]
Without DGs	—	242.1523	—	—	—	0.9–1.1	400
20% penetration
MVO	26/0.01	133.56324/44.8433	133.56871/44.8410	44.84	0.003	0.9385/69	252.5817
	61/583.13
	66/243.43
PSO	26/0	133.56262/44.8435	134.15470/44.5990	57.16	1.502	0.9385/69	252.5817
	61/580.16
	66/246.41
ALO	26/0	133.63334/44.8143	134.60680/44.4123	76.89	0.579	0.9390/69	252.6323
	61/546.38
	66/279.62
BH	26/9.55	133.94677/44.6849	137.80535/43.0915	38.64	1.499	0.9378/69	252.6825
	61/595.61
	66/220.52
CGA	26/4.08	133.69225/44.7900	134.20074/44.5800	43.18	0.165	0.9381/69	252.5921
	61/595.66
	66/226.83
40% penetration
MVO	26/152.51	86.45738/64.2963	86.45854/64.2958	45.11	0.002	0.9638/69	183.5712
	61/1253.71
	66/246.91
PSO	26/152.72	86.45736/64.2963	86.64928/64.2170	56.62	0.664	0.9638/69	183.5711
	61/1252.84
	66/247.57
ALO	26/152.77	86.48174/64.2862	87.06582/64.0450	81.02	0.626	0.9639/69	183.6309
	61/1243.67
	66/255.96
BH	26/208.65	86.98184/64.0797	90.47858/62.6357	45.23	1.924	0.9632/69	183.9434
	61/1110.03
	66/330.27
CGA	26/144.73	86.46711/64.2923	86.60059/64.2371	37.99	0.097	0.9638/69	183.5754
	61/1274.50
	66/233.87
60% penetration
MVO	26/382.16	76.95778/68.2193	76.95778/68.2193	44.49	1.31 × 10${}^{-6}$	0.9784/69	134.0951
	61/1641.63
	66/246.21
PSO	26/382.17	76.95778/68.2193	76.95778/68.2193	55.59	1.46 × 10${}^{-8}$	0.9784/69	134.0926
	61/1641.64
	66/246.23
ALO	26/386.59	76.95931/68.2186	77.39068/68.0405	86.72	0.741	0.9785/69	133.6689
	61/1637.61
	66/251.20
BH	26/358.03	76.99856/68.2024	79.07191/67.3462	43.35	1.824	0.9778/69	136.5195
	61/1653.47
	66/227.85
CGA	26/382.31	76.95929/68.2186	76.98586/68.2077	38.06	0.024	0.9784/69	134.4437
	61/1629.83
	66/253.45

,

Table 10. Simulation results in the 10-node mesh test system.

10-Node Mesh Test System
Method	Node/ Power [kW]	Power Losses				Vworst [p.u]/ Node	Imax [A]
		Minimum [kW]/ Reduction [%]	Average [kW]/ Reduction [%]	Time [s]	STD [%]
Without DGs	—	190.3237	—	—	—	0.9–1.1	590
20% penetration
MVO	5/0	104.7510/44.9617	104.7540/44.9601	4.09	0.002	0.9793/8	433.0907
	9/1039.96
	10/1471.71
PSO	5/0.02	104.7511/44.9616	105.3226/44.6613	4.72	1.807	0.9793/8	433.0907
	9/1038.24
	10/1473.40
ALO	5/32.05	104.7986/44.9367	105.0366/44.8116	6.53	0.180	0.9793/8	433.1153
	9/1012.16
	10/1466.94
BH	5/1.87	104.9699/44.8467	105.9958/44.3076	3.48	0.538	0.9793/8	433.4899
	9/1037.61
	10/1463.23
CGA	5/18.12	104.8075/44.9320	105.0660/44.7962	3.40	0.117	0.9793/8	433.1163
	9/1087.18
	10/1405.83
40% penetration
MVO	5/586.03	58.4855/69.2705	58.4882/69.2691	3.81	0.006	0.9838/7	321.8764
	9/1224.24
	10/3213.06
PSO	5/611.96	58.4859/69.2703	64.6277/66.0433	4.38	24.212	0.9838/7	321.8764
	9/1227.34
	10/3184.03
ALO	5/526.13	58.4985/69.2637	58.6598/69.1789	6.37	0.291	0.9838/7	321.9142
	9/1215.08
	10/3281.26
BH	5/1253.67	58.6297/69.1947	60.1293/68.4068	3.45	1.223	0.9838/7	321.8891
	9/1241.74
	10/2527.77
CGA	5/813.33	58.5195/69.2526	58.6400/69.1894	3.44	0.137	0.9838/7	321.8762
	9/1215.85
	10/2994.17
60% penetration
MVO	5/2440.87	39.3867/79.3054	39.3874/79.3050	3.88	0.002	0.9874/6	211.8432
	9/1396.49
	10/3697.63
PSO	5/2448.40	39.3867/79.3054	40.7435/78.5925	4.31	10.312	0.9874/6	211.8432
	9/1396.09
	10/3690.50
ALO	5/2445.34	39.3976/79.2997	39.6632/79.1601	6.56	0.690	0.9874/6	212.0355
	9/1399.98
	10/3685.25
BH	5/3065.27	39.5207/79.2350	40.6407/78.6465	3.40	1.577	0.9873/6	212.0846
	9/1368.25
	10/3096.05
CGA	5/2378.87	39.3908/79.3033	39.4689/79.2622	3.56	0.104	0.9874/6	211.8915
	9/1399.13
	10/3755.89

presents the electrical parameters of this system.

6. Simulations and Results

This section discusses the results obtained by each optimization algorithm used to solve the OPF problem in the four test systems mentioned above. All the simulations were performed in Matlab^® (version 2021b), a numerical computing system, running on a laptop with 4 GB of RAM, an Intel^® Core^TM i5-8250U @1.60 GHz 1.80 GHz processor, a 225-GB solid-state drive, and Windows 10 PRO. To guarantee the same conditions and evaluate the repeatability and precision of each solution technique, the codes were executed 100 times. The following subsections present the results obtained in each radial and mesh test system.

6.1. Results in the Radial Test Systems

This subsection presents and analyzes the results obtained in each radial system used as test scenario.

6.1.1. 10-Node Radial Test System

Table 7 reports the results obtained by each optimization algorithm after performing the simulations in the 10-node radial system at three levels of distributed generation penetration: 20%, 40%, and 60% of the power supplied by the slack generator. From left to right, this table details the optimization algorithm implemented; the node where the DGs are located and the power that each one of them injects into the system in kW; the minimum power losses ($P_{loss}$) in kW and the percentage of reduction with respect to the base case (%); the average $P_{loss}$ in kW and the percentage of reduction with respect to the base case (%); the computation time required by each technique to obtain the solution (s); the standard deviation of each optimization technique (%); the worst voltage profile (p.u) and the node where it occurs; and the maximum current in the electrical system (A). Additionally, the $P_{loss}$ in the base case (system without DGs), i.e., $223.4181$ kW, are shown in the upper part of the table.

Table 7 compares the results obtained by the five optimization algorithms employed to solve the OPF problem in the 10-node system. Figure 6 and Figure 7, which were constructed based on such results, illustrate the differences between these algorithms in terms of reduction of minimum and average power losses.

Figure 6 compares the reduction of minimum $P_{loss}$ obtained by each algorithm at the three penetration levels: 20%, 40%, and 60%. Considering that the MVO is the base scenario, this figure presents the reduction percentage obtained by the MVO in comparison to the other optimization algorithms. The number in red indicates that the proposed MVO was outperformed by the PSO. At 20% penetration, the MVO achieved a reduction of $47.6667\%$, which was outperformed by the PSO by 0.0001% but was better than those of the ALO, CGA, and BH by 0.0113%, 0.0535%, and 0.4486%, respectively. At 40% penetration, the MVO and PSO obtained a reduction percentage of 63.8522%, outperforming the CGA by 0.0089%, ALO by 0.0140%, and BH by 0.0965%. At 60% penetration, the MVO and PSO exhibited the same reduction, i.e., 67.7170%, thus outperforming ALO, the CGA, and BH by 0.0021%, 0.0038%, and 0.0107%, respectively.

Figure 7 compares the reduction of average $P_{loss}$ obtained by the optimization techniques at the three penetration levels: 20%, 40%, and 60% of the power provided by the slack generator in the base case. As in Figure 6, this figure presents the MVO as the base scenario. At 20% penetration, the MVO achieved the best reduction, i.e., 47.6654%, thus outperforming PSO by 0.1284%, the CGA by 0.2484%, ALO by 0.4448%, and BH by 2.0591%. At 40% penetration, the MVO obtained the best reduction of average $P_{loss}$, outperforming PSO, the CGA, ALO, and BH by 0.0969%, 0.1100%, 0.4888%, and 0.7498%, respectively. At 60% penetration, the MVO and PSO exhibited the best reduction of average $P_{loss}$, i.e., 67.7170%, thus outperforming ALO (in the third place) by 0.0021%, the CGA (fourth place) by $0.0038\%$, and BH (fifth place) by $0.0107\%$.

To complete the analysis of the 10-node system, Figure 8, which was created based on the results presented in Table 7, compares the standard deviation obtained by the optimization techniques at the three penetration levels: $20\%$, $40\%$, and $60\%$. At $20\%$ penetration, the MVO presented the best standard deviation, i.e., $0.005\%$, thus outperforming the CGA by $0.1685\%$, ALO by $0.7162\%$, PSO by $1.3230\%$, and BH by $1.7415\%$. At $40\%$ penetration, the MVO exhibited the best standard deviation, outperforming the other optimization algorithms by an average percentage of $0.9915\%$. At $60\%$ penetration, the MVO and PSO obtained standard deviations of $9.4\times {10}^{-7}$ and $1.22\times {10}^{-8}$, respectively; thus, the MVO outperformed the CGA by $0.0610\%$, BH by $1.1291\%$, and ALO by $1.6134\%$. This demonstrates that, when evaluated in small networks, the MVO produces excellent results in terms of the repeatability of the solution.

According to these results, the MVO has excellent precision and repeatability, which guarantees that a good quality solution is obtained every time it is executed. Moreover, it can be concluded that the MVO is the most appropriate technique to solve the OPF problem in small AC networks, as it ensures that a good quality solution is found in a relatively short time in any distributed generation scenario.

6.1.2. 33-Node Radial Test System

Table 8, which is organized in the same way as Table 7, reports the results of the simulations performed in the 33-node system after the algorithms were executed 100 times to solve the OPF problem. Importantly, the $P_{loss}$ in the base case were $210.9785$ kW, as shown in Table 8. The same as with the 10-node system above, Figure 9, Figure 10 and Figure 11 compare the minimum $P_{loss}$, average $P_{loss}$, and standard deviation, respectively, obtained by each algorithm at the three penetration levels (i.e., $20\%$, $40\%$, and $60\%$).

Figure 9 shows the reduction of minimum $P_{loss}$ obtained by each optimization method in the 33-node radial system at the three penetration levels. At $20\%$ penetration, the MVO and PSO achieved the same reduction of minimum $P_{loss}$ with respect to the base case, i.e., $39.5681\%$, thus outperforming ALO by $0.0021\%$, the CGA by $0.0098\%$, and BH by $0.0603\%$. At $40\%$ penetration, the MVO and PSO exhibited the same reduction percentage, i.e., $57.1629\%$, thus outperforming ALO by $0.0043\%$, the CGA by $0.0118\%$, and BH by $0.582\%$. At $60\%$ penetration, the MVO and PSO obtained the same reduction percentage once again, i.e., $59.3423\%$, thus outperforming ALO, the CGA, and BH by $0.0007$, $0.0011\%$, and $0.0121\%$, respectively.

Considering that the MVO is the base scenario, Figure 10 reports the differences in the reductions of average $P_{loss}$ obtained by the MVO and the other optimization algorithms at the three penetration levels. At $20\%$ penetration, the MVO presented a reduction of average $P_{loss}$ of $39.5676\%$, outperforming the CGA (in the second place) by $0.0496\%$, ALO (third place) by $0.0605\%$, PSO (fourth place) by $0.1857\%$, and BH (fifth place) by $0.4508\%$. At $40\%$ penetration, the MVO exhibited the best reduction of average $P_{loss}$, i.e., $57.1626\%$, thus outperforming the other algorithms by an average percentage of $0.2443\%$. At $60\%$ penetration, both the MVO and PSO achieved a reduction of $59.3423\%$, outperforming the CGA by $0.0100\%$, ALO by $0.1094\%$, and BH by $0.2806\%$.

To complete the analysis of the 33-node system, Figure 11 illustrates the standard deviation obtained by each technique used to solve the OPF problem in AC networks. As can be seen in this figure, the MVO is superior to the other optimization algorithms in each distributed generation scenario. At $20\%$ penetration, the MVO presented a standard deviation of $0.001\%$, outperforming the CGA by $0.0430\%$, ALO by $0.0901\%$, BH by $0.4034\%$, and PSO by $0.5231\%$. At $40\%$ penetration, the MVO exhibited the highest precision, with a standard deviation of $0.001\%$, outperforming the other optimization algorithms by an average percentage of $0.5510\%$. At $60\%$ penetration, the MVO obtained a standard deviation of $6.1\times {10}^{-7}\%$, thus outperforming PSO by $1\times {10}^{-5}\%$, the CGA by $0.0168\%$, ALO by $0.3471\%$, and BH by $0.6068\%$.

After a general analysis of these results, the MVO proves to be superior to the other algorithms in terms of standard deviation and precision, which guarantees that a good quality solution is obtained in a short computation time every time this algorithm is executed. Therefore, it can be concluded that the MVO is the technique that offers the best solution, in a short computation time, for medium-sized networks.

6.1.3. 69-Node Radial Test System

Table 9, which is organized in the same way as Table 7 and Table 8, presents the results obtained by the optimization algorithms used to solve the OPF problem in the 69-node radial test system.

The results reported in Table 9 were used to construct Figure 12, Figure 13 and Figure 14, which compare the minimum $P_{loss}$, average $P_{loss}$, and standard deviation, respectively, obtained by each optimization algorithm implemented here to solve the OPF problem in the 69-node radial test system. The same distributed generation scenarios considered in the 10- and 33-node radial networks above were employed for this system. Regarding minimum $P_{loss}$, Figure 12 shows the reduction obtained by the MVO in comparison to the other optimization algorithms. At $20\%$ penetration, the MVO presented a reduction of minimum $P_{loss}$ of $44.8433\%$ with respect to the base case, which was only outperformed by the PSO by $0.0003\%$ but was better than those of ALO, the CGA, and BH by $0.0289\%$, $0.0533\%$, and $0.1584\%$, respectively. At $40\%$ penetration, the MVO and PSO exhibited a reduction in minimum $P_{loss}$ of $64.2963\%$, thus outperforming the CGA by $0.0040\%$, ALO by $0.0101\%$, and BH by $0.2166\%$. At $60\%$ penetration, the MVO and PSO achieved a reduction of $68.2193\%$, outperforming ALO by $0.0006\%$, the CGA by $0.0006\%$, and BH by $0.0168\%$.

Figure 13 illustrates the differences in average $P_{loss}$ obtained by the MVO and the other optimization techniques. At $20\%$ penetration, the MVO achieved the best reduction of average $P_{loss}$, i.e., $44.8410\%$, thus outperforming the other optimization algorithms by an average percentage of $0.6703\%$. At $40\%$ penetration, the MVO exhibited the best reduction of average $P_{loss}$, i.e., $64.2958\%$, thus outperforming the CGA, PSO, ALO, and BH by $0.0587\%$, $0.0788\%$, $0.2508\%$, and $1.6601\%$, respectively. Finally, at $60\%$ penetration, the MVO and PSO presented the same reduction of average $P_{loss}$, i.e., $68.2193\%$, thus outperforming the CGA by $0.0116\%$, ALO by $0.1788\%$, and BH by $0.8731\%$.

To complete the analysis of the 69-node radial system, Figure 14 shows the standard deviation obtained by each optimization technique used to solve the OPF problem in in this network at the three penetration percentages. At $20\%$ penetration, the MVO presented a standard deviation of $0.003\%$, thus outperforming the other optimization algorithms by an average percentage of $0.9329\%$. At $40\%$ penetration, the MVO exhibited a standard deviation of $0.002\%$, thus outperforming the CGA, ALO, PSO, and BH by $0.0958\%$, $0.6241\%$, $1.6621\%$, and $1.9223\%$, respectively. Finally, at $60\%$ penetration, the MVO and PSO obtained standard deviations of $1.3\times {10}^{-6}$ and $1.5\times {10}^{-6}$, respectively; therefore, the MVO outperformed the CGA by $0.0237\%$, ALO by $0.7409\%$, and BH by $1.8238\%$.

These results demonstrate once again that the MVO is superior to the other techniques in terms of standard deviation, making it the most precise and appropriate method to solve the OPF problem in large AC networks because it guarantees that good quality solutions are obtained every time it is executed.

6.2. Results in the Mesh Test System

This section presents and analyzes the results obtained in the mesh system used as a test scenario.

10-Node Mesh Test System

Table 10 presents the results obtained by the optimization algorithms to solve the OPF problem in the 10-node mesh system after they were executed 100 times. The information appears in the same order as in Table 3, Table 4 and Table 5. Figure 15, Figure 16 and Figure 17 resulted from analyzing Table 10. These figures compare the results obtained by the optimization algorithms in terms of minimum $P_{loss}$, average $P_{loss}$, and standard deviation, respectively.

Figure 15 compares the results achieved by the optimization algorithms to obtain the minimum $P_{loss}$ in the 10-node mesh system with $20\%$, $40\%$, and $60\%$ penetration. In the figure mentioned, the y-axis denotes the improvement, in terms of minimum power loss reduction, obtained by the MVO compared to the other optimization algorithms; in turn, the x-axis specifies the methods used for comparison. At $20\%$ penetration, the MVO has the best reduction in minimum $P_{loss}$, outperforming PSO, ALO, the CGA, and BHO by $0.0001\%$, $0.0250\%$, $0.0296\%$, and $0.1150\%$, respectively. At $40\%$ penetration, the MVO presents a reduction in minimum $P_{loss}$ of $69.2705\%$, outperforming PSO by $0.0002\%$, ALO by $0.0068\%$, the CGA by $0.0179$, and BH by $0.0758\%$. Finally, at $60\%$ penetration, the MVO presents the best reduction in minimum $P_{loss}$ again, i.e., $79.3054\%$ (the same as that of PSO), thus outperforming the CGA by $0.0021\%$, ALO by $0.0057\%$, and BH by $0.0704\%$.

Figure 16 compares the average $P_{loss}$ obtained by the MVO and the other optimization algorithms in the 10-node mesh test system (with the MVO as the base case). This analysis was performed employing the same three penetration percentages as in Figure 15. At $20\%$ penetration, the MVO presents a reduction of average $P_{loss}$ of $44.9601\%$, outperforming ALO, the CGA, PSO, and BHO by $0.1485\%$, $0.1639\%$, $0.2987\%$, and $0.6524\%$, respectively. At $40\%$ penetration, the MVO exhibits a reduction of average $P_{loss}$ of $69.2691\%$, outperforming the other optimization algorithms by $1.0645\%$. At $60\%$ penetration, the MVO has the best reduction of average $P_{loss}$ again, outperforming the CGA, ALO, BHO, and PSO by $0.0428\%$, $0.1449\%$, $0.6585\%$, and $0.7125\%$, respectively.

To conduct the analysis of the mesh system, the precision and repeatability of all the algorithms are compared in Figure 17. As with the minimum and average $P_{loss}$, the standard deviation is assessed with $20\%$, $40\%$, and $60\%$ penetration. In the first case, the MVO presents an outstanding standard deviation of $0.002\%$, outperforming the CGA by $0.1152\%$, ALO by $0.1775\%$, BH by $0.5359\%$, and PSO by $1.8050\%$. In a $40\%$ penetration scenario, the MVO has a standard deviation of $0.006\%$, outperforming the other optimization algorithms by a significant average of $6.46\%$. Finally, at $60\%$ penetration, the MVO presents an outstanding solution precision with a standard deviation of $0.002\%$, outperforming the CGA by $0.1026\%$, ALO by $0.6884\%$, BH by $1.5748$, and PSO by $10.3097\%$.

Analyzing the results obtained and discussed in this section, it is possible to note that, in general, the MVO provides the best solution. It offers an outstanding solution quality, short processing time, and a good standard deviation; as a result, it finds an excellent solution every time the algorithm is run. Therefore, the MVO is the most suitable optimization methodology to solve the OPF problem in AC networks of any type and size.

7. Conclusions

In this paper, we proposed the implementation of the MVO to solve the OPF problem in AC networks using a master–slave methodology. The master stage uses the MVO to determine the optimal power to be injected by each DG in the AC network. The slave stage employs SA (a numerical method) to assess the impact of every solution provided by the master stage on the objective function and the constraints of the problem. In order to demonstrate the robustness of the proposed algorithm, it was compared with some of the best optimization techniques that have been reported in the specialized literature to solve the OPF problem in AC networks: PSO, ALO, BH, and the CGA. All the algorithms employed in this study were tuned so that they could find the best solution to the OPF problem. To test each algorithm, the simulations were performed in the 10-, 33-, and 69-node radial systems and the 10-node mesh system using three levels of distributed generation penetration: $20\%$, $40\%$, and $60\%$ of the power supplied by the slack generator in the base case. Moreover, each algorithm was executed 100 times to evaluate its standard deviation and precision.

According to the results in radial systems, the MVO obtained the best solution regarding the reduction of average $P_{loss}$ in an adequate computation time and presented the lowest standard deviation. Moreover, in most cases, the MVO achieved the best percentage of reduction of minimum $P_{loss}$, although it was outperformed only by PSO by an almost negligible difference in the 10- and 69-node radial systems at a $20\%$ penetration level. In terms of repeatability, the MVO presented low standard deviations (its highest value was $1\times {10}^{-3}$) and outperformed most of the other optimization techniques in the different test scenarios. Thus, this technique proves to be efficient in terms of precision and repeatability, obtaining good quality solutions to the OPF problem every time the algorithm is executed.

In the mesh topology, the MVO algorithm obtained the best solution in all the scenarios of distributed generation evaluated in this study, reducing minimum power losses by $0.029\%$ and average power losses by $0.59\%$ with respect to the other methods used here for comparison. The MVO achieved these results in a short processing time with the lowest standard deviation (under $0.006\%$). This proves its efficiency in terms of solution quality and processing times, as well as the repeatability of its solutions. Therefore, the MVO obtains a good-quality solution to the OPF problem in AC mesh networks every time its algorithm is run. From the paragraphs above, it is possible to conclude that the MVO is the best strategy to solve the OPF problem in mesh or radial AC networks.

Future studies can use this methodology for optimal power management in mesh or radial AC networks by employing power dispatch in energy storage devices and power loads considering their behavior in a 24-h cycle. This methodology can also be implemented in the planning of AC electrical systems to size distributed energy resources (generators, reactive elements, and energy storage) when the objective functions are to reduce the operating cost of the network, minimize CO₂ emissions, and improve the operating conditions. Finally, to reduce processing times and use parallel processing tools, future research can propose a parallel version of this methodology to shorten the processing times of the individuals that compose the populations at each iteration. This would considerably reduce the total processing times of the method.