Gain and Phase Calibration of Uniform Rectangular Arrays Based on Convex Optimization and Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ng, B.P.; Lie, J.P.; Er, M.H.; Feng, A. A Practical Simple Geometry and Gain/Phase Calibration Technique for Antenna Array Processing. IEEE Trans. Antennas Propag. 2009, 57, 1963–1972. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Er, M.H. Theoretical analyses of gain and phase error calibration with optimal implementation for linear equispaced array. IEEE Trans. Signal Process. 2006, 54, 712–723. [Google Scholar] [CrossRef]
- Yuan, L.; Jiang, R.; Chen, Y. Gain and Phase Autocalibration of Large Uniform Rectangular Arrays for Underwater 3-D Sonar Imaging Systems. IEEE J. Ocean. Eng. 2014, 39, 458–471. [Google Scholar] [CrossRef]
- Terada, T.; Nishimura, T.; Ogawa, Y.; Ohgane, T.; Yamada, H. DOA Estimation for Multi-Band Signal Sources Using Compressed Sensing Techniques with Khatri-Rao Processing. IEICE Trans. Commun. 2014, E97.B, 2110–2117. [Google Scholar] [CrossRef] [Green Version]
- Ogut, M.; Bosch-Lluis, X.; Reising, S.C. Deep Learning Calibration of the High-Frequency Airborne Microwave and Millimeter-Wave Radiometer (HAMMR) Instrument. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3391–3399. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, A.; Chen, X.; Wang, P.; Wang, Y.; Yang, H. A Deep Learning Approach for Blind Drift Calibration of Sensor Networks. IEEE Sens. J. 2017, 17, 4158–4171. [Google Scholar] [CrossRef] [Green Version]
- Goodman, J.; Salmond, D.; Davis, C.; Acosta, C. Ambiguity Resolution in Direction of Arrival Estimation using Mixed Integer Optimization and Deep Learning. In Proceedings of the 2019 IEEE National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 15–19 July 2019; pp. 317–322. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Thanthrige, U.S.K.P.M.; El Gamal, A.; Sezgin, A. Deep Learning for DOA Estimation in MIMO Radar Systems via Emulation of Large Antenna Arrays. IEEE Commun. Lett. 2021, 25, 1559–1563. [Google Scholar] [CrossRef]
- CVX: MATLAB Software for Disciplined Convex Programming. Available online: http://cvxr.com/cvx/ (accessed on 8 August 2021).
- Tütüncü, R.H.; Toh, K.C.; Todd, M.J. Solving semidefinite-quadratic-linear programs using SDPT3. Math. Program. 2003, 95, 189–207. [Google Scholar] [CrossRef]
- Helmberg, C.; Rendl, F.; Vanderbei, R.J.; Wolkowicz, H. An Interior-Point Method for Semidefinite Programming. SIAM J. Optim. 1996, 6, 342–361. [Google Scholar] [CrossRef]
- Kojima, M.; Shindoh, S.; Hara, S. Interior-Point Methods for the Monotone Semidefinite Linear Complementarity Problem in Symmetric Matrices. SIAM J. Optim. 1997, 7, 86–125. [Google Scholar] [CrossRef]
- Monteiro, R.D.C. Primal-Dual Path-Following Algorithms for Semidefinite Programming. SIAM J. Optim. 1997, 7, 663–678. [Google Scholar] [CrossRef] [Green Version]
- Nesterov, Y.E.; Todd, M.J. Self-Scaled Barriers and Interior-Point Methods for Convex Programming. Math. Oper. Res. 1997, 22, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Mehrotra, S. On the Implementation of a Primal-Dual Interior Point Method. SIAM J. Optim. 1992, 2, 575–601. [Google Scholar] [CrossRef]

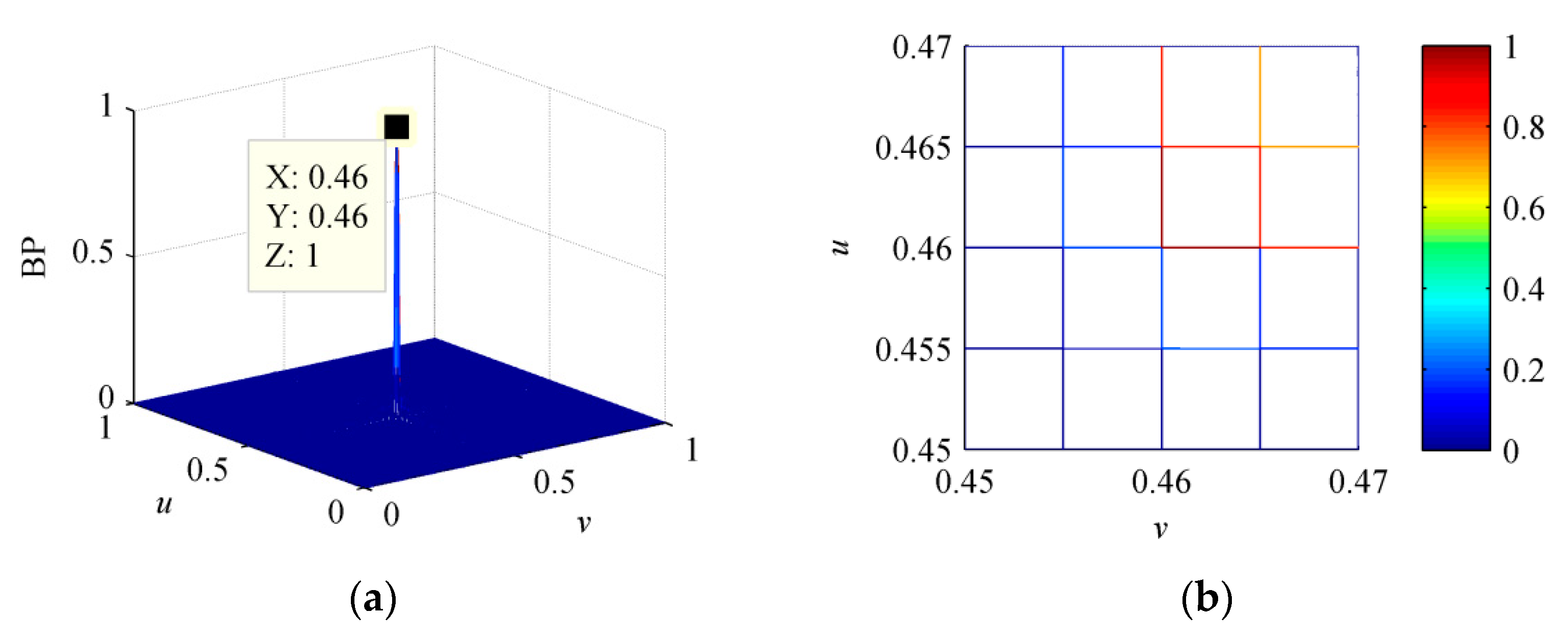





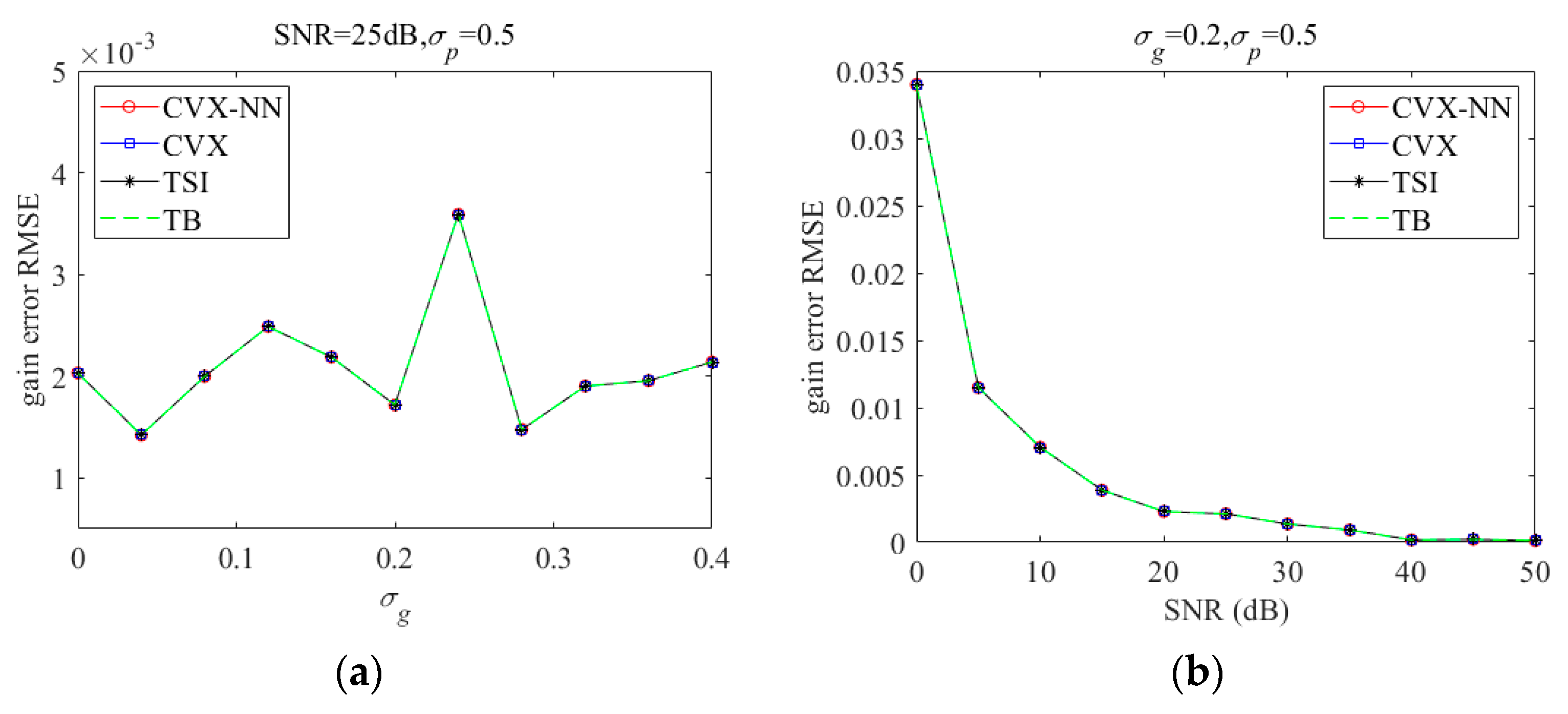
| Sensor Index | Gain Error Value (Normalized) | Phase Error Value (Rad) | ||
|---|---|---|---|---|
| Actual | Estimated | Actual | Estimated | |
| (1, 1) | 1.1380 | 1.1413 | −0.3866 | −0.3847 |
| (5, 5) | 0.8205 | 0.8227 | −0.4081 | −0.4093 |
| (10, 10) | 1.1534 | 1.1551 | −0.5294 | −0.5278 |
| (15, 15) | 0.9586 | 0.9600 | −1.0722 | −1.0712 |
| (20, 20) | 0.8177 | 0.8188 | −1.0361 | −1.0358 |
| (25, 25) | 1.0000 | 1.0000 | 0.0000 | 0.0000 |
| (30, 30) | 1.1298 | 1.1311 | −0.5637 | −0.5655 |
| (35, 35) | 0.6254 | 0.6261 | −0.3143 | −0.3129 |
| (40, 40) | 0.9555 | 0.9581 | 0.6357 | 0.6322 |
| (45, 45) | 1.1451 | 1.1459 | −0.2079 | −0.2127 |
| (50, 50) | 0.7934 | 0.7933 | 0.9309 | 0.9260 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jie, X.; Zheng, B.; Gu, B. Gain and Phase Calibration of Uniform Rectangular Arrays Based on Convex Optimization and Neural Networks. Electronics 2022, 11, 718. https://doi.org/10.3390/electronics11050718
Jie X, Zheng B, Gu B. Gain and Phase Calibration of Uniform Rectangular Arrays Based on Convex Optimization and Neural Networks. Electronics. 2022; 11(5):718. https://doi.org/10.3390/electronics11050718
Chicago/Turabian StyleJie, Xiran, Bolun Zheng, and Boxuan Gu. 2022. "Gain and Phase Calibration of Uniform Rectangular Arrays Based on Convex Optimization and Neural Networks" Electronics 11, no. 5: 718. https://doi.org/10.3390/electronics11050718
APA StyleJie, X., Zheng, B., & Gu, B. (2022). Gain and Phase Calibration of Uniform Rectangular Arrays Based on Convex Optimization and Neural Networks. Electronics, 11(5), 718. https://doi.org/10.3390/electronics11050718






