A Gradually Linearizing Kalman Filter Bank Designing for Product-Type Strong Nonlinear Systems
Abstract
:1. Introduction
2. A Strong Tracking Filter (STF) Method for Joint Estimation of the State and Parameters in a Nonlinear System
2.1. Description of Nonlinear Systems with Real Varying Parameters to Be Estimated
2.2. Design of STF for Joint Estimation of State and Parameter in the Nonlinear System
- (1)
- A strong tracking filter (STF) is composed of Equations (14)–(27), whenin Equation (19), and STF degenerates the traditional EKF.
- (2)
- The nonlinear functions in Equations (1) and (2) degenerate into the following:
3. A Class of Nonlinear Systems Described by the Product of States, Parameters and Nonlinear Functions
3.1. Description of Non-Linear System
3.2. Gradually Linearizing of the Strongly Nonlinear Systems
4. The Design of Three-Stage Kalman Filter for Estimating State, Parameters and Hidden Variables
4.1. The Linear Kalman Filter Design for Solving Hidden Variables
The Design of the Linear Kalman Filter to Estimate Value of the Hidden Variable
4.2. The Design of Linear Kalman Filter for Solving Parameters
The Design of Linear Filter for the Estimated Value of Parameter Variable
4.3. The Linear Kalman Filter Design for Solving State Variables
The Linear Filter Design of State Variable Estimates
5. Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, S.; Liu, W.; Cui, H. Multiple resolvable groups tracking using the GLMB filter. Acta Autom. Sin. 2017, 43, 2178–2189. [Google Scholar]
- Hu, Y.; Jin, Z.; Xue, X.; Sun, C. Fault diagnosis for networked systems by asynchronous IMM fusion filtering. Acta Autom. Sin. 2017, 43, 1329–1338. [Google Scholar]
- Thomas, C.; Thach, N.D.; Julien, M.; Wang, Z.; Tarek, R. Zonotopic Kalman Filter-Based Interval Estimation for Discrete-Time Linear Systems With Unknown Inputs. IEEE Control Syst. Lett. 2022, 6, 806–811. [Google Scholar]
- Shen, T.; Xue, A.; Zhou, Z. Multi-sensor Gaussian mixture PHD fusion for multi-target tracking. Acta Autom. Sin. 2017, 43, 1028–1037. [Google Scholar]
- Liu, J.; Sun, L.; Pu, J.; Hu, Z.; Wang, Y. Cooperative Localization in a Team of Two Mobile Robots Based on Rigid Constraints. Acta Electron. Sin. 2020, 48, 1777–1785. [Google Scholar]
- Alfakih, M.; Keche, M.; Benoudnine, H. A Kalman-filter-based fusion method for accurate urban localisation. IET Commun. 2021, 15, 653–663. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filter and prediction. Trans. ASME Ser. D J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Qiao, S.; Han, N.; Zhu, X.; Shu, H. A Dynamic Trajectory Prediction Algorithm Based on Kalman Filter. Acta Electron. Sin. 2018, 46, 418–423. [Google Scholar]
- Wang, X. Power Systems Dynamic State Estimation With the Two-Step Fault Tolerant Extended Kalman Filtering. IEEE Acesses 2021, 9, 137211–137223. [Google Scholar] [CrossRef]
- Li, H.; Zhao, S. The Optimal Distributed Kalman Filtering Fusion With Linear Equality Contraint. IEEE Acesses 2021, 9, 106283–106292. [Google Scholar] [CrossRef]
- Wen, C.; Cheng, X.; Xu, D.; Wen, C. Filter design based on characteristic functions for one class of multi-dimensional nonlinear non-Gaussian systems. Automatica 2017, 82, 171–180. [Google Scholar] [CrossRef]
- Wen, C.; Wang, Z.; Hu, J.; Liu, Q.; Fuad, E.A. Recursive filtering for state-saturated systems with randomly occurring nonlinearities and missing measurements. Int. J. Robust Nonlinearity Control 2018, 28, 1715–1727. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Sunahara, Y. An approximate method of state estimation for nonlinear dynamical systems. Fluids Eng. 1970, 11, 957–972. [Google Scholar] [CrossRef]
- Guo, H.; Chen, H.; Xu, F.; Wang, F.; Lu, G. Implementation of EKF for vehicle velocities estimation on FPGA. IEEE Trans. Ind. Electron. 2013, 60, 3823–3835. [Google Scholar] [CrossRef]
- Ye, S.; Daniel, B.W. Scaling the Kalman filter for large-scale traffic estimation. IEEE Trans. Control Netw. Syst. 2018, 5, 968–980. [Google Scholar]
- Zhao, J.; Marcos, N.; Lamine, M. A robust iterated extended Kalman filter for power system dyamic state estimation. IEEE Trans. Power Syst. 2017, 32, 3205–3216. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef] [Green Version]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef] [Green Version]
- Arasaratnam, I.; Haykin, S. Square-root quadrature Kalman filtering. IEEE Trans Signal Process. 2008, 56, 2589–2593. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, J. Nonlinear Filtering Based Joint Estimation of Parameters in Polynomial Systems. In Proceedings of the 26th China Control and Decision Conference, Changsha, China, 31 July 2014. [Google Scholar]
- Wen, C.; Chen, Z.; Zhou, D. Joint State and Parameter Estimation for Multisensor Nonlinear Dynamic Systems on the Basis of Strong Tracking Filter. Acta Electron. Sin. 2002, 30, 1715–1717. [Google Scholar]
- Sun, X.; Wen, C.; Wen, T. Maximum Correntropy High-Order Extended Kalman Filter. Chin. J. Electron. 2022, 31, 190–198. [Google Scholar] [CrossRef]
- Sun, X.; Wen, C.; Wen, T. A Novel Step-by-Step High-Order Extended Kalman Filter Design for a Class of Complex Systems with Multiple Basic Multipliers. Chin. J. Electron. 2021, 30, 313–321. [Google Scholar] [CrossRef]
- Sun, X.; Wen, C.; Wen, T. High-Order Extended Kalman Filter Design for a Class of Complex Dynamic Systems with Polynomial Nonlinearities. Chin. J. Electron. 2021, 30, 508–515. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, X.; Wen, C. Design Method for a Higher Order Extended Kalman Filter Based on Maximum Correlation Entropy and a Taylor Network System. Sensors 2021, 21, 5864. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wen, C.; Sun, X. Design Method of High-Order Kalman Filter for Strong Nonlinear System Based on Kronecker Product Transform. Sensors 2022, 22, 653. [Google Scholar] [CrossRef] [PubMed]
- Wen, T.; Xie, G.; Cao, Y.; Cai, B. A DNN-Based Channel Model for Network Planning in Train Control Systems. IEEE Trans. Intell. Transp. Syst. 2021, 1–8. [Google Scholar] [CrossRef]
- Kong, Y.; Ma, X.; Wen, C. A New Method of Deep Convolutional Neural Network Image Classification Based on Knowledge Transfer in Small Label Sample Environment. Sensors 2022, 22, 898. [Google Scholar] [CrossRef]
- Ye, L.; Ma, X.; Wen, C. Rotating Machinery Fault Diagnosis Method by Combining Time-Frequency Domain Features and CNN Knowledge Transfer. Sensor 2021, 21, 8168. [Google Scholar] [CrossRef]
- Ma, X.; Wen, C.; Wen, T. An Asynchronous and Real-time Update Paradigm of Federated Learning for Fault Diagnosis. IEEE Trans. Ind. Inform. 2021, 17, 8531–8540. [Google Scholar] [CrossRef]
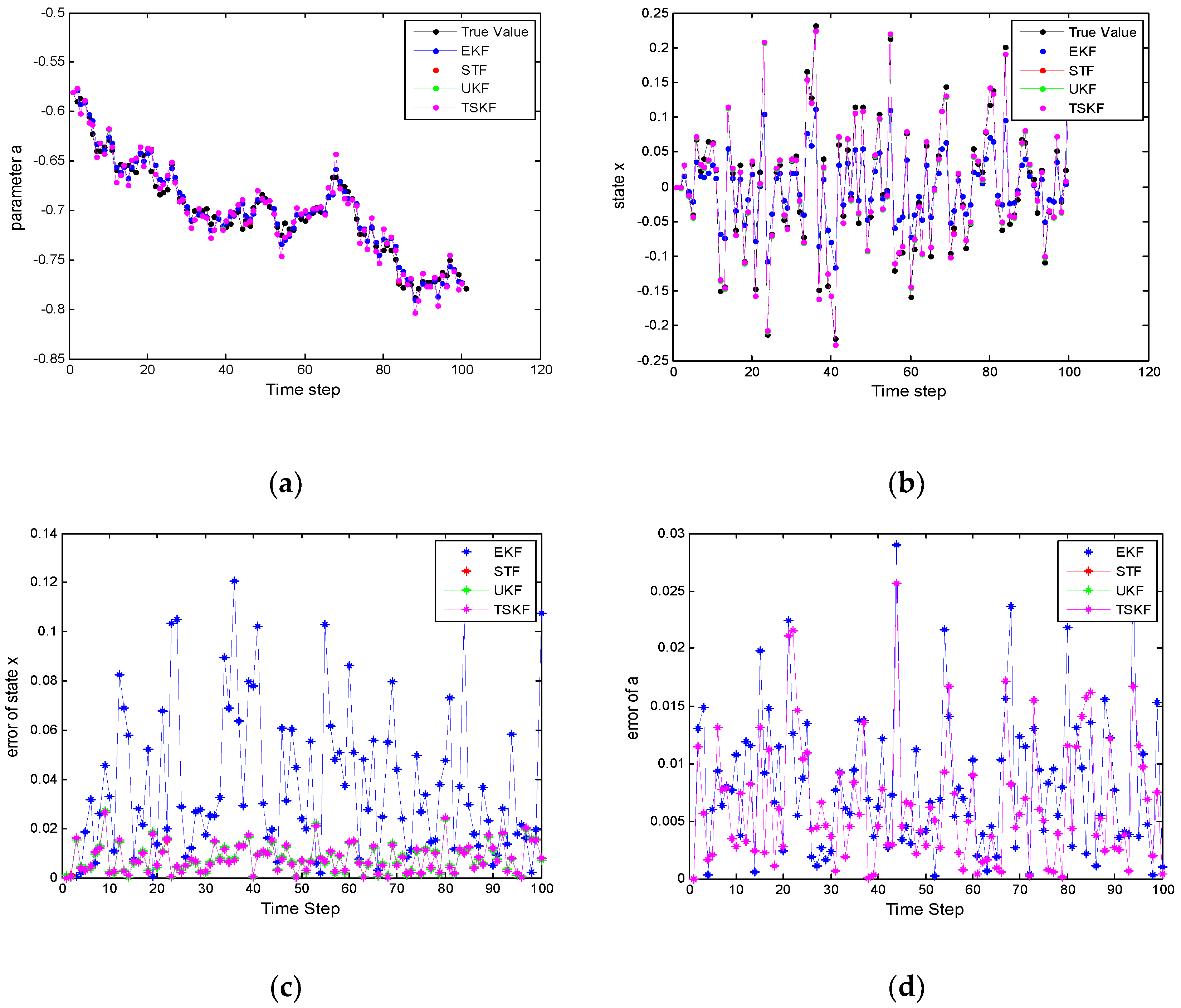
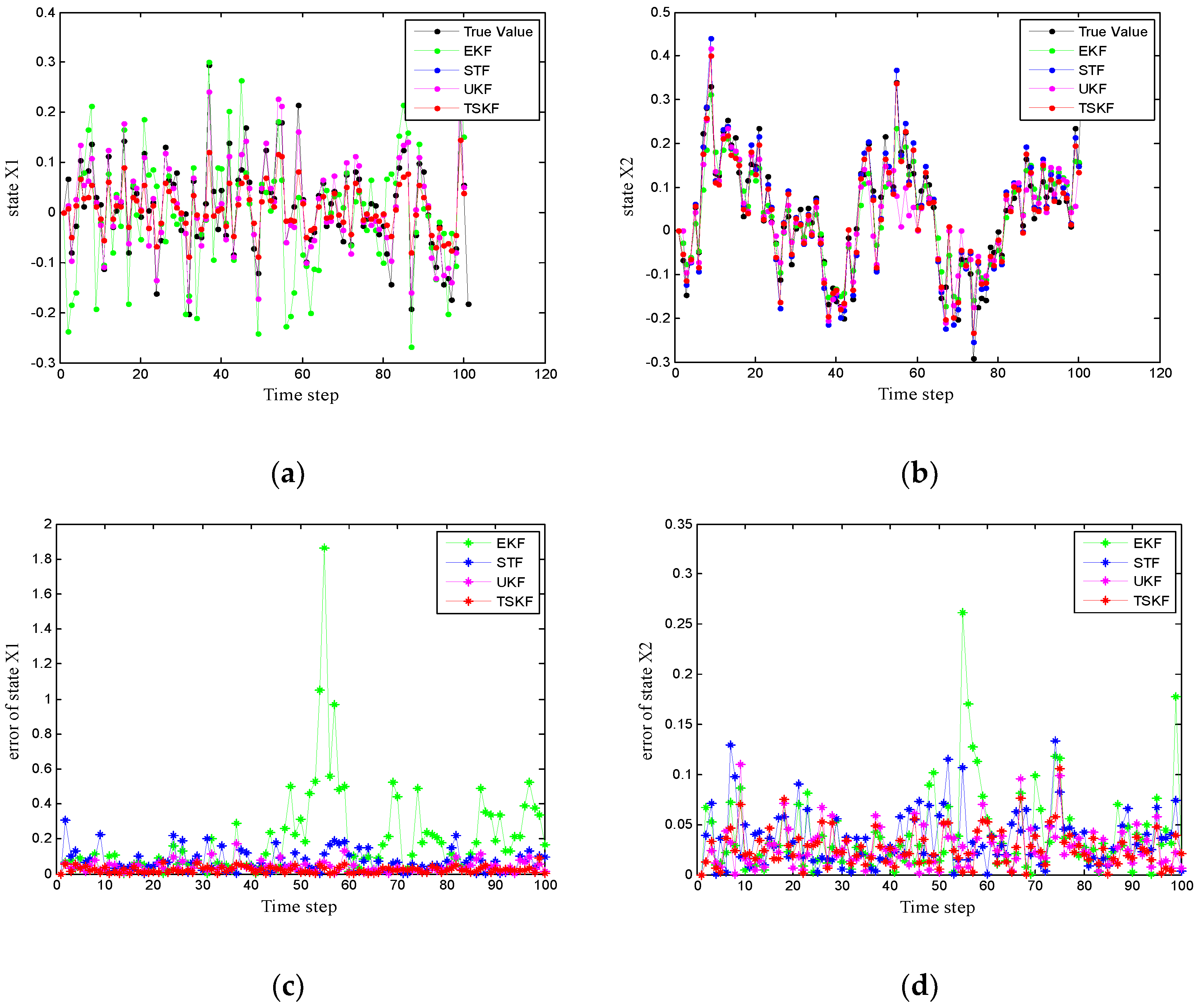

| Kalman Filter | Extended Kalman Filter | Strong Tracking Filter | Unscented Kalman Filter | Three Stage-Kalman Filter |
| Abbreviation | EKF | STF | UKF | TSKF |
| MSE | EKF | STF | UKF | TSKF | VS EKF | VS STF | VS UKF | |
|---|---|---|---|---|---|---|---|---|
| state | 0.0065 | 0.0063 | 3.3783 × 10−4 | 1.6557 × 10−4 | 97.4528% | 97.3719% | 50.9901% | |
| parameter | 0.0225 | 1.4868 × 10−4 | 1.0504 × 10−4 | 8.7584 × 10−5 | 99.6107% | 41.0923% | 16.6184% |
| MSE | EKF | STF | UKF | TSKF | VS EKF | VS STF | VS UKF | |
|---|---|---|---|---|---|---|---|---|
| state | 0.0091 | 0.0076 | 0.0024 | 0.0010 | 89.0110% | 86.8421% | 58.3333% | |
| 0.0035 | 0.0019 | 9.9575 × 10−4 | 8.8605 × 10−4 | 74.6843% | 53.3658% | 11.0168% |
| MSE | EKF | STF | UKF | TSKF | VS EKF | VS STF | VS UKF | |
|---|---|---|---|---|---|---|---|---|
| parameter | 0.0032 | 0.0030 | 0.0019 | 0.0011 | 65.6250% | 63.3333% | 42.1053% | |
| 0.0037 | 0.0031 | 0.0015 | 0.0009 | 75.6757% | 70.9677% | 40.0000% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, C.; Lin, Z. A Gradually Linearizing Kalman Filter Bank Designing for Product-Type Strong Nonlinear Systems. Electronics 2022, 11, 714. https://doi.org/10.3390/electronics11050714
Wen C, Lin Z. A Gradually Linearizing Kalman Filter Bank Designing for Product-Type Strong Nonlinear Systems. Electronics. 2022; 11(5):714. https://doi.org/10.3390/electronics11050714
Chicago/Turabian StyleWen, Chenglin, and Zhipeng Lin. 2022. "A Gradually Linearizing Kalman Filter Bank Designing for Product-Type Strong Nonlinear Systems" Electronics 11, no. 5: 714. https://doi.org/10.3390/electronics11050714
APA StyleWen, C., & Lin, Z. (2022). A Gradually Linearizing Kalman Filter Bank Designing for Product-Type Strong Nonlinear Systems. Electronics, 11(5), 714. https://doi.org/10.3390/electronics11050714






