3D Placement of a New Tethered UAV to UAV Relay System for Coverage Maximization
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
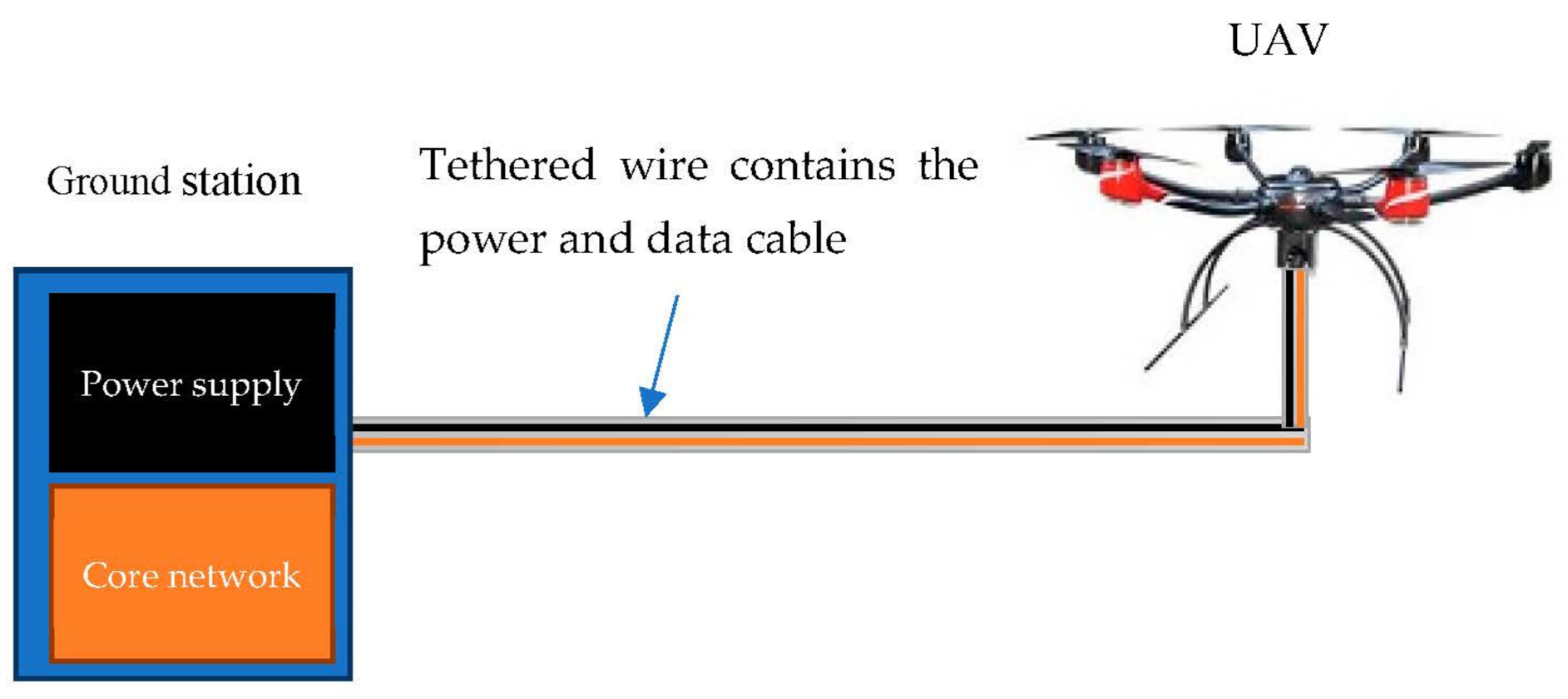
- Proposing a new relay system TU2U2G system. It uses the TUAV as a viable alternative to replace a BS and provide seamless service over a cable that simultaneously supplies a stable power and a reliable wired data-link connection from a ground control station [3]. Compared to the BS, TUAV improves the system coverage due to its high altitude. Also, it overcomes antenna down-tilting, which increases the path loss between the BS and the UAV in the cellular system [26].
- Formulating the optimization problem to maximize UAV relay station coverage under the power budget and maximum UAV height constraints. For simplicity, the 3D placement of the UAV is decoupled to the vertical and horizontal placement. Then, a 3D placement algorithm for the system is proposed.
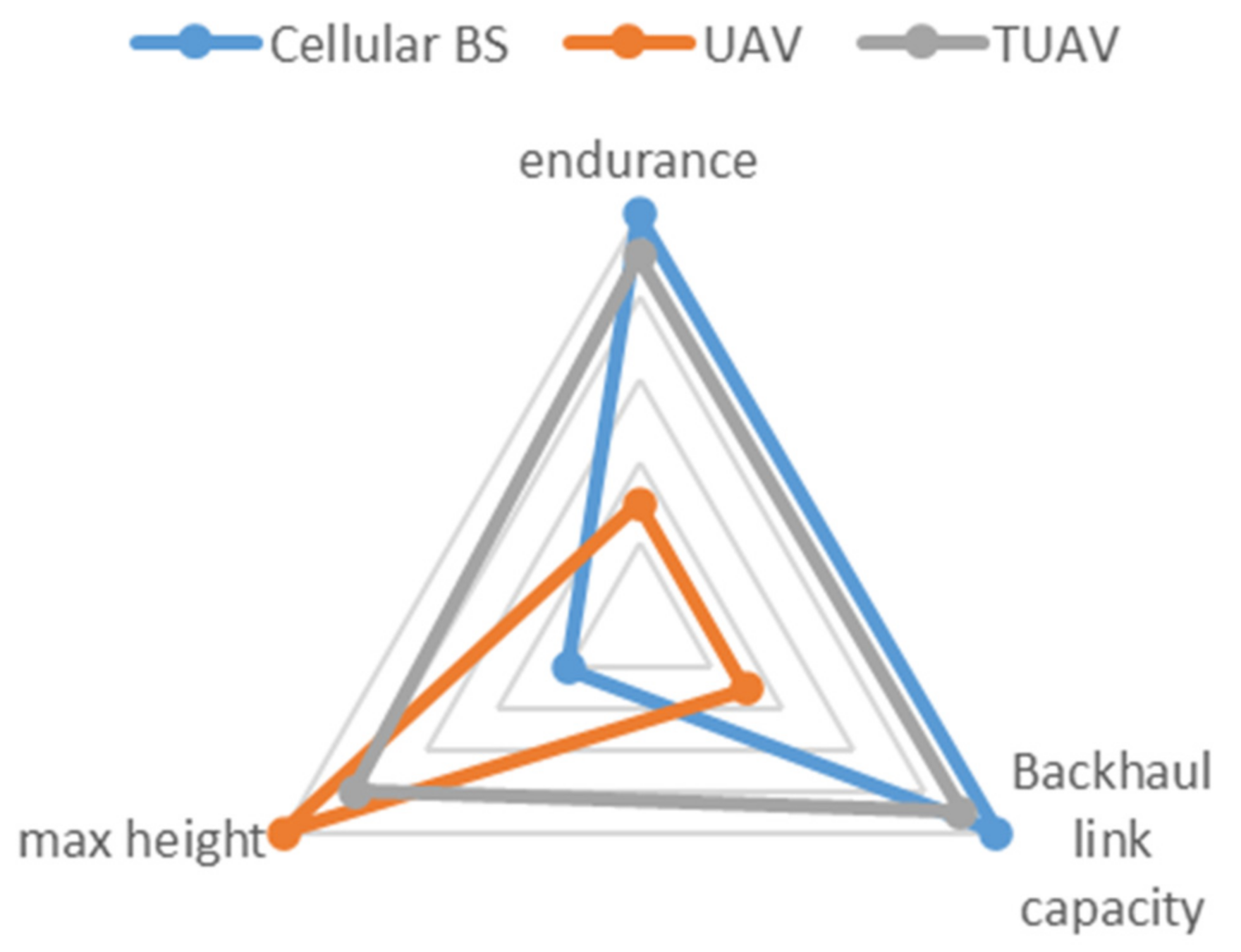
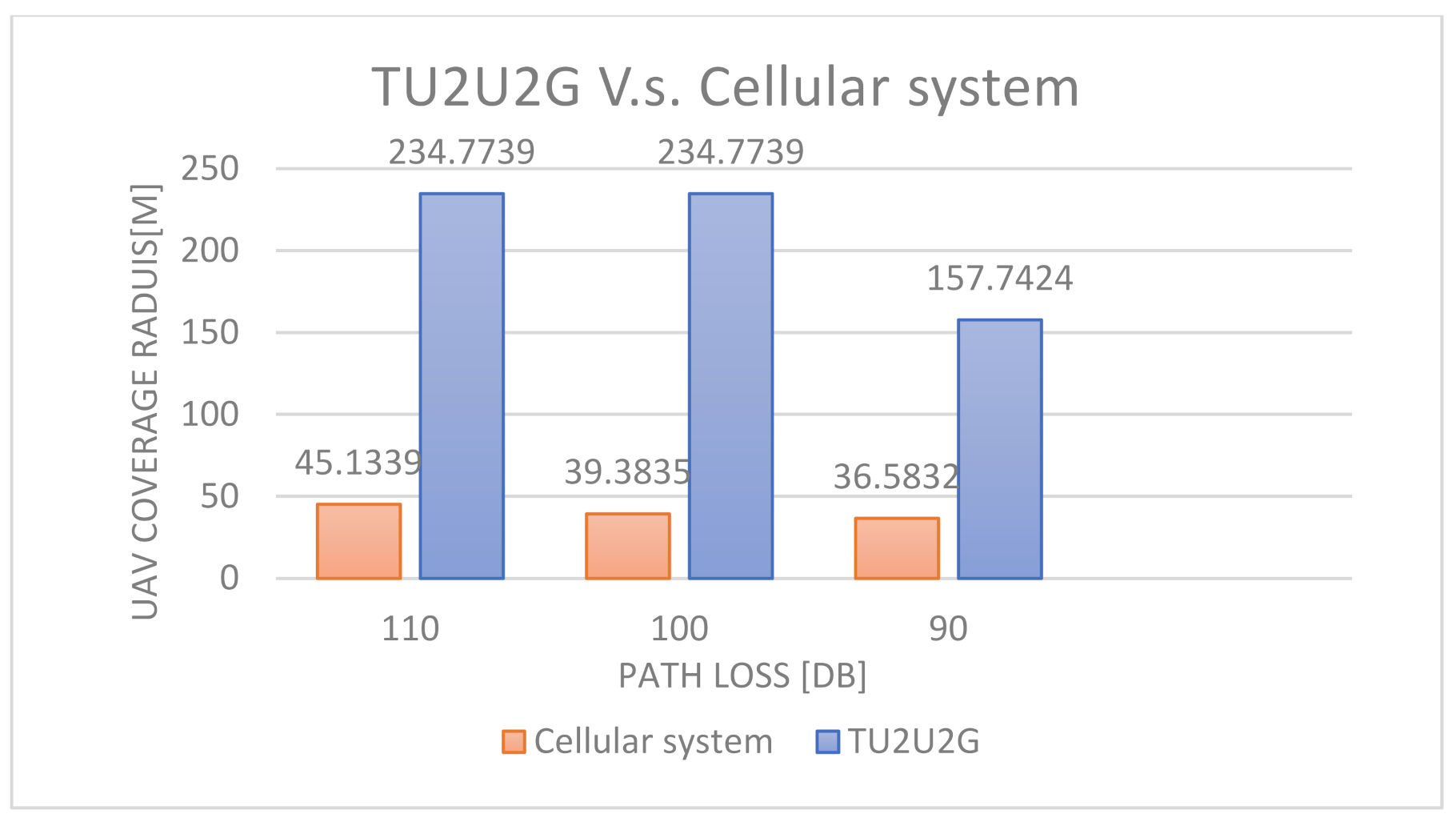
- Numerical results are presented. TU2U2G the system shows better results than the cellular system in terms of optimum UAV height, maximum coverage radius, and maximum distance between the BS and the UAV.
2. System Models
2.1. Channels Models
2.1.1. A2G Channel
2.1.2. U2U Channel
2.2. UAV Transmission Power, SNR, and Probability of Coverage
2.3. Problem Formulation
3. The Proposed 3D Placement of UAV
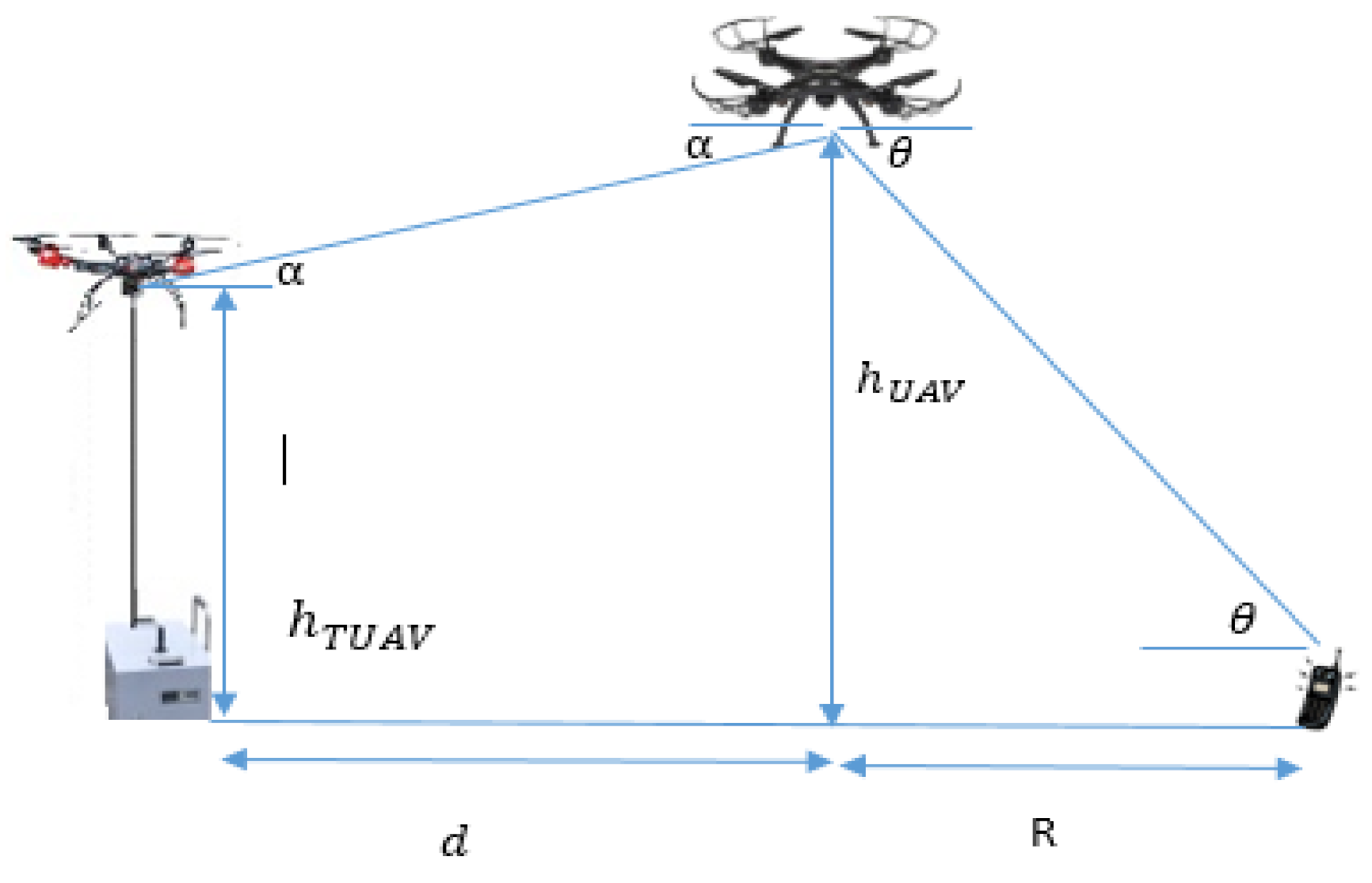
3.1. Altitude Optimization for Maximum Coverage
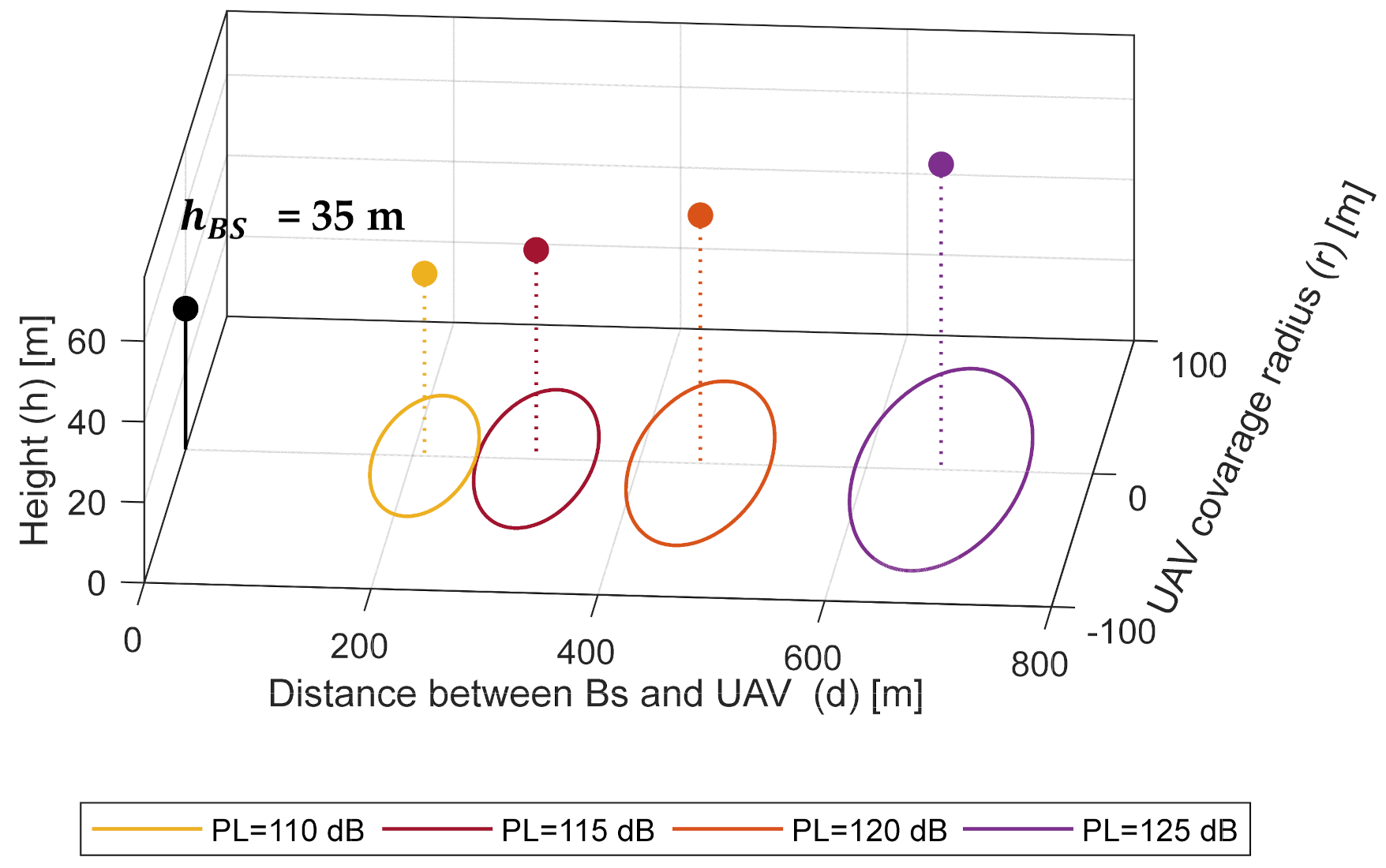
3.1.1. Finding the UAV Height for Maximum Coverage Radius between UAV and Ground User
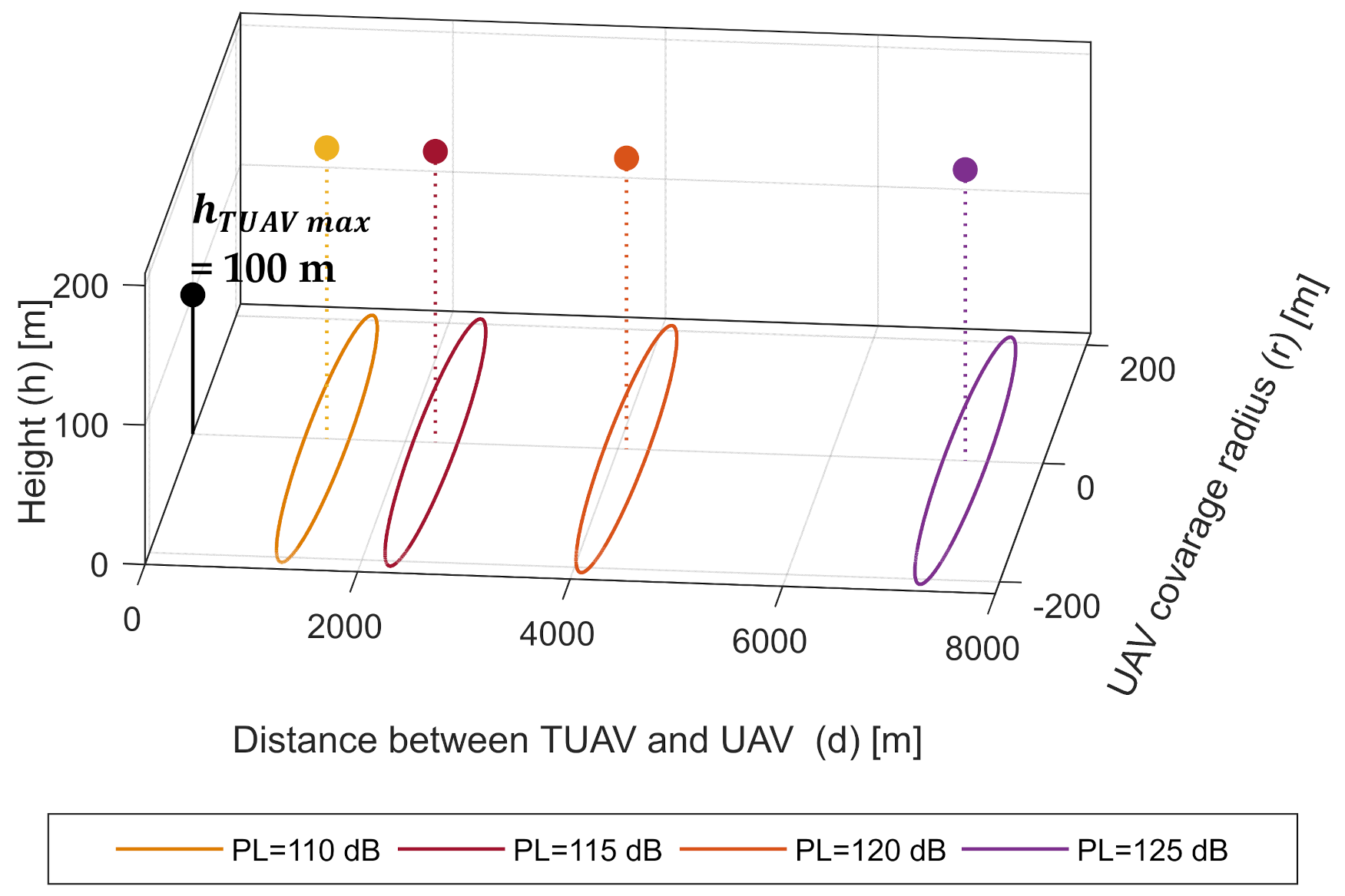
3.1.2. Finding the UAV Height for Maximum Distance between TUAV and UAV
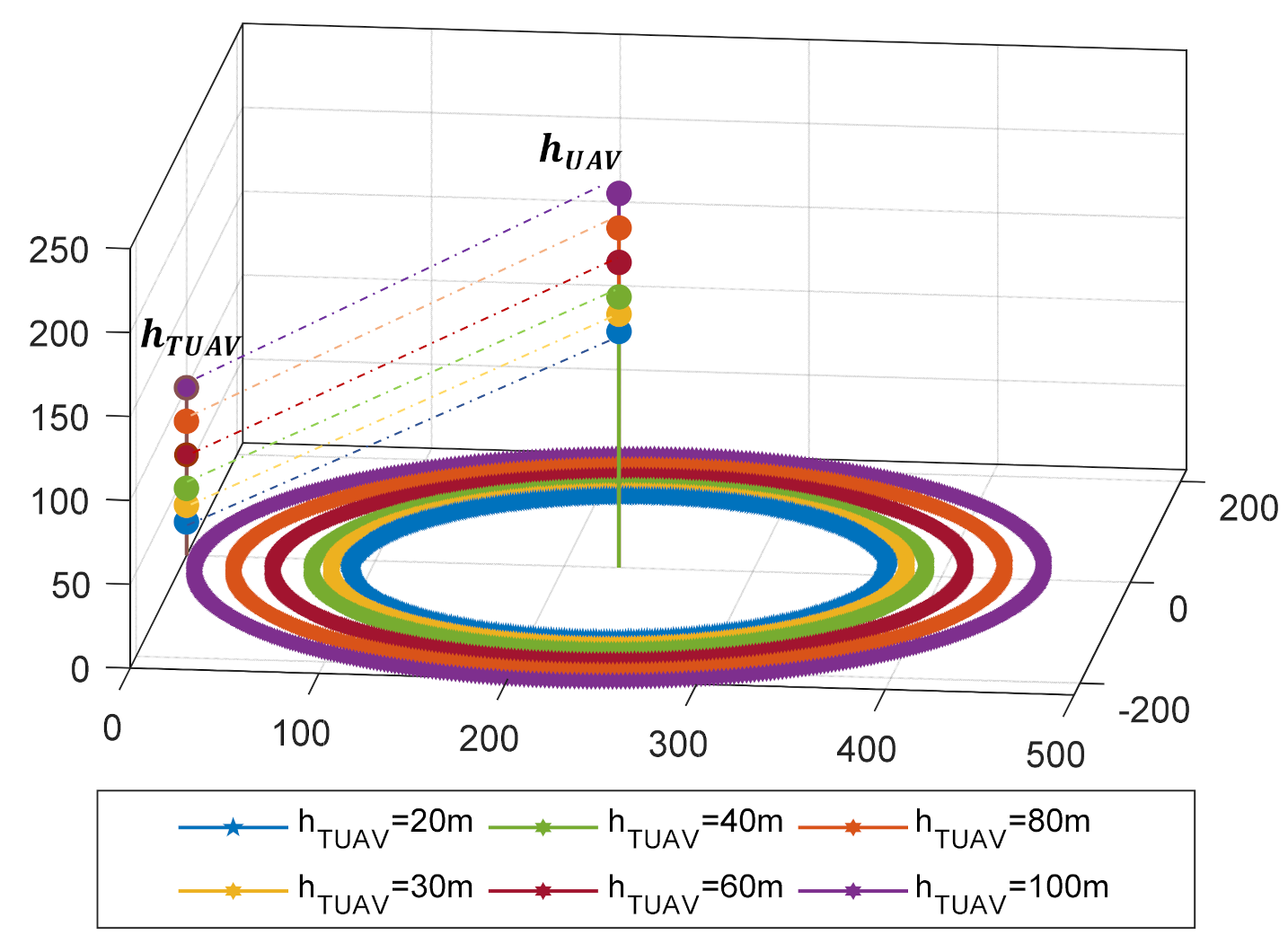
3.2. Horizontal Placement of UAV
3.3. 3D Placement Algorithm
| Algorithm 1: Obtain Optimal 3D Location (d, R, , ) |
| Input:,,,,,, f,,, |
| Output: (d,R,,) |
| 1 Obtain Finding by solving the problem in (24). Then, substituting by in (5) to calculate . Then, substituting by and in (25) to calculate . 2 Obtain ∆ Finding by solving the problem in (26). Then, substituting by in (7) to calculate . Then, substituting by and in (27) to calculate ∆. |
| 3 Calculate∆ = absolute value of () If (∆ > ∆) then ∆h = ∆ = else ∆h = ∆ If ( > ) then If (∆ = 0) then = else = + ∆ = end If else = + ∆ end If end If |
| 4 ObtainR from (25) |
| 5 Obtaind from (27) 6 Solve a problem: obtain UAV coverage center ( and users’ coverage N by solving the problem (15) |
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Merwaday, A.; Guvenc, I. UAV assisted heterogeneous networks for public safety communications. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), New Orleans, LA, USA, 9–12 March 2015; pp. 329–334. [Google Scholar]
- Kishk, M.; Bader, A.; Alouini, M.-S. Aerial Base Station Deployment in 6G Cellular Networks Using Tethered Drones: The Mobility and Endurance Tradeoff. IEEE Veh. Technol. Mag. 2020, 15, 103–111. [Google Scholar] [CrossRef]
- Kishk, M.A.; Bader, A.; Alouini, M.-S. On the 3-D Placement of Airborne Base Stations Using Tethered UAVs. IEEE Trans. Commun. 2020, 68, 5202–5215. [Google Scholar] [CrossRef]
- AT&T. AT&T’s First Official Deployment of Cell on Wings in Puerto Rico. 2017. Available online: https://www.youtube.com/watch?v=RgxVHbQaMIE (accessed on 14 January 2022).
- Shakoor, S.; Kaleem, Z.; Do, D.-T.; Dobre, O.A.; Jamalipour, A. Joint Optimization of UAV 3-D Placement and Path-Loss Factor for Energy-Efficient Maximal Coverage. IEEE Internet Things J. 2021, 8, 9776–9786. [Google Scholar] [CrossRef]
- Cui, J.; Shakhatreh, H.; Hu, B.; Chen, S.; Wang, C. Power-Efficient Deployment of a UAV for Emergency Indoor Wireless Coverage. IEEE Access 2018, 6, 73200–73209. [Google Scholar] [CrossRef]
- Alzenad, M.; El-Keyi, A.; Lagum, F.; Yanikomeroglu, H. 3-D Placement of an Unmanned Aerial Vehicle Base Station (UAV-BS) for Energy-Efficient Maximal Coverage. IEEE Wirel. Commun. Lett. 2017, 6, 434–437. [Google Scholar] [CrossRef] [Green Version]
- Alzenad, M.; El-Keyi, A.; Yanikomeroglu, H. 3-D Placement of an Unmanned Aerial Vehicle Base Station for Maximum Coverage of Users With Different QoS Requirements. IEEE Wirel. Commun. Lett. 2017, 7, 38–41. [Google Scholar] [CrossRef] [Green Version]
- Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wirel. Commun. Lett. 2014, 3, 569–572. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Xu, D.; Ng, D.W.K.; Dai, L.; Schober, R. Optimal 3D-Trajectory Design and Resource Allocation for Solar-Powered UAV Communication Systems. IEEE Trans. Commun. 2019, 67, 4281–4298. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Ren, G.; Chen, J.; Ding, G.; Yang, Y. Unmanned Aerial Vehicle-Aided Communications: Joint Transmit Power and Trajectory Optimization. IEEE Wirel. Commun. Lett. 2018, 7, 522–525. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint Trajectory and Communication Design for Multi-UAV Enabled Wireless Networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Wei, Z.; Li, R.; Ng, D.W.K.; Yuan, J. Joint Trajectory and Resource Allocation Design for Energy-Efficient Secure UAV Communication Systems. IEEE Trans. Commun. 2020, 68, 4536–4553. [Google Scholar] [CrossRef] [Green Version]
- El Hammouti, H.; Benjillali, M.; Shihada, B.; Alouini, M.-S. Learn-As-You-Fly: A Distributed Algorithm for Joint 3D Placement and User Association in Multi-UAVs Networks. IEEE Trans. Wirel. Commun. 2019, 18, 5831–5844. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Huang, L.; Zhong, S.; Zhang, P. UAV-Mounted Mobile Base Station Placement via Sparse Recovery. IEEE Access 2020, 8, 71775–71781. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, F.; Li, B.; Yang, Z.; Wu, Y.; Zhu, H. Placement optimization of caching UAV-assisted mobile relay maritime communication. China Commun. 2020, 17, 209–219. [Google Scholar] [CrossRef]
- Li, Y.; Feng, G.; Ghasemiahmadi, M.; Cai, L. Power Allocation and 3-D Placement for Floating Relay Supporting Indoor Communications. IEEE Trans. Mob. Comput. 2019, 18, 618–631. [Google Scholar] [CrossRef]
- Chen, J.; Gesbert, D. Optimal positioning of flying relays for wireless networks: A LOS map approach. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Larsen, E.; Landmark, L.; Kure, O. Optimal UAV relay positions in multi-rate networks. In 2017 Wireless Days; IEEE: Port, Portugal, 2017; pp. 8–14. [Google Scholar]
- Zeng, Y.; Zhang, R.; Lim, T.J. Throughput Maximization for UAV-Enabled Mobile Relaying Systems. IEEE Trans. Commun. 2016, 64, 4983–4996. [Google Scholar] [CrossRef]
- Kalantari, E.; Bor-Yaliniz, I.; Yongacoglu, A.; Yanikomeroglu, H. User association and bandwidth allocation for terrestrial and aerial base stations with backhaul considerations. In Proceedings of the 28th IEEE Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Chattopadhyay, A.; Ghosh, A.; Kumar, A. Asynchronous Stochastic Approximation Based Learning Algorithms for As-You-Go Deployment of Wireless Relay Networks Along a Line. IEEE Trans. Mob. Comput. 2017, 17, 1004–1018. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Feng, W.; Zheng, G. Optimum Placement of UAV as Relays. IEEE Commun. Lett. 2018, 22, 248–251. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Sabatini, R.; Ramasamy, S. UAVs Assisted Delay Optimization in Heterogeneous Wireless Networks. IEEE Commun. Lett. 2016, 20, 2526–2529. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Gomez, K. Modeling Cellular-to-UAV Path-Loss for Suburban Environments. IEEE Wirel. Commun. Lett. 2017, 7, 82–85. [Google Scholar] [CrossRef]



| Ref No. | UAV Placement for | Pros | Cons |
|---|---|---|---|
| [6] | Coverage maximization | Jointly optimizes the 3D UAV placement and path loss compensation factor | References [6,7,8,9,10,11,12,13,14,15,16] consider only the power constraints of the communication link between UAV and the ground user mobile station (MS) but do not consider the power constraints of the communication link between a UAV and the BS |
| [7] | Minimizes the total transmit power required to provide wireless coverage for indoor users | ||
| [8] | Maximizes the number of covered users with minimum transmission power | ||
| [9] | Maximizes the number of served users with different quality-of-service requirements | ||
| [10] | finds the optimum UAV altitude | ||
| [11] | Throughput maximization | A joint trajectory and resource allocation algorithm | |
| [12] | A joint transmit power and trajectory optimization algorithm | ||
| [13] | Optimizing the scheduling of multi-user communication and association jointly with the trajectory of UAVs and power control | ||
| [14] | Joint optimization of Trajectory and resource allocation | ||
| [15] | Algorithm for downlink sum-rate maximization | ||
| [16] | Algorithm for UAV placement based on sparse recovery | ||
| [17] | Throughput maximization | Maximizes the average achievable rate through the one-dimensional linear search | References [17,18,19,20,21,22,23,24,25] are proposed for UAVs to assist the cellular network. However, the antenna down-tilting and low height of the cellular base station (BS) limits the ability of the UAV relay station to reach high altitudes due to the power constraint on the path between a UAV and a BS. |
| [18] | The optimization problem is formulated to maximize the system throughput. | ||
| [19] | An algorithm to find the UAV optimal position based on LOS information | ||
| [20] | Explores the relationship between system throughput and placement of a UAV | ||
| [21] | Jointly optimizes throughput and the UAV’s trajectory | ||
| [22] | Sum logarithmic rate of the users maximize | An algorithm to find the 3D locations of UAVs besides the user-BS associations and bandwidth allocations of the wireless backhaul | |
| [23] | Data rate maximization | Algorithms for deploying a multi-relay network to maximize the end-to-end achievable rate | |
| [24] | Power loss, outage probability, and BER minimization | An approach to find the optimum altitude of UAV | |
| [25] | Optimizing the overall network delays | An approach to optimize the overall network delays | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safwat, N.E.-D.; Hafez, I.M.; Newagy, F. 3D Placement of a New Tethered UAV to UAV Relay System for Coverage Maximization. Electronics 2022, 11, 385. https://doi.org/10.3390/electronics11030385
Safwat NE-D, Hafez IM, Newagy F. 3D Placement of a New Tethered UAV to UAV Relay System for Coverage Maximization. Electronics. 2022; 11(3):385. https://doi.org/10.3390/electronics11030385
Chicago/Turabian StyleSafwat, Nour El-Din, Ismail Mohammed Hafez, and Fatma Newagy. 2022. "3D Placement of a New Tethered UAV to UAV Relay System for Coverage Maximization" Electronics 11, no. 3: 385. https://doi.org/10.3390/electronics11030385
APA StyleSafwat, N. E.-D., Hafez, I. M., & Newagy, F. (2022). 3D Placement of a New Tethered UAV to UAV Relay System for Coverage Maximization. Electronics, 11(3), 385. https://doi.org/10.3390/electronics11030385






