A Unified FPGA Realization for Fractional-Order Integrator and Differentiator
Abstract
:1. Introduction
2. Literature Review of GL-Based Fractional Operators Implementations
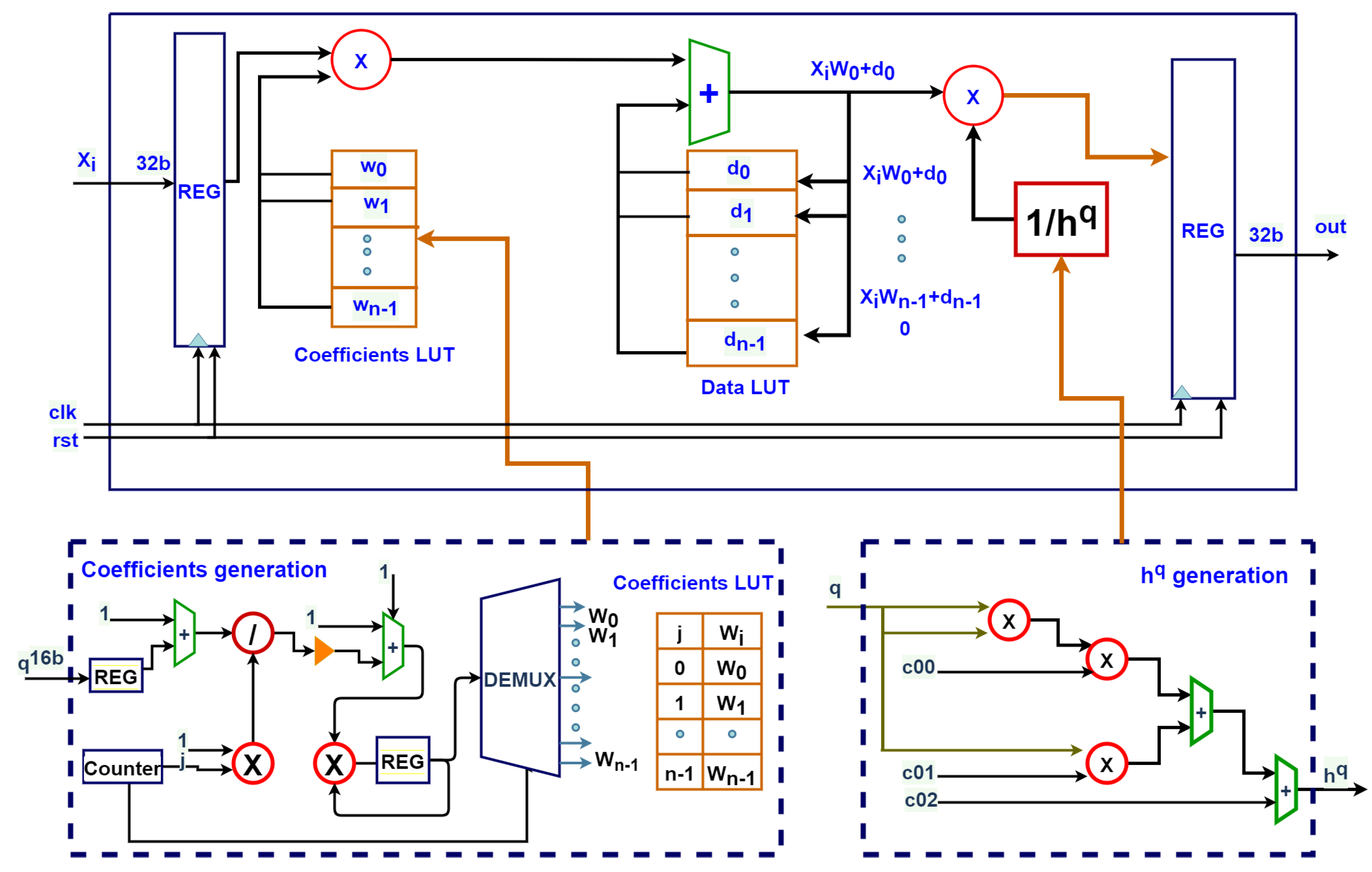
3. Proposed Generic Hardware Realization of Fractional-Order GL-Based Integrator and Differentiator
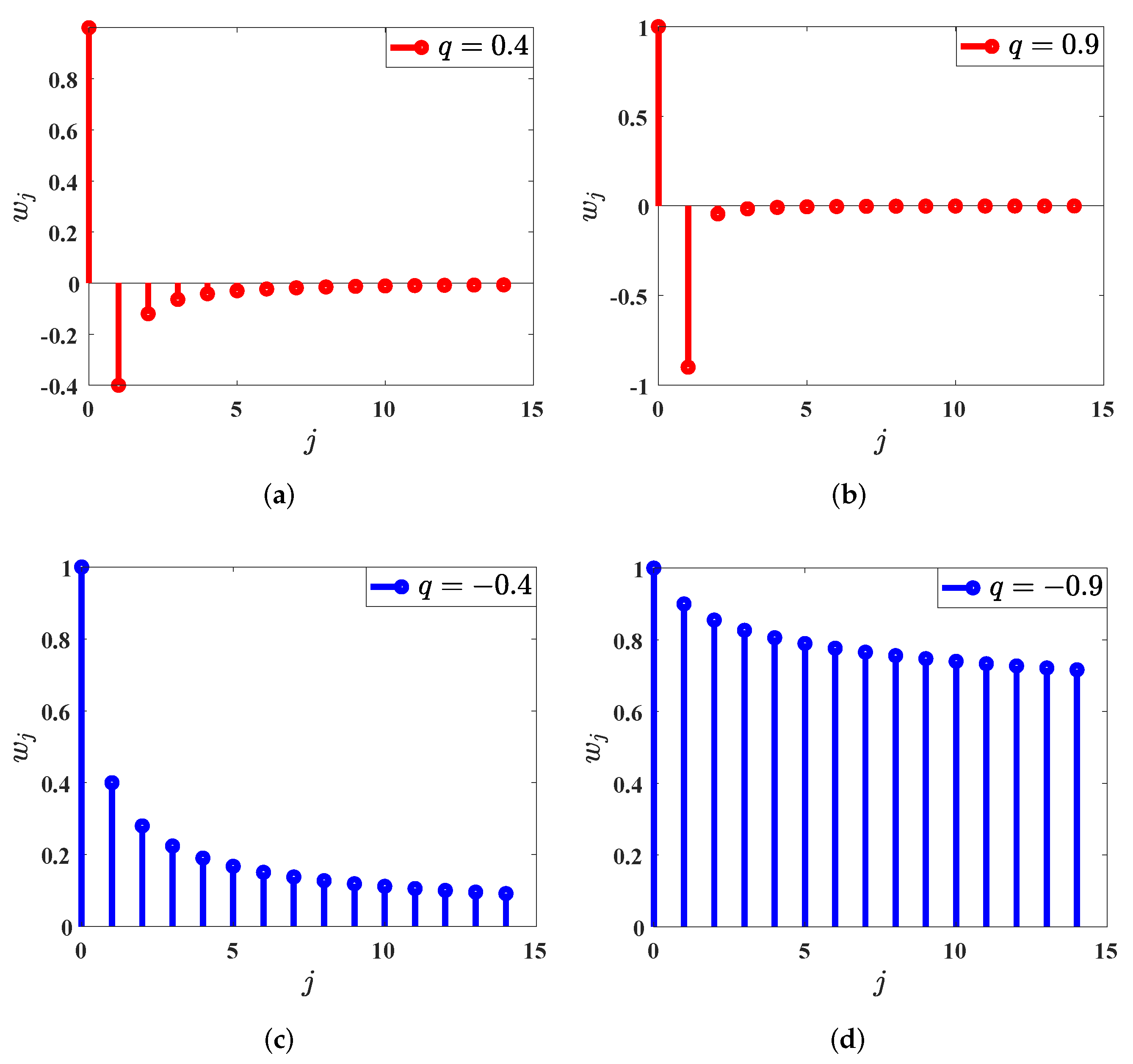
3.1. Binomial Coefficients Generation
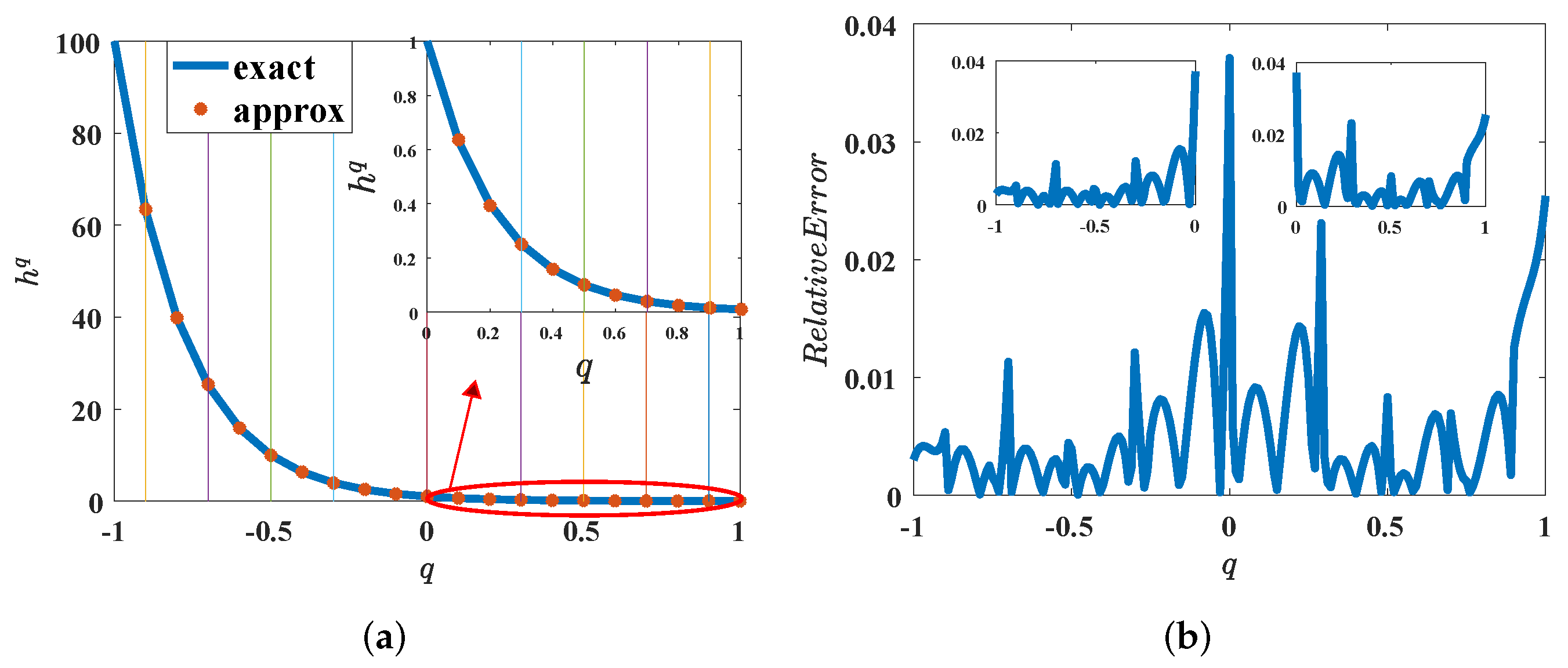
3.2. Generation
3.3. Fixed-Window Hardware Implementation:
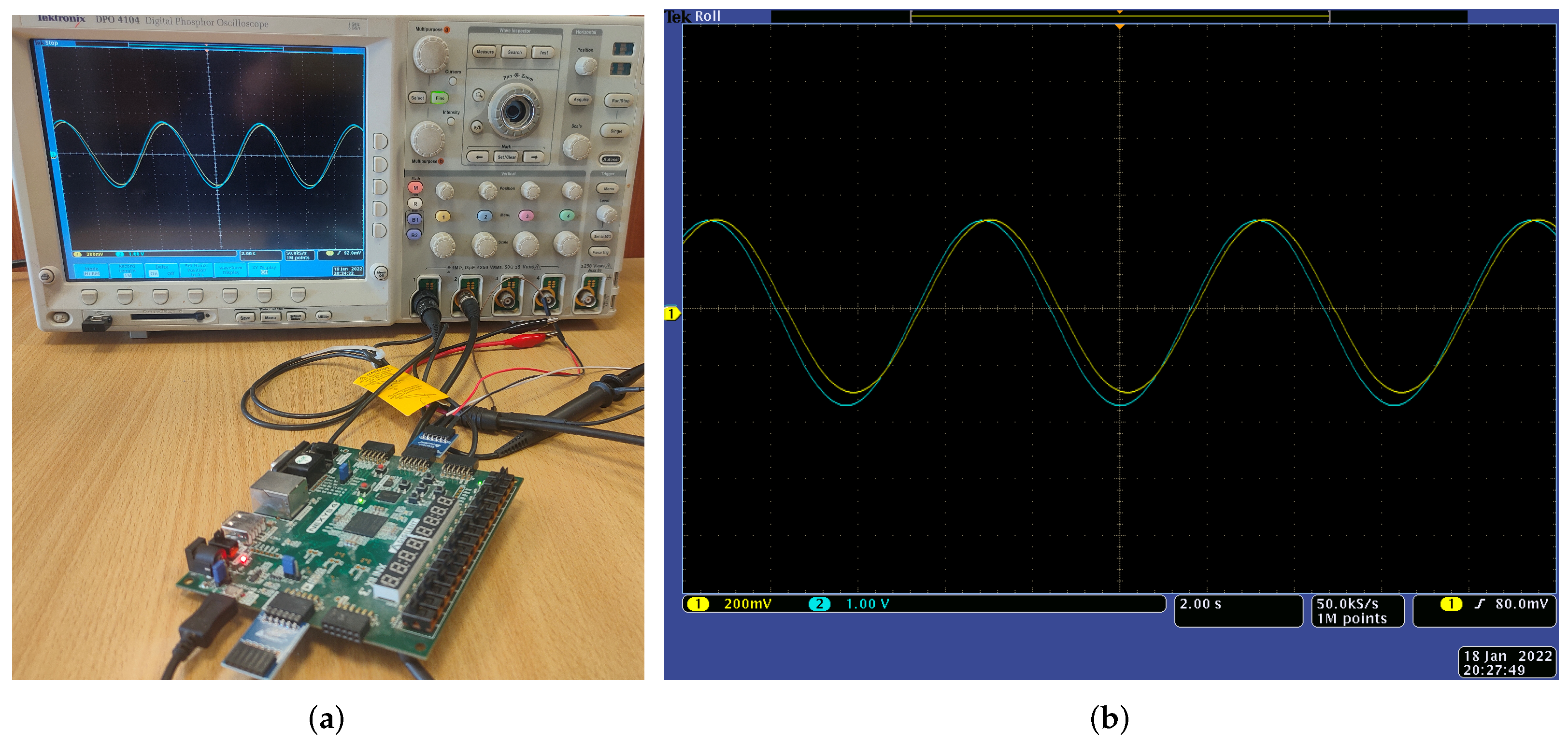
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Machado, J.T.; Kiryakova, V. Recent history of the fractional calculus: Data and statistics. Handb. Fract. Calc. Appl. 2019, 1, 1–21. [Google Scholar]
- Petráš, I.; Terpák, J. Fractional calculus as a simple tool for modeling and analysis of long memory process in industry. Mathematics 2019, 7, 511. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Kaskouta, E.; Kapoulea, S.; Psychalinos, C.; Elwakil, A.S. Implementation of a fractional-order electronically reconfigurable lung impedance emulator of the human respiratory tree. J. Low Power Electron. Appl. 2020, 10, 18. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Li, W. Periodically intermittent discrete observation control for synchronization of fractional-order coupled systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 74, 219–235. [Google Scholar] [CrossRef]
- Qiu, X.; Feng, H.; Hu, B. Fractional order graph filters: Design and implementation. Electronics 2021, 10, 437. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Grassi, G.; Pham, V.T.; El-Khazali, R.; Vo Hoang, D. A quadratic fractional map without equilibria: Bifurcation, 0–1 test, complexity, entropy, and control. Electronics 2020, 9, 748. [Google Scholar] [CrossRef]
- Alam, M.S.; Alotaibi, M.A.; Alam, M.A.; Hossain, M.A.; Shafiullah, M.; Al-Ismail, F.S.; Rashid, M.M.U.; Abido, M.A. High-level renewable energy integrated system frequency control with SMES-based optimized fractional order controller. Electronics 2021, 10, 511. [Google Scholar] [CrossRef]
- Gao, X.; Yu, J.; Banerjee, S.; Yan, H.; Mou, J. A new image encryption scheme based on fractional-order hyperchaotic system and multiple image fusion. Sci. Rep. 2021, 11, 15737. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.; Jasim, B.H.; Al-Yasir, Y.I.; Abd-Alhameed, R.A. High-Security Image Encryption Based on a Novel Simple Fractional-Order Memristive Chaotic System with a Single Unstable Equilibrium Point. Electronics 2021, 10, 3130. [Google Scholar] [CrossRef]
- Teodoro, G.S.; Machado, J.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef] [Green Version]
- Loverro, A. Fractional Calculus: History, Definitions and Applications for the Engineer; Rapport Technique; Univeristy of Notre Dame, Department of Aerospace and Mechanical Engineering: Notre Dame, IN, USA, 2004; pp. 1–28. Available online: https://www.academia.edu/9364104/Fractional_Calculus_History_Definitions_and_Applications_for_the_Engineer?from=cover_page (accessed on 24 May 2022).
- Maamri, N.; Trigeassou, J.C. A comparative analysis of two algorithms for the simulation of fractional differential equations. Int. J. Dyn. Control 2020, 8, 302–311. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999; Volume 198, pp. 41–119. Available online: https://cir.nii.ac.jp/crid/1573387449640571136 (accessed on 24 May 2022).
- Nuñez-Perez, J.C.; Adeyemi, V.A.; Sandoval-Ibarra, Y.; Pérez-Pinal, F.J.; Tlelo-Cuautle, E. FPGA realization of spherical chaotic system with application in image transmission. Math. Probl. Eng. 2021, 2021, 5532106. [Google Scholar] [CrossRef]
- MacLean, W.J. An evaluation of the suitability of FPGAs for embedded vision systems. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05)-Workshops, San Diego, CA, USA, 21–23 September 2005; p. 131. [Google Scholar]
- Tolba, M.F.; AbdelAty, A.M.; Said, L.A.; Elwakil, A.S.; Azar, A.T.; Madian, A.H.; Ounnas, A.; Radwan, A.G. FPGA realization of Caputo and Grünwald-Letnikov operators. In Proceedings of the 2017 6th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 4–6 May 2017; pp. 1–4. [Google Scholar]
- Li, C.; Chen, G. Chaos in the fractional order Chen system and its control. Chaos Solitons Fractals 2004, 22, 549–554. [Google Scholar] [CrossRef]
- Gutierrez, R.E.; Rosario, J.M.; Tenreiro Machado, J. Fractional order calculus: Basic concepts and engineering applications. Math. Probl. Eng. 2010, 2010, 375858. [Google Scholar] [CrossRef]
- Dimeas, I.; Petras, I.; Psychalinos, C. New analog implementation technique for fractional-order controller: A DC motor control. AEU-Int. J. Electron. Commun. 2017, 78, 192–200. [Google Scholar] [CrossRef]
- Tolba, M.F.; AbdelAty, A.M.; Soliman, N.S.; Said, L.A.; Madian, A.H.; Azar, A.T.; Radwan, A.G. FPGA implementation of two fractional order chaotic systems. AEU-Int. J. Electron. Commun. 2017, 78, 162–172. [Google Scholar] [CrossRef]
- Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. FPGA implementation of the fractional order integrator/differentiator: Two approaches and applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 66, 1484–1495. [Google Scholar] [CrossRef]
- Ricci, F.; Le-Huy, H. Modeling and simulation of FPGA-based variable-speed drives using Simulink. Math. Comput. Simul. 2003, 63, 183–195. [Google Scholar] [CrossRef]
- Tolba, M.F.; Saleh, H.; Mohammad, B.; Al-Qutayri, M.; Elwakil, A.S.; Radwan, A.G. Enhanced FPGA realization of the fractional-order derivative and application to a variable-order chaotic system. Nonlinear Dyn. 2020, 99, 3143–3154. [Google Scholar] [CrossRef]
- Peng, D.; Peng, L.; Zhang, X. A Generic FPGA Implementation of the Fractional-Order Derivative and Its Application; Research Square: Durham, NC, USA, 2021. [Google Scholar]
- Mohamed, S.M.; Sayed, W.S.; Said, L.A.; Radwan, A.G. Reconfigurable fpga realization of fractional-order chaotic systems. IEEE Access 2021, 9, 89376–89389. [Google Scholar] [CrossRef]
- Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. FPGA implementation of fractional-order integrator and differentiator based on Grünwald Letnikov’s definition. In Proceedings of the 2017 29th International Conference on Microelectronics (ICM), Beirut, Lebanon, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Tolba, M.F.; AboAlNaga, B.M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Fractional order integrator/differentiator: FPGA implementation and FOPID controller application. AEU-Int. J. Electron. Commun. 2019, 98, 220–229. [Google Scholar] [CrossRef]
- Pano-Azucena, A.D.; Tlelo-Cuautle, E.; Muñoz-Pacheco, J.M.; de la Fraga, L.G. FPGA-based implementation of different families of fractional-order chaotic oscillators applying Grünwald–Letnikov method. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 516–527. [Google Scholar] [CrossRef]
- Xu, B.; Chen, K.; Wang, Y.; Geng, H.; Zou, S.; Yu, B. A Method For Implementing Fractional Order Differentiator and Integrator Based on Digital Oscilloscope. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–6. [Google Scholar]
- Arlinghaus, S. Practical Handbook of Curve Fitting; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- MathWorks, Inc. MathWorks, Curve Fitting Toolbox 1: User’s Guide; MathWorks: Natick, MA, USA, 2006. [Google Scholar]
- Weisstein, E.W. Least Squares Fitting. 2002. Available online: https://mathworld.wolfram.com/ (accessed on 30 January 2022).
| Ref | Diff./Integ. | Application | Generality | Approaches | q Range | Window Size | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Diff. | Int. | |||||||||
| MATLAB | Hardware | MATLAB | Hardware | |||||||
| [22] | ✓ | — | chaotic systems | ✓ | — | ✓ | — | fixed window | 0 ≤ | 20,40,30 |
| [23] | ✓ | ✓ | fractional order systems | ✓ | — | ✓ | — | fixed-linear, fixed-quadratic and pwl | < ≤ | 64,512,20 |
| [30] | ✓ | — | oscillators | ✓ | — | ✓ | — | fixed window | < ≤ 1 | 256 |
| [29] | ✓ | ✓ | FOPID controller | ✓ | — | ✓ | — | fixed window-linear | — | 32,512,1024 |
| [18] | ✓ | ✓ | — | ✓ | — | ✓ | — | fixed window-linear | — | 32 |
| [25] | ✓ | — | chaotic systems | — | ✓ | — | ✓ | fixed window-linear | 0 < ≤ | 32 |
| [26] | — | — | chaotic systems | — | ✓ | — | ✓ | fixed window | < ≤ 1 | 28,56 |
| [27] | — | — | chaotic systems | — | ✓ | — | ✓ | fixed window | < ≤ 1 | 16,32 |
| [31] | ✓ | ✓ | — | — | — | — | — | — | — | — |
| L = 32 | L = 512 | L = 1024 | |
|---|---|---|---|
| Derivative | 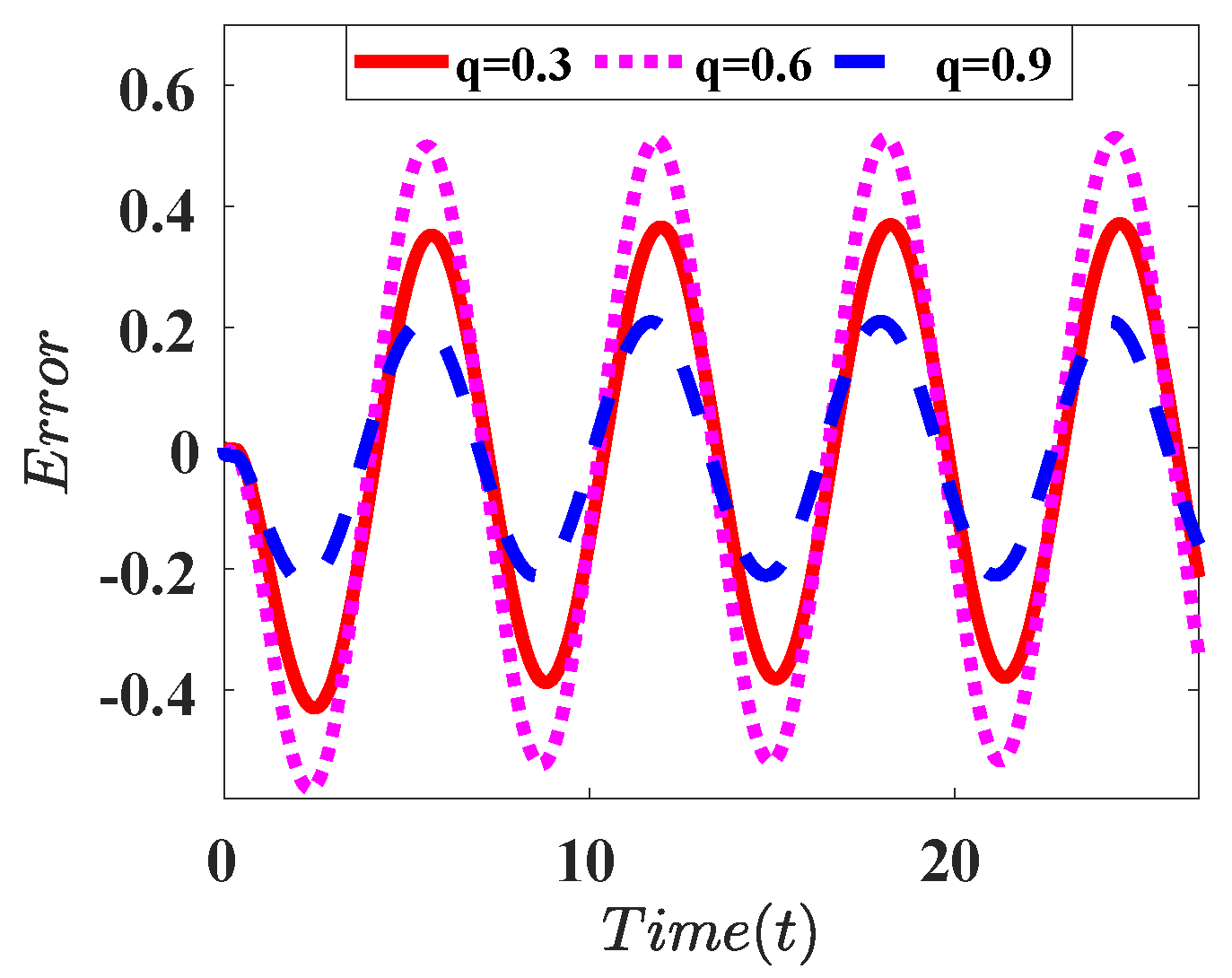 | 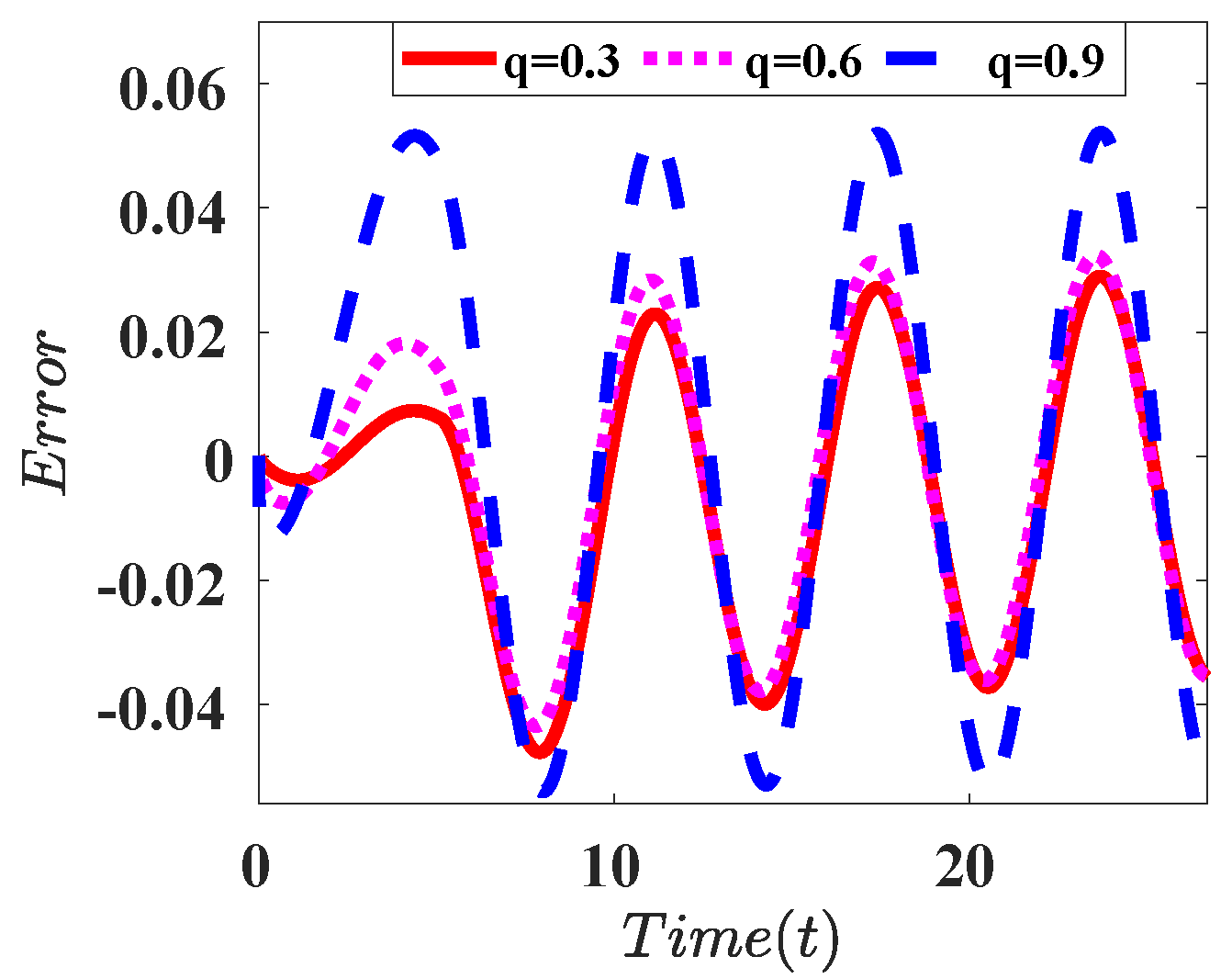 | 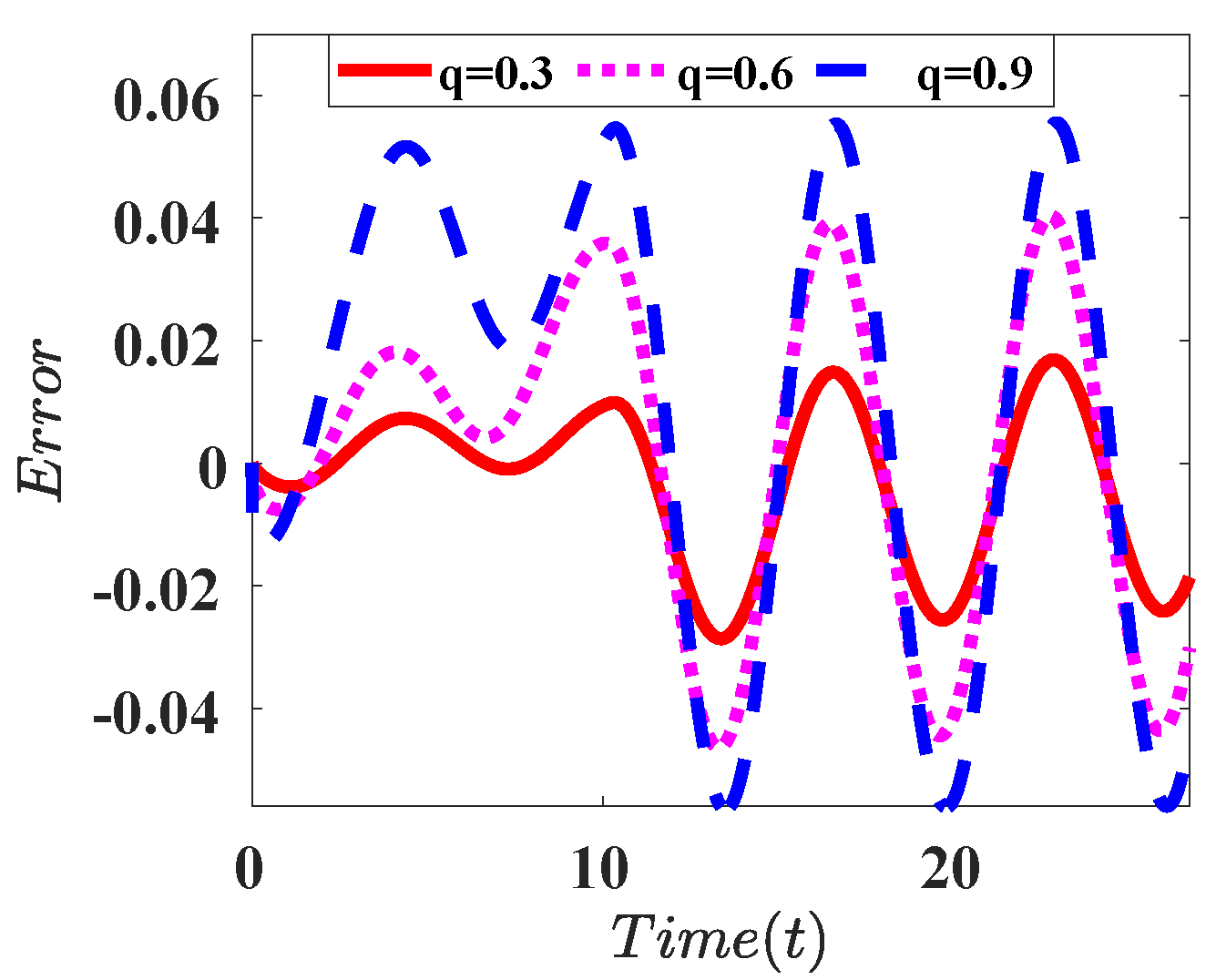 |
| Integral | 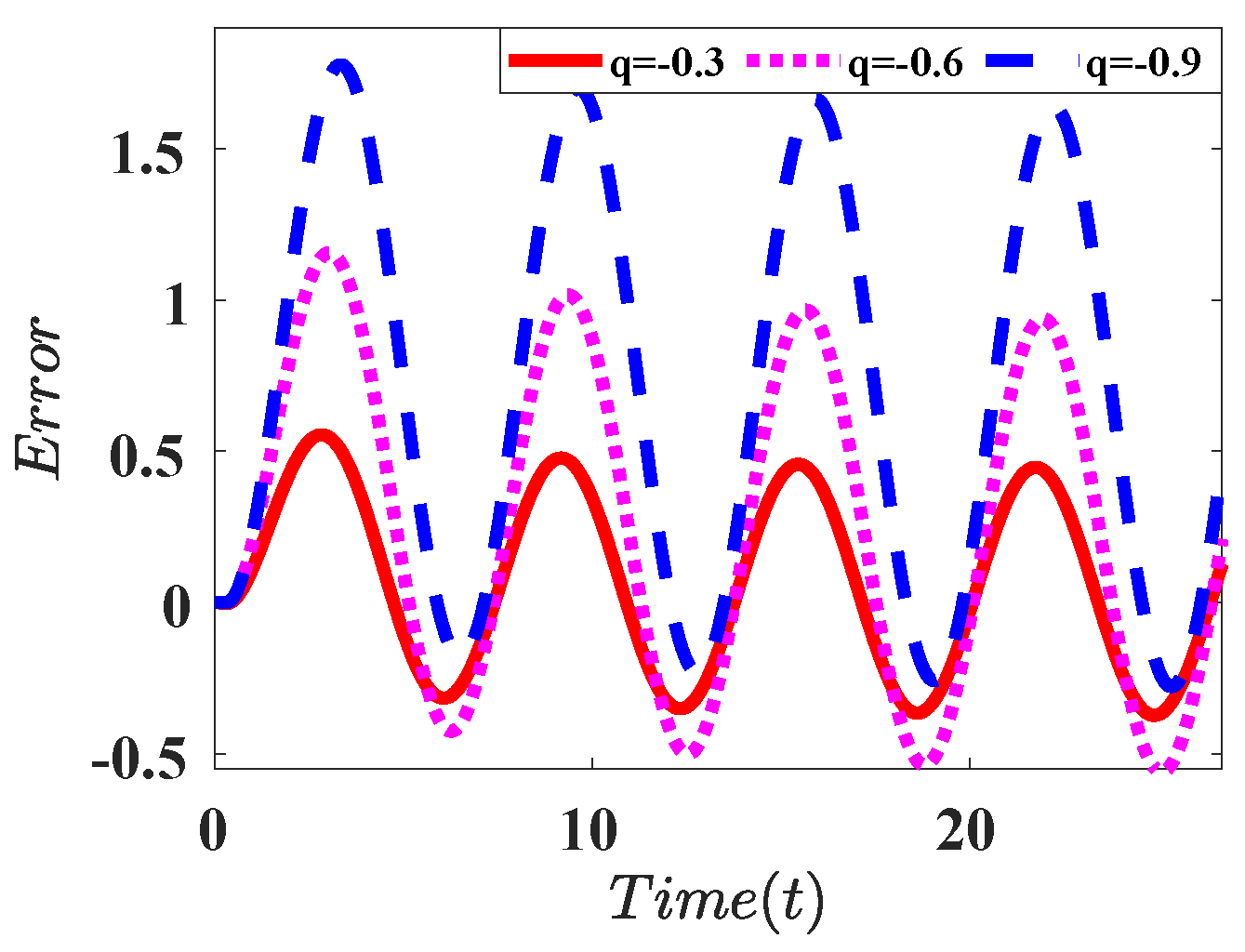 | 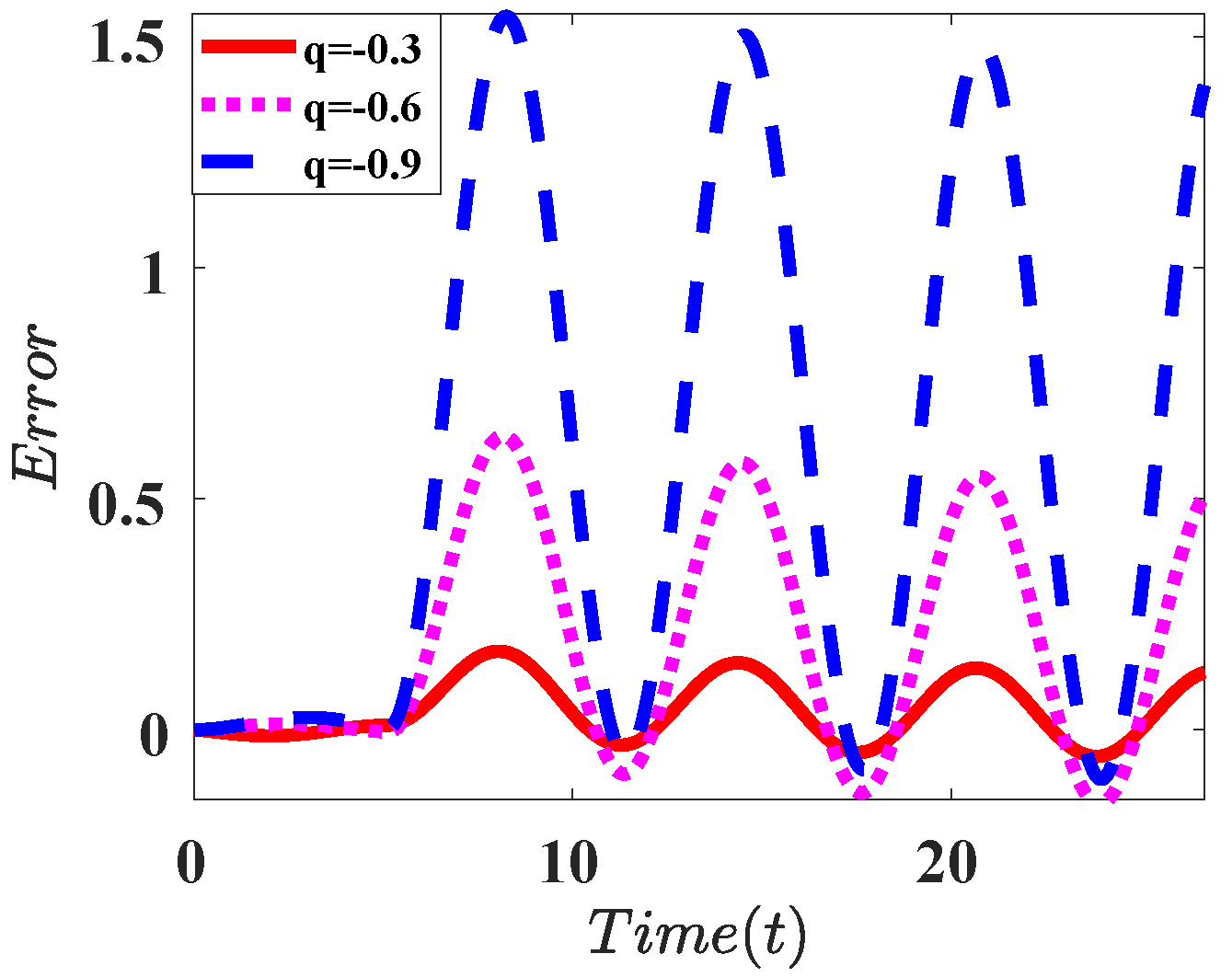 | 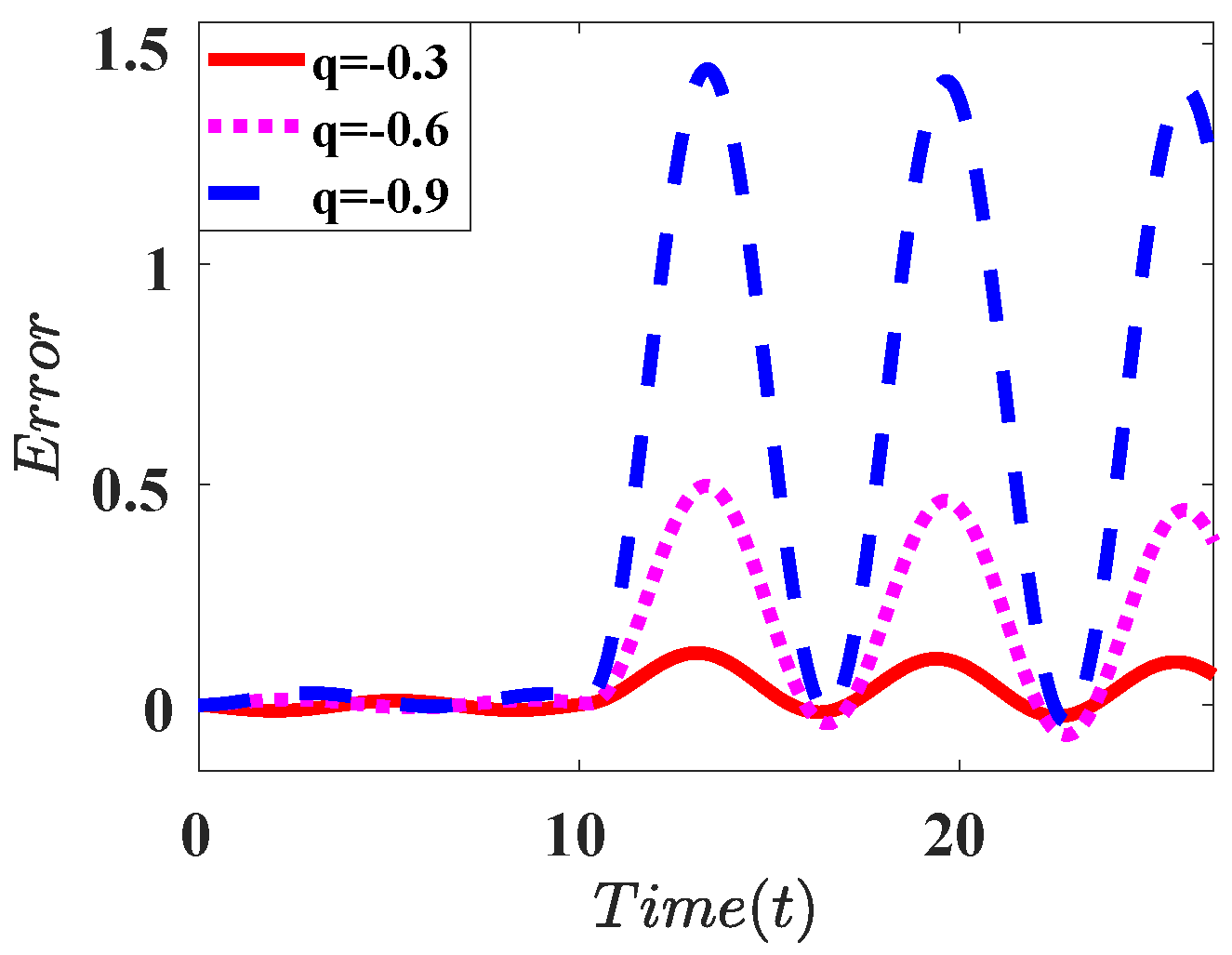 |
| L = 32 | L = 512 | L = 1024 | |
|---|---|---|---|
| Derivative | 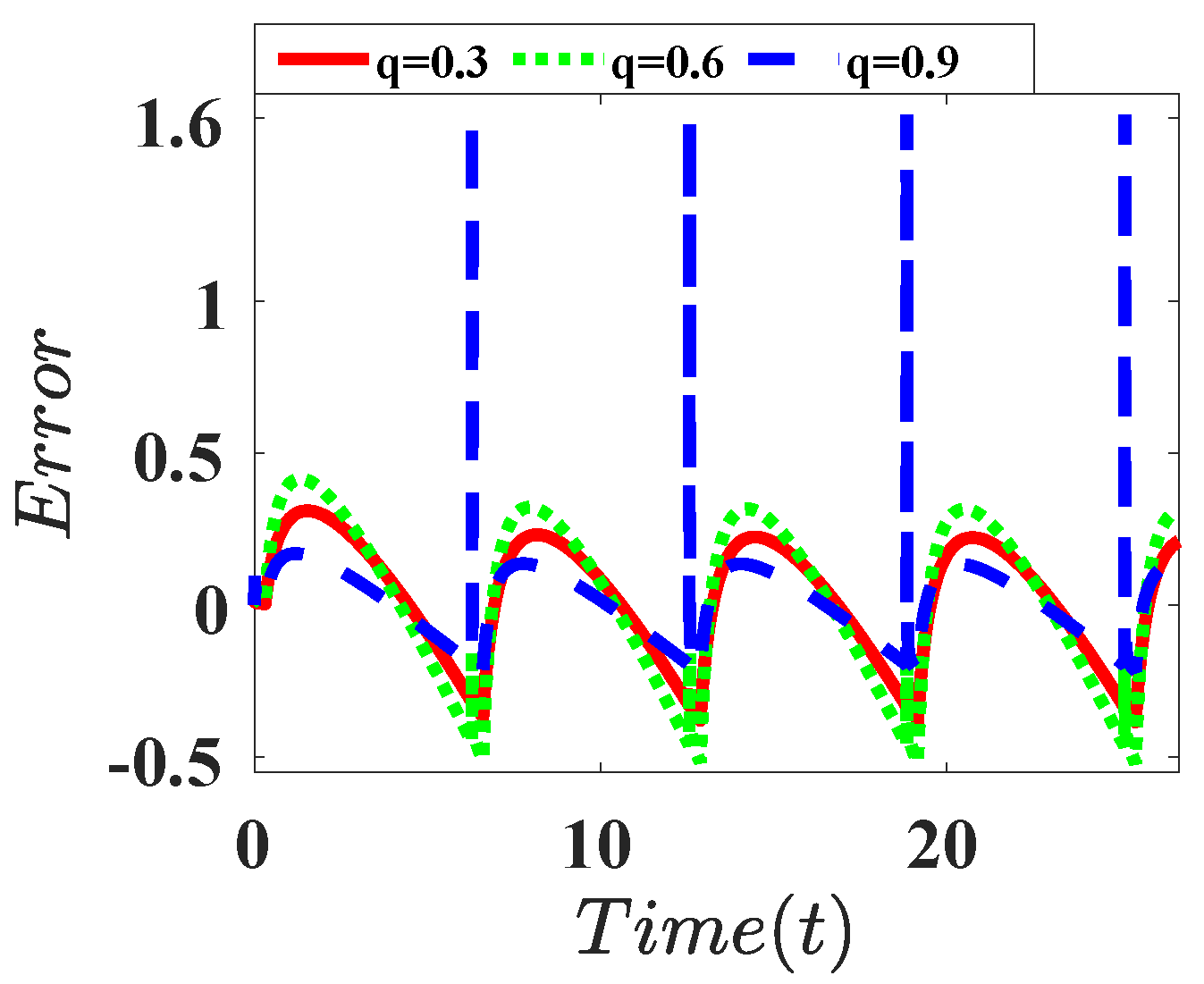 | 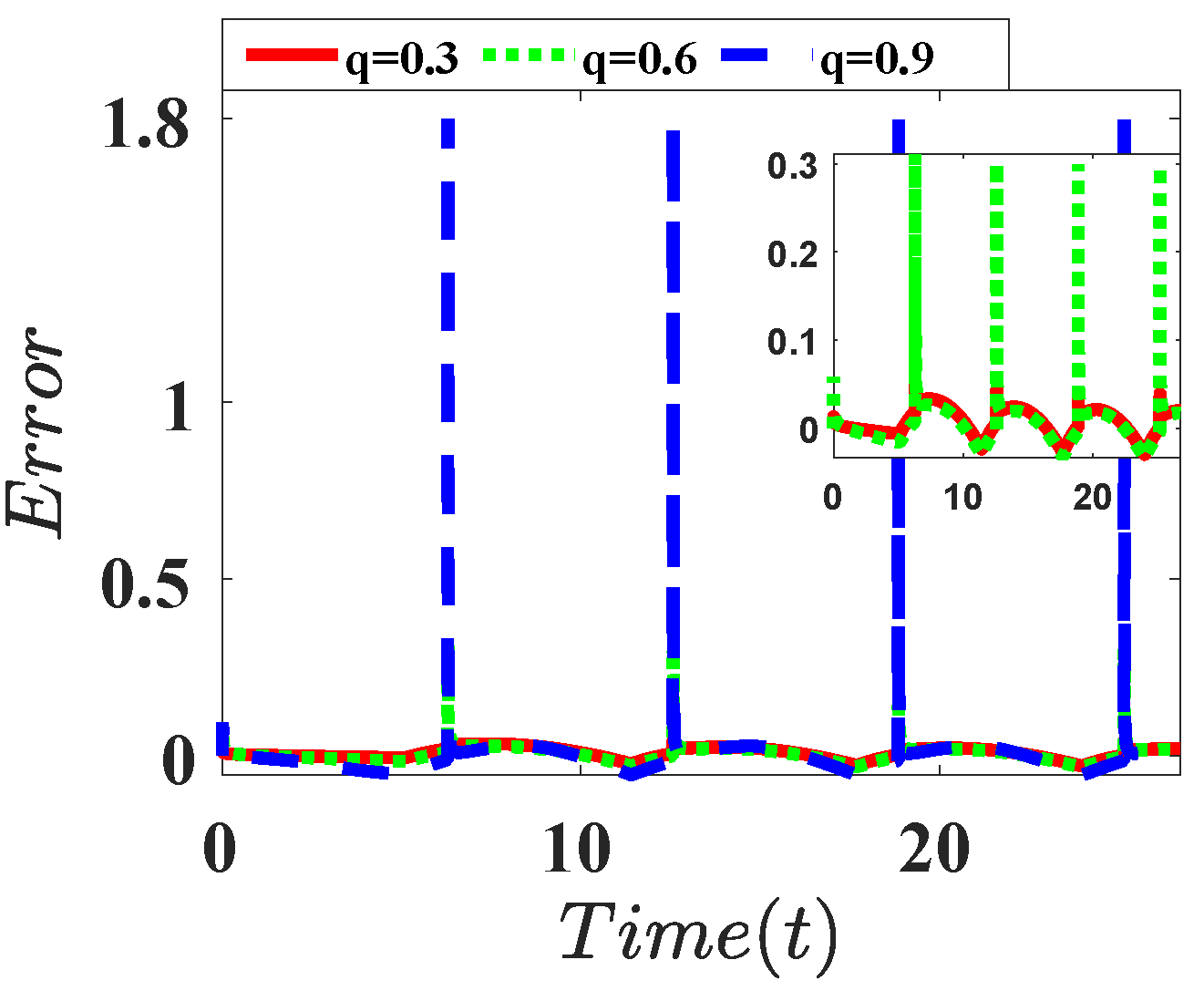 | 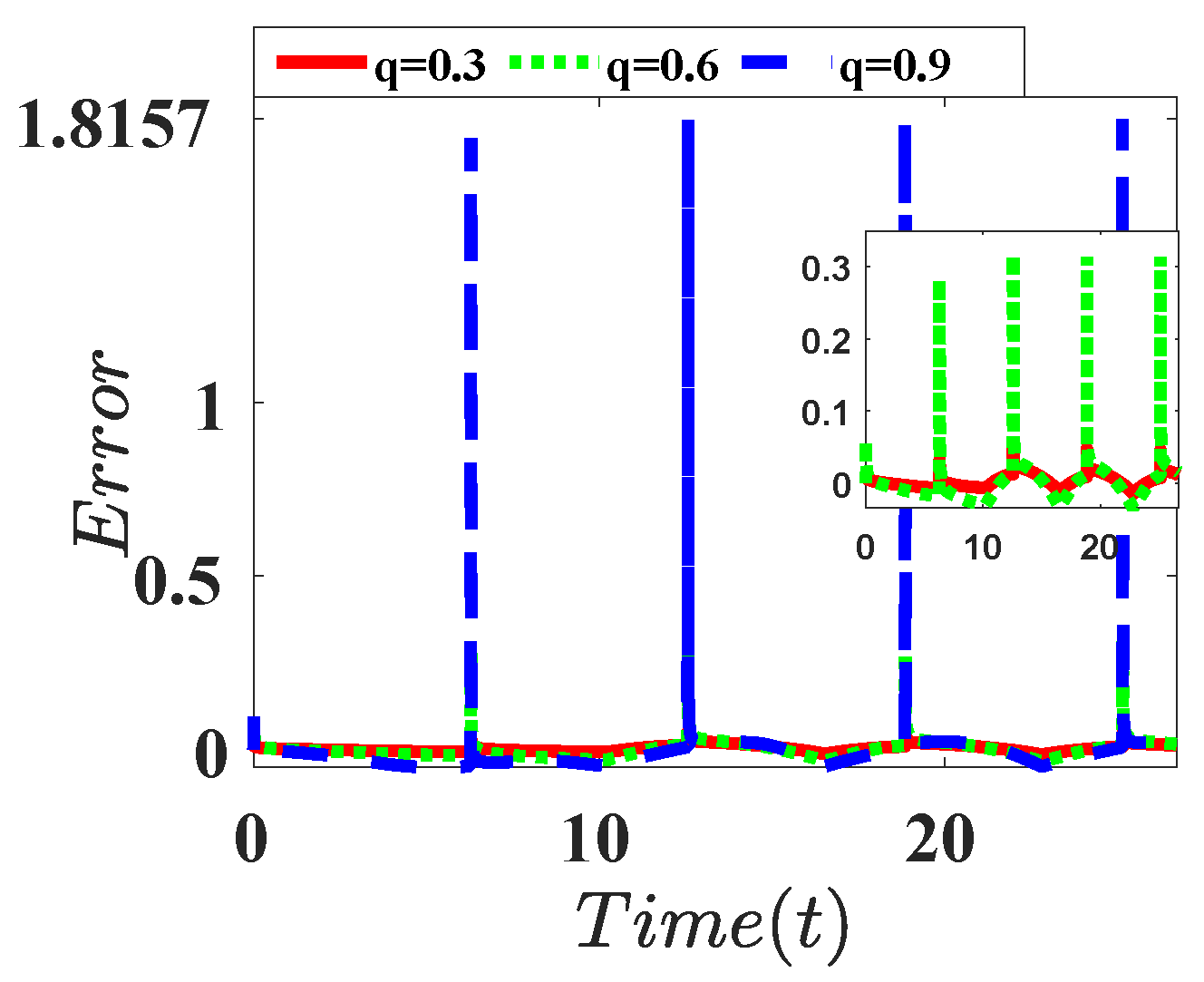 |
| Integral | 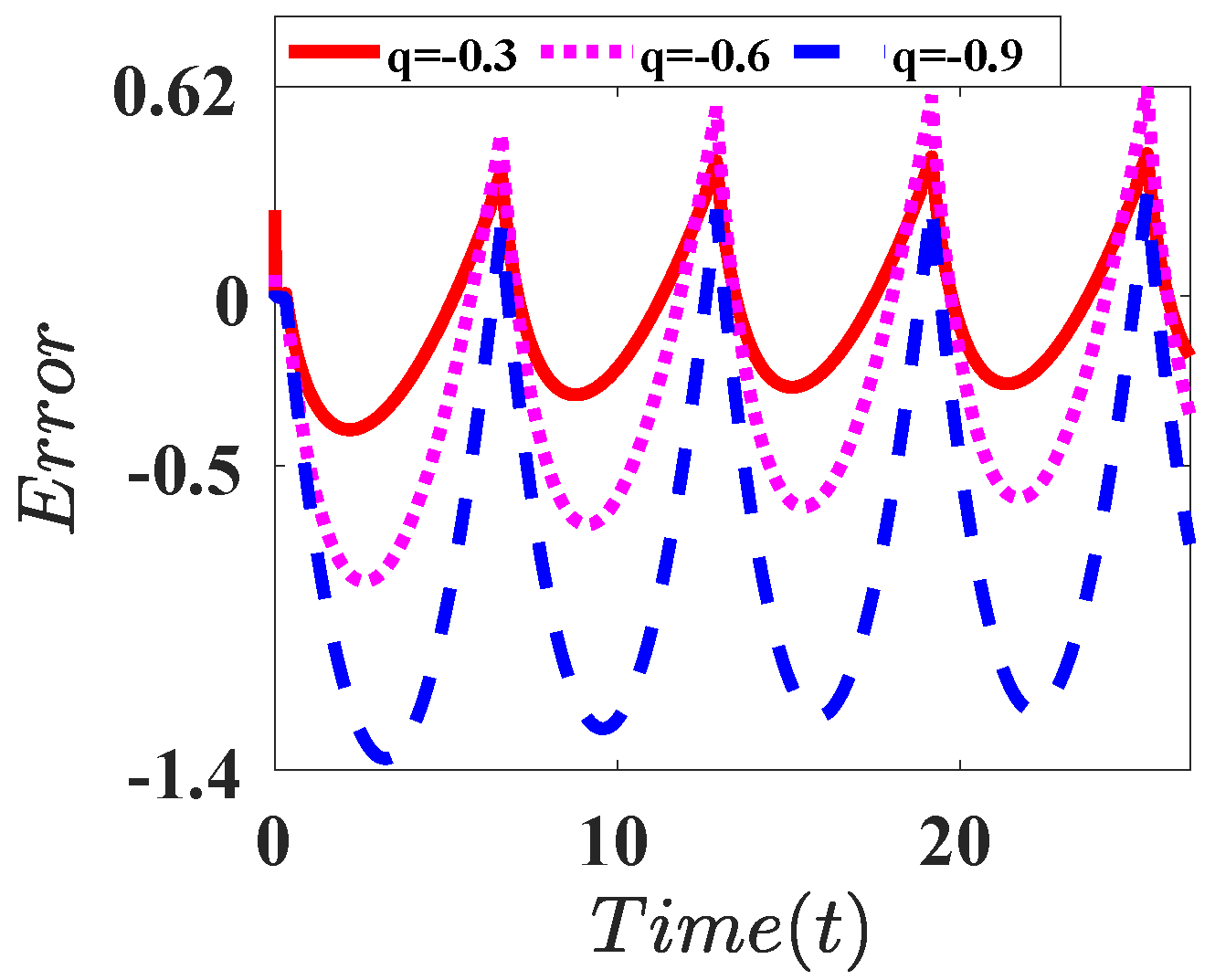 |  | 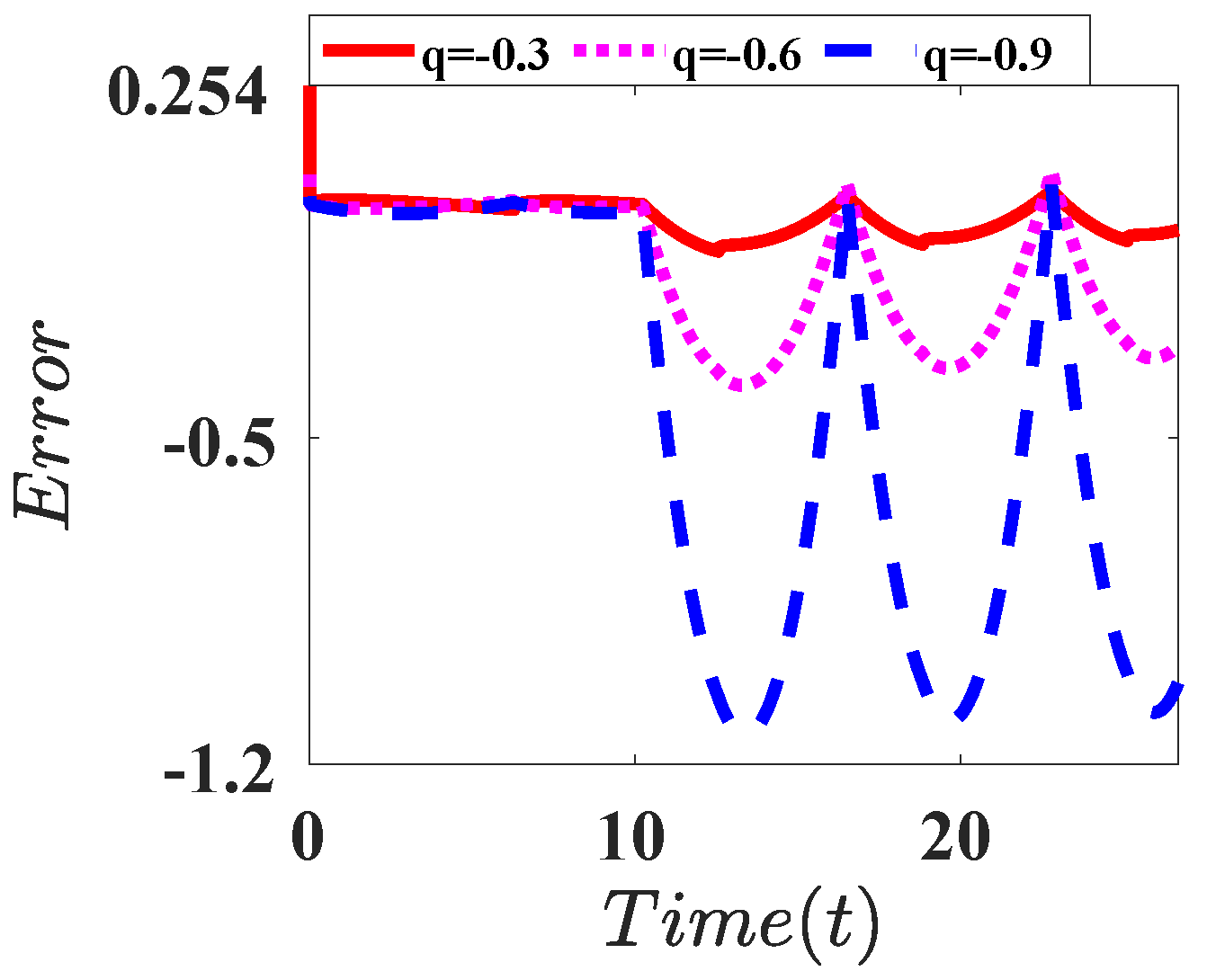 |
| L = 32 | L = 512 | L = 1024 | |
|---|---|---|---|
| Derivative | 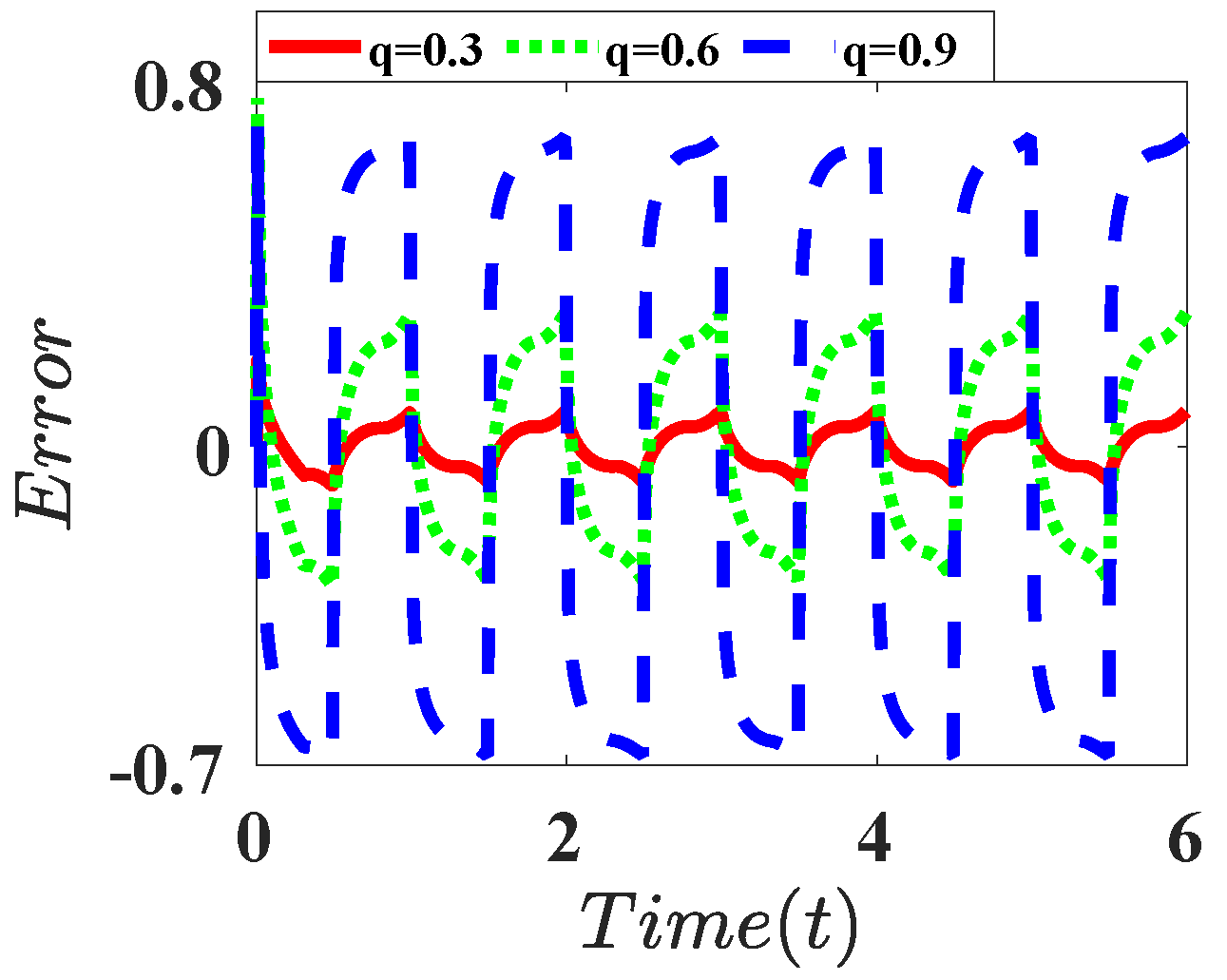 | 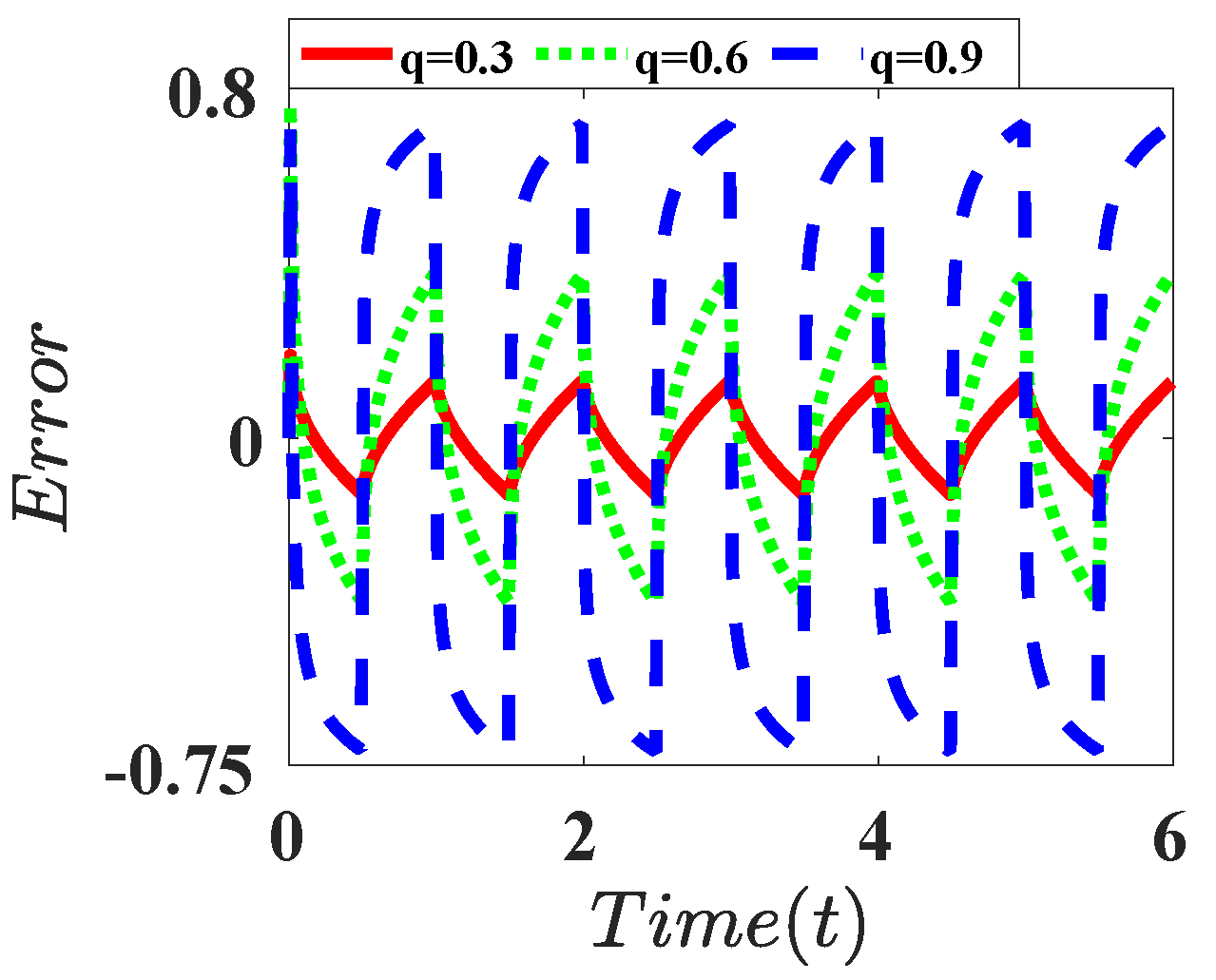 | 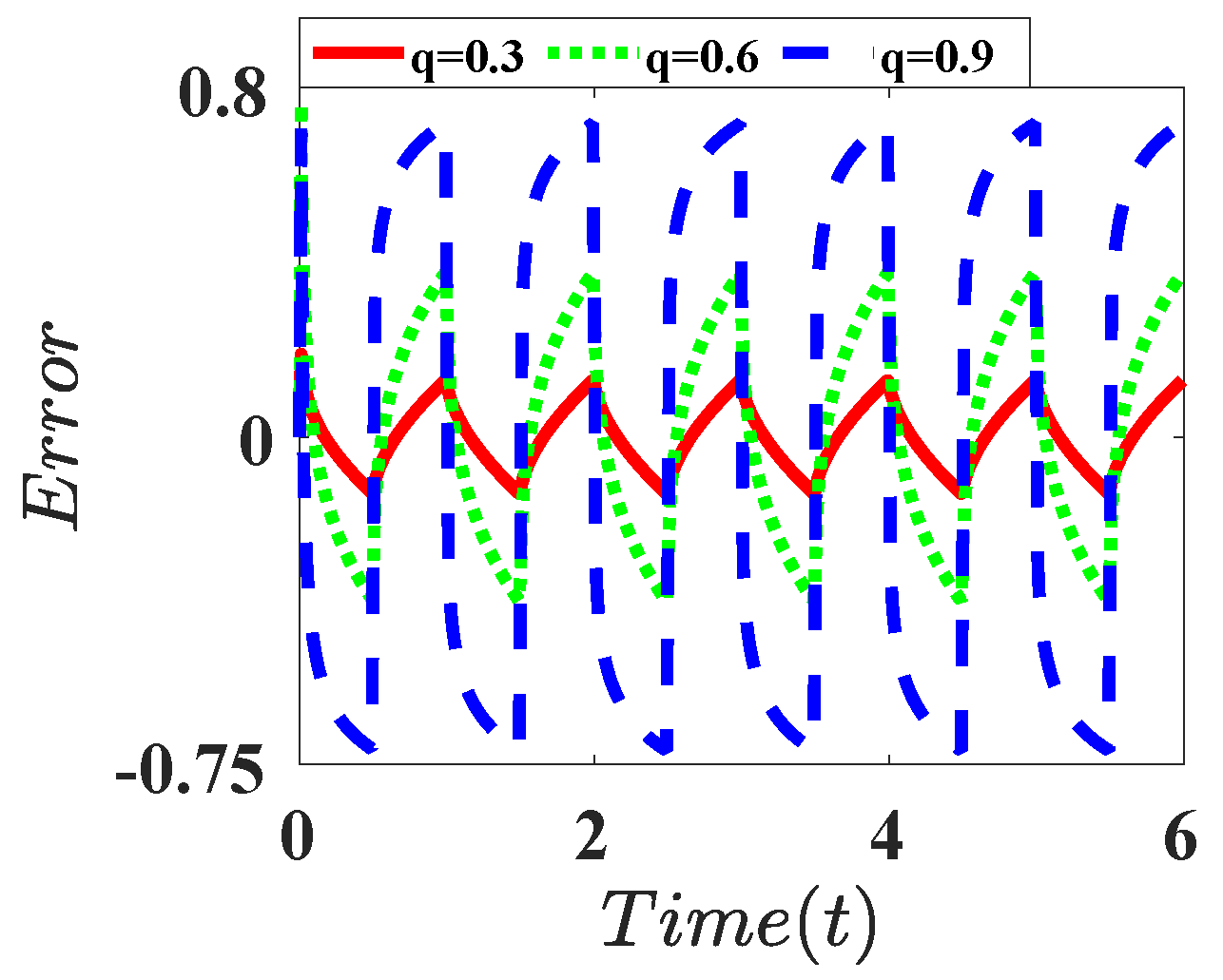 |
| Integral |  | 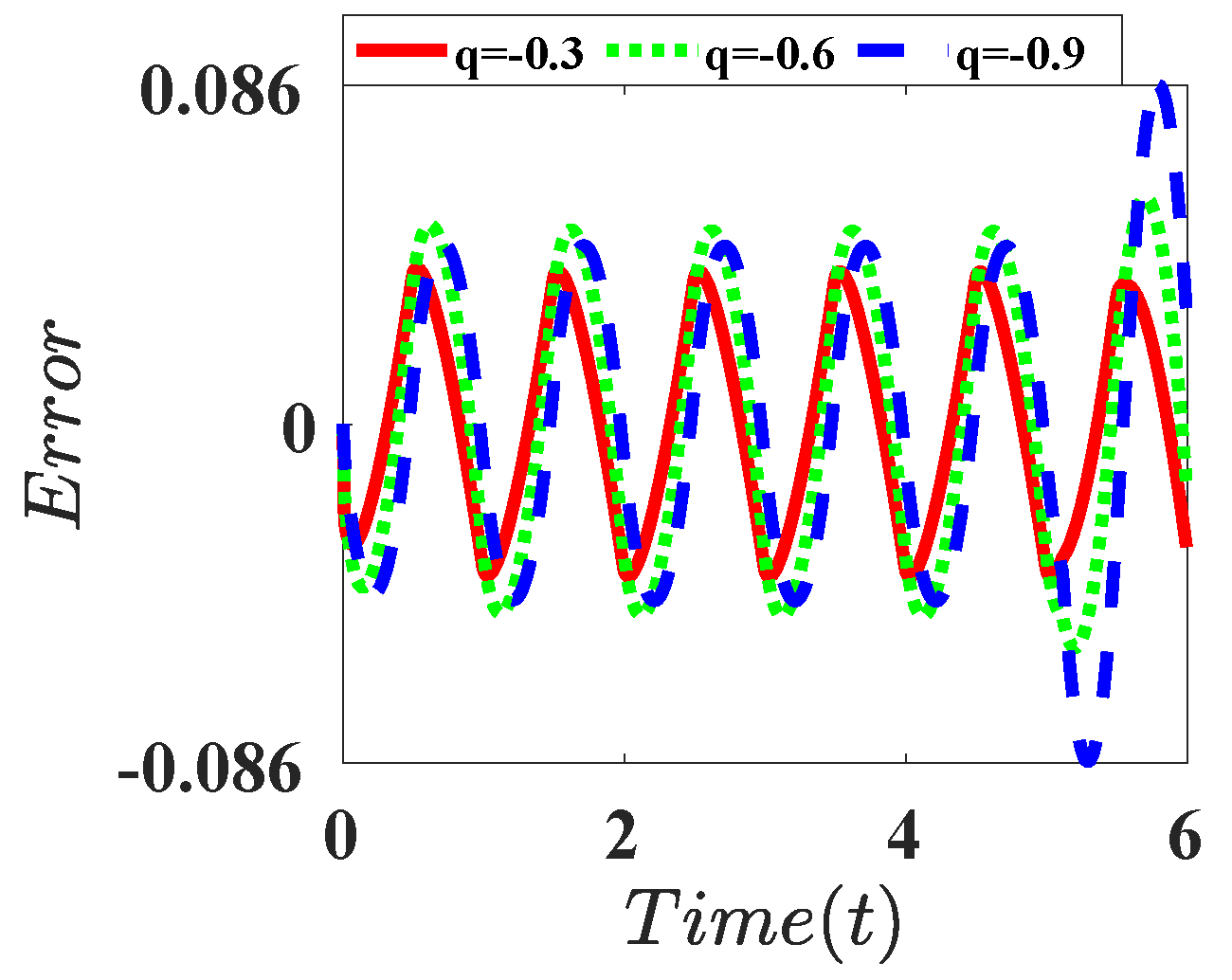 | 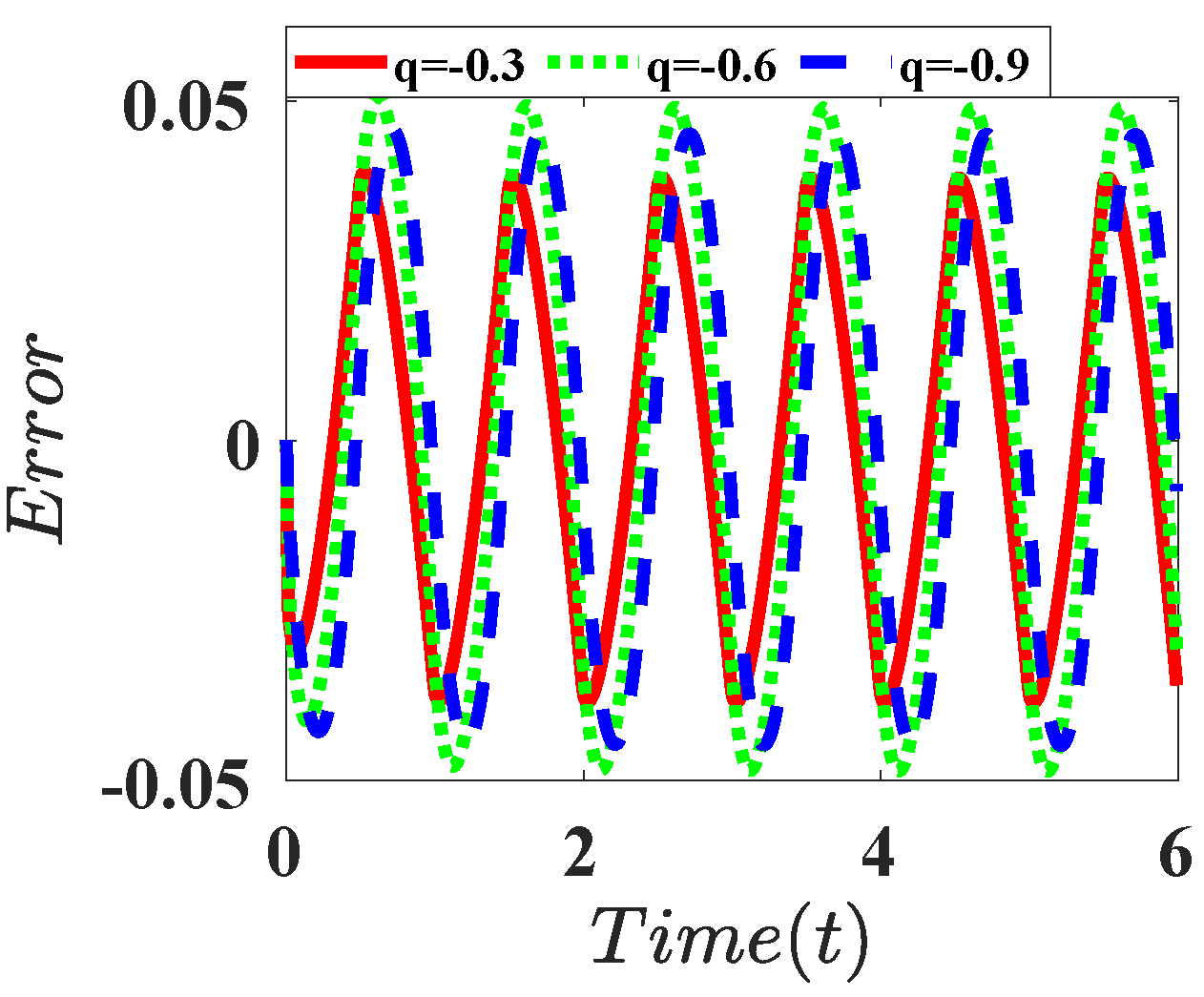 |
| The proposed Design | 0.22 | 1.7 | 0.05 | 1.4 |
| [29] | 0.22 | 1.8 | 0.01 | 1.5 |
| Logic Utilization | No. of Slice LUTs | No. of Slice Registers | Maximum Frequency (MHz) | DSP Multipliers |
|---|---|---|---|---|
| Proposed Design (L = 20) | 22,968 (36%) | 1072 (1%) | 9.328 | 64 (26%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monir, M.S.; Sayed, W.S.; Madian, A.H.; Radwan, A.G.; Said, L.A. A Unified FPGA Realization for Fractional-Order Integrator and Differentiator. Electronics 2022, 11, 2052. https://doi.org/10.3390/electronics11132052
Monir MS, Sayed WS, Madian AH, Radwan AG, Said LA. A Unified FPGA Realization for Fractional-Order Integrator and Differentiator. Electronics. 2022; 11(13):2052. https://doi.org/10.3390/electronics11132052
Chicago/Turabian StyleMonir, Mohamed S., Wafaa S. Sayed, Ahmed H. Madian, Ahmed G. Radwan, and Lobna A. Said. 2022. "A Unified FPGA Realization for Fractional-Order Integrator and Differentiator" Electronics 11, no. 13: 2052. https://doi.org/10.3390/electronics11132052
APA StyleMonir, M. S., Sayed, W. S., Madian, A. H., Radwan, A. G., & Said, L. A. (2022). A Unified FPGA Realization for Fractional-Order Integrator and Differentiator. Electronics, 11(13), 2052. https://doi.org/10.3390/electronics11132052








