Motion Tracking Algorithms Based on Wearable Inertial Sensor: A Focus on Shoulder
Abstract
:1. Introduction
2. Materials and Methods
2.1. Eligibility Criteria
2.1.1. Study Inclusion Criteria
- Only articles written in English.
- Articles published in peer-reviewed journals or presented at a conference.
- Wearable magnetic/inertial sensors to track upper limb kinematics, including the shoulder joint.
- Studies that developed an algorithm to extract shoulder joint variables of clinical relevance.
2.1.2. Study Exclusion Criteria
- Reviews, books, cadaver studies;
- Studies in which the shoulder joint was not included;
- Patients who underwent previous surgery (hemiarthroplasty, total joint arthroplasty, rotator cuff repair);
- Patients with neurological pathologies (e.g., stroke);
- Use of prosthesis, orthoses, exoskeleton or robotic devices;
- Studies where the analysis was done with a combination of inertial sensors and other types of sensors.
2.2. Search Strategy
2.3. Study Selection
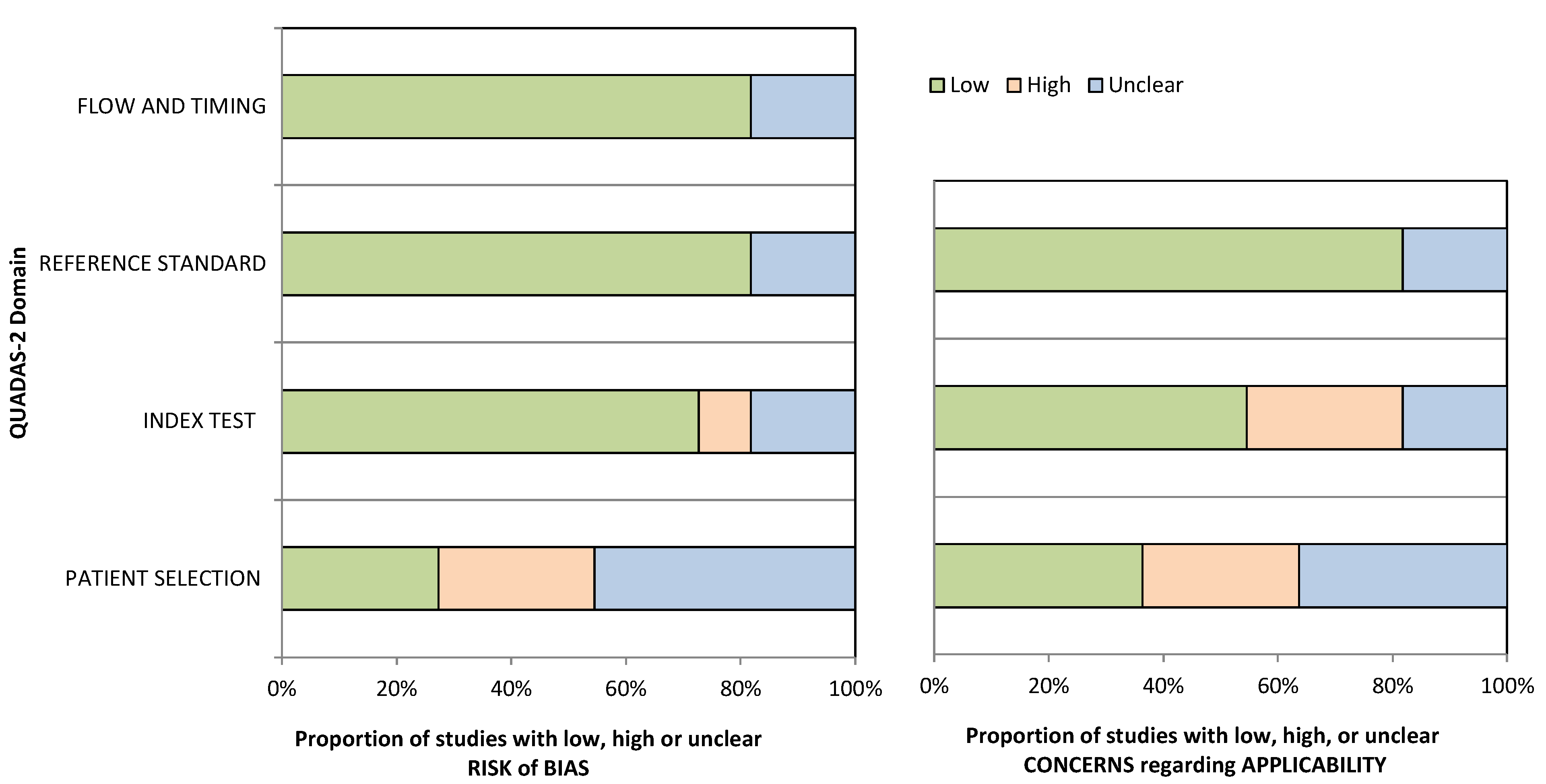
2.4. Quality Assessment
2.5. Data Synthesis and Analysis
3. Results
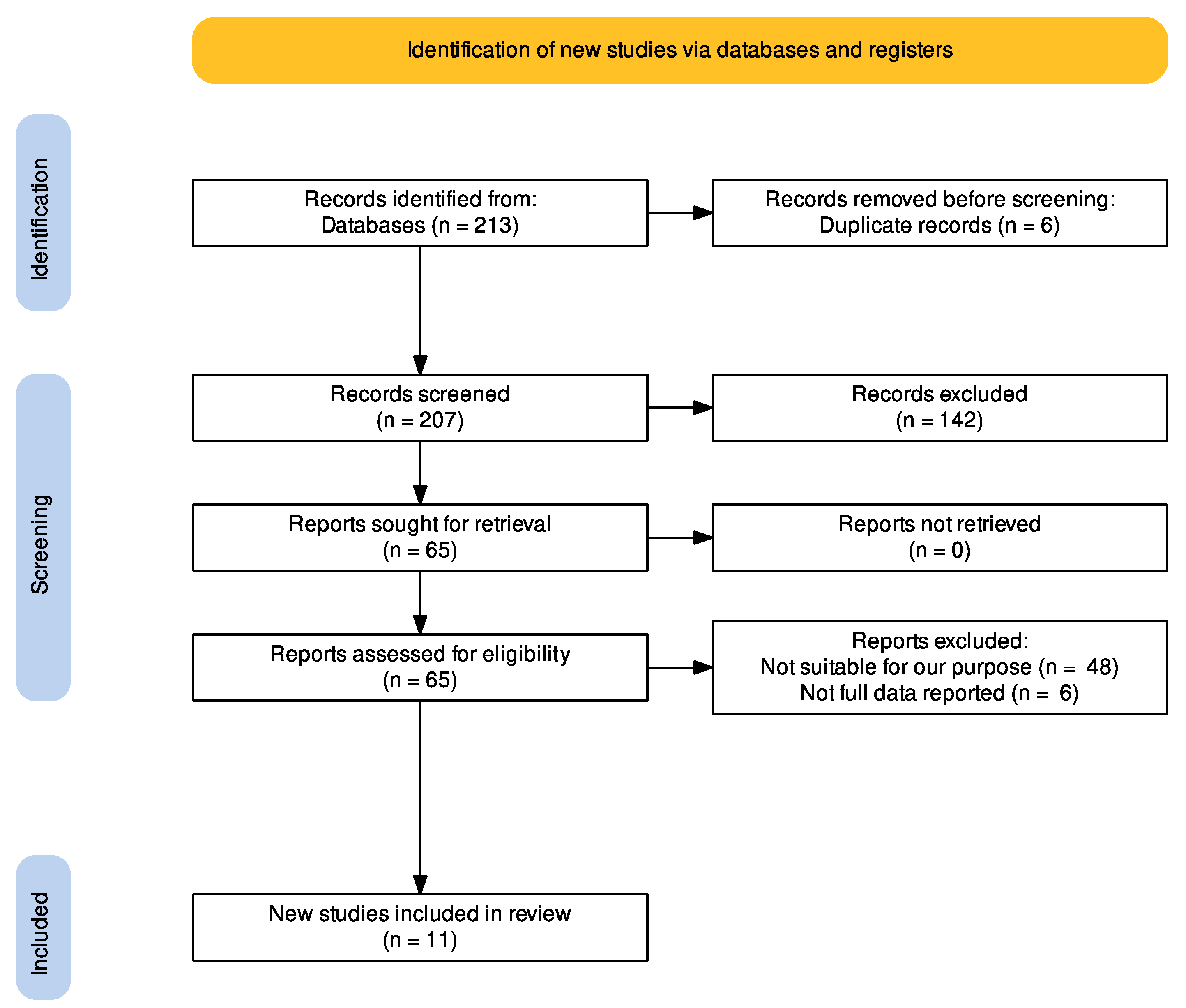
3.1. Study Selection
3.2. Study Characteristics and Risk of Bias Assessment
| First Author, Year | Participants (N) | Patients Characteristics | Sensors | Sensors (N), Placement | Upper Limb Kinematic Representation (Shoulder DoF) | ||
|---|---|---|---|---|---|---|---|
| Acc | Gyr | Magn | |||||
| El Gohary 2011, [19] | - | - | V | V | IMU (N = 2), APDM Opal sensor FA (near wrist), UA (between the shoulder and elbow) | - | |
| El-Gohary 2012, [20] | HS (N = 8) | Not specified | V | V | IMU (N = 2), APDM Opal UA, FA | Upper limb with 5 DOFs, 3 DOFs (Sh) | |
| Hsu 2013, [22] | HS (N = 10) | 8 males, 2 females Y: 23.3 ± 1.33, a mean height of 171 ± 7.45 cm, and a mean body mass of 62.8 ± 12.1 kg | V | V | V | N = 2 LSM303DLH (acc, magn) L3G4200D (gyr) UA, FA | - |
| Hyde 2008, [18] | - | - | V | V | IMU (N = 2), Distal end of Sh | - | |
| Lee 2012, [27] | HS (N = 1) | Not specified | V | Acc (N = 2), MMA7361L (Freescale) UA (near elb), FA (near wri) | - | ||
| Mazomenos 2016, [21] | HS (N = 18) Control group (N = 4) | HS: staff and students from the university, Y: 25–50, both male and female, both left and right arm dominance. Control group: stroke survivors, both men and women, Y: 45–73, at different post-stroke rehabilitation stages. | V | V | V | MARG (N = 2), FA (wri), UA (elb) | 2-link limb model of upper limb 3 DOFs (Sh) |
| Pathirana 2018, [24] | HS (N = 10) | 8 males and 2 females | V | V | V | MIMU (N = 1), elb | 3 DOFs (Sh) |
| Peppoloni 2013, [25] | - | - | V | V | V | MIMU (N = 3) | Upper limb with 7 DOFs |
| Salah 2014, [28] | - | - | V | V | IMU (N = 2) Trunk, thigh | - | |
| Zhang 2011, [23] | HS (N = 4) | Not specified | V | V | V | MIMU (N = 3), wlb, wri, SE | 2 Link limb model (UA, FA), revolute joint (elb) 3 DOFs (Sh) |
| Zhou 2006, [26] | HS (N = 4) | Healthy patients, Y = 20–40 | V | V | V | MIMU (N = 2), Xsens MT9B UA (near the wri), FA (elb joint) | Upper limb with 5 DOFs, |
| First Author, Year | Sensors Fusion Algorithm | Comparator | Movements | Shoulder Parameters | Accuracy |
|---|---|---|---|---|---|
| El Gohary 2011, [19] | UKF | O (Eagle Analog System) | AB-AD (Sh) IER (Sh) FLX-EXT (Sh) | - | R > 0.9 |
| El-Gohary 2012, [20] | UKF | O (Vicon) | AB-AD (Sh) IER (Sh) FLX-EXT (Sh) | - | R ≥ 0.95 RMSE < 8° |
| Hsu 2013, [22] | Quaternion-based CF | Xsens MTw inertial sensors | FLX-EXT, AB, IER | RMSE < 3.36° | |
| Hyde 2008, [18] | Composite filter | - | Depression-elevation (sh), Retraction-protraction (Sh) | Upper limb-orientation | <15 Hz |
| Lee 2012, [27] | Factorized quaternion Approach | IMU (MTx Xsens) | FLX-EXT (UA) IER (UA) | Orientation of the UA | Mean Difference < 3.68° |
| Mazomenos 2016, [21] | Quaternion-based gradient descent | - | AB-AD (Sh) IER (Sh) FLX-EXT (Sh) | Joint angles, position (UA, FA) | - |
| Pathirana 2018, [24] | EKF | O (Vicon, Kinect) | Forward FLX-EXT AB-AD Backward FLX-EXT Horizontal FLX-EXT | - | RMSE < 8.46° (Kinect) RMSE < 6.08° (VICON) |
| Peppoloni 2013, [25] | UKF | O (Vicon, Kinect) | AB-AD (Sh) Internal rotation (Sh) FLX-EXT (Sh) | - | RMSE = 7.85° (5 DOFs) R = 0.93 (5 DOFs) RMSE = 7.41° (7 DOFs) R = 0.82 (7 DOFs) |
| Salah 2014, [28] | ANFIS | VICON | - | - | RMSE < 0.018 m |
| Zhang 2011, [23] | UKF | MTx sensor units, BTS SMART-D | Free movements | Upper limb motion AB-AD (Sh) IER (Sh) FLX-EXT (Sh) | RMSE < 0.2276° R > 0.8912 |
| Zhou 2006, [26] | Lagrangian-based optimisation technique | CODA | shrugging | - | RMSE < 0.004 m R > 0.96 |
3.3. Results of Individual Studies
4. Discussion
4.1. Analysis of Sensor-Fusion Algorithms
4.2. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANFIS | adaptive neuro-fuzzy inference system, |
| O | optical tracking system |
| CF | complementary filter, |
| QUEST | quaternion estimator algorithm, |
| r | correlation coefficient, |
| RMSE | root mean square error, |
| SD | standard deviation, |
| UKF | unscented Kalman filter, |
References
- Krishnan, R.; Björsell, N.; Gutierrez-Farewik, E.M.; Smith, C. A survey of human shoulder functional kinematic representations. Med. Biol. Eng. Comput. 2019, 57, 339–367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Locher, J.; Wilken, F.; Beitzel, K.; Buchmann, S.; Longo, U.G.; Denaro, V.; Imhoff, A.B. Hill-Sachs Off-track Lesions as Risk Factor for Recurrence of Instability after Arthroscopic Bankart Repair. Arthrosc. J. Arthrosc. Relat. Surg. 2016, 32, 1993–1999. [Google Scholar] [CrossRef] [PubMed]
- Tondu, B. Estimating Shoulder-Complex Mobility. Appl. Bionics Biomech. 2007, 4, 19–29. [Google Scholar] [CrossRef] [Green Version]
- Kapandji, A. Physiology of the Joints; Upper Limb: Churchill Livingstone, UK, 1982; Volume 1. [Google Scholar]
- Karduna, A.R.; McClure, P.W.; Michener, L.A. Scapular kinematics: Effects of altering the Euler angle sequence of rotations. J. Biomech. 2000, 33, 1063–1068. [Google Scholar] [CrossRef]
- McClure, P.W.; Michener, L.A.; Sennett, B.J.; Karduna, A.R. Direct 3-dimensional measurement of scapular kinematics during dynamic movements in vivo. J. Shoulder Elb. Surg. 2001, 10, 269–277. [Google Scholar] [CrossRef] [Green Version]
- Dayanidhi, S.; Orlin, M.; Kozin, S.; Duff, S.; Karduna, A. Scapular kinematics during humeral elevation in adults and children. Clin. Biomech. 2005, 20, 600–606. [Google Scholar] [CrossRef]
- Holzbaur, K.R.; Murray, W.M.; Delp, S.L. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Ann. Biomed. Eng. 2005, 33, 829–840. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, M.; Li, J.; Cao, Q. A Modified Kinematic Model of Shoulder Complex Based on Vicon Motion Capturing System: Generalized GH Joint with Floating Centre. Sensors 2020, 20, 3713. [Google Scholar] [CrossRef]
- Carnevale, A.; Schena, E.; Formica, D.; Massaroni, C.; Longo, U.G.; Denaro, V. Skin Strain Analysis of the Scapular Region and Wearables Design. Sensors 2021, 21, 5761. [Google Scholar] [CrossRef]
- Beshara, P.; Chen, J.F.; Read, A.C.; Lagadec, P.; Wang, T.; Walsh, W.R. The Reliability and Validity of Wearable Inertial Sensors Coupled with the Microsoft Kinect to Measure Shoulder Range-of-Motion. Sensors 2020, 20, 7238. [Google Scholar] [CrossRef]
- Carnevale, A.; Longo, U.G.; Schena, E.; Massaroni, C.; Lo Presti, D.; Berton, A.; Candela, V.; Denaro, V. Wearable systems for shoulder kinematics assessment: A systematic review. BMC Musculoskelet. Disord. 2019, 20, 546. [Google Scholar] [CrossRef] [PubMed]
- Longo, U.G.; Huijsmans, P.E.; Maffulli, N.; Denaro, V.; De Beer, J.F. Video analysis of the mechanisms of shoulder dislocation in four elite rugby players. J. Orthop. Sci. 2011, 16, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Höglund, G.; Grip, H.; Öhberg, F. The importance of inertial measurement unit placement in assessing upper limb motion. Med. Eng. Phys. 2021, 92, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Group, P. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med. 2009, 6, e1000097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whiting, P.F.; Rutjes, A.W.; Westwood, M.E.; Mallett, S.; Deeks, J.J.; Reitsma, J.B.; Leeflang, M.M.; Sterne, J.A.; Bossuyt, P.M.; QUADAS-2 Group. QUADAS-2: A revised tool for the quality assessment of diagnostic accuracy studies. Ann. Intern. Med. 2011, 155, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Haddaway, N.R.; McGuinness, L.A.; Pritchard, C.C. PRISMA2020: R Package and Shinyapp for Producing PRISMA 2020 Compliant Flow Diagram. Zenodo. 2021. Available online: https://zenodo.org/record/5082518#.YpWQJu5Bw2w (accessed on 18 April 2022).
- Hyde, R.A.; Ketteringham, L.P.; Neild, S.A.; Jones, R.S. Estimation of upper-limb orientation based on accelerometer and gyroscope measurements. IEEE Trans. Biomed. Eng. 2008, 55, 746–754. [Google Scholar] [CrossRef]
- El-Gohary, M.; Holmstrom, L.; Huisinga, J.; King, E.; McNames, J.; Horak, F. Upper limb joint angle tracking with inertial sensors. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 5629–5632. [Google Scholar] [CrossRef]
- El-Gohary, M.; McNames, J. Shoulder and elbow joint angle tracking with inertial sensors. IEEE Trans. Biomed. Eng. 2012, 59, 2635–2641. [Google Scholar] [CrossRef]
- Mazomenos, E.B.; Biswas, D.; Cranny, A.; Rajan, A.; Maharatna, K.; Achner, J.; Klemke, J.; Jobges, M.; Ortmann, S.; Langendorfer, P. Detecting Elementary Arm Movements by Tracking Upper Limb Joint Angles With MARG Sensors. IEEE J. Biomed. Health Inform. 2016, 20, 1088–1099. [Google Scholar] [CrossRef]
- Hsu, Y.; Wang, J.; Lin, Y.; Chen, S.; Tsai, Y.; Chu, C.; Chang, C. A wearable inertial-sensing-based body sensor network for shoulder range of motion assessment. In Proceedings of the 2013 1st International Conference on Orange Technologies (ICOT), Tainan, Taiwan, 12–16 March 2013; pp. 328–331. [Google Scholar]
- Zhang, Z.; Wong, W.; Wu, J. Ubiquitous Human Upper-Limb Motion Estimation using Wearable Sensors. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 513–521. [Google Scholar] [CrossRef]
- Pathirana, P.N.; Karunarathne, M.S.; Williams, G.L.; Nam, P.T.; Durrant-Whyte, H. Robust and Accurate Capture of Human Joint Pose Using an Inertial Sensor. IEEE J. Transl. Eng. Health Med. 2018, 6, 1–11. [Google Scholar] [CrossRef]
- Peppoloni, L.; Filippeschi, A.; Ruffaldi, E.; Avizzano, C.A. A novel 7 degrees of freedom model for upper limb kinematic reconstruction based on wearable sensors. In Proceedings of the 2013 IEEE 11th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, Serbia, 26–28 September 2013; pp. 105–110. [Google Scholar]
- Zhou, H.; Stone, T.; Hu, H.; Harris, N. Use of multiple wearable inertial sensors in upper limb motion tracking. Med. Eng. Phys. 2008, 30, 123–133. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.X.; Low, K. A Factorized Quaternion Approach to Determine the Arm Motions Using Triaxial Accelerometers With Anatomical and Sensor Constraints. IEEE Trans. Instrum. Meas. 2012, 61, 1793–1802. [Google Scholar] [CrossRef]
- Salah, O.; Ramadan, A.A.; Sessa, S.; El-Bab, A.M.R.F.; Abo-Ismail, A.; Zecca, M.; Kobayashi, Y.; Takanishi, A.; Fujie, M. Sit to stand sensing using wearable IMUs based on adaptive Neuro Fuzzy and Kalman Filter. In Proceedings of the 2014 IEEE Healthcare Innovation Conference (HIC), Seattle, WA, USA, 8–10 October 2014; pp. 288–291. [Google Scholar]
- Filippeschi, A.; Schmitz, N.; Miezal, M.; Bleser, G.; Ruffaldi, E.; Stricker, D. Survey of Motion Tracking Methods Based on Inertial Sensors: A Focus on Upper Limb Human Motion. Sensors 2017, 17, 1257. [Google Scholar] [CrossRef] [Green Version]
- Roetenberg, D. Inertial and Magnetic Sensing of Human Motion. Ph.D. Thesis, Universiteit Twente, Enschede, The Netherlands, 2006. [Google Scholar]
- Bachmann, E.R.; Yun, X.; Peterson, C.W. An Investigation of the Effects of Magnetic Variations on Inertial/Magnetic Orientation. Sensors 2004, 2, 1115–1122. [Google Scholar]
- Yun, X.; Bachmann, E.R. Design, Implementation, and Experimental Results of a Quaternion-Based Kalman Filter for Human Body Motion Tracking. IEEE Trans. Robot. 2006, 22, 1216–1227. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Longo, U.G.; De Salvatore, S.; Sassi, M.; Carnevale, A.; De Luca, G.; Denaro, V. Motion Tracking Algorithms Based on Wearable Inertial Sensor: A Focus on Shoulder. Electronics 2022, 11, 1741. https://doi.org/10.3390/electronics11111741
Longo UG, De Salvatore S, Sassi M, Carnevale A, De Luca G, Denaro V. Motion Tracking Algorithms Based on Wearable Inertial Sensor: A Focus on Shoulder. Electronics. 2022; 11(11):1741. https://doi.org/10.3390/electronics11111741
Chicago/Turabian StyleLongo, Umile Giuseppe, Sergio De Salvatore, Martina Sassi, Arianna Carnevale, Giovanna De Luca, and Vincenzo Denaro. 2022. "Motion Tracking Algorithms Based on Wearable Inertial Sensor: A Focus on Shoulder" Electronics 11, no. 11: 1741. https://doi.org/10.3390/electronics11111741
APA StyleLongo, U. G., De Salvatore, S., Sassi, M., Carnevale, A., De Luca, G., & Denaro, V. (2022). Motion Tracking Algorithms Based on Wearable Inertial Sensor: A Focus on Shoulder. Electronics, 11(11), 1741. https://doi.org/10.3390/electronics11111741








