Study on Gibbs Optimization-Based Resource Scheduling Algorithm in Data Aggregation Networks
Abstract
:1. Introduction
2. Related Works
3. Problem Definition
3.1. Interference Model
3.2. Network Model
3.3. Multi-Channel Scheduling
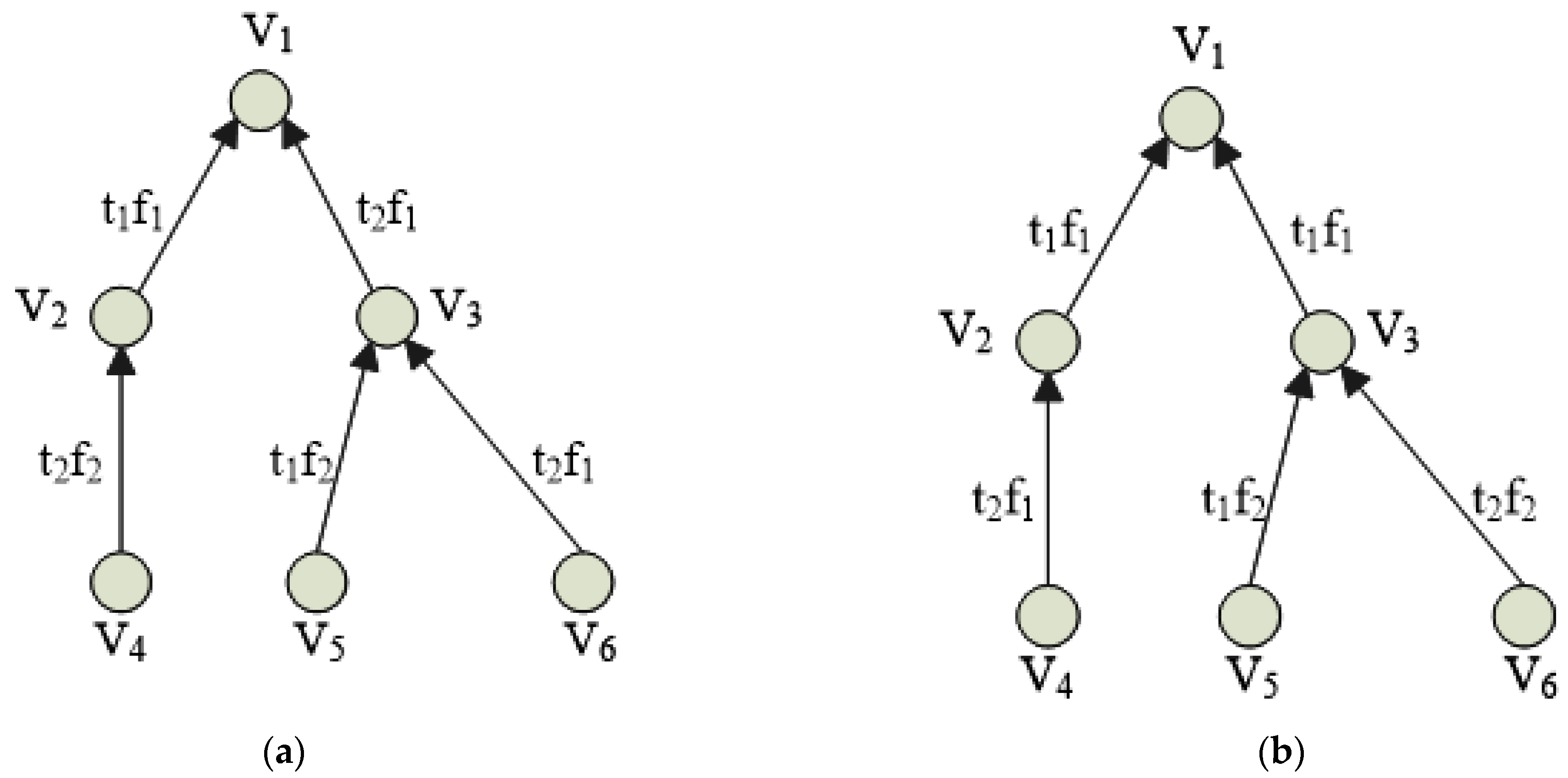
3.4. Interference Graph
3.5. Interference Graph
3.6. Minimization of Communication Conflict
- (2)
- The problem of minimizing the vertex coloring of graphs is a special case of minimizing network communication conflicts and is an NP-complete problem [25]. The problem of minimizing vertex coloring is described as follows: Given an undirected graph and a non-negative integer K. Whether there is a non-negative integer , divided by into k disjoint subsets (each subset represents a specific color) so that the nodes in the same subset are not adjacent in the graph . We can see that when the number of channels m = 1, , the problem of minimizing network communication conflicts is a typical problem of minimizing vertex coloring. □
4. Multi-Channel TDMA Scheduling Algorithm
- Constructing routing tree T on the basis of undirected graph G, and constructing the interference graph Ge based on graph G and routing tree T.
- Performing conditional double coloring for the vertex in the interference graph Ge to minimize the communication conflict.
4.1. Construction of Routing Trees
- (1)
- Nodes in the tree check their number of child nodes and broadcast the construction message if the number is less than d. Otherwise, the broadcast stops.
- (2)
- Upon receiving multiple construction messages, the node with the highest priority is selected for all the nodes that are not in the tree as the father node based on the power priority of the broadcasting node, which sends the father node a message requesting to join.
- (3)
- When receiving multiple request messages from nodes outside the tree, nodes in the tree select the node with higher priority based on its own number of child nodes and power priority and send an ACK message to the node with the higher priority.
- (4)
- A node outside the tree joins in the tree only after receiving an ACK message from its father node. Otherwise, the node with the higher priority is selected as the father node, and a message requesting to join is sent to it.
- (5)
- The above process is repeated until no nodes join the routing tree. When the timer is triggered, if the node has not yet joined the routing tree, it needs to broadcast to look for the message of the father node. The node in the tree receives the message and replies with its own number of child nodes. Based on the messages, the node selects a node in the tree with the number of child nodes less than d as its own father node. If there are no nodes with a number of child nodes less than d, the node with the least number of child nodes is selected.
| Algorithm 1. Construction of routing trees. |
| Input: G = (V, E), the max number of children d, the sink node S |
| Output: |
| 01. Initialization: = [1], ; |
| 02. do while |
| 03. for i 1 to || |
| 04. if (children() < d) |
| 05. for j 1 to deg () |
| 06. if ( == max(P(N1()))) |
| 07. = + {}; |
| 08. = + {(, )}; |
| 09. children () = children () + 1; |
| 10. N1() = N1() − {}; |
| 11. end if |
| 12. end for |
| 13. end if |
| 14. end for |
| 15. = − ; |
| 16. for i 1 to || |
| 17. for j 1 to || |
| 18. if (children () == min (children ())) |
| 19. = + {}; |
| 20. = + {(, )}; |
| 21. children () = children () + 1; |
| 22. end if |
| 23. end for |
| 24. end for |
| 25. end while ( == ) |
| 26. V = ; |
| 27. = ; |
4.2. Vertex Coloring
4.2.1. Gibbs Optimization
4.2.2. Methodology
| Algorithm 2. Graph vertex coloring based on the Gibbs optimization. |
| Input: The graph Ge = (V, E), the number of main color k, the number of secondary color m, the max number of iterations , Initial temperature |
| Output: Coloring result of every node in Ge |
| 01. Initialization: count = 0; |
| 02. do while |
| 03. count = 0; |
| 04. T = /log(2 + t) |
| 05. for 1 to |V| |
| 06. for 1 to k |
| 07. for z 1 to m |
| 08. Energy (, , z); |
| 09. end for |
| 10. end for |
| 11. for 1 to k DO |
| 12. for z 1 to m DO |
| 13. Probability (, T, Energy (, , z)); //Probability of the node selecting the present color combination |
| 14. end for |
| 15. end for |
| 16. count = count + Conflict (); //Total conflicts in the present network |
| 17. end for |
| 18. end while (count = 0 or t > ) |
5. Experiments and Analysis
5.1. Effects of Network Parameters on Scheduling Algorithms
5.2. Effect of Routing Tree’s Degree on Scheduling Algorithm
5.3. Network Throughput and Transmission Delay
- Network throughput: the number of packets sent in nodes of each time slot network.
- Transmission delay: the average waiting time between two successful transmissions.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dehkordi, S.A.; Farajzadeh, K.; Rezazadeh, J. A survey on data aggregation techniques in IoT sensor networks. Wirel. Netw. 2020, 26, 1243–1263. [Google Scholar] [CrossRef]
- Dumka, A.; Chaurasiya, S.K.; Biswas, A.; Mandoria, H.L. Data Aggregation in Wireless Sensor Networks. In A Complete Guide to Wireless Sensor Networks, 1st ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Ahmed, N.M.; Rikli, N. QoS-Based Data Aggregation and Resource Allocation Algorithm for Machine Type Communication Devices in Next-Generation Networks. IEEE Access 2021, 9, 119735–119754. [Google Scholar] [CrossRef]
- Azarhava, H.; Musevi Niya, J. Energy Efficient Resource Allocation in Wireless Energy Harvesting Sensor Networks. IEEE Wirel. Commun. Lett. 2020, 9, 1000–1003. [Google Scholar] [CrossRef]
- Osamy, W.; El-Sawy, A.A.; Khedr, A.M. Effective TDMA scheduling for tree-based data collection using genetic algorithm in wireless sensor networks. Peer-to-Peer Netw. Appl. 2020, 13, 796–815. [Google Scholar] [CrossRef]
- Xia, N.; Wang, C.; Peng, H.; Zhao, Z.; Chen, Y. Optimization algorithms in wireless monitoring networks: A survey. Neurocomputing 2022, in press. [Google Scholar] [CrossRef]
- Ying, X.; Chen, D.; Zhang, L. Research on spectrum scheduling based on discrete artificial bee colony algorithm. In Proceedings of the 2021 International Conference on Computer Network Security and Software Engineering (CNSSE 2021), Zhuhai, China, 26–28 February 2021. [Google Scholar]
- Cao, K.; Dong, C.; Yu, F. Dynamic Time-slot Allocation Algorithm Based on Environment Sensing in Wireless Sensor Network. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing, ICSIP 2019, Wuxi, China, 19–21 July 2019. [Google Scholar]
- Alghamdi, B.; Ayaida, M.; Fouchal, H. A dynamic slot scheduling for wireless sensors networks. In Proceedings of the 2014 IEEE Global Communications Conference, ICC 2014, Austin, TX, USA, 8–12 December 2014. [Google Scholar]
- Nguyen, N.T.; Liu, B.H.; Weng, H.Z. A Distributed Algorithm: Minimum-Latency Collision-Avoidance Multiple-Data-Aggregation Scheduling in Multi-Channel WSNs. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018. [Google Scholar]
- Zhang, J.; Zhou, G.; Huang, C.; Son, S.H.; Stankovic, J.A. TMMAC: An Energy Efficient Multi-Channel MAC Protocol for Ad Hoc Networks. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 3554–3561. [Google Scholar]
- Zhou, G.; Huang, C.; Yan, T.; He, T.; Stankovic, J.A. MMSN: Multi-Frequency Media Access Control for Wireless Sensor Networks. In Proceedings of the IEEE INFOCOM 2006, 25th IEEE International Conference on Computer Communications, Barcelona, Spain, 23–29 April 2006; pp. 1–13. [Google Scholar]
- Chen, H.; Baras, J.S. A distributed opportunistic scheduling protocol for multi-channel wireless ad-hoc networks. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 274–279. [Google Scholar]
- Incel, Ö.D.; Ghosh, A.; Krishnamachari, B.; Chintalapudi, K. Fast Data Collection in Tree-Based Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2012, 11, 86–99. [Google Scholar] [CrossRef]
- Kori, G.S.; Kakkasageri, M.S. Agent driven resource scheduling in wireless sensor networks: Fuzzy approach. Int. J. Inf. Technol. 2021, 14, 345–358. [Google Scholar] [CrossRef]
- Nguyen, T.; Le, D.T.; Vo, V.V.; Kim, M.; Choo, H. Fast Sensory Data Aggregation in IoT Networks: Collision-Resistant Dynamic Approach. IEEE Internet Things J. 2021, 8, 766–777. [Google Scholar] [CrossRef]
- Ren, M.; Li, J.; Guo, L.; Li, X.; Fan, W. Distributed Data Aggregation Scheduling in Multi-Channel and Multi-Power Wireless Sensor Networks. IEEE Access 2017, 5, 27887–27896. [Google Scholar] [CrossRef]
- Lenka, M.R.; Swain, A.R.; Nayak, B.P. A Hybrid based Distributed Slot Scheduling Approach for WSN MAC. J. Commun. Softw. Syst. 2019, 15, 109–117. [Google Scholar] [CrossRef]
- Incel, Ö.D.; Krishnamachari, B. Enhancing the Data Collection Rate of Tree-Based Aggregation in Wireless Sensor Networks. In Proceedings of the 2008 5th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, San Francisco, CA, USA, 16–20 June 2008; pp. 569–577. [Google Scholar]
- Uyanik, O.; Korpeoglu, I. Multi-channel TDMA Scheduling in Wireless Sensor Networks. Ad Hoc Sens. Wirel. Netw. 2019, 43, 109–138. [Google Scholar]
- Schmid, S.; Wattenhofer, R. Algorithmic models for sensor networks. In Proceedings of the 20th IEEE International Parallel & Distributed Processing Symposium, Rhodes, Greece, 25–29 April 2006. [Google Scholar]
- Dubhashi, A.S.; Mvs, S.; Pati, A.; Shashank, R. Channel Assignment for Wireless Networks Modelled as d-Dimensional Square Grids. In International Workshop on Distributed Computing (IWDC), 1st ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 130–141. [Google Scholar]
- Jain, K.K.; Padhye, J.; Padmanabhan, V.N.; Qiu, L. Impact of Interference on Multi-Hop Wireless Network Performance. Wirel. Netw. 2005, 11, 471–487. [Google Scholar] [CrossRef]
- Zhang, W.J.; Zhu, S.B.; Chang, L.; Wang, X. Channel Conflict Model Based on Graph N Multiple Coloring Theory. Sci. Technol. Eng. 2013, 13, 8166–8172. [Google Scholar]
- Hartmanis, J. Computers and Intractability A Guide to the Theory of Np Completeness. Siam Rev. 1982, 1, 90. [Google Scholar] [CrossRef]
- Karp, R.M. Reducibility among Combinatorial Problems. In 50 Years of Integer Programming; Springer: Berlin/Heidelberg, Germany, 2009; pp. 219–241. [Google Scholar]
- Hesterberg, T. Monte Carlo Strategies in Scientific Computing. Technometrics 2002, 44, 403–404. [Google Scholar] [CrossRef]
- Spall, J.C. Introduction to stochastic search and optimization estimation, simulation, and control. In Wiley-Interscience Series in Discrete Mathematics and Optimization; John Wiley & Sons: New York, NY, USA, 2005; pp. 1–595. [Google Scholar]
- Brémaud, P. Markov Chains. In Texts in Applied Mathematics, 2nd ed.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Xia, N.; Luo, L.; Du, H.; Wang, P.; Yu, Y. Channel Assignment Algorithm Based on Discrete BFO for Wireless Monitoring Networks. In Proceedings of the International Conference on Intelligent Computing, ICIC 2021, Xi’an, China, 9 August 2021. [Google Scholar]














| Notation | Description |
|---|---|
| graph G is an undirected graph, V is the set of vertices, E is the set of edges | |
| link between node i and node j | |
| number of hops between the vertices of the link | |
| SINR | signal to interference and noise ratio |
| the arrival power of node i detected on node j | |
| the noise interference near node j | |
| deg(Si) | the number of neighbor nodes of node Si |
| N1(Si) | the neighbor node set of node Si |
| the tree generated on the basis of the undirected graph G with S as the root node | |
| Children(Si) | the number of child nodes of node Si in the tree |
| the allocated time slot | |
| the allocated channel | |
| . | |
| the ratio of rectangle length to width | |
| a | a node’s choice of main and secondary colors in the interference graph |
| indicator function | |
| the interference degree of the node Si | |
| distribution functions for Gibbs sampling | |
| a solution vector of the system | |
| V(L) | non-negative expression |
| the probability of picking the color combination | |
| degree of graph |
| Maximum Number of Iterations | Degree of the Routing Tree | |
|---|---|---|
| 0.005 | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, S.; Du, H.; Xia, N.; Li, S.; Yu, Y. Study on Gibbs Optimization-Based Resource Scheduling Algorithm in Data Aggregation Networks. Electronics 2022, 11, 1695. https://doi.org/10.3390/electronics11111695
Ding S, Du H, Xia N, Li S, Yu Y. Study on Gibbs Optimization-Based Resource Scheduling Algorithm in Data Aggregation Networks. Electronics. 2022; 11(11):1695. https://doi.org/10.3390/electronics11111695
Chicago/Turabian StyleDing, Sheng, Huazheng Du, Na Xia, Shaojie Li, and Yongtang Yu. 2022. "Study on Gibbs Optimization-Based Resource Scheduling Algorithm in Data Aggregation Networks" Electronics 11, no. 11: 1695. https://doi.org/10.3390/electronics11111695
APA StyleDing, S., Du, H., Xia, N., Li, S., & Yu, Y. (2022). Study on Gibbs Optimization-Based Resource Scheduling Algorithm in Data Aggregation Networks. Electronics, 11(11), 1695. https://doi.org/10.3390/electronics11111695





