In-Memory Computing with Resistive Memory Circuits: Status and Outlook
Abstract
1. Introduction
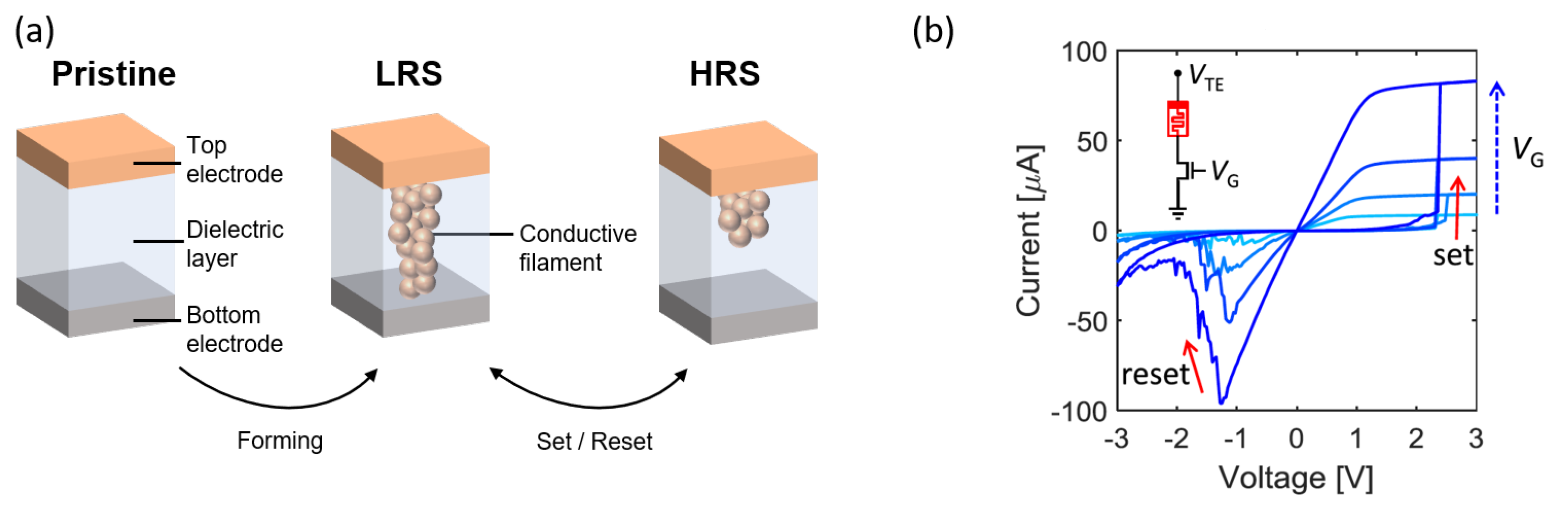
2. RRAM Device Structure
3. Analog Memory Programming Techniques and Variations
3.1. Program-Verify Algorithms and Device-to-Device Variations
3.2. Conductance Drift and Fluctuations
4. RRAM Conductance Mapping Techniques
4.1. Multilevel
4.2. Binary
4.3. Unary
4.4. Multilevel with Redundancy
4.5. Slicing
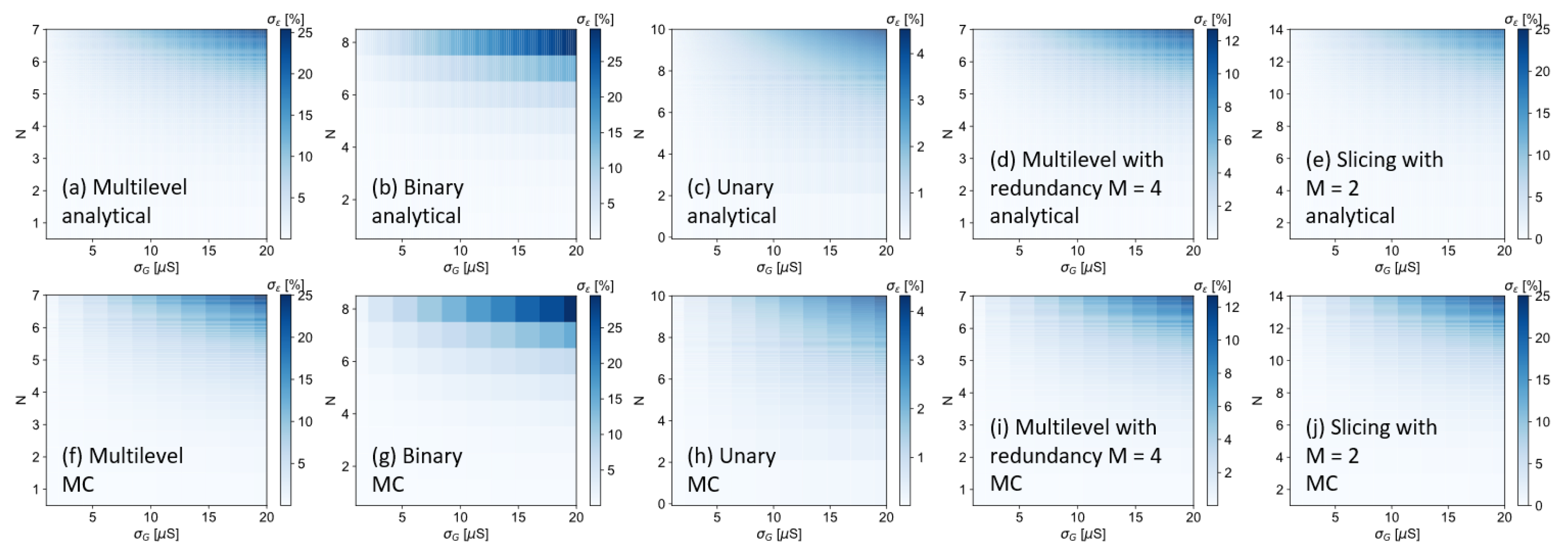
4.6. Simulation Results
| Technique | |||
|---|---|---|---|
| Multilevel | |||
| Binary | |||
| Unary | |||
| Multilevel with redundancy | |||
| Slicing |
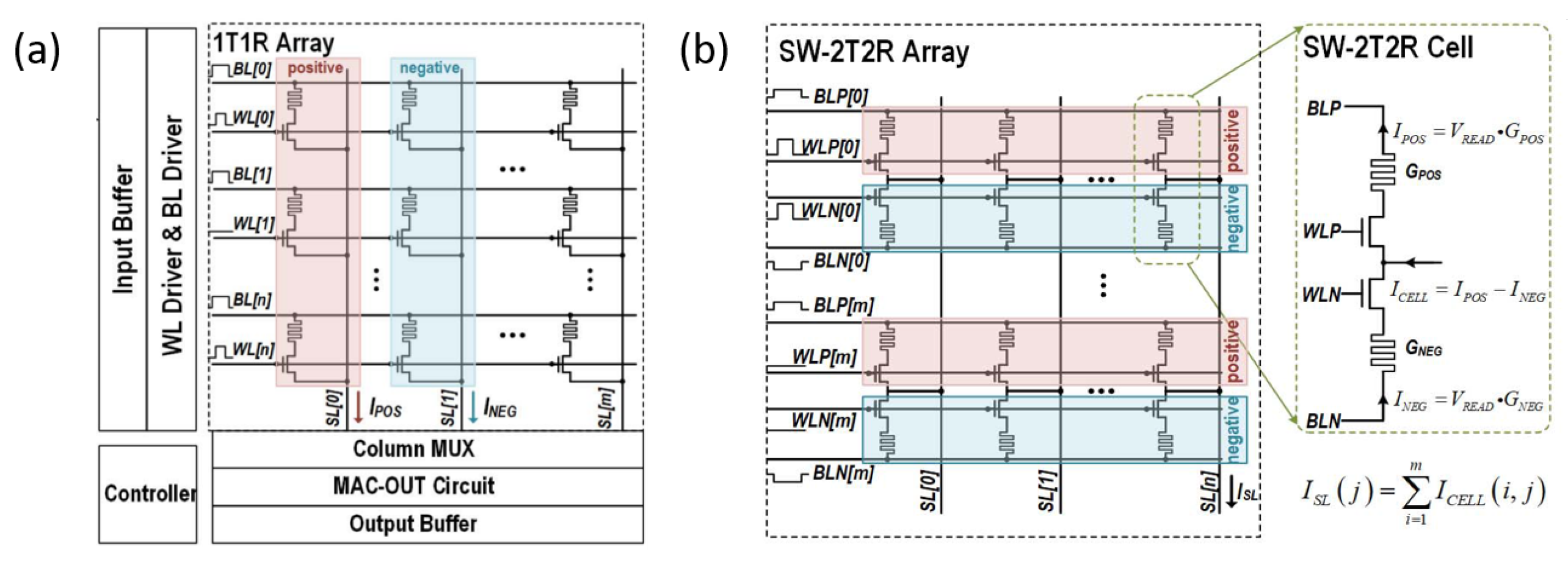
5. Array-Level Reliability Issues
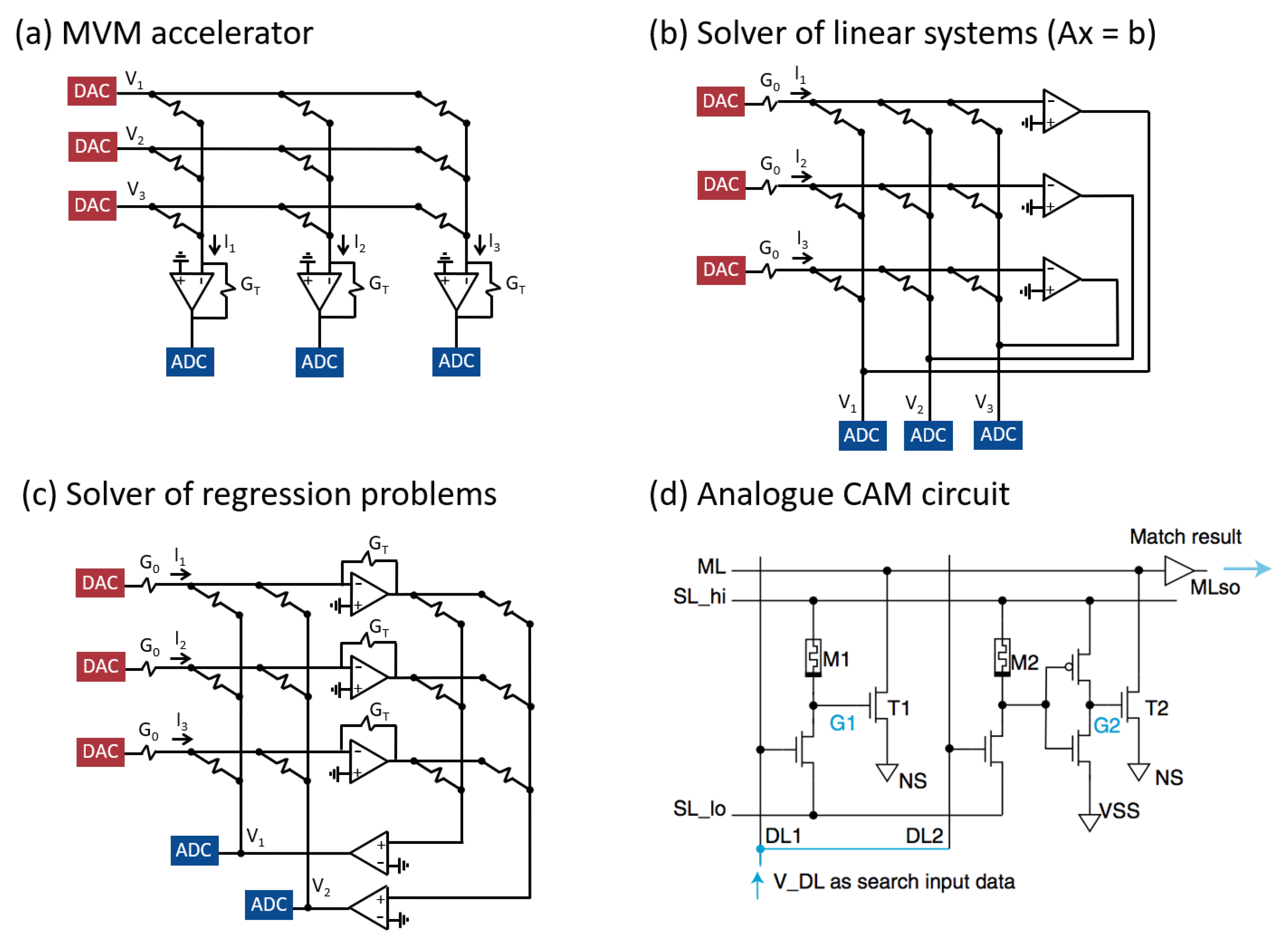
6. Circuit Primitives for Analog Computing
6.1. MVM Accelerator
6.2. Analog Closed-Loop Accelerators
6.3. Analog CAM
7. Outlook on Memory Technologies and Computing Applications
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ielmini, D.; Wong, H.S.P. In-memory computing with resistive switching devices. Nat. Electron. 2018, 1, 333–343. [Google Scholar] [CrossRef]
- Zidan, M.A.; Strachan, J.P.; Lu, W.D. The future of electronics based on memristive systems. Nat. Electron. 2018, 1, 22–29. [Google Scholar] [CrossRef]
- Yu, S. Neuro-Inspired Computing with Emerging Nonvolatile Memorys. Proc. IEEE 2018, 106, 260–285. [Google Scholar] [CrossRef]
- Borghetti, J.; Snider, G.S.; Kuekes, P.J.; Yang, J.J.; Stewart, D.R.; Williams, R.S. ‘Memristive’ switches enable ‘stateful’ logic operations via material implication. Nature 2010, 464, 873–876. [Google Scholar] [CrossRef] [PubMed]
- Reuben, J.; Ben-Hur, R.; Wald, N.; Talati, N.; Ali, A.H.; Gaillardon, P.E.; Kvatinsky, S. Memristive logic: A framework for evaluation and comparison. In Proceedings of the 2017 27th International Symposium on Power and Timing Modeling, Optimization and Simulation (PATMOS), Thessaloniki, Greece, 25–27 September 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Jeong, D.S.; Kim, K.M.; Kim, S.; Choi, B.J.; Hwang, C.S. Memristors for Energy-Efficient New Computing Paradigms. Adv. Electron. Mater. 2016, 2, 1600090. [Google Scholar] [CrossRef]
- Balatti, S.; Ambrogio, S.; Ielmini, D. Normally-off Logic Based on Resistive Switches—Part I: Logic Gates. IEEE Trans. Electron Devices 2015, 62, 1831–1838. [Google Scholar] [CrossRef]
- Chen, A. Utilizing the Variability of Resistive Random Access Memory to Implement Reconfigurable Physical Unclonable Functions. IEEE Electron Device Lett. 2015, 36, 138–140. [Google Scholar] [CrossRef]
- Gao, L.; Chen, P.Y.; Liu, R.; Yu, S. Physical Unclonable Function Exploiting Sneak Paths in Resistive Cross-point Array. IEEE Trans. Electron Devices 2016, 63, 3109–3115. [Google Scholar] [CrossRef]
- Nili, H.; Adam, G.C.; Hoskins, B.; Prezioso, M.; Kim, J.; Mahmoodi, M.R.; Bayat, F.M.; Kavehei, O.; Strukov, D.B. Hardware-intrinsic security primitives enabled by analogue state and nonlinear conductance variations in integrated memristors. Nat. Electron. 2018, 1, 197–202. [Google Scholar] [CrossRef]
- Carboni, R.; Ambrogio, S.; Chen, W.; Siddik, M.; Harms, J.; Lyle, A.; Kula, W.; Sandhu, G.; Ielmini, D. Modeling of Breakdown-Limited Endurance in Spin-Transfer Torque Magnetic Memory Under Pulsed Cycling Regime. IEEE Trans. Electron Devices 2018, 65, 2470–2478. [Google Scholar] [CrossRef]
- Jo, S.H.; Chang, T.; Ebong, I.; Bhadviya, B.B.; Mazumder, P.; Lu, W. Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef]
- Yu, S.; Wu, Y.; Jeyasingh, R.; Kuzum, D.; Wong, H.S.P. An Electronic Synapse Device Based on Metal Oxide Resistive Switching Memory for Neuromorphic Computation. IEEE Trans. Electron Devices 2011, 58, 2729–2737. [Google Scholar] [CrossRef]
- Yu, S.; Gao, B.; Fang, Z.; Yu, H.; Kang, J.; Wong, H.S.P. A Low Energy Oxide-Based Electronic Synaptic Device for Neuromorphic Visual Systems with Tolerance to Device Variation. Adv. Mater. 2013, 25, 1774–1779. [Google Scholar] [CrossRef]
- Pedretti, G.; Milo, V.; Ambrogio, S.; Carboni, R.; Bianchi, S.; Calderoni, A.; Ramaswamy, N.; Spinelli, A.S.; Ielmini, D. Memristive neural network for on-line learning and tracking with brain-inspired spike timing dependent plasticity. Sci. Rep. 2017, 7, 5288. [Google Scholar] [CrossRef]
- Wang, Z.; Joshi, S.; Savel’ev, S.; Song, W.; Midya, R.; Li, Y.; Rao, M.; Yan, P.; Asapu, S.; Zhuo, Y.; et al. Fully memristive neural networks for pattern classification with unsupervised learning. Nat. Electron. 2018, 1, 137–145. [Google Scholar] [CrossRef]
- Truong, S.N.; Min, K.S. New Memristor-Based Crossbar Array Architecture with 50-% Area Reduction and 48-% Power Saving for Matrix-Vector Multiplication of Analog Neuromorphic Computing. JSTS J. Semicond. Technol. Sci. 2014, 14, 356–363. [Google Scholar] [CrossRef]
- Li, C.; Hu, M.; Li, Y.; Jiang, H.; Ge, N.; Montgomery, E.; Zhang, J.; Song, W.; Dávila, N.; Graves, C.E.; et al. Analogue signal and image processing with large memristor crossbars. Nat. Electron. 2018, 1, 52–59. [Google Scholar] [CrossRef]
- Hu, M.; Graves, C.E.; Li, C.; Li, Y.; Ge, N.; Montgomery, E.; Davila, N.; Jiang, H.; Williams, R.S.; Yang, J.J.; et al. Memristor-Based Analog Computation and Neural Network Classification with a Dot Product Engine. Adv. Mater. 2018, 30, 1705914. [Google Scholar] [CrossRef] [PubMed]
- Chi, P.; Li, S.; Xu, C.; Zhang, T.; Zhao, J.; Liu, Y.; Wang, Y.; Xie, Y. PRIME: A Novel Processing-in-Memory Architecture for Neural Network Computation in ReRAM-Based Main Memory. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016; pp. 27–39. [Google Scholar] [CrossRef]
- Gokmen, T.; Vlasov, Y. Acceleration of Deep Neural Network Training with Resistive Cross-Point Devices: Design Considerations. Front. Neurosci. 2016, 10, 333. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Eryilmaz, S.B.; Huang, X.; Zhang, W.; Zhang, Q.; Deng, N.; Shi, L.; Wong, H.S.P.; et al. Face classification using electronic synapses. Nat. Commun. 2017, 8, 15199. [Google Scholar] [CrossRef] [PubMed]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. ISAAC: A Convolutional Neural Network Accelerator with In-Situ Analog Arithmetic in Crossbars. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016; pp. 14–26. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully hardware-implemented memristor convolutional neural network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Xue, C.X.; Chiu, Y.C.; Liu, T.W.; Huang, T.Y.; Liu, J.S.; Chang, T.W.; Kao, H.Y.; Wang, J.H.; Wei, S.Y.; Lee, C.Y.; et al. A CMOS-integrated compute-in-memory macro based on resistive random-access memory for AI edge devices. Nat. Electron. 2021, 4, 81–90. [Google Scholar] [CrossRef]
- Le Gallo, M.; Sebastian, A.; Mathis, R.; Manica, M.; Giefers, H.; Tuma, T.; Bekas, C.; Curioni, A.; Eleftheriou, E. Mixed-precision in-memory computing. Nat. Electron. 2018, 1, 246–253. [Google Scholar] [CrossRef]
- Zidan, M.A.; Jeong, Y.; Lee, J.; Chen, B.; Huang, S.; Kushner, M.J.; Lu, W.D. A general memristor-based partial differential equation solver. Nat. Electron. 2018, 1, 411–420. [Google Scholar] [CrossRef]
- Sun, Z.; Pedretti, G.; Ambrosi, E.; Bricalli, A.; Wang, W.; Ielmini, D. Solving matrix equations in one step with cross-point resistive arrays. Proc. Natl. Acad. Sci. USA 2019, 116, 4123–4128. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Pedretti, G.; Bricalli, A.; Ielmini, D. One-step regression and classification with cross-point resistive memory arrays. Sci. Adv. 2020, 6, eaay2378. [Google Scholar] [CrossRef]
- Cassinerio, M.; Ciocchini, N.; Ielmini, D. Logic Computation in Phase Change Materials by Threshold and Memory Switching. Adv. Mater. 2013, 25, 5975–5980. [Google Scholar] [CrossRef] [PubMed]
- Ielmini, D.; Pedretti, G. Device and Circuit Architectures for In-Memory Computing. Adv. Intell. Syst. 2020, 2, 2000040. [Google Scholar] [CrossRef]
- Chappert, C.; Fert, A.; Van Dau, F.N. The emergence of spin electronics in data storage. Nat. Mater. 2007, 6, 813–823. [Google Scholar] [CrossRef] [PubMed]
- Raoux, S.; Wełnic, W.; Ielmini, D. Phase Change Materials and Their Application to Nonvolatile Memories. Chem. Rev. 2010, 110, 240–267. [Google Scholar] [CrossRef] [PubMed]
- Burr, G.W.; Breitwisch, M.J.; Franceschini, M.; Garetto, D.; Gopalakrishnan, K.; Jackson, B.; Kurdi, B.; Lam, C.; Lastras, L.A.; Padilla, A.; et al. Phase change memory technology. J. Vac. Sci. Technol. Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2010, 28, 223–262. [Google Scholar] [CrossRef]
- Ielmini, D. Resistive switching memories based on metal oxides: Mechanisms, reliability and scaling. Semicond. Sci. Technol. 2016, 31, 063002. [Google Scholar] [CrossRef]
- Govoreanu, B.; Kar, G.; Chen, Y.Y.; Paraschiv, V.; Kubicek, S.; Fantini, A.; Radu, I.; Goux, L.; Clima, S.; Degraeve, R.; et al. 10 × 10 nm2 Hf/HfOx crossbar resistive RAM with excellent performance, reliability and low-energy operation. In 2011 International Electron Devices Meeting; IEEE: Washington, DC, USA, 2011; pp. 31.6.1–31.6.4. [Google Scholar] [CrossRef]
- Pi, S.; Li, C.; Jiang, H.; Xia, W.; Xin, H.; Yang, J.J.; Xia, Q. Memristor crossbar arrays with 6-nm half-pitch and 2-nm critical dimension. Nat. Nanotechnol. 2019, 14, 35–39. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Ambrosi, E.; Pedretti, G.; Bricalli, A.; Ielmini, D. In-Memory PageRank Accelerator With a Cross-Point Array of Resistive Memories. IEEE Trans. Electron Devices 2020, 67, 1466–1470. [Google Scholar] [CrossRef]
- Yang, J.J.; Strukov, D.B.; Stewart, D.R. Memristive devices for computing. Nat. Nanotechnol. 2013, 8, 13–24. [Google Scholar] [CrossRef]
- Prezioso, M.; Merrikh-Bayat, F.; Hoskins, B.D.; Adam, G.C.; Likharev, K.K.; Strukov, D.B. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 2015, 521, 61–64. [Google Scholar] [CrossRef]
- Ambrogio, S.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Boybat, I.; di Nolfo, C.; Sidler, S.; Giordano, M.; Bodini, M.; Farinha, N.C.P.; et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 2018, 558, 60–67. [Google Scholar] [CrossRef]
- Li, C.; Belkin, D.; Li, Y.; Yan, P.; Hu, M.; Ge, N.; Jiang, H.; Montgomery, E.; Lin, P.; Wang, Z.; et al. Efficient and self-adaptive in situ learning in multilayer memristor neural networks. Nat. Commun. 2018, 9, 2385. [Google Scholar] [CrossRef]
- Milo, V.; Zambelli, C.; Olivo, P.; Pérez, E.; K. Mahadevaiah, M.; G. Ossorio, O.; Wenger, C.; Ielmini, D. Multilevel HfO2 -based RRAM devices for low-power neuromorphic networks. APL Mater. 2019, 7, 081120. [Google Scholar] [CrossRef]
- Prezioso, M.; Mahmoodi, M.R.; Bayat, F.M.; Nili, H.; Kim, H.; Vincent, A.; Strukov, D.B. Spike-timing-dependent plasticity learning of coincidence detection with passively integrated memristive circuits. Nat. Commun. 2018, 9, 5311. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, T.; Ren, Y.; Lin, Y.; Xu, H.; Zhao, X.; Liu, Y.; Ielmini, D. Toward a generalized Bienenstock-Cooper-Munro rule for spatiotemporal learning via triplet-STDP in memristive devices. Nat. Commun. 2020, 11, 1510. [Google Scholar] [CrossRef]
- Sheridan, P.M.; Cai, F.; Du, C.; Ma, W.; Zhang, Z.; Lu, W.D. Sparse coding with memristor networks. Nat. Nanotechnol. 2017, 12, 784–789. [Google Scholar] [CrossRef]
- Shin, J.H.; Jeong, Y.J.; Zidan, M.A.; Wang, Q.; Lu, W.D. Hardware Acceleration of Simulated Annealing of Spin Glass by RRAM Crossbar Array. In Proceedings of the 2018 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 1–5 December 2018; pp. 3.3.1–3.3.4. [Google Scholar] [CrossRef]
- Mahmoodi, M.R.; Kim, H.; Fahimi, Z.; Nili, H.; Sedov, L.; Polishchuk, V.; Strukov, D.B. An Analog Neuro-Optimizer with Adaptable Annealing Based on 64x64 0T1R Crossbar Circuit. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 14.7.1–14.7.4. [Google Scholar] [CrossRef]
- Cai, F.; Kumar, S.; Van Vaerenbergh, T.; Sheng, X.; Liu, R.; Li, C.; Liu, Z.; Foltin, M.; Yu, S.; Xia, Q.; et al. Power-efficient combinatorial optimization using intrinsic noise in memristor Hopfield neural networks. Nat. Electron. 2020. [Google Scholar] [CrossRef]
- Pedretti, G.; Mannocci, P.; Hashemkhani, S.; Milo, V.; Melnic, O.; Chicca, E.; Ielmini, D. A Spiking Recurrent Neural Network With Phase-Change Memory Neurons and Synapses for the Accelerated Solution of Constraint Satisfaction Problems. IEEE J. Explor. Solid State Comput. Devices Circ. 2020, 6, 89–97. [Google Scholar] [CrossRef]
- Pedretti, G.; Ambrosi, E.; Ielmini, D. Conductance variations and their impact on the precision of in-memory computing with resistive switching memory (RRAM). In Proceedings of the 2021 IEEE International Reliability Physics Symposium (IRPS), live virtual conference, 21–24 March 2021; pp. 2C.1–1–2C.1–4. [Google Scholar]
- Ambrogio, S.; Balatti, S.; Cubeta, A.; Calderoni, A.; Ramaswamy, N.; Ielmini, D. Statistical Fluctuations in HfOx Resistive-Switching Memory: Part II—Random Telegraph Noise. IEEE Trans. Electron Devices 2014, 61, 2920–2927. [Google Scholar] [CrossRef]
- Bricalli, A.; Ambrosi, E.; Laudato, M.; Maestro, M.; Rodriguez, R.; Ielmini, D. Resistive Switching Device Technology Based on Silicon Oxide for Improved ON—OFF Ratio—Part I: Memory Devices. IEEE Trans. Electron Devices 2018, 65, 115–121. [Google Scholar] [CrossRef]
- Balatti, S.; Ambrogio, S.; Ielmini, D.; Gilmer, D.C. Variability and failure of set process in HfO2 RRAM. In Proceedings of the 2013 5th IEEE International Memory Workshop, Monterey, CA, USA, 26–29 May 2013; pp. 38–41. [Google Scholar] [CrossRef]
- Balatti, S.; Ambrogio, S.; Gilmer, D.C.; Ielmini, D. Set Variability and Failure Induced by Complementary Switching in Bipolar RRAM. IEEE Electron Device Lett. 2013, 34, 861–863. [Google Scholar] [CrossRef]
- Fantini, A.; Goux, L.; Degraeve, R.; Wouters, D.; Raghavan, N.; Kar, G.; Belmonte, A.; Chen, Y.Y.; Govoreanu, B.; Jurczak, M. Intrinsic switching variability in HfO2 RRAM. In Proceedings of the 2013 5th IEEE International Memory Workshop, Monterey, CA, USA, 26–29 May 2013; pp. 30–33. [Google Scholar] [CrossRef]
- Milo, V.; Anzalone, F.; Zambelli, C.; Perez, E.; Mahadevaiah, M.; Ossorio, O.; Olivo, P.; Wenger, C.; Ielmini, D. Optimized programming algorithms for multilevel RRAM in hardware neural networks. In Proceedings of the 2021 IEEE International Reliability Physics Symposium (IRPS), live virtual conference, 21–24 March 2021; pp. 2C.4–1–2C.4–4. [Google Scholar]
- Lin, Y.H.; Wang, C.H.; Lee, M.H.; Lee, D.Y.; Lin, Y.Y.; Lee, F.M.; Lung, H.L.; Wang, K.C.; Tseng, T.Y.; Lu, C.Y. Performance Impacts of Analog ReRAM Non-ideality on Neuromorphic Computing. IEEE Trans. Electron Devices 2019, 66, 1289–1295. [Google Scholar] [CrossRef]
- Ambrogio, S.; Balatti, S.; McCaffrey, V.; Wang, D.C.; Ielmini, D. Noise-Induced Resistance Broadening in Resistive Switching Memory—Part II: Array Statistics. IEEE Trans. Electron Devices 2015, 62, 3812–3819. [Google Scholar] [CrossRef]
- Peng, X.; Huang, S.; Luo, Y.; Sun, X.; Yu, S. DNN+NeuroSim: An End-to-End Benchmarking Framework for Compute-in-Memory Accelerators with Versatile Device Technologies. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 32.5.1–32.5.4. [Google Scholar] [CrossRef]
- Alibart, F.; Gao, L.; Hoskins, B.D.; Strukov, D.B. High Precision Tuning of State for Memristive Devices by Adaptable Variation-Tolerant Algorithm. Nanotechnology 2012, 23, 075201. [Google Scholar] [CrossRef]
- Yu, S.; Li, Z.; Chen, P.Y.; Wu, H.; Gao, B.; Wang, D.; Wu, W.; Qian, H. Binary neural network with 16 Mb RRAM macro chip for classification and online training. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 16.2.1–16.2.4. [Google Scholar] [CrossRef]
- Ma, C.; Sun, Y.; Qian, W.; Meng, Z.; Yang, R.; Jiang, L. Go Unary: A Novel Synapse Coding and Mapping Scheme for Reliable ReRAM-based Neuromorphic Computing. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 1432–1437. [Google Scholar] [CrossRef]
- Boybat, I.; Le Gallo, M.; Nandakumar, S.R.; Moraitis, T.; Parnell, T.; Tuma, T.; Rajendran, B.; Leblebici, Y.; Sebastian, A.; Eleftheriou, E. Neuromorphic computing with multi-memristive synapses. Nat. Commun. 2018, 9, 2514. [Google Scholar] [CrossRef]
- Hu, M.; Williams, R.S.; Strachan, J.P.; Li, Z.; Grafals, E.M.; Davila, N.; Graves, C.; Lam, S.; Ge, N.; Yang, J.J. Dot-product engine for neuromorphic computing: Programming 1T1M crossbar to accelerate matrix-vector multiplication. In Proceedings of the 53rd Annual Design Automation Conference on-DAC ’16; ACM Press: Austin, TX, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Gokmen, T.; Rasch, M.J.; Haensch, W. The marriage of training and inference for scaled deep learning analog hardware. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 22.3.1–22.3.4. [Google Scholar] [CrossRef]
- Cosemans, S.; Verhoef, B.; Doevenspeck, J.; Papistas, I.A.; Catthoor, F.; Debacker, P.; Mallik, A.; Verkest, D. Towards 10000TOPS/W DNN Inference with Analog in-Memory Computing—A Circuit Blueprint, Device Options and Requirements. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 22.2.1–22.2.4. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, M. Mitigate Parasitic Resistance in Resistive Crossbar-based Convolutional Neural Networks. ACM J. Emerg. Technol. Comput. Syst. 2020, 16, 1–20. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, B.; Yao, P.; Wu, D.; Chen, J.; Pang, Y.; Zhang, W.; Liao, Y.; Xue, C.X.; Chen, W.H.; et al. 33.2 A Fully Integrated Analog ReRAM Based 78.4TOPS/W Compute-In-Memory Chip with Fully Parallel MAC Computing. In Proceedings of the 2020 IEEE International Solid- State Circuits Conference-(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 500–502. [Google Scholar] [CrossRef]
- Ankit, A.; Hajj, I.E.; Chalamalasetti, S.R.; Ndu, G.; Foltin, M.; Williams, R.S.; Faraboschi, P.; Hwu, W.M.W.; Strachan, J.P.; Roy, K.; et al. PUMA: A Programmable Ultra-efficient Memristor-based Accelerator for Machine Learning Inference. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems, Providence, RI, USA, 13–17 April 2019; pp. 715–731. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Lee, S.H.; Meng, F.H.; Lu, W.D. A Deep Neural Network Accelerator Based on Tiled RRAM Architecture. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 14.4.1–14.4.4. [Google Scholar] [CrossRef]
- Ni, K.; Yin, X.; Laguna, A.F.; Joshi, S.; Dünkel, S.; Trentzsch, M.; Müller, J.; Beyer, S.; Niemier, M.; Hu, X.S.; et al. Ferroelectric ternary content-addressable memory for one-shot learning. Nat. Electron. 2019, 2, 521–529. [Google Scholar] [CrossRef]
- Li, C.; Graves, C.E.; Sheng, X.; Miller, D.; Foltin, M.; Pedretti, G.; Strachan, J.P. Analog content-addressable memories with memristors. Nat. Commun. 2020, 11, 1638. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Oh, S.; Shi, Y.; Liu, X.; Song, J.; Kuzum, D. Drift-Enhanced Unsupervised Learning of Handwritten Digits in Spiking Neural Network With PCM Synapses. IEEE Electron Device Lett. 2018, 39, 1768–1771. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Song, W.; Rao, M.; Belkin, D.; Li, Y.; Yan, P.; Jiang, H.; Lin, P.; Hu, M.; et al. Reinforcement learning with analogue memristor arrays. Nat. Electron. 2019, 2, 115–124. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Lin, P.; Rao, M.; Nie, Y.; Song, W.; Qiu, Q.; Li, Y.; Yan, P.; Strachan, J.P.; et al. In situ training of feed-forward and recurrent convolutional memristor networks. Nat. Mach. Intell. 2019, 1, 434–442. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Rao, M.; Belkin, D.; Song, W.; Jiang, H.; Yan, P.; Li, Y.; Lin, P.; Hu, M.; et al. Long short-term memory networks in memristor crossbar arrays. Nat. Mach. Intell. 2019, 1, 49–57. [Google Scholar] [CrossRef]
- Cai, F.; Correll, J.M.; Lee, S.H.; Lim, Y.; Bothra, V.; Zhang, Z.; Flynn, M.P.; Lu, W.D. A fully integrated reprogrammable memristor–CMOS system for efficient multiply—Accumulate operations. Nat. Electron. 2019, 2, 290–299. [Google Scholar] [CrossRef]
- Li, C.; Ignowski, J.; Sheng, X.; Wessel, R.; Jaffe, B.; Ingemi, J.; Graves, C.; Strachan, J.P. CMOS-integrated nanoscale memristive crossbars for CNN and optimization acceleration. In Proceedings of the 2020 IEEE International Memory Workshop (IMW), Dresden, Germany, 17–20 May 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Hopfield, J.; Tank, D. Computing with neural circuits: A model. Science 1986, 233, 625–633. [Google Scholar] [CrossRef] [PubMed]
- Eryilmaz, S.B.; Kuzum, D.; Jeyasingh, R.; Kim, S.; BrightSky, M.; Lam, C.; Wong, H.S.P. Brain-like associative learning using a nanoscale non-volatile phase change synaptic device array. Front. Neurosci. 2014, 8, 205. [Google Scholar] [CrossRef]
- Milo, V.; Ielmini, D.; Chicca, E. Attractor networks and associative memories with STDP learning in RRAM synapses. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; pp. 11.2.1–11.2.4. [Google Scholar] [CrossRef]
- Tank, D.; Hopfield, J. Simple ’neural’ optimization networks: An A/D converter, signal decision circuit, and a linear programming circuit. IEEE Trans. Circ. Syst. 1986, 33, 533–541. [Google Scholar] [CrossRef]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 5. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef]
- Mahmoodi, M.R.; Prezioso, M.; Strukov, D.B. Versatile stochastic dot product circuits based on nonvolatile memories for high performance neurocomputing and neurooptimization. Nat. Commun. 2019, 10, 5113. [Google Scholar] [CrossRef]
- Le Gallo, M.; Sebastian, A.; Cherubini, G.; Giefers, H.; Eleftheriou, E. Compressed Sensing with Approximate Message Passing Using In-Memory Computing. IEEE Trans. Electron Devices 2018, 65, 4304–4312. [Google Scholar] [CrossRef]
- Cai, R.; Ren, A.; Soundarajan, S.; Wang, Y. A low-computation-complexity, energy-efficient, and high-performance linear program solver based on primal–dual interior point method using memristor crossbars. Nano Commun. Netw. 2018, 18, 62–71. [Google Scholar] [CrossRef]
- Agarwal, S.; Plimpton, S.J.; Hughart, D.R.; Hsia, A.H.; Richter, I.; Cox, J.A.; James, C.D.; Marinella, M.J. Resistive memory device requirements for a neural algorithm accelerator. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 929–938. [Google Scholar] [CrossRef]
- Ielmini, D.; Ambrogio, S. Emerging neuromorphic devices. Nanotechnology 2019, 31, 092001. [Google Scholar] [CrossRef]
- Sun, Z.; Pedretti, G.; Mannocci, P.; Ambrosi, E.; Bricalli, A.; Ielmini, D. Time Complexity of In-Memory Solution of Linear Systems. IEEE Trans. Electron Devices 2020, 67, 2945–2951. [Google Scholar] [CrossRef]
- Bryan, K.; Leise, T. The $25,000,000,000 Eigenvector: The Linear Algebra behind Google. SIAM Rev. 2006, 48, 569–581. [Google Scholar] [CrossRef]
- Sun, Z.; Pedretti, G.; Ambrosi, E.; Bricalli, A.; Ielmini, D. In-Memory Eigenvector Computation in Time O (1). Adv. Intell. Syst. 2020, 2000042. [Google Scholar] [CrossRef]
- Pagiamtzis, K.; Sheikholeslami, A. Content-Addressable Memory (CAM) Circuits and Architectures: A Tutorial and Survey. IEEE J. Solid State Circ. 2006, 41, 712–727. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, X.; Bai, Y.; İpek, E. A resistive TCAM accelerator for data-intensive computing. In Proceedings of the 44th Annual IEEE/ACM International Symposium on Microarchitecture—MICRO-44 ’11; ACM Press: Porto Alegre, Brazil, 2011; p. 339. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, X.; Patel, R.; Ipek, E.; Friedman, E.G. AC-DIMM: Associative Computing with STT-MRAM. In Proceedings of the 40th Annual International Symposium on Computer Architecture; Association for Computing Machinery: New York, NY, USA, 2013; pp. 189–200. [Google Scholar] [CrossRef]
- Graves, C.E.; Li, C.; Sheng, X.; Miller, D.; Ignowski, J.; Kiyama, L.; Strachan, J.P. In-Memory Computing with Memristor Content Addressable Memories for Pattern Matching. Adv. Mater. 2020, 32, 2003437. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Muller, F.; Ali, T.; Olivo, R.; Imani, M.; Deng, S.; Zhuo, C.; Kampfe, T.; Yin, X.; Ni, K. A Scalable Design of Multi-Bit Ferroelectric Content Addressable Memory for Data-Centric Computing. In Proceedings of the 2020 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 12–18 December 2020; pp. 29.3.1–29.3.4. [Google Scholar] [CrossRef]
- Pedretti, G.; Graves, C.E.; Li, C.; Serebryakov, S.; Sheng, X.; Foltin, M.; Mao, R.; Strachan, J.P. Tree-based machine learning performed in-memory with memristive analog CAM. arXiv 2021, arXiv:2103.08986. [Google Scholar]
- Burr, G.W.; Shelby, R.M.; Sidler, S.; di Nolfo, C.; Jang, J.; Boybat, I.; Shenoy, R.S.; Narayanan, P.; Virwani, K.; Giacometti, E.U.; et al. Experimental Demonstration and Tolerancing of a Large-Scale Neural Network (165,000 Synapses) Using Phase-Change Memory as the Synaptic Weight Element. IEEE Trans. Electron Devices 2015, 62, 3498–3507. [Google Scholar] [CrossRef]
- Jang, J.W.; Park, S.; Burr, G.W.; Hwang, H.; Jeong, Y.H. Optimization of Conductance Change in Pr1–x Cax MnO3 -Based Synaptic Devices for Neuromorphic Systems. IEEE Electron Device Lett. 2015, 36, 457–459. [Google Scholar] [CrossRef]
- Wang, Z.; Ambrogio, S.; Balatti, S.; Sills, S.; Calderoni, A.; Ramaswamy, N.; Ielmini, D. Postcycling Degradation in Metal-Oxide Bipolar Resistive Switching Memory. IEEE Trans. Electron Devices 2016, 63, 4279–4287. [Google Scholar] [CrossRef]
- Chen, P.Y.; Yu, S. Reliability perspective of resistive synaptic devices on the neuromorphic system performance. In Proceedings of the 2018 IEEE International Reliability Physics Symposium (IRPS), Burlingame, CA, 11–15 March 2018; pp. 5C.4–1–5C.4–4. [Google Scholar] [CrossRef]
- Nardi, F.; Larentis, S.; Balatti, S.; Gilmer, D.C.; Ielmini, D. Resistive Switching by Voltage-Driven Ion Migration in Bipolar RRAM—Part I: Experimental Study. IEEE Trans. Electron Devices 2012, 59, 2461–2467. [Google Scholar] [CrossRef]
- Yang, T.J.; Sze, V. Design Considerations for Efficient Deep Neural Networks on Processing-in-Memory Accelerators. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 22.1.1–22.1.4. [Google Scholar] [CrossRef]
- Pedretti, G.; Milo, V.; Ambrogio, S.; Carboni, R.; Bianchi, S.; Calderoni, A.; Ramaswamy, N.; Spinelli, A.S.; Ielmini, D. Stochastic Learning in Neuromorphic Hardware via Spike Timing Dependent Plasticity With RRAM Synapses. IEEE J. Emerg. Sel. Top. Circ. Syst. 2018, 8, 77–85. [Google Scholar] [CrossRef]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. arXiv 2020, arXiv:cs.CL/2005.14165. [Google Scholar]
- Wong, H.S.P.; Raoux, S.; Kim, S.; Liang, J.; Reifenberg, J.P.; Rajendran, B.; Asheghi, M.; Goodson, K.E. Phase Change Memory. Proc. IEEE 2010, 98, 2201–2227. [Google Scholar] [CrossRef]
- Le Gallo, M.; Sebastian, A. An overview of phase-change memory device physics. J. Phys. D Appl. Phys. 2020, 53, 213002. [Google Scholar] [CrossRef]
- Dieny, B.; Prejbeanu, I.L.; Garello, K.; Gambardella, P.; Freitas, P.; Lehndorff, R.; Raberg, W.; Ebels, U.; Demokritov, S.O.; Akerman, J.; et al. Opportunities and challenges for spintronics in the microelectronics industry. Nat. Electron. 2020, 3, 446–459. [Google Scholar] [CrossRef]
- Ielmini, D.; Sharma, D.; Lavizzari, S.; Lacaita, A.L. Reliability Impact of Chalcogenide-Structure Relaxation in Phase-Change Memory (PCM) Cells—Part I: Experimental Study. IEEE Trans. Electron Devices 2009, 56, 1070–1077. [Google Scholar] [CrossRef]
- Chang, C.; Wu, M.; Lin, J.; Li, C.; Parmar, V.; Lee, H.; Wei, J.; Sheu, S.; Suri, M.; Chang, T.; et al. NV-BNN: An Accurate Deep Convolutional Neural Network Based on Binary STT-MRAM for Adaptive AI Edge. In Proceedings of the 2019 56th ACM/IEEE Design Automation Conference (DAC), Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- Hirtzlin, T.; Penkovsky, B.; Bocquet, M.; Klein, J.O.; Portal, J.M.; Querlioz, D. Stochastic Computing for Hardware Implementation of Binarized Neural Networks. IEEE Access 2019, 7, 76394–76403. [Google Scholar] [CrossRef]
- Milo, V.; Malavena, G.; Monzio Compagnoni, C.; Ielmini, D. Memristive and CMOS Devices for Neuromorphic Computing. Materials 2020, 13, 166. [Google Scholar] [CrossRef]
- Jerry, M.; Chen, P.; Zhang, J.; Sharma, P.; Ni, K.; Yu, S.; Datta, S. Ferroelectric FET analog synapse for acceleration of deep neural network training. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; pp. 6.2.1–6.2.4. [Google Scholar] [CrossRef]
- Tang, J.; Bishop, D.; Kim, S.; Copel, M.; Gokmen, T.; Todorov, T.; Shin, S.; Lee, K.T.; Solomon, P.; Chan, K.; et al. ECRAM as Scalable Synaptic Cell for High-Speed, Low-Power Neuromorphic Computing. In Proceedings of the 2018 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 1–5 December 2018; pp. 13.1.1–13.1.4. [Google Scholar] [CrossRef]
- Guo, X.; Bayat, F.M.; Bavandpour, M.; Klachko, M.; Mahmoodi, M.R.; Prezioso, M.; Likharev, K.K.; Strukov, D.B. Fast, energy-efficient, robust, and reproducible mixed-signal neuromorphic classifier based on embedded NOR flash memory technology. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 26 December 2017; pp. 6.5.1–6.5.4. [Google Scholar] [CrossRef]
- Kim, S.; Ott, J.A.; Ando, T.; Miyazoe, H.; Narayanan, V.; Rozen, J.; Todorov, T.; Onen, M.; Gokmen, T.; Bishop, D.; et al. Metal-oxide based, CMOS-compatible ECRAM for Deep Learning Accelerator. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 35.7.1–35.7.4. [Google Scholar] [CrossRef]
- Li, Y.; Fuller, E.J.; Sugar, J.D.; Yoo, S.; Ashby, D.S.; Bennett, C.H.; Horton, R.D.; Bartsch, M.S.; Marinella, M.J.; Lu, W.D.; et al. Filament-Free Bulk Resistive Memory Enables Deterministic Analogue Switching. Adv. Mater. 2020, 32, 2003984. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedretti, G.; Ielmini, D. In-Memory Computing with Resistive Memory Circuits: Status and Outlook. Electronics 2021, 10, 1063. https://doi.org/10.3390/electronics10091063
Pedretti G, Ielmini D. In-Memory Computing with Resistive Memory Circuits: Status and Outlook. Electronics. 2021; 10(9):1063. https://doi.org/10.3390/electronics10091063
Chicago/Turabian StylePedretti, Giacomo, and Daniele Ielmini. 2021. "In-Memory Computing with Resistive Memory Circuits: Status and Outlook" Electronics 10, no. 9: 1063. https://doi.org/10.3390/electronics10091063
APA StylePedretti, G., & Ielmini, D. (2021). In-Memory Computing with Resistive Memory Circuits: Status and Outlook. Electronics, 10(9), 1063. https://doi.org/10.3390/electronics10091063






