1. Introduction
With the developments of different kinds of control techniques, Buck circuits can be used widely to help converters to achieve impressive performance. As a research hot spot, many scholars have proposed a number of control techniques [
1,
2,
3,
4,
5,
6] to develop the performance of Buck circuits. However, most of the mainstream control methods are linear control methods and digital control methods, both of which are based on pulse-width modulation (PWM) technology. These research results show that PWM-based controllers bring signals from PWM drivers with a fixed frequency into feedback signals, which do not reflect the dynamic situations of systems. As a result, it is difficult to separate the signals without digital control design, and so the cost is high. Even if a digital control design were embedded, the dynamic performance of the PWM-based controller would be limited.
In the authors’ previous work [
7], an improved hybrid hysteresis voltage mode for Buck circuits was proposed. When controlling a synchronous rectifier Buck circuit, a hysteresis voltage mode improved by hysteresis voltage schemes can provide a lower voltage drop ratio in the case of proper LC (inductance and capacitance) parameter design, a high dynamic response speed with a high frequency and low ripple rate of steady-state output and large load current change, as well as an acceptable range of steady-state operating frequency change. The hysteresis voltage mode can greatly improve the single-phase current output capacity and effect of the Buck circuit, which is conducive to improve the power supply performance when the dynamic capacity of the single-phase power supply is greatly required, such as in the case of a high-level operation equipment power supply, class-D power amplifier, precision experimental instrument and precision inverter welding machine. The results from [
7] showed that the accuracy and robustness of the system were much better than PWM-based control modes. When the load current changed greatly, the controller began to adjust the power semiconductors immediately based on the feedback voltage. The output voltage was also barely sensitive to the changes of the load and the input voltage. However, when we tried to adjust the system parameters, a small error in the parameters due to factors such as manufacturing deviation or thermal influence would make the steady state frequency change suddenly and greatly. Furthermore, when the current was high, the inductor spread unnecessary electromagnetic waves, which was a kind of pollution.
Thus, it can be concluded that the steady-state frequency of the hysteresis voltage mode is determined by the control parameter ratio, equivalent serial resistance (ESR) of the capacitance and the half hysteresis width. A high ratio and low resistance lead to a small width and high frequency, which is unreasonable. To simplify the design process, a control mode with only one logical judgment point (a singularity point for a control dynamical system) should be adopted; in contrast, the hybrid hysteresis voltage proposed in [
7] has two points of this kind. The constant on-time (COT) voltage mode is confirmed to be such a kind of controlling mode, which is designed for light-load applications to achieve high efficiency and a fast transient response. The basic COT voltage workflow is demonstrated by Algorithm 1. In Algorithm 1,
U_transistor represents the status of the upper transistor and
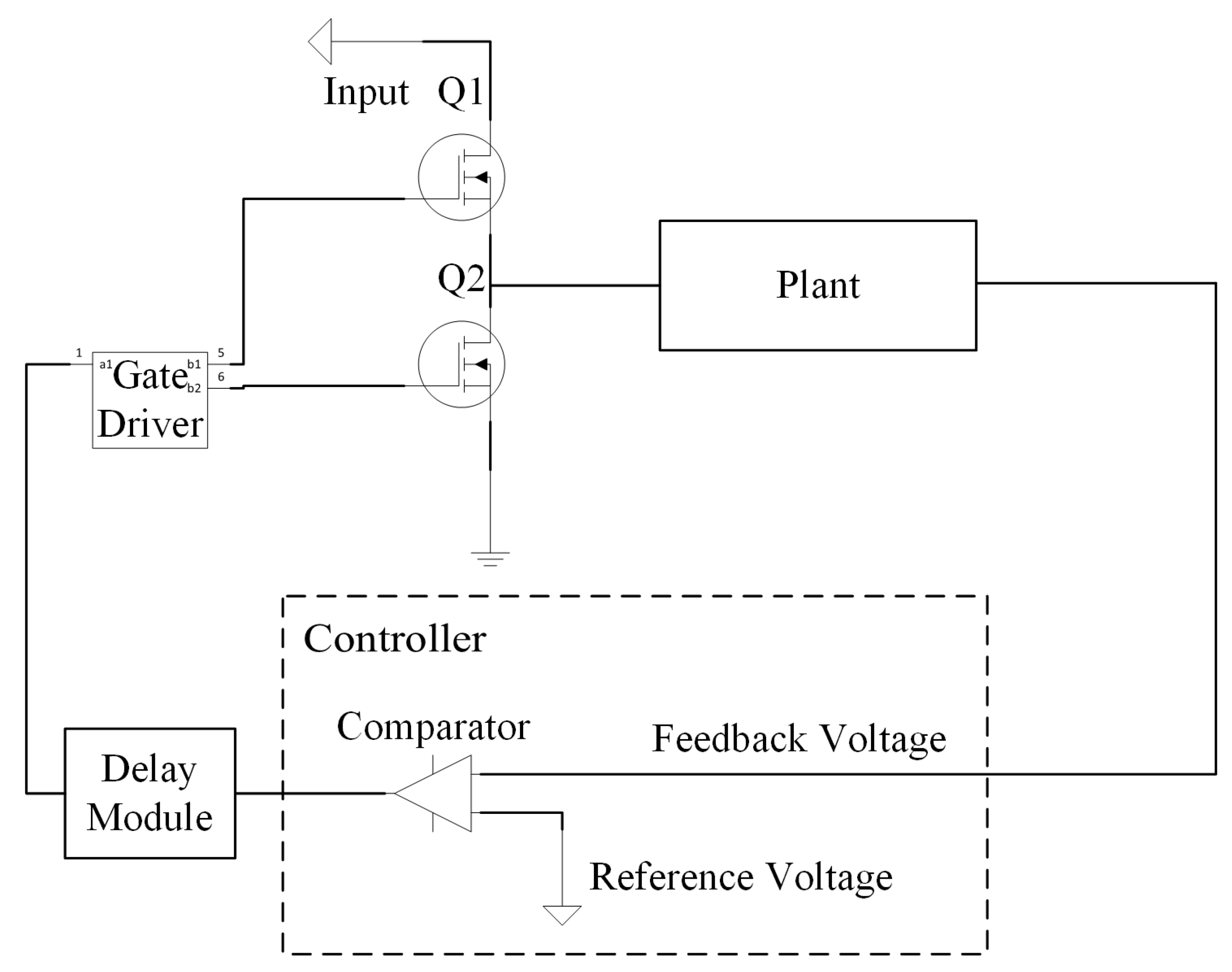
L_transistor represents the status of the lower transistor. The number 1 means on, and 0 means off. The system is initialized at the beginning of the process and then starts to work. By comparing the feedback voltage with the reference voltage, the status of the transistors switches. Thus, it is a nonlinear control method. The block diagram of Algorithm 1 is presented in
Figure 1. In the diagram, the Delay module is implemented after the compensator, with t_on being a fixed value and t_off being a minimal value.
| Algorithm 1 COT voltage mode. |
1: U_transistor = 0; 2: L_transistor = 1; 3: while 1 { 4: If V_FB < V_ref 5: { U_transistor = 1; 6: L_transistor = 0; 7: delay(t_on); 8: //Delay for a period of time// 9: //which lasts t_on. // 10: U_transistor = 0; 11: L_transistor = 1; 12: delay(t_off); 13: //Delay for a period of time// 14: //which lasts t_off. // 15: } 16: } |
Many technologies [
8,
9,
10,
11,
12,
13,
14,
15] have been proposed to improve the performance of COT under light loads, including various trajectory control technologies [
8,
13], time-optimized technology [
9], various adaptive technologies [
10,
11,
12] and current-mode control technologies [
14,
15]. In more detail, to follow the natural state trajectory of the system, Li et al. [
8] proposed a state-trajectory-based control with a single-cycle transient response. To remove the need for a large ESR, Yang et al. [
13] proposed the pseudowave tracking (PWT) technique to reduce the load-dependent DC offset voltage. Li et al. [
9] studied a constant on-time Buck converter with analog time-optimized on-time control (OTC) to achieve a fast load-current step-up transient response for high slew-rate loads. Including a transient-enhanced technique for fast dynamic voltage scaling (DVS) and load-transient response, an adaptive constant on time (ACOT) control was proposed by Ting et al. [
10]. Zhao et al. [
11] introduced a ripple-based adaptive on-time controlled Buck converter with pseudo triangular ramp compensation. Bari et al. [
12] solved the issue of the slow transient response caused by the fixed T_on operation that plagued the control of the constant on-time current mode (COTCM) by a new fast adaptive on-time control method. Zhen et al. [
14] improved the transient response and voltage scaling speed by using current mode variable on-time (CM-VOT) control. Zhang et al. investigated the sub-harmonic instability of Constant On-time Current-mode Controlled (COT-CMC) Buck converters with a proportional–integral (PI) compensator by using accurate reduced-order asynchronous-switching mapping and constant on-time current-mode control. However, the COT voltage mode is unstable in continuous conduction mode (CCM). In order to make its dynamic performance appropriate for heavy-load applications and its semi-fixed-frequency characteristic suitable for a CCM Buck circuit with a large current, a novel technology should be introduced to the COT voltage mode.
This paper is organized as follows. In the first section, the motivation of this work and an introduction are presented. The modeling process is described in
Section 2. The proposal and the controlling process of the hybrid COT voltage mode design are detailed in
Section 3. To verify the fixed frequency, an observation is shown in
Section 4. Some comparisons are made in
Section 5. Finally, this work is concluded in
Section 6.
2. Modeling
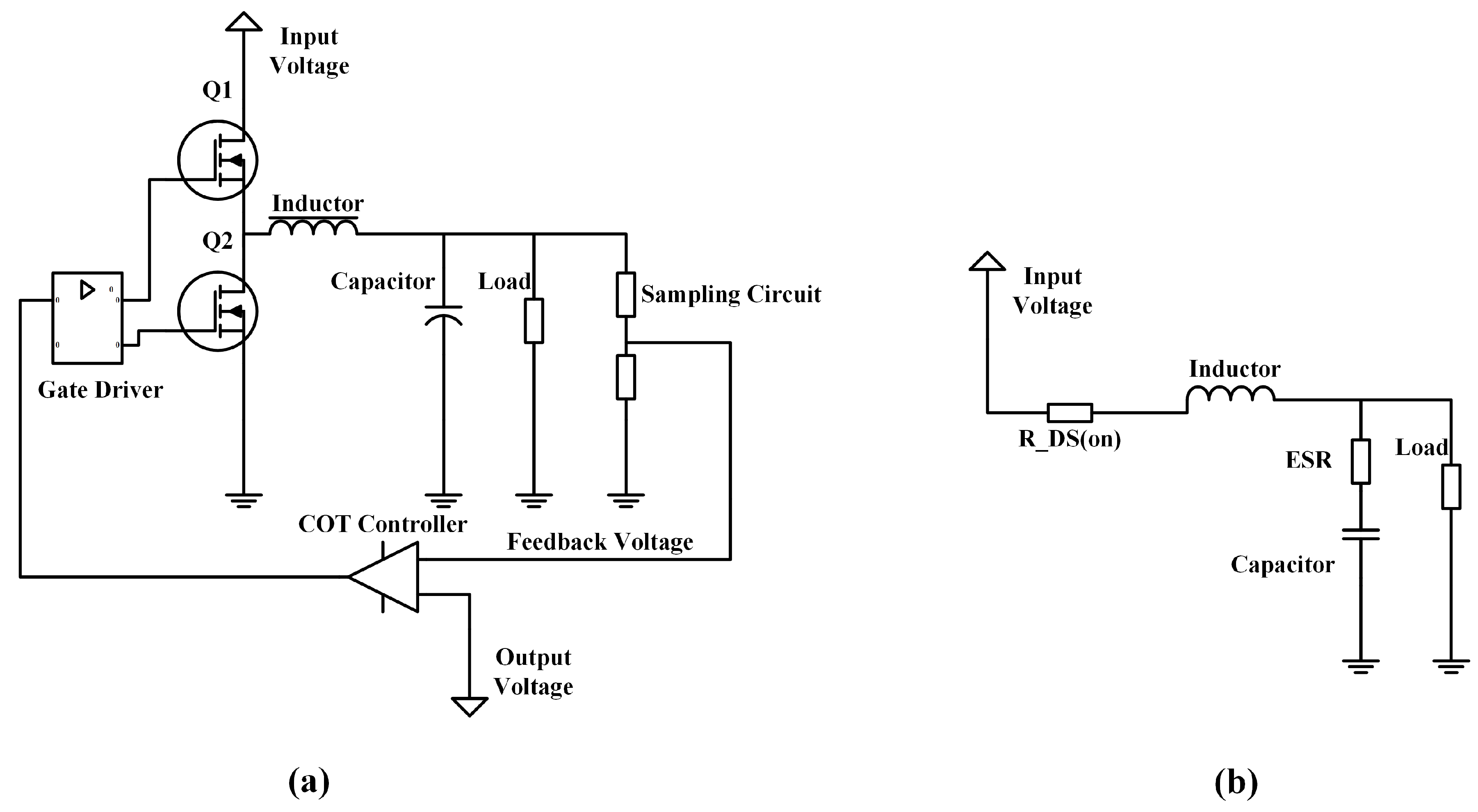
A classical Buck circuit’s equivalent model is shown in
Figure 2a, and its simplified model is shown in
Figure 2b.
Following the same modeling process described in [
7], the second-order differential equation for the Buck circuit, whose structure is given in
Figure 1, can be derived step by step.
For an ideal Buck circuit, one has
For the inductance, we have
Combining all the ideal relationship expressions gives us
Deriving Equation (
5), we can get
Then, we can describe the circuit as a second-order differential equation as follows:
where the output voltage is
and all parameters needed are defined in
Table 1.
Table 1 also lists the default values for the constant parameters.
Based on the dynamics equation of the Buck circuit described in Equation (
7), the stability can be analyzed with the eigenvalues of the Jacobian matrix of the left side of the Equation (
7). When the real parts of all the eigenvalues are negative, the system will converge to the equilibrium point. That means the system is stable. The eigenvalues of Equation (
7) are determined by the parameters of general mass, general damping and general stiffness. Among all these parameters,
and
are determined by the working condition and expect an output of
. When other values of system parameters are fixed as listed values in
Table 1, the system does not lose its stability, satisfying the condition of
, and
A.
It is widely known that the on-time and off-time of the steady state of a PWM-controlled CCM Buck circuit are fixed if
,
and
are definite. In other words, if
,
and the on-time of every period of the controller are definite, the
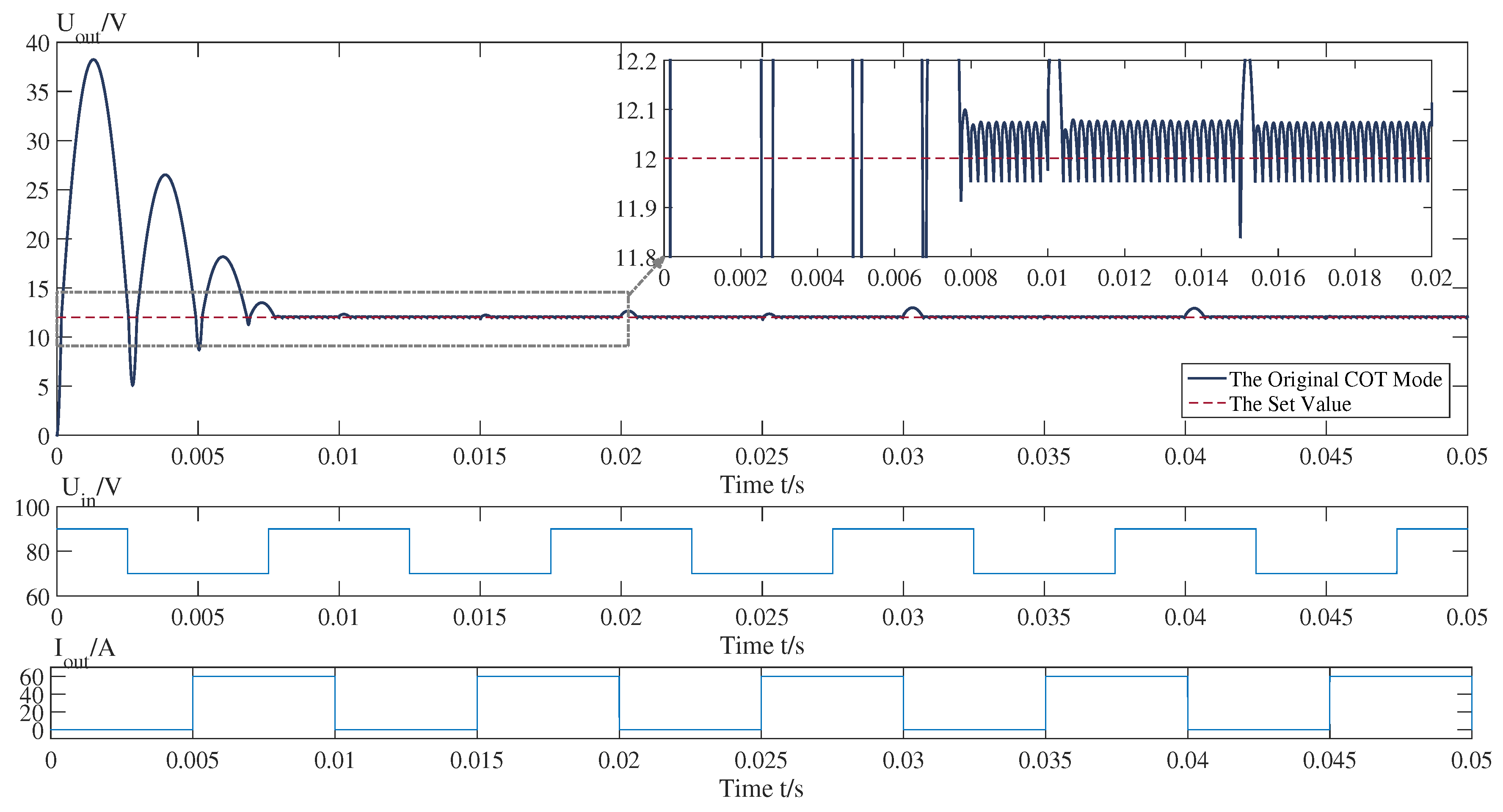
under a steady state is fixed. For these, the COT voltage mode could be a semi-constant-frequency time-domain-based control scheme. The output voltage with COT voltage mode is simulated in
Figure 3.
It can be seen from
Figure 3 that the output voltage (dark blue dotted line) vibrates around the set value with the evolution of time and is insensitive to the sudden changes of the inputs. The amplitude is acceptable in steady state and the transient time is reasonable. This means the COT control also has strong robustness. However, its large start-up overshoot amplitude and high steady-state peak-to-peak voltage are unacceptable, and the circuit is not in the proper steady state, because the output frequency is lower than the designed frequency. The COT voltage mode has two kinds of steady states, while the controller only works with an alternating frequency between the highest frequency and zero in the abnormal steady state.
3. Proposal of the Algorithm
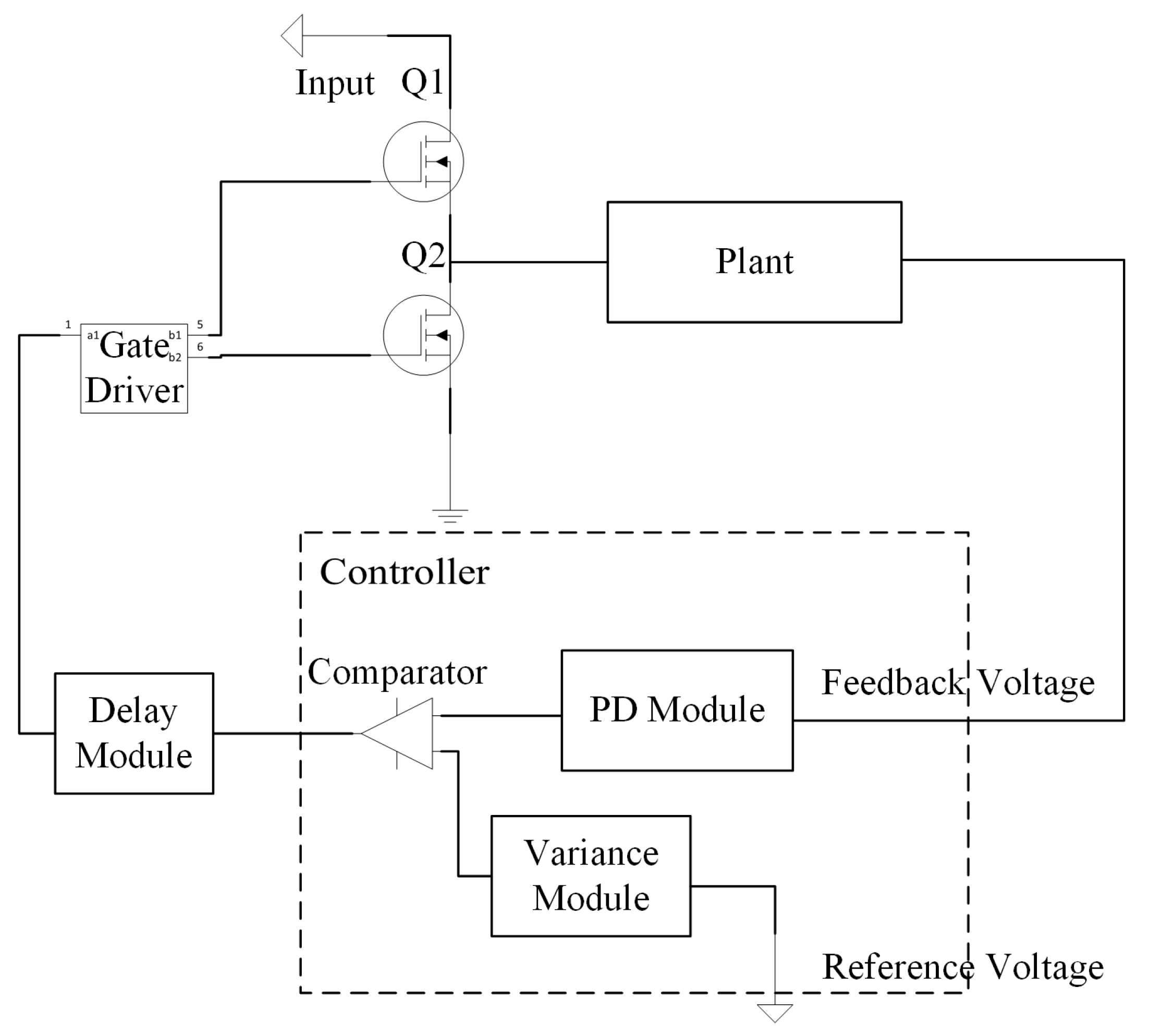
To overcome the disadvantages shown in the previous simulation, the dynamic reference voltage method as well as a PD module were introduced to the COT mode. The control scheme is given in Algorithm 2. In Algorithm 2,
V_dy_ref represents the dynamic reference voltage, function
Delta shows the variation of the argument and function
Diff shows the differential of the argument. The initial conditions are set equal to those in Algorithm 1. At the very beginning of each loop, the direction of the dynamic reference voltage is adjusted to the opposite one of the static difference. After a comparison is made in the PD module, the status of the transistors switches as in Algorithm 1.
Figure 4 gives the block diagram of Algorithm 2. Compared to
Figure 1, the controller module is adjusted by the introduction of the PD module and variance module to compute the feedback signal and reference signal.
| Algorithm 2 Proposed PD-COT voltage mode. |
01: U_transistor = 0; 02: L_transistor = 1; 03: while 1 { 04: If V_FB < V_ref 05: { V_dy_ref = Delta(V_ref);} 06: Else if V_FB > V_ref 07: { V_dy_ref = - Delta(V_ref);} 08: If P * (V_FB - V_ref) + D * 09: Diff(V_FB) < V_dy_ref 10: { U_transistor = 1; 11: L_transistor = 0; 12: delay(t_on); 13: //Delay for a period of time // 14: //which lasts t_on. // 15: U_transistor = 0; 16: L_transistor = 1; 17: delay(t_off); 18: //Delay for a period of time // 19: // which lasts t_off. // 20: } 21: } |
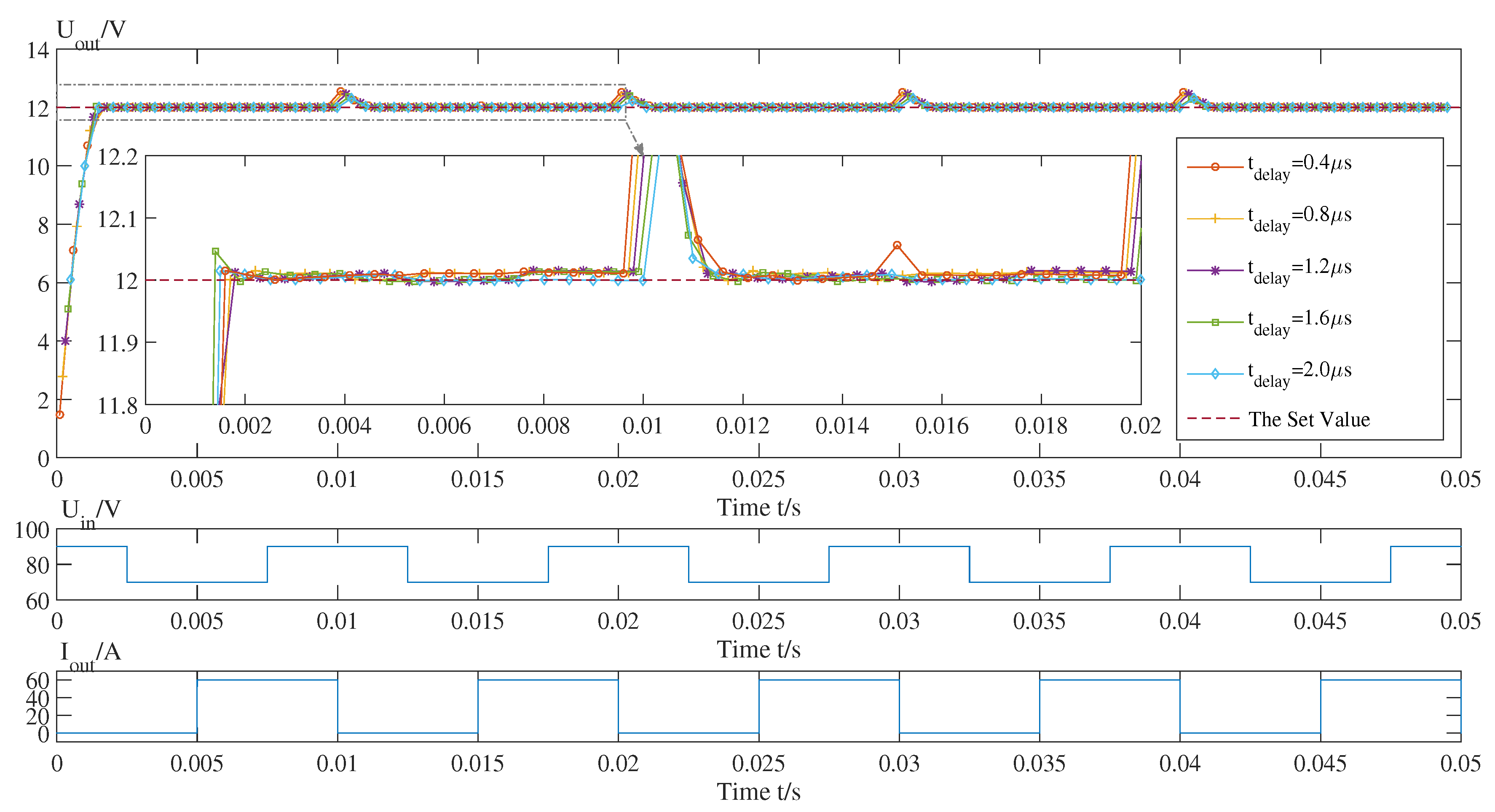
Setting the control scheme described in Algorithm 2, the performances of the hybrid control scheme with different total delays are simulated. The results are given in
Figure 5.
Considering
Figure 5 and taking the red dot line (
μs) as an example, the static differences almost disappear when the system works in a steady state. The output voltage matches the set value well. The transient time is short, and the overshoot is repressed well. The model even copes well with a sudden change: the system can recover to a steady state quickly and the surge is acceptable. The other lines (different delays) follow the same rule.
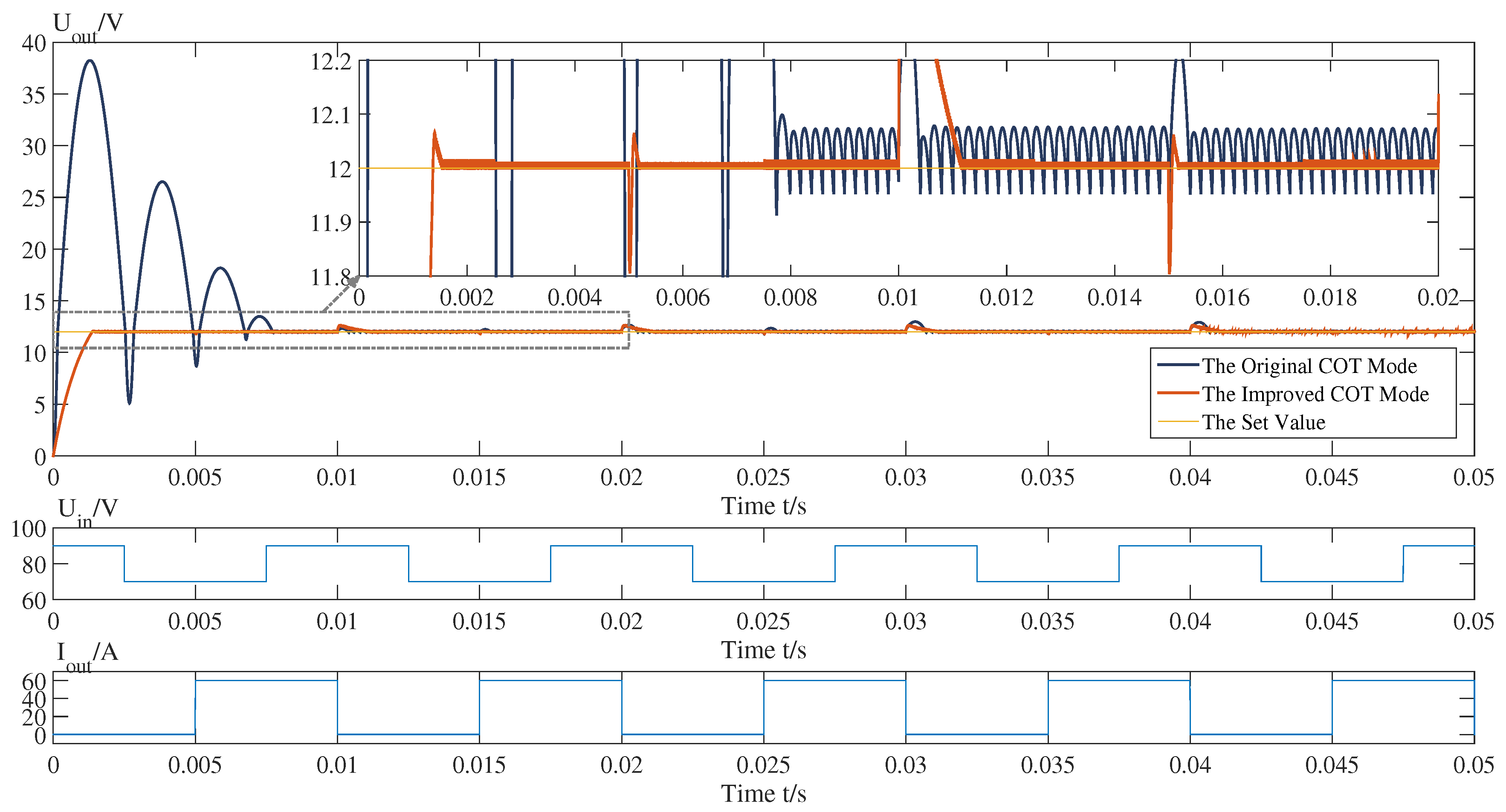
In order to clarify the advantages of the proposed scheme, a comparison of the performances of the same Buck circuit with COT and PD-COT methods is made. The results are displayed in
Figure 6. From
Figure 6, it can be seen that, compared with the dark blue line (classical COT), the orange line (proposed PD-COT) performs well. The advantages are stated in the preceding paragraph. Although the static difference should be increased by the introduction of the PD module, the control scheme keeps it at an extremely low level with the help of the dynamic reference voltage. Furthermore, with the game mechanism, the system maintains its ability to repress overshoot and recover quickly from sudden changes. Because the structure of the PD module is simple, the cost of the controller is not greatly increased, and the controller has only four core parameters, which can be set and optimized easily.
It is worth noting that, when designing a control system, the optimal parameters should be determined by the working conditions, such as and , and the expected performance, such as . However, and could change with time; once the hardware parameters have been fixed, a change of the working condition should only be tackled by a robust control method. Thus, when using the analysis method of a second-order linear system, we should pay attention to the impact of a sudden and large change of load resistance and input voltage in the system and make sure the control strategy has robustness. With the introduction of the PD link and dynamic reference voltage, the robustness of the control is significantly strengthened. Even when the load changes suddenly, the steady-state frequency is effectively limited in a narrow range, and the generated electromagnetic interference is also within the acceptable range.
4. Operating Frequency Analysis
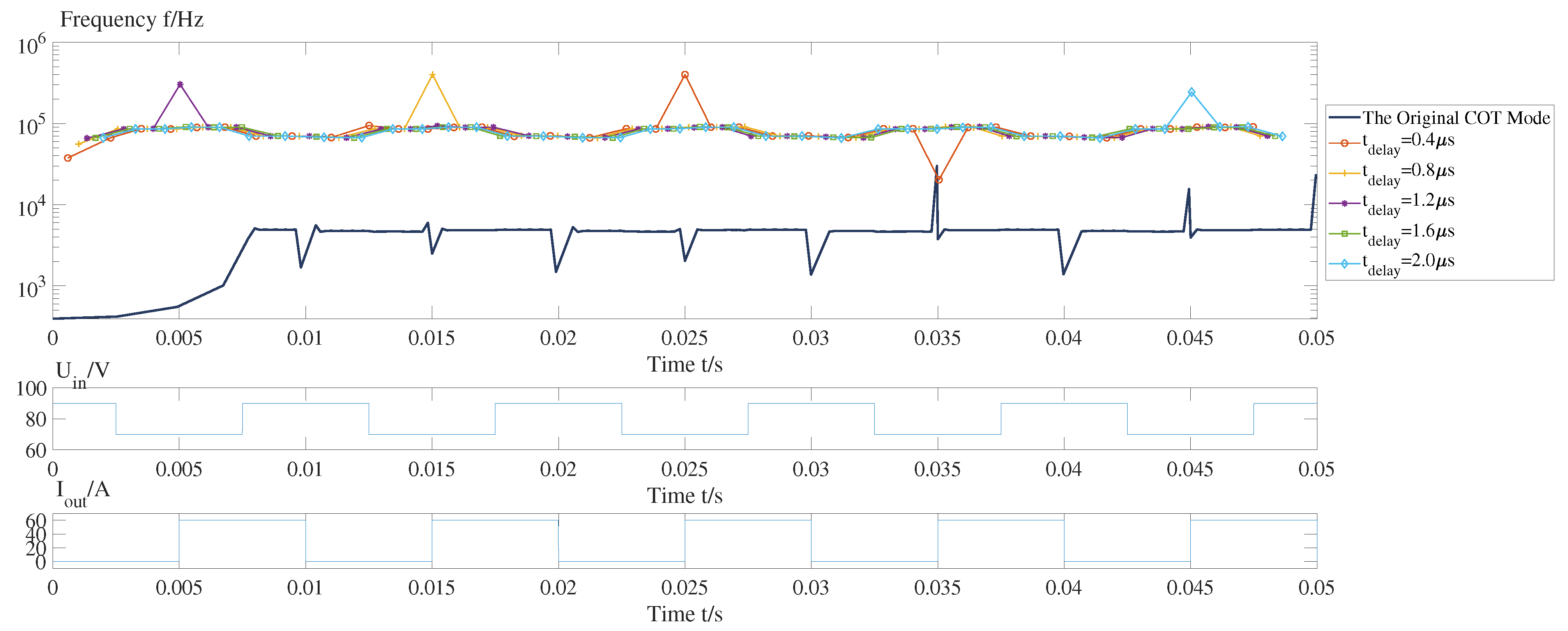
Working with a designed and fixed operating frequency under CCM is the main advantage of the COT mode compared with the hysteresis mode. In this study, the variation of the operating frequency is focused not only when the system is working in a steady state but also when the system suffers a sudden change of load. The operating frequencies of the COT and PD-COT with different delays are simulated, and the results are shown in
Figure 7.
Considering
Figure 7, it can be seen that the operating frequency of the COT (dark blue dotted line) is lower than the designed point, while the operating frequencies of the proposed method are fixed and match designed values in the steady state. This is the contribution from the parameters of the voltage ratio and on-time, which are easy to calculate and design. Meanwhile, the total delays of the feedback and control links barely affect the operating frequency. However, the operating frequencies jump at some points that follow the delay and the sudden jump of the input and output voltage ratio.
Taking the red line as an example, the frequency jump phenomenon occurs due to the step impacts of the load. However, the physically realizable impact strength is limited and occurs in a step-wise manner. Thus, these peaks can be ignored.
5. Comparison and Application Analysis
A monolithic voltage-mode DC–DC buck converter with advanced burst mode (ABM) and PWM was presented in a paper by Yuan [
6]. Yuan proposed a counter-based method to make the transition between ABM and PWM smooth. Thus, the load transient response was improved significantly. Using the parameter configurations given in [
6], comparisons of this work with Yuan’s work [
6] and our previous work [
7] can be made. The results are listed in
Table 2.
By horizontal comparisons of the performances with different control schemes as listed in
Table 2, the recovery time of the proposed method is shorter than those in [
6,
7]. The overshoot and undershoot voltages are lower than Yuan’s work. The Buck circuits with the proposed control method work under a fixed and lower frequency but show a similar ripple voltage to the hysteresis mode [
7].
To further prove the validity of the proposed method, choosing similar external inductor and capacitor configurations, the performances of the method in this work are compared with the results from Hsu’s work. In Hsu’s work [
2], to achieve a fast transient response for a DC–DC Buck converter, a proposed operational trans-conductance amplifier with a dual operating modes (DOM) control circuit was used as an error amplifier in the pulse-width modulation (PWM) control circuit. This approach leads to a transient response by accelerating the output level shifting of the error amplifier. Thus, the PWM control circuit generates the proper signal to drive the power transistors. Finally, the output voltage of the DC–DC buck converter is rapidly recovered when the load transient occurs. The comparison results are shown in
Table 3 and indicate that, with the same recovery time, the ripple voltage of our approach is much smaller than that in Hsu’s work.
Through the comparisons, it is noting that, as the main performance indexes are competitive, the proposed method is reasonable. Meanwhile, it must be noted that in the simulations and comparisons, all the parameter values are set to be in normal ranges. That means the implementation is physically realizable as all electronic components needed are common.