Motion Planning for Vibration Reduction of a Railway Bridge Maintenance Robot with a Redundant Manipulator
Abstract
:1. Introduction
- (1)
- Developing a nonlinear programming-based framework that can solve the collision-free and vibration-reduction problem of the trajectory of a mobile redundant manipulator at the same time.
- (2)
- Developing the vibration-reduction trajectory planning algorithm of a mobile redundant manipulator by smoothing the joints’ jerk and minimizing the total torque exerted on the mobile base.
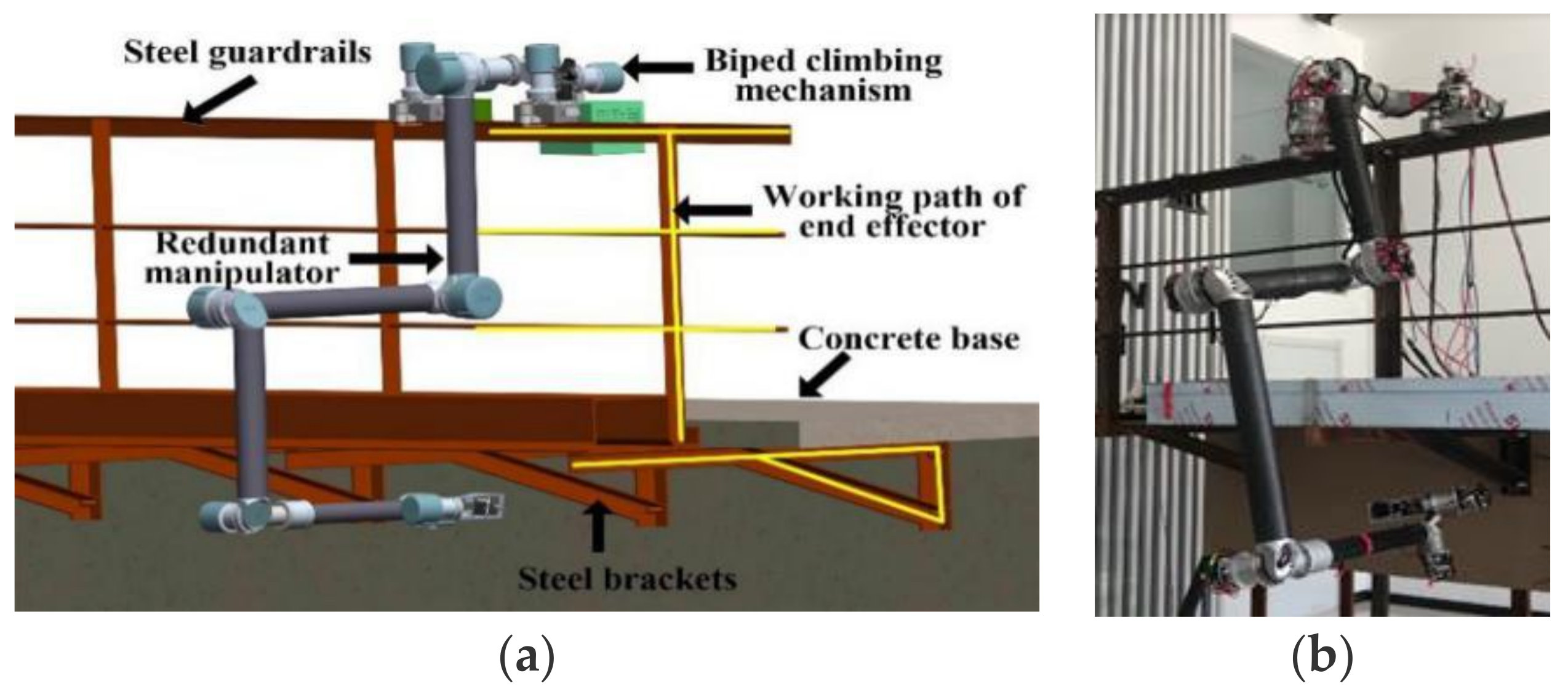
2. Kinematic and Dynamic Modeling of the Outdoor Redundant Manipulator
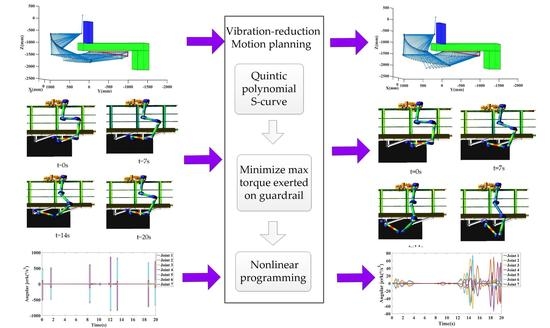
3. Vibration-Reduction Motion Planning Algorithm for the Redundant Manipulator of COMBOT
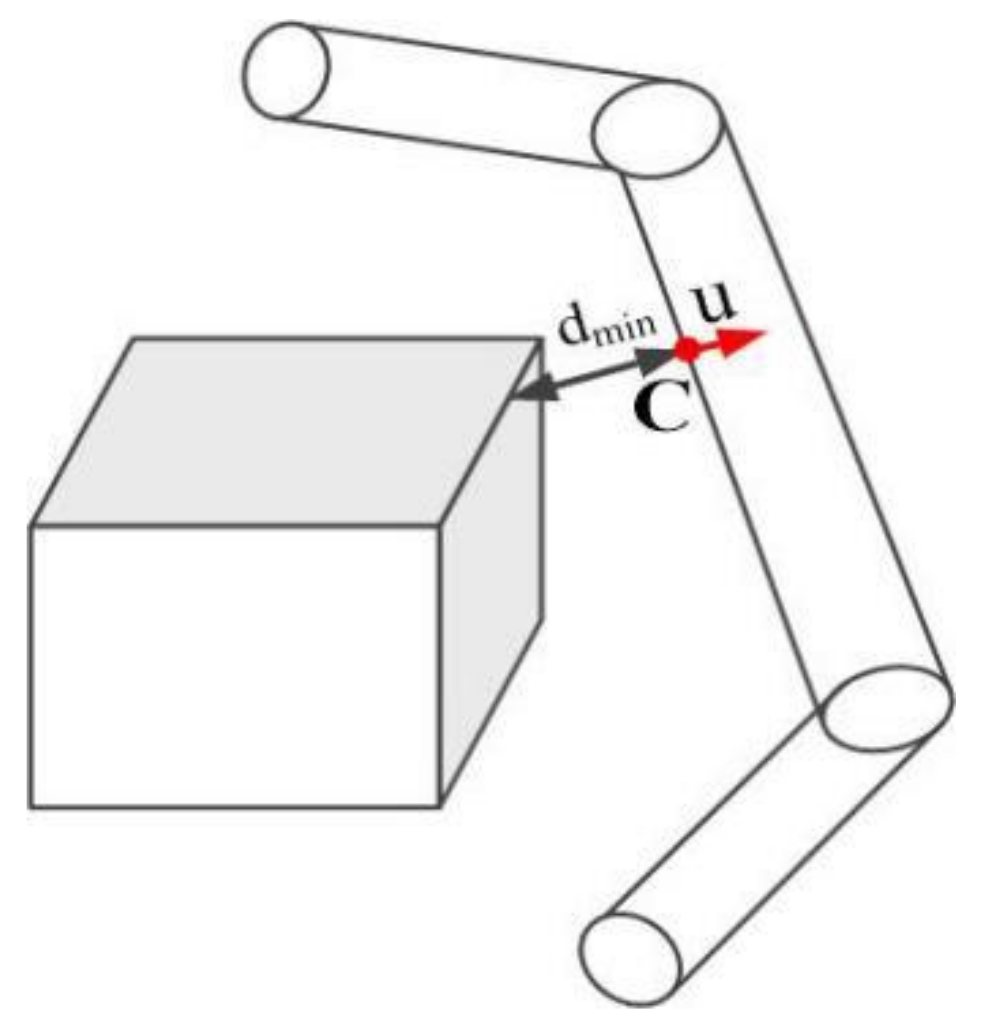
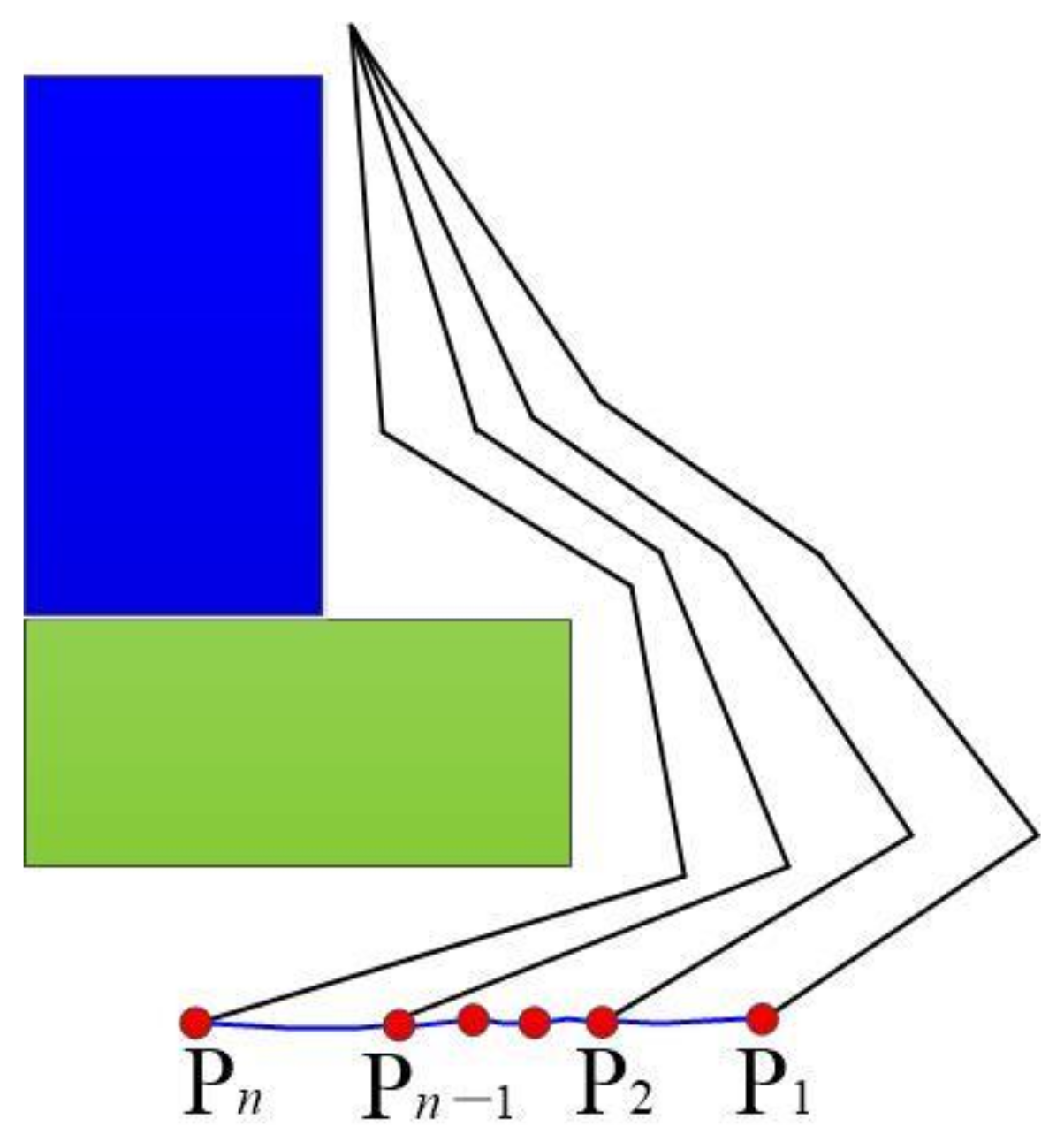
3.1. Collision-Free Geometric Path Planning Based on the Gradient Method with A Singularity-Robust Inverse
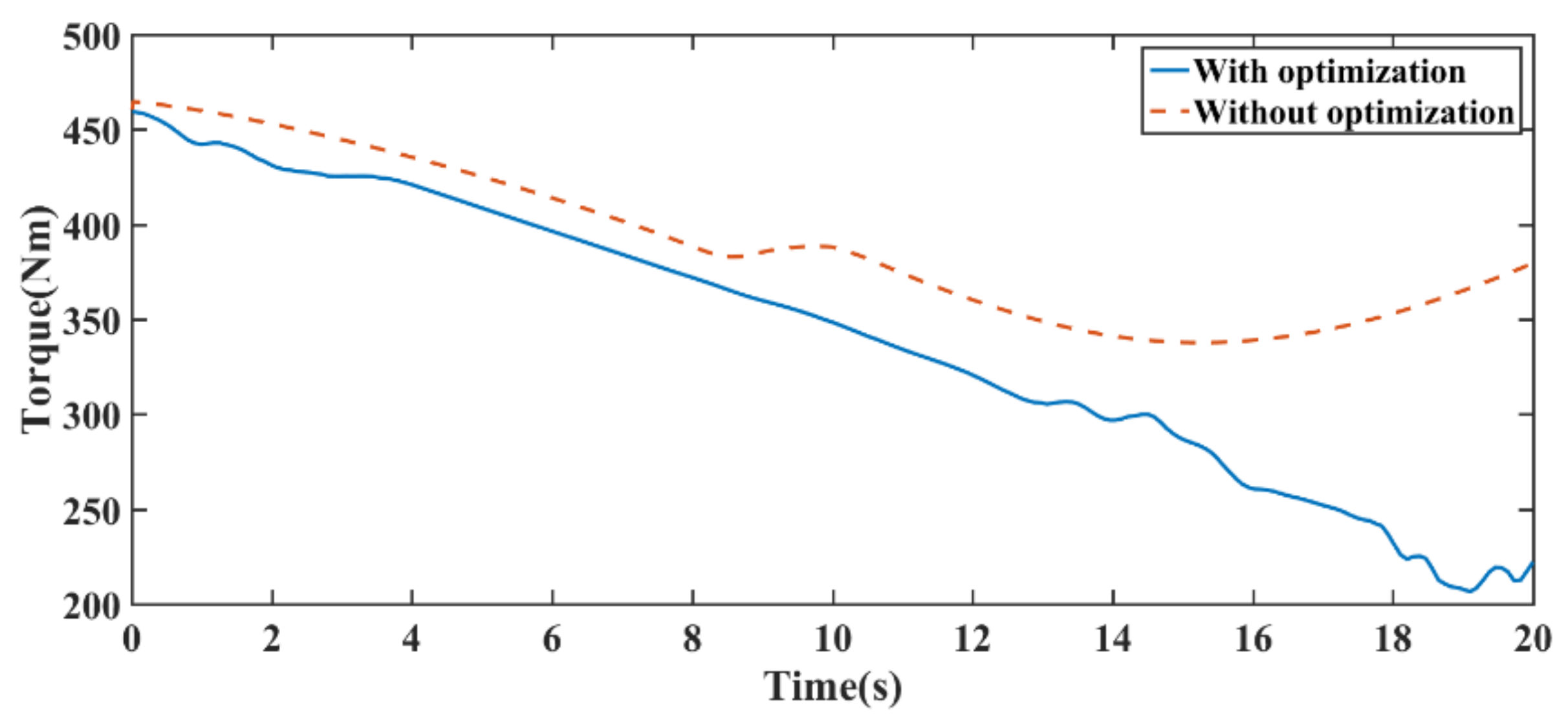
3.2. A Smooth and Vibration-Reduction Trajectory Planning Based on Nonlinear Programming
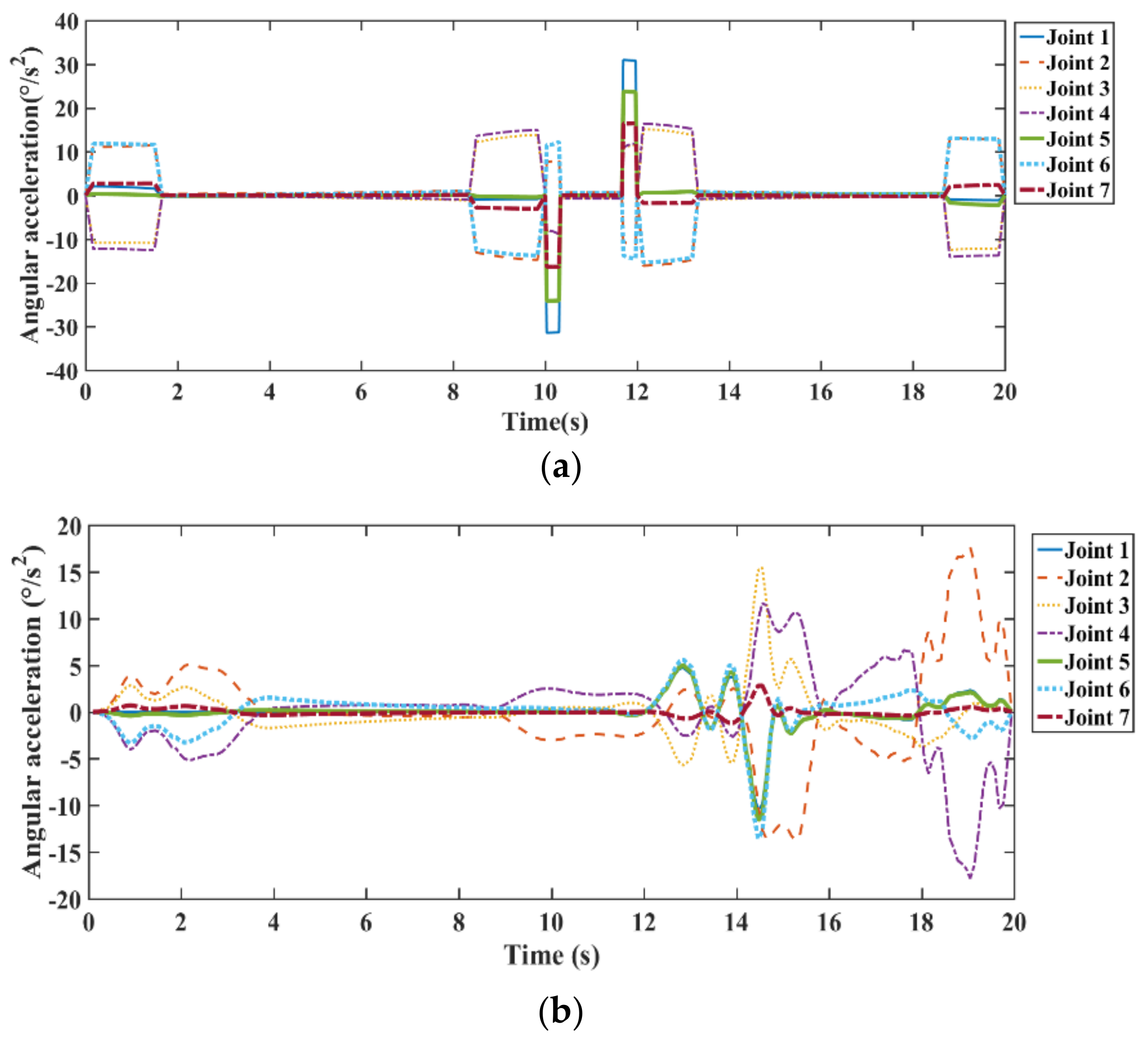
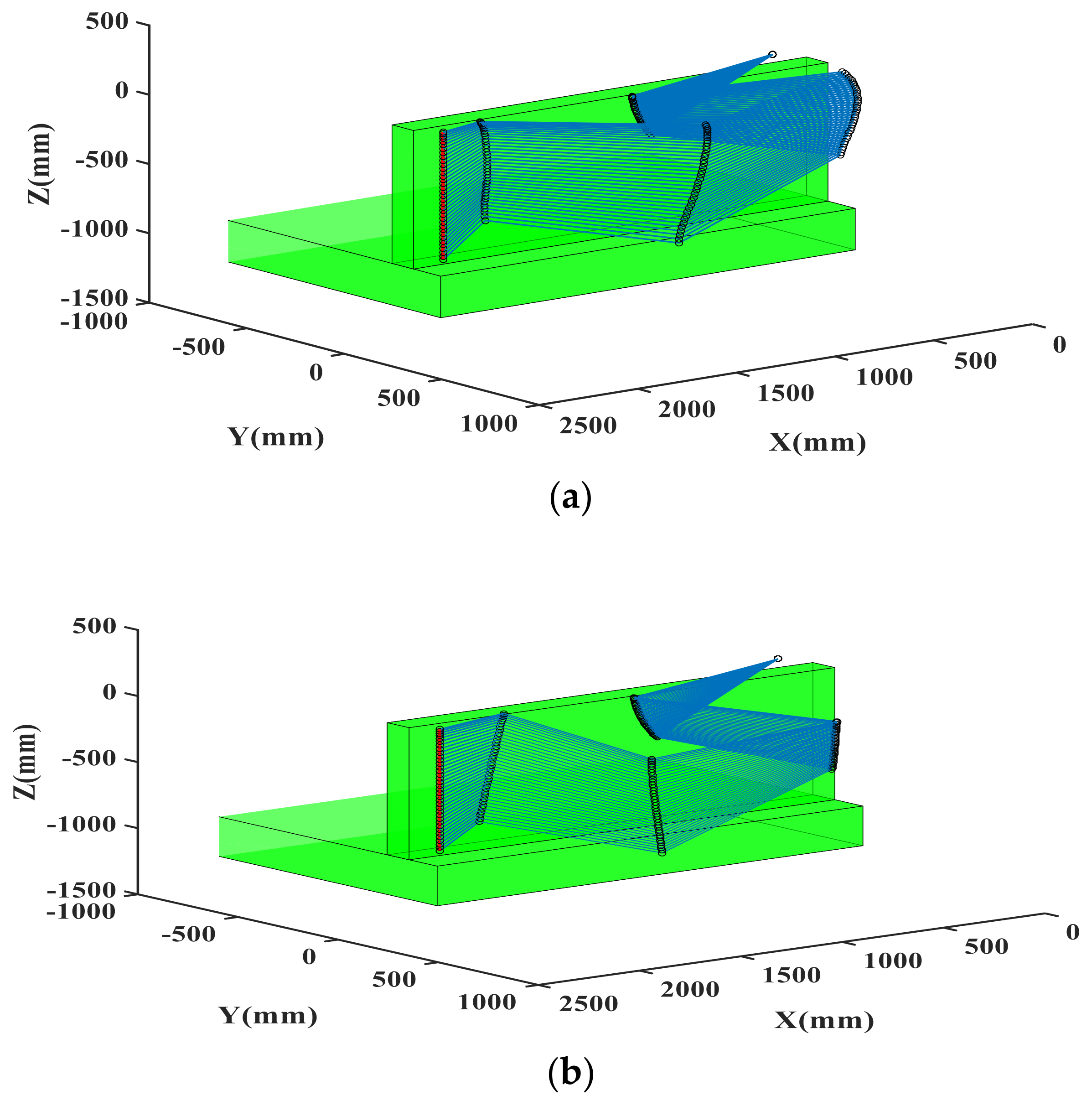
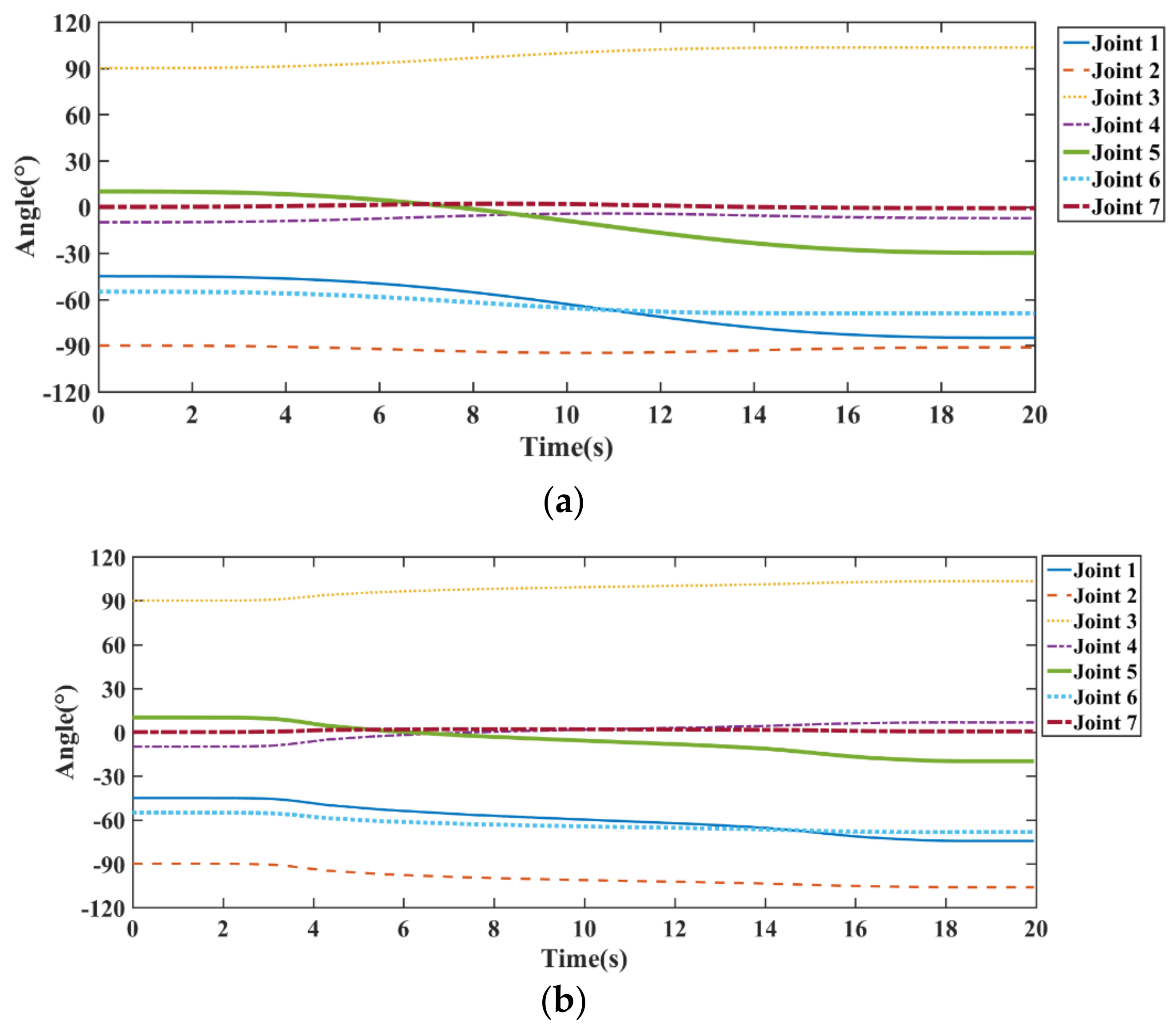
4. Simulation and Experiments
4.1. Triangle Working Path along the Steel Brackets
4.2. Linear Working Path along the Vertical Angle Steel of the Guardrails
5. Conclusions
6. Future Works
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Variables or Acronyms | Description |
|---|---|
| Oi | The local coordinate system of each link in manipulator |
| Unit vector of z-axis of Oi | |
| θi | Angle of joint i |
| αi | Twist angle of link i |
| δi | Length of link i |
| di | Offset of link i |
| Rotation matrix which represents the orientation of Oi+1 with respect to Oi | |
| iωi | Angular velocity and angular acceleration of Oi expressed in Oi |
| iγi | Angular acceleration of Oi expressed in Oi |
| iFi | Force acting on the COM of link i |
| iNi | Torque acting on the COM of link i |
| Mass matrix of the manipulator | |
| Matrix representing the coefficients of the Coriolis and centrifugal effects | |
| Vector accounting for gravity | |
| Jacobian matrix of the manipulator | |
| Pseudoinverse matrix of J | |
| Torque exerted on the guardrail by the manipulator | |
| VCi | Velocity bound of joint i |
| ACi | Acceleration bound of joint i |
| JCi | Jerk bound of joint i |
| τCi | Torque bound of joint i |
References
- Dorafshan, S.; Maguire, M. Bridge inspection: Human performance, unmanned aerial systems and automation. J. Civ. Struct. Health Monit. 2018, 8, 443–476. [Google Scholar] [CrossRef] [Green Version]
- Chu, B.; Jung, K.; Han, C.S.; Hong, D. A survey of climbing robots: Locomotion and adhesion. Int. J. Precis. Eng. Manuf. 2010, 11, 633–647. [Google Scholar] [CrossRef]
- Huang, H.; Li, D.; Xue, Z.; Chen, X.; Liu, S.; Leng, J.; Wei, Y. Design and performance analysis of a tracked wall-climbing robot for ship inspection in shipbuilding. Ocean Eng. 2017, 131, 224–230. [Google Scholar] [CrossRef]
- Pagano, D.; Liu, D. An approach for real-time motion planning of an inchworm robot in complex steel bridge environments. Robotica 2017, 35, 1280–1309. [Google Scholar] [CrossRef]
- Muthugala, M.A.V.J.; Le, A.V.; Cruz, E.S.; Elara, M.R.; Veerajagadheswar, P.; Kumar, M. A self-organizing fuzzy logic classifier for benchmarking robot-aided blasting of ship hulls. Sensors 2020, 20, 3215. [Google Scholar] [CrossRef]
- Muthugala, M.A.V.J.; Vega-Heredia, M.; Vengadesh, A.; Sriharsha, G.; Elara, M.R. Design of an adhesion-aware façade cleaning robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1441–1447. [Google Scholar]
- Eldred, R.; Lussier, J.; Pollman, A. Design and Testing of a Spherical Autonomous Underwater Vehicle for Shipwreck InteriorExploration. J. Mar. Sci. Eng. 2021, 9, 320. [Google Scholar] [CrossRef]
- Chang, Q.; Luo, X.; Qiao, Z. Design and Motion Planning of a Biped Climbing Robot with Redundant Manipulator. Appl. Sci. 2019, 9, 3009. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Ding, B.; Li, Y. Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation. Adv. Mech. Eng. 2020, 12, 1–18. [Google Scholar] [CrossRef]
- Li, L.; Xiao, J.; Zou, Y. Time-optimal path tracking for robots a numerical integration-like approach combined with an iterative learning algorithm. Ind. Robot. 2019, 46, 763–777. [Google Scholar] [CrossRef]
- Pham, H.; Pham, Q. A new approach to time-optimal path parameterization based on reachability analysis. IEEE Trans. Robot. 2018, 34, 645–659. [Google Scholar] [CrossRef] [Green Version]
- Consolini, L.; Locatelli, M.; Minari, A. Optimal time-complexity speed planning for robot manipulators. IEEE Trans. Robot. 2019, 35, 790–797. [Google Scholar] [CrossRef]
- Verscheure, D.; Demeulenaere, B.; Swevers, J. Time-optimal path tracking for robots: A convex optimization approach. IEEE Trans. Autom. Control. 2009, 54, 2318–2327. [Google Scholar] [CrossRef]
- Reiter, A.; Müller, A.; Gattringer, H. On higher order inverse kinematics methods in time-optimal trajectory planning for kinematically redundant manipulators. IEEE Trans. Ind. Inform. 2018, 14, 1681–1690. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, J.; Liu, W. Smooth and time-optimal S-curve trajectory planning for automated robots and machines. Mech. Mach. Theory 2019, 137, 127–153. [Google Scholar] [CrossRef]
- Brossog, M.; Bornschlegl, M.; Franke, J. Reducing the energy consumption of industrial robots in manufacturing systems. Int. J. Adv. Manuf. Technol. 2015, 78, 1315–1328. [Google Scholar]
- Sands, T. Optimization provenance of whiplash compensation for flexible space robotics. Aerospace 2019, 6, 93. [Google Scholar] [CrossRef] [Green Version]
- Saramago, S.; Junior, V. Optimal trajectory planning of robot manipulators in the presence of moving obstacles. Mech. Mach. Theory 2000, 35, 1079–1094. [Google Scholar] [CrossRef]
- Li, Y.; Huang, T.; Chetwynd, D. An approach for smooth trajectory planning of high-speed pick-and-place parallel robots using quintic B-splines. Mech. Mach. Theory 2018, 126, 479–490. [Google Scholar] [CrossRef] [Green Version]
- Piazzi, A.; Visioli, A. Global minimum-jerk trajectory planning of robot manipulators. IEEE Trans. Ind. Inform. 2000, 47, 140–149. [Google Scholar] [CrossRef] [Green Version]
- Macfarlane, S.; Croft, E. Jerk-bounded manipulator trajectory planning: Design for real-time applications. IEEE Trans. Robot. Autom. 2003, 19, 42–52. [Google Scholar] [CrossRef] [Green Version]
- Gasparetto, A.; Zanotto, V. A technique for time-jerk optimal planning of robot trajectories. Robot. Comput. Integr. Manuf. 2008, 24, 415–426. [Google Scholar] [CrossRef]
- Gasparetto, A.; Lanzutti, A.; Vidoni, R. Validation of minimum time-jerk algorithms for trajectory planning of industrial robots. J. Mech. Robot. 2011, 3, 031003. [Google Scholar] [CrossRef]
- Bianco, C. Minimum-jerk velocity planning for mobile robot applications. IEEE Trans. Robot. 2013, 29, 1317–1326. [Google Scholar] [CrossRef]
- Huang, T.; Wang, P.; Mei, J. Time minimum trajectory planning of a 2-DOF translational parallel robot for pick-and-place operations. CIRP Ann. 2007, 56, 365–368. [Google Scholar] [CrossRef]
- Rocha, C.; Tonetto, A.; Dias, A. A comparison between the Denavit–Hartenberg and the screw-based methods used in kinematic modeling of robot manipulators. Robot. Comput. Integr. Manuf. 2011, 27, 723–728. [Google Scholar] [CrossRef]
- Bianco, C. Evaluation of generalized force derivatives by means of a recursive Newton–Euler approach. IEEE Trans. Robot. 2009, 25, 954–959. [Google Scholar] [CrossRef]
- Gilbert, E.; Johnson, D.; Keerthi, S. A fast procedure for computing the distance between complex objects in three-dimensional space. IEEE Trans. Rob. Autom. 1988, 4, 193–203. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Li, H. Weighted UDV*-decomposition and weighted spectral decomposition for rectangular matrices and their applications. Appl. Math. Comput. 2008, 198, 150–162. [Google Scholar] [CrossRef]



















| Link i | Twist Angle αi (°) | Length of Link δi (m) | Offset of Link di (m) | Joint Angle θi/(°) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | θ1 |
| 2 | −90 | l1 = 0.83 | 0 | θ2 |
| 3 | 0 | l2 = 1.00 | 0 | θ3 |
| 4 | 0 | l3 = 0.78 | 0 | θ4 |
| 5 | 90 | 0 | l4 = 0.87 | θ5 |
| 6 | −90 | 0 | 0 | θ6 |
| 7 | 90 | 0 | 0 | θ7 |
| Link i | Link Mass (kg) | Inertia of Link (Ixx, Iyy, Izz, Ixy, Ixz, Iyz) (kg · m2) | Joint Torque Range (Nm) |
|---|---|---|---|
| 1 | 7.8 | (0.02, 0.32, 0.32, 0, −0.01, 0) | ±240 |
| 2 | 7.4 | (0.04, 0.46, 0.45, −0.01, 0.06, 0) | ±240 |
| 3 | 7.7 | (0.06, 0.56, 0.59, 0.011, 0.12, 0) | ±240 |
| 4 | 4.9 | (0.05, 0.03, 0.03, −0.01, 0.01, 0) | ±160 |
| 5 | 3.7 | (0.25, 0.25, 0.01, 0, 0.01, 0.01) | ±160 |
| 6 | 2.5 | (0.01, 0.01, 0.003, 0, 0, 0.001) | ±160 |
| 7 | 3.62 | (0.03, 0.09, 0.07, −0.01, 0.01, 0) | ±160 |
| Constraint Parameters | Joint 1 | Joint 2 | Joint 3 | Joint 4 | Joint 5 | Joint 6 | Joint 7 |
|---|---|---|---|---|---|---|---|
| VCi (°/s) | 20 | 20 | 20 | 30 | 30 | 30 | 30 |
| ACi (°/s2) | 60 | 60 | 60 | 90 | 90 | 90 | 90 |
| JCi (°/s3) | 160 | 160 | 160 | 240 | 240 | 240 | 240 |
| (Nm) | 240 | 240 | 240 | 160 | 160 | 160 | 160 |
| Statistical Results of Tracking Errors | X-Axis | Y-Axis | Z-Axis | |
|---|---|---|---|---|
| Without optimization | Mean deviation (mm) | −1.22 | 3.94 | −9.23 |
| Standard deviation (mm) | 1.28 | 3.99 | 8.22 | |
| With optimization | Mean deviation (mm) | −2.44 | 11.52 | −24.48 |
| Mean deviation (mm) | 4.21 | 16.20 | 26.78 | |
| Statistical Results of Tracking Errors | X-Axis | Y-Axis | Z-Axis | |
|---|---|---|---|---|
| Without optimization | Mean deviation (mm) | −2.13 | −2.03 | −2.55 |
| Standard deviation (mm) | 2.01 | 2.26 | 3.39 | |
| With optimization | Mean deviation (mm) | −6.17 | −3.93 | −5.36 |
| Mean deviation (mm) | 7.62 | 4.63 | 7.87 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Q.; Wang, H.; Wang, D.; Zhang, H.; Li, K.; Yu, B. Motion Planning for Vibration Reduction of a Railway Bridge Maintenance Robot with a Redundant Manipulator. Electronics 2021, 10, 2793. https://doi.org/10.3390/electronics10222793
Chang Q, Wang H, Wang D, Zhang H, Li K, Yu B. Motion Planning for Vibration Reduction of a Railway Bridge Maintenance Robot with a Redundant Manipulator. Electronics. 2021; 10(22):2793. https://doi.org/10.3390/electronics10222793
Chicago/Turabian StyleChang, Qing, Huaiwen Wang, Dongai Wang, Haijun Zhang, Keying Li, and Biao Yu. 2021. "Motion Planning for Vibration Reduction of a Railway Bridge Maintenance Robot with a Redundant Manipulator" Electronics 10, no. 22: 2793. https://doi.org/10.3390/electronics10222793
APA StyleChang, Q., Wang, H., Wang, D., Zhang, H., Li, K., & Yu, B. (2021). Motion Planning for Vibration Reduction of a Railway Bridge Maintenance Robot with a Redundant Manipulator. Electronics, 10(22), 2793. https://doi.org/10.3390/electronics10222793