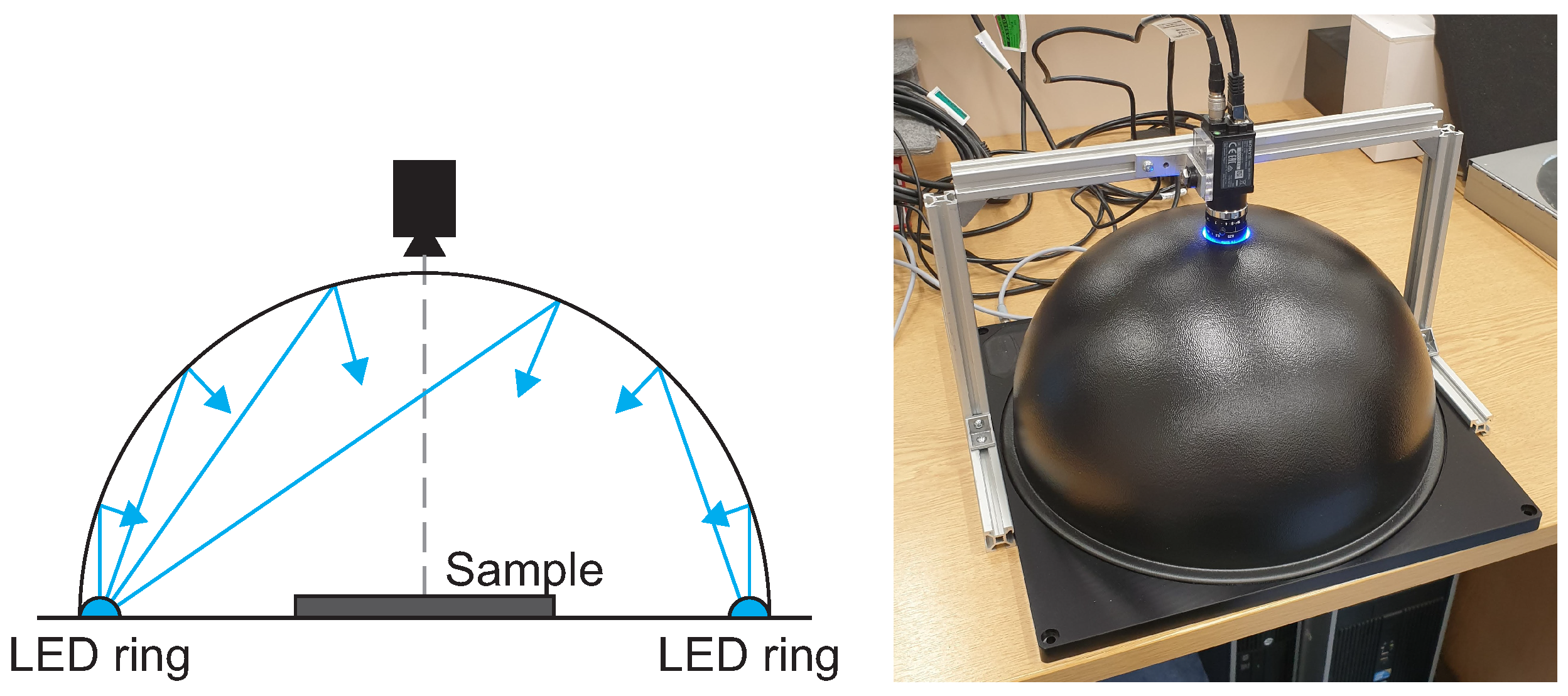
1. Introduction
The use of composite structures in various industries has increased in recent decades due to their advantages over conventional materials. Most notably, carbon fibre reinforced polymer (CFRP) components offer exceptionally high strength-to-weight ratios and are, thus, highly attractive for aerospace engineering. Other advantages of CFRP include high stiffness, corrosion resistance and low thermal expansion. Consequently, CFRP usage is becoming increasingly popular in other areas such as maritime, civil and automotive engineering [
1].
Due to this increased use of CFRP—in addition to its higher manufacturing costs—the need for inspection and repair technologies for such materials has increased accordingly. This is particularly important since the strength and stiffness of composite parts are highly dependent on the placement and orientation of fibres during manufacture [
2]: a 5° angular error in orientation, for example, can result in a 20% reduction in component strength [
3]. Due to this importance and the time consuming nature of inspection, a great deal of resources are often devoted to the inspection of parts. Rudberg et al., for example, stated that 33% of the time taken for automated fibre placement in aerostructures can be devoted to inspection and repair [
4]. Therefore, precise measurement of fibre orientation plays an important role during manufacturing quality assurance.
Motivated by the above, the aim of this paper is to assess the accuracy and reliability of an emerging non-destructive technology used for the analysis of composite parts: polarisation vision. Specifically, the paper presents research into the feasibility of this technology for widespread adoption in the field with a primary focus on fibre orientation measurement of carbon fibre materials. The paper considers both dry materials (i.e., raw and untreated carbon fibre fabrics) and cured materials (those with the fibres set in resin, forming a hardened composite part). It should be noted that only minor changes to the presented method would be required to make the inspection more general (e.g., to localise specific defects such as waviness or fuzzballs) since many such defects manifest as local unexpected variations in fibre angle. Only
carbon fibres are considered here since other types, such as glass fibres, do not possess the requisite anisotropic conductivity for the appropriate theory (
Section 2.1) to apply.
Polarisation vision is a growing sub-field of computer vision that uses polarisation data to extract useful information about a scene or object. It can be defined as “the acquisition and use of images that encode information about the polarisation state of incoming light” [
5]. Images captured with this technology typically encode polarisation data in a three channel image, where each channel contains the following information [
5]:
Intensity, I: Identical to a standard monochrome image;
Phase or angle of linear polarisation (AoLP), : Angle of polarisation of incoming light at each pixel;
Degree of polarisation (DoP), ρ: Fraction of the incoming light that is polarised at each pixel, ranging from 0 (unpolarised) to 1 (completely linearly polarised).
This paper primarily uses the AoLP since it aligns with the fibre angles on the surface under investigation, as explained in
Section 2.1.
The remainder of this paper is organised as follows. First, a summary of the existing literature in the field is presented followed by a list of the main contributions of this research study.
Section 2 then describes the underlying principles of the physics of reflectance used for this research study as well as the hardware used and algorithmic approach to data processing.
Section 3 covers the detailed numerical results of the study, demonstrating the levels of precision expected in both ideal and non-ideal conditions. The primary focus is on planar surfaces, although non-planar surfaces are briefly considered in
Section 3.3. A discussion of the significance of the research with respect to real application areas is provided in
Section 4 before
Section 5 concludes the paper.
1.1. Related Work
The following subsections cover existing research in composite part inspection before reviewing polarisation vision hardware and its applications.
1.1.1. Composite Part Inspection
Many non-destructive methods currently exist for quality assurance during manufacturing and damage detection on composite structures. Most of these are highlighted in [
6,
7], such as acoustics, shearography, thermography, etc. One particularly sophisticated non-destructive method is X-ray computed tomography (CT) as it provides geometrically accurate subsurface imaging of a component [
8]. Researchers have exploited this technology to develop an interactive tool for visual analysis of fibre properties on CFRP components [
9]. This tool often uses parallel coordinates to define and configure initial fibre classes before applying polar plots to render fibre orientation distributions [
9]. Further work on the application of X-ray CT for composite inspection can be found in [
10,
11]. Nelson et al. highlighted that one disadvantage of the method is that the physical size of typical aerospace components often precludes inspection using X-ray CT methods because spatial resolution requirements cannot be achieved [
8]. However, spatial resolution is improving and different strategies can be adopted to overcome sample size/resolution issues [
12]. Certainly, CT scanners remain expensive and unwieldy.
Another dominant non-destructive method for composite inspection is ultrasound. Pulse-echo ultrasound is commonly used in aerospace for analysis of large composite components; however, data generated from the technique do not intuitively reveal ply and fibre features [
8]. Nelson et al. demonstrate that ultrasonic instantaneous-phase data can be analysed by using image processing algorithms to produce three-dimensional maps of ply orientations [
8]. Unfortunately, the researchers concluded that further work was necessary to produce robust measurements.
Computer vision methods for inspection have proved challenging on CFRP surfaces due to their black and shiny nature. Several attempts have been proposed based on traditional image processing and edge detection, but these inherently need very high quality and high resolution images that are not always tractable [
13,
14]. Furthermore, the methods were not proven on materials with plain appearance such as unidirectional surfaces with no visible stitching. In order to overcome the difficult reflectance properties, Zambal et al. [
15] used a specialised lighting rig and modelled the reflectance properties of fibres to determine their orientations. This provided sub-degree precision for more general CFRP surfaces at the expense of longer capture times and the need for highly controlled illumination.
Recently, polarisation vision has been applied to the analysis of carbon fibre composite structures since the anisotropic conductance of such materials means that the angle of polarisation of reflected light matches the fibre orientation of each point on a surface [
16,
17]. The key elements demonstrated from these works are as follows:
The angle of linear polarisation corresponds to the angle of orientation of the fibres (both dry and cured), as predicted by the underlying physics theory.
Reflection from CFRP materials causes unpolarised incident light to become partially polarised. As such, an unpolarised light source is sufficient for data capture.
Light intensity and distribution are important factors to consider as some illuminations will result in no light being reflected from certain fibres. A dome illumination can be used for ensuring uniform illumination throughout the entire component.
The degree of polarisation shows the amount of polarised vs. unpolarised light, which can add confidence levels to individual measurements.
Further studies on the application of polarisation vision for composite part inspection can be found in [
18] where Atkinson et al. first focused on demonstrating the ability of polarisation technology for image recovery on diffuse, non-fibrous surfaces before performing a brief test on a planar CFRP sample. The results gathered from the experiments in [
18] highlight that the fibre orientation distribution corresponds to the angle of linear polarisation, as stated in [
16], and that the AoLP histogram allows for the determination of the main angles present. The pros and cons of polarisation compared to alternative methods are summarised in
Table 1.
1.1.2. Polarisation Vision Hardware
The field of polarisation vision initially developed in the 1980s with several major contributions from Wolff and coworkers in the 1990s [
19,
20,
21]. Without specialist hardware, polarisation data have been captured by using a standard, typically monochrome, camera with a mechanically rotating linear polarising filter placed in front of the lens. With this method, at least three images are needed at different polariser orientations to obtain a complete measurement of partial linear polarisation [
5,
21,
22]. This assumes that there is no circular/elliptical polarisation present. However, due to the need for rotating optics, the measurements of AoLP and DoP are slow and, thus, limited to static scenes.
The development of liquid crystal polarisation cameras opened up further applications as the polariser transmission axis could be switched much more rapidly [
23,
24]. These “polarisation cameras” then allowed for faster data acquisition as there was no longer a mechanically rotating part. However, captured data were highly susceptible to noise, and capture time was still longer than a standard camera [
5]. For these reasons, widespread adoption of the technology was still limited well after the turn of the century.
An alternative approach to data capture was to use a polarising beam splitter that allows for real-time measurements of partial linear polarisation [
25,
26]. Indeed Pezzaniti et al. were able to recover full Stokes vector parameters at 60 frames per second [
26]. While this provides higher frame rates than the above mentioned liquid crystal polarisation cameras, this comes as a trade-off as such an arrangement is expensive and difficult to calibrate [
5].
Since the development of the above capture methods, many cameras have emerged that overcome some of their issues by incorporating polarising filters directly onto the sensor chip [
17,
27,
28]. One of the earliest, the “POLKA”, was developed at the Fraunhofer Institute for Integrated Circuits and is compared to the rotating filter method in [
5], showing comparable precision but at much faster frame rates. The POLKA was also used in early efforts for determining strand orientation in CFRP components for contactless quality inspection [
16]. This is even demonstrated on moving parts. This paper uses a similar sensor to POLKA, the Sony IMX250MZR. Similarly to the POLKA, the Sony sensor uses monochrome quad-polarised filters to capture polarised light in four planes [
29], as detailed in
Section 2.2.
1.1.3. Other Polarisation Vision Applications
Perhaps the most widely studied application for polarisation vision in computer vision literature is three-dimensional shape analysis [
19,
22,
30,
31] where polarisation information is used to estimate the geometry of an object. In 2004, Atkinson et al. applied the Fresnel theory to recover the shape of an object in diffuse polarisation cases and concluded that diffuse polarisation had potential for such application when combined with other computer vision techniques [
22]. Atkinson later, therefore, incorporated binocular [
30] and photometric [
31] stereo in order to improve precision. Miyazaki et al. [
24] used polarisation on transparent surfaces for shape estimation of particularly challenging material types. Other example applications include bio-medicine [
32], haze reduction [
33], underwater geo-localization [
34] and eye tracking [
35]. A more detailed survey of general applications of polarisation vision can be found in [
5].
1.2. Contributions
The above literature survey shows that, while the wider field of polarisation vision has now become established, its use in the specific area of composite part inspection is still relatively new. In particular, a detailed numerical study into its performance in such an application has been lacking, forming the primary motivation for this paper. The main novel contributions of this research are as follows:
Evidence that polarisation imaging offers a viable approach to the challenging problem of composite part inspection;
Determination of the capture conditions necessary to obtain the most reliable measurements;
Quantitative analysis of performance for both optimal capture conditions and more general scenarios;
Demonstration that, while the general polarisation phenomena for non-planar components can be qualitatively understood, further research is required for accurate inspection of most three-dimensional parts in an industrial setting;
Generally improved understanding of the polarising optical properties of carbon fibres with and without being cured in resin.
Compared to many of the non-polarisation methods described above, the method in this paper is exceptionally fast and cheap, requiring minimal physical footprint on an inspection/manufacturing line, while maintaining competitive precision relative to the state of the art. The main drawback is that the approach is limited to analysis of the top (visible) layer of a part only.
3. Results
As it will become clear, the optimal conditions from those in
Table 2 are 23 mm lens with dark field illumination. The performance of the system for this particular arrangement will be presented in detail in
Section 3.1. Other conditions will be described in
Section 3.2. A preliminary study for non-planar components can then be found in
Section 3.3.
For most tests in this paper, the UD samples are positioned such that the mean fibre angle is at 90° (i.e., vertical in the images). For woven cases, half of the fibres are nominally at 90° with the remainder at 0°/180°. The sample orientation was initially set by hand, aligning the fibres with the edges of the image display in a live feed from the camera. In practice, this was rather difficult, and the ground truth orientation for all experiments has approximately 1° of uncertainty. This is the reason for the choice of
relative angle measurements for the analysis (see
Section 3.1) rather than the practically difficult
absolute angle. It should be noted that for test samples in good imaging conditions, the difference between manually measured absolute fibre angles and that from the polarisation data fell within experimental uncertainty.
3.1. Optimal Conditions
The best results were found for the case of dark-field illumination; thus, these are analysed in detail first.
3.1.1. UD Samples
For the first test, a UD sample was placed on a computer-controlled turntable that was able to rotate the part with very high (≪1°) precision. Due to the difficulty in manually positioning the sample at a required angle, the approach was to initially align the part by trial-and-error until the polarisation method returned an average of 0° estimates across the image. The test was then to observe whether the subsequent fibre angles were correctly estimated as the table was rotated. Of course, it would have been better to test the absolute orientation of the sample by comparing the polarisation method to absolute ground truth fibre angle from the outset had the latter been more readily available. However, it is worth reiterating that estimates of the absolute angles of the fibres from polarisation data did fall within experimental error of manual measurements made with a simple protractor.
For various ROIs within the image, the estimated median angles were plotted against the turntable angle as shown in
Figure 8. This shows exceptionally robust performance in the given conditions, with marginally inferior results for dry samples compared to cured ones (although this may be simply due to the greater difficulty in lining up the tows in the dry sample for data capture). Note that the turntable rotates by 360°, while outputs from the algorithm only allow angles up to 180°. For the sake of presentation, 180° has been manually added to the second half of the data points for ease of comparison.
Figure 9 shows images of AoLP and DoP data for the cured sample. The AoLP image is very uniform except for a few speckles—presumably due to imperfections on the top layer and/or marks on the resin. The DoP image mostly shows high values (>0.4), meaning a correspondingly high SNR is present.
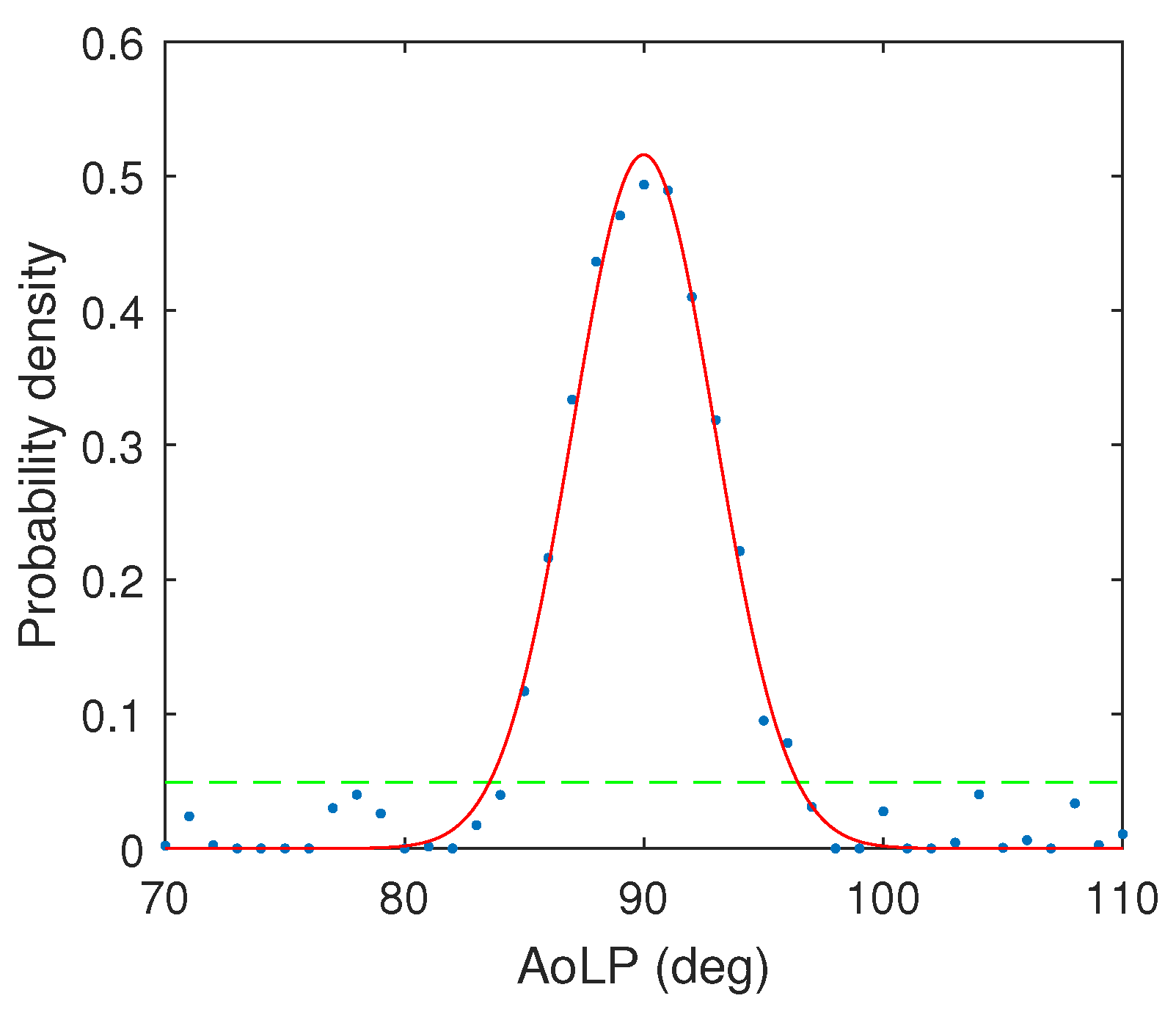
Figure 9 also shows the histograms of AoLP measurements for each ROI with Gaussian curve fitting and corresponding standard deviations. Again, this demonstrates strong uniformity and values close to the expected 90°. Indeed, the results suggest that sub-degree accuracy in relative angle estimation can be attained.
Figure 10 shows a close-up of the histogram and various statistical measures used to emphasise the robustness of the AoLP to confirm the angle of orientation of carbon fibres. As observed, the difference between the mean and the median is minimal, which indicates that the likelihood of reliable estimates is high. The figure also indicates robustness of the fibre angle estimation method against the performance metric used—i.e., to show that results are not biased by the specific choice of metrics.
Figure 11 and
Figure 12 show equivalent results for an uncured UD sample. The performance is comparable but slightly inferior with respect to the cured case in terms of the spread of data. This is presumably a consequence of both genuinely more distributed fibre angles and loose fibres reflecting light directly to the camera and would, thus, vary for different quality materials. There is also evidence of a slight shift in measured angles between different parts of the image, which will be studied further in
Section 3.2.
Figure 13 shows a close-up image of a portion of dry fibre cloth (with the camera placed approximately 10 cm from the surface for this image). This shows that very fine details of the fibres can be obtained if necessary—up to single strands. However, the image also demonstrates that small particles (dust, binding agents, etc.) potentially contaminate the fibre orientation measurements. Furthermore, the AoLP values for individual fibres vary from one side of their axis to the other, as shown by the loose fibre near the top of the image at about 15°, for example. This may be a result of the three-dimensional geometry of single fibres affecting polarisation measurements, as previously observed for non-fibrous surfaces [
30].
3.1.2. Non-UD Samples
Figure 14,
Figure 15,
Figure 16 and
Figure 17 show results in optimal conditions for cured and dry woven samples. The main observation here is that both errors relative to ground truth and the standard deviations are larger. The latter is mostly explained by the presence of small but numerous transition regions between tows of fibres at each angle. A close inspection of individual tows reveals only small local variations in measurements. Data for the dry fibres clearly show the presence of waviness as, for example, in the upper-left ROI of
Figure 16. Furthermore, ground truth angles are clearly not consistently 90° throughout the image. For these reasons,
Figure 16 should act more as a demonstration to indicate the capabilities of the approach, rather than a test of precision.
An interim conclusion at this point is that the approach has the capability to estimate average fibre angles to a precision of at least 1° but that pixel-by-pixel estimates can be affected by a few factors such as the location of the pixel within the image (discussed below) and the transition regions between fibre directions in woven samples.
3.2. Alternative Capture Conditions
While the results above represent the best-case scenario, it is not always possible to attain such capture conditions in real-world industrial settings. This section demonstrates alternative capture conditions for comparison. The standard deviation results for various test cases are shown in
Table 3 with results from the turntable shown for the extreme case of a point source shown in
Figure 18. The first observation from the table and figure is that global/large ROI measurements are still typically robust (at least with a 23 mm lens) but that pixel-level variations are often high.
As observed in
Table 3, the results for bright field illumination are inferior to the dark field case for most test samples. Furthermore, the capture process was more complicated since the lights caused a specularity in the images necessitating multiple exposures to obtain the figures quoted in the table, as per the method described in
Section 2.5. The dark field case by contrast, did not require this step. Indeed, the dark field and dome illuminators were the only two lighting types that did not generally require multiple exposures in order for reliable measurements to be made.
For dry samples, results from the dome light were comparable or even superior to those with dark field illumination. However, results were comparatively poor for the basic case of a cured UD sample. Upon further inspection, it was found that the reason for this is the presence of non-normal specular reflections from the resin surface to the camera, for which Fresnel Theory predicts finite polarisation even in the absence of fibres. In other words, the assumption that all polarisation is a result of the fibres breaks down.
This phenomenon is best illustrated with a 12 mm lens: The representative results for which are shown in
Table 4. By comparing results in this table to the corresponding cells from
Table 3, the only significant difference relates to the cured UD material under the dome illuminator. This can be understood by considering that, for the shorter focal length, more of the resin surface is reflected towards the camera at a non-normal direction (strictly speaking, one should say “far-from-normal direction”), as shown in the schematic of
Figure 19.
To demonstrate this effect further,
Figure 20 shows AoLP and DoP images for a pure cured resin surface (i.e., the planar resin matrix with no fibres embedded). In this case, there are no anisotropic conducting fibres to polarise light, meaning that any observed pattern is due to specular reflection following phenomena studied elsewhere in the literature [
5,
22]. This is apparent from the fact that the four corners of the image follow an obvious pattern, but that the effect is less noticeable for the longer focal length, where less non-normal specular reflectances are present.
Figure 21 shows results for the cured UD sample with a 12 mm lens under the dome. The AoLP image demonstrates that the phenomenon in
Figure 20, unfortunately, carries over into an image with carbon fibre in the resin. The histogram peaks for the central and full ROIs show good estimates of the true fibre angles, but the outer ROIs show huge (>5°) deviations as a result of the specular reflections from the resin. While this effect is particularly extreme here (the experiment for obtaining
Figure 21 was specifically devised to exaggerate the effect), it is still apparent to a lesser-degree when using a 23 mm lens, as in
Figure 22. It can also be observed to a small extent in some of the earlier results, such as in
Figure 11.
The fourth row of
Table 3 shows the measured standard deviations under ambient illumination—in this case, light from overhead fluorescent strip lights in a small laboratory and a multitude of consequent reflections around the room. Not surprisingly, the results are inferior to the optimal case. Furthermore, other forms of ambient light would presumably generate different results. However, this test does demonstrate scope for
some measurements to be taken without specialised illumination in certain environments depending on the variability of conditions and the required precision.
The final results from
Table 3 show standard deviations with the surface illuminated by a single LED. These tests are included to help understand the optical properties of the materials, rather than as realistic scenarios for industrial environments. The results for the point sources are generally poor—especially for cured samples with a parallel reflectance plane (a less dramatic reverse of this trend is true for dry samples for reasons not yet fully understood). In the table, the standard deviations for woven materials are simply listed in numerical order; although upon close examination, it was found that the direction corresponding to the higher values followed a similar trend to the UD samples. While this wide distribution of measured angles limits the applicability of data at the pixel level, the average angle measurements over wider ROIs proved more useful, as shown by results of a cured UD sample on the turntable, for example (
Figure 18).
3.3. Non-Planar Surfaces
So far, this paper has considered planar components that are parallel to the image plane. The first experiment for investigating more general components aimed to image the planar UD cured sample under dark field illumination but with the surface inclined at an angle of 15° to the image plane. This was performed twice: The first was performed such that the fibres themselves were inclined relative to the image plane, and the second was performed such that each fibre was parallel to the image plane with neighbouring fibres moving progressively further from the camera. The purpose of this test was to assess the importance of any angular offset between the image plane and the sample part. The results were very promising, with numerical differences to the non-inclined plane that were insufficiently large to establish any real difference (full experimental data are available in Data Availability Statement).
Unfortunately, the results for non-planar surfaces mostly demonstrated poor accuracy. However, they are briefly presented here as discoveries have been made that may prove useful for future research.
Figure 23 shows polarisation data for a section of a cured UD tube under dark field illumination. The tube is constructed in a manner such that the angle between the fibres and the axis of the tube is 45°. The DoP image shows a nonuniform pattern with especially high values near the occluding contours. This is most likely due to specular and/or diffuse reflection obeying the Fresnel theory [
5,
22] in combination with the tendency of AoLP to align with the fibres. As a result, specular reflections from the light sources caused erroneous angle measurements where this occurred. The graphs in
Figure 23 further demonstrate these complications, with specularities at positions of approximately −0.5 and +0.5 across the tube.
In an effort to minimise the complications above, the data for the tube were recaptured by using ambient and dome illumination, as shown in
Figure 24 and
Figure 25, respectively. The motivation for this was that the complications with dark field illumination might be reduced with more uniform lighting. It should be noted that the component was not completely inside the dome for
Figure 24 for practical reasons, meaning that the lighting was not truly hemispherical, with only minimal illumination emerging from grazing angles. The results are indeed superior but still inadequate for most real industrial applications.
Figure 26,
Figure 27 and
Figure 28 show the results for a similar tube but with UD dry material wrapped around. Here, we see much more predictable results since the complications of non-normal specular reflections from the resin are no longer present. The bumps on the dome illuminator image are thought to be due to the fact that the component did not fit fully inside.
In summary, the results for the tube correctly showed AoLP approaching 90° at the occluding contours (see Data Availability Statement for details of theoretical prediction) and 45° in the centre of the tube. However, competition between the effects described by the Fresnel theory for specularities and the alignment of the electric field of the reflected light with the fibres means that many parts of the images follow a very complicated (and difficult to model) pattern. This is further complicated by the difficulty in manufacturing the tube to a high degree of precision, as can be seen in some parts of the AoLP in
Figure 24 that have lower-than-expected values, for example.
4. Discussion
The results presented in the previous section are highly varied in terms of accuracy and applicability. At best, they demonstrate highly repeatable sub-degree measurements of fibre angles in dark field illumination. At worst, non-planar components proved difficult to inspect—although the nature of the inaccuracies were, at least, well understood in a phenomenological sense.
For the best-case results, it is easy to imagine an inspection system based on the proposed method that is integrated into a manufacturing line. This could take many forms. For instance, it could be used for small scale inspection of a high-precision component that is either planar or possesses a large radius of curvature. Alternatively, for some lower-precision/resolution applications, the method may be beneficial with a large working distance. However, installation and control of dark field illumination may be impractical in such a case.
A different approach might be to employ an integrated system, whereby the dark field lights and the camera are all attached to an end effector of a robot arm or gantry system that traverses the surface, scanning the part sequentially. This would maximise the uniformity of illumination throughout the capture. Indeed, it may prove beneficial to switch the technology to a line-scanning approach for some applications should such a version of the polarisation sensor ever be commercialised. An area-scan surface-traversal approach has already been proven by applying non-polarisation machine vision technology by Profactor [
39]. If a three-dimensional CAD model of the part is available (typically the case), then a three-dimensional part can be inspected provided that the curvature is sufficiently low as to prevent complications such as those described in
Section 3.3. The inclined-plane experiments in
Section 3.3 support this possibility, showing that a small misalignment between the image plane and surface patch has negligible implications on precision. In any case, given the inferior results of ambient illumination compared to that of dark field in
Table 3, the dark field lights should be sufficiently bright as to drown out ambient light as much as possible. In fact, a few experiments were conducted as part of this research study involving the capture of two images in rapid succession: one with dark field
and ambient light and one with only ambient light. The latter image was then subtracted from the former, effectively only leaving the dark field component. However, the improvement in results was too small/negligible to be reported in this paper.
Dome illumination might be an effective option for situations that are both practical for such an illuminator to be present on the production line/inspection system and where ambient illumination is unpredictable. The results in this paper suggest superior results for woven materials using the dome illuminator, although this is minor and inconclusive. Under ambient illumination, the results are less predictable, as one might have expected. However, they do demonstrate potential application for lower-precision applications. Indeed, this might be regarded as a strength of the method because inspection using uncontrolled illumination is a highly desirable but is a seldom attained goal—even at low-precision.
While the results for the tube were of low quality, there is some hope for the inspection of parts during a draping process for some applications based on the promising output for dry fibres wrapped around the tube under dome and ambient illumination (
Figure 27 and
Figure 28).
One weakness of the paper is the difficulty in obtaining reliable ground truth absolute angle values for comparison to the experiment. Regardless of this, the relative values are all well within 1° precision for planar surfaces, provided that there is some initial reference to which other results can be measured against. Finally, it should be noted that, in most cases, individual pixel measurements are of limited use due to relatively high (typically >1°) standard deviations in values. Instead, global measurements or average values over small regions should be used as outputs from the method.
In relation to alternative technologies for composite part inspection, the methods in this paper are largely complementary. The approach is financially and computationally much cheaper than most others and relatively straightforward to incorporate into manufacturing lines. The method is also fast and requires little installation time or infrastructure. On the other hand, polarisation methods do require careful consideration of illumination—especially for high-precision applications—and are only able to inspect top layers. That said, such a system could potentially be embedded onto a production line such that each layer is inspected in situ during the layup process. Another weakness of polarisation is that the method is only sensitive to defects/misalignments that occur within the plane of the surface. While this precludes the detection of certain problems, it is believed that the majority of defects do at least partially manifest within the plane and so are theoretically detectable using polarisation information.
5. Conclusions
This paper has demonstrated the capabilities and limitations of polarisation imaging technology as applied to CFRP component inspections. In the best cases, the average relative angles over specific regions of interest were measured to less than one quarter of a degree, with standard deviations less than one degree. Other situations, however, had much higher standard deviations, often over 2°, as shown in
Table 3. Cases have been identified where the approach can be embedded into an existing production line (e.g., close-up inspection of UD and woven materials under dome illumination or mid-range measurements of UD components under dark-field illumination). Cases have also been identified where the outputs are of poor quality such as for highly curved surfaces or short focal lengths where specularities are present on resin. In summary, the paper has shown great promise for the technology but also that there are many potential complications present, meaning that the design features of an inspection system may vary depending on the application in question.
The aim of future work will be to more closely inspect the small differences in precision for woven materials compared to UD and to parametrise the limits of curvature for which robust measurements can be made—or even design illumination to permit full-scale inspection of three-dimensional parts. We also hope to further study the effects of specular reflection to introduce corrective factors for short focal lengths (i.e., to address the weaknesses identified in
Figure 21). As mentioned in the introduction, the method theoretically allows a more general inspection process to localise defects in CFRP samples; thus, a natural follow-on study would verify this. Finally, the methods should be trialed in real-world manufacturing and inspection settings such as in a layup laboratory or above a ply cutter.