An Arrow-Curve Path Planning Model for Mobile Beacon Node Aided Localization in Air Pollution Monitoring System IoT

Abstract

In wireless sensor networks, it is crucial to support the collected data of sensor nodes with position information. One of the promising ways to acquire the position of unknown nodes is using a mobile anchor node that traverses throughout the network, stops at determined points, and sends its position to aid in obtaining the location of other unknown nodes. The main challenge in using mobile anchor nodes lies in designing the path model with the highest localization accuracy, shortest path length, full coverage area, and minimal power consumption. In this paper, a path model named the Arrow-Curve path model is proposed for mobile node aided localization. The proposed path model can effectively localize all the static unknown sensor positions in the network field with high positioning accuracy and low power consumption while pledging full coverage area. The sensor network is implemented using MATLAB simulation and MCU node in both static unknown nodes and the mobile anchor node. The realtime environment guarantees a realistic environmental model with reliable results. The path model is implemented in realtime in indoor and outdoor environments and compared to the H-Curve path model using a trilateration technique. The results show that the suggested path model achieves better results compared to H-Curve model. The proposed path model achieves an average position error less than that of H-Curve by 10.6% in a simulation environment, 5% in an outdoor realtime environment, and 9% in an indoor realtime environment, and it decreases power consumption by 62.65% in the simulation environment, 50% in the outdoor realtime environment, and 75% in the realtime environment in indoor compared to H-Curve.

1. Introduction

A wireless sensor network (WSN) is formed of numerous sensors that observe the network field and connect wirelessly among each other [1]. WSNs are used in many applications such as in the army, health, field monitoring, air pollution monitoring systems, and object tracking [2]. The collected data of these applications are not meaningful without knowing the location of the source [3]. The mechanism of locating sensor nodes is defined as localization. There are classic methods to obtain the positions of unknown sensor nodes, such as GPS, which is usually utilized as an accurate method for localization. However, it wastes a lot of power and comes with a very high cost. Moreover, GPS is not able to function in all environments, such as closed areas [4]. To overcome the problems of GPS, we use localization methods that use nodes called anchor nodes located via GPS or by placing them in predetermined positions, which are then used to find the positions of other unknown nodes in the network. Although this solution is effective, it has been observed, however, that the accuracy of this solution depends on the number of anchor nodes [5,6], but raising the number of anchor nodes means increasing the power utilization and cost. Taking all these problems into consideration has led researchers to propose path planning models using one mobile anchor node rather than many stationary anchor nodes. Finding the position using one mobile anchor node is more precise and there is less cost and lower power consumption [7,8,9,10,11]. The mobile anchor node moves through the network field in a predefined path and starts sending messages to unknown sensor nodes that are posited in the field [12]. The messages contain information related to each point it stops at. The success of path planning models depends on designing the most efficient path for the mobile anchor node that guarantees covering all sensor nodes in the network field. Moreover, it has to achieve high position accuracy while reducing the power consumption of the mobile node.

In paper, a new path model for mobile anchor aided localization in WSNs is proposed. The proposed path model achieves high localization accuracy and low power consumption and path length. An air pollution monitoring system framework is built in simulation and in realtime using Node MCU (ESP8266 Wi-Fi module and (ESP32 (Wi-Fi–Bluetooth) module) hardware to apply and inspect the proposed localization models in comparison to previously proposed models in literature. The main contributions of this paper are:

• Introducing two path models for mobile anchor-based localization in WSN.
• Solving the problem of having three pausing points on one straight line for the mobile anchor node (collinearity problem).
• Finding the average localization error, standard deviation of error, power consumption, and path length as evaluation metrics for the proposed path models.
• Finding the average localization error, standard deviation of error, power consumption, and path length as evaluation metrics for the proposed path models.
• Comparing the proposed models with previously proposed models in literature using simulation and a hardware realtime model.

The rest of this paper is organized as follows. In Section 2, the work related to localization algorithms based on mobility is presented. In Section 3, the path modeling design is introduced. Section 4 presents the results of the model evaluation. In Section 5, the conclusions and future work are provided.

2. Related Work

Extensive research on proposing localization methods in wireless sensor networks has recently been published. Most of this research can be categorized based on reliance on the type of surroundings as follows: range-based techniques or range-free techniques. Range-based techniques rely on the features of the surroundings, such as received signal strength indicator (RSSI), time of arrival (TOA), and angle of arrival (AOA).

In [13,14,15], the authors proposed a number of range-based techniques. On the other side, range-free techniques as in [16,17] rely on connectivity information such as the number of hops among the sensor nodes. Although this categorization is effective in the case of static anchor nodes and static unknown sensor nodes, it does not however take into consideration the case of the mobile anchor node or mobile unknown sensor nodes. Thus, another category based on node mobility was proposed.

This categorizes sensor nodes into four classes, as in Figure 1: static sensor nodes, static anchor nodes—for example, as presented in [18,19,20]; static sensor nodes, mobile anchor nodes—for example, as presented in [8,21,22,23,24]; mobile sensor nodes, static anchor nodes—for example, as presented in [5,25,26,27]; and mobile sensor nodes, mobile anchor nodes—for example, as presented in [28,29].

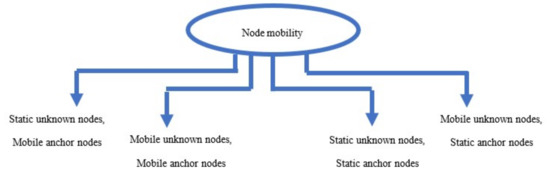
Figure 1. Classification of node mobility.

The main focus of localization algorithms depending on mobile anchor node path design is to find the best path model for the mobile node which achieves the required goals, such as whole coverage area, low position error, short path length, and low power consumption. Some of the existing path length models will be listed in this section.

In [30], the authors proposed SCAN and HILBERT models, which are the first proposed path models. SCAN is an elementary model; in this model, the mobile node moves directly in one extent, the x axis line or y axis line. The resolution in this path model is defined as the interval between two anchor stop points in each line. The strength of SCAN model is that it is easy to implement, though it does not solve the collinearity problem. To solve the problem of collinearity, HILBERT was proposed. In the HILBERT path model, the network field is divided into four equivalent sub-fields and links the stop points between these sub-fields. Using the information from non-collinear pausing points, the unknown nodes can estimate their positions with higher position accuracy than the SCAN model. The point of weakness for the HILBERT path mode is that it cannot apply full coverage area because the unknown nodes that are set at the margin of the network field cannot receive sufficient information to determine their positions. This problem affects the value of the position error.

In [31], the authors presented an effective path model for the mobile anchor node called the LMAT path model. In this path model, the mobile node traverses through the symmetrical triangles and regularly transmits messages at each edge of the triangle. The unknown nodes estimate their positions using the calculated distance between themselves and the mobile anchor node via RSSI. This model solves the collinearity problem and reduces the position error. However, the position error on the border is high, and the path length of the mobile node is high.

In [32], the authors presented a new path model called Z-curve path model. This model solves the collinearity problem and has a short path length. Moreover, it can deal with obstacles in the network field. However, this advantage causes higher energy consumption by the mobile anchor node.

In [33], the authors proposed a path model called the H-Curve path model. This model, as shown in Figure 2, solves the collinearity problem, achieves high results of position accuracy, has short path length. However, it does not deal with the obstacles and has a high number of pausing points for the mobile node.

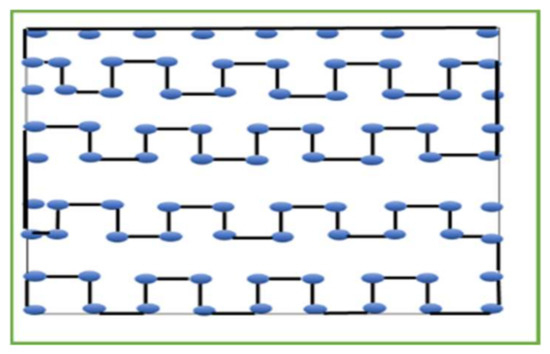
Figure 2. H-Curve path model.

3. Path Model Design

The main contribution of this paper is to design an effective path model for the mobile anchor node to acquire the locations of unknown nodes in the area. A preliminary and final model have been proposed to reach the final required goal. The proposed paths were designed to achieve the following:

• High localization accuracy;
• Full coverage area;
• Low power consumption;
• Solving the problem of collinearity.

The challenges of the first depend on many criteria, such as the environmental characteristics, indoor or outdoor, and the path trajectory model of the mobile anchor node. The second achievement is very important as the mobile node trajectory must ensure that the whole area of the network is reached; to achieve that goal, suitable paths were chosen to guarantee that all the unknown nodes receive at least three different messages from the mobile anchor node. The low power consumption challenge mainly depends on the path length, the obstacles that it needs to turn around, and the number of pausing points it stops at.

To solve the problem of collinearity, the value of x-axis parameter is checked for each pausing point, which is used to obtain the location of the unknown node. If it is the same value, we replace any pausing point with another one that has a different x-axis value. The same process is carried out for the y-axis value parameter.

Wireless sensor network model assumptions:

• The unknown nodes are spread in fixed locations.
• Each node has a determined communication range which differs depending on the surrounding criteria.
• The mobile anchor node traverses through the network deterministic path. It can move around any obstacle it meets through its journey.
• The mobile anchor sends messages at each pausing point it rests at, and the unknown nodes in its scope receive the messages from it.
• The mobile anchor node can determine its position at each pausing point.
• The unknown node can compute its position via the position information from three different mobile node positions.

3.1. R-Curve Path Model

In the first preliminary proposed mobile anchor node path planning model, the primary curve of the path model appears as in Figure 3, designed based on the letter R Pattern. This algorithm has been designed as a primary step for reaching the final model proposed by this paper. The presented path can cover the entire network area so, all unknown sensor nodes guarantee that they receive at least three different mobile beacon messages.

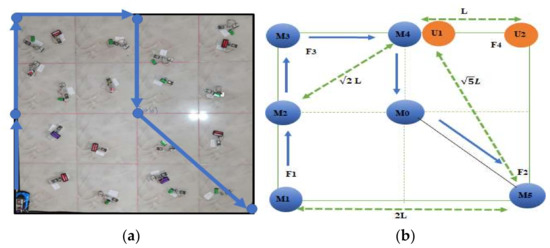
Figure 3. (a) Applied R-Curve path model; (b) R-Curve path model (le = 1).

In the proposed path model, the theory of the level used in [32] has been adopted. The level is referred to as le. The network area is split into $4^{\mathrm{le}}$ sub-fields and the mobile node connects the $4^{\mathrm{le}}$ sub-fields during its movement. The basic model is defined for R-Curve as $\mathrm{le}=1$, as shown in Figure 3. We present $\mathrm{le}=2$ and $\mathrm{le}=3$ of the path model in Figure 4a and b, respectively. The introduced path model involved two stages:

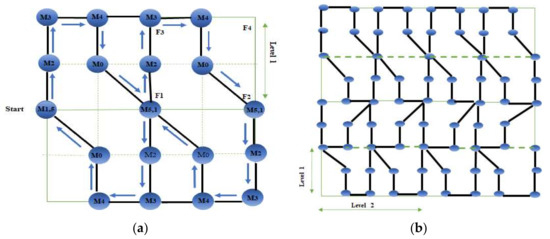
Figure 4. (a) R-Curve path model (le = 2); (b) R-Curve path model (le = 3).

3.1.1. Stage 1: Experiment Preparation

The target in this stage is to guarantee that all unknown sensors can determine their positions. First, we test the communication range of the mobile node at the environments where we execute the experiments. From [28], all the non-localized sensors can obtain their positions if:

$$\forall {\mathrm{U}}_{\mathrm{x}\left(\mathrm{x}=1,2,3\dots \mathrm{r}\right)}\exists {\{\mathrm{M}}_{\mathrm{y}\left(\mathrm{y}=1,2,3\right)}|\mathrm{distance}\left({\mathrm{U}}_{\mathrm{x}},{\mathrm{M}}_{\mathrm{y}}\right)\le \mathrm{CR}$$

(1)

where ${\mathrm{U}}_{\mathrm{x}}$ signifies non-localized sensors, ${\mathrm{M}}_{\mathrm{y}}$ signifies the mobile node pausing points positions, distance (${\mathrm{U}}_{\mathrm{x}},{\mathrm{M}}_{\mathrm{y}}$) is the distance between non-localized nodes and mobile node positions, and CR is the communication range of mobile node.

We then adjust the model level based on the communication ratio. First, as we illustrated above, the network area in le = 1, is split into four square sub-fields, defined as ${\mathrm{SF}}_{\mathrm{f}}$ (f = 1, …, 4). The mobile node pauses for one minute at pausing points ${\mathrm{M}}_{\mathrm{p}\left(\mathrm{p}=0,1,\dots .\right)}$. We define the resolution of the introduced path model as the side length L of a square sub-field. Each non-localized sensor node should receive messages from different mobile node positions to guarantee a successful positioning process.

In Figure 3b, ${\mathrm{U}}_1$ is an unknown sensor which is located in the farthest point from ${\mathrm{M}}_5$. If ${\mathrm{U}}_1$ receives a message from ${\mathrm{M}}_5$, it confirms that all unknown nodes in ${\mathrm{F}}_4$ can receive messages from ${\mathrm{M}}_5$. As has been recognized from Figure 3b:

$$\mathrm{distance}({\mathrm{M}}_5,{\mathrm{U}}_1)=\sqrt{5}\mathrm{L}\le \mathrm{CR}$$

(2)

where distance $\left({\mathrm{M}}_5,{\mathrm{U}}_1\right)$ is the distance between unknown sensor ${\mathrm{U}}_1$ and the mobile node position at ${\mathrm{M}}_5$. In this way, all the non-localized sensors can receive three different messages and achieve full coverage area.

3.1.2. Stage 2: Mobility Motion Description

As shown in Figure 3b, the mobile node will begin at point ${\mathrm{M}}_1$ in the sub-field ${\mathrm{F}}_1$ and will travel in a straight line vertically to the upper direction, pausing for one minute at point ${\mathrm{M}}_2$. After that, it will move in a straight line vertically to the upper direction stopping for one minute at ${\mathrm{M}}_3$ in sub-field${\mathrm{F}}_3$. Then, it will move in straight line horizontally to the right direction stopping for one minute at ${\mathrm{M}}_4$. Then, it moves in straight line vertically downwards and reaches ${\mathrm{M}}_0$, which is the center point of the four sub-fields. Finally, it moves in a diagonal line with an angle ${45}^{°}$ toward ${\mathrm{M}}_5$, stopping for one minute at ${\mathrm{M}}_5$ in sub-field ${\mathrm{F}}_2$.

There are two scenarios for the role of the mobile anchor node; in the first scenario as shown in Figure 5, the mobile anchor node acts as an access point with a specific IP address and creates a network, and the mobile node pauses at each position for one minute and sends messages to the unknown nodes with the pausing point number and position X, Y. Hence, every unknown sensor acts as a server in each sub-field that has at least information from three different mobile pausing points in its communication range. Then, it will select the three saved messages which have the largest RSS values and acquire its position using the accuracy-priority trilateration technique (APT), which evaluates the positions of non-localized nodes by taking the three nearest messages from the all-accepted messages [32]. APT has high localization accuracy in comparison with the trilateration technique [32]. The data are available on requirement from the webpage of the specified IP.

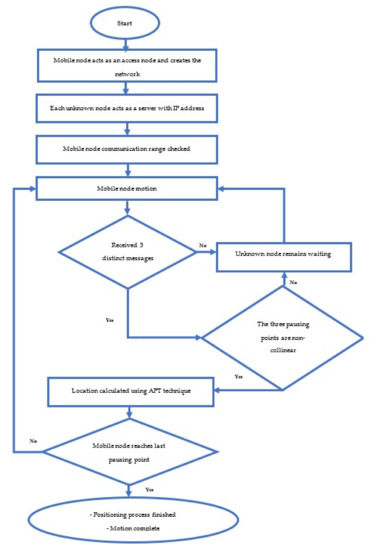
Figure 5. First scenario.

In the second scenario, as shown in Figure 6 the mobile anchor node acts as a server, which saves the positions of all pausing points and their numbers. It pauses at each position for one minute and sends “Hello” messages to all the unknown sensor nodes, then each unknown sensor plays two roles, the access point which starts the network, and the client which replies at each “Hello” message from the server with a message containing its number. The mobile node saves each message and the equivalent RSSI. Then, for each unknown node, it selects the largest RSSI values and the pausing point position where it acquires them and calculates the position using APT. Then, it automatically sends all the data to its webpage with the nodes number and their positions.

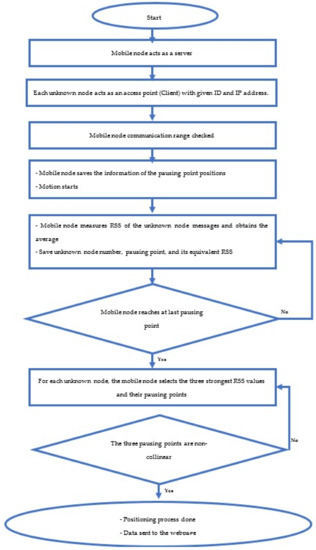
Figure 6. Second scenario.

Using the two scenarios, the accuracy of the position of the unknown sensor node depends on selecting an effective path model for the existing obstacle.

The overall distance taken by the mobile node at le = 1 and resolution L is denoted by (3):

$$4\ast \mathrm{L}+\sqrt{2}\mathrm{L}$$

(3)

At $\mathrm{le}=2$ as in Figure 4a the overall distance is denoted by (4):

$$(4\ast \mathrm{L}+\sqrt{2}\mathrm{L})\ast 4^{\mathrm{le}-1}$$

(4)

At $\mathrm{le}=3$ as in Figure 4b, the overall distance is denoted by (5):

$$(4\ast \mathrm{L}+\sqrt{2}\mathrm{L})\ast 4^{\mathrm{le}-1}+4\ast \mathrm{L}$$

(5)

3.2. Arrow-Curve Path Model

R-Curve, despite being a promising path model, has encountered some problems in having uniform pausing points along the field and, thus, this increased the error percentage in localization. This deficiency in performance was a motive for proposing a final model that overcomes these problems.

In the final proposed mobile anchor node path planning model, the designed curve of the path model appears as in Figure 7, and it is designed in an arrow form. As discussed in R-Curve path model, the final path also can cover the entire network area, so all unknown sensor nodes guarantee that they receive at least three different mobile beacon messages. In the Arrow-Curve path model, the same concepts used for experimental preparation of R-Curve have been used as discussed in R-Curve stage 1. We present $\mathrm{le}=2$ and $\mathrm{le}=3$ of the path model in Figure 8a and b, respectively.

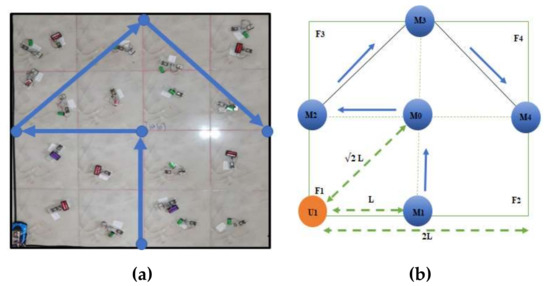
Figure 7. (a) Applied Arrow-Curve path model; (b) Arrow-Curve path model (le = 1).

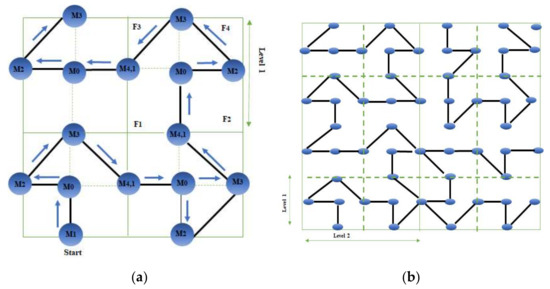
Figure 8. (a) Arrow-Curve path model (le = 2); (b) Arrow-Curve path model (le = 3).

Stage 2: Mobility Motion Description

As presented in Figure 7b, the mobile node will begin at point ${\mathrm{M}}_1$ and will travel in a straight line to the upper direction, pausing for one minute at point ${\mathrm{M}}_0$, which is the center point of the four sub-fields. After that, it will move in a straight line horizontally to the left stopping for one minute at${\mathrm{M}}_2$.

Then, it will move in a diagonal with an angle ${45}^0$ toward ${\mathrm{M}}_3$, stopping for one minute at${\mathrm{M}}_3$. Then, it moves in a diagonal line with an angle ${45}^0$ toward at ${\mathrm{M}}_4$, stopping for one minute at${\mathrm{M}}_4$.

The overall distance taken by the mobile node at $\mathrm{le}=1$ and resolution L is denoted by (6):

$$2\ast \mathrm{L}+2\sqrt{2}\mathrm{L}$$

(6)

At $\mathrm{le}=2$ as in Figure 9, the overall distance is denoted by (7):

$$(2\ast \mathrm{L}+2\sqrt{2}\ast \mathrm{L})\ast 4^{\mathrm{le}-1}-\sqrt{2}\mathrm{L}$$

(7)

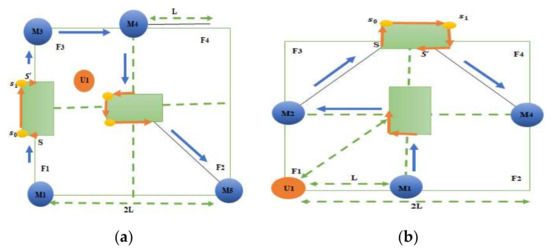
Figure 9. (a) R-Curve obstacle existence; (b) Arrow-Curve obstacle existence.

At $\mathrm{le}=3$ as in Figure 10, the overall distance is denoted by (8):

$$(2\ast \mathrm{L}+2\sqrt{2}\mathrm{L})*4^{\mathrm{le}-1}+10\ast \mathrm{L}-10\sqrt{2}\mathrm{L}$$

(8)

3.3. Obstacle—Reluctant Path

In a realtime environment, obstacles may be found in the experimental area that may prevent radio contact between the mobile anchor node and other sensor nodes. In [12], the mobile anchor node turns around the obstacle and propagates the messages sent to the unknown nodes with a detour flag. The unknown sensor nodes calculate their positions using the information in the messages that contain a detour flag to compute the virtual mobile anchor node positions paused at to turn around the obstacle. When the mobile node walks away from the obstacle, it returns back to the main path and resumes propagating the mobile node normal messages.

In [34], the mobile node can find out any anonymous obstacle once it existed in the communication range. The R-Curve and Arrow-Curve are static and deterministic paths, the path pattern and the mobile node pausing points are fixed so the mobile node knows the position of the obstacles and can resume its path after it moves away from the obstacle. The R-Curve and Arrow-Curve obstacle-reluctant path is introduced to resolve the obstacle problem in the real environment to improve R-Curve and Arrow-Curve path pattern at the presence of an obstacle.

We define an obstacle mode as illustrated in Figure 9, where the mobile node firstly moves on the path trajectory. Then, when and if it detects an obstacle in its trajectory, it first broadcasts the arriving point S, then the mobile node switches on the obstacle mode. It starts to broadcast messages containing its position ${\mathrm{s}}_0,{\mathrm{s}}_1$ with a detour flag for each detour to inform the sensor nodes that it is turning around an obstacle. When the anchor node crosses the obstacle, it switches back to the normal mode and returns to the original path. Once it reaches the departure position ${\mathrm{s}}^{\prime }$, it starts to broadcast messages containing ${\mathrm{s}}^{\prime }$. R-Curve and Arrow-Curve obstacle-reluctant paths are illustrated in Figure 11; Figure 12. The green blocks illustrate the obstacles and the orange lines illustrate the path around the obstacle.

4. Performance Evaluation

In this section, the performance of R-Curve, Arrow-Curve, and the previously proposed H-Curve is applied and compared using MATLAB simulation [35] and hardware prototype using the Node MCU hardware tool. This section is organized as follows: firstly, the performance parameters used to measure the efficiency of each model in simulation and hardware are defined; in the second section, performance evaluation using MATLAB simulation is presented; in the third section, performance evaluation using Node MCU is presented; in the fourth section, the results of simulation and hardware evaluations are compared and, at last, replacing fixed anchors rather than one mobile anchor is studied.

4.1. Performance Parameters

The metrics used to evaluate the algorithms’ performance using MATLAB simulation and hardware prototype using Node MCU are average position error, standard deviation of localization error, localization coverage ratio, path length, and power consumption.

• Average localization error.

Localization error is an important parameter for evaluating any proposed path model. Two metrics are applied to find the localization error of the proposed path models, average localization error, and the standard deviation of the localization error. The average localization error [30] is calculated using (9):

$${\mathrm{localization}\mathrm{error}}_{\mathrm{j}}=\sqrt{{\left({\mathrm{x}}_{\mathrm{j}}-{\mathrm{est}}_{\mathrm{j}}\right)}^2+{\left({\mathrm{y}}_{\mathrm{j}}-{\mathrm{est}}_{\mathrm{j}}\right)}^2}$$

(9)

where (${\mathrm{x}}_{\mathrm{j}},{\mathrm{y}}_{\mathrm{j}})$ is the real location of node j, and $\left({\mathrm{est}}_{\mathrm{j}},{\mathrm{est}}_{\mathrm{j}}\right)$ is the estimated location of node j using the localization models. Hence, the average localization error is:

$${\mathrm{localization}\mathrm{error}}_{\mathrm{av}}={{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{n}}({\mathrm{localization}\mathrm{error}}_{\mathrm{j}})/\mathrm{n}$$

(10)

where n is the total number of unknown nodes.

2.

Standard deviation of position error.

We compute the standard deviation of position error to estimate how it differs from the average position error. If the value of the standard deviation of position error is low, the estimated position error values of nodes tend to vary near to the average position error of all nodes in the network. The equation of standard deviation of position error is as follows:

$${\mathrm{position}\mathrm{error}}_{\mathrm{std}}={{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{position}\mathrm{error}}_{\mathrm{j}}-{\mathrm{position}\mathrm{error}}_{\mathrm{av}}\right)}^2$$

(11)

where n is total number of unknown nodes, ${\mathrm{position}\mathrm{error}}_{\mathrm{j}}$ is the position error of node j, and the ${\mathrm{position}\mathrm{error}}_{\mathrm{av}}$ is the average position error.

3.

Coverage ratio.

Coverage ratio is the percentage of nodes localized successfully in the network.

4.

Number of pausing points.

The mobile node stops at each pausing point for a predefined period in each algorithm. Increasing the number of pausing points impacts on networking time and power consumption.

5.

Path length.

The path length is defined as the distance wrapped by the mobile anchor to follow the suggested path model in the network. The path length does not have influence on the position error. However, it impacts the power consumed by the mobile node and the overall time of the localization procedure. The unpretentious solution for decreasing the power consumption is to reduce the path length covered by the mobile anchor node. The path length of Arrow-Curve and R-Curve are compared to that of H-Curve trajectory [33] using the following equations:

$$\mathrm{Pathlength}\mathrm{of}\mathrm{H}-\mathrm{Curve}=\frac{{\mathrm{A}}^2}{\mathrm{L}}+18\mathrm{L}$$

(12)

where A is the network area and L is the resolution as defined in previous sections.

$$\mathrm{Path}\mathrm{length}\mathrm{of}\mathrm{Arrow}-\mathrm{Curve}=(2\ast \mathrm{L}+2\sqrt{2} \mathrm{L})*4^{\mathrm{le}-1}+10\mathrm{L}-10\sqrt{2}\mathrm{L}$$

(13)

$$\mathrm{Path}\text{\_}\mathrm{length}\mathrm{of}\mathrm{R}-\mathrm{Curve}=(4\ast \mathrm{L}+\sqrt{2} \mathrm{L})*4^{\mathrm{le}-1}+4\ast \mathrm{L}$$

(14)

6.

Energy or power consumption.

Energy or power consumption is an important metric to be taken into consideration when proposing path models. However, the path models that take energy or power consumption parameter into consideration in literature are limited [33]. Most of the energy or power consumed by the mobile anchor node is dissipated while traveling through the network.

To evaluate the energy consumption by the mobile anchor, we first need to determine the value of the path length and the amount of energy needed to move one meter, which can be calculated from the following equation:

$$E_{traveling}=pat{h}_l*E_d+E_{dissipated\_send}$$

(15)

where $E_{traveling}$ is the energy dissipated through travelling, $pat{h}_l$ is the path length of the mobile node, $E_d$ is the energy dissipated through moving 1 m which is calculated to be 2 J [22,36], and $E_{dissipated\_send}$ is the energy consumed during sending.

The dissipated energy of one mobile anchor node is only dissipated through sending messages at each pausing point, and it is calculated from the following equation:

$$E_{dissipated}=message{s}_{send}*E_{send}$$

(16)

where $message{s}_{send}$, $E_{send}$ are number of sending messages and energy dissipated for sending one message, respectively. The energy dissipated for sending one message is calculated from this equation:

$$E_{send}=P_{send}*\frac{packet size}{data rate}$$

(17)

where $p_{send}$ is the sending power, and its value is 18.5 m In ESP 32, the value of data rate is 100 Mbps, and we assume packet size 25 kbps.

In Node MCU, to evaluate the power consumed by the mobile anchor, we first need to obtain the value of the volt and current consumption of the two 18,650 rechargeable batteries, which are connected in series. The nominal capacity is 3800 mAH and nominal voltage is 3.7 V, and the values of voltage and current are measured using MAX471 Voltage and Current Sensor Module shown in Figure 10 The equations used for voltage and current measurement are as follows:

Figure 10. Mobile anchor node with MAX471 Voltage and Current Sensor Module Consume Voltage Load Detection Module.

V = Analog reading of sensor value ∗ (8.4/4095)

(18)

I = Analog reading of sensor value ∗ (1/4095)

(19)

$$\mathrm{The}\mathrm{equation}\mathrm{for}\mathrm{power}\mathrm{is}:\mathrm{P}=\left(\mathrm{V}*\mathrm{I}\right)$$

(20)

Power dissipated is converted to energy using this equation:

$${\mathrm{E}}_{\left(\mathrm{J}\right)}={\mathrm{P}}_{\left(\mathrm{W}\right)}{*\mathrm{T}}_{\sec }$$

(21)

where E, P, T is the energy dissipated, power dissipated and time of dissipation, respectively.

4.2. Performance Evaluation Using MATLAB Simulation

The performance of the proposed path models is first compared using MATLAB simulation. For wireless model, the specifications of wireless nodes that was equipped with ESP 23 node are employed in simulation. The network area is assumed to be a square area of size s = 50 × 50 ${\mathrm{m}}^2$, 40 unknown nodes deployed with communication range 15 m, and one mobile anchor node is used. Each point in the results is the average of 10 experimental runs. The distance between the mobile node and the unknown node at each pausing point is calculated as follows:

$$\mathrm{D}={\mathrm{D}}_0*{10}^{\frac{\mathrm{RSSI}-{\mathrm{RSSI}}_0}{10{\mathrm{n}}_{\mathrm{p}}}}+\mathsf{\sigma }$$

(22)

where RSSI is the received signal strength indicated at distance D, ${\mathrm{RSSI}}_0$ is the received signal strength indicated at the reference distance ${\mathrm{D}}_0$, ${\mathrm{n}}_{\mathrm{p}}$ is the power loss exponent, and σ is the standard deviation of noise. Estimating the distance using RSSI measurement suffers from high errors caused by signal fading and blockage of the signal by obstacles. To overcome the problem of blockage of signals due to obstacles, in the path design, the mobile node has to move around obstacle and not crash with it. For noise fading through simulation, we should guarantee that σ and ${\mathrm{n}}_{\mathrm{p}}$ values chosen during calculations are suitable to the nature of the noise and obstacles in the environment. The list of parameters is shown in Table 1.

Table 1. Experimental Parameters.

Parameter	Value
Network area size	50 × 50 ${\mathrm{m}}^2$
Number of mobile anchor nodes	1
Number of unknown nodes	40
Resolution L	L = 10, 12.5, 15, 17.5
Path loss exponent (${\mathrm{n}}_{\mathrm{p}}$)	3.3
${\mathrm{RSSI}}_0$ (${\mathrm{D}}_0)$	−59
${\mathrm{D}}_0$	1 m
Standard deviation of noise (σ)	4
Communication range	15
Simulation run times	10

The performance of the proposed of the proposed models is evaluated using the following metrics: average localization error, standard deviation of localization error, localization coverage ratio, path length, and power consumption.

• Average localization error.

Figure 11 shows the average localization error of the two path models compared to H-Curve.

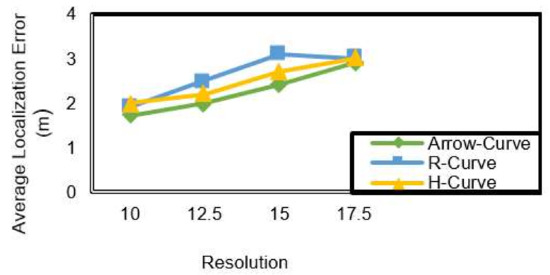
Figure 11. Average localization error (m) corresponding to resolution (L) in Arrow-Curve model, R-Curve model, and H-Curve.

In simulation results, as observed from Figure 11, the Arrow-Curve achieves higher accuracy results in comparison to H-Curve and R-Curve. Arrow-Curve achieves an average localization error less than H-Curve by 11%. R-Curve model has the lowest accuracy values in most resolutions near to H-Curve model results, however, because it is not a symmetric path model as shown previously in Figure 3, where the non-localized nodes that exist in the second and fourth sub-fields do not receive sufficient localization information from the mobile anchor node and, hence, their position accuracy will decrease. In the analysis of sub-field(s) shown in Figure 12, the Arrow-Curve has the lowest average localization error in each sub-field because the locations of the mobile anchor node pausing points is at the middle of each edge. However, the R-Curve achieves the lowest results because it is non-symmetric in shape. The value of localization error in each sub-field depends on the location status of the unknown node, whether it is in the corner of the sub-field or in the middle, and also depends on the type of path model.

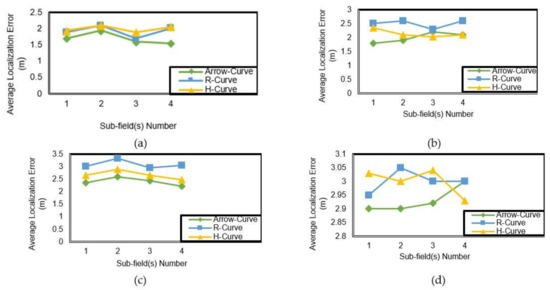
Figure 12. Average localization error (m) corresponding to sub-field (S) number at resolution (L): (a) L = 10.; (b) L = 12.5; (c) L = 15; (d) L = 17.5.

2.

Standard deviation of position error.

The standard deviation error is calculated at different values of resolution. Figure 13 illustrates the standard deviation error values at different resolutions. Arrow-Curve achieves lower standard deviation values, which means it is very close to average. For Arrow-Curve, average${\mathrm{position}\mathrm{error}}_{\mathrm{std}}$ = 1.4. For H-Curve, average${\mathrm{position}\mathrm{error}}_{\mathrm{std}}$ = 1.5125. For R-Curve, average${\mathrm{position}\mathrm{error}}_{\mathrm{std}}$ = 1.55. R-Curve achieves the highest values of standard deviation of error because of the nature of unsymmetric models. Hence, there are non-located nodes in the corner which have higher error in localization than others, which affects the values of the standard deviation of error.

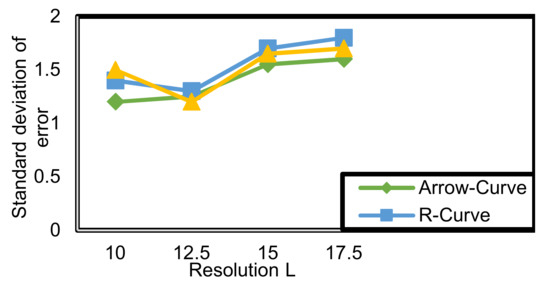
Figure 13. Standard deviation of error (SDE) corresponding to resolution (L) in Arrow-Curve model, R-Curve path model, and H-Curve.

3.

Coverage ratio.

As noted from Figure 14, the position coverage ratio at high resolutions is 100%. However, as the resolution decreases, the coverage ratio in the three path models also deceases.

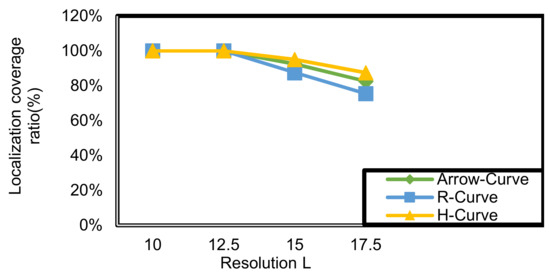
Figure 14. Localization coverage ratio corresponding to resolution (L) in Arrow-Curve path model, R-Curve path model, and H-Curve.

4.

Path length.

As noted from Figure 15, the path length is affected by the network size and the path model. Arrow-Curve and R-Curve have a shorter path model length than H-Curve because of the nature of the two paths, and H-Curve path as described extensively in previous sections.

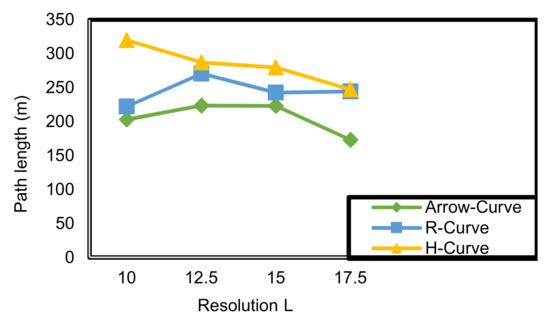
Figure 15. Path length (PL) corresponding to resolution (L) in Arrow-Curve model, R-Curve path model, and H-Curve.

5.

Energy consumption.

As noted from Figure 16, Arrow-Curve achieves lower energy consumption results than H-Curve by 62.65%. R-Curve achieves energy consumption results lower than H-Curve by 24.12%. The energy consumption in simulation tool is affected by the network size, path length, and the communication process, where Arrow-Curve and R-Curve dissipate less energy, while H-Curve has high energy consumption because of the nature of the path length of H-Curve. The energy dissipation on simulation tools is calculated using two parameters, the energy dissipation through movement and the energy dissipation through sending messages from the mobile node to the unknown nodes. To reduce power dissipation, we should choose the path model with small length and reduce energy dissipation through sending by reducing the number of transmitted messages and reducing the time of experiment.

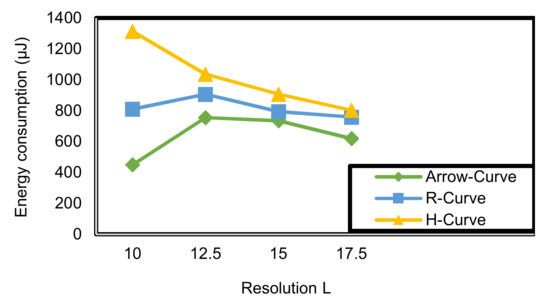
Figure 16. Power consumption (mw) corresponding to resolution (L) in Arrow-Curve model, R-Curve path model, and H-Curve.

4.3. Performance Evaluation Using Node MCU

In this section, we apply and compare the performances of R-Curve, Arrow-Curve, and the previously proposed H-Curve.

Parameter Settings: The proposed models were implemented in hardware using Node MCU (ESP 32 (Wi-Fi–Bluetooth module)) [37] as a mobile anchor node and Node MCU (ESP 8266 (Wi-Fi module)) [38] and (ESP 32 (Wi-Fi–Bluetooth module)) as unknown nodes. The network area is assumed to be a square area of size s = 20 × 20 ${\mathrm{m}}^2$ in the outdoor with communication range 28 m and has a size s = 8 × 8 ${\mathrm{m}}^2$ in indoor environment with communication range 9 m. A total of 20 unknown nodes are deployed in the outdoor square area and 10 unknown nodes are deployed in the indoor square area. The used sensors are Dust and Smoke sensors [39,40], as shown in Figure 17a,b. We program the node using Arduino IDE software [41].

Figure 17. (a) Dust sensor; (b) smoke sensor.

The experiment was run in an open-door environment where there are no obstacles and an indoor environment with obstacles. We find the distance between mobile node and the unknown node at each pausing point as illustrated in the following equation:

$$\mathrm{D}={\mathrm{D}}_0*{10}^{\frac{\mathrm{RSSI}-{\mathrm{RSSI}}_0}{10{\mathrm{n}}_{\mathrm{p}}}}$$

(23)

where RSSI is the received signal strength indicated at distance D, ${\mathrm{RSSI}}_0$ is the received signal strength indicated at the reference distance ${\mathrm{D}}_0$, and ${\mathrm{n}}_{\mathrm{p}}$ is the power loss exponent. The list of parameters is shown in Table 2.

Table 2. Experimental parameters.

Parameter	Value
Network area size	20 × 20 ${\mathrm{m}}^2$(outdoor); 8 × 8 ${\mathrm{m}}^2$ (indoor)
Number of mobile anchor nodes	1
Number of unknown nodes	20 (outdoor); 10 (indoor)
Resolution L	L = 20, 17.5, 15, 12.5, 10, 7.5 (outdoor); L = 8, 7, 6, 5, 4, 3 (indoor)
Path loss exponent (${\mathrm{n}}_{\mathrm{p}}$)	2.3 (outdoor); 5.2 (indoor)
${\mathrm{RSSI}}_0$ (${\mathrm{D}}_0)$	−54.
${\mathrm{D}}_0$	0.4 m
Number of beacons received at each pausing point.	50
Communication range	28 m outdoor; 9 m indoor with obstacles

The performance of the proposed models is evaluated using the following metrics: average position error, standard deviation of localization error, localization coverage ratio, number of pausing points, path length, and power consumption.

• Average localization error.

Figure 18 shows the average localization error of the two path models compared to H-Curve.

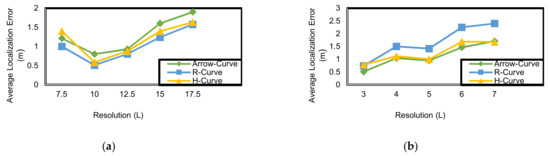
Figure 18. Average localization error (m) corresponding to resolution (L) in Arrow-Curve model, R-Curve model, and H-Curve (outdoor environment): (a) (outdoor environment); (b) (indoor environment).

Arrow-Curve achieves high accuracy results in comparison to H-Curve and R-Curve in indoor and outdoor environments. Arrow-Curve achieves average localization error results less than H-Curve by 5% in outdoor and 9.6% in indoor. R-Curve is the worst model in both cases because it is not a symmetric path model. As shown in Figure 3, the non-localized nodes that exist in the second and the fourth sub-fields do not receive sufficient localization information from the mobile anchor node so, their position accuracy will decrease. In analysis of sub-field(s) (outdoor environment) as shown in Figure 19, the Arrow-Curve has the lowest average localization error in each sub-field because the locations of the mobile anchor node pausing points is at the middle of each edge. However, the R-Curve achieves the lowest results because it is non-symmetric in shape. Moreover, in sub-field (indoor environment) as shown in Figure 20, Arrow-Curve achieves high results in comparison to R-Curve and H-Curve as the mobile anchor node pausing points locations are at the corners of each sub-field. The value of localization error in each sub-field depends on the location status of the unknown node; whether it is in the corner of the sub-field or in the middle and the type of path model, and in indoor environment, it depends on the existence of obstacles in the mobile node path in each sub-field.

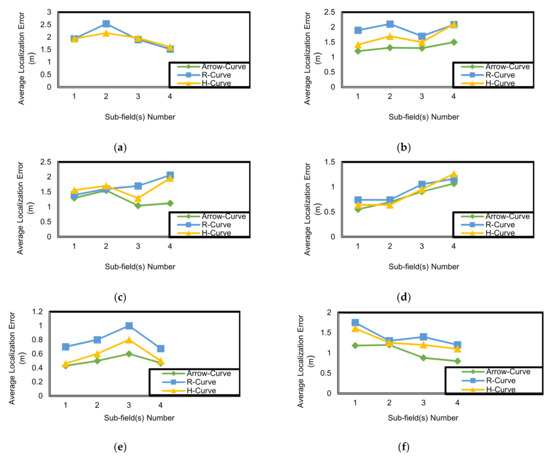
Figure 19. Average localization error (m) corresponding to sub-field (S) number at resolution (L) in outdoor environment: (a) L = 20; (b) L = 17.5; (c) L = 15; (d) L = 12.5; (e) L = 10; (f) L = 7.5.

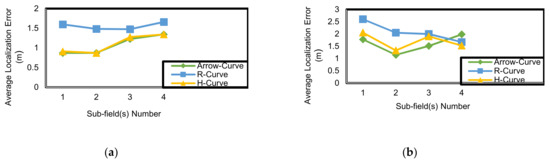
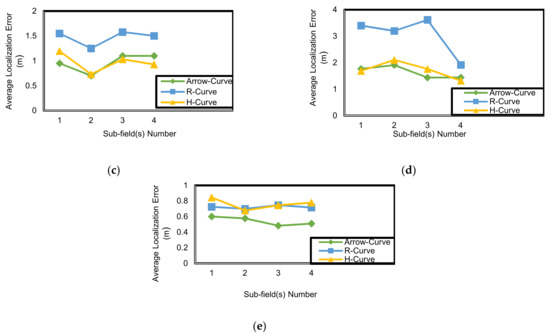
Figure 20. Average localization error (m) corresponding to sub-field (S) number at resolution (L) in indoor environment: (a) L = 7; (b) L = 6; (c) L = 5; (d) L = 4; (e) L = 3.

2.

Standard deviation of position error.

The standard deviation error is calculated at different values of resolution. Figure 21 illustrates the standard deviation error values at different resolutions in outdoor environment and indoor environment. Arrow-Curve achieves lower standard deviation values, which means it is very close to the average. Arrow-Curve achieves lower values of standard deviation in indoor environment than in outdoor environment. For Arrow-Curve, the average${\mathrm{position}\mathrm{error}}_{\mathrm{std}}$ = 1.0267 in outdoor environment and 0.4719 in indoor environment. For H-Curve, the average${\mathrm{position}\mathrm{error}}_{\mathrm{std}}$ = 1.1164 in outdoor environment and 0.5681 in indoor environment. For R-Curve, the average${\mathrm{position}\mathrm{error}}_{\mathrm{std}}$ = 1.14395 in outdoor environment and 0.8134 in indoor environment. R-Curve achieves the highest values of standard deviation of error because of the nature of unsymmetric models. Hence, there are non-localized nodes in the corner which have higher error than others, which affects the values for standard deviation of error.

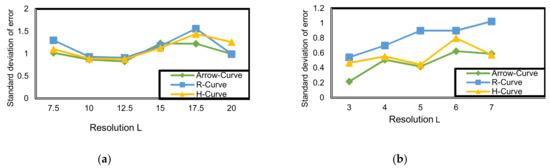
Figure 21. Standard deviation of error (SDE) corresponding to resolution (L) in Arrow-Curve model, R-Curve path model, and H-Curve: (a) outdoor environment; (b) indoor environment.

3.

Coverage ratio.

Coverage ratio is the percentage of nodes localized successfully in the network.

As noted from Figure 22, the position coverage ratio at all resolutions in outdoor equals 100%, which means that all unknown nodes have been localized. The two proposed models achieve full coverage area in addition to the H-Curve model.

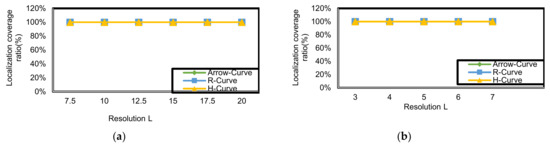
Figure 22. Localization coverage ratio corresponding to resolution (L) in Arrow-Curve path model, R-Curve path model, and H-Curve: (a) outdoor environment; (b) indoor environment.

4.

Number of pausing points.

As noted from Figure 23, the number of pausing points depend on the number of edges of the path model. The number of pausing points outdoor is higher than those indoor because the network size is larger.

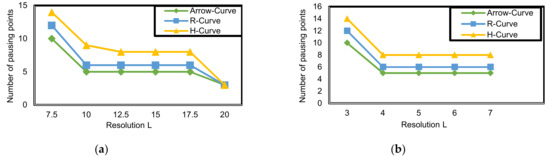
Figure 23. Number of pausing points (PP) corresponding to resolution (L) in Arrow-Curve model, R-Curve path model, and H-Curve: (a) outdoor environment; (b) indoor environment.

5.

Path length.

The path length does not influence the position error. However, it impacts the power consumed by the mobile node and the overall time of the localization procedure. The unpretentious solution for decreasing the power consumption is to reduce the path length covered by the mobile anchor node. The path length of H-curve trajectory [33] is compared to that of the proposed models.

As noted from Figure 24, the path length is affected by the network size and the path model. Arrow-Curve and R-Curve have a shorter path model length in both outdoor and indoor environments than H-Curve because of the nature of the two paths and H-Curve path.

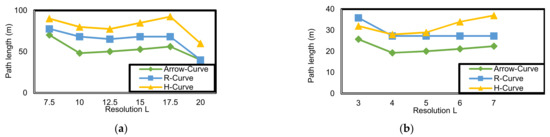
Figure 24. Path length (PL) corresponding to resolution (L) in Arrow-Curve model, R-Curve path model, and H-Curve (outdoor environment): (a) outdoor environment; (b) indoor environment.

6.

Power consumption.

As noted from Figure 25, Arrow-Curve achieves lower power consumption results than H-Curve by 50% (outdoor) and 75% (indoor). R-Curve achieves power consumption results lower than H-Curve by 27% in outdoor and 24% in indoor. The power consumption is affected by the network size, path length, number of pausing points, and energy dissipated during communication. Arrow-Curve and R-Curve dissipate less power in both outdoor and indoor environments. On the other hand, H-Curve has high power consumption because of the nature of the path length of H-Curve and high number of pausing points. The power consumption is reduced through choosing the path model, with the lowest path length, and by reducing time at each pausing point.

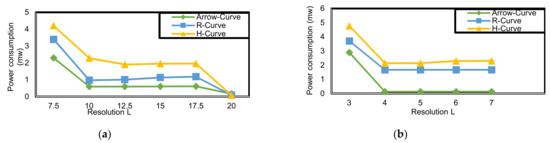
Figure 25. Power consumption (mW) corresponding to resolution (L) in Arrow-Curve model, R-Curve path model, and H-Curve: (a) outdoor environment; (b) indoor environment.

4.4. Performance Evaluation Comparison

In this section, the results for an ideal MATLAB simulation environment are compared to an outdoor realtime environment. The path length and the coverage ratio metrics show the same results as it depends on the path model. However, the average localization error and energy consumption show different results. The list of parameters used in both simulation and hardware comparison are shown in Table 3.

Table 3. Experimental parameters.

Parameter	Value
Network area size	20 × 20 ${\mathrm{m}}^2$
Number of mobile anchor nodes	1
Number of unknown nodes	20 (outdoor)
Resolution L	L = 10, 12.5, 15, 17.5,
Path loss exponent (${\mathrm{n}}_{\mathrm{p}}$)	2.3
${\mathrm{RSSI}}_0$ (${\mathrm{D}}_0)$	−54
${\mathrm{D}}_0$	0.4 m
Number of beacons received at each pausing point (Node MCU)	50
Simulation run times (MATLAB)	10
Communication range	28 m

The comparison metrics used to evaluate the proposed models are average position error and power consumption.

• Average localization error

Figure 26 shows the average localization error of the two path models using MATLAB simulation compared to using Node MCU.

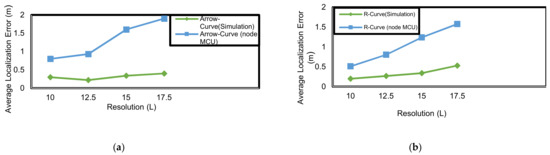
Figure 26. Average localization error (m) corresponding to resolution (L) in both simulation and real environment: (a) Arrow-Curve path model; (b) R-Curve path model.

As shown in Figure 26, Arrow-Curve and R-Curve average localization error results in both simulation environment and real environment achieve high accuracy results. Arrow-Curve achieves average localization error results in simulation environment that are less than those of the real environment by 75.9%. R-Curve achieves average localization error results in simulation environment less than those of the real environment by 67.5%. That is because in the real environment, there is no ideal situation such as in the simulation, and we cannot keep all nodes on the line of sight with the mobile anchor node and cannot keep the outdoor area free from all kinds of noise. Hence, the signal will be dissipated in such circumstances more than in simulation, and the error will increase.

2.

Energy Consumption

As shown in Figure 27, Arrow-Curve and R-Curve energy consumption results in both simulation environment and real environment. Both of dissipate high energy in the real environment. Arrow-Curve dissipates 93% less energy in the simulation environment than in the real environment. R-Curve dissipates 96.68% less energy in the simulation environment less than in the real environment. That is because the battery specifications are far more limiting in real hardware than in simulation.

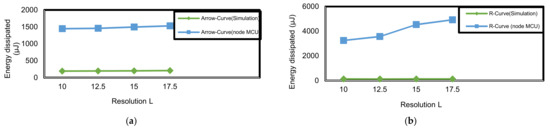
Figure 27. Energy dissipated (µJ) corresponding to resolution (L) in both simulation and real environment: (a) Arrow-Curve path model; (b) R-Curve path model.

4.5. Replacing One Mobile Anchor Node by Fixed Anchor Nodes

We will study the case where we replace one mobile anchor node by fixed anchor nodes in a MATLAB simulation environment with the specifications depicted in Section 4.2. The number of fixed nodes equals the number of pausing points of the mobile anchor node.

In Figure 28, we compare between energy dissipated by one mobile anchor node including the energy dissipated through sending messages and the total energy dissipated by all fixed anchor nodes replaced by one mobile anchor node. As shown, the mobile anchor node consumes more energy by fixed anchor nodes due the power dissipated through moving. Moreover, the cost of using fixed anchor nodes rather than one mobile node is very high.

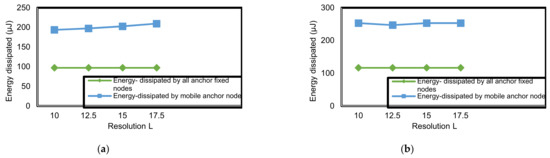
Figure 28. Energy dissipated (µJ) corresponding to resolution (L) in both one mobile anchor node and fixed anchor nodes: (a) Arrow-Curve path model; (b) R-Curve path model.

5. Conclusions and Future Work

In this paper, a path model for mobile anchor node aided localization in Wireless Air Pollution Monitoring System (WAPMS) named the Arrow-Curve path model was proposed. The model guarantees full coverage area. It achieves high position accuracy results. It has a small path length and consumes low power and can handle obstacles met in its way. The experimental results of the model in both simulation environment and realtime environment are compared to the H-Curve model. The results of simulation environment are more ideal than the realtime environment as it is an environment with zero noise effects. Arrow-Curve achieves average position error results lower than H-Curve by 10.6% in the simulation environment. The Arrow-Curve achieves an average position error lower than H-Curve by 5% in outdoor and 10% in the realtime environment, and the proposed model has higher efficiency in terms of average position error, standard deviation of position error, position coverage ratio, path length, number of pausing points, and power or energy consumption. It achieves high results in indoor environment with high obstacles compared to outdoor environment because of the nature of the path, in which it moves around any obstacle to overcome the obstacle problem. The model can be used in many applications, such as in healthcare and any indoor applications. In future work, to reduce power dissipated, we plan to use different mobility techniques and find the optimal number of mobile anchor nodes for more scalability and program each of them to work at a period of time and cause the others to sleep to reduce power consumption, and we can also use other wireless sensor nodes that allow other wireless communication protocols that consume less power, such as the Zigbee wireless technology protocol.