Overview of Signal Processing and Machine Learning for Smart Grid Condition Monitoring
Abstract
1. Introduction
- A systematic review of smart grid disturbances, PMU requirements for PQ measurement, and European and international PQ standards is presented,
- An in-depth and comprehensive survey of methods for grid frequency, rate of change of frequency (ROCOF) and synchronized phasor estimation is provided.
- A survey on classification methods for intelligent system application to disturbances diagnosis in power systems is conducted. A critical analysis on signal processing and machine learning is presented and a brief discussion on relevant topics for future developments is conducted.
2. Power Quality Measurement
2.1. Power Grid Disturbances
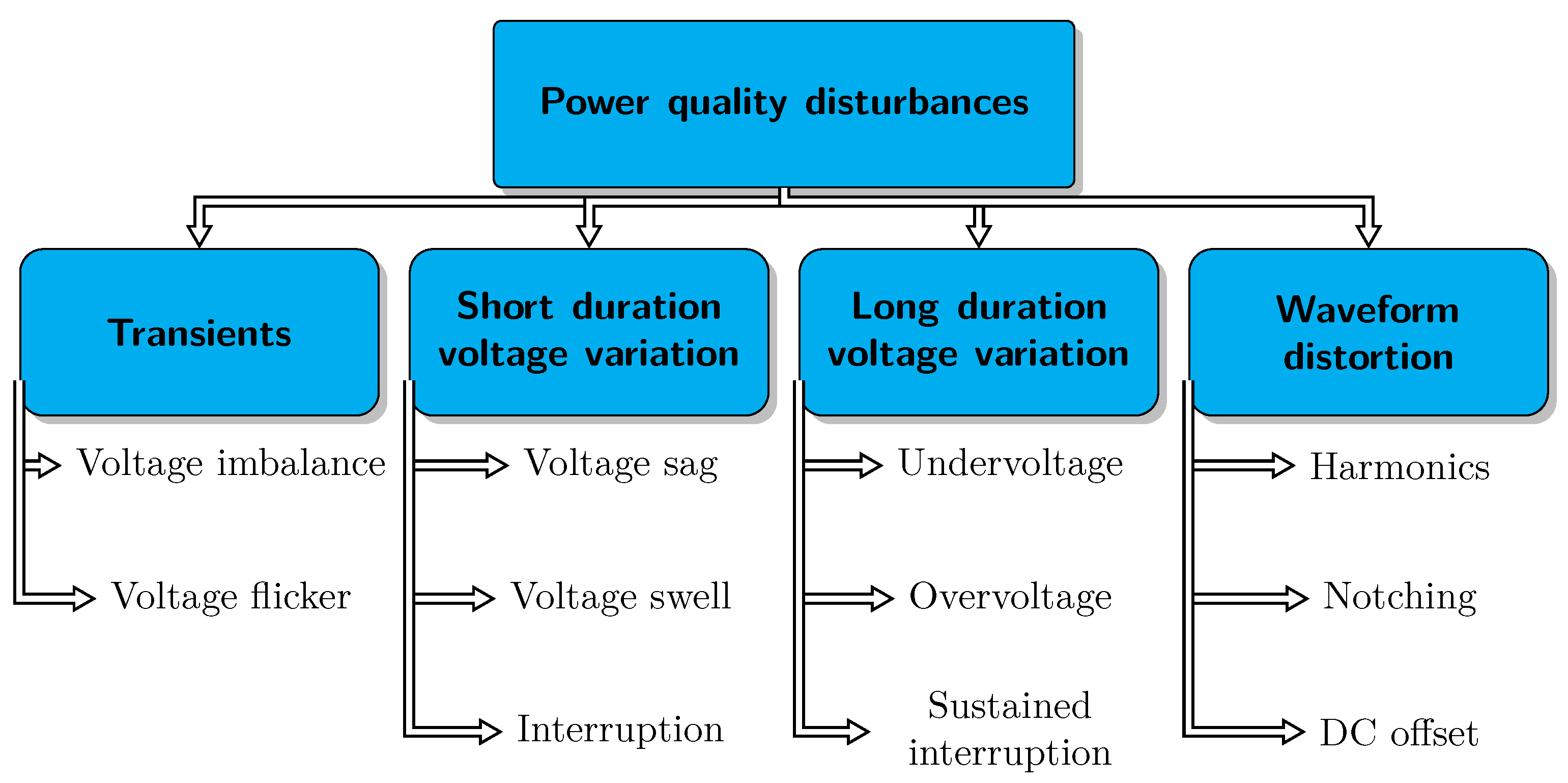
2.1.1. Typical Power Quality Disturbances
2.1.2. Causes and Consequences
2.2. Power Quality Analysis
2.2.1. Definition
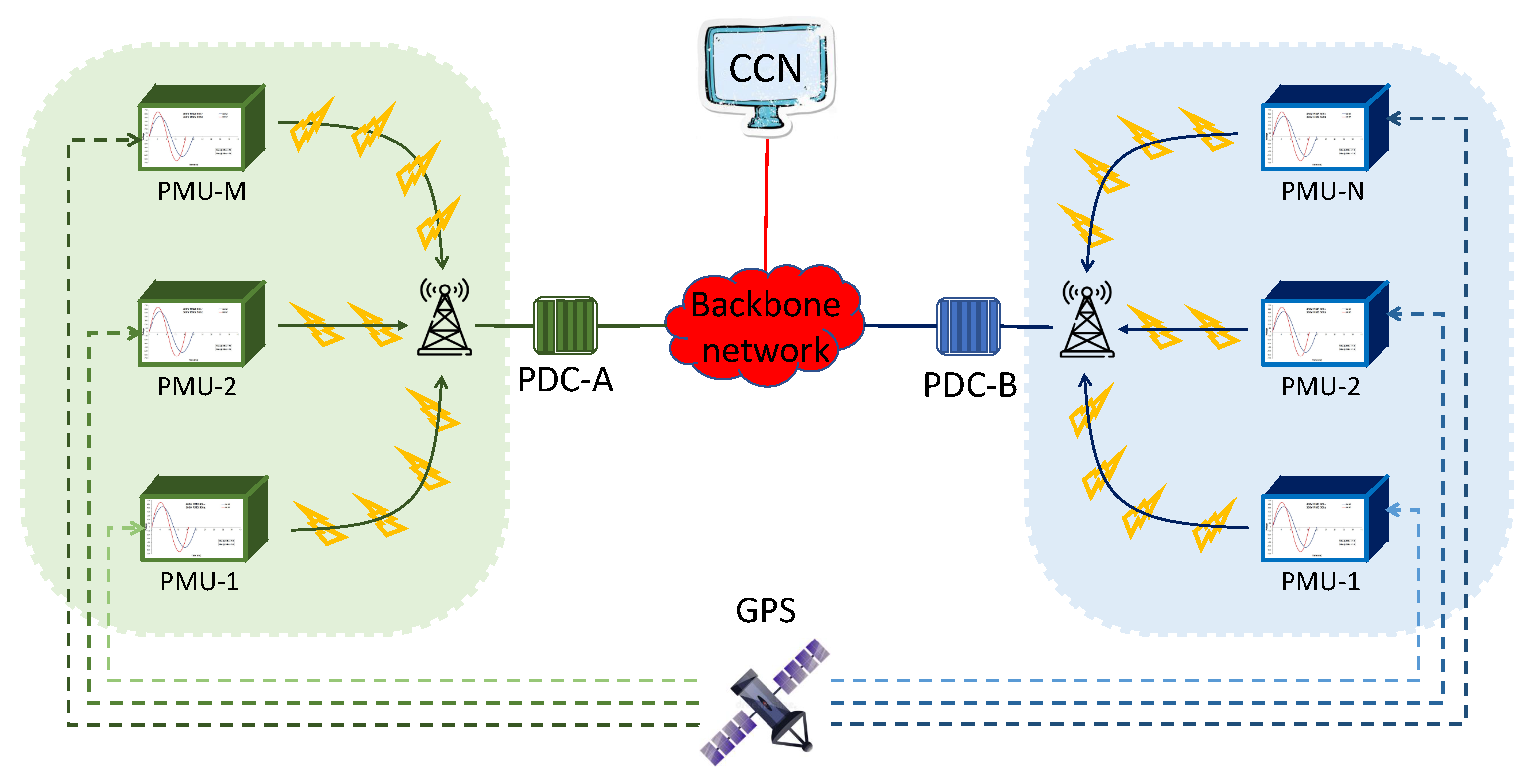
2.2.2. Wide Area Measurement System
2.2.3. Phasor Measurement Units
2.2.4. International Standards
- IEC/IEEE 60255-118-1:2018 is used for synchrophasor measurement systems in power systems. It defines PMU, synchrophasor, frequency, and ROCOF measurements. Even though it does not provide hardware and software for computing these quantities, it specifies methods for evaluating the compliance of these measurements with standard requirements under both static and dynamic conditions.
- EN50160 is the European standard for power quality measurement, defining the acceptable limits of voltages and currents RMS values with respect to nominal values and the disturbance duration in AC power.
- IEEE-519 is the North American guideline for power systems. It is intended as “recommended practice” and refers to both current and voltage distortion.
- IEC 61000-4-30 is the standard defining methods for power quality monitoring. Specifically, it provides a description of measurement methods and PQ parameters interpretation [17]. Unlike earlier editions, the 2015 Edition 3 includes current measurements as well as voltage measurement.
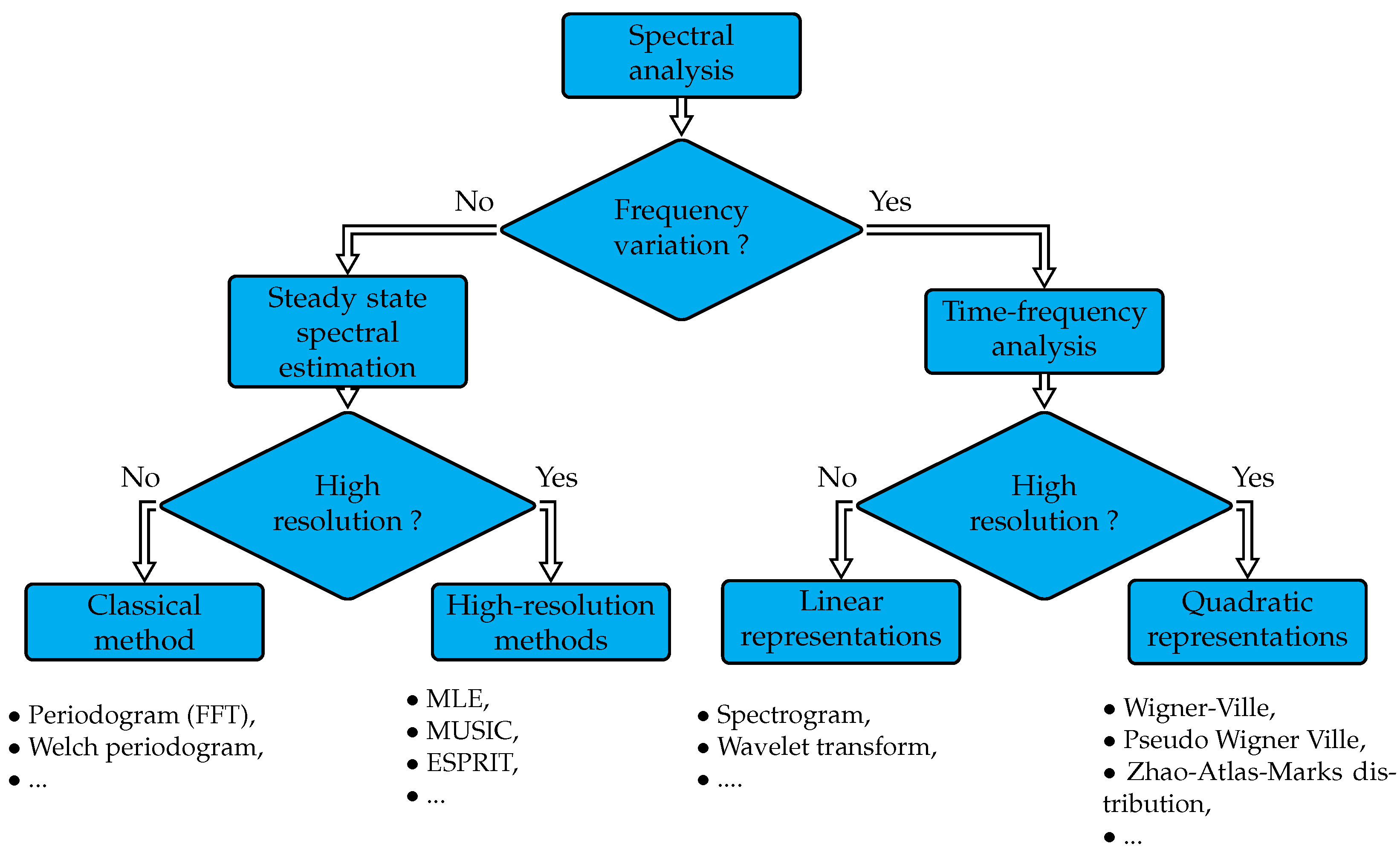
3. Grid Frequency and Phasor Estimation
- is the instantaneous amplitude,
- is the instantaneous phase. denotes the normalized instantaenous fundamental frequency and corresponds to the initial phase.
- includes all possible disturbances, such as harmonics, inter-harmonics, and wideband noise.
3.1. Conventional Approaches
3.1.1. Zero-Crossing and Root Mean Square
3.1.2. Taylor Weighted Least-Squares Algorithm
3.1.3. Kalman Filtering
3.2. Power Spectral Density Estimation Techniques
3.2.1. Periodogram and Its Extensions
3.2.2. High-Resolution Techniques
Subspace Techniques
| Algorithm 1 MUSIC [123]. |
Require:N observations of the signal .
|
| Algorithm 2 ESPRIT [123]. |
Require:N observations the signal .
|
Maximum Likelihood Estimation
- is a matrix containing the measured three-phase samples and is given by
- is a real-valued matrix and is given by
- is a real-valued matrix given by
- is the Frobenius norm.
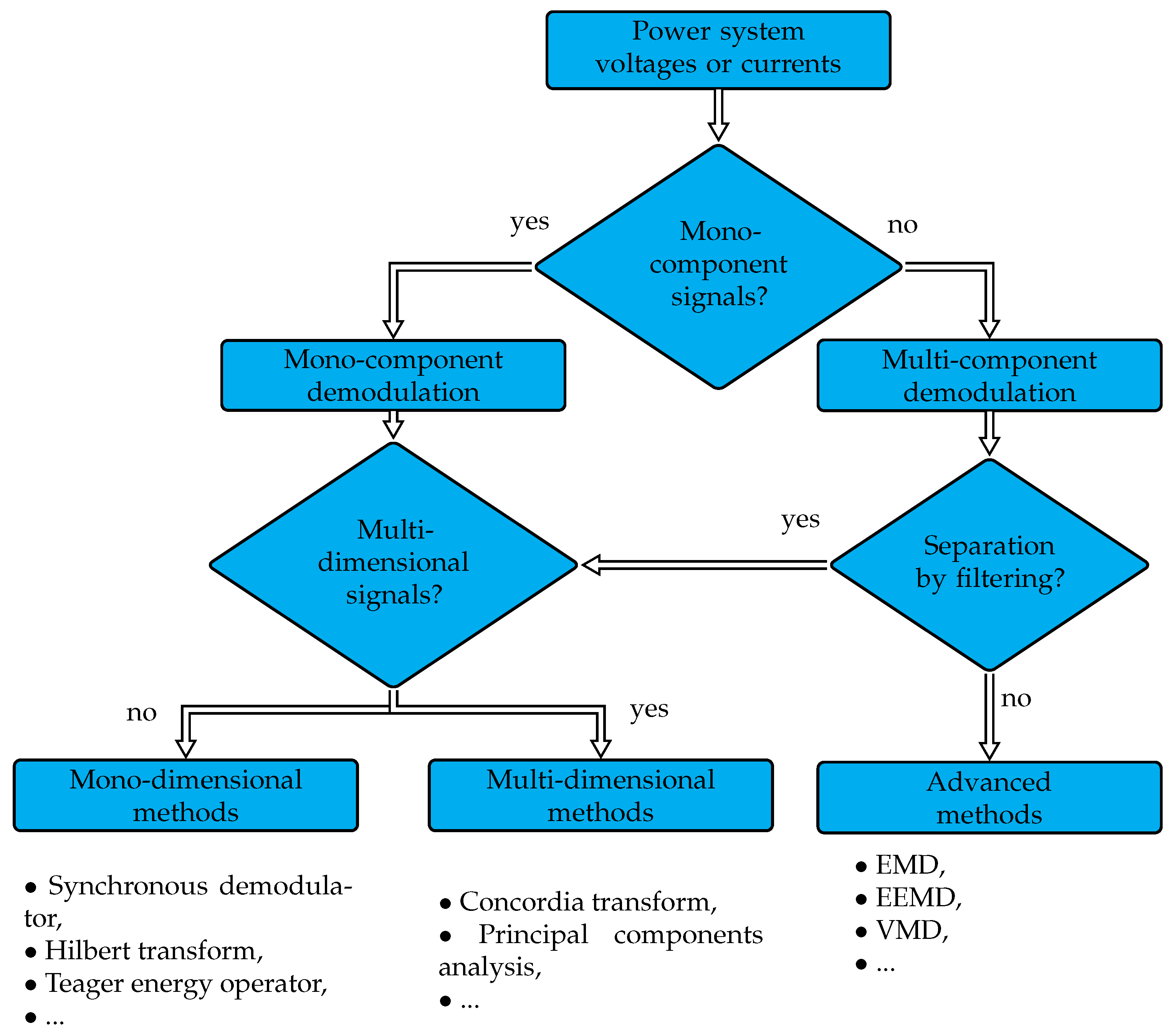
3.3. Demodulation Techniques
3.3.1. Mono-Dimensional Techniques
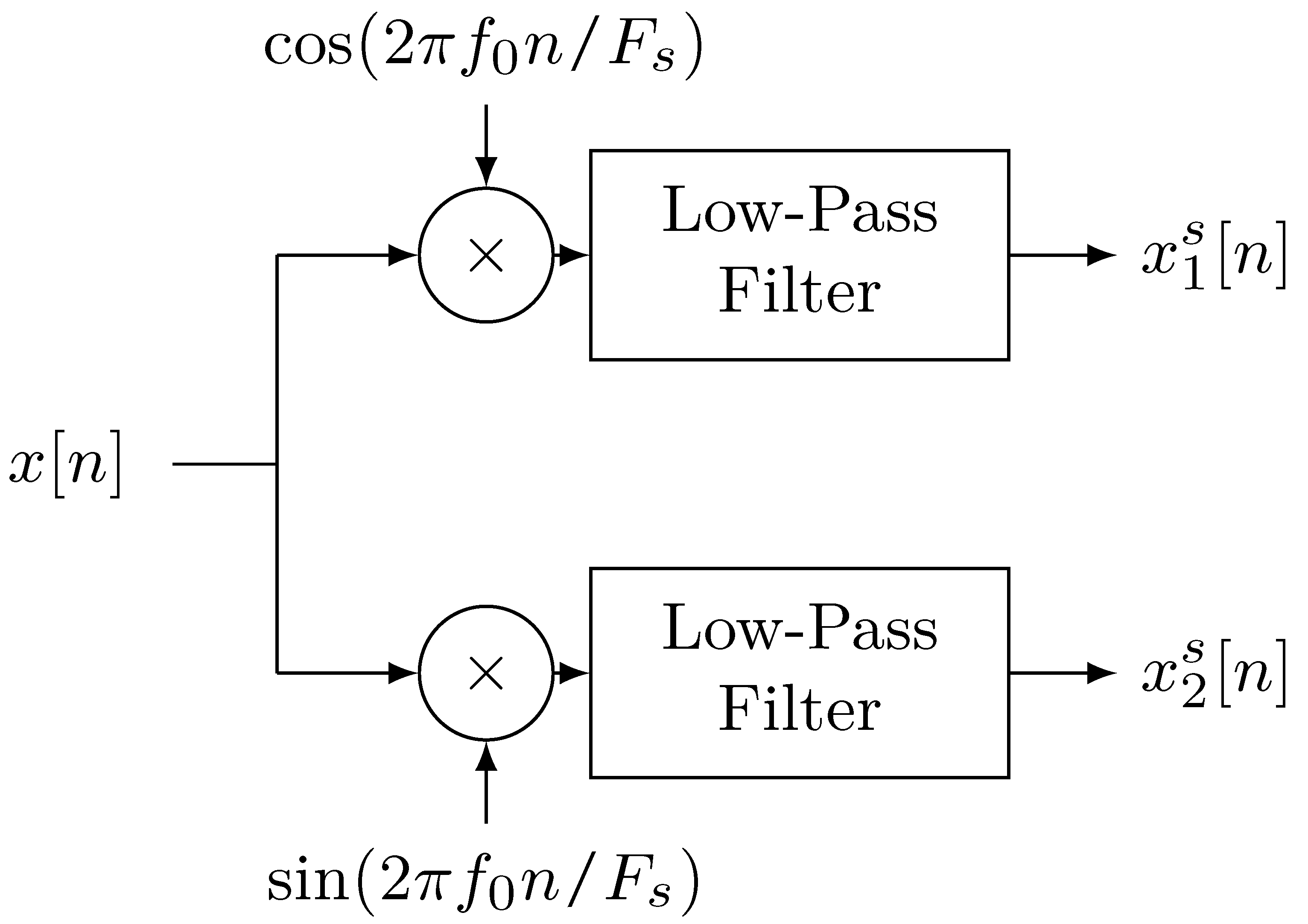
Synchronous Demodulator
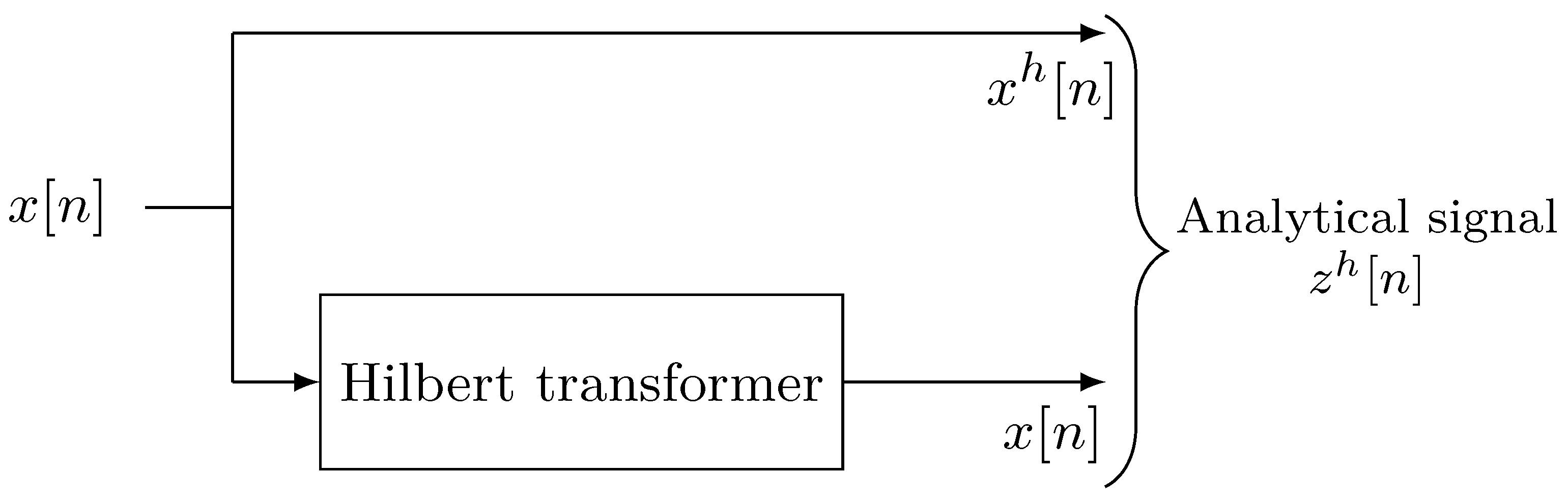
Hilbert Transform
Teager Energy Operator
3.3.2. Multi-Dimensional Techniques
Concordia Transform
Principal Component Analysis
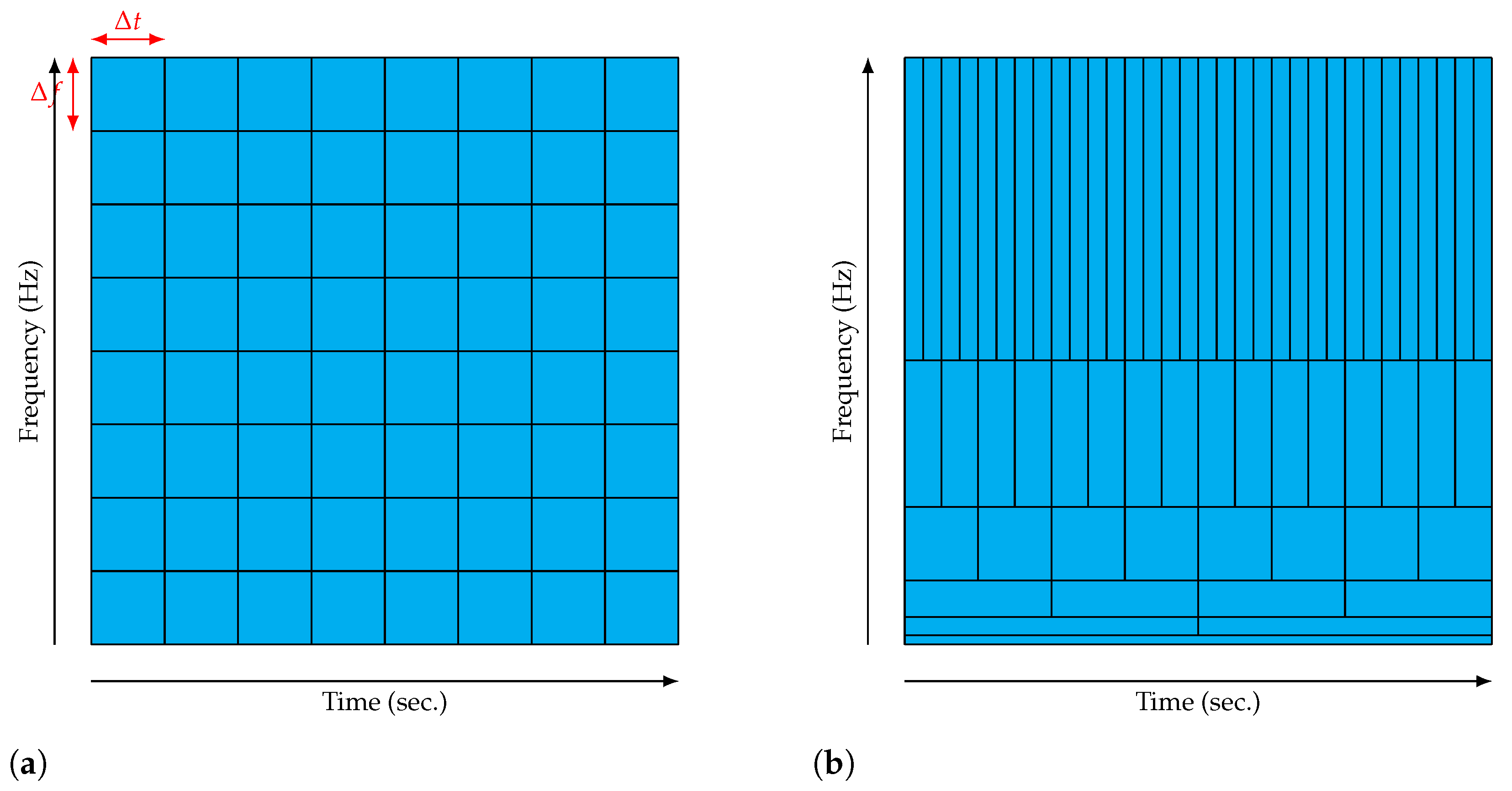
3.4. Time-Frequency, Time-Scale Analysis
3.4.1. Spectrogram
- The electric signal is divided into time segments,
- A time window is applied to each segment to reduce side-lobe effects. Classical choices for is the rectangular, Hanning, Hamming or Gaussian windows.
- PSD estimation of each windowed time segment is calculated based on the Fourier transform.
3.4.2. Scalogram
3.4.3. Wigner–Ville and Other Quadratic Distributions
3.4.4. Hilbert–Huang Transform
- The electrical signal is decomposed into a sum of amplitude- and frequency- modulated mono-component sine waves using an EMD algorithm. EMD has been proposed by Huang and is described by the following algorithm [158]:
- –
- Identification of all extrema of
- –
- Interpolation between minima (resp. maxima) ending up with some envelope (resp. ).
- –
- Computation of the mean:
- –
- Extraction of the detail:
- –
- Iteration on the residual .
- Instantaneous amplitude and instantaneous frequency of each IMF are extracted using a demodulation technique described in Section 3.3. In general, to achieve IA and IF calculation, the Hilbert transform is used. In this case, the transformation is called HHT.
- The time-frequency representation is obtained by displaying the time evolution of the instantaneous amplitude and frequency for each sine wave in the time-frequency plane.
3.5. Discussion
4. Disturbances Classification Techniques
4.1. Conventional Approaches for Quality Monitoring
4.1.1. ABC Classifier
- Fault type, which includes single-line-to-ground fault, line-to-line fault, double-line-to-ground fault, three-phase fault,
- Transformer winding connection,
- Load connection.
4.1.2. Symmetrical Component Classifier
Fundamental Frequency Deviation
Fundamental Amplitude and Phase Shift Related Disturbances
Harmonics Disturbances
4.1.3. Information Criteria Rules
- : Zero and negative sequences are null,
- : Zero sequence is null,
- : Negative sequence is null,
- : All sequences are not null.
4.2. Machine Learning Techniques
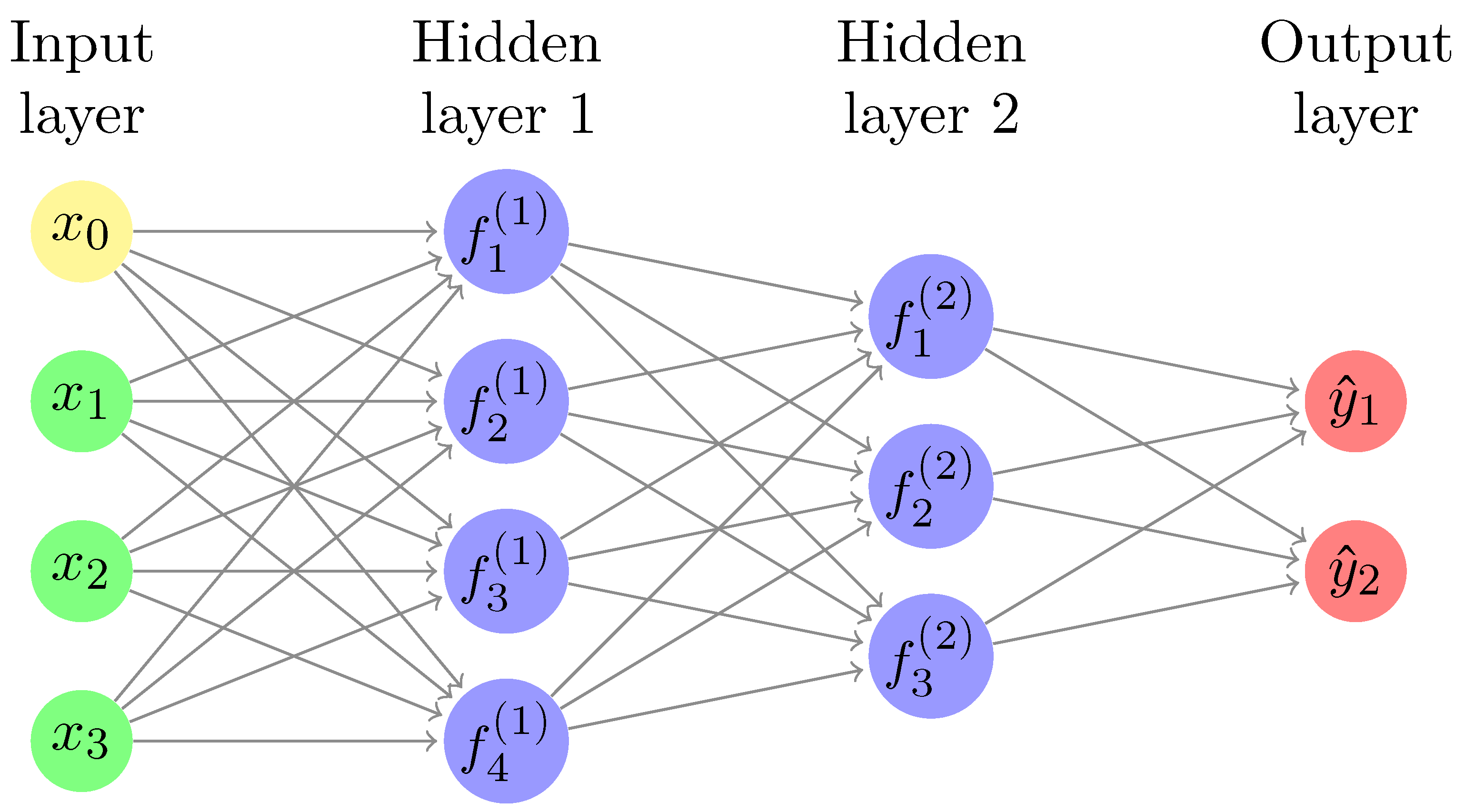
4.2.1. Artificial Neural Networks Technique
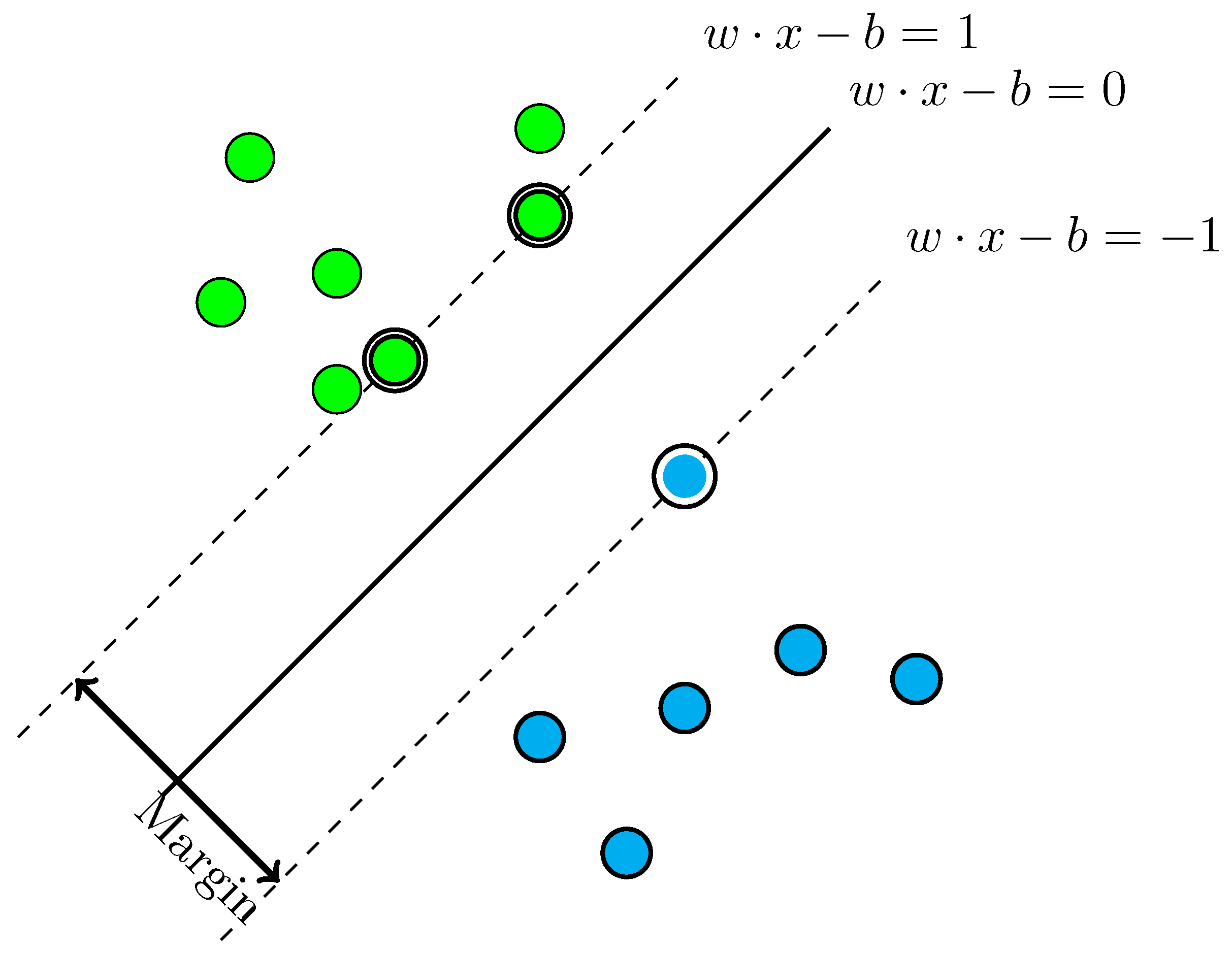
4.2.2. Support Vector Machines Technique
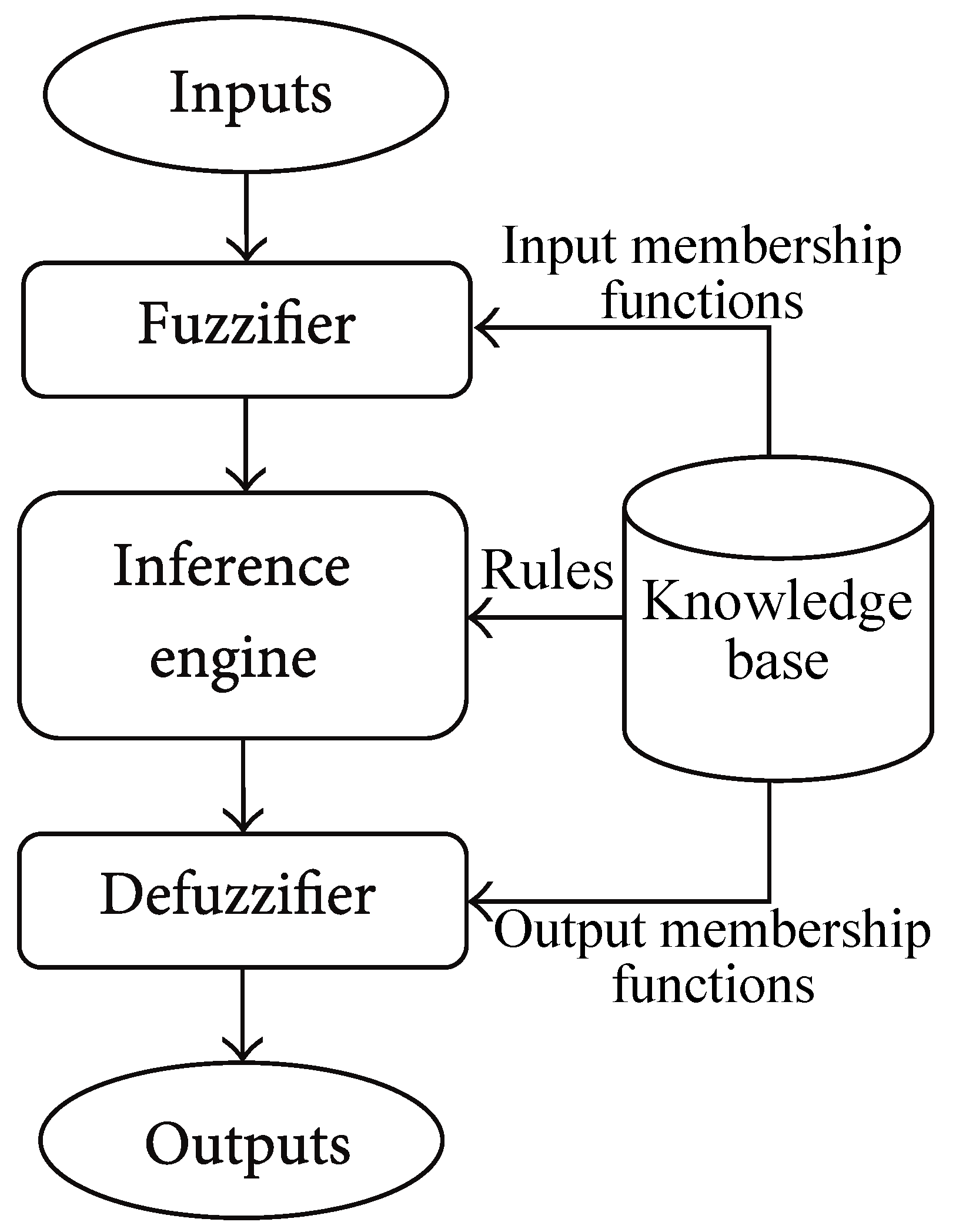
4.2.3. Fuzzy Expert Systems
4.2.4. Deep Learning Approaches
4.3. Critical Analysis and Future Research Topics and Challenges
5. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PQ | Power Quality |
| PMU | Phasor Measurement Unit |
| DSP | Digital Signal Processing |
| IoT | Internet of Things |
| MLE | Maximum Likelihood Estimation |
| MUSIC | Multiple Signal Classification |
| ESPRIT | Estimation of Signal Parameters via Rotational Invariance Techniques |
| ARMA | AutoRegressive Moving Average |
| EMD | Empirical Mode Decomposition |
| DWT | Discrete Wavelet transform |
| ANN | Artificial Neural Network |
| SVM | Support Vector Machine |
| CNN | Convolution Neural Network |
| RNN | Recurrent Neural Network |
| I-RNN | Identity-Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Units |
| CNN-LSTM | Convolutional Neural Network-Long Short-Term Memory |
| AI | Artificial Intelligence |
| SCADA | Supervisory Control and Data Acquisition |
| GPS | Global Positioning System |
| PDC | Phasor Data Concentrator |
| CCN | Central Control Network |
| IEC | International Electrotechnical Commission |
| IEEE | Institute of Electrical and Electronics Engineers |
| TVE | Total Vector Error |
| RMS | Root Mean Square |
| PSD | Power Spectral Density |
| FFT | Fast Fourier Transform |
| DTFT | Discrete Time Fourier transform |
| SVD | Singular Value Decomposition |
| EVD | EigenValues Decomposition |
| SNR | Signal to Noise Ratio |
| IF | Instantaneous Frequency |
| IAm | Instantaneous Amplitude |
| TEO | Teager energy operator |
| ESA | Energy Separation Algorithm |
| CT | Concordia Transform |
| PCA | Principal Component Analysis |
| STFT | Short-Time Fourier Transform |
| CWT | Continuous Wavelet Transform |
| WVD | Wigner–Ville Distribution |
| HHT | Hilbert–Huang Transform |
| HAS | Hilbert Spectral Analysis |
| IMF | Intrinsic Mode Function |
| VMD | Variational Mode Decomposition |
| EEMD | Ensemble EMD |
| SD | Synchronous Demodulator |
| ROCOF | Rate Of Change Of Frequency |
| MLP | Multilayer Perceptron |
| DL | Deep Learning |
| QoS | Quality of Service |
| SCADA | Supervisory Control And Data Acquisition |
| WAMS | Wide Area Measurement System |
| IpDFT | Interpolated Discrete Fourier Transform |
| DCF | Down-Conversion and low-pass Filtering |
| TFT | Taylor Fourier Transform |
References
- Ekanayake, J.B.; Jenkins, N.; Liyanage, K.; Wu, J.; Yokoyama, A. Smart Grid: Technology and Applications; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2011, 14, 944–980. [Google Scholar] [CrossRef]
- Gungor, V.C.; Sahin, D.; Kocak, T.; Ergut, S.; Buccella, C.; Cecati, C.; Hancke, G.P. A survey on smart grid potential applications and communication requirements. IEEE Trans. Ind. Inform. 2012, 9, 28–42. [Google Scholar] [CrossRef]
- Gungor, V.C.; Sahin, D.; Kocak, T.; Ergut, S.; Buccella, C.; Cecati, C.; Hancke, G.P. Smart grid technologies: Communication technologies and standards. IEEE Trans. Ind. Inform. 2011, 7, 529–539. [Google Scholar] [CrossRef]
- Mwasilu, F.; Justo, J.J.; Kim, E.K.; Do, T.D.; Jung, J.W. Electric vehicles and smart grid interaction: A review on vehicle to grid and renewable energy sources integration. Renew. Sustain. Energy Rev. 2014, 34, 501–516. [Google Scholar] [CrossRef]
- Phuangpornpitak, N.; Tia, S. Opportunities and challenges of integrating renewable energy in smart grid system. Energy Procedia 2013, 34, 282–290. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Feld, G.; Amirat, Y.; Benbouzid, M.; Le Gall, F. Design and experimental implementation of a wind energy conversion platform with education and research capabilities. Comput. Electr. Eng. 2020, 85, 106661. [Google Scholar] [CrossRef]
- Mortaji, H.; Ow, S.H.; Moghavvemi, M.; Almurib, H.A.F. Load shedding and smart-direct load control using internet of things in smart grid demand response management. IEEE Trans. Ind. Appl. 2017, 53, 5155–5163. [Google Scholar] [CrossRef]
- Hui, H.; Ding, Y.; Shi, Q.; Li, F.; Song, Y.; Yan, J. 5G network-based Internet of Things for demand response in smart grid: A survey on application potential. Appl. Energy 2020, 257, 113972. [Google Scholar] [CrossRef]
- Mortaji, H.; Hock, O.S.; Moghavvemi, M.; Almurib, H.A. Smart grid demand response management using internet of things for load shedding and smart-direct load control. In Proceedings of the 2016 IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016; pp. 1–7. [Google Scholar]
- Kabalci, Y. A survey on smart metering and smart grid communication. Renew. Sustain. Energy Rev. 2016, 57, 302–318. [Google Scholar] [CrossRef]
- Keshtkar, A.; Arzanpour, S. An adaptive fuzzy logic system for residential energy management in smart grid environments. Appl. Energy 2017, 186, 68–81. [Google Scholar] [CrossRef]
- Zhao, C.; He, J.; Cheng, P.; Chen, J. Consensus-based energy management in smart grid with transmission losses and directed communication. IEEE Trans. Smart Grid 2016, 8, 2049–2061. [Google Scholar] [CrossRef]
- Worighi, I.; Maach, A.; Hafid, A.; Hegazy, O.; Van Mierlo, J. Integrating renewable energy in smart grid system: Architecture, virtualization and analysis. Sustain. Energy Grids Netw. 2019, 18, 100226. [Google Scholar] [CrossRef]
- Yang, K.; Walid, A. Outage-storage tradeoff in frequency regulation for smart grid with renewables. IEEE Trans. Smart Grid 2013, 4, 245–252. [Google Scholar] [CrossRef]
- Standard British. Voltage Characteristics of Electricity Supplied by Public Distribution Networks. October 2007. Available online: https://webstore.ansi.org/standards/bsi/bsen501602007 (accessed on 21 September 2007).
- International Standard. Testing and Measurement Techniques—Power Quality Measurement Methods. March 2021. Available online: https://webstore.iec.ch/publication/68642 (accessed on 13 October 2021).
- IEEE Recommended Practice for Monitoring Electric Power Quality. IEEE 1159-2019 (Revision of IEEE Standard 1159-2009). 13 August 2019. Available online: https://ieeexplore.ieee.org/document/8796486 (accessed on 13 October 2021). [CrossRef]
- Fuchs, E.; Masoum, M.A. Power Quality in Power Systems and Electrical Machines; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Bollen, M.H. What is power quality? Electr. Power Syst. Res. 2003, 66, 5–14. [Google Scholar] [CrossRef]
- Kusko, A. Power Quality in Electrical Systems; McGraw-Hill Education: New York, NY, USA, 2007. [Google Scholar]
- Mishra, S.; Bhende, C.; Panigrahi, B. Detection and classification of power quality disturbances using S-transform and probabilistic neural network. IEEE Trans. Power Deliv. 2007, 23, 280–287. [Google Scholar] [CrossRef]
- Bollen, M.H.; Gu, I.Y. Signal Processing of Power Quality Disturbances; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 30. [Google Scholar]
- Muscas, C. Power quality monitoring in modern electric distribution systems. IEEE Instrum. Meas. Mag. 2010, 13, 19–27. [Google Scholar] [CrossRef]
- Elphick, S.; Ciufo, P.; Drury, G.; Smith, V.; Perera, S.; Gosbell, V. Large scale proactive power-quality monitoring: An example from Australia. IEEE Trans. Power Deliv. 2016, 32, 881–889. [Google Scholar] [CrossRef]
- Parle, J.; Madrigal, M.; Acha, E. Trends in power quality monitoring. IEEE Power Eng. Rev. 2001, 21, 3–21. [Google Scholar] [CrossRef]
- Yildirim, O.; Eristi, B.; Eristi, H.; Unal, S.; Erol, Y.; Demir, Y. FPGA-based online power quality monitoring system for electrical distribution network. Measurement 2018, 121, 109–121. [Google Scholar] [CrossRef]
- Venkatraman, K.; Reddy, B.D.; Selvan, M.; Moorthi, S.; Kumaresan, N.; Gounden, N.A. Online condition monitoring and power management system for standalone micro-grid using FPGAs. IET Gener. Transm. Distrib. 2016, 10, 3875–3884. [Google Scholar] [CrossRef]
- Nilsson, J.; Bertling, L. Maintenance management of wind power systems using condition monitoring systems—Life cycle cost analysis for two case studies. IEEE Trans. Energy Convers. 2007, 22, 223–229. [Google Scholar] [CrossRef]
- Liu, J.; Tang, J.; Ponci, F.; Monti, A.; Muscas, C.; Pegoraro, P.A. Trade-offs in PMU deployment for state estimation in active distribution grids. IEEE Trans. Smart Grid 2012, 3, 915–924. [Google Scholar] [CrossRef]
- IEEE/IEC. International Standard—Measuring Relays and Protection Equipment—Part 118-1: Synchrophasor for Power Systems Measurements. IEC/IEEE 60255-118-1:2018. 19 December 2018. Available online: https://standards.ieee.org/standard/60255-118-1-2018.html (accessed on 13 October 2021).
- Tai, X.; Marelli, D.; Rohr, E.; Fu, M. Optimal PMU placement for power system state estimation with random component outages. Int. J. Electr. Power Energy Syst. 2013, 51, 35–42. [Google Scholar] [CrossRef]
- Bashian, A.; Assili, M.; Anvari-Moghaddam, A. A security-based observability method for optimal PMU-sensor placement in WAMS. Int. J. Electr. Power Energy Syst. 2020, 121, 106157. [Google Scholar] [CrossRef]
- Bashian, A.; Assili, M.; Anvari-Moghaddam, A.; Catalão, J.P.S. Optimal Design of a Wide Area Measurement System Using Hybrid Wireless Sensors and Phasor Measurement Units. Electronics 2019, 8, 1085. [Google Scholar] [CrossRef]
- Macii, D.; Belega, D.; Petri, D. IpDFT-Tuned Estimation Algorithms for PMUs: Overview and Performance Comparison. Appl. Sci. 2021, 11, 2318. [Google Scholar] [CrossRef]
- Belega, D.; Fontanelli, D.; Petri, D. Low-complexity least-squares dynamic synchrophasor estimation based on the discrete Fourier transform. IEEE Trans. Instrum. Meas. 2015, 64, 3284–3296. [Google Scholar] [CrossRef]
- Singh, A.K.; Pal, B.C. Rate of change of frequency estimation for power systems using interpolated DFT and Kalman filter. IEEE Trans. Power Syst. 2019, 34, 2509–2517. [Google Scholar] [CrossRef]
- Macii, D.; Petri, D. Digital filters for phasor measurement units: Design criteria, advantages and limitations. In Proceedings of the 2019 IEEE 10th International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 25–27 September 2019; pp. 1–6. [Google Scholar]
- Kamwa, I.; Samantaray, S.; Joos, G. Wide frequency range adaptive phasor and frequency PMU algorithms. IEEE Trans. Smart Grid 2013, 5, 569–579. [Google Scholar] [CrossRef]
- Zhan, L.; Liu, Y.; Liu, Y. A Clarke transformation-based DFT phasor and frequency algorithm for wide frequency range. IEEE Trans. Smart Grid 2016, 9, 67–77. [Google Scholar] [CrossRef]
- Xia, T.; Liu, Y. Single-phase phase angle measurements in electric power systems. IEEE Trans. Power Syst. 2009, 25, 844–852. [Google Scholar] [CrossRef]
- Kang, S.H.; Lee, D.G.; Nam, S.R.; Crossley, P.A.; Kang, Y.C. Fourier transform-based modified phasor estimation method immune to the effect of the DC offsets. IEEE Trans. Power Deliv. 2009, 24, 1104–1111. [Google Scholar] [CrossRef]
- Derviškadić, A.; Romano, P.; Paolone, M. Iterative-interpolated DFT for synchrophasor estimation: A single algorithm for P- and M-class compliant PMUs. IEEE Trans. Instrum. Meas. 2017, 67, 547–558. [Google Scholar] [CrossRef]
- Petri, D.; Fontanelli, D.; Macii, D. A frequency-domain algorithm for dynamic synchrophasor and frequency estimation. IEEE Trans. Instrum. Meas. 2014, 63, 2330–2340. [Google Scholar] [CrossRef]
- Huang, C.; Xie, X.; Jiang, H. Dynamic phasor estimation through DSTKF under transient conditions. IEEE Trans. Instrum. Meas. 2017, 66, 2929–2936. [Google Scholar] [CrossRef]
- Nanda, S.; Dash, P.K. A Gauss–Newton ADALINE for dynamic phasor estimation of power signals and its FPGA implementation. IEEE Trans. Instrum. Meas. 2016, 67, 45–56. [Google Scholar] [CrossRef]
- De la O Serna, J.A.; Rodriguez-Maldonado, J. Instantaneous oscillating phasor estimates with Taylor K-Kalman filters. IEEE Trans. Power Syst. 2011, 26, 2336–2344. [Google Scholar] [CrossRef]
- Zečević, Ž.; Krstajić, B.; Popović, T. Improved frequency estimation in unbalanced three-phase power system using coupled orthogonal constant modulus algorithm. IEEE Trans. Power Deliv. 2016, 32, 1809–1816. [Google Scholar] [CrossRef]
- Messina, F.; Marchi, P.; Vega, L.R.; Galarza, C.G.; Laiz, H. A novel modular positive-sequence synchrophasor estimation algorithm for PMUs. IEEE Trans. Instrum. Meas. 2016, 66, 1164–1175. [Google Scholar] [CrossRef]
- Vejdan, S.; Sanaye-Pasand, M.; Malik, O.P. Accurate dynamic phasor estimation based on the signal model under off-nominal frequency and oscillations. IEEE Trans. Smart Grid 2015, 8, 708–719. [Google Scholar] [CrossRef]
- Chauhan, K.; Reddy, M.V.; Sodhi, R. A novel distribution-level phasor estimation algorithm using empirical wavelet transform. IEEE Trans. Ind. Electron. 2018, 65, 7984–7995. [Google Scholar] [CrossRef]
- Narduzzi, C.; Bertocco, M.; Frigo, G.; Giorgi, G. Fast-TFM—Multifrequency phasor measurement for distribution networks. IEEE Trans. Instrum. Meas. 2018, 67, 1825–1835. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, Q.; Wang, F.; Huang, S. Dynamic harmonic synchrophasor estimator based on sinc interpolation functions. IEEE Trans. Instrum. Meas. 2018, 68, 3054–3065. [Google Scholar] [CrossRef]
- Zečević, Ž.; Jokić, I.; Popović, T.; Krstajić, B. An efficient phasor and frequency estimation algorithm for wide frequency range. Electr. Power Syst. Res. 2020, 180, 106124. [Google Scholar] [CrossRef]
- Song, J.; Zhang, J.; Wen, H. Accurate Dynamic Phasor Estimation by Matrix Pencil and Taylor Weighted Least Squares Method. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar]
- Xu, S.; Liu, H.; Bi, T.; Martin, K. An improved Taylor weighted least squares method for estimating synchrophasor. Int. J. Electr. Power Energy Syst. 2020, 120, 105987. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G.; Gupta, N. A critical review of detection and classification of power quality events. Renew. Sustain. Energy Rev. 2015, 41, 495–505. [Google Scholar] [CrossRef]
- Tu, C.; He, X.; Shuai, Z.; Jiang, F. Big data issues in smart grid—A review. Renew. Sustain. Energy Rev. 2017, 79, 1099–1107. [Google Scholar] [CrossRef]
- Mishra, M. Power quality disturbance detection and classification using signal processing and soft computing techniques: A comprehensive review. Int. Trans. Electr. Energy Syst. 2019, 29, e12008. [Google Scholar] [CrossRef]
- Hossain, E.; Khan, I.; Un-Noor, F.; Sikander, S.S.; Sunny, M.S.H. Application of big data and machine learning in smart grid, and associated security concerns: A review. IEEE Access 2019, 7, 13960–13988. [Google Scholar] [CrossRef]
- Rivas, A.E.L.; Abrão, T. Faults in smart grid systems: Monitoring, detection and classification. Electr. Power Syst. Res. 2020, 189, 106602. [Google Scholar] [CrossRef]
- Khetarpal, P.; Tripathi, M.M. A critical and comprehensive review on power quality disturbance detection and classification. Sustain. Comput. Inform. Syst. 2020, 28, 100417. [Google Scholar]
- Ibrahim, M.S.; Dong, W.; Yang, Q. Machine learning driven smart electric power systems: Current trends and new perspectives. Appl. Energy 2020, 272, 115237. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G.; Shaik, M.; Padmanaban, S.; Holm-Nielsen, J.B.; Mahela, O.P.; Kaliannan, P. Comprehensive review on detection and classification of power quality disturbances in utility grid with renewable energy penetration. IEEE Access 2020, 8, 146807–146830. [Google Scholar] [CrossRef]
- Gargoom, A.M.; Ertugrul, N.; Soong, W. A comparative study on effective signal processing tools for power quality monitoring. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005. [Google Scholar] [CrossRef]
- Karasu, S.; Saraç, Z. Classification of power quality disturbances by 2D-Riesz Transform, multi-objective grey wolf optimizer and machine learning methods. Digit. Signal Process. 2020, 101, 102711. [Google Scholar] [CrossRef]
- Khokhar, S.; Zin, A.A.B.M.; Mokhtar, A.S.B.; Pesaran, M. A comprehensive overview on signal processing and artificial intelligence techniques applications in classification of power quality disturbances. Renew. Sustain. Energy Rev. 2015, 51, 1650–1663. [Google Scholar] [CrossRef]
- Yilmaz, A.S.; Alkan, A.; Asyali, M.H. Applications of parametric spectral estimation methods on detection of power system harmonics. Electr. Power Syst. Res. 2008, 78, 683–693. [Google Scholar] [CrossRef]
- Zolfaghari, R.; Shrivastava, Y.; Agelidis, V.G.; Chu, G.L. Using windowed ESPRIT spectral estimation for measuring power quality indices. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010; pp. 1–8. [Google Scholar]
- Zygarlicki, J.; Mroczka, J. Variable-frequency Prony method in the analysis of electrical power quality. Metrol. Meas. Syst. 2012, 19, 39–48. [Google Scholar] [CrossRef]
- Liu, X.; Liu, C.; Wang, J.; Xing, J. Inter-harmonic parameter estimation based on FFT and MUSIC. Power Syst. Prot. Control 2009, 5, 12–15. [Google Scholar]
- Kapoor, R.; Saini, M.K. Hybrid demodulation concept and harmonic analysis for single/multiple power quality events detection and classification. Int. J. Electr. Power Energy Syst. 2011, 33, 1608–1622. [Google Scholar] [CrossRef]
- Jayasree, T.; Devaraj, D.; Sukanesh, R. Power quality disturbance classification using Hilbert transform and RBF networks. Neurocomputing 2010, 73, 1451–1456. [Google Scholar] [CrossRef]
- Senroy, N.; Suryanarayanan, S.; Ribeiro, P.F. An improved Hilbert–Huang method for analysis of time-varying waveforms in power quality. IEEE Trans. Power Syst. 2007, 22, 1843–1850. [Google Scholar] [CrossRef]
- Liu, J.; Song, H.; Sun, H.; Zhao, H. High-Precision Identification of Power Quality Disturbances Under Strong Noise Environment Based on FastICA and Random Forest. IEEE Trans. Ind. Inform. 2020, 17, 377–387. [Google Scholar] [CrossRef]
- Ucar, F.; Alcin, O.F.; Dandil, B.; Ata, F. Power quality event detection using a fast extreme learning machine. Energies 2018, 11, 145. [Google Scholar] [CrossRef]
- Masoum, M.; Jamali, S.; Ghaffarzadeh, N. Detection and classification of power quality disturbances using discrete wavelet transform and wavelet networks. IET Sci. Meas. Technol. 2010, 4, 193–205. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, J.J.; Gao, W.; Wu, Z. Fault detection, identification, and location in smart grid based on data-driven computational methods. IEEE Trans. Smart Grid 2014, 5, 2947–2956. [Google Scholar] [CrossRef]
- Thirumala, K.; Umarikar, A.C.; Jain, T. Estimation of single-phase and three-phase power-quality indices using empirical wavelet transform. IEEE Trans. Power Deliv. 2014, 30, 445–454. [Google Scholar] [CrossRef]
- Adamo, F.; Attivissimo, F.; Di Nisio, A.; Savino, M.; Spadavecchia, M. A spectral estimation method for nonstationary signals analysis with application to power systems. Measurement 2015, 73, 247–261. [Google Scholar] [CrossRef]
- Xu, S.; Liu, H.; Bi, T. A novel frequency estimation method based on complex Bandpass filters for P-class PMUs with short reporting latency. IEEE Trans. Power Deliv. 2020. [Google Scholar] [CrossRef]
- Tosato, P.; Macii, D.; Luiso, M.; Brunelli, D.; Gallo, D.; Landi, C. A tuned lightweight estimation algorithm for low-cost phasor measurement units. IEEE Trans. Instrum. Meas. 2018, 67, 1047–1057. [Google Scholar] [CrossRef]
- Bollen, M.H.; Zhang, L. Different methods for classification of three-phase unbalanced voltage dips due to faults. Electr. Power Syst. Res. 2003, 66, 59–69. [Google Scholar] [CrossRef]
- Bollen, M.H. Algorithms for characterizing measured three-phase unbalanced voltage dips. IEEE Trans. Power Deliv. 2003, 18, 937–944. [Google Scholar] [CrossRef]
- Sahani, M.; Dash, P.K. Automatic power quality events recognition based on Hilbert Huang transform and weighted bidirectional extreme learning machine. IEEE Trans. Ind. Inform. 2018, 14, 3849–3858. [Google Scholar] [CrossRef]
- Lee, C.; Nam, S. Efficient feature vector extraction for automatic classification of power quality disturbances. Electron. Lett. 1998, 34, 1059–1061. [Google Scholar] [CrossRef]
- Monedero, I.; Leon, C.; Ropero, J.; Garcia, A.; Elena, J.M.; Montano, J.C. Classification of electrical disturbances in real time using neural networks. IEEE Trans. Power Deliv. 2007, 22, 1288–1296. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; de Jesus Romero-Troncoso, R.; Osornio-Rios, R.A.; Garcia-Perez, A. Detection and classification of single and combined power quality disturbances using neural networks. IEEE Trans. Ind. Electron. 2013, 61, 2473–2482. [Google Scholar] [CrossRef]
- Bhende, C.; Mishra, S.; Panigrahi, B. Detection and classification of power quality disturbances using S-transform and modular neural network. Electr. Power Syst. Res. 2008, 78, 122–128. [Google Scholar] [CrossRef]
- Ekici, S. Classification of power system disturbances using support vector machines. Expert Syst. Appl. 2009, 36, 9859–9868. [Google Scholar] [CrossRef]
- Lin, W.M.; Wu, C.H.; Lin, C.H.; Cheng, F.S. Detection and classification of multiple power-quality disturbances with wavelet multiclass SVM. IEEE Trans. Power Deliv. 2008, 23, 2575–2582. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, Y.; Li, W. A classification method for complex power quality disturbances using EEMD and rank wavelet SVM. IEEE Trans. Smart Grid 2015, 6, 1678–1685. [Google Scholar] [CrossRef]
- Erişti, H.; Uçar, A.; Demir, Y. Wavelet-based feature extraction and selection for classification of power system disturbances using support vector machines. Electr. Power Syst. Res. 2010, 80, 743–752. [Google Scholar] [CrossRef]
- Yang, H.; Liu, X.; Zhang, D.; Chen, T.; Li, C.; Huang, W. Machine learning for power system protection and control. Electr. J. 2021, 34, 106881. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Fernandes, R.A.S.; da Silva, I.N.; Oleskovicz, M. Load profile identification interface for consumer online monitoring purposes in smart grids. IEEE Trans. Ind. Inform. 2012, 9, 1507–1517. [Google Scholar] [CrossRef]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Disturbances classification based on a model order selection method for power quality monitoring. IEEE Trans. Ind. Electron. 2017, 64, 9421–9432. [Google Scholar] [CrossRef]
- Ignatova, V.; Granjon, P.; Bacha, S. Space vector method for voltage dips and swells analysis. IEEE Trans. Power Deliv. 2009, 24, 2054–2061. [Google Scholar] [CrossRef]
- Bollen, M.H. Understanding power quality problems. In Voltage Sags and Interruptions; IEEE Press: Piscataway, NJ, USA, 2000. [Google Scholar]
- Dahal, O.P.; Brahma, S.M.; Cao, H. Comprehensive clustering of disturbance events recorded by phasor measurement units. IEEE Trans. Power Deliv. 2013, 29, 1390–1397. [Google Scholar] [CrossRef]
- Saini, M.K.; Kapoor, R. Classification of power quality events–a review. Int. J. Electr. Power Energy Syst. 2012, 43, 11–19. [Google Scholar] [CrossRef]
- Oubrahim, Z. On Electric Grid Power Quality Monitoring Using Parametric Signal Processing Techniques. Ph.D. Thesis, Thèse de Doctorat de l’Université de Bretagne Occidentale, Brest, France, November 2017. [Google Scholar]
- De Almeida, A.; Moreira, L.; Delgado, J. Power quality problems and new solutions. In Proceedings of the International Conference on Renewable Energies and Power Quality, Vigo, Spain, 9–11 April 2003; Volume 3. [Google Scholar]
- Bollen, M.H.; Gu, I.Y.; Santoso, S.; McGranaghan, M.F.; Crossley, P.A.; Ribeiro, M.V.; Ribeiro, P.F. Bridging the gap between signal and power. IEEE Signal Process. Mag. 2009, 26, 12–31. [Google Scholar] [CrossRef]
- Monti, A.; Muscas, C.; Ponci, F. Phasor Measurement Units and Wide Area Monitoring Systems; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chakrabarti, S.; Kyriakides, E. Optimal placement of phasor measurement units for power system observability. IEEE Trans. Power Syst. 2008, 23, 1433–1440. [Google Scholar] [CrossRef]
- Tholomier, D.; Kang, H.; Cvorovic, B. Phasor measurement units: Functionality and applications. In Proceedings of the 2009 Power Systems Conference, Clemson, SC, USA, 10–13 March 2009; pp. 1–12. [Google Scholar]
- Singh, B.; Sharma, N.; Tiwari, A.; Verma, K.; Singh, S. Applications of phasor measurement units (PMUs) in electric power system networks incorporated with FACTS controllers. Int. J. Eng. Sci. Technol. 2011, 3. [Google Scholar] [CrossRef]
- Khan, R.H.; Khan, J.Y. A comprehensive review of the application characteristics and traffic requirements of a smart grid communications network. Comput. Netw. 2013, 57, 825–845. [Google Scholar] [CrossRef]
- Radulović, M.; Zečević, Ž.; Krstajić, B. Dynamic phasor estimation by symmetric Taylor weighted least square filter. IEEE Trans. Power Deliv. 2019, 35, 828–836. [Google Scholar] [CrossRef]
- Belega, D.; Fontanelli, D.; Petri, D. Dynamic phasor and frequency measurements by an improved Taylor weighted least squares algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 2165–2178. [Google Scholar] [CrossRef]
- Ferrero, R.; Pegoraro, P.A.; Toscani, S. Synchrophasor Estimation for Three-Phase Systems Based on Taylor Extended Kalman Filtering. IEEE Trans. Instrum. Meas. 2020, 69, 6723–6730. [Google Scholar] [CrossRef]
- Fan, L.; Wehbe, Y. Extended Kalman filtering based real-time dynamic state and parameter estimation using PMU data. Electr. Power Syst. Res. 2013, 103, 168–177. [Google Scholar] [CrossRef]
- De la O Serna, J.A.; Rodríguez-Maldonado, J. Taylor–Kalman–Fourier filters for instantaneous oscillating phasor and harmonic estimates. IEEE Trans. Instrum. Meas. 2012, 61, 941–951. [Google Scholar] [CrossRef]
- Kay, S. Modern Spectral Estimation: Theory and Application; Prentice Hall, Englewood Cliffs: Hoboken, NJ, USA, 1998. [Google Scholar]
- Ribeiro, P.F.; Duque, C.A.; Ribeiro, P.M.; Cerqueira, A.S. Power Systems Signal Processing for Smart Grids; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kay, S.; Marple, S. Spectrum Analysis—A Modern Perspective. Proc. IEEE 1981, 69, 1380–1419. [Google Scholar] [CrossRef]
- Alkan, A.; Yilmaz, A.S. Frequency domain analysis of power system transients using Welch and Yule–Walker AR methods. Energy Convers. Manag. 2007, 48, 2129–2135. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. Enhanced interpolated-DFT for synchrophasor estimation in FPGAs: Theory, implementation, and validation of a PMU prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Fast procedures for accurate parameter estimation of sine-waves affected by noise and harmonic distortion. Digit. Signal Process. 2021, 114, 103035. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Accuracy analysis of the multicycle synchrophasor estimator provided by the interpolated DFT algorithm. IEEE Trans. Instrum. Meas. 2013, 62, 942–953. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Introduction to Spectral Analysis; Prentice-Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Elbouchikhi, E.; Choqueuse, V.; Benbouzid, M. Induction machine diagnosis using stator current advanced signal processing. Int. J. Energy Convers. 2015, 3, 76–87. [Google Scholar]
- Stoica, P.; Selen, Y. Model-order selection: A review of information criterion rules. IEEE Signal Process. Mag. 2004, 21, 36–47. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, Maximum Likelihood, and Cramer-Rao Bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Zhang, S.; Luo, R.C.; Hu, Z.Y.; Huang, B. Root-MUSIC and Prony based parameter estimation of voltage flicker. J. Electr. Power Sci. Technol. 2013, 4, 43–48. [Google Scholar]
- Zolfaghari, R.; Shrivastava, Y.; Agelidis, V.G. Evaluation of windowed ESPRIT virtual instrument for estimating Power Quality Indices. Electr. Power Syst. Res. 2012, 83, 58–65. [Google Scholar] [CrossRef]
- Kay, S. Fundamentals of Statistical Signal Processing: Estimation Theory; Signal Processing Series; 17th Printing; Prentice-Hall: Upper Saddle River, NJ, USA, 26 March 1993. [Google Scholar]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Maximum-likelihood frequency and phasor estimations for electric power grid monitoring. IEEE Trans. Ind. Inform. 2017, 14, 167–177. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Choqueuse, V.; Benbouzid, M. Induction machine faults detection using stator current parametric spectral estimation. Mech. Syst. Signal Process. 2015, 52, 447–464. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Choqueuse, V.; Benbouzid, M. Condition monitoring of induction motors based on stator currents demodulation. Int. Rev. Electr.-Eng.—IREE 2015, 10, 704–715. [Google Scholar] [CrossRef]
- Vakman, D. On the analytic signal, the Teager-Kaiser energy algorithm, and other methods for defining amplitude and frequency. Signal Process. IEEE Trans. 1996, 44, 791–797. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; Xiao, H. An approach to measure interharmonics-flicker based on synchronous demodulation. Proc. CSEE 2011, 31, 67–72. [Google Scholar]
- Hahn, S.L. Hilbert Transforms in Signal Processing; Artech House: Norwell, MA, USA, 1996. [Google Scholar]
- Oppenheim, A.; Schafer, R.; Padgett, W. Discrete-Time Signal Processing, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2009. [Google Scholar]
- Picinbono, B. On instantaneous amplitude and phase of signals. IEEE Trans. Signal Process. 1997, 45, 552–560. [Google Scholar] [CrossRef]
- Boashash, B. Time-Frequency Signal Analysis. In Advances in Spectrum Estimation; Haykin, S., Ed.; Engewood Cliffs, Prentice-Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Marple, L., Jr. Computing the discrete-time “analytic” signal via FFT. Signal Process. IEEE Trans. 1999, 47, 2600–2603. [Google Scholar] [CrossRef]
- Maragos, P.; Kaiser, J.; Quatieri, T. Energy Separation in Signal Modulations with Application to Speech Analysis. IEEE Trans. Signal Process. 1993, 10, 3024–3051. [Google Scholar] [CrossRef]
- Maragos, P.; Kaiser, J.; Quartieri, T. On Amplitude and Frequency Demodulation Using Energy Operators. IEEE Trans. Signal Process. 1993, 41, 1532–1550. [Google Scholar] [CrossRef]
- Subasi, A.; Yilmaz, A.S.; Tufan, K. Detection of generated and measured transient power quality events using Teager Energy Operator. Energy Convers. Manag. 2011, 52, 1959–1967. [Google Scholar] [CrossRef]
- Cho, S.H.; Hur, J.; Chung, I.Y. An applicability of teager energy operator and energy separation algorithm for waveform distortion analysis: Harmonics, inter-harmonics and frequency variation. J. Electr. Eng. Technol. 2014, 9, 1210–1216. [Google Scholar] [CrossRef]
- Aller, J.M.; Bueno, A.; Pagá, T. Power system analysis using space-vector transformation. Power Syst. IEEE Trans. 2002, 17, 957–965. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.A. A review on distribution grid fault location techniques. Electr. Power Components Syst. 2017, 45, 807–824. [Google Scholar] [CrossRef]
- Shen, Y.; Abubakar, M.; Liu, H.; Hussain, F. Power quality disturbance monitoring and classification based on improved PCA and convolution neural network for wind-grid distribution systems. Energies 2019, 12, 1280. [Google Scholar] [CrossRef]
- Flandrin, P. Time-Frequency/Time-Scale Analysis; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Auger, F.; Flandrin, P.; Goncalves, P.; Lemoine, O. Time-Frequency Toolbox, for Use with Matlab; Technical Report; CNRS, GDR ISIS, 1995–1996; Available online: http://tftb.nongnu.org/refguide.pdf (accessed on 8 August 2021).
- Rilling, G.; Flandrin, P.; Goncalvs, P. On Empirical Mode Decomposition and its algorithms. In Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03, Grado, Italy, 20–23 June 2003. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Jopri, M.; Abdullah, A.; Manap, M.; Yusoff, M.; Sutikno, T.; Habban, M. An improved detection and classification technique of harmonic signals in power distribution by utilizing spectrogram. Int. J. Electr. Comput. Eng. 2017, 7, 12. [Google Scholar] [CrossRef]
- Avdakovic, S.; Nuhanovic, A.; Kusljugic, M.; Music, M. Wavelet transform applications in power system dynamics. Electr. Power Syst. Res. 2012, 83, 237–245. [Google Scholar] [CrossRef]
- Mroczka, J.; Szmajda, M.; Górecki, K. Gabor transform, spwvd, gabor-wigner transform and wavelet transform-tools for power quality monitoring. Metrol. Meas. Syst. 2010, 17, 383–396. [Google Scholar]
- Abdullah, A.R.B.; Sha’ameri, A.Z.B.; Jidin, A.B. Classification of power quality signals using smooth-windowed Wigner-Ville distribution. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Korea, 10–13 October 2010; pp. 1981–1985. [Google Scholar]
- Cohen, L. Time-frequency Distributions: A Review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Camarena-Martinez, D.; Valtierra-Rodriguez, M.; Perez-Ramlu2005empiricalirez, C.A.; Amezquita-Sanchez, J.P.; de Jesus Romero-Troncoso, R.; Garcia-Perez, A. Novel downsampling empirical mode decomposition approach for power quality analysis. IEEE Trans. Ind. Electron. 2015, 63, 2369–2378. [Google Scholar] [CrossRef]
- Lu, Z.; Smith, J.; Wu, Q.; Fitch, J. Empirical mode decomposition for power quality monitoring. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 18 August 2005; pp. 1–5. [Google Scholar]
- Huang, N.; Shen, Z.; Long, S.; Wu, M.; Shih, H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H. The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Amirat, Y.; Benbouzid, M.; Wang, T.; Turri, S. An ensemble empirical mode decomposition approach for voltage sag detection in a smart grid context. Int. Rev. Electr. Eng. 2013, 8, 1503–1508. [Google Scholar]
- Ozgonenel, O.; Yalcin, T.; Guney, I.; Kurt, U. A new classification for power quality events in distribution systems. Electr. Power Syst. Res. 2013, 95, 192–199. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.R.; Manikandan, M.S. Variational mode decomposition and decision tree based detection and classification of power quality disturbances in grid-connected distributed generation system. IEEE Trans. Smart Grid 2016, 9, 3122–3132. [Google Scholar] [CrossRef]
- Sahani, M.; Dash, P.; Samal, D. A real-time power quality events recognition using variational mode decomposition and online-sequential extreme learning machine. Measurement 2020, 157, 107597. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Sahani, M.; Dash, P. Variational mode decomposition and weighted online sequential extreme learning machine for power quality event patterns recognition. Neurocomputing 2018, 310, 10–27. [Google Scholar] [CrossRef]
- Zhao, C.; Li, K.; Li, Y.; Wang, L.; Luo, Y.; Xu, X.; Ding, X.; Meng, Q. Novel method based on variational mode decomposition and a random discriminative projection extreme learning machine for multiple power quality disturbance recognition. IEEE Trans. Ind. Inform. 2018, 15, 2915–2926. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Choqueuse, V.; Granjon, P.; Belouchrani, A.; Auger, F.; Benbouzid, M. Monitoring of three-phase signals based on singular-value decomposition. IEEE Trans. Smart Grid 2019, 10, 6156–6166. [Google Scholar] [CrossRef]
- Chouhy Leborgne, R. Voltage Sags Characterisation and Estimation; ProQuest Chalmers Tekniska Hogskola, Dissertations Publishing: Gothenburg, Sweden, 2005. [Google Scholar]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications; Springer: Cham, Switzerland; New York, NY, USA, 2008; Volume 1. [Google Scholar]
- Zjavka, L. Power quality multi-step predictions with the gradually increasing selected input parameters using machine-learning and regression. Sustain. Energy Grids Netw. 2021, 26, 100442. [Google Scholar] [CrossRef]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition; Elsevier Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Rahul; Choudhary, B. An Advanced Genetic Algorithm with Improved Support Vector Machine for Multi-Class Classification of Real Power Quality Events. Electr. Power Syst. Res. 2021, 191, 106879. [Google Scholar] [CrossRef]
- Karasu, S.; Saraç, Z. Investigation of power quality disturbances by using 2D discrete orthonormal S-transform, machine learning and multi-objective evolutionary algorithms. Swarm Evol. Comput. 2019, 44, 1060–1072. [Google Scholar] [CrossRef]
- Motlagh, S.Z.; Foroud, A.A. Power quality disturbances recognition using adaptive chirp mode pursuit and grasshopper optimized support vector machines. Measurement 2021, 168, 108461. [Google Scholar] [CrossRef]
- Nagata, E.A.; Ferreira, D.D.; Bollen, M.H.; Barbosa, B.H.; Ribeiro, E.G.; Duque, C.A.; Ribeiro, P.F. Real-time voltage sag detection and classification for power quality diagnostics. Measurement 2020, 164, 108097. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mlakić, D.; Nikolovski, S.; Dragicević, T. Support vector machine-based islanding and grid fault detection in active distribution networks. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 2385–2403. [Google Scholar] [CrossRef]
- Kandel, A. Fuzzy Expert Systems; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Liao, Y.; Lee, J.B. A fuzzy-expert system for classifying power quality disturbances. Int. J. Electr. Power Energy Syst. 2004, 26, 199–205. [Google Scholar] [CrossRef]
- Dash, P.; Mishra, S.; Salama, M.; Liew, A. Classification of power system disturbances using a fuzzy expert system and a Fourier linear combiner. IEEE Trans. Power Deliv. 2000, 15, 472–477. [Google Scholar] [CrossRef]
- Reaz, M.B.I.; Choong, F.; Sulaiman, M.S.; Mohd-Yasin, F.; Kamada, M. Expert system for power quality disturbance classifier. IEEE Trans. Power Deliv. 2007, 22, 1979–1988. [Google Scholar] [CrossRef]
- Abdelsalam, A.A.; Eldesouky, A.A.; Sallam, A.A. Characterization of power quality disturbances using hybrid technique of linear Kalman filter and fuzzy-expert system. Electr. Power Syst. Res. 2012, 83, 41–50. [Google Scholar] [CrossRef]
- Biswal, M.; Dash, P.K. Measurement and classification of simultaneous power signal patterns with an S-transform variant and fuzzy decision tree. IEEE Trans. Ind. Inform. 2012, 9, 1819–1827. [Google Scholar] [CrossRef]
- Pires, V.F.; Amaral, T.G.; Martins, J.F. Power quality disturbances classification using the 3-D space representation and PCA based neuro-fuzzy approach. Expert Syst. Appl. 2011, 38, 11911–11917. [Google Scholar] [CrossRef]
- Styvaktakis, E.; Bollen, M.H.; Gu, I.Y. Expert system for classification and analysis of power system events. IEEE Trans. Power Deliv. 2002, 17, 423–428. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H. A novel deep learning method for the classification of power quality disturbances using deep convolutional neural network. Appl. Energy 2019, 235, 1126–1140. [Google Scholar] [CrossRef]
- Gonzalez-Abreu, A.D.; Delgado-Prieto, M.; Osornio-Rios, R.A.; Saucedo-Dorantes, J.J.; Romero-Troncoso, R.D.J. A Novel Deep Learning-Based Diagnosis Method Applied to Power Quality Disturbances. Energies 2021, 14, 2839. [Google Scholar] [CrossRef]
- Liu, H.; Hussain, F.; Shen, Y.; Arif, S.; Nazir, A.; Abubakar, M. Complex power quality disturbances classification via curvelet transform and deep learning. Electr. Power Syst. Res. 2018, 163, 1–9. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, J.; Xiao, L.; Chen, K.; Wu, J. Classification of power quality disturbances via deep learning. IETE Tech. Rev. 2017, 34, 408–415. [Google Scholar] [CrossRef]
- Xiao, F.; Lu, T.; Wu, M.; Ai, Q. Maximal overlap discrete wavelet transform and deep learning for robust denoising and detection of power quality disturbance. IET Gener. Transm. Distrib. 2020, 14, 140–147. [Google Scholar] [CrossRef]
- Balouji, E.; Salor, O. Classification of power quality events using deep learning on event images. In Proceedings of the 2017 3rd International Conference on Pattern Recognition and Image Analysis (IPRIA), Shahrekord, Iran, 19–20 April 2017; pp. 216–221. [Google Scholar]
- Varga, E.D.; Beretka, S.F.; Noce, C.; Sapienza, G. Robust real-time load profile encoding and classification framework for efficient power systems operation. IEEE Trans. Power Syst. 2014, 30, 1897–1904. [Google Scholar] [CrossRef]
- Claessens, B.J.; Vrancx, P.; Ruelens, F. Convolutional neural networks for automatic state-time feature extraction in reinforcement learning applied to residential load control. IEEE Trans. Smart Grid 2016, 9, 3259–3269. [Google Scholar] [CrossRef]
- Liao, H.; Milanović, J.V.; Rodrigues, M.; Shenfield, A. Voltage sag estimation in sparsely monitored power systems based on deep learning and system area mapping. IEEE Trans. Power Deliv. 2018, 33, 3162–3172. [Google Scholar] [CrossRef]



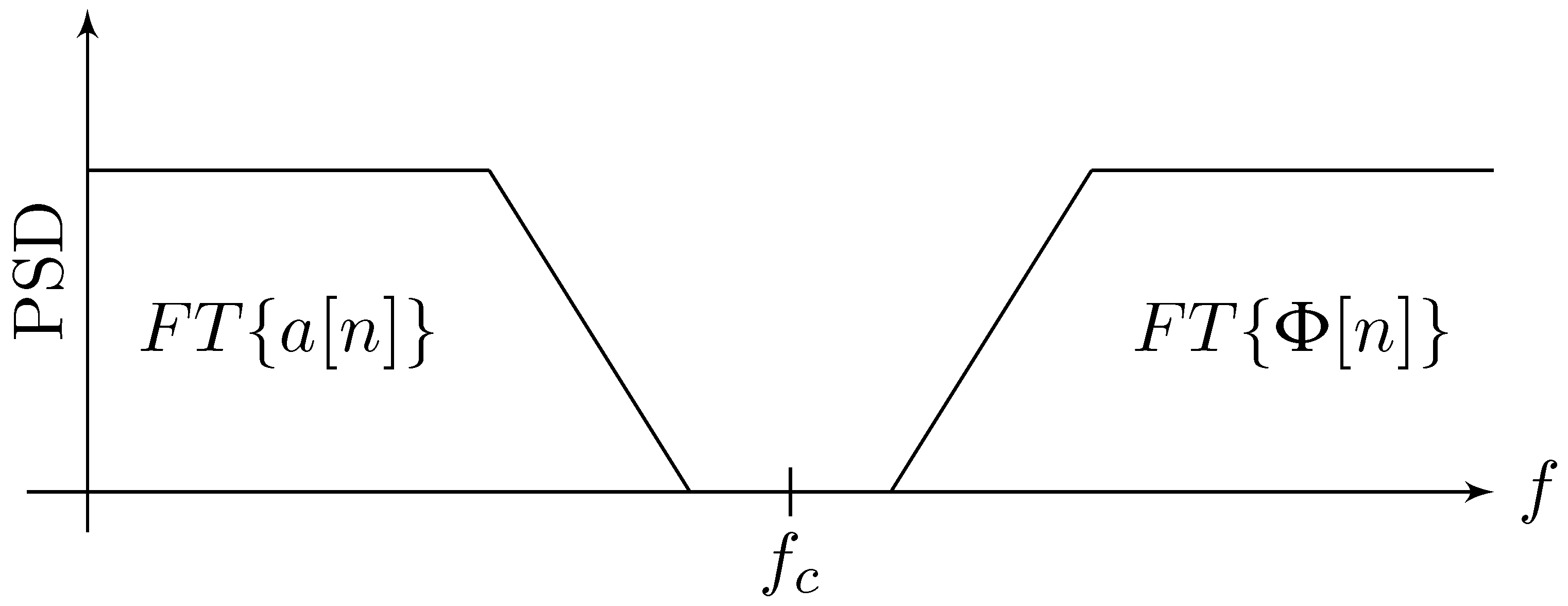
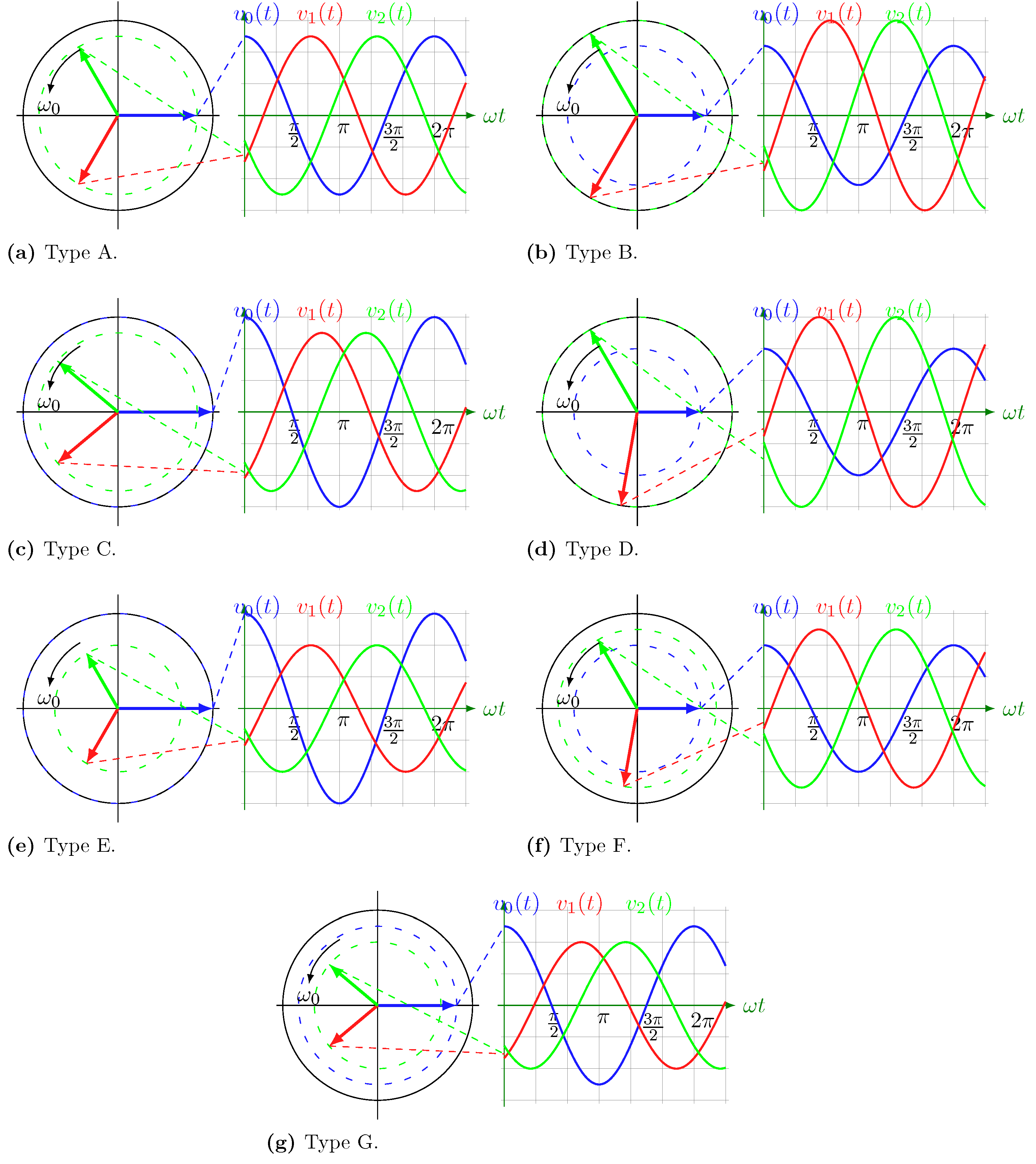

| Year | Ref. | Contributions |
|---|---|---|
| 2015 | [57] | This paper provides a comprehensive review of digital signal processing and machine learning techniques for automatic classification of power quality (PQ) events by investigating the effect of noise on these approaches’ performance. |
| 2017 | [58] | This paper reviews smart grid features and data issued from various energy resources and discusses techniques used for big data analysis in smart grid applications. |
| 2019 | [59] | This article provides a comprehensive review on digital signal processing (DSP) methods for fault detection and machine learning for fault classification and causes identification. The focus is to provide an overview of techniques used for automatic recognition of PQ events. Specifically, microgrid applications have been considered where the use of power electronic technology in renewable energy systems and distributed generators increases the risk of PQ issues. |
| [60] | This paper reviews machine learning and big data techniques for efficiently processing the massive data volume generated by Internet of Things (IoT) devices for reliable decision-making and ensuring the safety of both data and infrastructure against cyber attacks in a smart grid. | |
| 2020 | [61] | This paper presents failures in smart grid components (conventional energy systems, renewable resources, cables and transmission lines, power electronics and power transformers) and describes sensors, communication tools, including 5G, and monitoring infrastructure. Moreover, it discusses procedures associated with smart grids fault detection and location and provides an insight into lessons learned and future trends. |
| [62] | This paper reviews signal processing techniques and machine learning approaches used in the field of power quality disturbance detection and classification. | |
| [63] | This review paper highlights the interest of machine learning techniques for the efficient handling of a massive amount of data generated from smart meters and phasor measurement units in the next generation of power systems. | |
| [64] | This paper provides a critical review of approaches used for PQ disturbances detection and classification in the utility grid with renewable energy integration. It presents various concepts utilized for features extraction for detecting and classifying PQ disturbances in a noisy environment. |
| Category | Typical Causes | Main Consequences |
|---|---|---|
| Notching | Lightning strike, transformer energization, capacitor switching, disconnection of heavy loads, power electronic rectifiers commutation | Destruction of components and insulation materials, data processing error, electromagnetic interference, etc. |
| Voltage spikes | Lightning, switching of lines or power factor correction capacitors, disconnection of heavy loads | Destruction of components and of insulation materials, data processing errors or data loss, electromagnetic interference |
| Voltage flicker | Line, capacitor or load switching, frequent start/stop of electric motors and oscillating loads, arc furnace | Light flickering, unsteadiness of visual perception |
| Overvoltage | Switching large load, energizing a capacitor bank, incorrect tap settings on transformers | Light flicker, stoppage or damage of sensitive equipment |
| Harmonic | Nonlinear loads (variable speed drives, SMPS), data processing equipment, high efficiency lighting, arc furnaces, electric machines working above the knee of the magnetization curve | Transformers overheating, neutral overload, overheating of cables and equipment, loss of efficiency in electric machines, increased probability in the occurrence of resonance, electromagnetic interference with communication systems, errors in measures when using average reading meters, nuisance tripping of thermal protections. |
| Undervoltage | Switching on a large load or switching off a large capacitor bank | Light flicker, unsteadiness of visual perception |
| Voltage swell | Start or stop of heavy loads, badly dimensioned power sources and regulated transformers, system faults, load and capacitor switching | Light flicker, data loss, stoppage or damage of sensitive equipment |
| Voltage sag | Faulty consumer installations, faulty transmission or distribution electric network, start-up of large motors and connection of heavy loads | Malfunction of information technology equipment, tripping of contactors and electromechanical relays and loss of efficiency in electric rotating machines |
| Interruptions | Equipment failure in the power system network, tripping of protection devices, storms, human errors, failure of protection devices | Stoppage of all equipment |
| Type | Balanced or A | C, D, F and G | H and I | B and E |
|---|---|---|---|---|
| Proposed class |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elbouchikhi, E.; Zia, M.F.; Benbouzid, M.; El Hani, S. Overview of Signal Processing and Machine Learning for Smart Grid Condition Monitoring. Electronics 2021, 10, 2725. https://doi.org/10.3390/electronics10212725
Elbouchikhi E, Zia MF, Benbouzid M, El Hani S. Overview of Signal Processing and Machine Learning for Smart Grid Condition Monitoring. Electronics. 2021; 10(21):2725. https://doi.org/10.3390/electronics10212725
Chicago/Turabian StyleElbouchikhi, Elhoussin, Muhammad Fahad Zia, Mohamed Benbouzid, and Soumia El Hani. 2021. "Overview of Signal Processing and Machine Learning for Smart Grid Condition Monitoring" Electronics 10, no. 21: 2725. https://doi.org/10.3390/electronics10212725
APA StyleElbouchikhi, E., Zia, M. F., Benbouzid, M., & El Hani, S. (2021). Overview of Signal Processing and Machine Learning for Smart Grid Condition Monitoring. Electronics, 10(21), 2725. https://doi.org/10.3390/electronics10212725









