A Comprehensive Modeling of the Discrete and Dynamic Problem of Berth Allocation in Maritime Terminals
Abstract
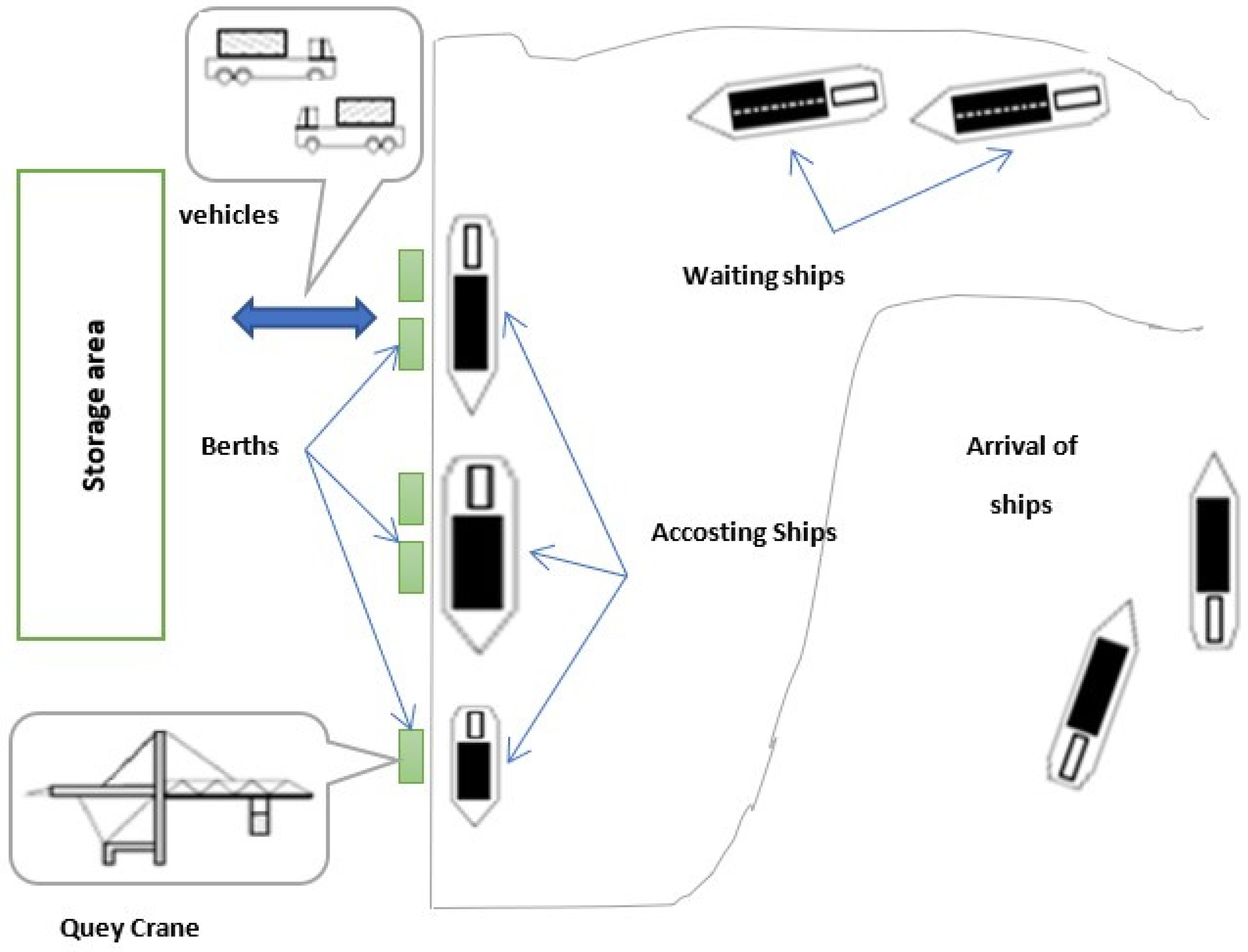
1. Presentation and Motivations for the Berth Allocation
- -
- The discrete and dynamic berth allocation problem is introduced and formulated as an integer linear problem with a set of constraints based on real world assumptions.
- -
- An efficient multi-agent system (MAS) is introduced to resolve the introduced DDBAP. The proposed multi-agent modeling is based on Multi-Agent-Systems-Engineering (O-MaSE), a modeling methodology dedicated for agent-based dynamic contexts and systems. O-MaSE relies on a set of specific diagrams which are detailed and explained for the context of the DDBAP.
- -
- The proposed multi-agent architecture is implemented and developed. Then, a set of experiments are achieved using the Jade multi-agent platform to assess the behavior of the proposed system with other heuristic methods such as the genetic algorithms.
2. Related Works
3. Mathematical Formulation of the DDBAP
- -
- i from 1 to I in B is the set of the available berths.
- -
- j from 1 to T in V is the set of the available ships.
- -
- k from 1 to T in O is the set of the available service orders.
- -
- Si is the time in which the location i becomes free and may be added to the schedule.
- -
- Aj the time of arrival of j.
- -
- Cij the needed time for handling the vessel j in the location i.
- -
- Xijk is equal to 1 if the vessel j is handled as the kth ship in the location i, 0 else.
- -
- Pk sub-set from O where Pk = {p|p < k € O}
- -
- Wi sub-set of ships such as Aj ≥ Si.
- -
- Yijk free time (from location i) separating the arrival of the kth ship from the departure of the (k − 1)th ship when the vessel j is served as the kth ship.
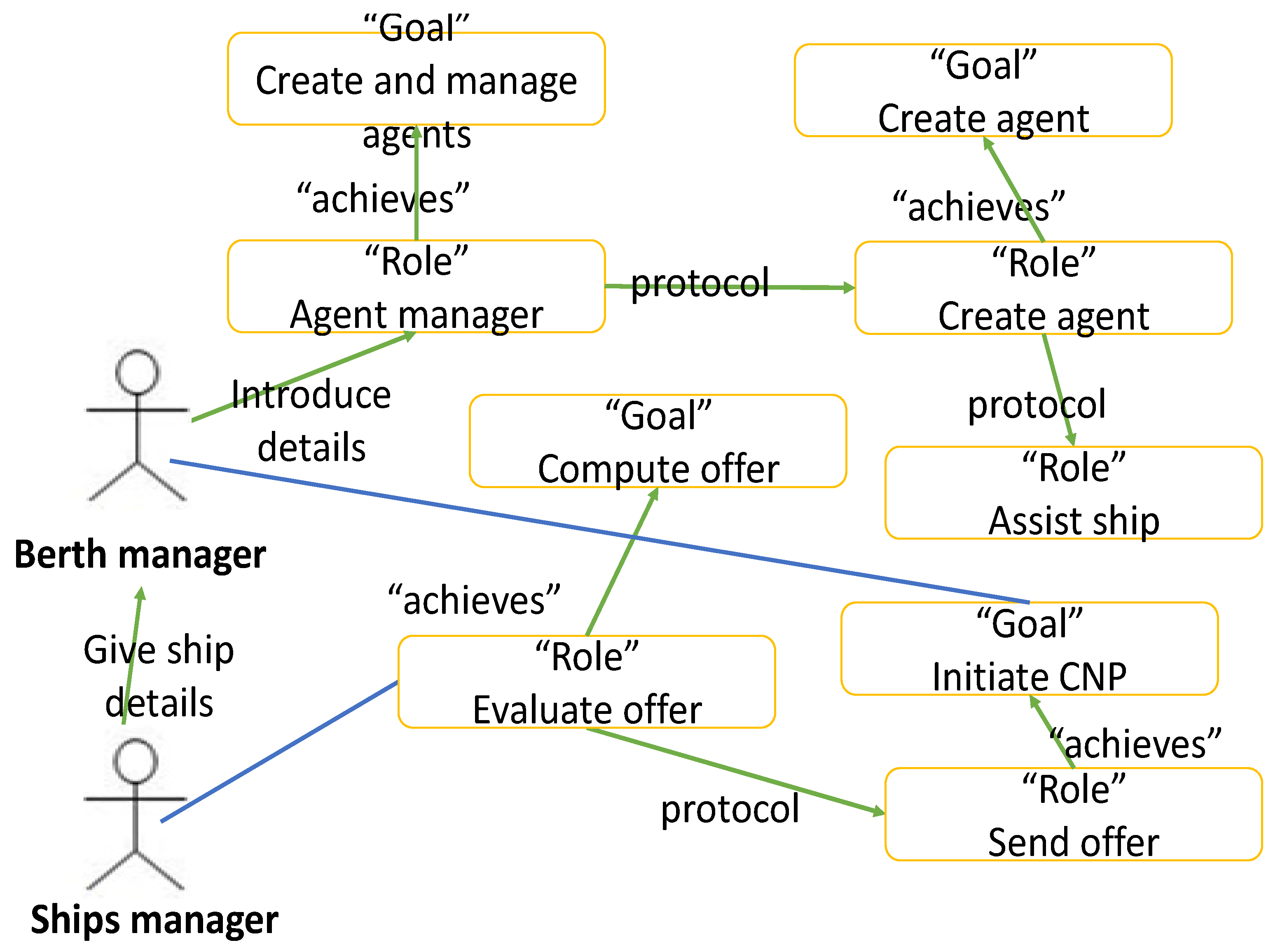
4. O-MaSE Modeling Methodology
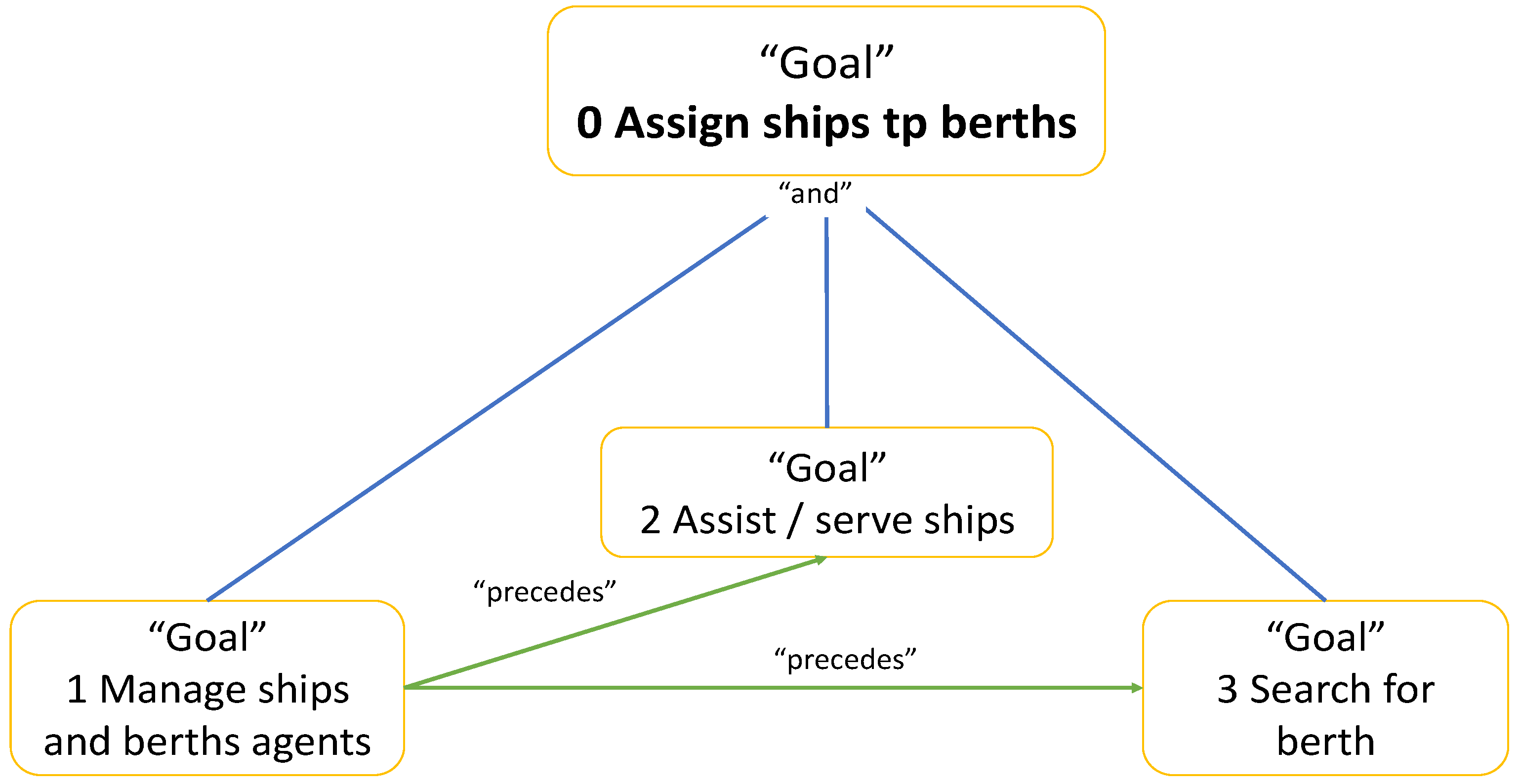
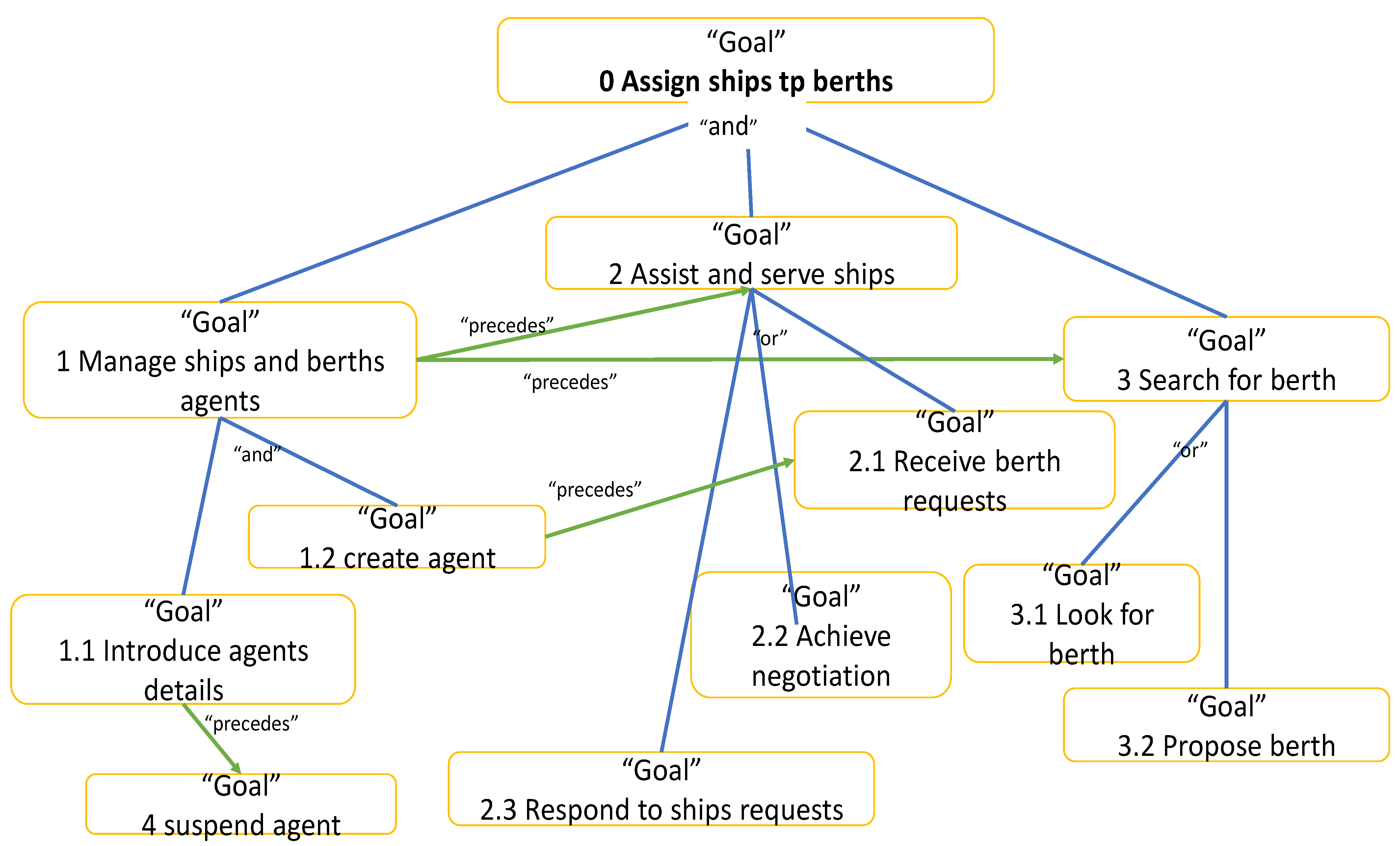
- The analysis phase: it is made up of the following three stages:
- -
- Identify goals: a “goal” is considered as an objective of the system. The goals are structured and organized according to their importance.
- -
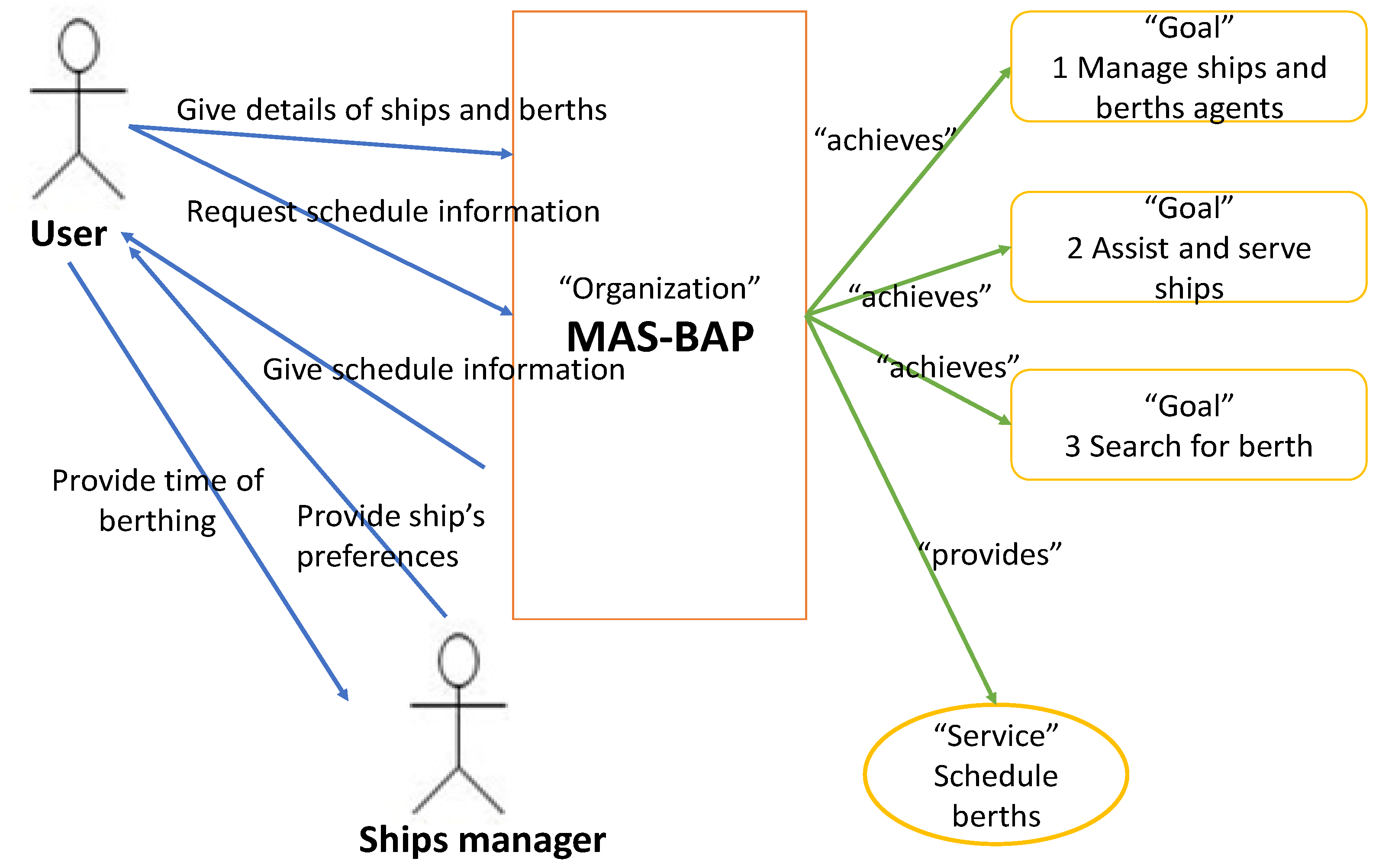
- Determine the desired behaviors of the system and describe the exchanged messages.
- -
- Define roles: each goal is transformed into a role and this role will be played by an agent.
- The design phase: composed of four stages:
- -
- Create agent’s classes: agent’s classes are identified from roles.
- -
- Build conversations: define protocols between agents.
- -
- Assemble the classes of agents: This step is concerned with the creation of internal classes of agents according to the chosen architectural model (Belief-Desire-Intention or others).
- -
- Define the structure of the system: this structure is presented by the O-MaSE deployment diagrams.
- The implementation phase: AgentTool facilitates the development of applications modeled by this methodology. It allows the verification, code generation, and reuse of components.
4.1. Analysis Phase
4.1.1. Goal Model
4.1.2. Organizational Model
4.1.3. Role-Model
4.2. The Design Phase
4.2.1. Agent Behaviors
4.2.2. Interactions and Communications between Agents
5. Experimental Results
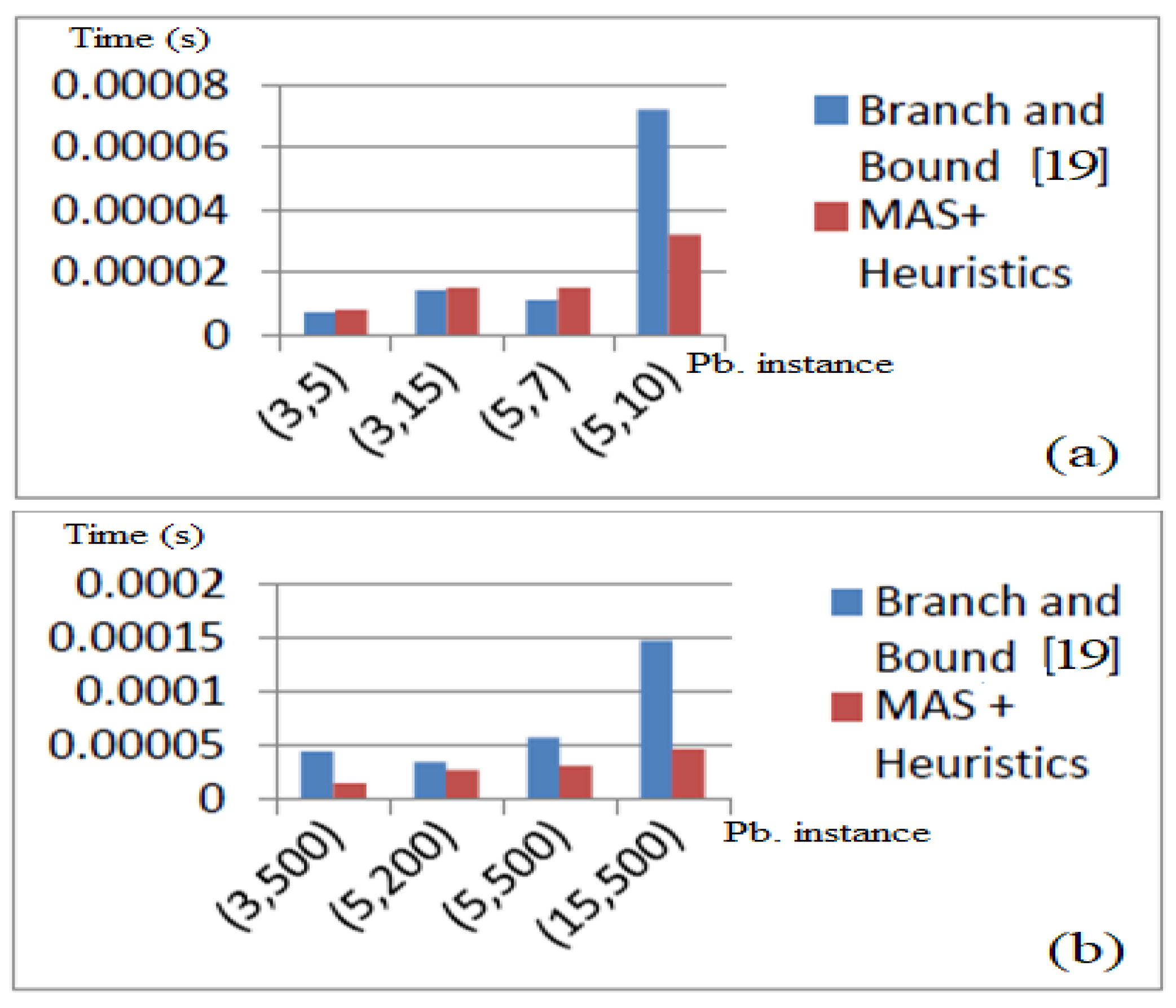
5.1. Comparison with Branch-and-Bound and Genetic Algorithm
5.1.1. Obtained Results for Small Size Instances of DellAmico and E. Mokotoff
5.1.2. Obtained Results for Big Size Instances of DellAmico and E. Mokotoff
5.1.3. Comparing with Adriana and Celso and the Genetic Algorithm
5.2. Performance Analysis of Genetic Algorithms
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giallombardo, G.; Moccia, L.; Salani, M.; Vacca, I. The tactical berth problem with quay crane assignment and transshipment-related quadratic yard costs. In Proceedings of the European Transport Conference (ETC), Noordwijkerhout, The Netherlands, 6 October 2008. [Google Scholar]
- Wang, F.; Lim, A. A stochastic beam search for the berth allocation problem. Decis. Support Syst. 2007, 42, 2186–2196. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Laporte, G.; Legato, P.; Moccia, L. Models and Tabu Search Heuristics for the Berth Allocation Problem. J. Transp. Sci. 2005, 39, 526–538. [Google Scholar] [CrossRef]
- Mnasri, S.; Zidi, K. A heuristic approach based on the multi-agents negotiation for the resolution of the DDBAP. In Proceedings of the 4th International Conference on Metaheuristics and Nature Inspired Computing, Sousse, Tunisia, 27–31 October 2012. [Google Scholar]
- Nasri, N.; Mnasri, S.; Val, T. 3D node deployment strategies prediction in wireless sensors network. Int. J. Electron. 2019, 107, 808–838. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Kan, R.; Brucker, A.H.G. Complexity of machine scheduling problems. Ann. Discret. Math. 1997, 1, 343–362. [Google Scholar]
- Hassanat, A.B.; Alkasassbeh, M.; Al-Awadi, M.; Alhasanat, E.A. Colour-based lips segmentation method using artificial neural networks. In Proceedings of the 2015 6th International Conference on Information and Communication Systems (ICICS), Amman, Jordan, 7–9 April 2015; pp. 188–193. [Google Scholar] [CrossRef]
- Hassanat, A.B.A. Furthest-Pair-Based Decision Trees: Experimental Results on Big Data Classification. Informations 2018, 9, 284. [Google Scholar] [CrossRef]
- Cahyono, R.T.; Flonk, E.J.; Jayawardhana, B. Discrete-Event Systems Modeling and the Model Predictive Allocation Algorithm for Integrated Berth and Quay Crane Allocation. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1321–1331. [Google Scholar] [CrossRef]
- Lassoued, R.; Elloumi, A. The discrete and dynamic berth allocation problem in bulk port. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1976–1980. [Google Scholar] [CrossRef]
- Arram, A.; Nazri, M.Z.A.; Ayob, M.; Abunadi, A. Bird mating optimizer for discrete berth allocation problem. In Proceedings of the 2015 International Conference on Electrical Engineering and Informatics (ICEEI), Denpasar, Indonesia, 10–11 August 2015; pp. 450–455. [Google Scholar] [CrossRef]
- Schepler, X.; Absi, N.; Feillet, D.; Sanlaville, E. The stochastic discrete berth allocation problem. EURO J. Transp. Logist. 2019, 8, 363–396. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Models for continuous berth allocation and quay crane assignment: Computational comparison. In Proceedings of the 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 10–13 December 2017; pp. 374–378. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y. A dynamic continuous berth allocation method based on genetic algorithm. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017; pp. 770–773. [Google Scholar] [CrossRef]
- Nourmohammadzadeh, A.; Voß, S. A robust multiobjective model for the integrated berth and quay crane scheduling problem at seaside container terminals. Ann. Math. Artif. Intell. 2021, 1–23. [Google Scholar] [CrossRef]
- Kasm, O.A.; Diabat, A.; Cheng, T.C.E. The integrated berth allocation, quay crane assignment and scheduling problem: Mathematical formulations and a case study. Ann. Oper. Res. 2020, 291, 435–461. [Google Scholar] [CrossRef]
- Atencio, F.N.; Casseres, D.M. A comparative analysis of metaheuristics for berth allocation in bulk ports: A real world application. IFAC PapersOnLine 2018, 51, 1281–1286. [Google Scholar] [CrossRef]
- Li, Y.; Chu, F.; Zheng, F.; Liu, M. A Bi-Objective Optimization for Integrated Berth Allocation and Quay Crane Assignment with Preventive Maintenance Activities. IEEE Trans. Intell. Transp. Syst. 2020, 1–18. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C. An expanded robust optimisation approach for the berth allocation problem considering uncertain operation time. Omega 2021, 103, 102444. [Google Scholar] [CrossRef]
- Liu, B.; Li, Z.-C.; Sheng, D.; Wang, Y. Integrated planning of berth allocation and vessel sequencing in a seaport with one-way navigation channel. Transp. Res. Part B Methodol. 2021, 143, 23–47. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C. An almost robust optimization model for integrated berth allocation and quay crane assignment problem. Omega 2021, 104, 102455. [Google Scholar] [CrossRef]
- Thanos, E.; Toffolo, T.; Santos, H.G.; Vancroonenburg, W.; Berghe, G.V. The tactical berth allocation problem with time-variant specific quay crane assignments. Comput. Ind. Eng. 2021, 155, 107168. [Google Scholar] [CrossRef]
- Guo, L.; Wang, J.; Zheng, J. Berth allocation problem with uncertain vessel handling times considering weather conditions. Comput. Ind. Eng. 2021, 158, 107417. [Google Scholar] [CrossRef]
- Bacalhau, E.T.; Casacio, L.; de Azevedo, A.T. New hybrid genetic algorithms to solve dynamic berth allocation problem. Expert Syst. Appl. 2021, 167, 114198. [Google Scholar] [CrossRef]
- Jiménez, P.; Gómez-Fuster, J.M.; Pavón-Mariño, P. HADES: A Multi-Agent Platform to Reduce Congestion Anchoring Based on Temporal Coordination of Vessel Arrivals—Application to the Multi-Client Liquid Bulk Terminal in the Port of Cartagena (Spain). Appl. Sci. 2021, 11, 3109. [Google Scholar] [CrossRef]
- Dkhil, H.; Diarrassouba, I.; Benmansour, S.; Yassine, A. Modelling and solving a berth allocation problem in an automotive transshipment terminal. J. Oper. Res. Soc. 2021, 72, 580–593. [Google Scholar] [CrossRef]
- Cervellera, C.; Gaggero, M.; Maccio, D. Policy Optimization for Berth Allocation Problems. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, W.; Ji, M.; Zhu, H. Multi-Period Coordinated Optimization on Berth Allocation and Yard Assignment in Container Terminals Based on Truck Route. IEEE Access 2021, 9, 83124–83136. [Google Scholar] [CrossRef]
- DeLoach, S.A.; Garcia-Ojeda, J.C. O-MaSE: A customisable approach to designing and building complex, adaptive multi-agent systems. Int. J. Agent Oriented Softw. Eng. 2010, 4, 244–280. [Google Scholar] [CrossRef]
- Official Site of AgentTools AT3. Available online: http://agenttool.cis.ksu.edu/ (accessed on 9 May 2021).
- Dell’Amico, M.; Martello, S. A note on exact algorithms for the identical parallel machine scheduling problem. Eur. J. Oper. Res. 2005, 160, 576–578. [Google Scholar] [CrossRef][Green Version]
- Mokotoff, E. An exact algorithm for the identical parallel machine scheduling problem. Eur. J. Oper. Res. 2004, 152, 758–769. [Google Scholar] [CrossRef]
- Akinnuwesi, B.A.; Yama, O.B.; Rahman, A.M.; Fashoto, S.G. Berth Allocation Model for Container Terminal using Genetic Algorithm Technique: Case of Apapa Wharf, Lagos, Nigeria. J. Comput. Sci. Appl. 2021, 28, 1. [Google Scholar] [CrossRef]
- Alvim, A.C.F.; Ribeiro, C.C. A Hybrid Heuristic for Bin-Packing and Multiprocessor Scheduling. J. Heuristics 2010. [Google Scholar] [CrossRef]
- Mnasri, S.; Nasri, N.; Val, T. The Deployment in the Wireless Sensor Networks: Methodologies, Recent Works and Applications. In Proceedings of the International Conference on Performance Evaluation and Modeling in Wired and Wireless Networks (PEMWN-2014), Sousse, Tunisia, 4–7 November 2014. [Google Scholar]






| Type of Berth Problem | Author/Year | Used Approach | Considered Objective(s) | Deductions/Discussion of the Study |
|---|---|---|---|---|
| Discrete problem | Cahyono et al., 2020 [9] | Dynamic predictive scheduling using Monte Carlo algorithm. | Minimization of total service time (standby time + handling time). | (+) Dataset from a real terminal (Tanjung Priuk, Jakarta) is used. (+) A dynamic formulation of the berthing process is proposed. |
| Lassoued et al., 2019 [10] | Mathematical model was introduced then solved by CPLEX. | Minimization of the global time of service of the vessels. | Resolution of the dynamic berth allocation problem in bulk ports. | |
| Arram et al., 2015 [11] | A bio-inspired Bird mating algorithm (BMO). | Minimization of the global waiting and processing time of the vessels. | The waiting time indicates the relevance of ships. The performance of the BMO algorithm is compared with other optimizers. | |
| Schepler et al., 2019 [12] | Probabilistic optimization based on Dynamic programming and Iterated tabu search. | Minimization of the global weighted flow-time. | Instances from the literature were used to evaluate the algorithms. Obtained results indicate the adaptability of the introduced algorithm to both reactive and proactive phases regarding the needed computation times. | |
| Continuous problem | Iris et al., 2017 [13] | Integer linear programming | Identifying berthing positions in partitioned continuous berth. Identifying berthing start and end time. Determining quay cranes for ships | (+) The state-of-the-art methods are investigated for the dynamic and the continuous berth allocation and quay crane problem. (−) A larger benchmark for the problem should be used. |
| Chen et al., 2017 [14] | Genetic Algorithms | Minimizing the penalty cost. | The distance of deviation from the reference point of berth and the delay of leaving time are considered in the modeled problem. | |
| Nourmohammadzadeh et al., 2020 [15] | Pareto Simulated Annealing (PSA) and a multi-Objective Simulated Annealing (MOSA) algorithm | Minimization of the deviations from target locations. Minimization of the departure delays of the vessels. | The introduced PSA and MOSA algorithm outperform other traditional methods (tests achieved using exact solver and with ϵ-constraint). | |
| Simultaneous berth and quay crane allocation problem | Abou kasm et al., 2019 [16] | Optimization modeling | Minimize the needed time for handling of the containers. | Three terminal problems are integrated and simultaneously resolved: the quay crane scheduling problem (QCSP), the quay crane assignment problem (QCAP), and the berth allocation problem (BAP). Real experimental tests were achieved on the terminal of Abu Dhabi. |
| Atencio et al., 2018 [17] | genetic algorithm, and colony optimization and simulated annealing. | Minimization of the total penalty cost. | Experimental tests were achieved on a real case in bulk ports, and using additional instances. | |
| Chu et al., 2020 [18] | ϵ-constraint based two-phase iterative algorithm. | Minimization of the global turnaround time of ships. Minimization of the global penalty cost of maintenance of the quay cranes. | Additional constraints are considered, such as the preventive activities of maintenance. Small size and large size instances of the problem are considered. |
| Mokotoff | Dell’Amico | Multi-Agent Approach (Our System) | Genetic Algorithm [33] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M | n | Time (In Seconds) | Non-Resolved Instances | Time (In Seconds) | Non-Resolved Instances | Time (In Seconds) | Non-Resolved Instances | Time (in Seconds) | Non-Resolved Instances |
| 3 | 20 | 0.12 | 0 | 0.000014 | 0 | 0.000015 | 0 | 0.00491 | 0 |
| 3 | 50 | 0.10 | 0 | 0.000017 | 0 | 0.000013 | 0 | 0.00582 | 0 |
| 3 | 100 | 0.22 | 0 | 0.000013 | 0 | 0.0000124 | 0 | 0.00611 | 0 |
| 3 | 200 | 0.12 | 0 | 0.000020 | 0 | 0.000014 | 0 | 0.00638 | 0 |
| 5 | 20 | 0.57 | 0 | 0.000753 | 0 | 0.00042 | 0 | 0.00518 | 0 |
| 5 | 50 | 0.35 | 0 | 0.000021 | 0 | 0.000019 | 0 | 0.00542 | 0 |
| 5 | 100 | 0.67 | 0 | 0.000026 | 0 | 0.000022 | 0 | 0.00566 | 0 |
| 5 | 200 | 1.23 | 0 | 0.000034 | 0 | 0.000027 | 0 | 0.00597 | 0 |
| 15 | 20 | 0.01 | 0 | 0.000004 | 0 | 0.000025 | 0 | 0.00643 | 0 |
| 15 | 50 | 864.47 | 2 | 0.000062 | 0 | 0.000039 | 0 | 0.00681 | 0 |
| 15 | 100 | 329.66 | 0 | 0.000059 | 0 | 0.000037 | 0 | 0.00729 | 0 |
| 15 | 200 | 348.79 | 0 | 0.000104 | 0 | 0.000041 | 0 | 0.00783 | 0 |
| 100 | 200 | 2042.08 | 0 | 0.058836 | 0 | 0.00078 | 0 | 0.00852 | 0 |
| Pi | M | n | Genetic Algorithm | Tabu Search (Adriana and Celso) | Multi-Agent Approach (Our System) |
|---|---|---|---|---|---|
| 1–1000 | 5 | 100 | 0.00985 | 0.01 | 0.000022 |
| 1–10,000 | 5 | 10 | 0.00368 | 0.22 | 0.000036 |
| 1–10,000 | 5 | 50 | 0.00492 | 0.15 | 0.000019 |
| 1–10,000 | 5 | 100 | 0.00643 | 0.01 | 0.000022 |
| Nbr of Generations | 10 | 30 | 70 | 100 | 150 | |
|---|---|---|---|---|---|---|
| Population size | 20 | 95.09 | 95.01 | 94.39 | 92.28 | 89.13 |
| 50 | 93.42 | 93.39 | 93.16 | 91.16 | 86.22 | |
| 100 | 81.28 | 81.12 | 80.72 | 78.71 | 76.16 | |
| 200 | 73.31 | 73.34 | 72.28 | 70.14 | 68.01 | |
| 500 | 44.46 | 43.17 | 41.17 | 40.28 | 37.74 | |
| 700 | 42.42 | 42.19 | 40.74 | 38.24 | 35.97 | |
| 1000 | 39.39 | 37.21 | 35.15 | 33.59 | 29.45 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mnasri, S.; Alrashidi, M. A Comprehensive Modeling of the Discrete and Dynamic Problem of Berth Allocation in Maritime Terminals. Electronics 2021, 10, 2684. https://doi.org/10.3390/electronics10212684
Mnasri S, Alrashidi M. A Comprehensive Modeling of the Discrete and Dynamic Problem of Berth Allocation in Maritime Terminals. Electronics. 2021; 10(21):2684. https://doi.org/10.3390/electronics10212684
Chicago/Turabian StyleMnasri, Sami, and Malek Alrashidi. 2021. "A Comprehensive Modeling of the Discrete and Dynamic Problem of Berth Allocation in Maritime Terminals" Electronics 10, no. 21: 2684. https://doi.org/10.3390/electronics10212684
APA StyleMnasri, S., & Alrashidi, M. (2021). A Comprehensive Modeling of the Discrete and Dynamic Problem of Berth Allocation in Maritime Terminals. Electronics, 10(21), 2684. https://doi.org/10.3390/electronics10212684







