Optimization of UAV-Aided Millimeter-Wave IoT Systems

Abstract

Due to their maneuverability, unmanned aerial vehicles (UAVs) have grown into a promising enabler of the Internet of Things (IoTs). In addition to the benefits of the bandwidth and communication quality of millimeter-wave (mmWave) systems, a UAV-aided mmWave multiple-input and multiple-output (MIMO) communication system is investigated in this paper for the data collection of IoT systems, in which single-antenna IoT devices are divided into several clusters, and the UAV aided mmWave base station (UAV-BS) collects data from each cluster using the time division scheme. The joint optimization of the beam selection, UAV trajectory, user clustering, power allocation and transmission duration is studied in this paper to improve the data collection efficiency. The solution of the problem is then given in three steps. Firstly, the incremental K-means clustering and ant colony optimization algorithm are utilized to handle the UAV trajectory planning and user clustering problem. Secondly, an incremental beam selection scheme is employed to ensure that all the devices in each cluster can communicate with the UAV. Thirdly, an iterative algorithm is proposed by alternately optimizing the power allocation and transmission duration of the IoT devices. Finally, the simulation results demonstrate the effectiveness of the proposed solution for the UAV-aided mmWave communication system.

1. Introduction

Unmanned aerial vehicles (UAVs) have been investigated in a wide range of applications, such as security monitoring, smart agriculture, aerial photography and cargo delivery [1]. UAV-assisted wireless communication has attracted a great deal of attention due to its mobility, flexibility and low cost and the high probability of establishing line of sight (LoS) air-to-ground communication links [2]. UAVs, which have been involved in mainly three applications of wireless communication—aerial relays, data collection and seamless coverage—can significantly assist the existing terrestrial communications to obtain better performance [3]. In particular, one of the leading challenges in the Internet of Things (IoT) is to achieve efficient data collection from massive IoT devices. The employment of UAVs can effectively enhance the coverage of IoT devices and significantly reduce the overhead [4].

Aiming to improve the efficiency of UAV-assisted data collection, several works have been proposed to optimize the UAV trajectory and the communication systems. By properly adjusting the placement or trajectory design of the UAV, the communication distances between the UAV and ground devices can be greatly decreased, and hence better channel gain can be obtained [5]. In [6], the data collection time allocation, energy transfer and UAV trajectory planning were jointly optimized to minimize the average age of information for the data collection, where the UAV was utilized to transfer energy and collect data from the ground devices. In [7], the UAV was employed as an aerial relay to minimize the average peak age of information by jointly optimizing the UAV trajectory, energy allocation and service time allocation. In [8], a multiantenna UAV was utilized to collect data from a cluster of IoT devices, in which both large-scale fading and small-scale fading were considered. The transmitting power and duration were jointly optimized to maximize the data collection efficiency. Besides, the distances between the UAV and the ground devices could be adjusted by employing user clustering, which was mainly dependent on the coverage of the UAV and improved the performance of the wireless communication system. In [9], the authors established a mathematical model of LoS probability and pointed out that the LoS probability was dependent on the covering radius, the UAV flying height and the type of environment parameter including suburban, urban, dense urban and high-rise urban. In [10], the UAV placement problem was formulated as a circle deployment problem to maximize the number of covered users with minimum transmitting power. In [11], a successive deployment method and a K-means clustering-based deployment method were proposed to place multiple UAVs in order to cover a maximal number of users in a target area.

The previous works mainly focused on the deployment and trajectory optimization of a UAV which was widely equipped with a single antenna and mainly worked in the microwave frequencies. Recently, millimeter-wave (mmWave) multiple-input multiple-output (MIMO) communication has been introduced into the UAV, since the small wavelength of mmWave enables antenna arrays to be packed in a small space [12,13]. However, mmWave systems have to face the challenge of propagation associated with mmWave frequencies, since the transmission at high frequencies will result in severe attenuation [14]. UAV-aided mmWave communication systems can combat the path-loss of mmWave systems through the beamforming of antenna arrays and also the mobility of UAV [15], and these systems have many other advantages, such as sufficient spectrum resources, seamless coverage and improved energy efficiency [16]. A 3D beamforming scheme for a UAV mmWave communication system was proposed to achieve efficient and flexible coverage in [17], where the phased uniform planar array was adopted. Besides, the joint optimization of UAV deployment and constant modulus analog beamforming of a mmWave base station (BS) was studied to maximize the sum rate of all users [18].

However, large numbers of radio frequency (RF) chains were employed in the previous UAV mmWave communication systems, which resulted in a high energy consumption and would further reduce the efficiency of the systems, especially when the transmitting power is limited at the UAV. In order to decrease the required RF chains, an effective solution is the beamspace MIMO. By utilizing the lens antenna array, the traditional channel can be transformed to the beamspace channel, and in this way, each beam only contains the signal from a specific direction [19]. Beamspace MIMO can reduce the number of RF chains, since the beamspace channel in UAV mmWave communication systems is sparse. Signal power is mainly focused on a small part of beams that are selected for transmission, and then the RF chains are attached to the selected beams [20]. Consequently, beamspace MIMO was introduced into UAV mmWave communication systems to reduce the number of RF chains without significant performance loss [21].

Furthermore, the IoT network is a fast-growing technology due to its wide range of applications [22]. In [23], a trust model based on a non-zero-sum game approach for clustered WSN (CWSN) security was proposed to maximize the data trustworthiness of transmission. In [24], game theory was adopted in the security issues of an IoT network. A game-theoretic protection approach was proposed to detect malicious sensor nodes. In [25], a modified Stackelberg game approach was proposed to reduce the required number of IoT nodes involved in achieving the trustworthiness of data. In particular, IoT devices suffer from weaknesses such as the security and data trustworthiness aspects, low processing capabilities and limited power [26]. Considering the limited energy of IoT devices, the transmission strategy should also be properly designed to achieve high data collection efficiency for IoT applications [8].

Motivated by the existing research, a UAV-aided mmWave communication system for data collection in the IoT is considered in this paper, where the UAV-aided BS (UAV-BS) is equipped with multiple antennas and operates in mmWave frequencies. The UAV-BS hovers at a fixed height to collect data from several clusters of ground IoT devices in a time-division scheme. In the proposed UAV-BS, the lens array is adopted by the UAV-BS to perform the receiver beamforming. As a result, the sparse beamspace MIMO channel is formed, and the parts of the beams containing the most signal power for ground devices are near LoS paths. Meanwhile, the UAV trajectory is optimized to obtain better channels. Consequently, we formulate a joint optimization problem of UAV trajectory planning, user clustering, beam selection, power allocation and transmission duration to maximize the data collection efficiency, subject to the practical energy constraints of IoT devices. As the problem is nonconvex and the variables are coupling with each other, it is challenging to directly address the problem.

To tackle the proposed complex problem, we decompose it into three subproblems. The first is to attain the optimal beams given the optimal UAV trajectory. The last problem is the joint allocation of power and transmission duration to maximize the data collection efficiency. For the first subproblem, an incremental K-means clustering algorithm and the ant colony optimization (ACO) algorithm are utilized to solve the problem. For the second subproblem, an incremental beam selection algorithm is proposed by incrementally maximizing the sum rate of the mmWave UAV system. The beams that make the highest contribution to the sum rate are selected by the UAV-BS. For the third subproblem, an iterative algorithm is proposed, and the power allocation and transmission duration allocation is optimized in an iterative way. The main contributions of this paper are summarized as follows:

• With the UAV trajectory obtained by the incremental K-means clustering and ACO algorithm, an incremental beam selection algorithm for the UAV-BS is proposed to maximize the sum rate of the IoT devices. Zero forcing (ZF) beamforming is utilized to eliminate the interference between IoT devices.
• Based on the obtained UAV trajectory, user clusters and the selected beams, the allocations of the transmitting power and transmission duration of the UAV-BS are optimized by alternately optimizing the power allocation and transmission duration, aiming to maximize the data collection efficiency of the UAV-aided mmWave communication systems.
• The sum-rate performance of the proposed incremental beam selection scheme and the iterative algorithm are investigated. Simulation results demonstrate the effectiveness of the proposed incremental beam selection scheme and the iterative algorithm.

The symbol notation is summarized in Table 1.

Table 1. Symbol Notation.

Symbol	Defination
a	Scalar variable
a	Vector
A	Matrix
$\mathbb{C}$	Complex number field
$|·|$	Absolute value
$\parallel ·\parallel$	Euclidean norm
${(·)}^{\mathrm{T}}$	Transpose
${(·)}^{\mathrm{H}}$	Hermitian transpose
${(·)}^{-1}$	inverse
${\left[A\right]}_{i,j}$	ith row and jth column elements of A
$\mathcal{A}\setminus \mathcal{B}$	The set consisting of all elements in $\mathcal{A}$ excluding those in $\mathcal{B}$

The rest of the paper is organized as follows. In Section 2, we present the system model to formulate the optimization problem. In Section 3, the data collection efficiency of the mmWave UAV communication is optimized. Section 4 shows the simulation results and discussion. Finally, Section 5 provides a summary of the main contributions of the study.

2. System Model

2.1. Transmission Model

As shown in Figure 1, we consider a mmWave uplink communication system consisting of K IoT devices and a rotary-wing UAV-BS. Each IoT device is equipped with a single antenna. The UAV-BS is equipped with $N_r$ antennas to improve the data collection efficiency. All the devices are divided into N orthogonal clusters. The number of devices in the nth cluster is denoted as $M_n,n=1,2,\dots ,N$. The N clusters are scheduled under a time-division regime. The UAV-BS utilizes $L_n,n=1,2,\dots ,N$ RF chains to achieve data collection from IoT devices in cluster n. In particular, $L_n\le N_r$. Furthermore, the UAV-BS adopts the fly-hover protocol [27] to collect data from the devices. Specially, for this fly-hover communication protocol, the UAV-BS successively visits the N hovering locations and communicates with the devices when it is hovering at the optimized locations. Since the UAV-BS has limited on-board energy, the energy for hovering is restrained. Thus, the communication duration between the UAV-BS and the devices is restricted by total transmission duration T. The adjustable transmission duration for cluster n is defined as ${\tau }_n$, and ${\tau }_n$ should satisfy the following constraints:

$$\begin{array}{c}\hfill \sum _{n=1}^N{\tau }_n\le T.\end{array}$$

(1)

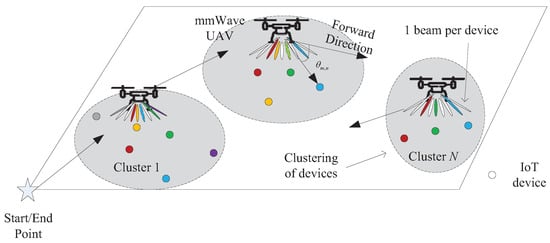
Figure 1. The proposed UAV-aided mmWave MIMO communication system.

Since the energy of each device is also restrained, the transmitting power $p_{m,n}$ of the mth device in cluster n should satisfy

$$\begin{array}{c}\hfill 0\le p_{m,n}\le P_{\max }^{m,n},\forall m,n,\end{array}$$

(2)

$$\begin{array}{c}\hfill p_{m,n}{\tau }_n\le E_{\max }^{m,n},\forall m,n,\end{array}$$

(3)

where $P_{\max }^{m,n}$ denotes the peak transmitting power of the mth device in cluster n, and $E_{\max }^{m,n}$ is the total energy of the mth device in cluster n. In particular, due to the limited energy, the total serving time T for UAV is relatively short. We assume that $p_{m,n}$ is constant during the transmission duration ${\tau }_n$.

Furthermore, for cluster n, the budget power $P_{\mathrm{budget}}^n$ and the budget transmission duration ${\tau }_{\mathrm{budget}}^n$ are adopted to fit the dynamically changing amount of data [8]. If the amount of the data is not very large, the budget power and budget transmission duration should be relatively small. Otherwise, ${\tau }_{\mathrm{budget}}^n$ and $P_{\mathrm{budget}}^n$ are set to be large for data transmission. Then, the following constrains can be derived:

$$\begin{array}{c}\hfill \sum _{m=1}^M{p}_{m,n}\le P_{\mathrm{budget}}^n,\forall n,\end{array}$$

(4)

$$\begin{array}{c}\hfill {\tau }_n\le {\tau }_{\mathrm{budget}}^n,\forall n.\end{array}$$

(5)

Without loss of generality, we consider a 3D Cartesian coordinate, and thereby the horizontal coordinates of the mth device in cluster n are defined as ${\mathit{u}}_{m,n}={[x_{m,n},y_{m,n}]}^T$. We consider that the UAV is flying at a fixed height $H_U$. The coordinates of the UAV projected on the ground for cluster n can be defined as ${\mathit{q}}_n={[q_{x,n},q_{y,n}]}^T$. Thus, the distance between the mth device in cluster n and the UAV is given by

$$\begin{array}{c}\hfill d_{m,n}=\sqrt{H_U^2+{\parallel {\mathit{q}}_n-{\mathit{u}}_{m,n}\parallel }^2}.\end{array}$$

(6)

2.2. Channel Model

The channels between the devices and the UAV-BS are mmWave channels. Taking the limitation of scattering in mmWave frequency into account [17], we assume that the air-to-ground links between the UAV-BS and the devices are dominated by line-of-sight (LoS) channels. Thus, the large-scale path loss between the UAV-BS and the mth device in cluster n can be expressed as [14,28]

$$\begin{array}{c}\hfill L_{m,n}^{\mathrm{LoS}}=32.4+20{log}_{10}\left(f_{mm}\right)+20{log}_{10}\left(d_{m,n}\right),\end{array}$$

(7)

where $f_{mm}$ is the carrier frequency in gigahertz, and $d_{m,n}$ is the distance in meters. Consequently, the gain of the LoS path from the mth device in the cluster n to the UAV-BS can be derived as

$$\begin{array}{c}\hfill {\beta }_{m,n}={10}^{-L_{m,n}^{\mathrm{LoS}}/10}.\end{array}$$

(8)

Then, the channel vector between the UAV-BS and the mth device in the nth cluster can be modeled as [29]

$$\begin{array}{c}\hfill {\mathit{h}}_{m,n}={\beta }_{m,n}\mathit{a}\left({\theta }_{m,n}\right),\end{array}$$

(9)

where $\mathit{a}\left({\theta }_{m,n}\right)\in {\mathbb{C}}^{N_r\times 1}$ is the array steering vector of the mth device in cluster n. We adopt a uniform linear array (ULA) in the mmWave UAV-BS, and the array steering vector for the mth device in cluster n is expressed as

$$\begin{array}{cc}\hfill \mathit{a}\left({\theta }_{m,n}\right)=& [1,e^{\mathsf{j}2\pi \frac{d}{\lambda }{\theta }_{m,n}},e^{\mathsf{j}2\pi \frac{d}{\lambda }2{\theta }_{m,n}},\hfill \\ \hfill & \dots ,e^{\mathsf{j}2\pi \frac{d}{\lambda }(N_r-1){\theta }_{m,n}}{]}^T,\hfill \end{array}$$

(10)

where $\lambda$ is the signal wavelength, and d is the antenna spacing satisfying $d=\lambda /2$. In addition, ${\theta }_{m,n}$ is the steering angle defined as ${\theta }_{m,n}=cos\left({\varphi }_{m,n}\right)$, where ${\varphi }_{m,n}$ represents the real angle of arrival of the mth device in cluster n. In particular, in this article, ${\theta }_{m,n}$ is defined as the cosine value of the direction value between the mth device in cluster n and the forward direction of the UAV [18]. The forward direction of the UAV is dependent on the next location of the UAV and is defined as ${\mathit{q}}_n^f={[q_{x,n+1}-q_{x,n},q_{y,n+1}-q_{y,n},0]}^T$. Thus, ${\theta }_{m,n}$ can be expressed as

$$\begin{array}{cc}\hfill {\theta }_{m,n}& =\frac{([x_{m,n},y_{m,n},0]-[q_{x,n},q_{y,n},H_U])·{\mathit{q}}_n^f}{\parallel {\left[x_{m,n}{y}_{m,n}0\right]}^{\mathrm{T}}-{\left[q_n^x{q}_n^y{H}_U\right]}^{\mathrm{T}}\parallel ·\parallel {\mathit{q}}_n^f\parallel }.\hfill \end{array}$$

(11)

The received signal at UAV-BS for cluster n is given by

$$\begin{array}{cc}\hfill {\mathit{y}}_n& ={\mathit{H}}_n{\mathit{s}}_n+{\mathit{n}}_n\hfill \\ \hfill & =\sum _{m=1}^M{\mathit{h}}_{m,n}{s}_{m,n}+{\mathit{n}}_n,\hfill \end{array}$$

(12)

where ${\mathit{H}}_n\in {\mathbb{C}}^{N_r\times M_n}$ is channel matrix for cluster n. ${\mathit{s}}_n\in {\mathbb{C}}^{M_n\times 1}$ is the signal vector for $M_n$ devices in cluster n, and $s_{m,n}$ is the transmitted signal of device m in cluster n with $E\left(\right|s_{m,n}{|}^2)=p_{m,n}$. ${\mathit{n}}_n\in {\mathbb{C}}^{N_r\times 1}$ is the additive white Gaussian noise (AWGN), and each entry of ${\mathit{n}}_n$ has the distribution $\mathcal{CN}(0,{\sigma }^2)$.

2.3. Beamspace Communication

Beamspace MIMO architecture adopts a lens antenna array as the analog beamforming module. By employing the lens antenna array, the signals are transformed into the beam domain or angular domain, and in this way, each beam only contains the signal from a specific direction [20]. Mathematically, the lens antenna array operates a spatial discrete Fourier transform (DFT) matrix $\mathit{U}$ to the antenna domain signals. The DFT matrix $\mathit{U}$ consists of the steering vectors for $N_r$ fixed spatial frequencies/angles with uniform spacing, and thereby the DFT matrix $\mathit{U}$ is defined as

$$\begin{array}{cc}\hfill & \mathit{U}=\frac{1}{\sqrt{N_r}}\left[\mathit{u}\left({\psi }_1\right),\mathit{u}\left({\psi }_2\right),\dots ,\mathit{u}\left({\psi }_{N_r}\right)\right],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & \mathit{u}\left({\psi }_i\right)={[1,e^{-j2\pi {\psi }_i},\dots ,e^{-j2\pi {\psi }_i(N_r-1)}]}^T,\hfill \end{array}$$

(14)

where ${\psi }_i=\frac{i}{N_r}$ and $i=0,1,\dots ,N_r-1$, are the predefined uniform spacings. Thus, $N_r$ candidate beams could be selected by each cluster of devices. In order to avoid multiple selections of the same beams for different users, we assume $M_n\le N_r$.The beamforming matrix $\mathit{U}\in {\mathbb{C}}^{N_r\times N_r}$ makes $N_r$ orthogonal spatial beams form the basis of the spatial signal space. $\mathit{U}$ is unitary and satisfies $\mathit{U}{\mathit{U}}^H={\mathit{U}}^H\mathit{U}=\mathit{I}$.

Then, the signal after receiving spatial discrete DFT can be expressed as

$$\begin{array}{cc}\hfill {\mathit{y}}_n^b=& {\mathit{H}}_n^b{\mathit{s}}_n+{\mathit{n}}_{n,b}\hfill \\ \hfill =& {\mathit{U}}^T{\mathit{H}}_n{\mathit{s}}_n+{\mathit{U}}^T{\mathit{n}}_n,\hfill \end{array}$$

(15)

where $n_b\in {\mathbb{C}}^{N_r\times 1}$ is the beamspace noise vector for cluster n. $H_n^b\in {\mathbb{C}}^{N_r\times M}$ is the beamspace channel matrix for cluster n and also can be expressed as

$$\begin{array}{cc}\hfill {\mathit{H}}_n^b& =\left[{\mathit{h}}_{1,n}^b,{\mathit{h}}_{2,n}^b,\dots ,{\mathit{h}}_{M,n}^b\right]\hfill \\ \hfill & =\left[{\mathit{U}}^T{\mathit{h}}_{1,n},{\mathit{U}}^T{\mathit{h}}_{2,n,}\dots ,{\mathit{U}}^T{\mathit{h}}_{M,n}\right],\hfill \end{array}$$

(16)

where ${\mathit{h}}_{m,n}^b\in {\mathbb{C}}^{N_r\times 1}$ is the beamspace channel of the mth device in cluster n.

Due to the sparse nature of the beamspace channel [30], each device has only a few dominant entries of the beamspace channel. As a result, a small number of beams can be chosen to reduce the dimension of the UAV mmWave communication system without significant performance loss. Let ${\mathit{A}}_n^L\in {\mathbb{C}}^{L_n\times N_r}$ denote the beam selection matrix; thus, the received signal can be rewritten as

$$\begin{array}{cc}\hfill {\mathit{y}}_n^B=& {\mathit{A}}_n^L{\mathit{y}}_n^b\hfill \\ \hfill =& {\mathit{A}}_n^L{\mathit{U}}^T{\mathit{H}}_n{\mathit{s}}_n+{\mathit{A}}_L{\mathit{U}}^T{\mathit{n}}_n\hfill \\ \hfill =& {\widehat{\mathit{H}}}_n{\mathit{s}}_n+{\mathit{A}}_L{\mathit{U}}^T{\mathit{n}}_n,\hfill \end{array}$$

(17)

where ${\mathit{A}}_n^L=[{\mathit{e}}_{i_{1,n}};{\mathit{e}}_{i_{2,n}};\dots ;{\mathit{e}}_{i_{L,n}}]$, and ${\mathit{e}}_{i_{l,n}}\in {\mathbb{C}}^{1\times N_r},1\le l\le L_n$ represents the $i_l$th row of the $N_r$-dimensional identity matrix $I_{N_r}$ for the cluster n. ${\widehat{\mathit{H}}}_n$ is the reduced beamspace channel matrix.

2.4. Digital Beamforming

In order to detect users’ uplink signals, ZF beamforming is adopted to eliminate multiuser interference. According to the criterion of ZF, the received digital beamforming matrix for the nth cluster consists of the pseudo inverse of ${\widehat{\mathit{H}}}_n$, which is given by

$$\begin{array}{c}\hfill {\mathit{W}}_n={\left({\widehat{\mathit{H}}}_n^H{\widehat{\mathit{H}}}_n\right)}^{-1}{\widehat{\mathit{H}}}_n^H.\end{array}$$

(18)

After the ZF beamforming process, the detected signal at the receiver can be written as

$$\begin{array}{cc}\hfill {\tilde{\mathit{y}}}_n& ={\mathit{W}}_n{\mathit{y}}_n^B\hfill \\ \hfill & ={\left({\widehat{\mathit{H}}}_n^H{\widehat{\mathit{H}}}_n\right)}^{-1}{\widehat{\mathit{H}}}_n^H{\mathit{y}}_n^B\hfill \\ \hfill & ={\mathit{s}}_n+{\left({\widehat{\mathit{H}}}_n^H{\widehat{\mathit{H}}}_n\right)}^{-1}{\widehat{\mathit{H}}}_n^H{\mathit{n}}_n.\hfill \end{array}$$

(19)

2.5. Problem Formulation

Based on (19), the uplink sum rate of the UAV mmWave communication system can be expressed as

$$\begin{array}{c}\hfill R_n=\sum _{m=1}^{M_n}{log}_2(1+{\gamma }_{m,n}),\end{array}$$

(20)

where ${\gamma }_{m,n}$ is the signal-to-interference-plus-noise ratio (SINR) of the mth device in cluster n, which is given by [31]

$$\begin{array}{c}\hfill {\gamma }_{m,n}=\frac{p_{m,n}}{{\sigma }^2{\left[{\left({\widehat{\mathit{H}}}_n^H{\widehat{\mathit{H}}}_n\right)}^{-1}\right]}_{m,m}}.\end{array}$$

(21)

On the basis of (20) and (21), it is obvious that the SINR of the mth device in cluster n is dependent on the reduced beamspace channel ${\widehat{\mathit{H}}}_n$ and the transmitting power $p_{m,n}$ of the mth device in cluster n. With the aim of achieving the maximal data collection efficiency, an immediate and basic problem is finding the best UAV trajectory. The clustering method is also quite important for the maximization of the data collection efficiency of the UAV mmWave communication system. Moreover, according to (17), we can know that the reduced beamspace channel is involved with beam selection. Thus, each device needs to select appropriate beams to maximize the data collection efficiency.

To maximize the data collection efficiency, we also need to take account of the UAV-BS transmission duration constraint, the peak transmitting power and the energy limitation of each device, as well as the budget power and budget transmission duration constraints of each cluster. Thus, the problem can be formulated as

$$\begin{array}{cc}\hfill \underset{\left\{{\mathit{q}}_n\right\},\left\{{\tau }_n\right\},\left\{{\mathit{A}}_n^L\right\},\left\{p_{m,n}\right\}}{max}& \sum _{n=1}^N{\tau }_n{R}_n\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \sum _{n=1}^N{\tau }_n\le T,\hfill \end{array}$$

(22b)

$$\begin{array}{cc}\hfill & 0\le {\tau }_n\le {\tau }_{\mathrm{budget}}^n,\forall n,\hfill \end{array}$$

(22c)

$$\begin{array}{cc}\hfill & 0\le p_{m,n}\le P_{\max }^{m,n},\forall m,n,\hfill \end{array}$$

(22d)

$$\begin{array}{cc}\hfill & p_{m,n}{\tau }_n\le E_{\max }^{m,n},\forall m,n,\hfill \end{array}$$

(22e)

$$\begin{array}{cc}\hfill & \sum _{m=1}^M{p}_{m,n}\le P_{\mathrm{budget}}^n,\forall n.\hfill \end{array}$$

(22f)

Based on the above, in order to maximize the data collection efficiency, the UAV would collect a large amount of data from the devices with a high sum rate, whereas a small amount would be collected from others.The above problem is nonconvex [32] and challenging, not only due to the complicated objective function with an expectation operator but also due to the fact that the variables to be optimized are coupled with each other.

3. Solution of the Problem

It is difficult to directly solve the problem in (22) because of the coupling variables and the nonconvex objective function and constraint (22e). Motivated by the “divide and conquer” concept, the original problem is tackled in three steps. First, since the UAV trajectory is entangled with the clustering strategy, by introducing the K means clustering algorithm and ACO algorithm, the UAV trajectory and the user clustering can be determined. Secondly, giving the trajectory of the UAV and the user clustering, a beam selection scheme is proposed to determine the selected beam set. After finding the optimal trajectory of the UAV, user clustering and the selected beam set, the coupled transmitting power and transmission duration can be solved in an iterative way.

3.1. Solution of the UAV Trajectory and User Clustering

Our proposed solution is to use a K-means clustering algorithm to partition the K devices into N subsets that represent N coverage areas of the UAV-BS. If the UAV-BS is assigned to service a subset, it will position itself in the subset centroid and serve up to $N_r$ devices inside of that subset. This is because the maximal $N_r$ beams can be utilized to serve devices. In order to avoid multiuser interference, each beam can be selected by a single device, namely $L_n=M_n$. Then, the UAV successively visits N hovering locations, and the trajectory planning of the UAV can be solved by the ACO algorithm.

In this paper, we assume the wireless links between the UAV and the devices are dominated by LoS. According to [9], it has been demonstrated that the UAV altitude $H_U$ and the coverage radius $R^{\mathrm{cov}}$ determine the LoS probability. Meanwhile, the LoS probability is also dependent on the environment condition. In particular, in suburban areas, given a fixed UAV altitude $H_U$, when the maximal coverage radius of the UAV $R_{\max }^{\mathrm{cov}}\approx H_U/tan\left(0.52\right)$, the wireless channels in the coverage area are dominated by the LoS.

We assume that the locations of K devices before clustering are defined as ${\mathit{u}}_k={[x_k,y_k]}^T,1\le k\le K$. In the K-means clustering algorithm, the partition criterion is based on a sum-of-squared-error criterion [11], which can be expressed as

$$\begin{array}{c}\hfill e=\sum _{n=1}^N\sum _{k=1}^K{u}_{k,n}\parallel {\mathit{u}}_k-{\mathit{q}}_n\parallel ,\end{array}$$

(23)

where $u_{k,n}\in 0,1$ is a binary variable, denoting whether the kth device belongs to the nth cluster. $u_{k,n}=1$ means that the kth device belongs to the nth cluster, and we define ${\mathit{u}}_{m,n}={\mathit{u}}_k,1\le m\le M_n$. When $u_{k,n}=0$, the kth device will not be assigned to the cluster n. ${\mathit{q}}_n$ is the center location of the nth cluster, denoting the UAV location in cluster n. In particular, the center location of a certain cluster is calculated by all devices in that cluster, which is given by

$$\begin{array}{cc}\hfill {\mathit{q}}_n& ={[q_{x,n},q_{y,n}]}^T\hfill \\ \hfill & =\frac{1}{M_n}{[\sum _{m=1}^{M_n}{x}_{m,n},\sum _{m=1}^{M_n}{y}_{m,n}]}^T\hfill \\ \hfill & =\frac{1}{M_n}{[\sum _{k=1}^K{u}_{k,n}{x}_k,\sum _{k=1}^K{u}_{k,n}{y}_k]}^T,\hfill \end{array}$$

(24)

where $n=1,2,\dots ,N$. Hence, we utilize the K-means clustering algorithm to partition the devices and determine the UAV locations. Since the K-means clustering algorithm assumes that the number of clusters is known, we determine the cluster number in an incremental way. We first start with a minimum cluster number $K=1$. Then, we increase the number of N until both constraints of the maximum UAV coverage area and the maximal number of devices that the UAV can serve at the same time are satisfied. The proposed solution of the UAV trajectory and user clustering with an incremental K-means clustering algorithm is summarized in Algorithm  1.

Algorithm 1 The proposed solution of the UAV trajectory and user clustering with an incremental K-means clustering algorithm.

Require: ${\mathit{u}}_k$,for $1\le k\le K$, $R_{\max }^{\mathrm{cov}}$, $N_r$

Ensure: N, ${\mathit{q}}_n$, ${\mathit{u}}_{m,n}$,for $1\le m\le M_n$ and $1\le n\le N$

1: Initialization: initial clustering number $N_{}=1$.

2: Repeat

3: Randomly select $N_{ini}$ points in the target area as the center points ${\mathit{q}}_n,1\le n\le N_{ini}$.

4:   Repeat

5:   Calculate the Euclidean distance between each device and any center of cluster.

6:    if $\parallel {\mathit{u}}_k-{\mathit{q}}_n\parallel <\parallel {\mathit{u}}_k-{\mathit{q}}_j\parallel$ $1\le k\le K,1\le n\le N_{ini},j\ne n$

7:     ${\mathit{u}}_{m,n}={\mathit{u}}_k$, the kth device is allocated in the cluster n

8:      end if

9:   Recalculate the center of the clusters based on (24)

10:    Until none of the ${\mathit{q}}_m$ is updated.

11: Calculate the maximal distance $r_{\max }$ between the devices and the its cluster center, and count the amount of devices in each cluster $M_n$.

12:  if $r_{\max }\le R_{\max }^{\mathrm{cov}}$ and $M_n\le N_r$

13:     $N=N_{ini}$

14:    break

15:  else

16:     $N_{ini}=N_{ini}+1$

17:  end if

In order to collect data from each cluster, these N clusters are scheduled under multiple access time division. UAV trajectory planning is performed to utilize the minimum energy required for visiting N clusters. Since a UAV’s flying energy consumption is dependent on the flying distance, the UAV trajectory planning can be transformed into finding the shortest route to visit N clusters in turn. Therefore, the UAV trajectory problem is a classic traveling salesperson problem, which can be solved by the ACO algorithm [33].

3.2. Incremental Beam Selection Scheme

Owing to the sparse structure of the beamspace channel, the beamspace channel for the mth device in the cluster n has dominant beams, and the number of RF chains can be reduced [34]. Given the UAV position of the nth cluster ${\mathit{q}}_{\mathit{n}}$ and the transmitting power of the mth device in cluster n, the beamspace channel ${\mathit{H}}_n^b$ and the sum rate are known. The proposed beam selection scheme selects the beams whose contribution is the best in terms of the sum rate. With the aim of minimizing the number of RF chains $L_n$ of cluster n, we assume that each device is served by only one beam, and thereby $L_n=M_n$. The number of candidate beams is $N_r$, and the indices of the beams which are selected by the devices in the nth cluster are stored in beam set ${\mathcal{L}}_n$.

Based o (18)–(21), we can select the required beams for the devices in the nth cluster one by one based on the incremental beam selection algorithm, which identifies the beams with the maximal gains in terms of sum rate. This incremental beam selection algorithm is summarized in Algorithm 2.

Algorithm 2 Proposed incremental beam selection scheme.

Require: ${\mathit{H}}_n^b$

Ensure${\mathit{A}}_n^L$

1: ${\mathcal{L}}_n=\varnothing$

2: ${\mathcal{L}}_n^R=\{1,2,\dots ,N_t\}$

3: for $j^{\prime }=1\to M_n$

4:   $j=\{1,2,\dots ,M_n\}\left(j^{\prime }\right)$

5:   for $i^{\prime }=1\to N_t$

6:     $i=\{1,2,\dots ,N_t\}\left(i^{\prime }\right)$

7:     ${\mathit{C}}_n^{\left(i\right)}={\mathit{H}}_n^b{(a,:)}_{a\in ({\mathcal{L}}_n\cup i)}$

8:     ${\mathit{F}}_n^{\left(i\right)}={\left({\left({\mathit{C}}_n^{\left(i\right)}\right)}^{\mathrm{H}}{\mathit{C}}_n^{\left(i\right)}\right)}^{-1}$

9:     for $ii=1:j^{\prime }$

10:    $\alpha \left(ii\right)={log}_2(1+\frac{p_{ii,n}}{{\sigma }^2{\left[{\mathit{F}}_n^{\left(i\right)}\right]}_{ii,ii}})$

11:    end

12:    $R^{\left(i\right)}={\sum }_{ii=1}^{j^{\prime }}\alpha \left(ii\right)$

13:  end

14:   $i_j^{★}=arg\underset{\forall i}{max}{R}^{\left(i\right)}$

15:   ${\mathcal{L}}_n={\mathcal{L}}_n\cup i_j^{★}$

16:   ${\mathcal{L}}_n^R\leftarrow {\mathcal{L}}_n^R\setminus i_j^{★}$

17: end

18: ${\mathit{A}}_n^L=[{\mathit{e}}_{i_{1,n}};{\mathit{e}}_{i_{2,n}};\dots ;{\mathit{e}}_{i_{L,n}}],i_l\in {\mathcal{L}}_n$

3.3. Iterative Solution

Given the UAV positions ${\mathit{q}}_n$ and the beam selection scheme, the main problem of tackling the optimization problem (22) is the coupling relationship between the transmission duration ${\tau }_n$ and the transmitting power $p_{m,n}$. To solve this problem effectively, we recast it into two subproblems. One is power allocation for a given transmission duration, and the other is allocating the transmission duration given the transmitting power $p_{m,n}$. The two subproblems are solved alternately. Finally, the proposed iterative optimization algorithm is summarized.

3.3.1. Power Allocation

For a given transmission duration ${\tau }_n^{t-1}$, the power allocation problem can be expressed as

$$\begin{array}{cc}\hfill \underset{\left\{p_{m,n}\right\}}{max}& R_n\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& 0\le p_{m,n}\le P_{\max }^{m,n},\forall m,n,\hfill \\ \hfill & p_{m,n}{\tau }_n^{t-1}\le E_{\max }^{m,n}\forall m,n,\hfill \\ \hfill & \sum _{m=1}^M{p}_{m,n}\le P_{\mathrm{budget}}^n,\forall n.\hfill \end{array}$$

(25)

where $t\ge 1$ represents the number of iterations. The optimization problem (25) is greatly simplified. According to (20)–(21), the achievable rate of the mth device in cluster n is given by

$$\begin{array}{c}\hfill R_{m,n}={log}_2(1+\frac{p_{m,n}}{{\sigma }^2{\left[{\left({\widehat{\mathit{H}}}_n^H{\widehat{\mathit{H}}}_n\right)}^{-1}\right]}_{m,m}}).\end{array}$$

(26)

It is easy to observe that

$$\begin{array}{c}\hfill \frac{d^2{R}_{m,n}}{d{p}_{m,n}^2}<0.\end{array}$$

(27)

Consequently, $R_{m,n}$ is concave with respect to $p_{m,n}$. The constraint is also convex with respect to $p_{m,n}$. Therefore, the problem (25) is a convex optimization problem which can be solved by CVX effectively.

3.3.2. Transmission Duration Allocation

With the power allocation $p_{m,n}^{t-1}$ obtained by solving (25), the transmission duration optimization can be formulated as

$$\begin{array}{cc}\hfill \underset{\left\{{\tau }_n\right\}}{max}& \sum _{n=1}^N{\tau }_n{R}_n\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \sum _{n=1}^N{\tau }_n\le T,\hfill \\ \hfill & 0\le {\tau }_n\le {\tau }_{\mathrm{budget}}^n,\forall n,\hfill \\ \hfill & p_{m,n}^{t-1}{\tau }_n\le E_{\max }^{m,n}\forall m,n.\hfill \end{array}$$

(28)

It is easy to see that the objective function and constraints are both convex. Thus, the problem (28) is a convex optimization problem. In order to efficiently solve the optimization problem (28), the communication duration T should be considered in three cases. The first one is $T\le {\tau }_1$; the second one is ${\tau }_1<T\le {\sum }_{n=1}^{\widehat{N}}{\tau }_{\widehat{N}},2\le \widehat{N}<N$; the third one is $T\ge {\sum }_{n=1}^N$. If T is not large enough to complete the communication mission of all clusters, the cluster with the highest sum rate will be served as a priority. As a result, the clusters are reordered according to

$$\begin{array}{c}\hfill R_1\ge R_2\ge \dots \ge R_N.\end{array}$$

(29)

For the first case, $T\le {\tau }_1$, which also can be written as

$$\begin{array}{c}\hfill T\le min\{\frac{E_{\max }^{1,1}}{p_{1,1}^{t-1}},\frac{E_{\max }^{2,1}}{p_{2,1}^{t-1}},\dots ,\frac{E_{\max }^{M_n,1}}{p_{M_n,1}^{t-1}},{\tau }_{\mathrm{budget}}^1\}.\end{array}$$

(30)

Thereby, the optimal solution of optimization problem (28) is given by

$$\begin{array}{cc}\hfill & {\tau }_1=T,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & {\tau }_n=0,1<n\le N.\hfill \end{array}$$

(32)

For the second case, ${\tau }_1<T<{\sum }_{n=1}^{\widehat{N}}{\tau }_{\widehat{N}},2\le \widehat{N}<N$ can be rewritten as

$$\begin{array}{c}\hfill T>min\{\frac{E_{\max }^{1,1}}{p_{1,1}^{t-1}},\frac{E_{\max }^{2,1}}{p_{2,1}^{t-1}},\dots ,\frac{E_{\max }^{M_n,1}}{p_{M_n,1}^{t-1}},{\tau }_{\mathrm{budget}}^1\},\end{array}$$

(33)

$$\begin{array}{c}\hfill T<\sum _{n=1}^{\widehat{N}}min\{\frac{E_{\max }^{1,n}}{p_{1,n}^{t-1}},\frac{E_{\max }^{2,n}}{p_{2,n}^{t-1}},\dots ,\frac{E_{\max }^{M_n,n}}{p_{M_n,n}^{t-1}},{\tau }_{\mathrm{budget}}^n\}.\end{array}$$

(34)

The optimal solution of (28) can be written as

$$\begin{array}{cc}\hfill {\tau }_n& =min\{\frac{E_{\max }^{1,n}}{p_{1,n}^{t-1}},\frac{E_{\max }^{2,n}}{p_{2,n}^{t-1}},\dots ,\frac{E_{\max }^{M_n,n}}{p_{M_n,n}^{t-1}},{\tau }_{\mathrm{budget}}^n\},\hfill \\ \hfill & 1\le n\le \widehat{N}-1,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\tau }_{\widehat{N}}& =T-min\{\frac{E_{\max }^{1,\widehat{N}}}{p_{1,\widehat{N}}^{t-1}},\frac{E_{\max }^{2,\widehat{N}}}{p_{2,\widehat{N}}^{t-1}},\dots ,\frac{E_{\max }^{M_n,\widehat{N}}}{p_{M_n,\widehat{N}}^{t-1}},{\tau }_{\mathrm{budget}}^{\widehat{N}}\},\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill {\tau }_n& =0,\widehat{N}\le n\le N.\hfill \end{array}$$

(37)

For the third case, $T\ge {\sum }_{n=1}^N$ can be rewritten as

$$\begin{array}{c}\hfill T\ge \sum _{n=1}^{N}min\{\frac{E_{\max }^{1,n}}{p_{1,n}^{t-1}},\frac{E_{\max }^{2,n}}{p_{2,n}^{t-1}},\dots ,\frac{E_{\max }^{M_n,n}}{p_{M_n,n}^{t-1}},{\tau }_{\mathrm{budget}}^n\}.\end{array}$$

(38)

The optimized solution of optimization problem (28) is shown as

$$\begin{array}{cc}\hfill {\tau }_n& =min\{\frac{E_{\max }^{1,n}}{p_{1,n}^{t-1}},\frac{E_{\max }^{2,n}}{p_{2,n}^{t-1}},\dots ,\frac{E_{\max }^{M_n,n}}{p_{M_n,n}^{t-1}},{\tau }_{\mathrm{budget}}^n\},\hfill \\ \hfill & 1\le n\le N.\hfill \end{array}$$

(39)

Based on the above discussion, an iterative algorithm is proposed to alternately solve the optimization problems (25) and (28), as summarized in Algorithm 3.

Algorithm 3 Iterative algorithm

1: Initialization: ${\tau }_0=T/N$, for $1\le n\le N$, $t=1$.

2: Repeat

3:  $\left\{{\tau }_n^{t-1}\right\}$, solve problem (25) to obtain the optimal solution $\left\{p_{m,n}^t\right\}$.

4:   For $\left\{p_{m,n}^t\right\}$, solve problem (28) with the consideration of three cases to obtain the optimal solution denoted as $\left\{{\tau }_n^t\right\}$.

5:  Update:$t=t+1$.

6: Until The increase of the ${\sum }_{n=1}^N{\tau }_n{R}_n$ is less than a threshold $\epsilon >0$, or the maximal number of iterations is reached.

It is clear that the achievable data collection efficiency increases with the increased number of iterations, which can be shown as

$$\begin{array}{c}\hfill \sum _{n=1}^N{\tau }_n^t{R}_n\left(p_{m,n}^t\right)\ge \sum _{n=1}^N{\tau }_n^{t-1}{R}_n\left(p_{m,n}^{t-1}\right).\end{array}$$

(40)

Thus, Algorithm 3 exhibits convergence.

4. Performance Analysis

In this section, we evaluate the performance of the proposed algorithm. We consider that a UAV visits N clusters in turn and collects data in a mmWave system. The terrestrial devices are randomly distributed in the square area of ${[0,500]}^T\times {[0,500]}^T$ (m${}^2$), and the UAV flies right above the coverage area. The UAV flying trajectory starts from ${\mathit{q}}_I={[0,0]}^T$ and ends at the same point. The CPU of our computer was Intel i9, and the RAM was 16 GB. The main default parameters of this simulated UAV mmWave communication system are listed in Table 2.

Table 2. Default System Parameters.

Parameter	Value
Coverage area	$[0,500]\times [0,500]$ m${}^2$
Start point of UAV	$[0,0]$
End point of UAV	$[0,0]$
Number of receive antennas at UAV $N_r$	16
AWGN ${\sigma }^2$	−94 dBm
Frequency $f_{m,m}$	28 GHz
Peak transmitting power $P_{\max }^{m,n},\forall m,n$	300 mW
Budget power $P_{\mathrm{budget}}^n,\forall n$	500 mW

Figure 2 depicts the optimized UAV trajectory and the square UAV trajectory, both with the aid of the proposed incremental beam selection scheme and the iterative algorithm. The number of devices is $K=20$. All the devices are divided into $N=4$ clusters. Each cluster has an unequal number of devices. The total communication duration T is set as $T=200$ s, and the budget transmission duration $T_{\mathrm{budget}}^n,\forall n$ is $T_{\mathrm{budget}}^n=100$ s. The total energy constraint of each device $E_{\max }^{m,n},\forall m,n$ is equal to 4 J. The UAV flies at a fixed height of $H_U=100$ m. Figure 2a shows the optimized UAV trajectory and the corresponding clustered devices, while Figure 2b shows the square UAV trajectory and the devices in each cluster. Specifically, the data collection efficiency of the optimized UAV trajectory is about 1764 bits/Hz higher than that achieved by the square UAV trajectory.

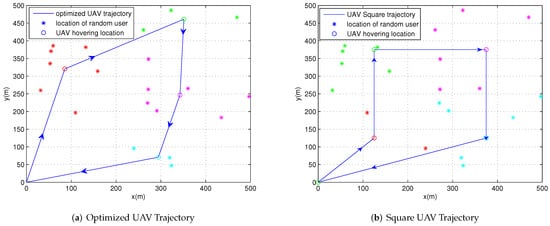
Figure 2. Comparison of the optimized UAV trajectory and the square UAV trajectory, both with the aid of the incremental beam selection and the iterative algorithm.

Figure 3 depicts the data collection efficiency as the function of the total energy constraint of each device for the proposed optimized UAV trajectory, in comparison with the performance attained by the square UAV trajectory. The both trajectories are aided by the incremental beam selection and iterative algorithm. The system has $K=20$, $N=4$, $T=200$ s, $T_{\mathrm{budget}}^n=100$ s, and $H_U=100$ m. As expected, the optimized UAV trajectory outperforms the square UAV trajectory. In particular, for the system with $E_{\max }^{m,n}=8\mathrm{J},\forall m,n$, the data collection efficiency attained by the proposed optimized approach is about 2868 bits/Hz higher than that of the square UAV trajectory.

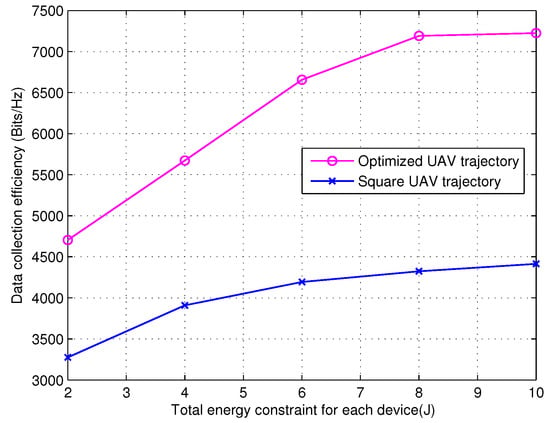
Figure 3. Comparison of data collection efficiency versus total energy constraint of each device for the optimized trajectory and square deployment, both with the aid of the incremental beam selection and iterative algorithm.

In Figure 4, we investigate the cluster results versus the number of devices of the proposed scheme. Figure 2a shows the cluster number and the maximum distance $r_{\max }$ between the UAV and the device versus the number of devices of the proposed scheme. Figure 2b shows the maximum number of employed beams versus the number of devices of the proposed scheme. The number of devices in each cluster is unequal. When the UAV flies at a fixed height $H_U=100$ m, and the maximum coverage radius of the UAV is $R_{\max }^{\mathrm{cov}}=174$ m. When the height of UAV is 80 m, the maximum coverage radius of the UAV is $R_{\max }^{\mathrm{cov}}=140$ m. The maximum number of devices in each cluster is 16. Each device is served by a single beam. It can observed from Figure 4 that the number of clusters increases with the increasing number of devices, due to the limited coverage area $R_{\max }^{\mathrm{cov}}$ and the constraint of the maximum number of devices in each cluster. From Figure 4, the tight constraint of $R_{\max }^{\mathrm{cov}}$ has an influence on the number of clusters. When $K=80$, the cluster number of $H=100$ m is 6, and $r_{\max }\approx 132$ m. Meanwhile, the maximum number of employed beams is 16. However, for $K=80$ and $H=80$ m, the cluster number is 7, and $r_{\max }\approx 140$ m. Meanwhile, the maximum number of employed beams is 16.

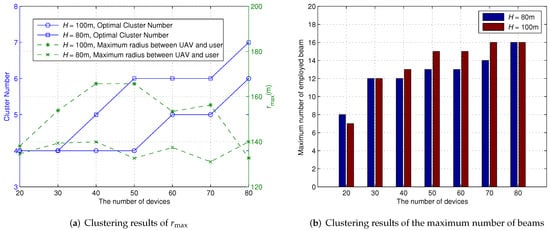
Figure 4. Optimized clustering results with different numbers of devices with a fixed UAV height of $H=80/100$ m.

In Figure 5, we compare the data collection efficiency as a function of the total energy constraint of each for device for the proposed scheme and the square trajectory with average time and power. The system setup is $K=20$, $N=4$, $T=300$ s, $T_{\mathrm{budget}}^n=200$ s, $\forall n$, and $H_U=100$ m. For the square trajectory with average time and power, ${\tau }_n=T/N$, $\forall n$, and $p_{m,n}=min\{P_{\max },E_{\max }^{m,n}/{\tau }_n,P_{\mathrm{budget}}/M_n\}$, $\forall n$ [29]. The MCMS scheme is utilized for the square trajectory with average time and power scheme. From Figure 5, the proposed scheme shows better performance than the square trajectory scheme with average time and power.

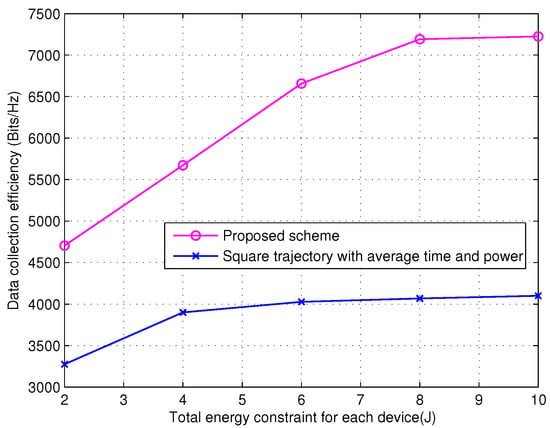
Figure 5. Comparison of data collection efficiency versus total energy constraint of each device for proposed scheme and the square trajectory with average time and power.

Figure 6 compares the data collection efficiency as a function of the total energy constraint of each device for the proposed incremental beam selection scheme and the maximum channel magnitude scheme (MCMS) [34], both adopting the proposed UAV trajectory and user clustering scheme and the iterative algorithm. Since the proposed scheme selects one beam for each device, the MCMS with one beam per device is selected as a reference. There are $K=20$ devices randomly distributed in the specific area. All the devices are separated into $N=4$ clusters, and the number of devices in each cluster is different. The total communication duration T is 400 s, and the budget transmission duration $T_{\mathrm{budget}}^n,\forall n$ is set as $T_{\mathrm{budget}}^n=200$ s. The UAV flies at a fixed height of $H_U=100$ m. As shown in Figure 6, the data collection efficiency of the incremental beam selection scheme significantly outperforms that of the MCMS. This is because the MCMS select the strongest beam for each device, and thereby some devices may share the same beam, which causes interference from the same beams for different devices.

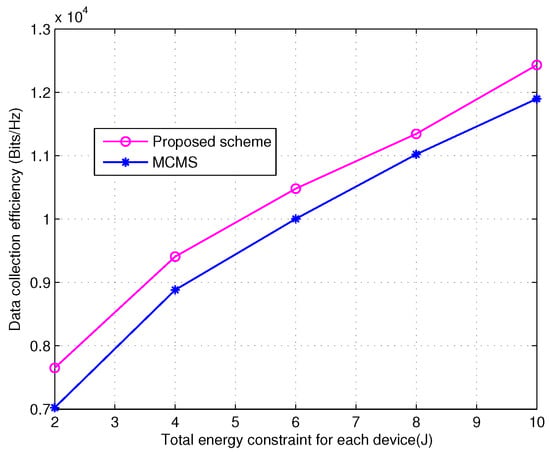
Figure 6. Comparison of data collection efficiency versus total energy constraint of each device for the incremental beam selection scheme and the MCMS beam selection scheme, both with the aid of the proposed trajectory planning scheme and iterative algorithm.

In Figure 7, we compare the data collection efficiency as a function of the total energy constraint of each device for the proposed iterative algorithm and traditional scheme, both with the aid of the proposed UAV trajectory and user clustering scheme and the incremental beam selection scheme. The system setup is $K=20$, $N=4$, $T=300$ s, $T_{\mathrm{budget}}^n=200$ s, $\forall n$ and $H_U=100$ m. In the traditional scheme, ${\tau }_n=T/N$, $\forall n$, and $p_{m,n}=min\{P_{\max },E_{\max }^{m,n}/{\tau }_n,P_{\mathrm{budget}}/M_n\}$, $\forall n$, which is widely used in the literature [8]. From Figure 7, the proposed iterative scheme shows better performance than the traditional scheme. For $E_{\max }^{m,n}=8$ J, $\forall m,n$, the data collection efficiency of our proposed iterative scheme is about 1000 bits/Hz higher than that of the traditional scheme.

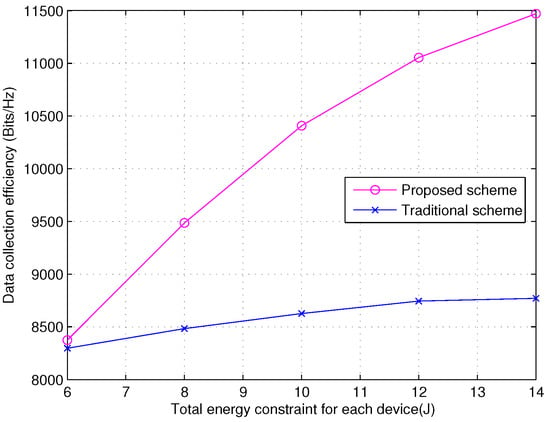
Figure 7. Comparison of data collection efficiency versus total energy constraint of each device for the proposed iterative algorithm and the traditional scheme, both with the aid of the proposed trajectory planning scheme and beam selection scheme.

Figure 8 investigates the data collection efficiency versus the total serving time for the proposed scheme with a different total energy constraint for each device. The system setup is $K=20$, $N=4$, $T_{\mathrm{budget}}^n=200$ s and $H_U=100$ m. The total energy constraint for each device $E_{\max }^{m,n}$ is 8 J or 14 J, $\forall n$. It can be observed from Figure 8 that, given the total energy constraint for each device, the data collection efficiency increases with the increased serving time T. When $T=300$ s, the data collection efficiency of $E_{\max }^{m,n}=14$ J is about 1780 bits/Hz higher than that of $E_{\max }^{m,n}=8$ J.

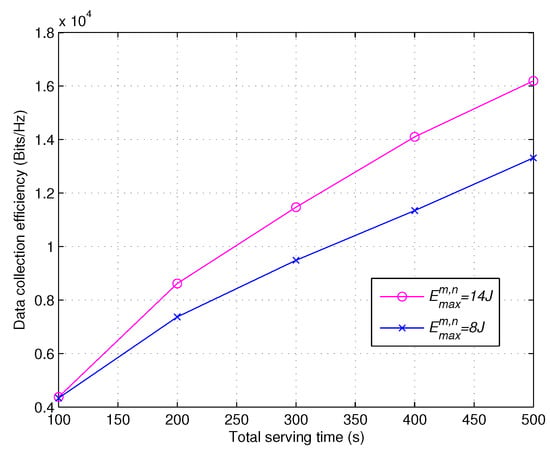
Figure 8. Comparison of data collection efficiency versus the total serving time for proposed scheme with $E_{\max }^{m,n}=8/14$ J.

5. Conclusions

In this paper, a UAV-aided mmWave communication system for the IoT is considered, and the maximization problem of the data collection efficiency is investigated, where the UAV trajectory planning, user clustering, beam selection, power allocation and transmission duration allocation are jointly optimized. To tackle this complex and nonconvex problem, we have decomposed it into three subproblems. Firstly, the incremental K-means clustering algorithm and ACO algorithm are proposed to solve the joint subproblem of UAV trajectory planning and user clustering, in which the cluster number, clustering method and hovering location of UAV are optimized according to the incremental K-means cluster algorithm. The UAV trajectory planning is transformed into a traveling distance minimization problem, which is solved by the ACO algorithm. Then, an incremental beam selection scheme is proposed to implement beam selection with one beam per device. With the aid of optimal UAV trajectory planning and the incremental beam selection scheme, an iterative algorithm is proposed to maximize the data collection efficiency by alternately solving the power allocation and transmission duration allocation problems. The data collection efficiency is finally evaluated for the proposed algorithm, and the results demonstrate that the proposed solutions can achieve excellent performance.

Our future work may focus on the unitary planar array (UPA). The UAV-BS utilizing UPA could place more antennas in small area. The UPA includes the elevation angle and azimuth angle, and thereby the beamforming of UAV-BS can be carefully designed to achieve better performance.