Adaptive Sliding Mode Neural Network Control and Flexible Vibration Suppression of a Flexible Spatial Parallel Robot
Abstract
:1. Introduction
- (1)
- Unlike previous models, in order to reduce the influence of deformation uncertainty on the dynamic performance of the system, this model uses the FFR method to establish an accurate dynamic model with rigid–flexible coupling effects and a small displacement of the moving platform caused by flexible deformation. Based on the established precise dynamics model of the system, the pre-calculated driving torque with coupling effects is subjected to feedforward compensation, and the adaptive sliding mode controller is used to ensure the tracking performance and improve the response speed of the system.
- (2)
- The dynamics equation of a flexible spatial beam with high-frequency vibrations is established through a combination of the finite element method and the Lagrange equation.
- (3)
- The displacement field of the flexible spatial link is described based on a floating frame of reference so that the coupling effects in the dynamic model can be considered. Through the boundary conditions and the coordination matrix, the dynamics equation of the moving platform that causes a small displacement of the moving platform due to elastic deformation is considered.
- (4)
- Approximating the effects of nonlinear errors and unknown interference through neural networks is crucial for achieving high positioning accuracy.
- (5)
- The controller can reach the optimal control performance with only a small number of hidden layer nodes, which shows that the controller has a simple structure, easy implementation, and universal applicability.
2. Flexible Spatial Parallel Robot
3. Dynamic Model of the Flexible Spatial Parallel Robot
3.1. Dynamic Model of the Flexible Spatial Link
3.2. Dynamic Model of Rigid Links
3.3. Dynamic Model of Flexible Spatial Parallel Robot
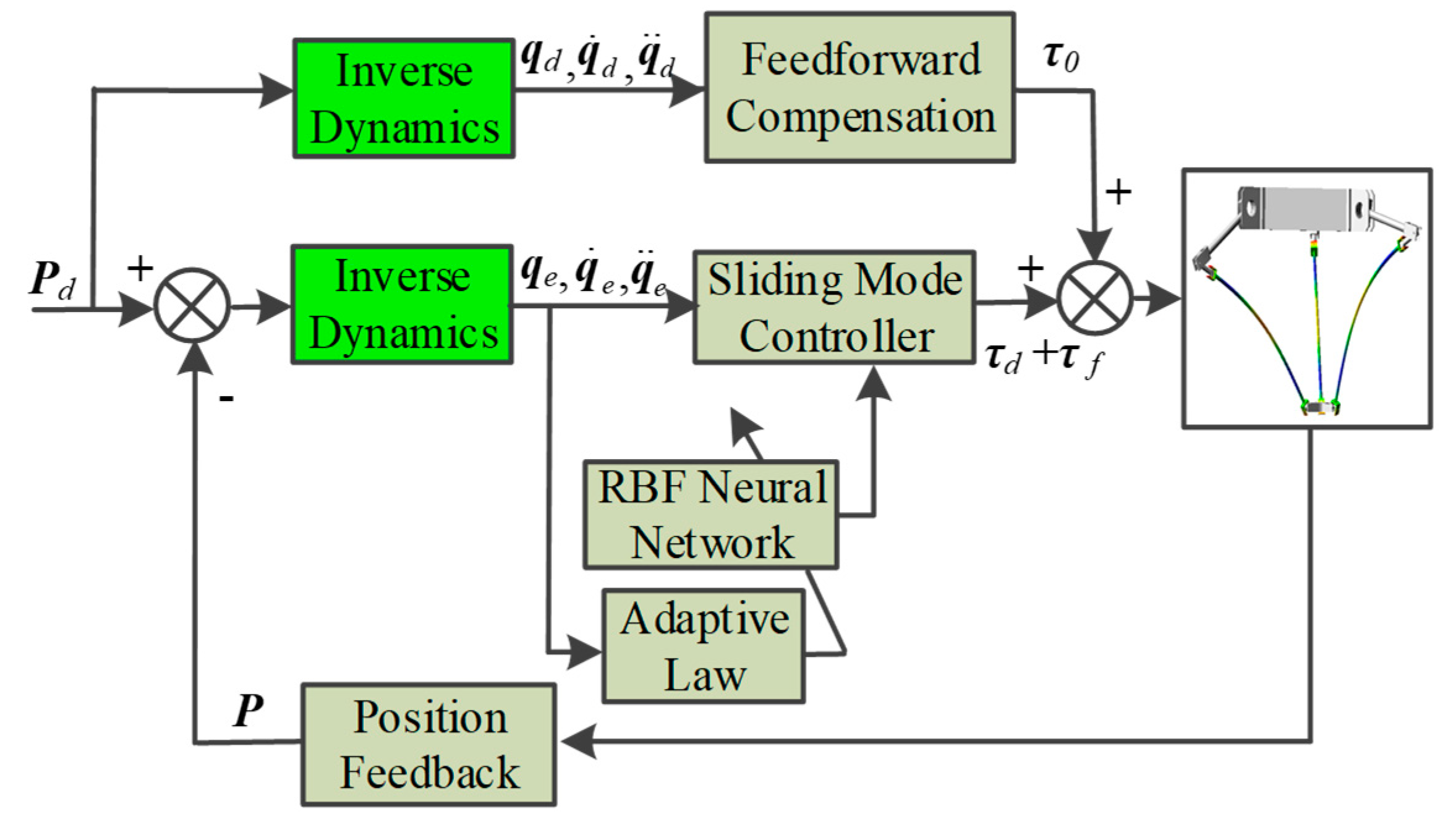
4. Intelligent Control
4.1. Problem Statement
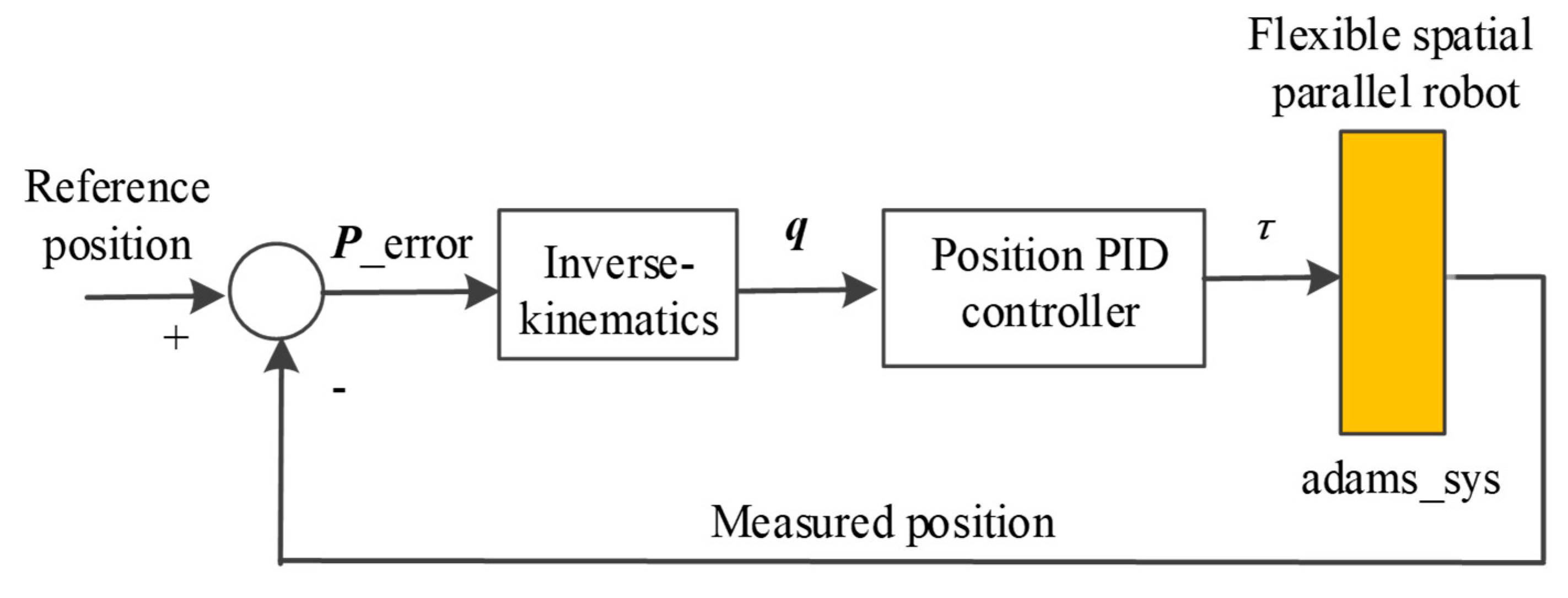
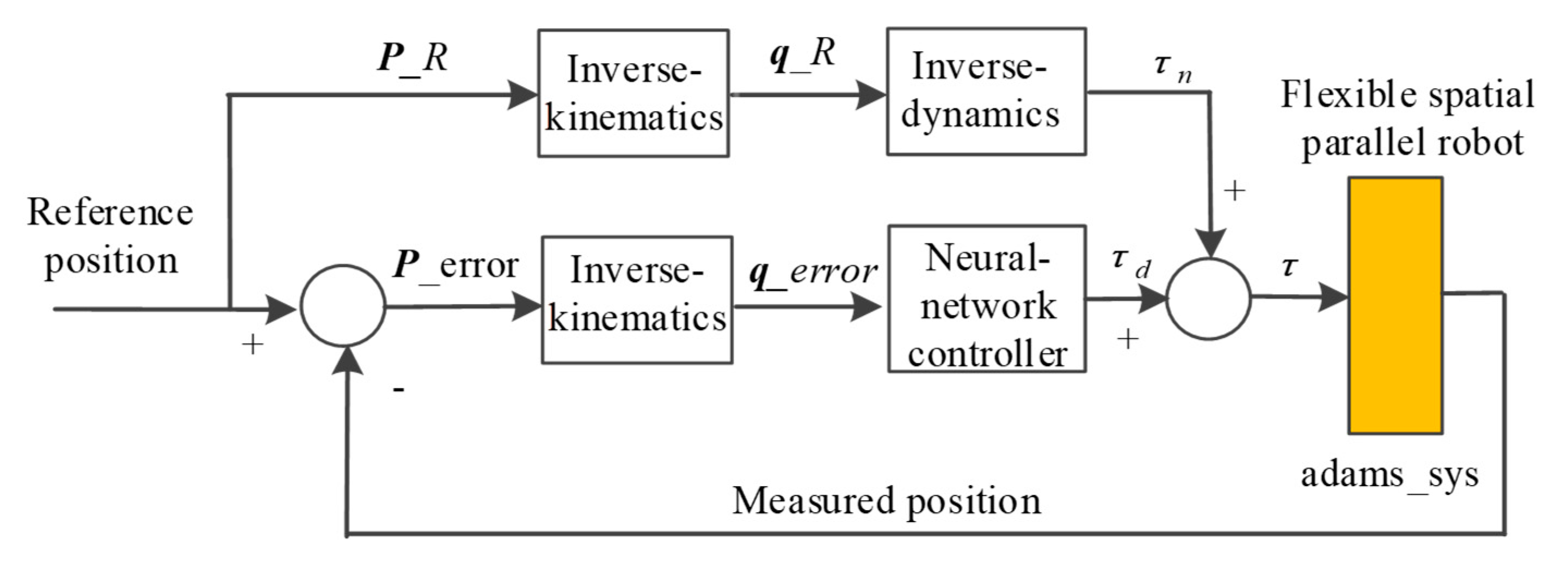
4.2. Feedforward Compensation
4.3. Sliding Mode Variable Structure Control
4.4. Adaptive Sliding Mode Neural Network Control
4.5. Stability Analysis
5. Simulation Results
5.1. Dynamic Simulation Model
- (1)
- Based on the SOLIDWORKS software, a three-dimensional model of the spatial parallel robot was constructed, and it was saved in (‘x_t’) format.
- (2)
- The three-dimensional model was imported into ADAMS, the constraint relationship between the components was set as shown in Table 1, and the material properties were defined as shown in Table 2. Since the flexible link was a simple homogeneous component, it was softened directly through the ADAMS/FLEX module, and the original rigid link was deleted. The constraints between the flexible link and its connected components were then reset.
- (3)
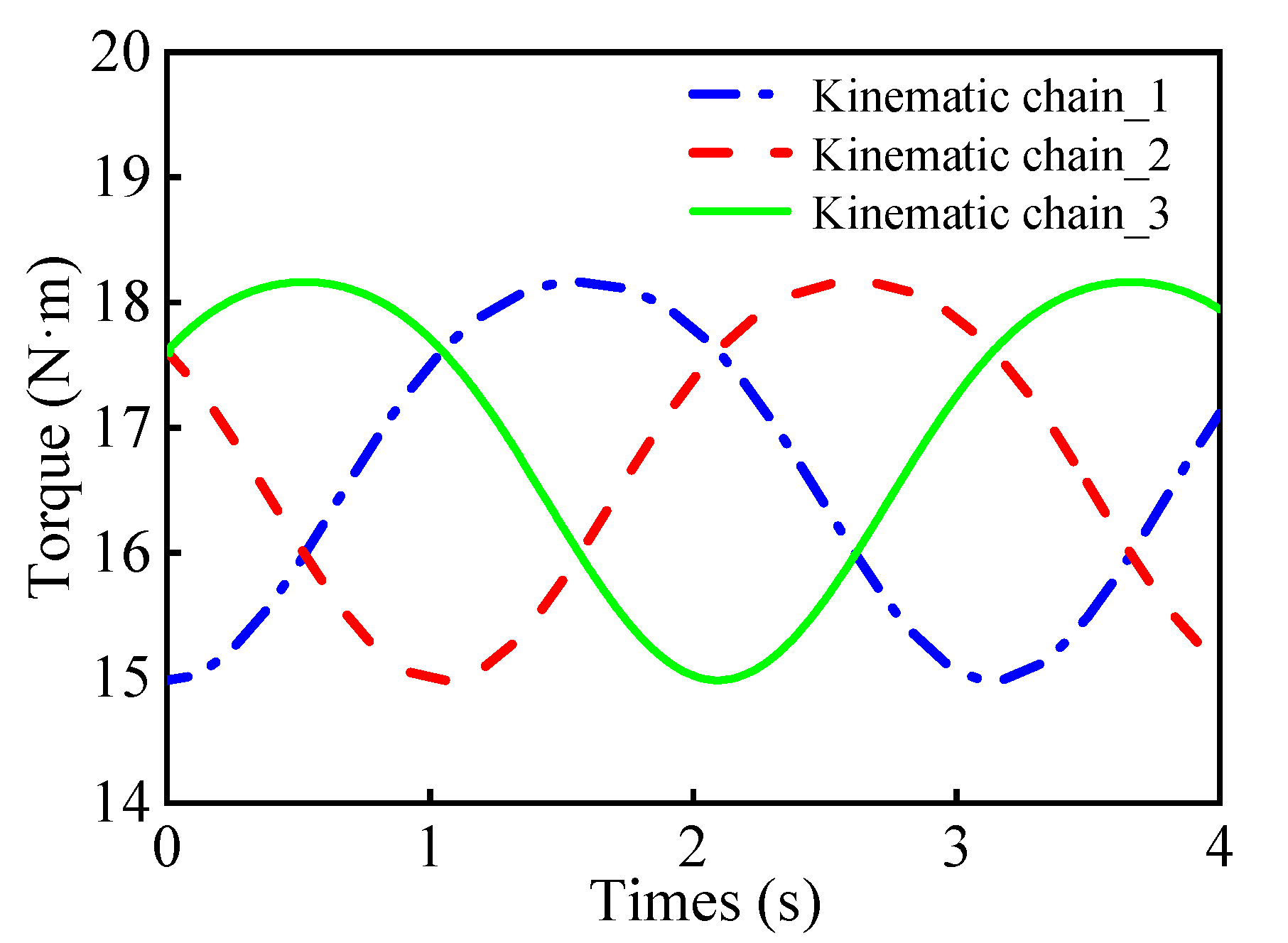
- An inverse dynamics analysis was performed on the dynamic simulation model by setting the moving platform drive.
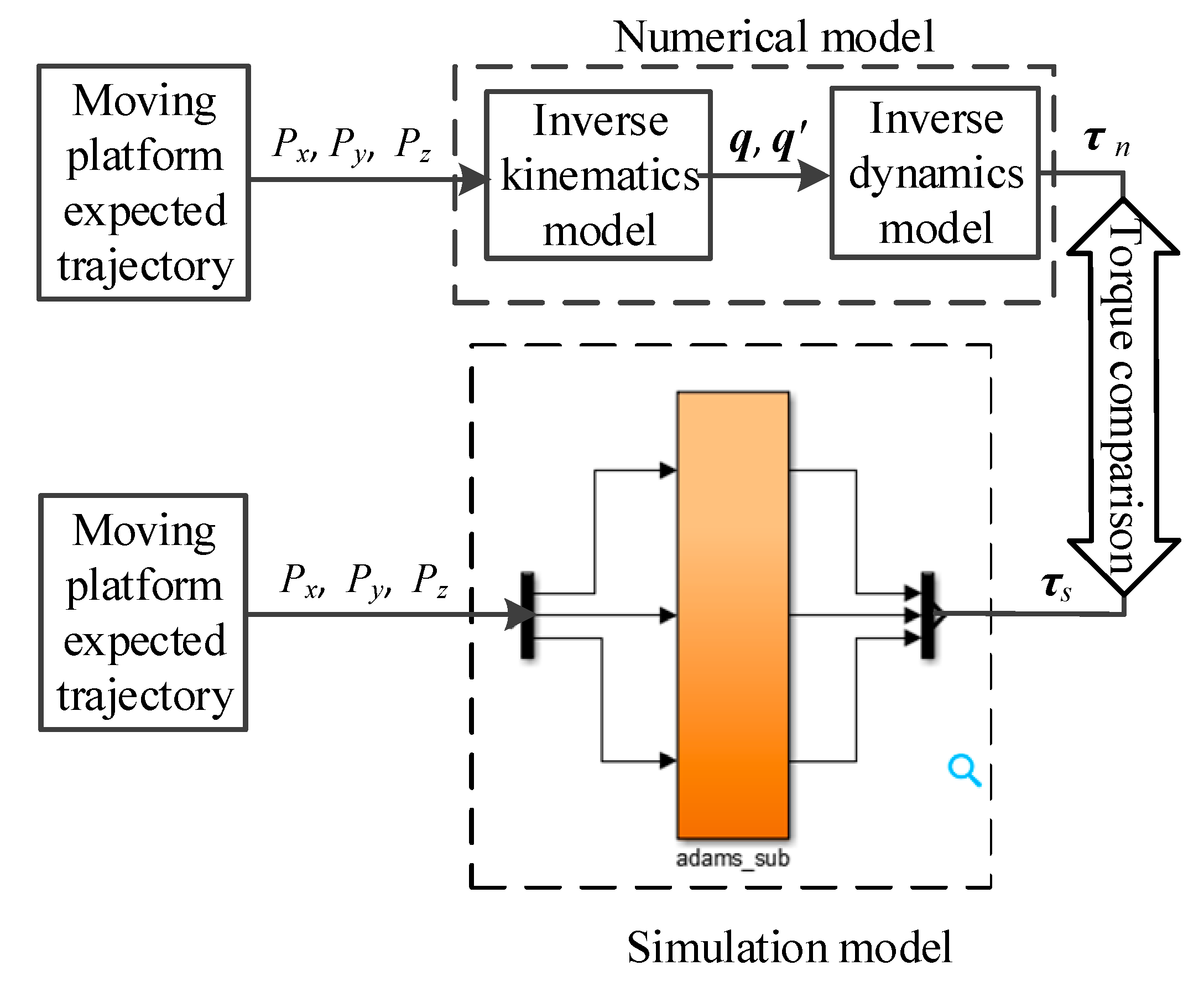
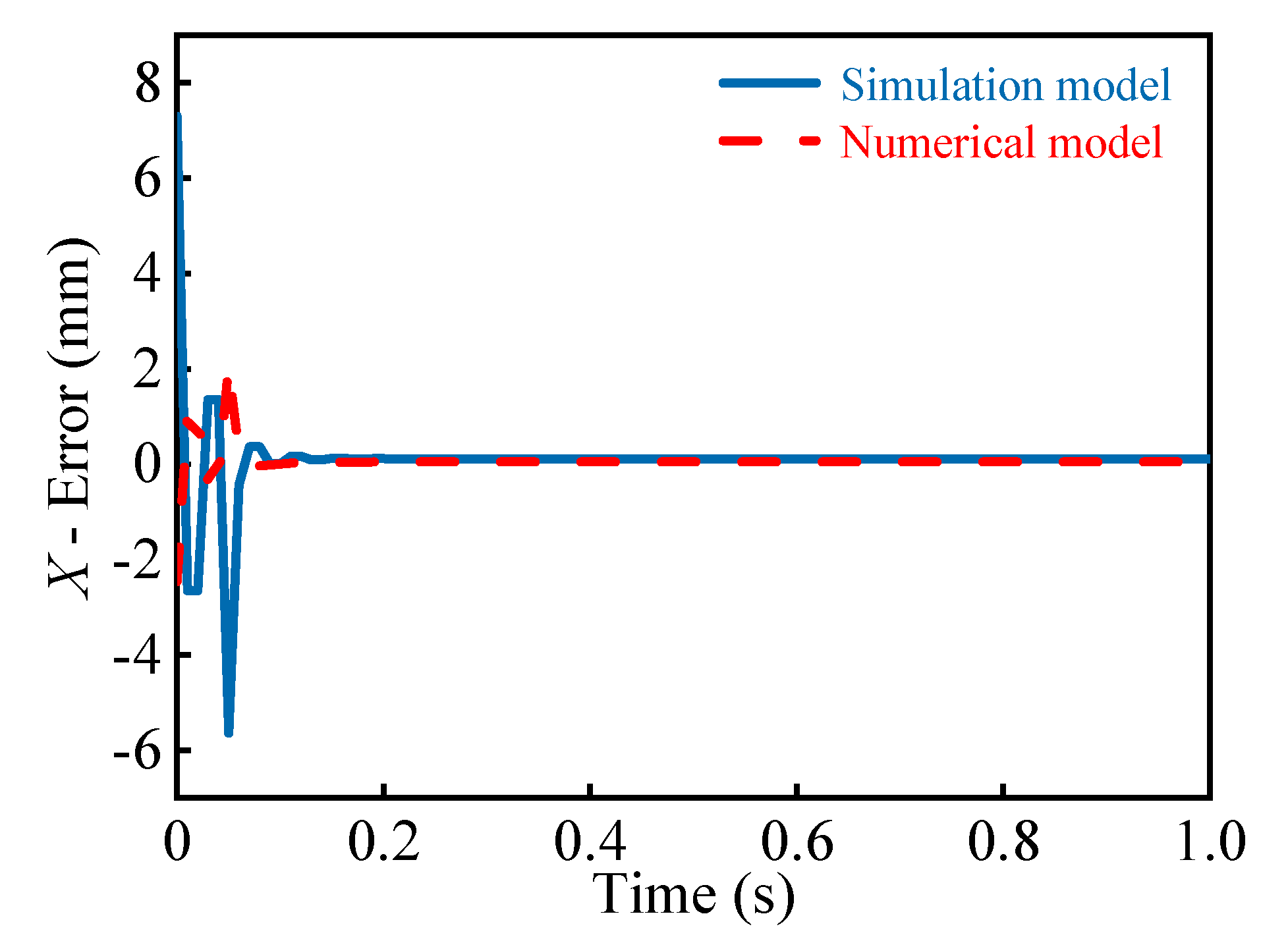
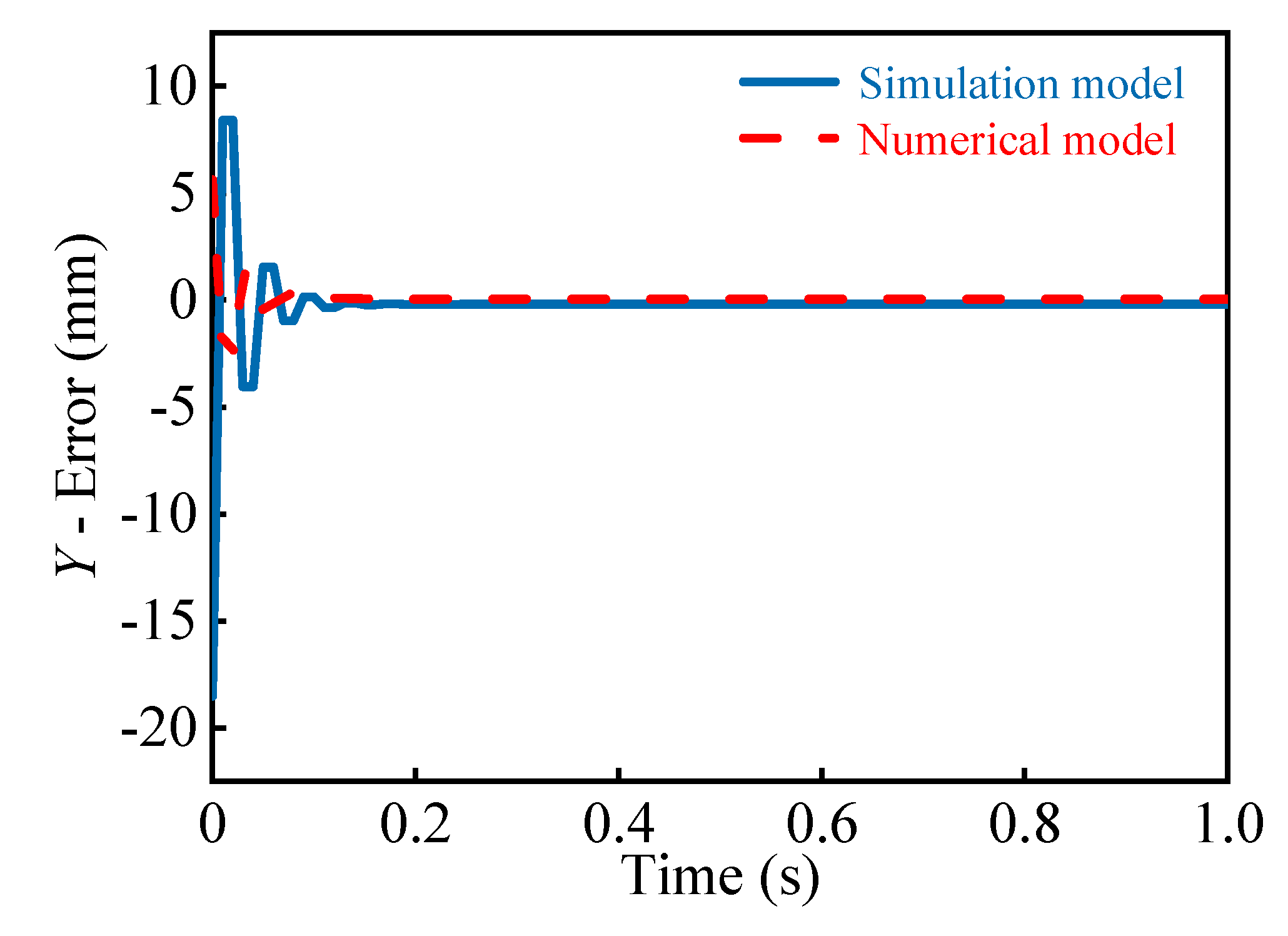
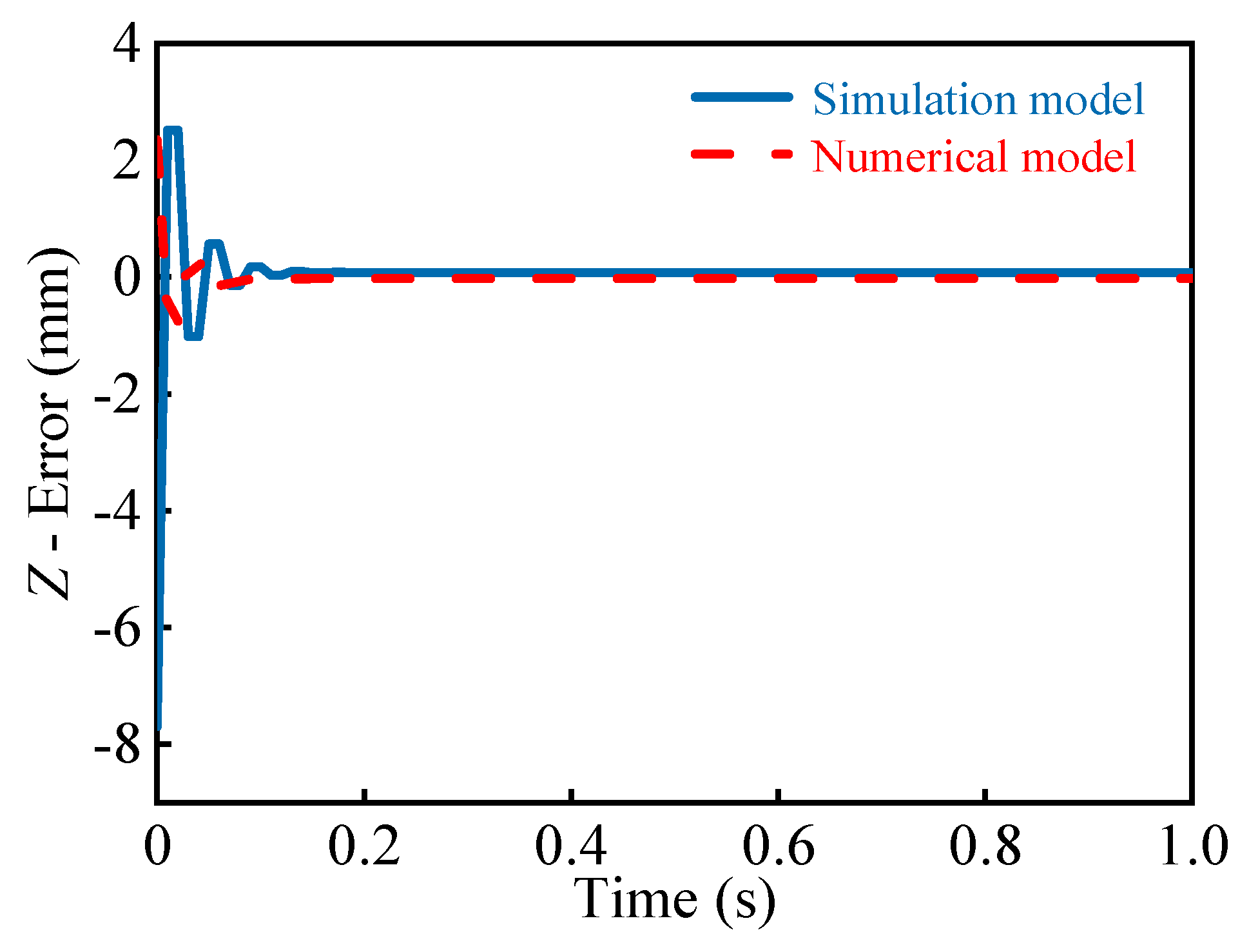
5.2. Numerical Model
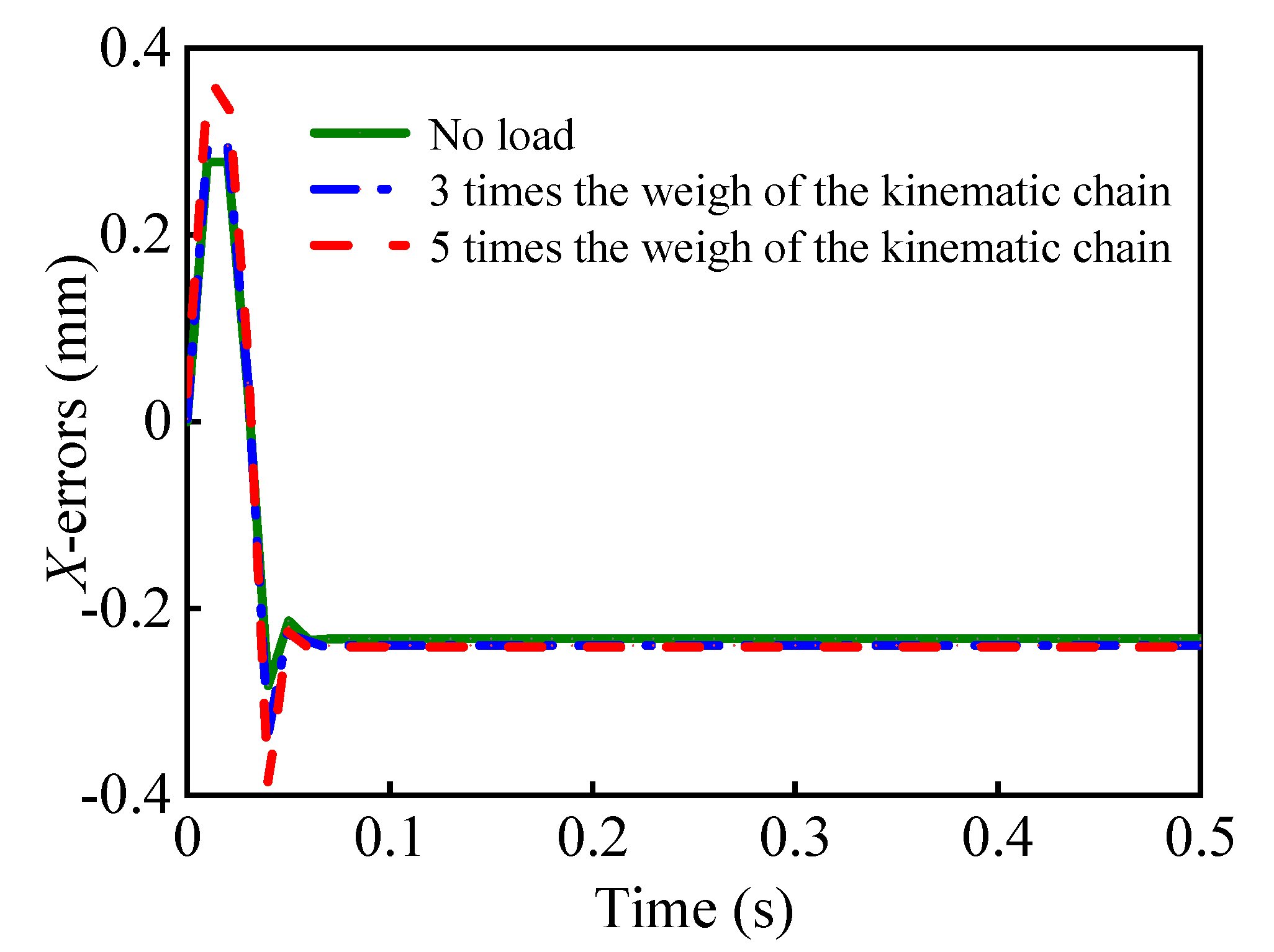
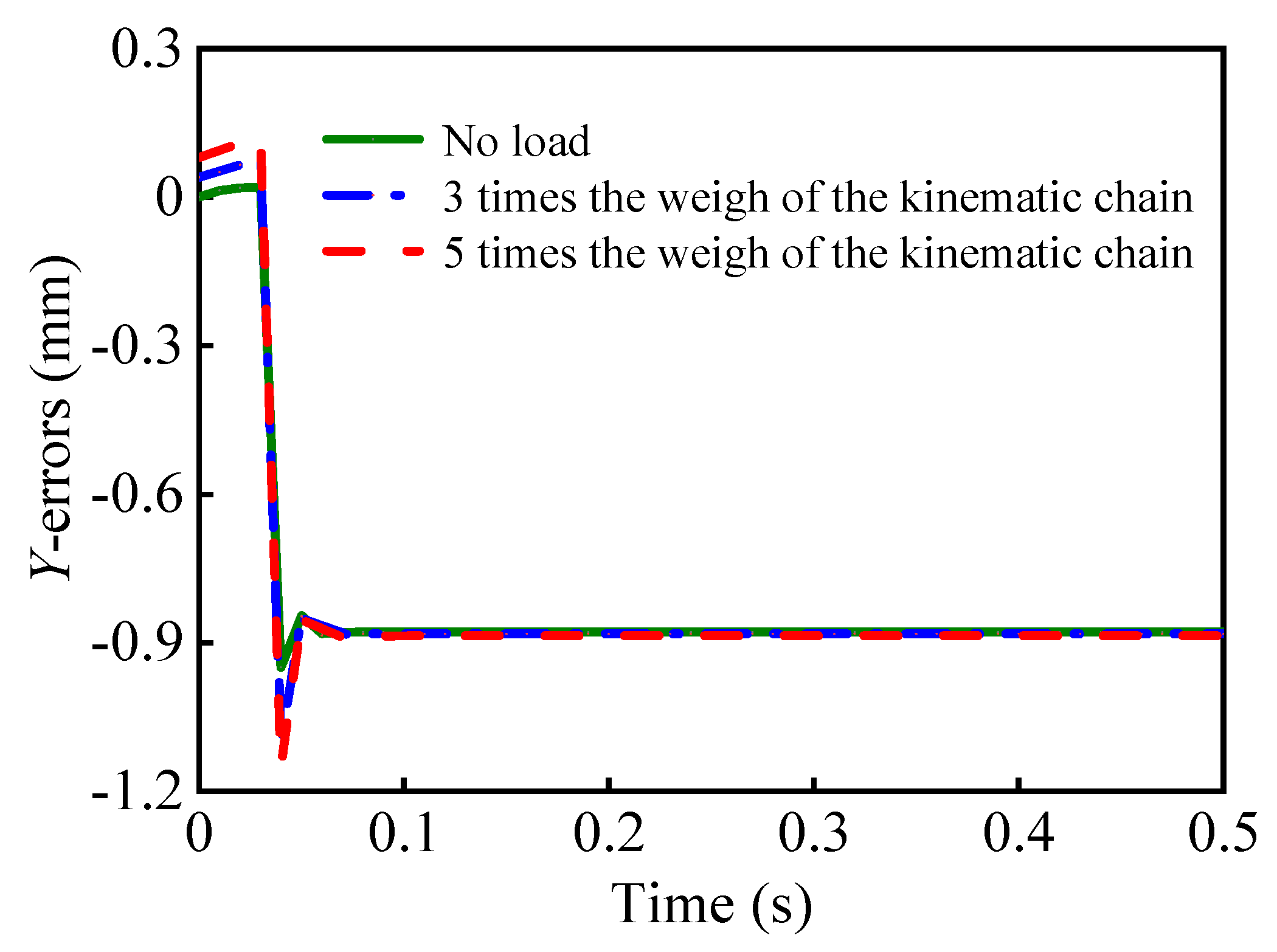
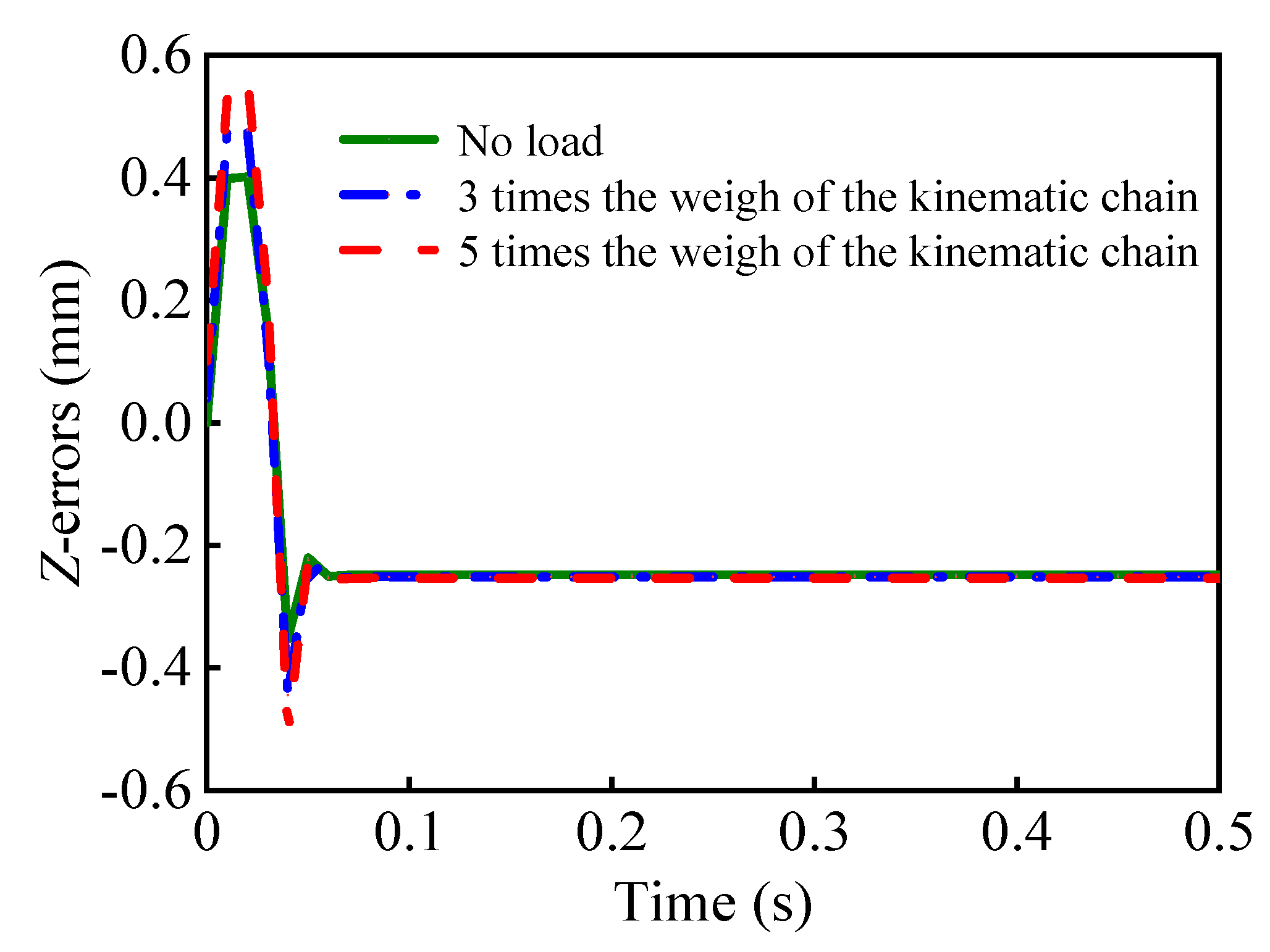
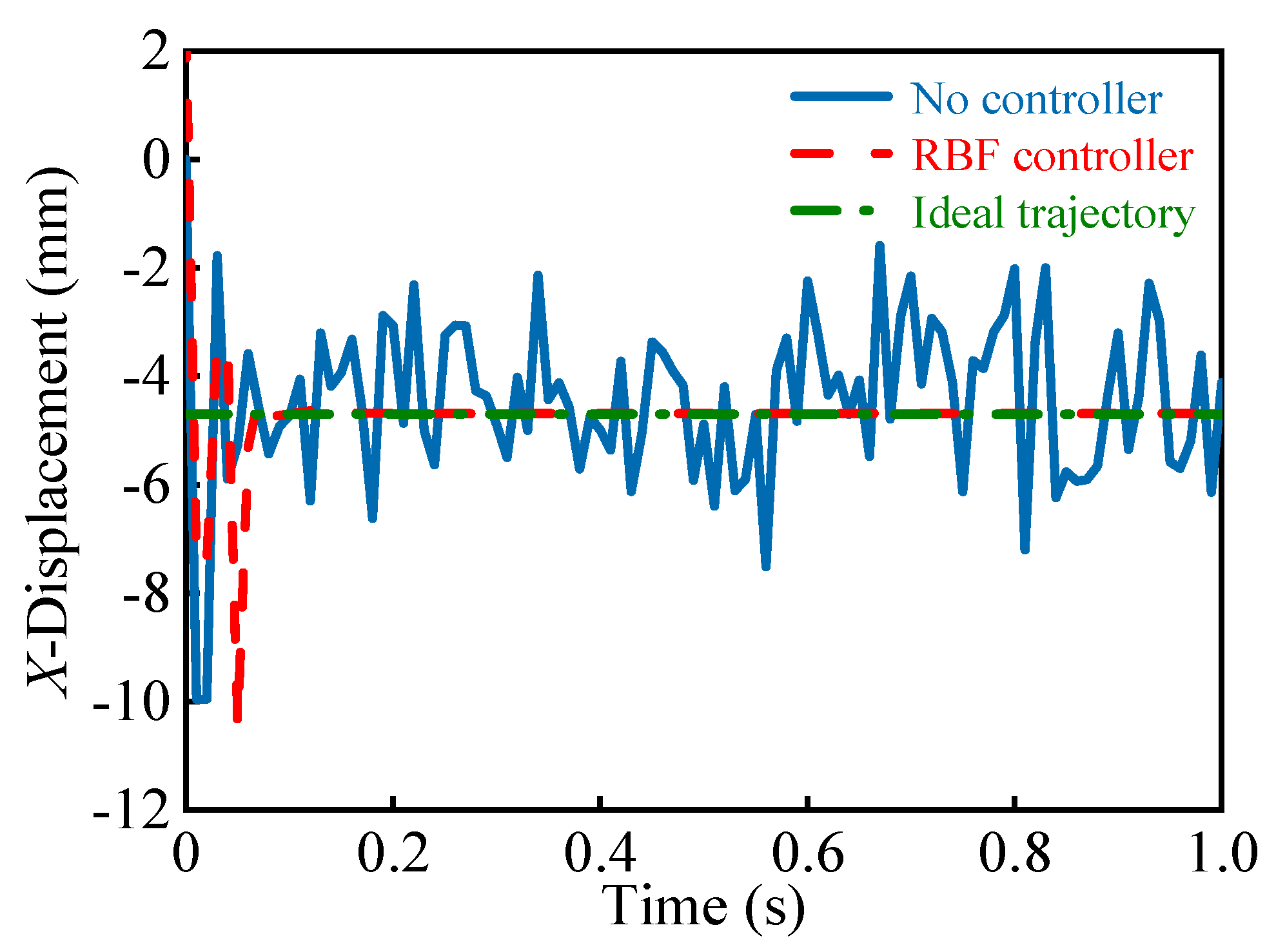
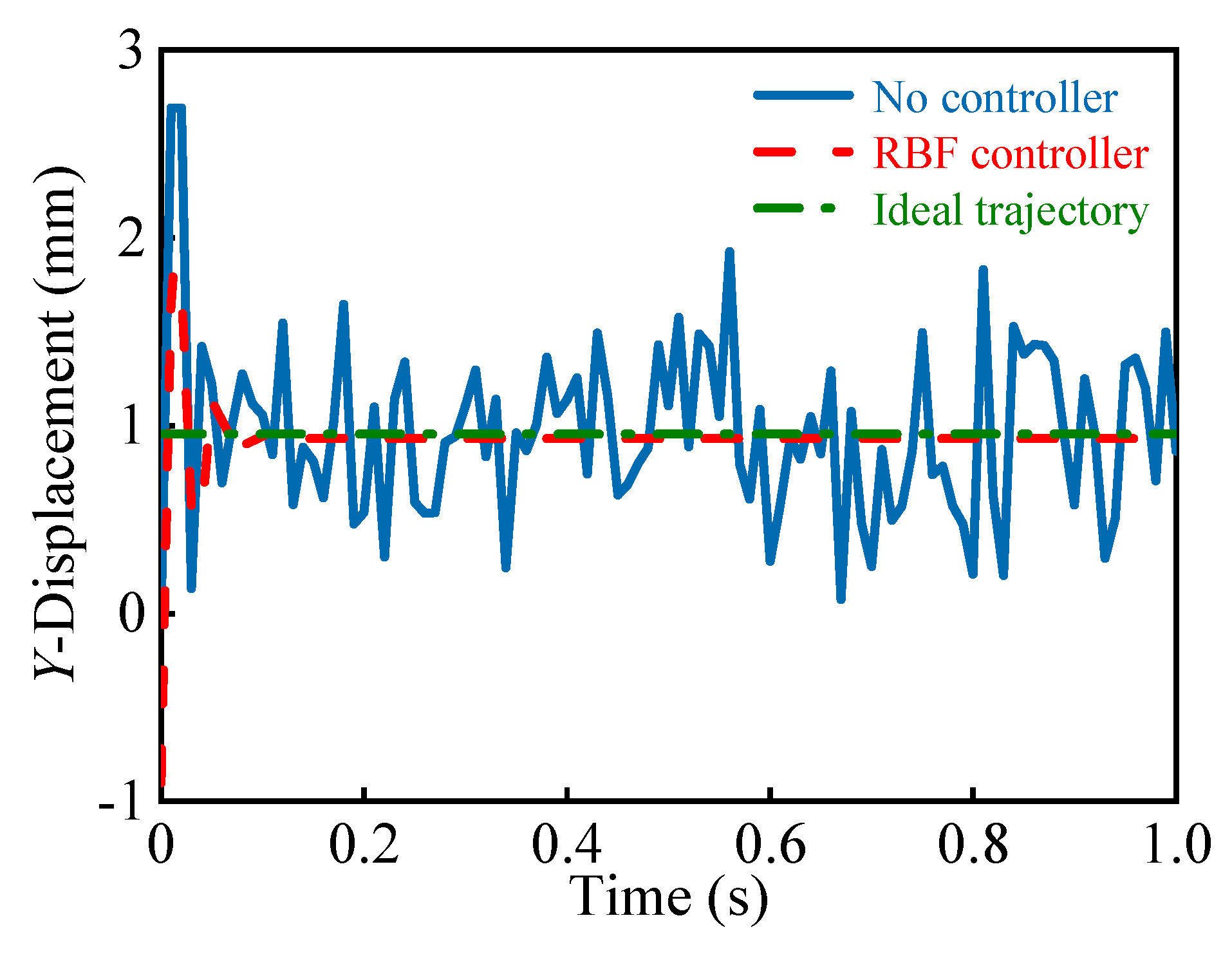
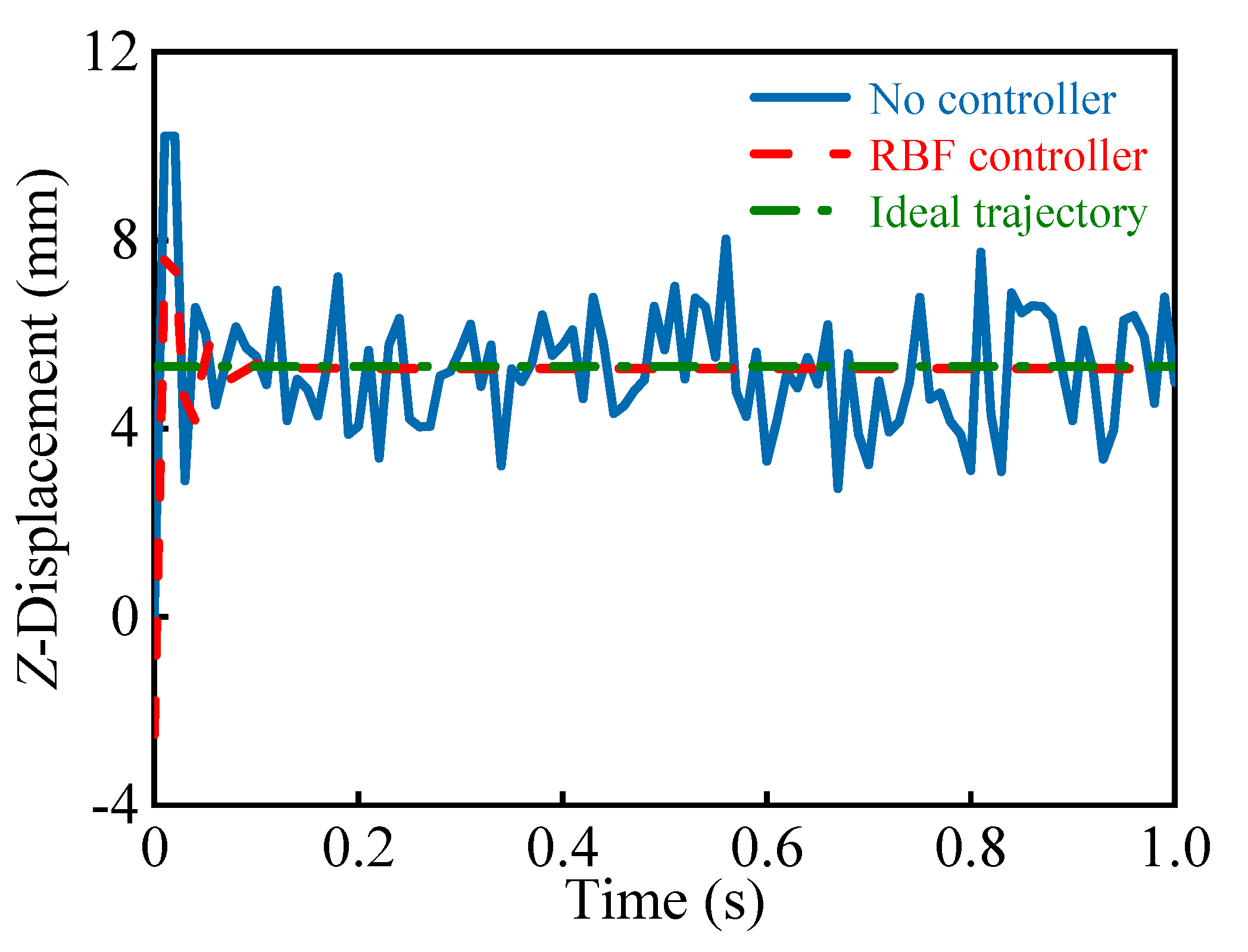
5.3. Control Simulation Results
- (1)
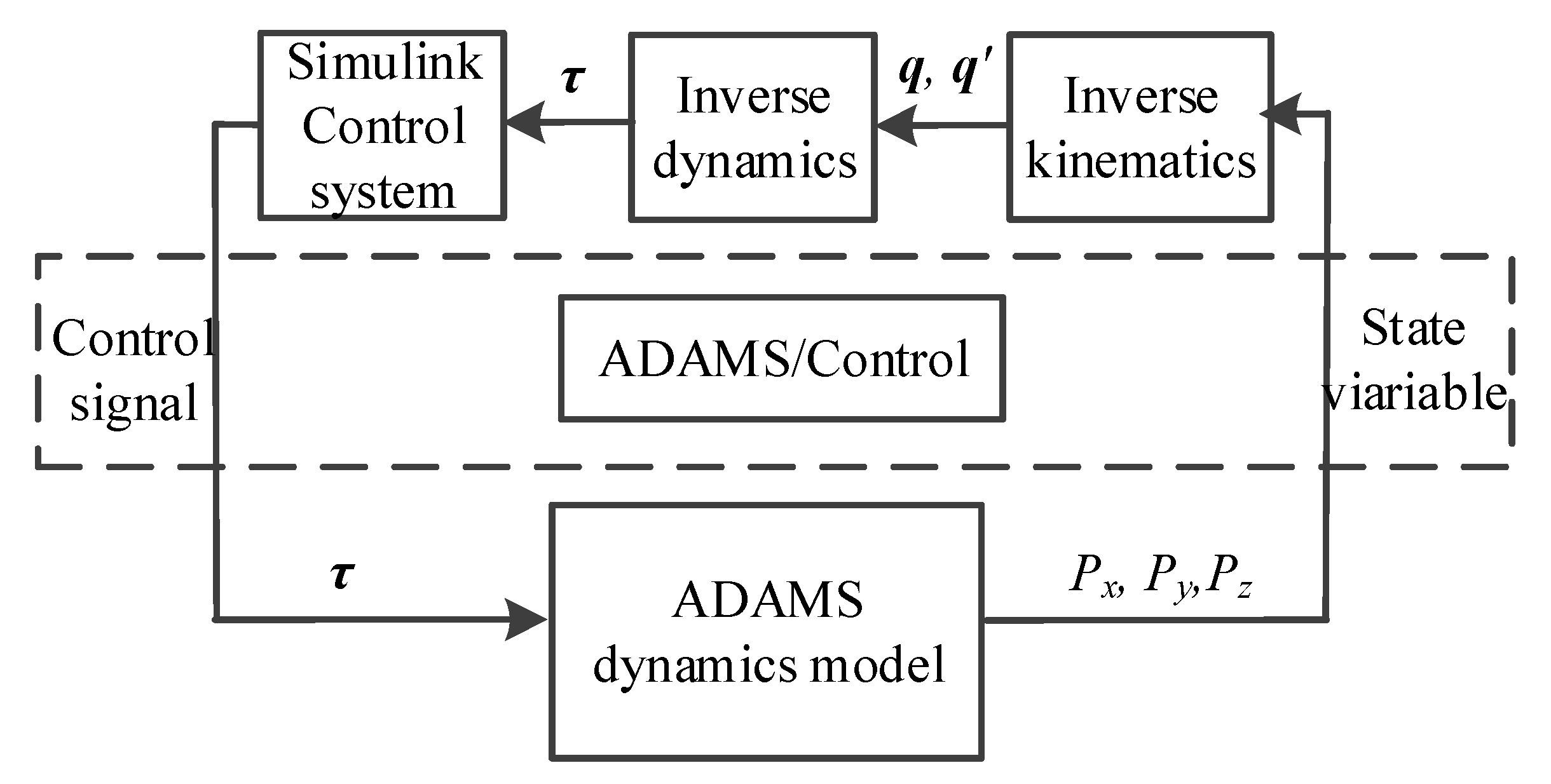
- The output variable of the ADAMS model was the input variable of the MATLAB/Simulink control model. According to the control algorithm we proposed, the three driving torques of the kinematic chain were set as control input signals, and the actual trajectory of the rigid moving platform was the control output signal. The dynamic model and the control model were connected through the ADAMS/Control module.
- (2)
- MATLAB/Simulink were used to build the control system of the flexible spatial parallel robot. The information exchange diagram of the co-simulation control model is shown in Figure 9.
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Wang, Y.Q.; Lin, Q.; Wang, X.G.; Zhou, F.G.; Liu, J. Force/position hybrid control for a wire-driven parallel robot support system based on RBF neural network compensation. Control Decis. 2020, 35, 536–546. [Google Scholar]
- Pham, C.B.; Yeo, S.H.; Yang, G.; Kurbanhusen, M.S.; Chen, I.M. Force-closure workspace analysis of cable-driven parallel mechanisms. Mech. Mach. Theory 2006, 41, 53–69. [Google Scholar] [CrossRef]
- Liang, Y.; Liang, Q.; Wu, G.; Wu, W.; Sun, W.; Wang, Y. 3RPS/UPS parallel robot back-stepping control based on network observer. Eng. Comput. Appl. 2019, 55, 255–262. [Google Scholar]
- Shi, L.L.; Chen, Q. Backstepping sliding mode control for flexible-joint robotic manipulators based on neural network. Control Eng. China 2017, 24, 2268–2273. [Google Scholar]
- Chen, Q.; Tao, L.; Nan, Y.; Ren, X. Adaptive nonlinear sliding mode control of mechanical servo system with LuGre friction compensation. J. Dyn. Sys. Meas. Control 2015, 138, 021003. [Google Scholar] [CrossRef]
- Korayem, M.H.; Yousefzadeh, M.; Beyranvand, B. Dynamics and control of a 6-dof cable-driven parallel robot with visco-elastic cables in presence of measurement noise. J. Intell. Robot. Syst. 2017, 88, 73–95. [Google Scholar] [CrossRef]
- Zubizarreta, A.; Cabanes, I.; Marcos, M.; Pinto, C. Dynamic modeling of planar parallel robots considering passive joint sensor data. Robotica 2009, 28, 649–661. [Google Scholar] [CrossRef]
- Nevmerzhitskiy, M.N.; Notkin, B.S.; Vara, A.V.; Zmeu, K.V. Friction model of industrial robot joint with temperature correction by example of KUKA KR10. J. Robot. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Talole, S.E.; Kolhe, J.P.; Phadke, S.B. Extended-state-observer-based control of flexible-joint system with experimental validation. IEEE Trans. Ind. Electron. 2010, 57, 1411–1419. [Google Scholar] [CrossRef]
- Tan, X.; Chen, G.; Sun, D.; Chen, Y. Dynamic analysis of planar mechanical systems with clearance joint based on LuGre friction model. J. Comput. Nonlinear Dyn. 2018, 13, 061003. [Google Scholar] [CrossRef]
- Shen, X.; Wang, B.; Yu, R.; Cui, X.H. Friction modeling and computed torque control of robot joints with adaptive RBF neural network compensation. J. China Univ. Metrol. 2020, 31, 71–78. [Google Scholar]
- Liu, S.Z.; Yu, Y.Q.; Du, Z.C.; Liu, Q.B. A summary of the dynamics analysis and control strategy of flexible manipulators. Ind. Instrum. Autom. 2008, 200, 18–24. [Google Scholar]
- Zhang, Q.; Zhang, X. Active residual vibration control of planar 3-RRR flexible parallel robots. Trans. Chin. Soc. Agric. Mach. 2013, 44, 232–237. [Google Scholar]
- Rahimi, H.N.; Nazemizadeh, M. Dynamic analysis and intelligent control techniques for flexible manipulators: A review. Adv. Robot. 2013, 28, 63–76. [Google Scholar] [CrossRef]
- Liang, J.; Chen, L.; Liang, P. The rigid-flexible coupling dynamics simulation and wavelet based fuzzy neural network control for space manipulator. Manned Spaceflight 2015, 21, 286–294. [Google Scholar]
- Yang, J.; Qiu, Z.; Zhang, X. Self-excited vibration control of a planar 3-RRR flexible parallel robot. J. Vib. Shock 2017, 36, 138–143. [Google Scholar]
- Zhang, Q.; Wang, R.; Zhou, L.; Tan, Z. Dynamic modeling and active vibration control of flexible parallel manipulator. J. Vib. Meas. Diag. 2013, 33, 1025–1031. [Google Scholar]
- Hu, J.; Zhang, X. Active vibration control and its simulation of a novel 2-DOF flexible parallel manipulator. China Mech. Eng. 2010, 21, 2017–2021. [Google Scholar]
- Zhang, X.; Mills, J.K.; Cleghorn, W.L. Multi-mode vibration control and position error analysis of parallel manipulator with multiple flexible links. Trans. Can. Soc. Mech. Eng. 2010, 34, 197–213. [Google Scholar] [CrossRef]
- Gan, D.; Dai, J.S.; Dias, J.; Seneviratne, L. Reconfigurability and unified kinematics modeling of a 3rTPS metamorphic parallel mechanism with perpendicular constraint screws. Robot. Comput. Integr. Manuf. 2013, 29, 121–128. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Mills, J.K.; Cleghorn, W.L. Dynamic Modeling and Active Vibration Control of a 3-PRR Flexible Parallel Manipulator with PZT Transducers. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 461–466. [Google Scholar]
- Zhang, F.T.; Han, Y.F. Elastic vibration control for delta parallel robot. Mach. Design Manuf. 2016, 9, 166–172. [Google Scholar]
- Stefan, P.; Zbigniew, Z.; Adam, C. Basic aspects related to operation of engine catalytic converters. Int. J. Thermodyn. 2004, 7, 9–13. [Google Scholar]
- Huang, Z.; Kong, L.F.; Fang, Y.F. Mechanism Theory and Control of Parallel Robot; Machinery Industry Press: Beijing, China, 1997. [Google Scholar]
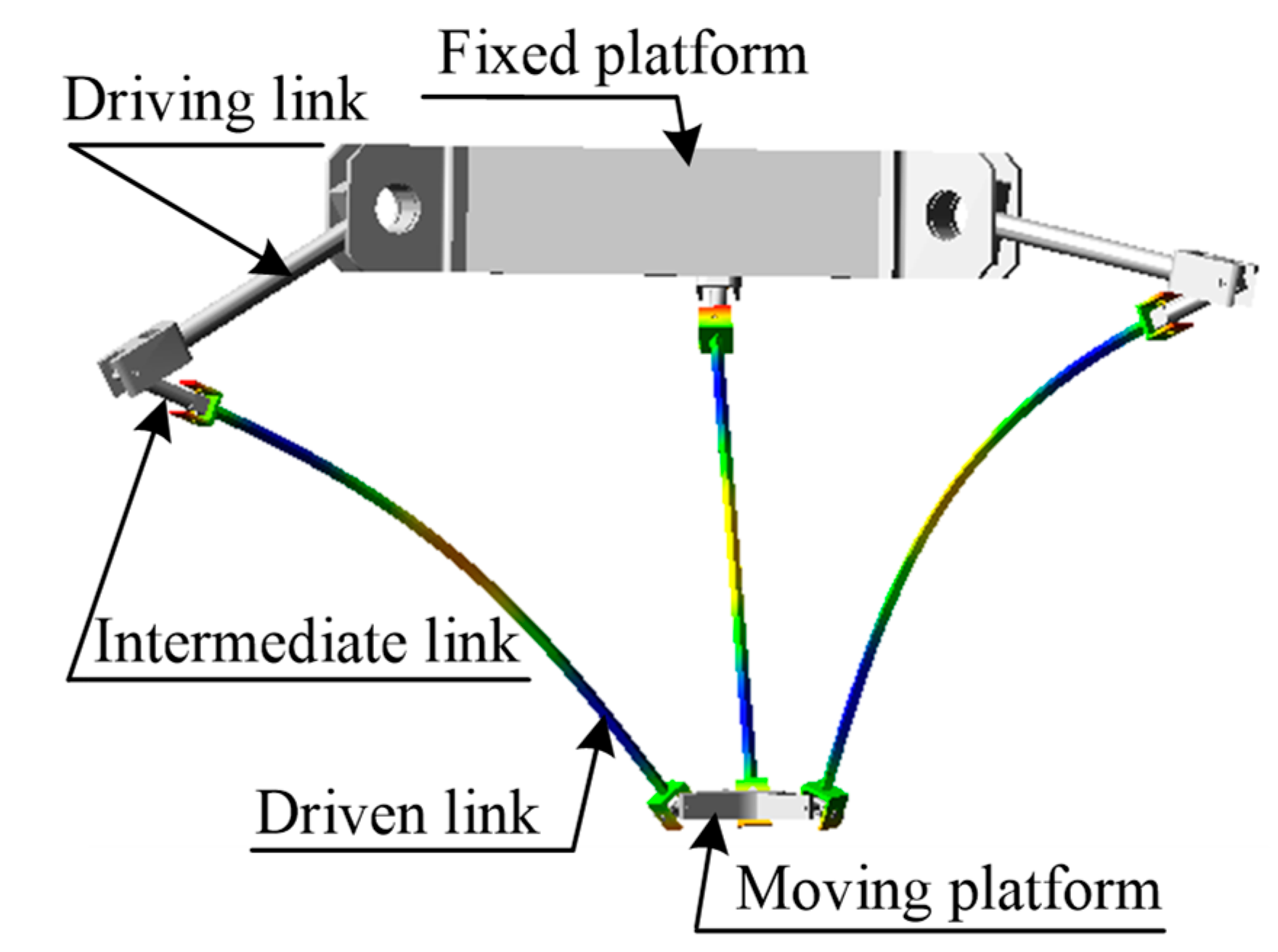
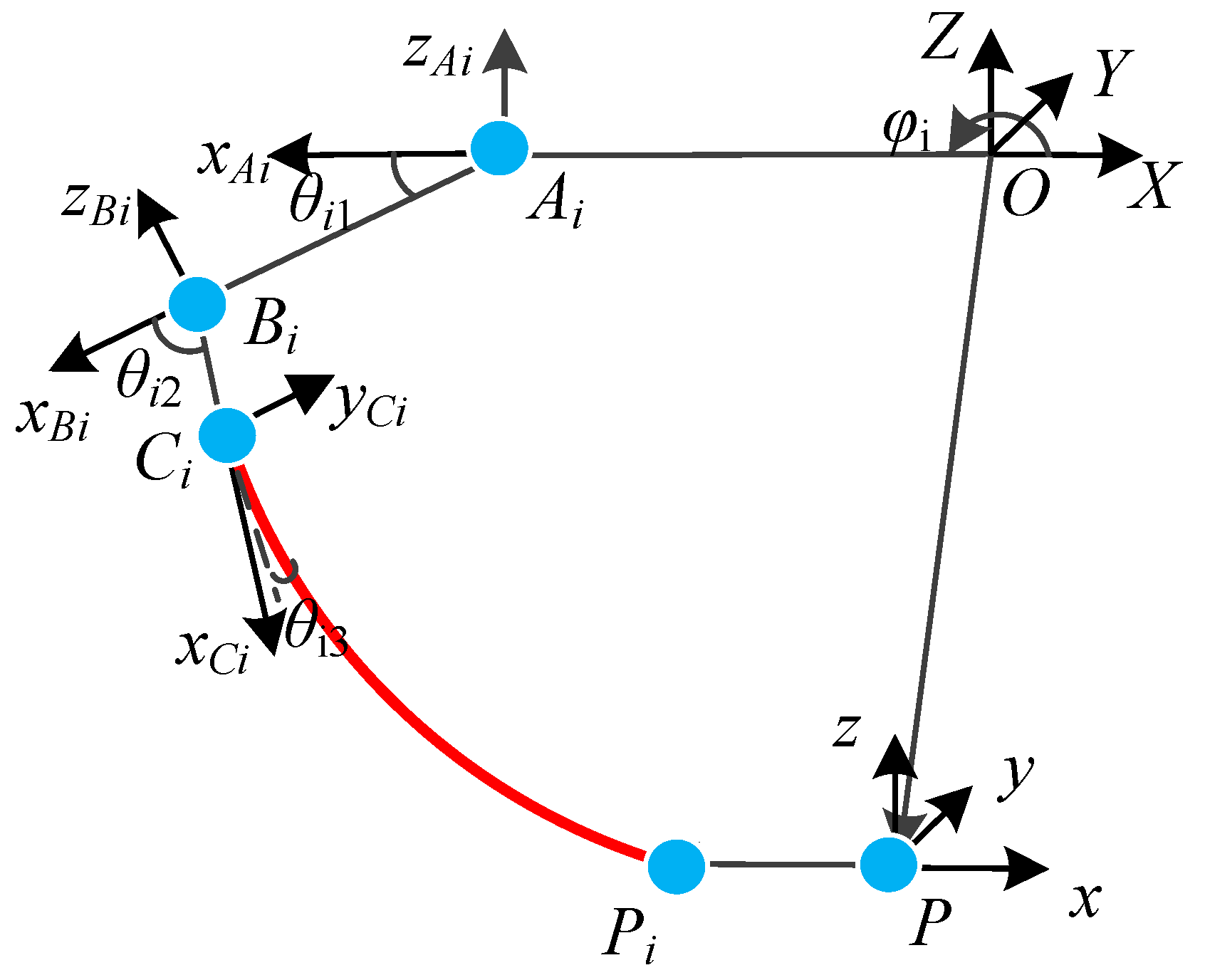
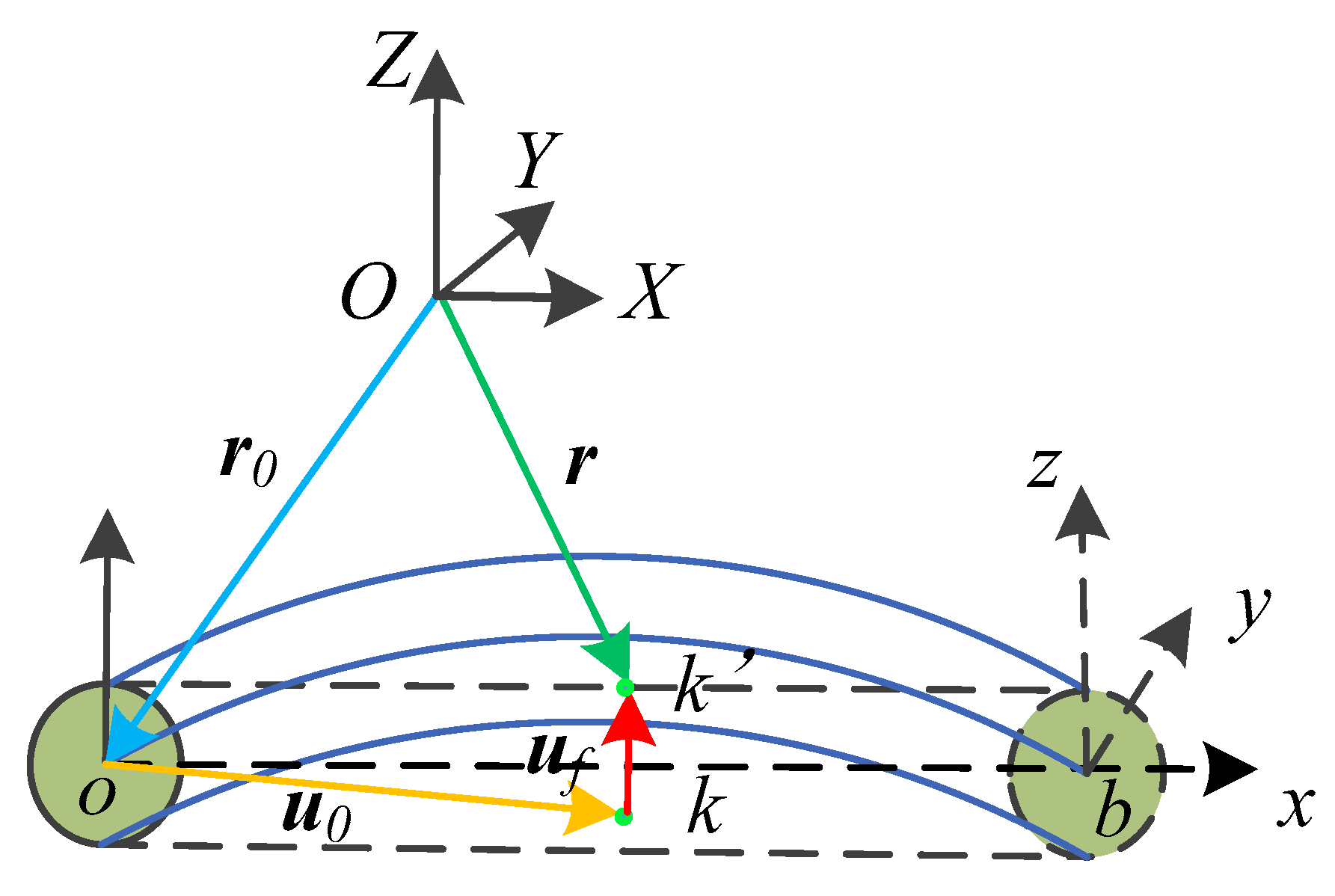
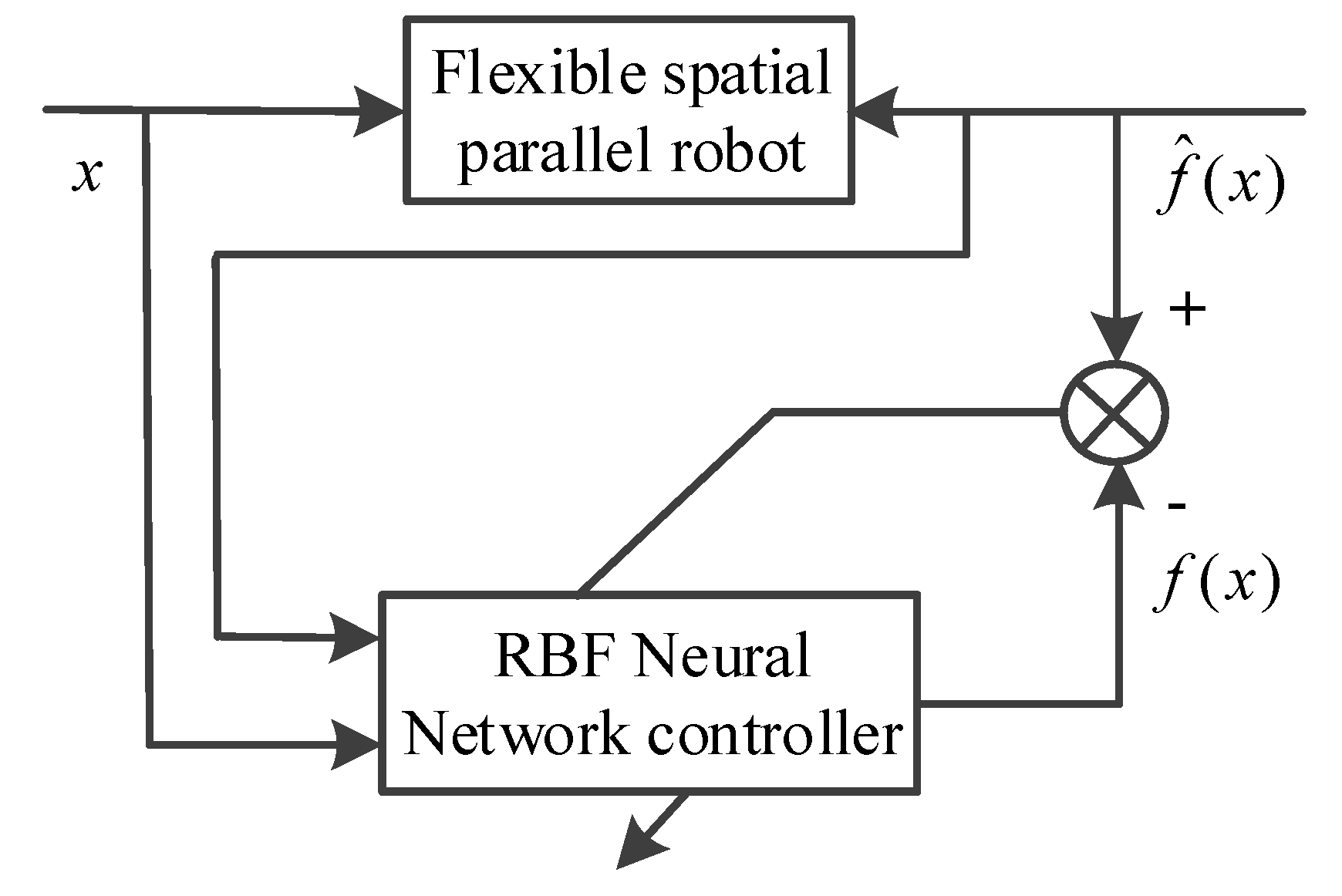


| Kinematic Pair | Component |
|---|---|
| Rotating pair | Driving link, fixed platform |
| Rotating pair | Intermediate link, driving link |
| Rotating pair | Driven link, intermediate link |
| Hook hinge | Moving platform, driven link |
| Component | Driving Link | Intermediate Link | Driven Link |
|---|---|---|---|
| Mass (kg) | 1.8 | 0.3 | 1.5 |
| Length (m) | 0.4 | 0.1 | 0.8 |
| Density (kg/m3) | 7801 | 7801 | 2740 |
| Poisson’s ratio | 0.29 | 0.29 | 0.33 |
| Elastic Modulus (N/m2) | 2.07 × 1011 | 2.07 × 1011 | 2.07 × 1011 |
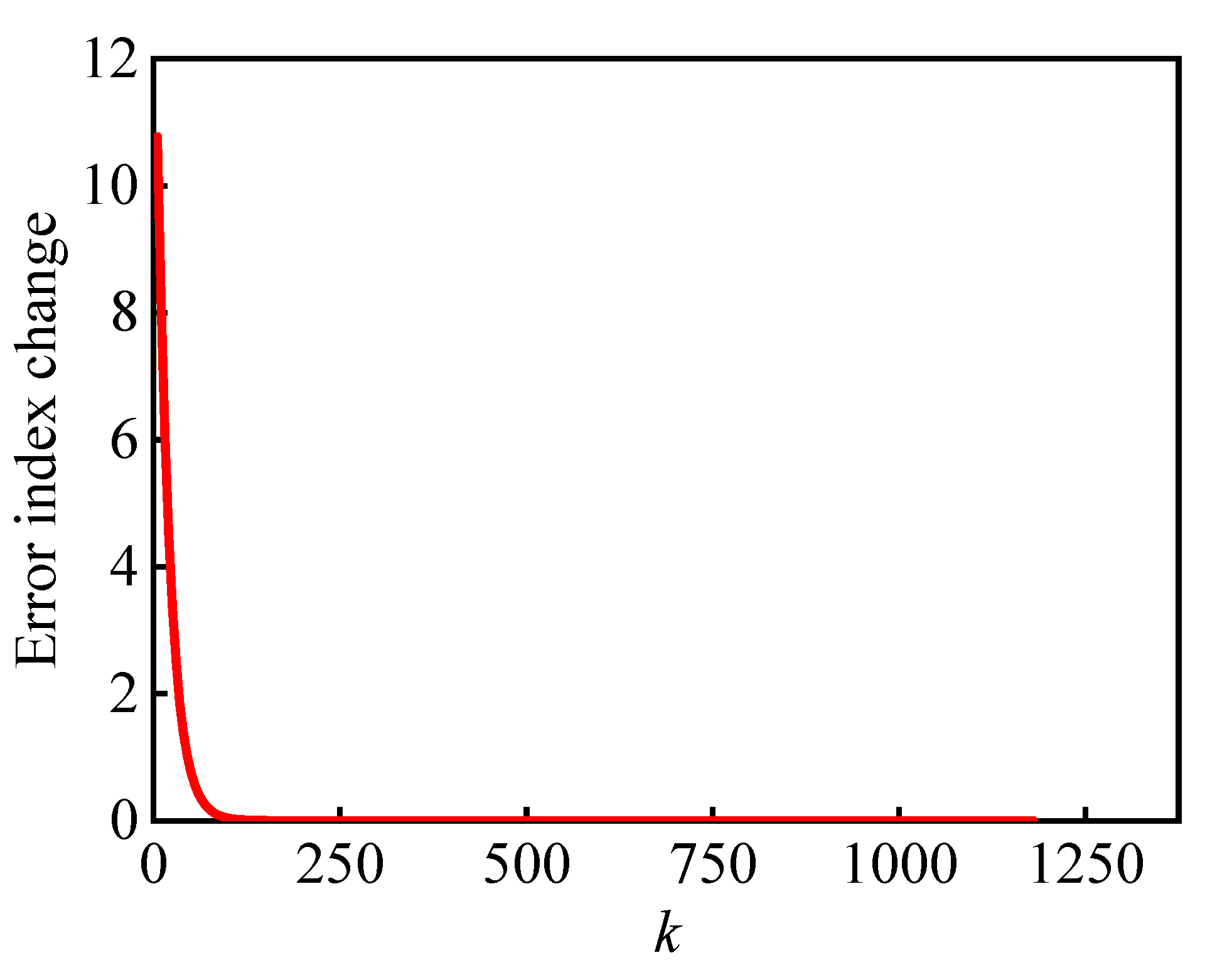
| Number of Hidden Layer Nodes | Steps to Reach the Target Number of Training | Error (mm) |
|---|---|---|
| 3 | 4376 | 5.215 |
| 5 | 2947 | 2.016 |
| 7 | 3542 | 3.962 |
| 9 | 4608 | 4.372 |
| Input | Output | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 1 | 0.967 | 0.022 | −0.089 |
| 0.97 | 0.1 | 0 | 0 | 0 | 1.011 | 0.002 | −0.007 |
| 1 | 1 | 0.1 | 0 | 1 | 0.977 | 0.033 | −0.140 |
| Deviation | Control Algorithm | X | Y | Z |
|---|---|---|---|---|
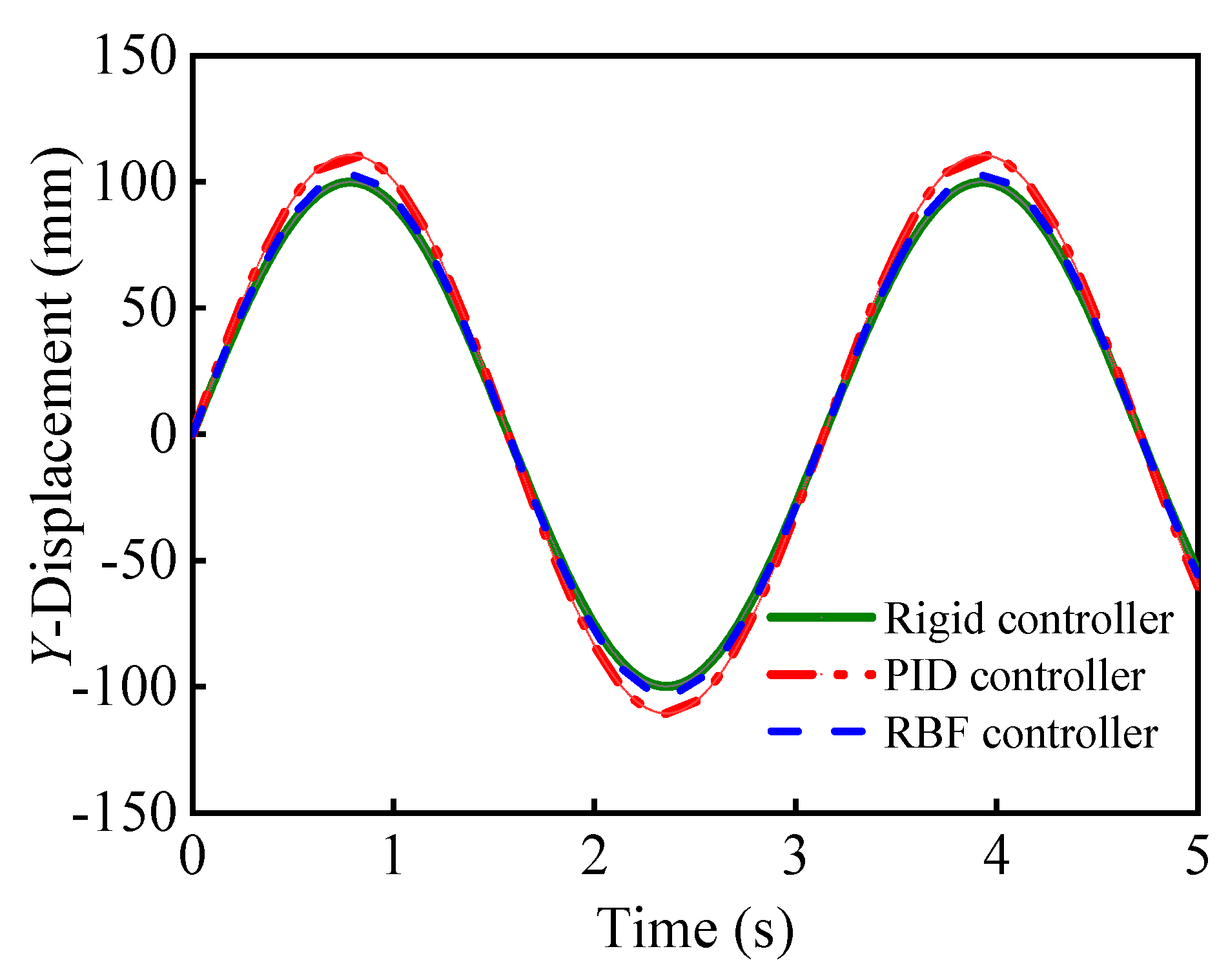
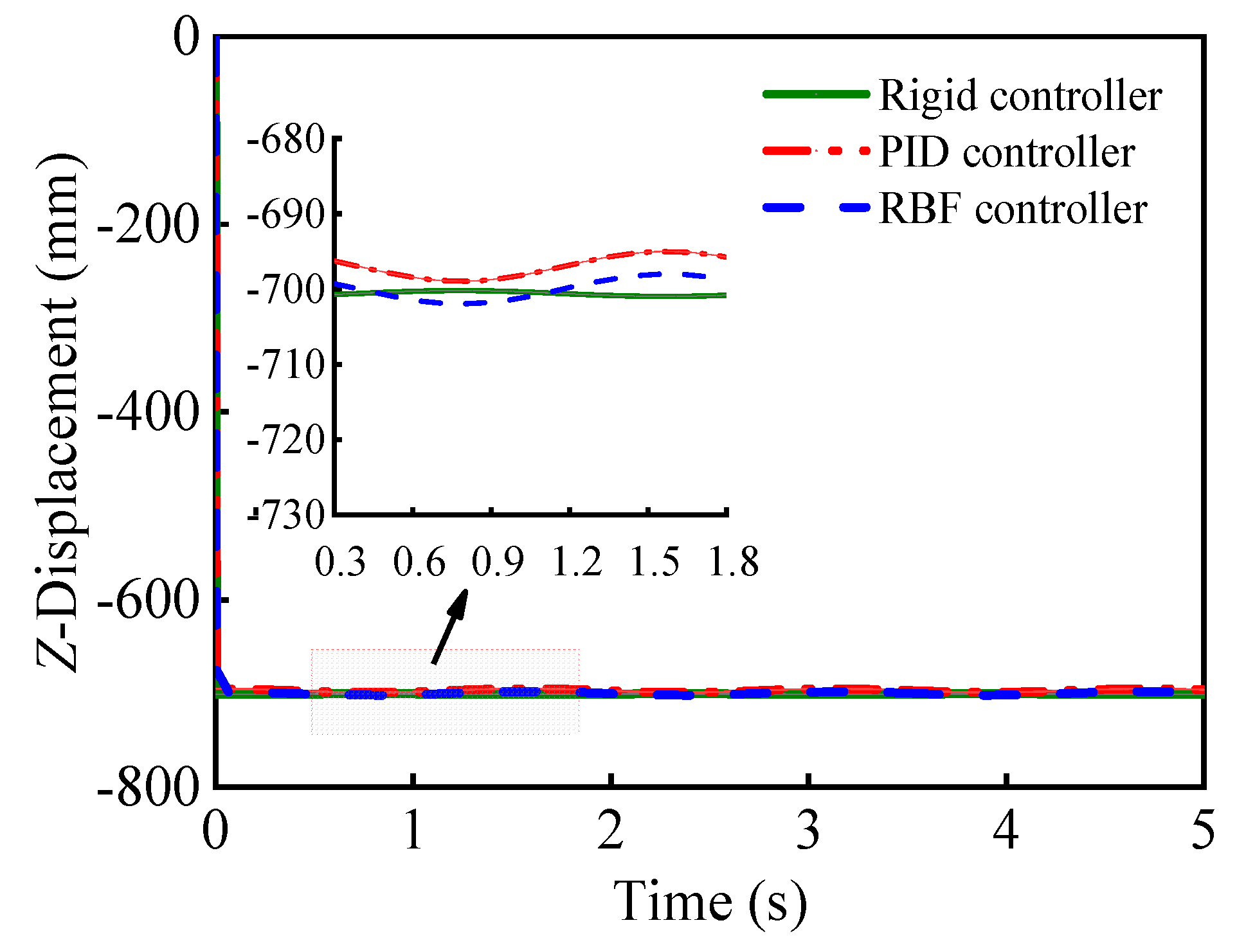
| Maximum deviation | RBF | 2.936 | 1.268 | 2.96 |
| PID | 3.372 | 2.072 | 5.961 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhao, X.; Liu, L.; Dai, T. Adaptive Sliding Mode Neural Network Control and Flexible Vibration Suppression of a Flexible Spatial Parallel Robot. Electronics 2021, 10, 212. https://doi.org/10.3390/electronics10020212
Zhang Q, Zhao X, Liu L, Dai T. Adaptive Sliding Mode Neural Network Control and Flexible Vibration Suppression of a Flexible Spatial Parallel Robot. Electronics. 2021; 10(2):212. https://doi.org/10.3390/electronics10020212
Chicago/Turabian StyleZhang, Qingyun, Xinhua Zhao, Liang Liu, and Tengda Dai. 2021. "Adaptive Sliding Mode Neural Network Control and Flexible Vibration Suppression of a Flexible Spatial Parallel Robot" Electronics 10, no. 2: 212. https://doi.org/10.3390/electronics10020212
APA StyleZhang, Q., Zhao, X., Liu, L., & Dai, T. (2021). Adaptive Sliding Mode Neural Network Control and Flexible Vibration Suppression of a Flexible Spatial Parallel Robot. Electronics, 10(2), 212. https://doi.org/10.3390/electronics10020212




