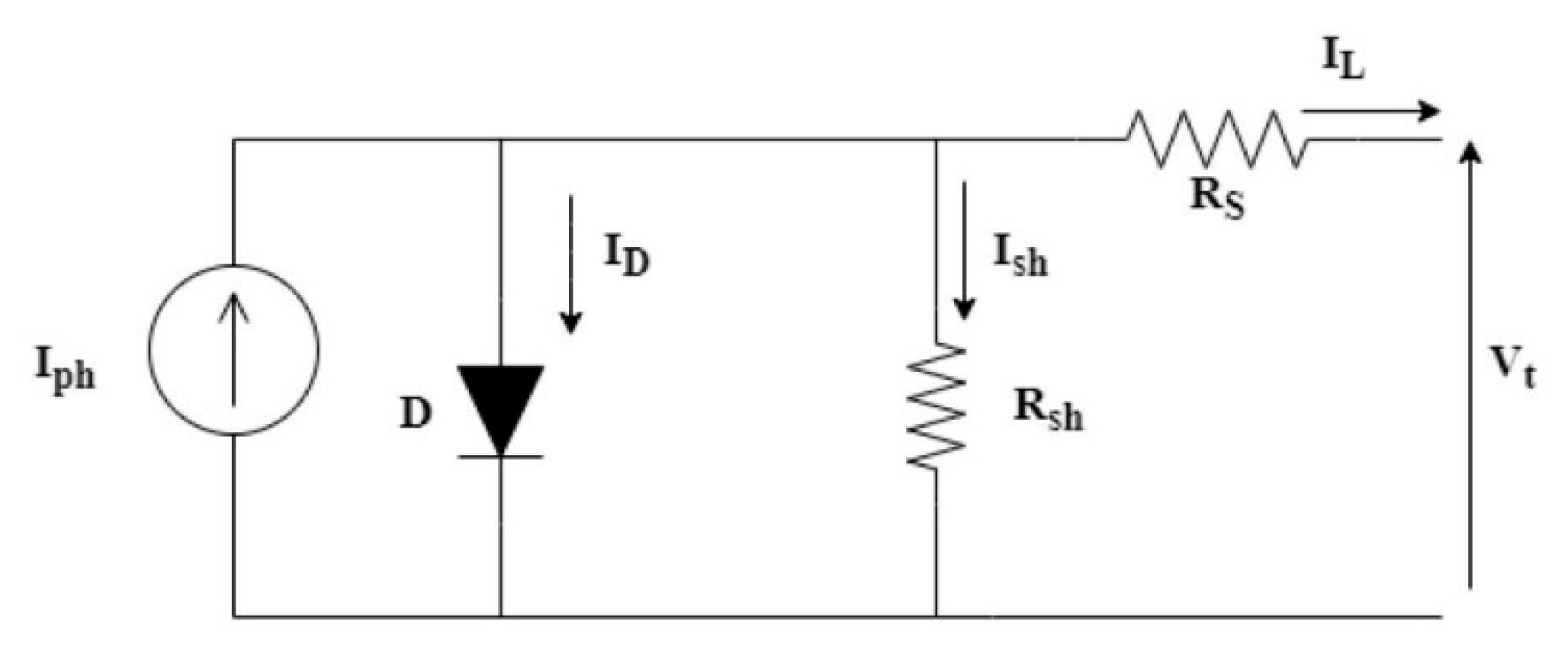
Figure 1.
Single Diode Model (SDM) of the solar PV cell.
Figure 1.
Single Diode Model (SDM) of the solar PV cell.
Figure 2.
Double Diode Model (DDM) of the solar PV cell.
Figure 2.
Double Diode Model (DDM) of the solar PV cell.
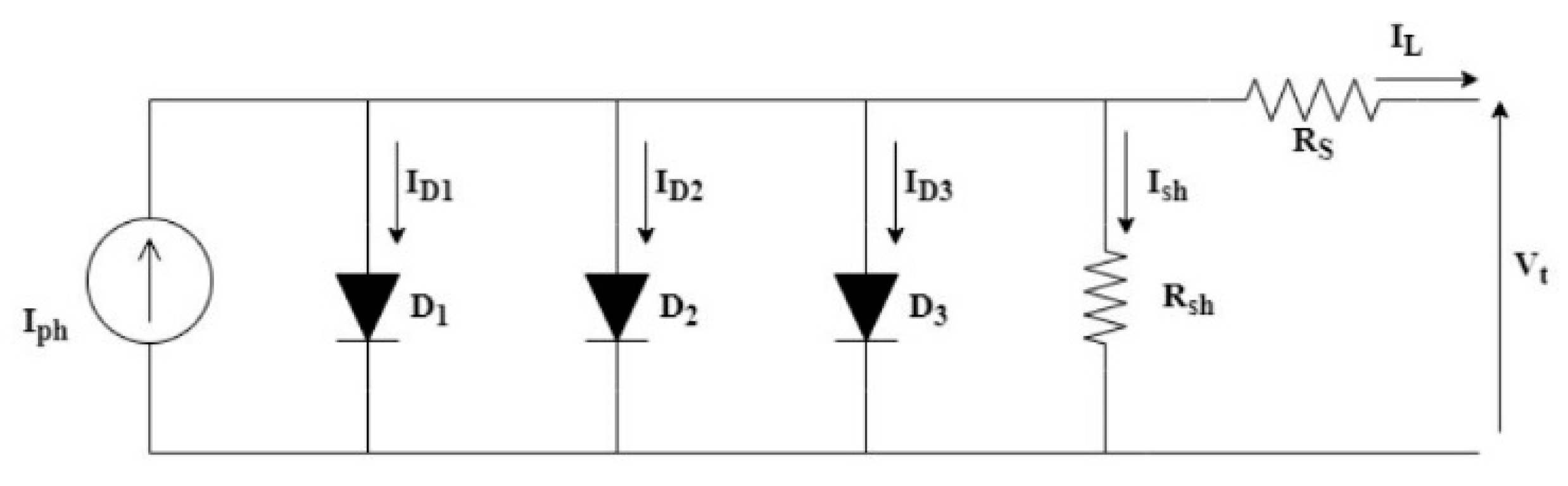
Figure 3.
Three Diode Model (TDM) of the PV cell.
Figure 3.
Three Diode Model (TDM) of the PV cell.
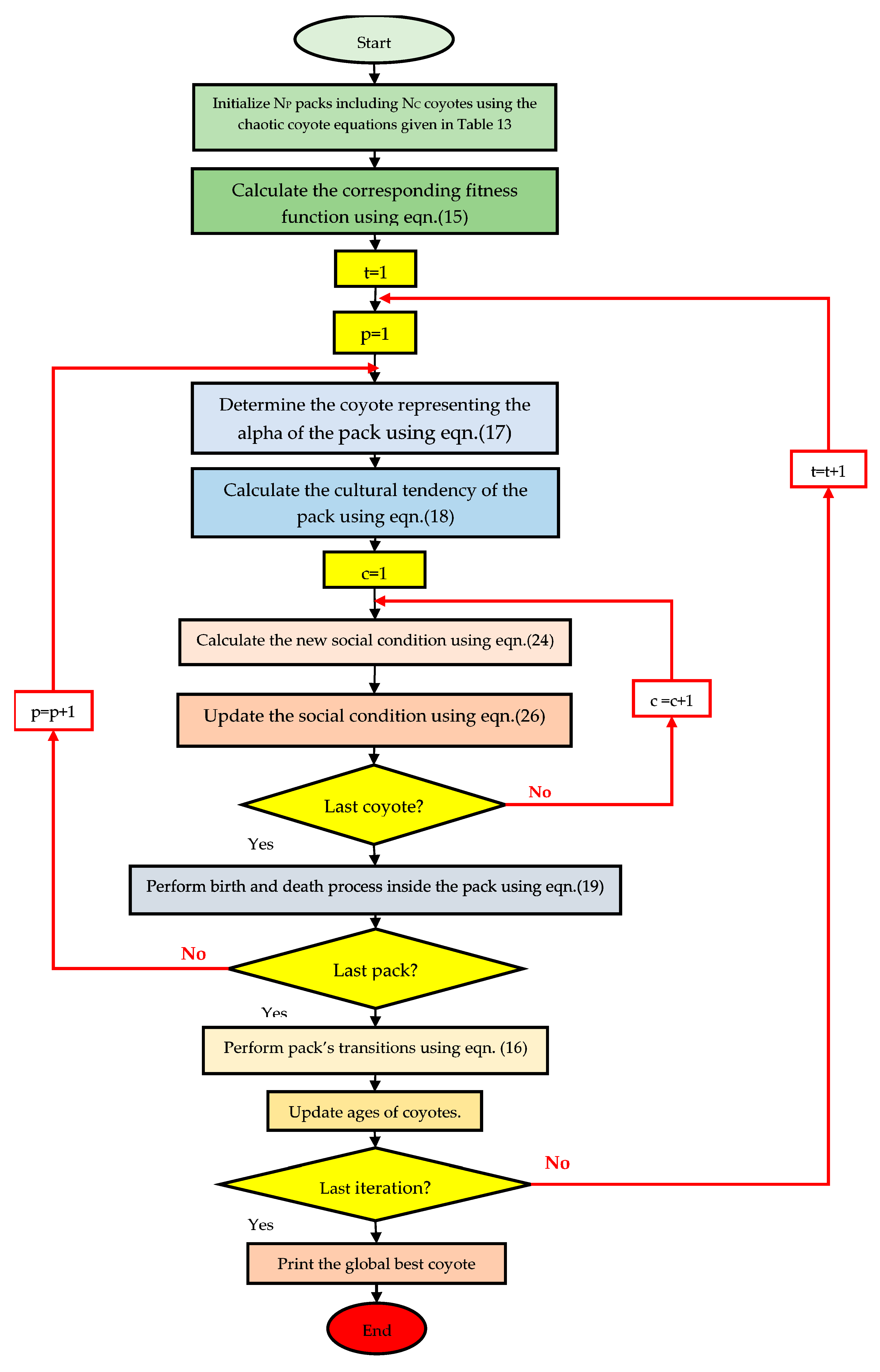
Figure 4.
Chaotic COA Flowchart.
Figure 4.
Chaotic COA Flowchart.
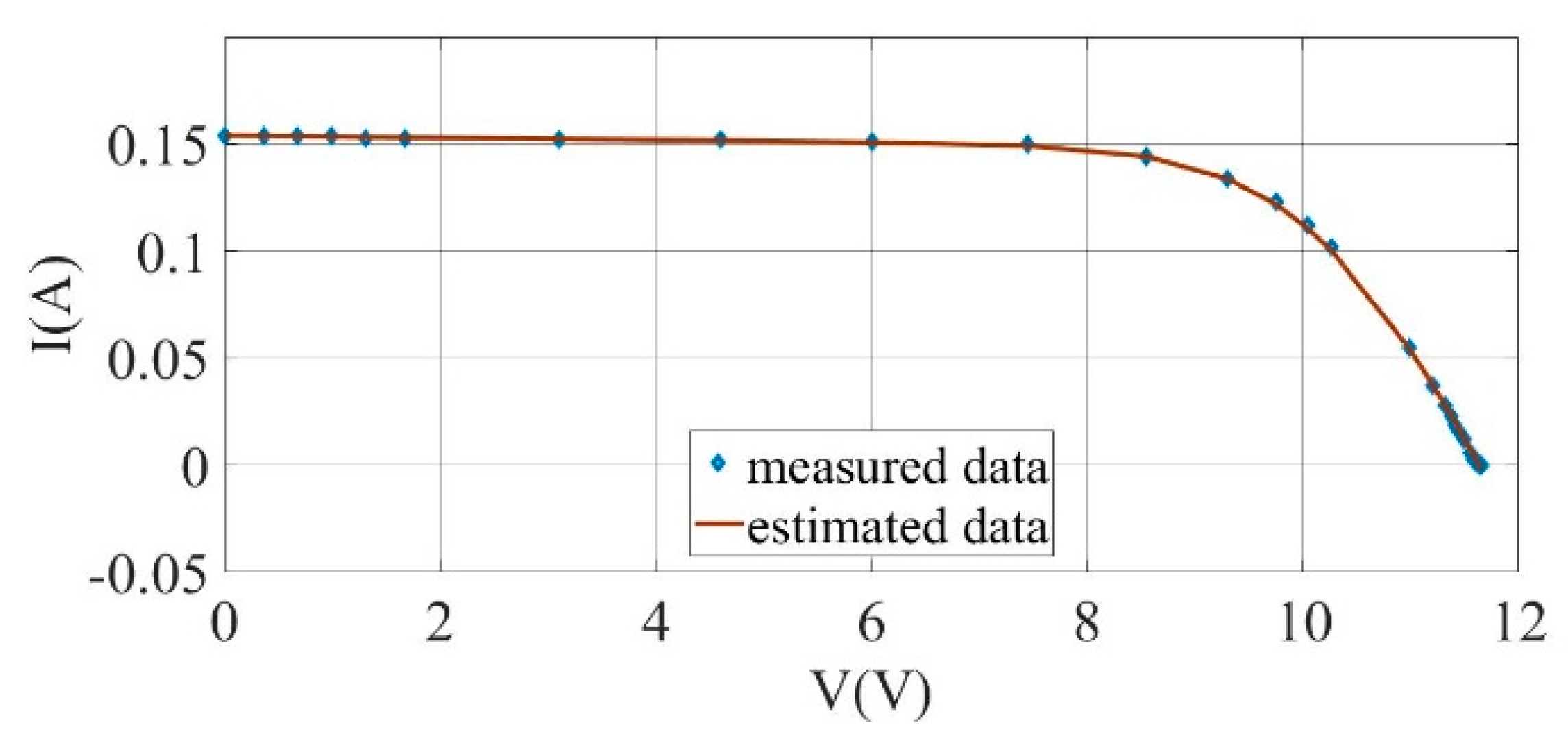
Figure 5.
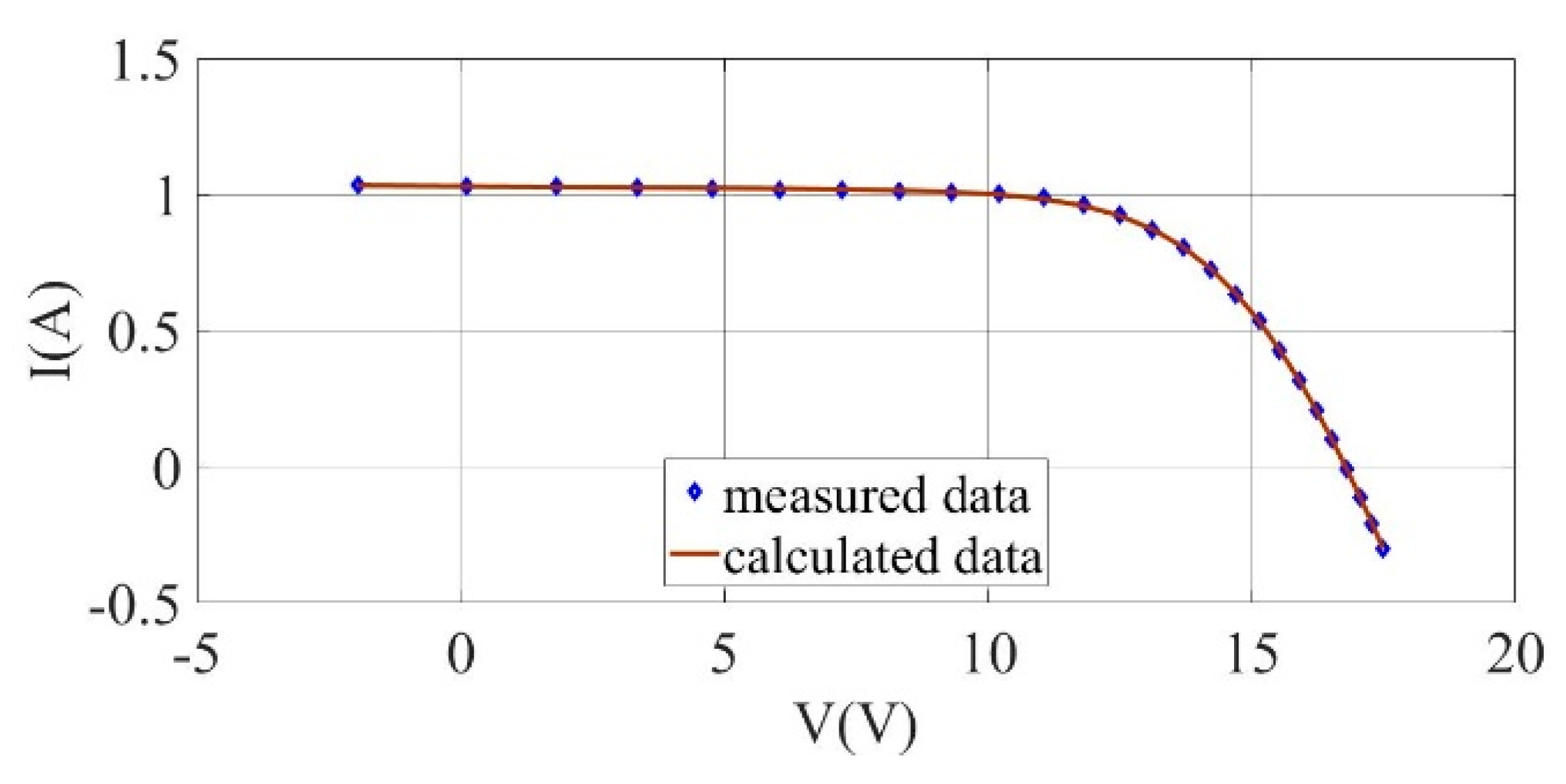
I–V curves for the experimentally measured data and the estimated results for a mono-crystalline LSM20 solar cell module (SDM).
Figure 5.
I–V curves for the experimentally measured data and the estimated results for a mono-crystalline LSM20 solar cell module (SDM).
Figure 6.
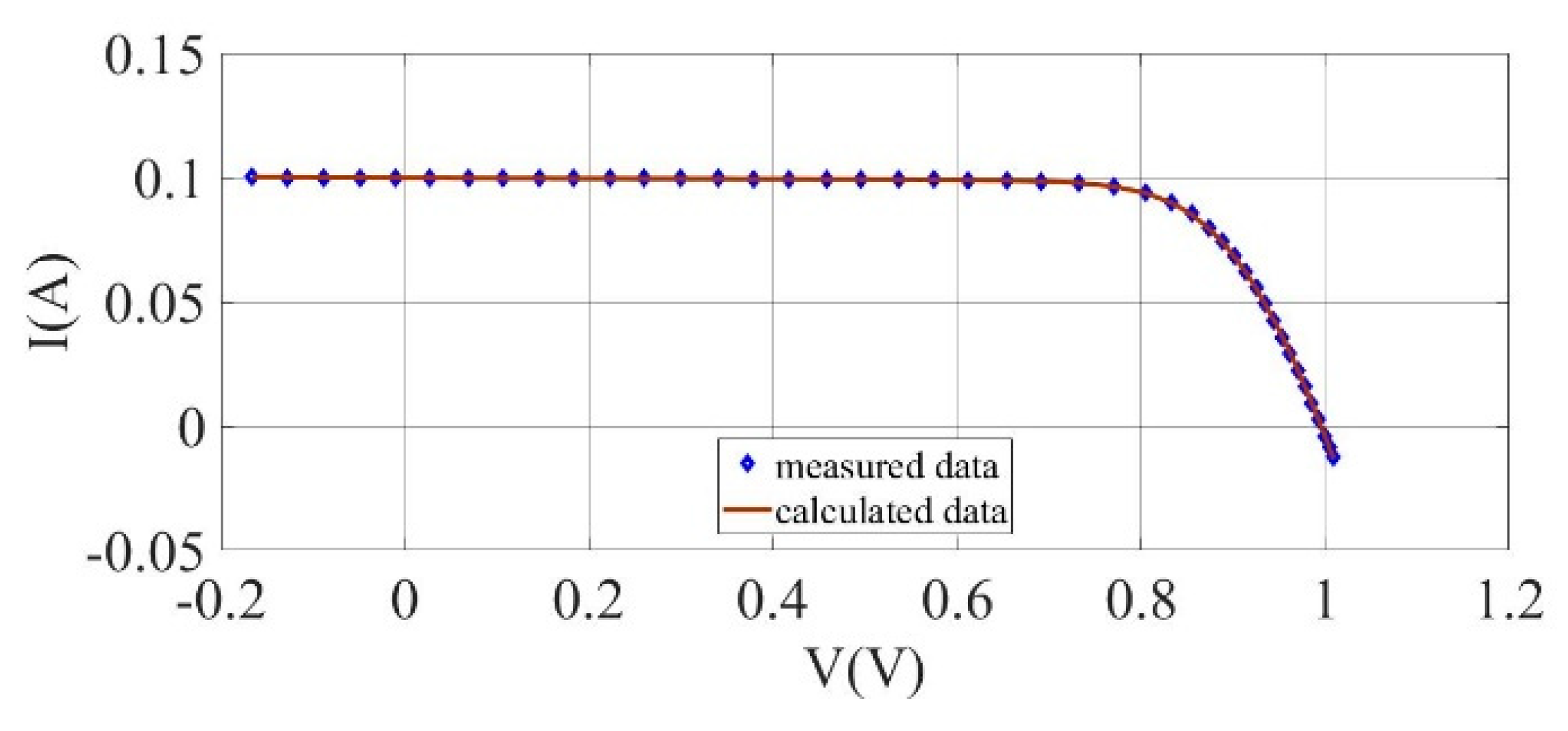
I–V curves for the experimentally measured data and the estimated results for Photowatt-PWP201 solar cell module (SDM).
Figure 6.
I–V curves for the experimentally measured data and the estimated results for Photowatt-PWP201 solar cell module (SDM).
Figure 7.
I–V curves for the experimentally measured data and the estimated results for GaAs thin-film solar cell (SDM).
Figure 7.
I–V curves for the experimentally measured data and the estimated results for GaAs thin-film solar cell (SDM).
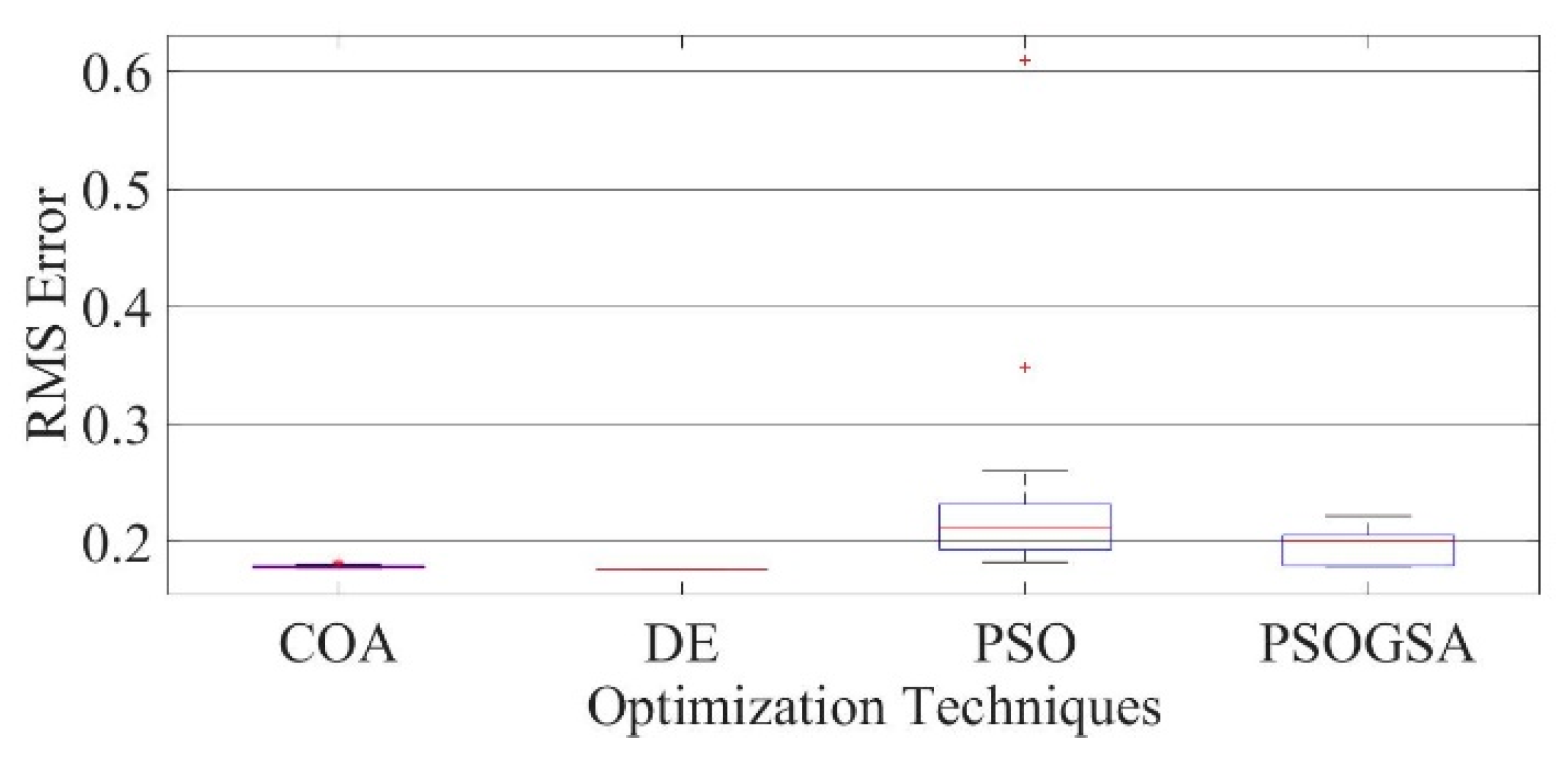
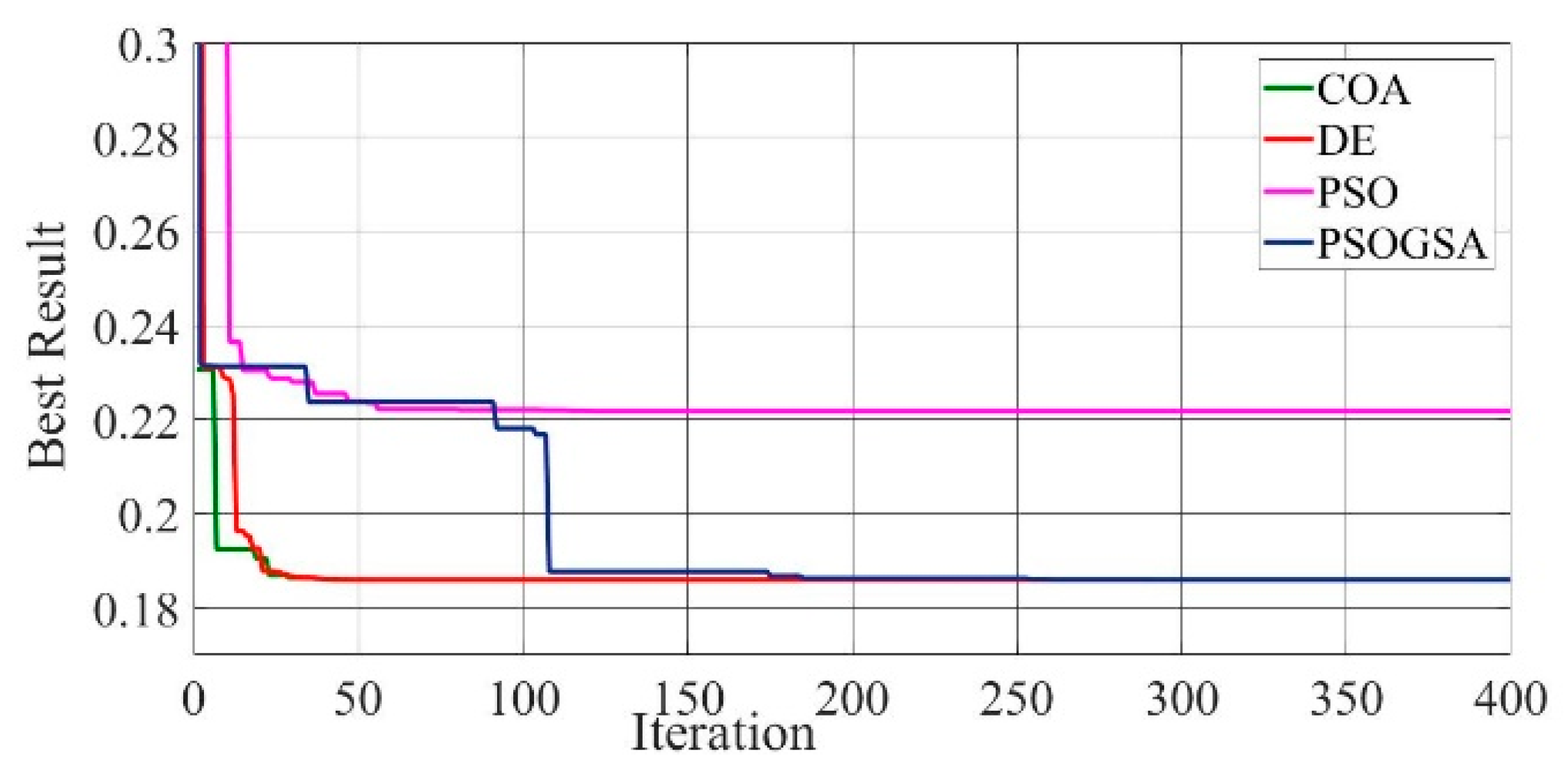
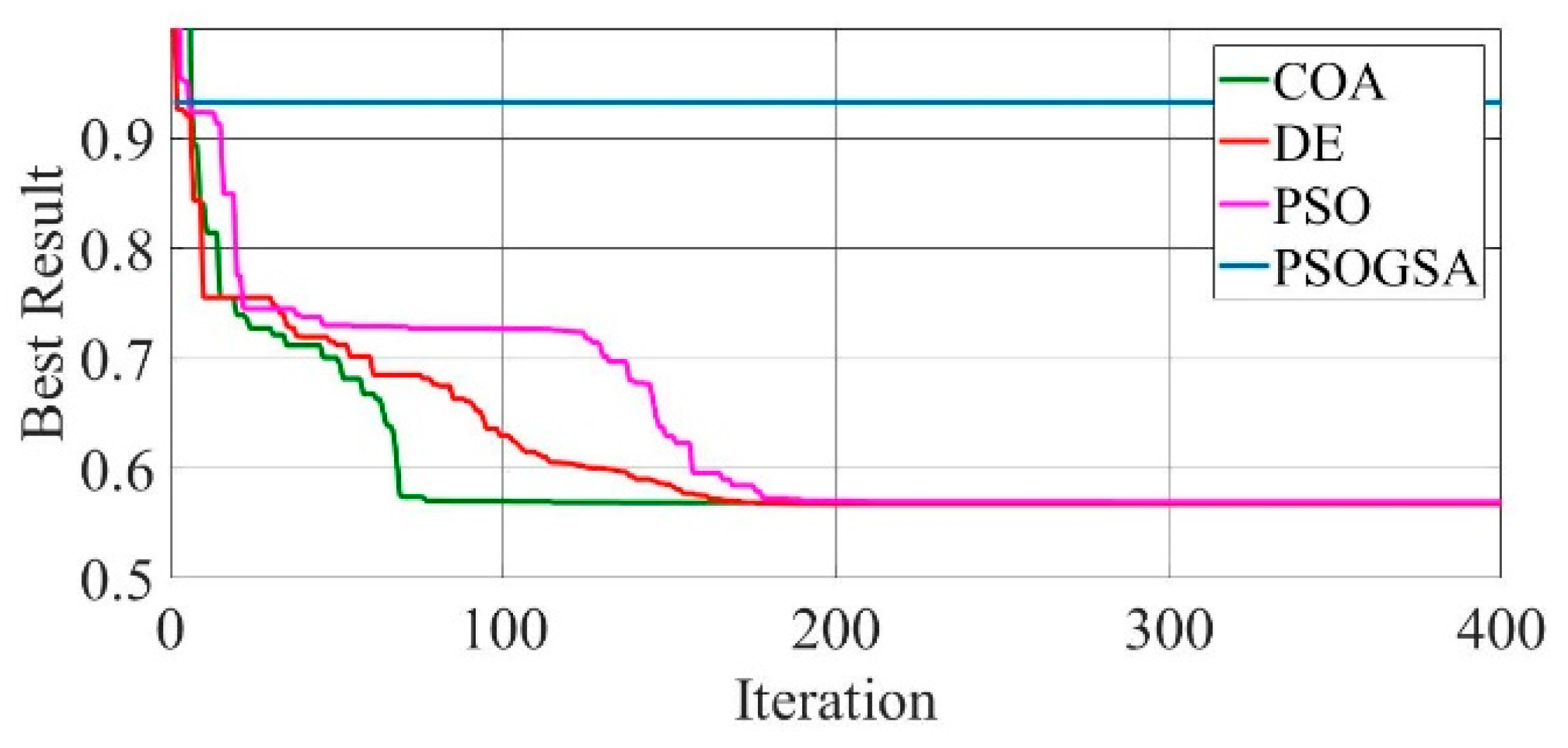
Figure 8.
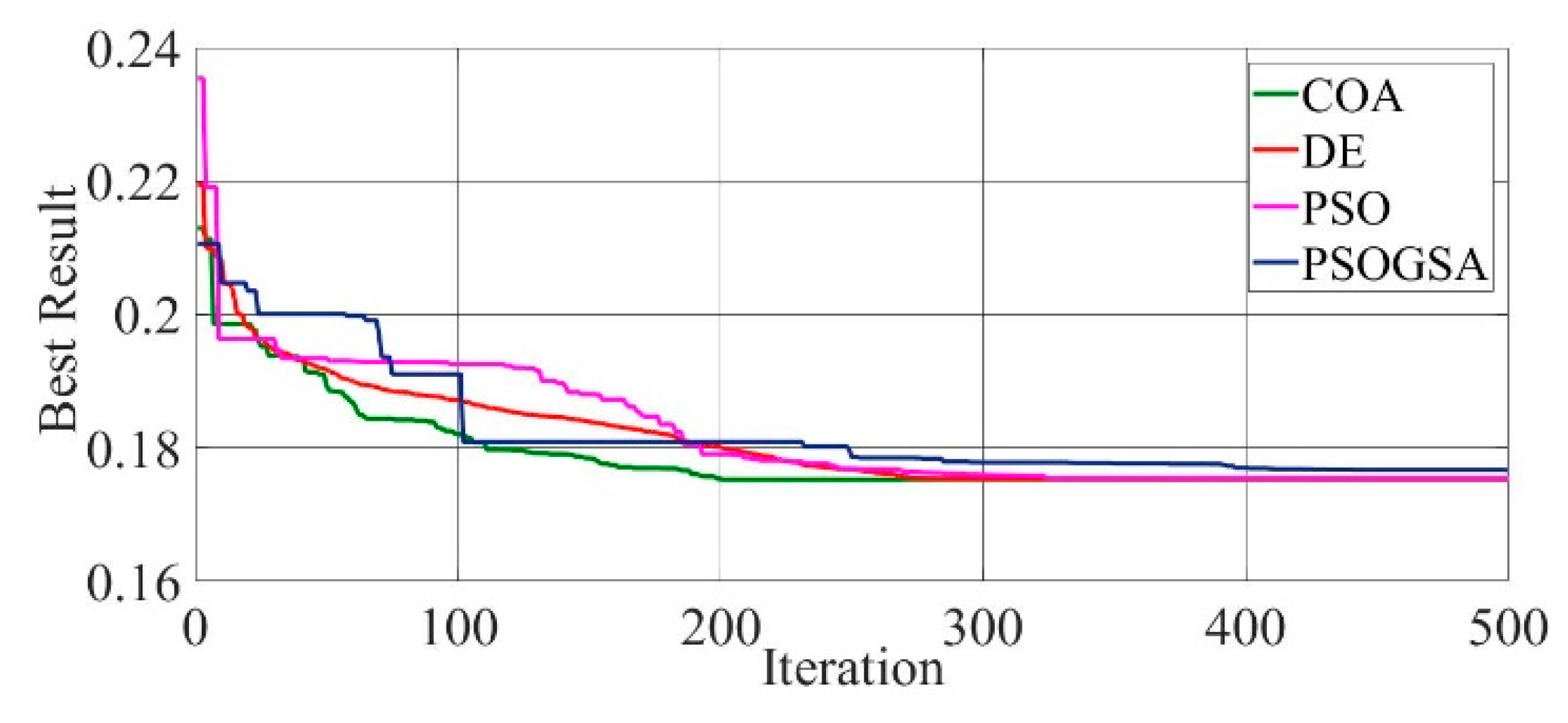
Convergence curves of mono-crystalline LSM20 solar cell module (SDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 8.
Convergence curves of mono-crystalline LSM20 solar cell module (SDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
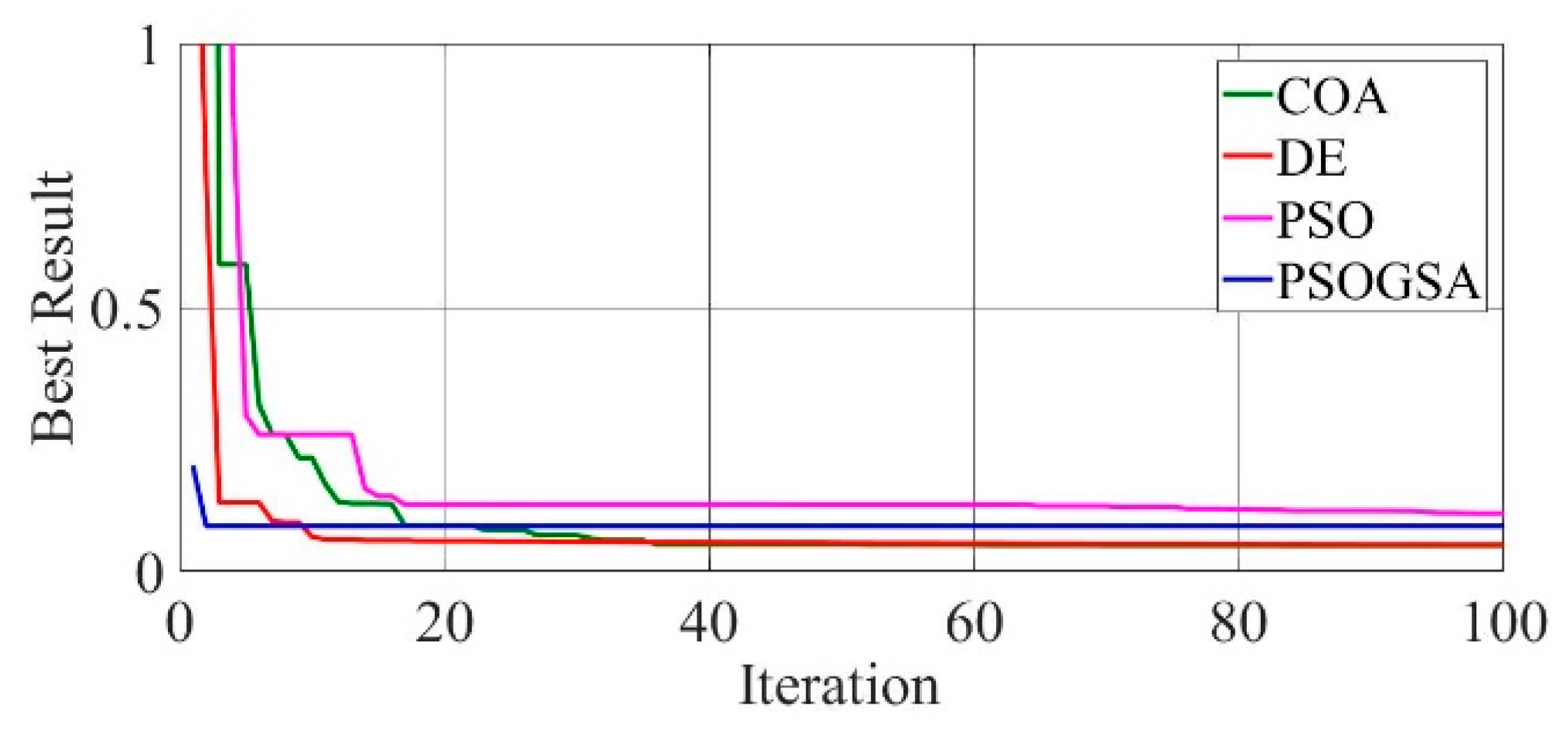
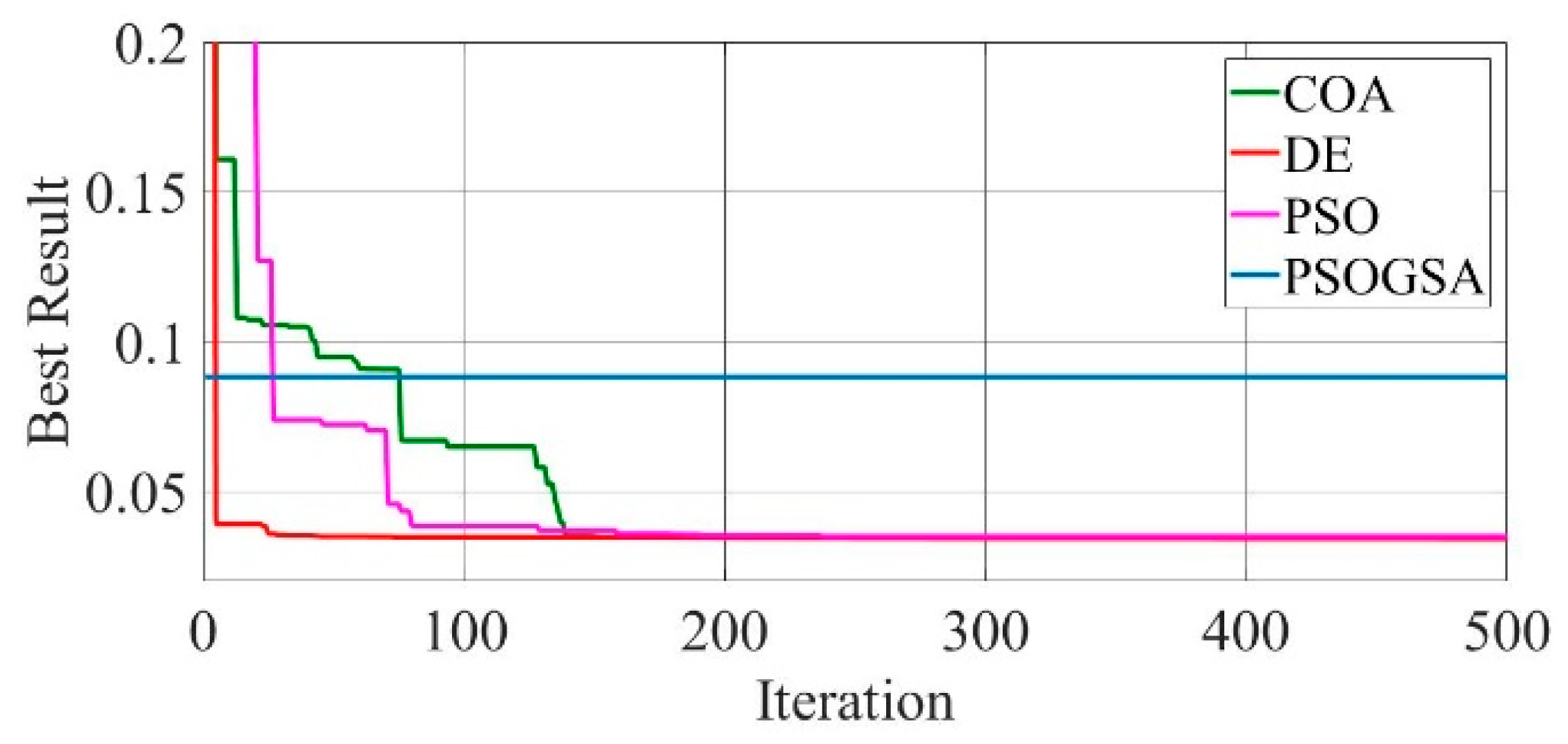
Figure 9.
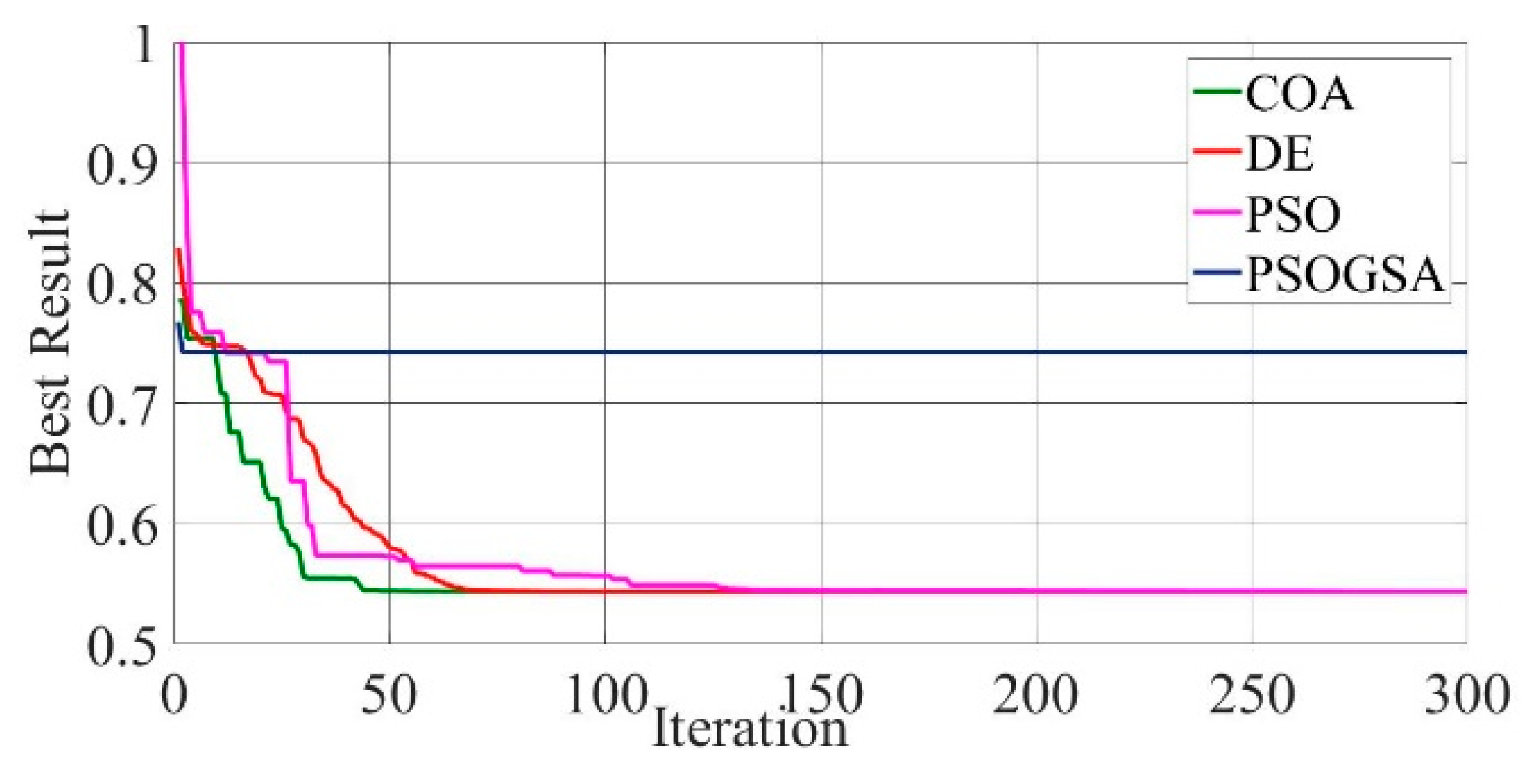
Convergence curves of Photowatt-PWP201 solar cell module (SDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 9.
Convergence curves of Photowatt-PWP201 solar cell module (SDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
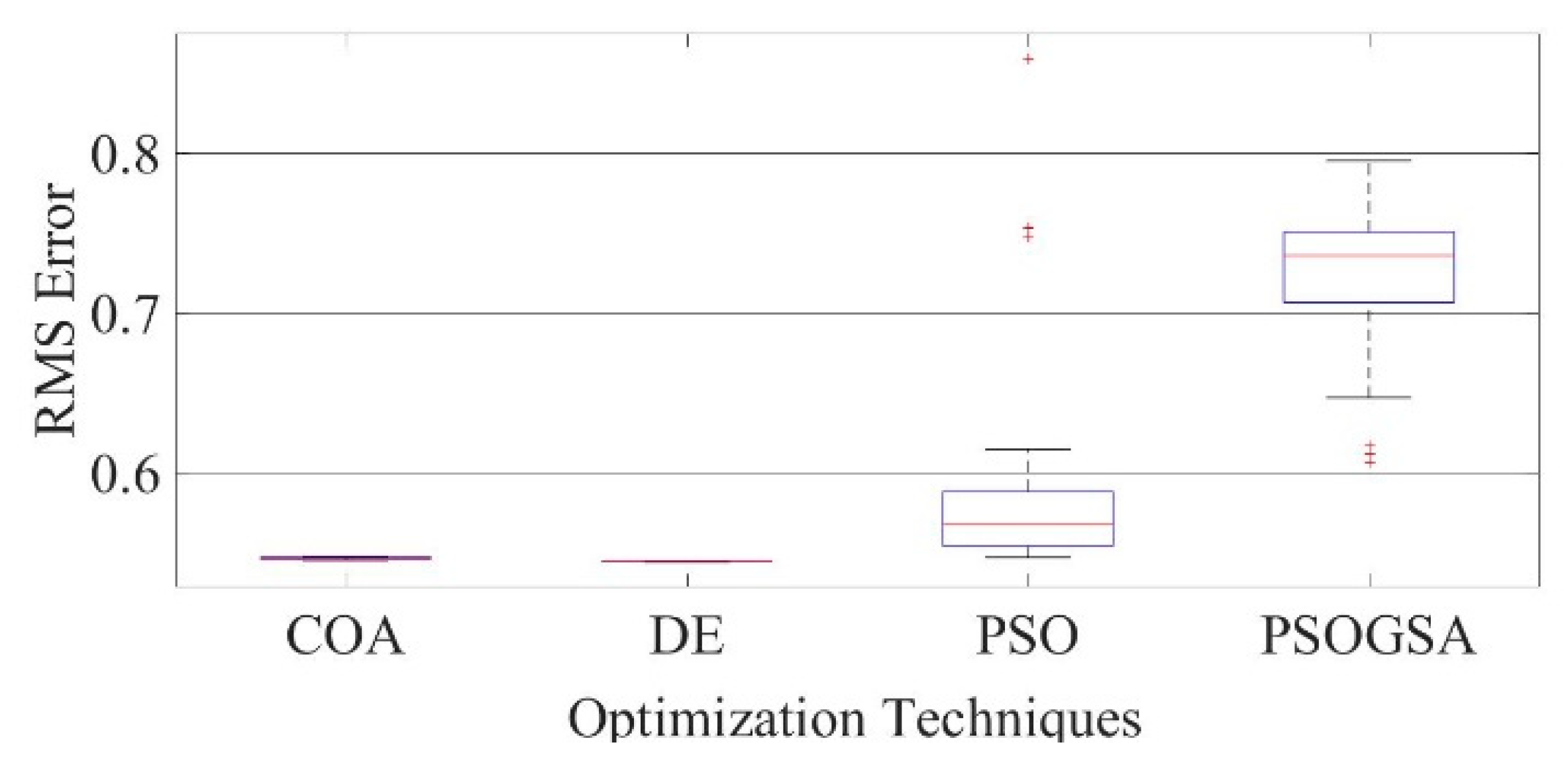
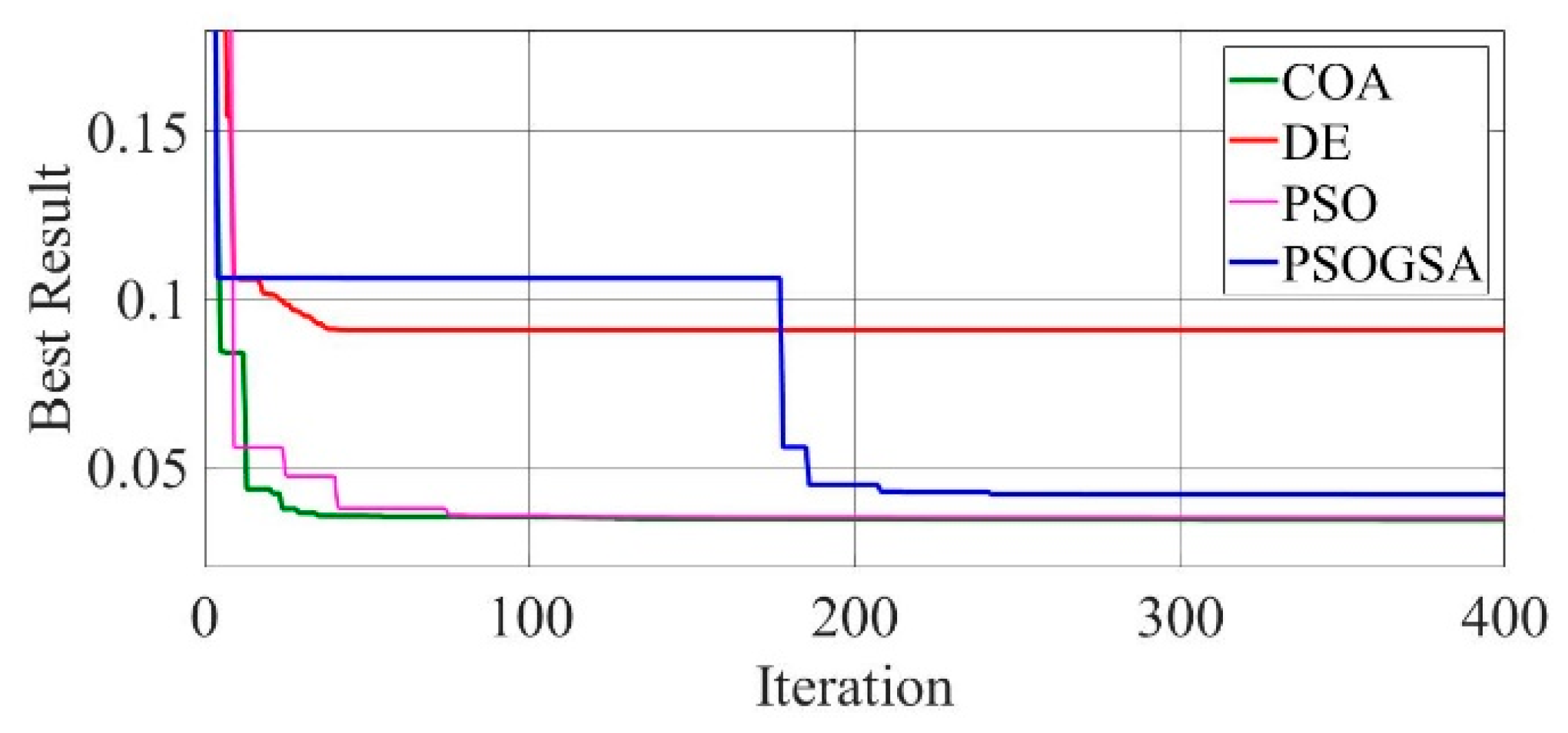
Figure 10.
Convergence curves of GaAs thin-film solar cell-PVM752 (SDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 10.
Convergence curves of GaAs thin-film solar cell-PVM752 (SDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
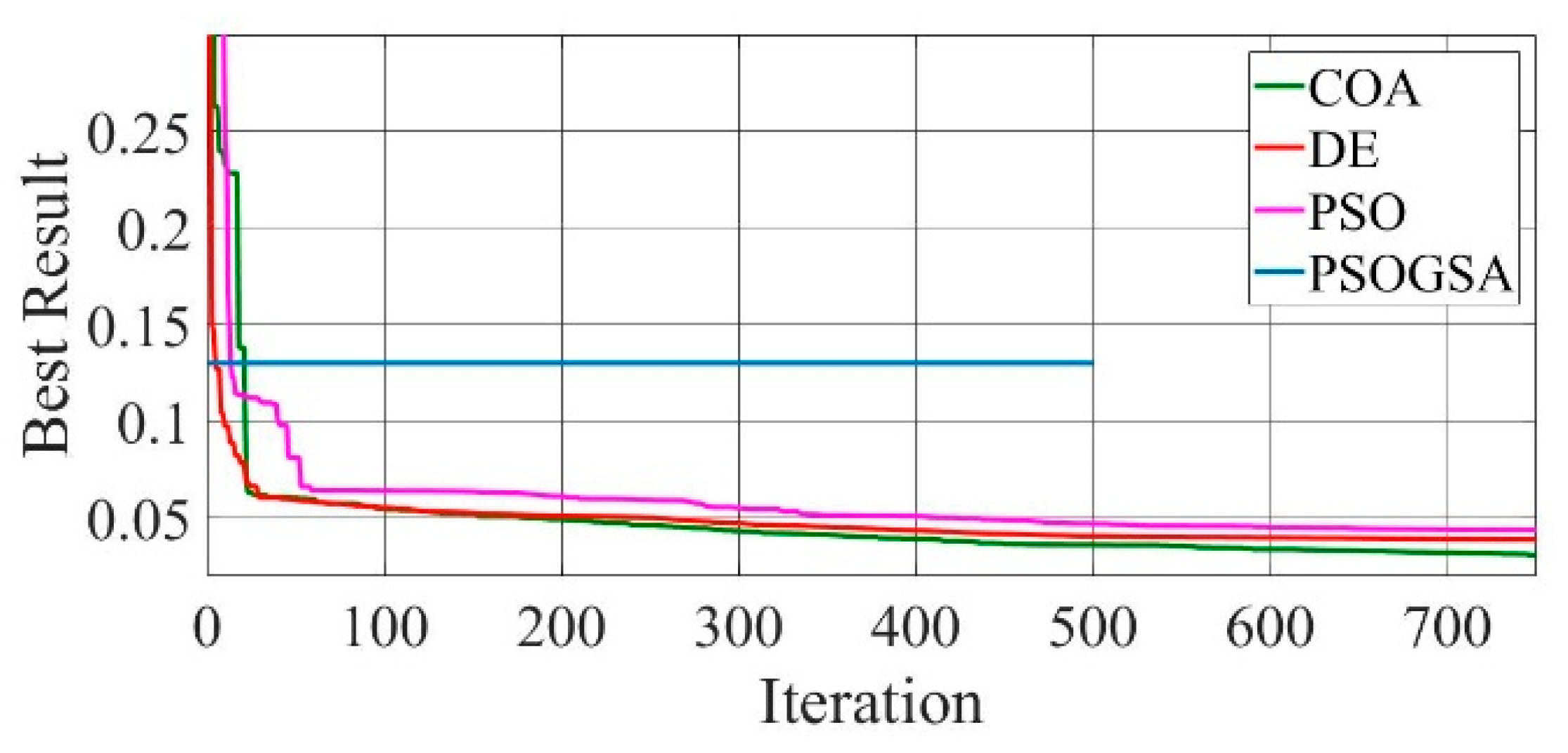
Figure 11.
Convergence curves of mono-crystalline LSM20 solar cell module (DDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 11.
Convergence curves of mono-crystalline LSM20 solar cell module (DDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
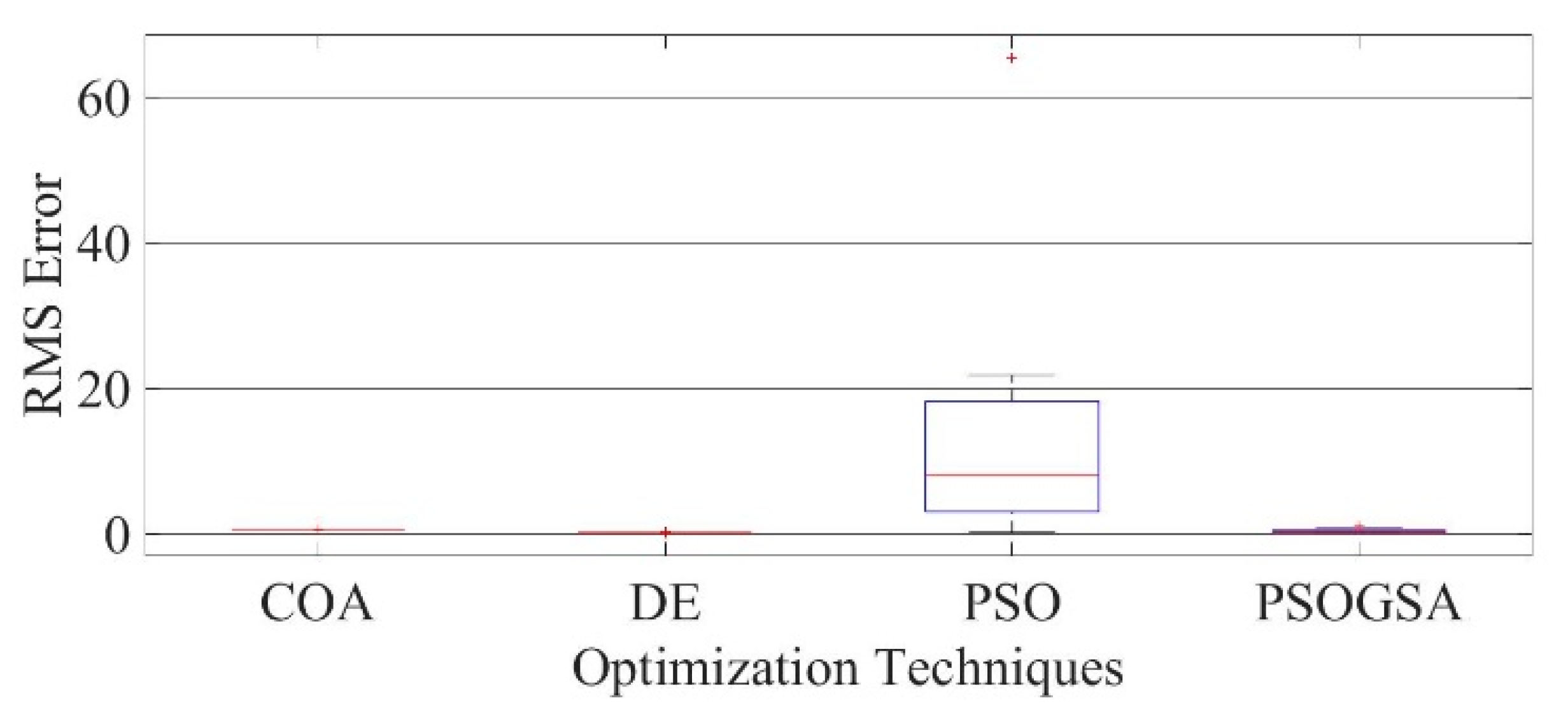
Figure 12.
Convergence curves of Photowatt-PWP201 solar cell module (DDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 12.
Convergence curves of Photowatt-PWP201 solar cell module (DDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 13.
Convergence curves of GaAs thin-film solar cell-PVM752 (DDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 13.
Convergence curves of GaAs thin-film solar cell-PVM752 (DDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 14.
Convergence curves of mono-crystalline LSM20 solar cell module (TDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 14.
Convergence curves of mono-crystalline LSM20 solar cell module (TDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
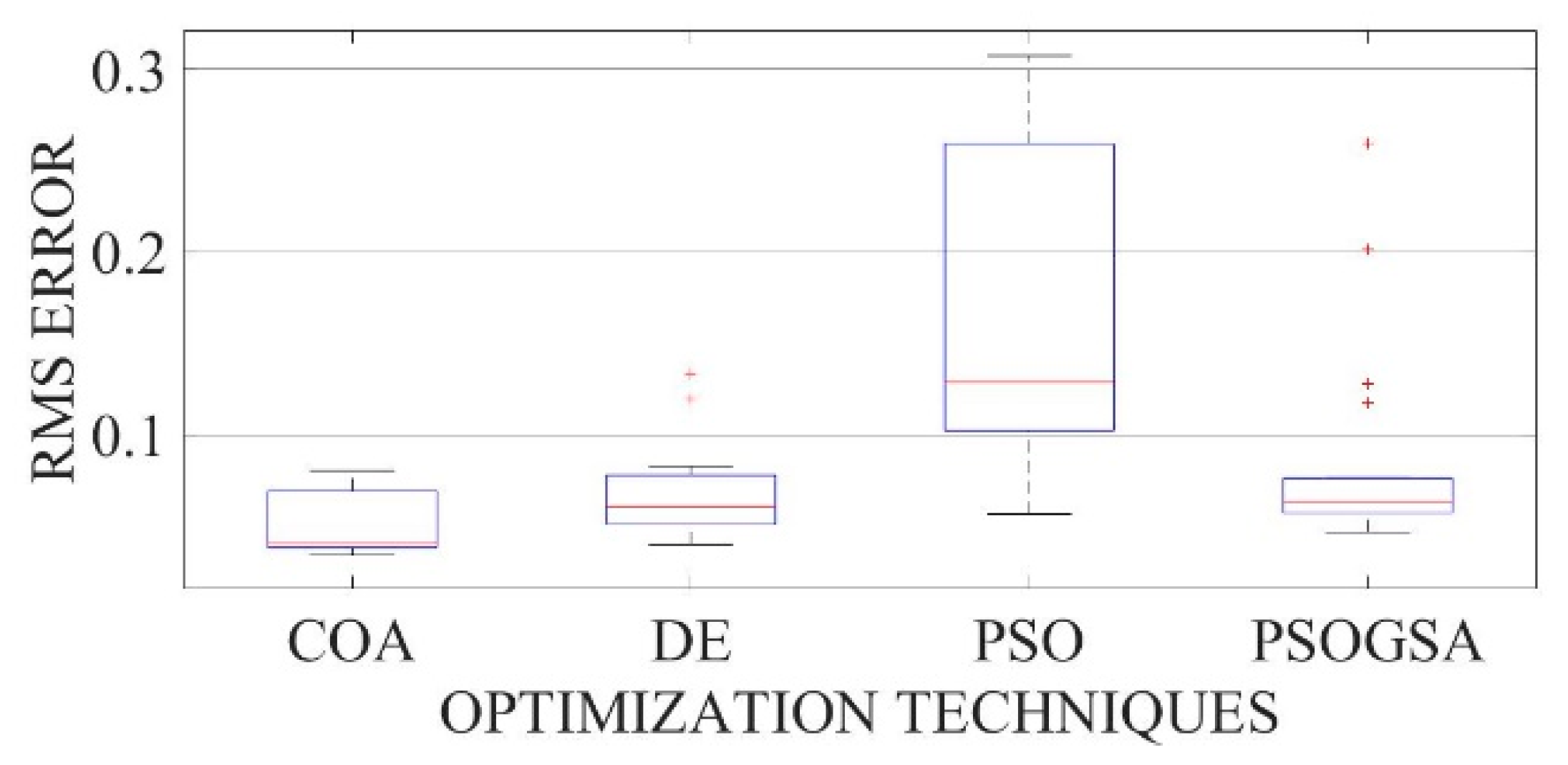
Figure 15.
Convergence curves of Photowatt-PWP201 solar cell module (TDM) comparing the convergence characteristics of COA, DE, PSO and PSOGSA.
Figure 15.
Convergence curves of Photowatt-PWP201 solar cell module (TDM) comparing the convergence characteristics of COA, DE, PSO and PSOGSA.
Figure 16.
Convergence curves of GaAs thin-film solar cell-PVM752 (TDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
Figure 16.
Convergence curves of GaAs thin-film solar cell-PVM752 (TDM) comparing the convergence characteristics of COA, DE, PSO, and PSOGSA.
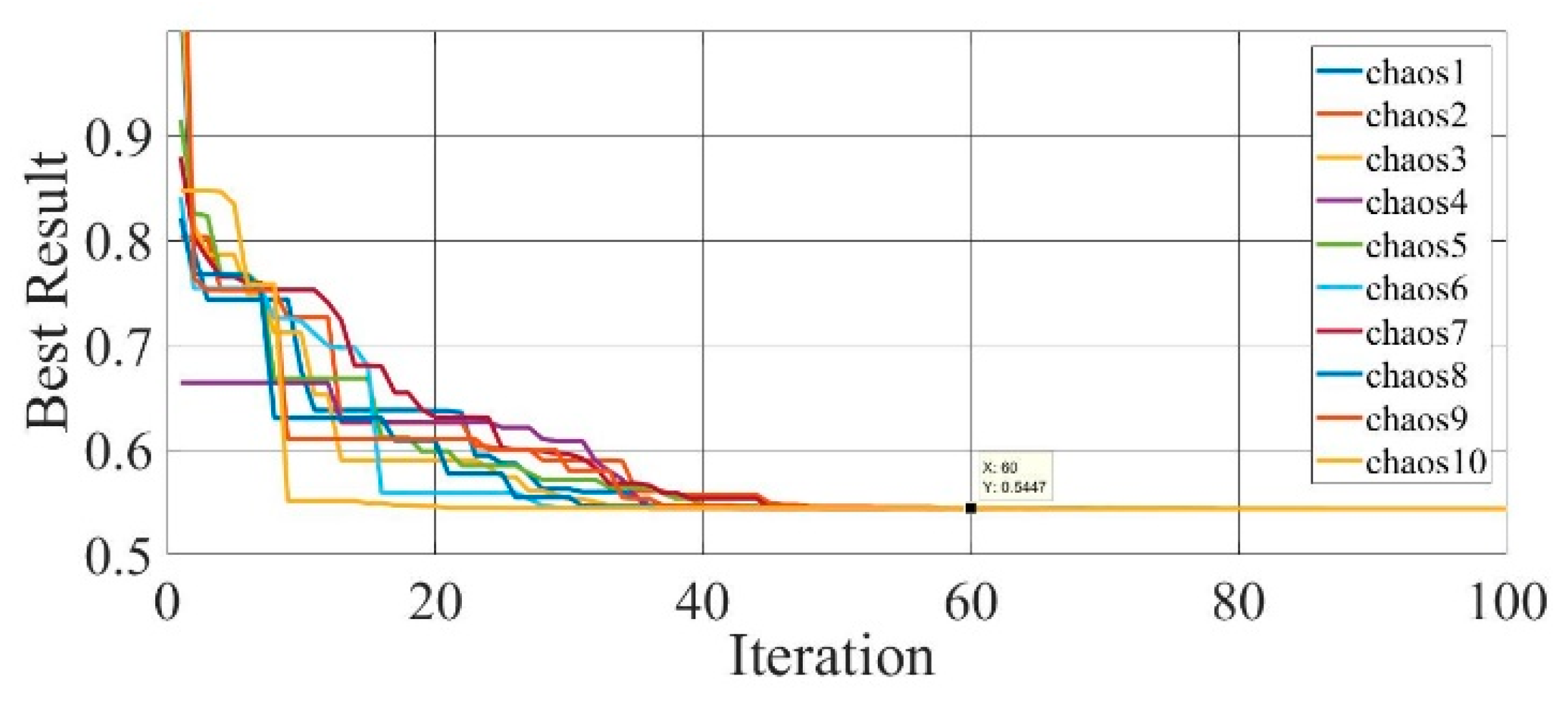
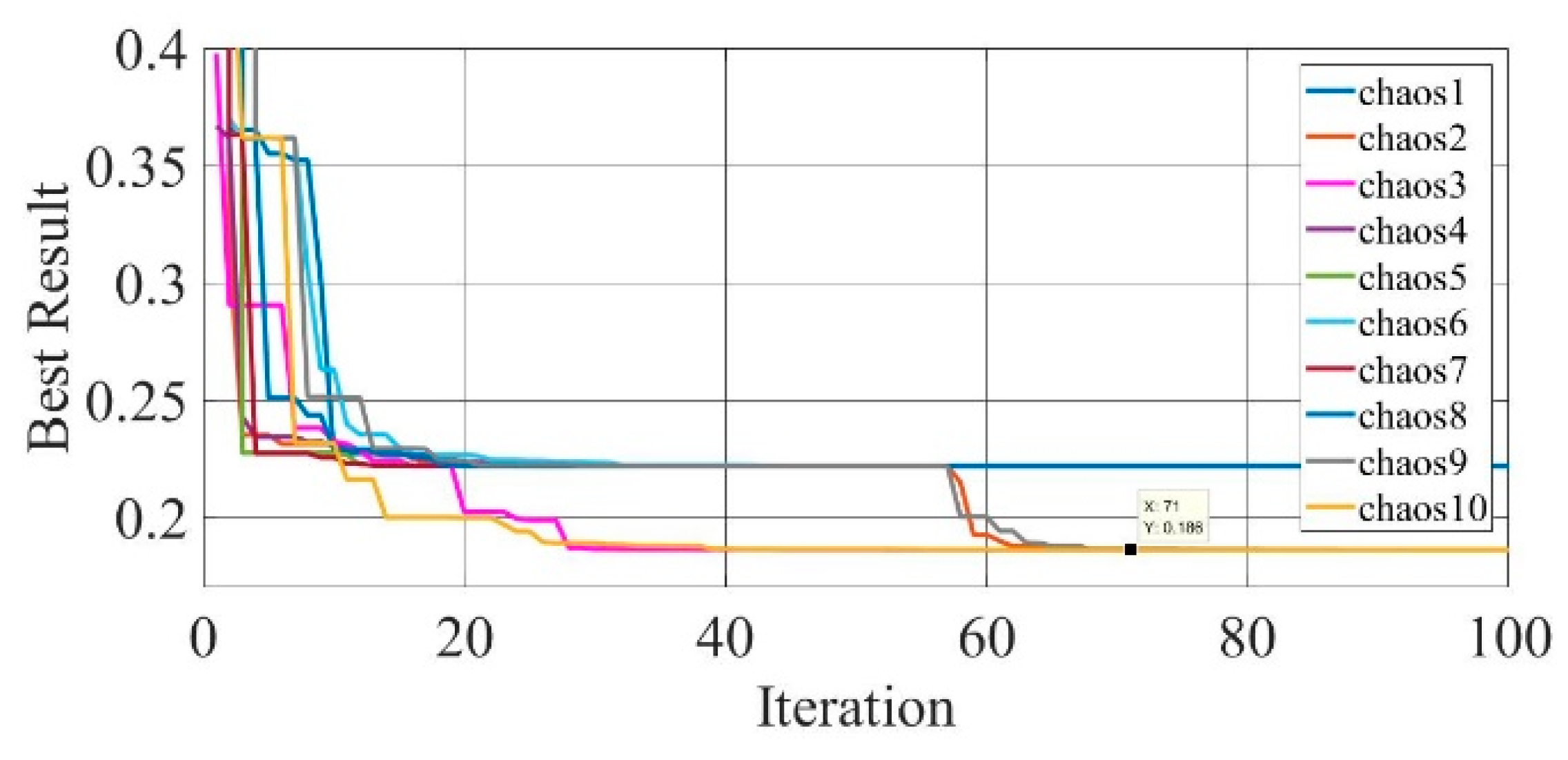
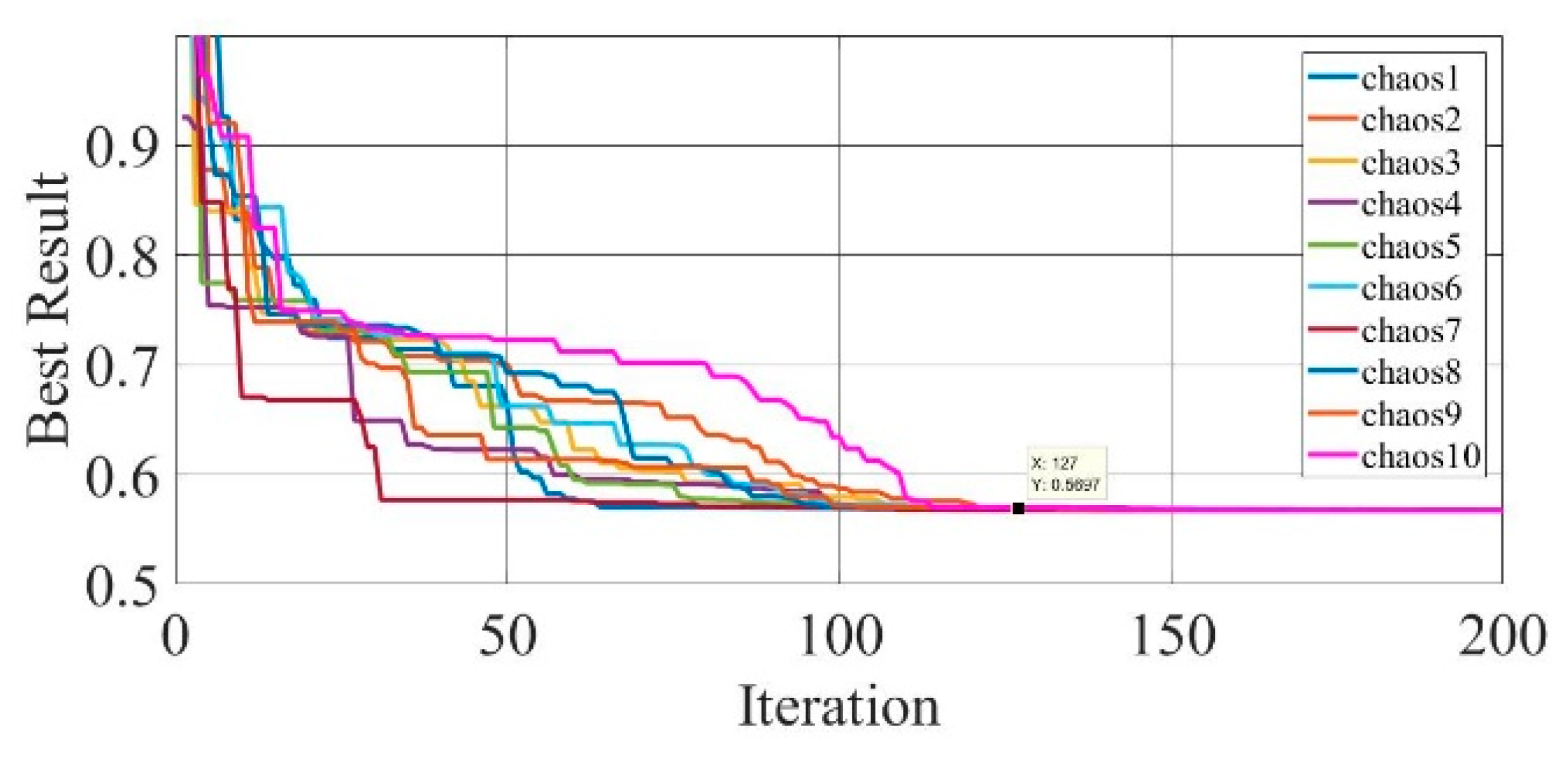
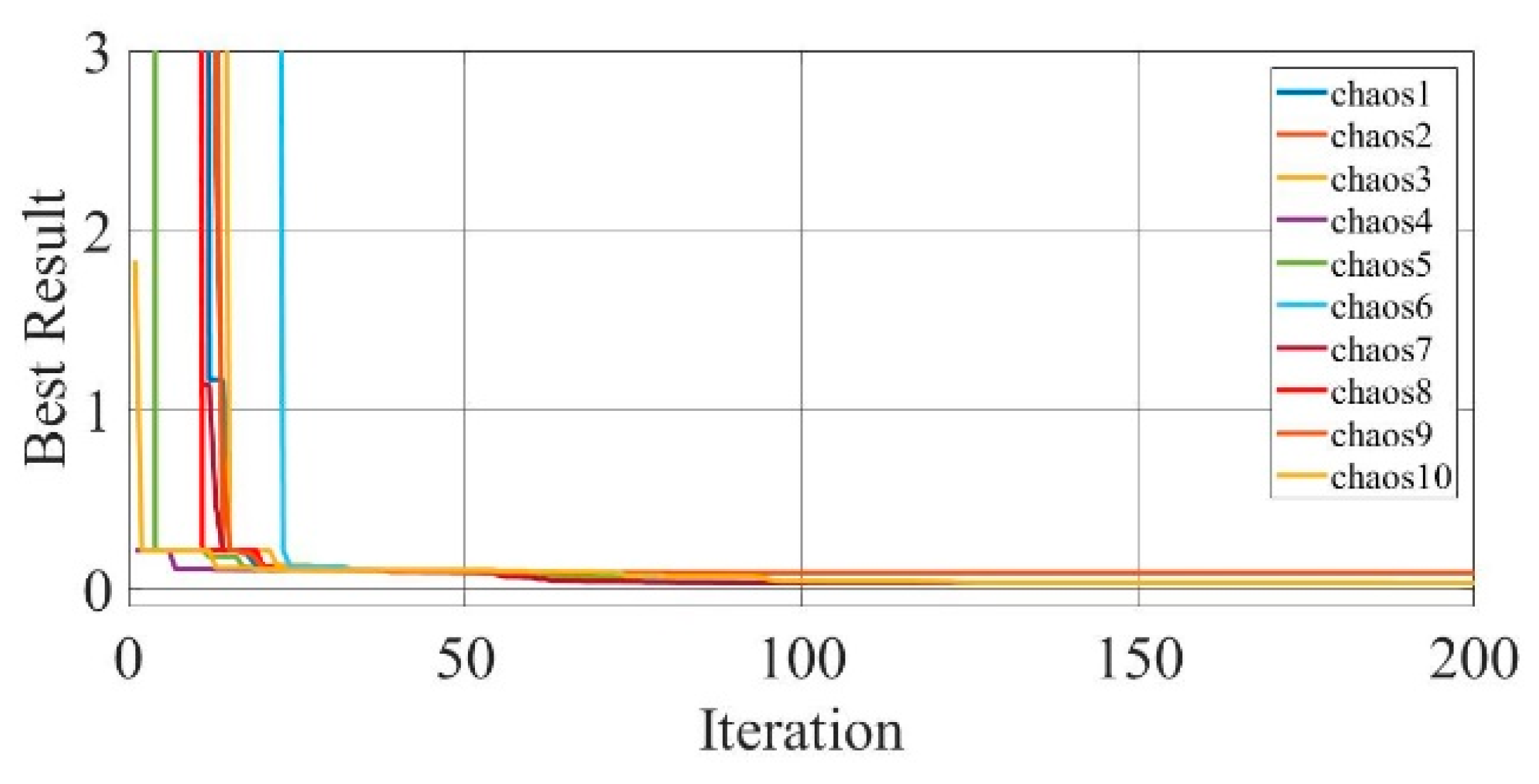
Figure 17.
Convergence curves of chaotic COA optimization technique during parameter extraction for a mono-crystalline solar cell LSM20 module (SDM).
Figure 17.
Convergence curves of chaotic COA optimization technique during parameter extraction for a mono-crystalline solar cell LSM20 module (SDM).
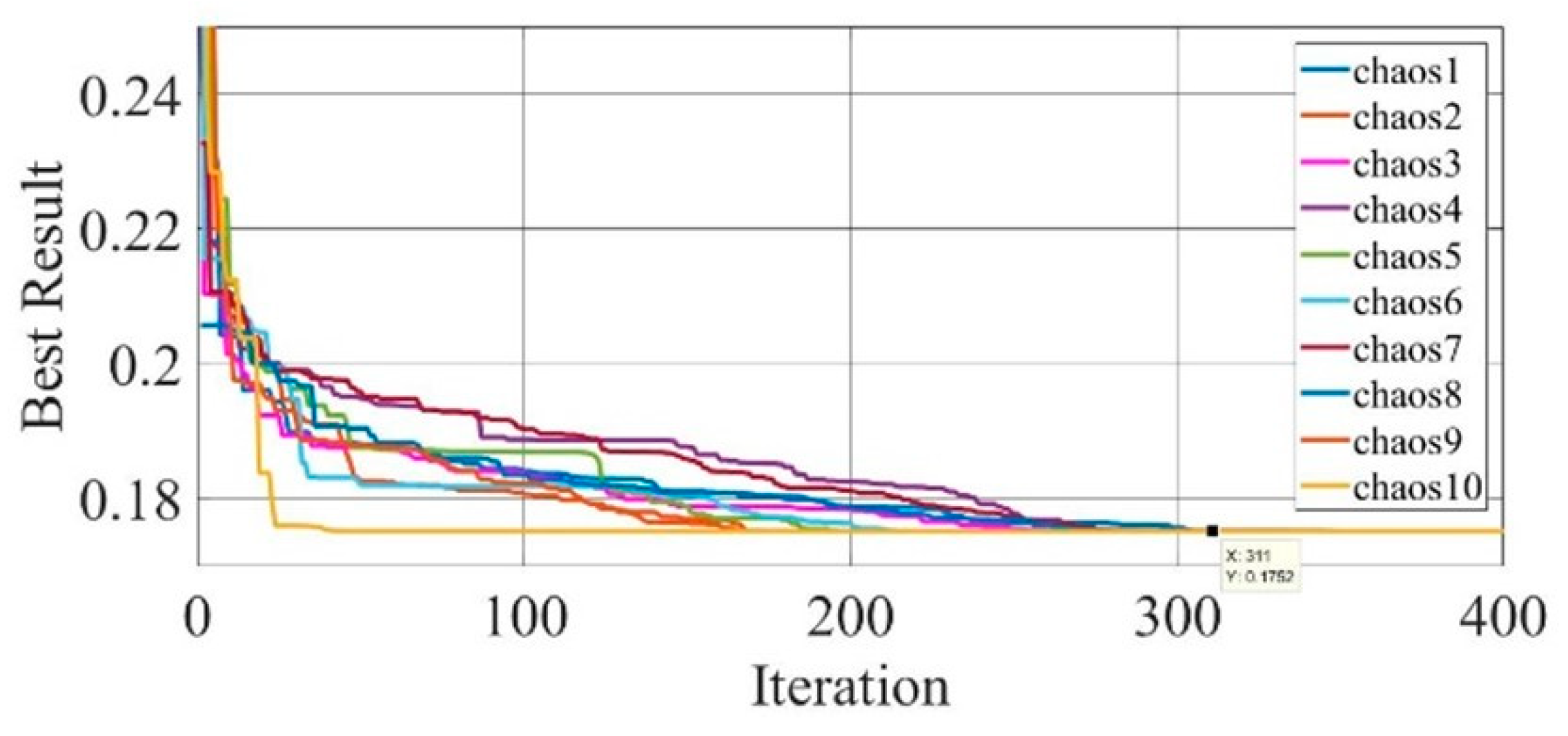
Figure 18.
Convergence curves of chaotic COA optimization technique during parameter extraction for Photowatt-PWP201 solar cell module (SDM).
Figure 18.
Convergence curves of chaotic COA optimization technique during parameter extraction for Photowatt-PWP201 solar cell module (SDM).
Figure 19.
Convergence curves of chaotic COA optimization technique during parameter extraction for GaAs thin-film solar cell PVM752 (SDM).
Figure 19.
Convergence curves of chaotic COA optimization technique during parameter extraction for GaAs thin-film solar cell PVM752 (SDM).
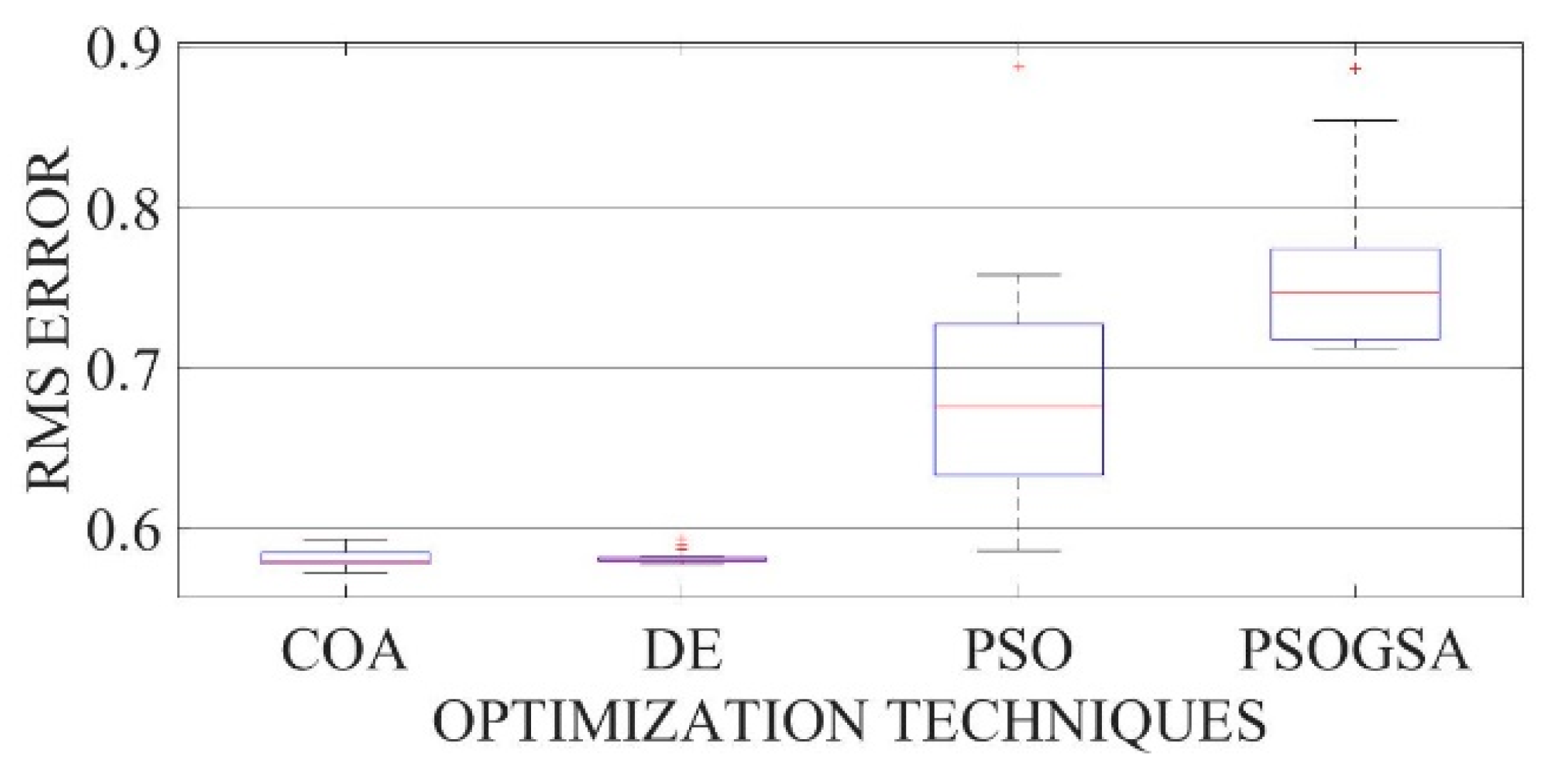
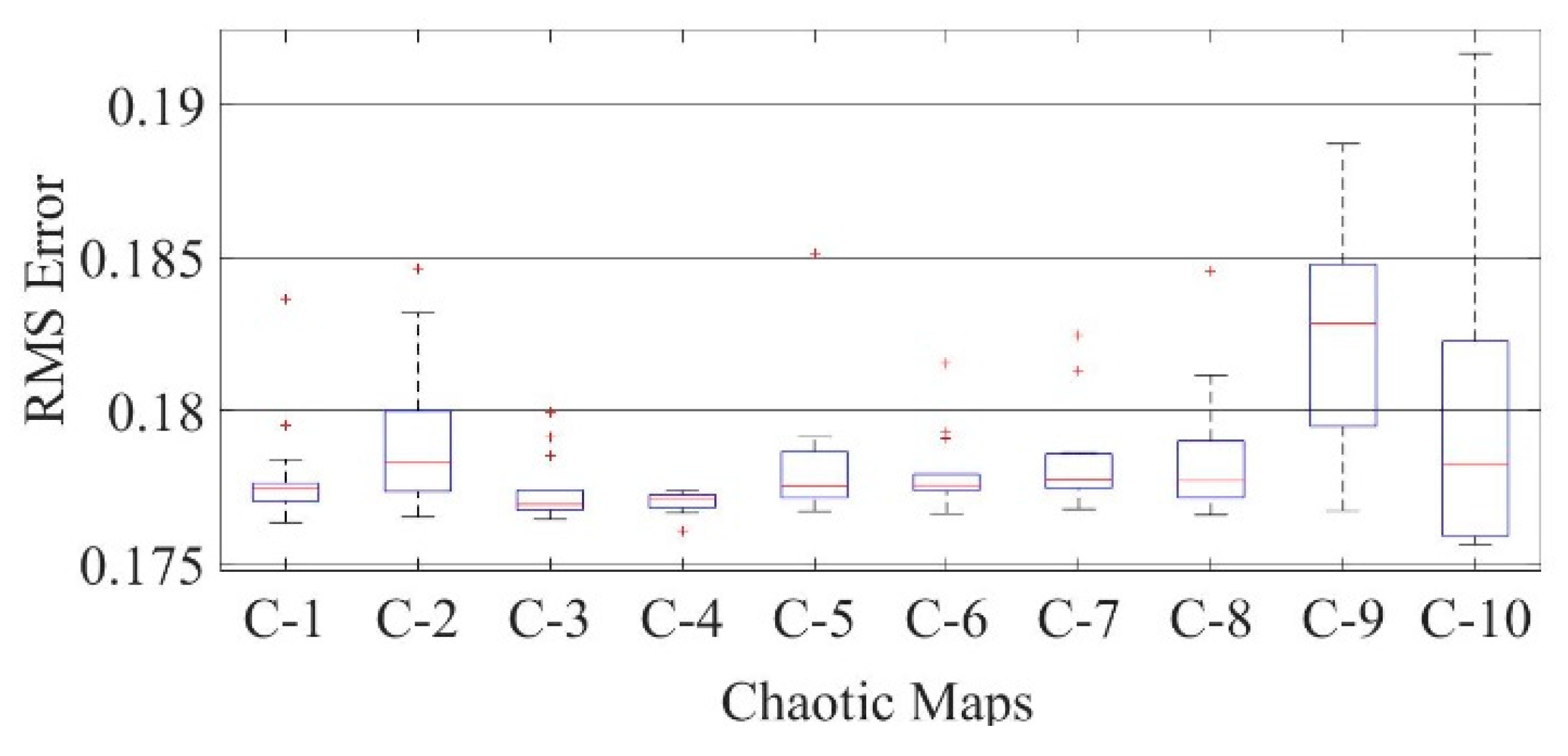
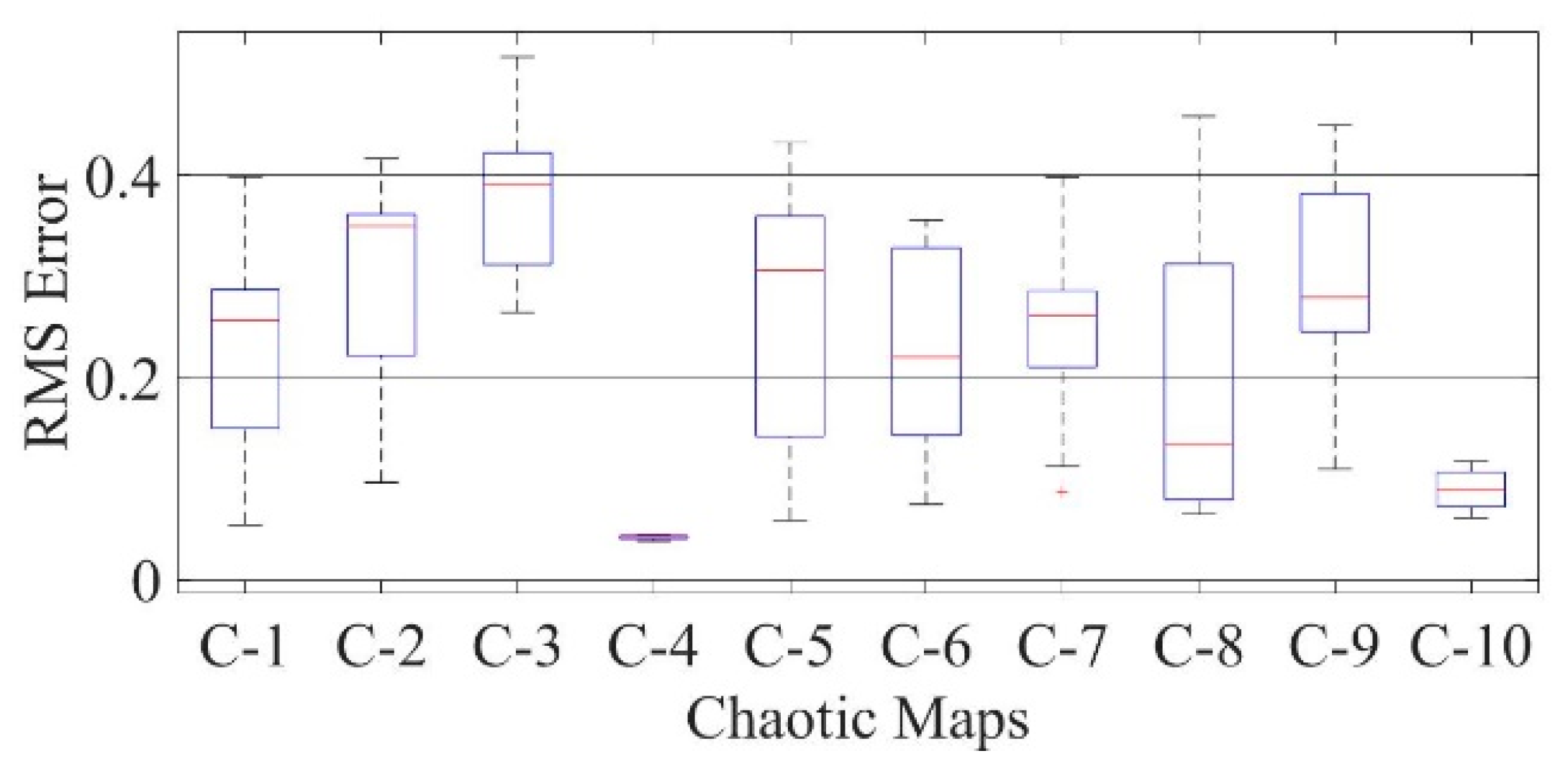
Figure 20.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a mono-crystalline LSM20 solar cell module (SDM).
Figure 20.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a mono-crystalline LSM20 solar cell module (SDM).
Figure 21.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a polycrystalline PWP-201 solar cell module (SDM).
Figure 21.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a polycrystalline PWP-201 solar cell module (SDM).
Figure 22.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a thin-film solar cell PVM752 (SDM).
Figure 22.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a thin-film solar cell PVM752 (SDM).
Figure 23.
Convergence curves of chaotic COA optimization technique during parameter extraction for a mono-crystalline solar cell LSM20 module (DDM).
Figure 23.
Convergence curves of chaotic COA optimization technique during parameter extraction for a mono-crystalline solar cell LSM20 module (DDM).
Figure 24.
Convergence curves of chaotic COA optimization technique during parameter extraction for Photowatt-PWP201 solar cell module (DDM).
Figure 24.
Convergence curves of chaotic COA optimization technique during parameter extraction for Photowatt-PWP201 solar cell module (DDM).
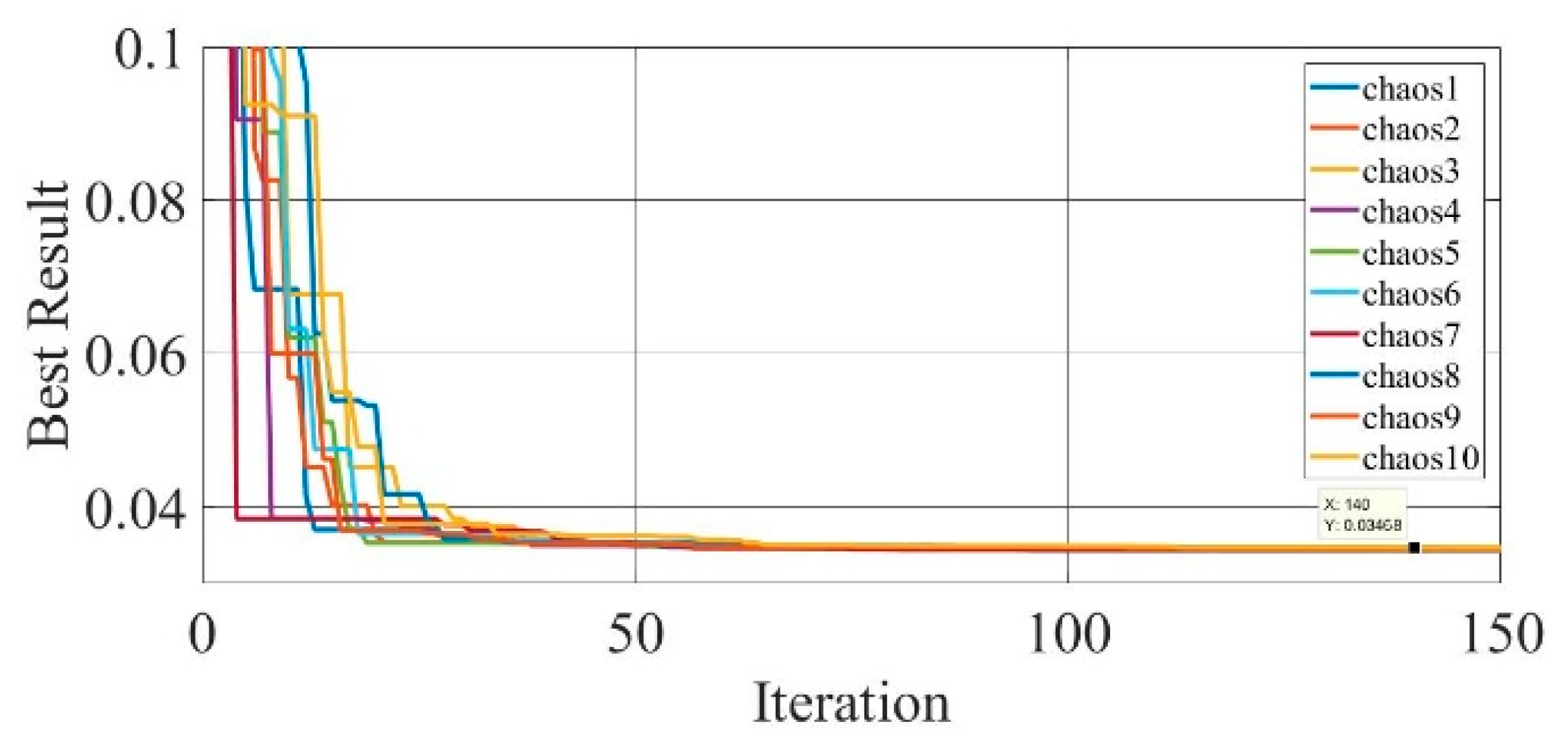
Figure 25.
Convergence curves of chaotic COA optimization technique during parameter extraction for GaAs thin-film solar cell PVM752 (DDM).
Figure 25.
Convergence curves of chaotic COA optimization technique during parameter extraction for GaAs thin-film solar cell PVM752 (DDM).
Figure 26.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a mono-crystalline LSM20 solar cell module (DDM).
Figure 26.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a mono-crystalline LSM20 solar cell module (DDM).
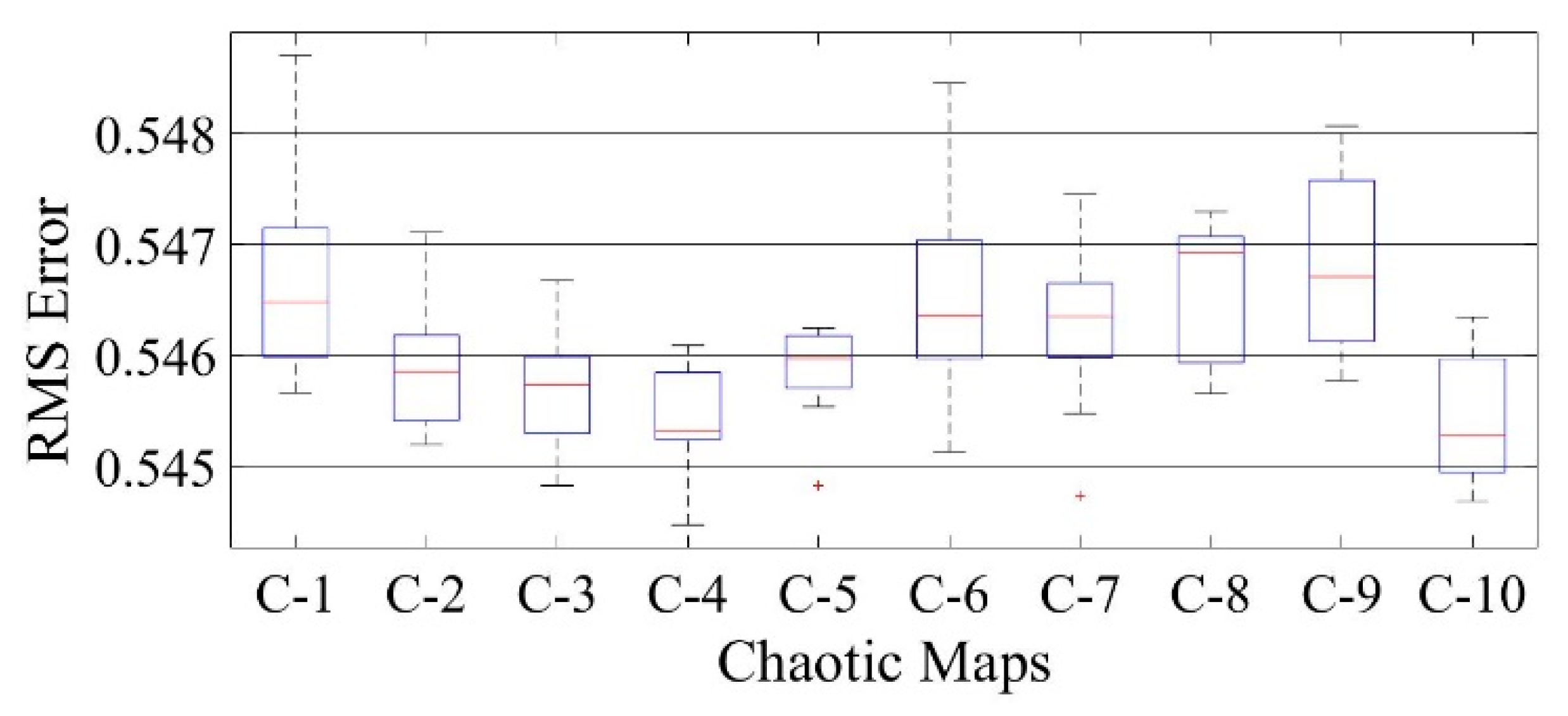
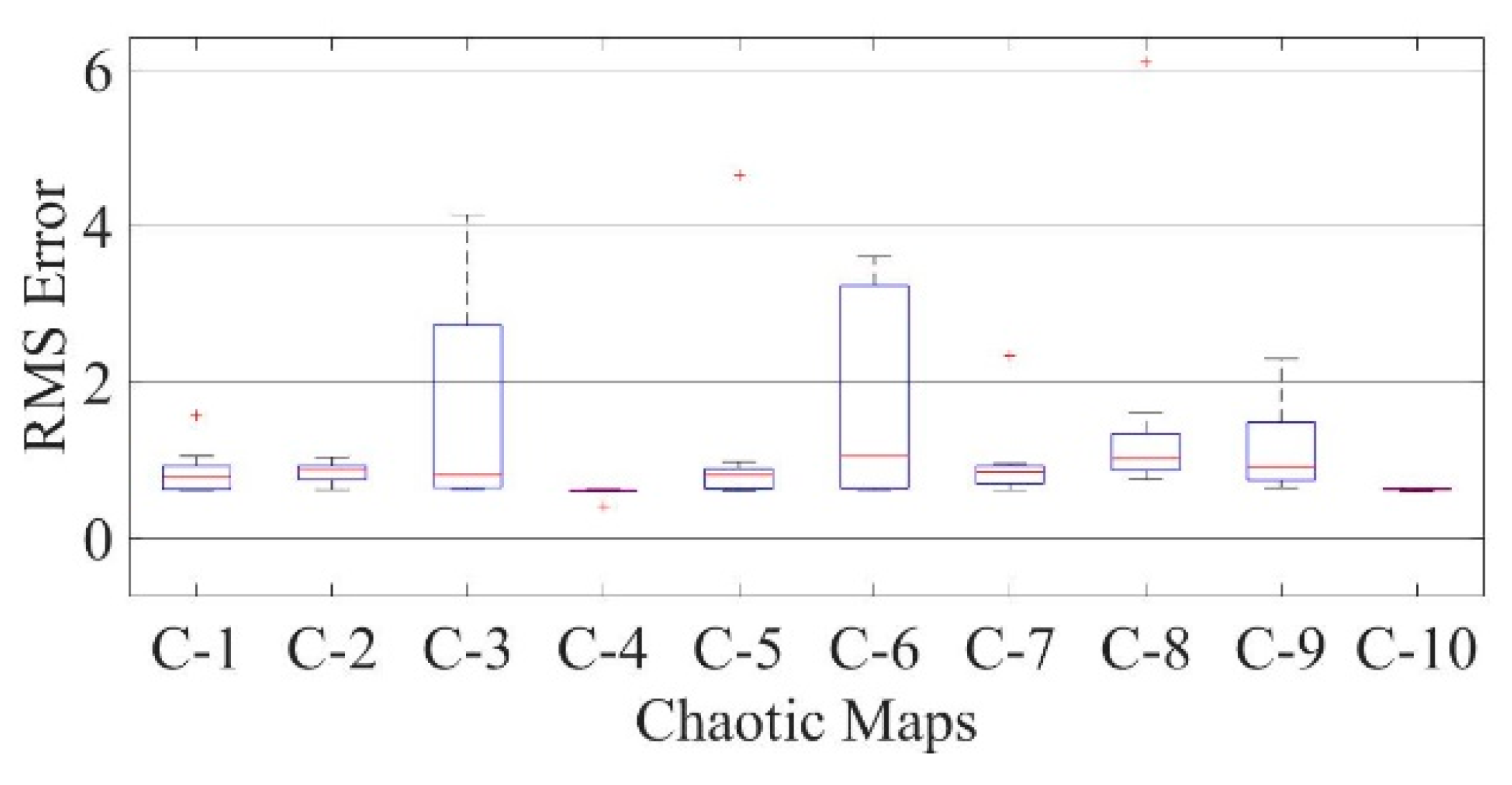
Figure 27.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a polycrystalline PWP-201 solar cell module (DDM).
Figure 27.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a polycrystalline PWP-201 solar cell module (DDM).
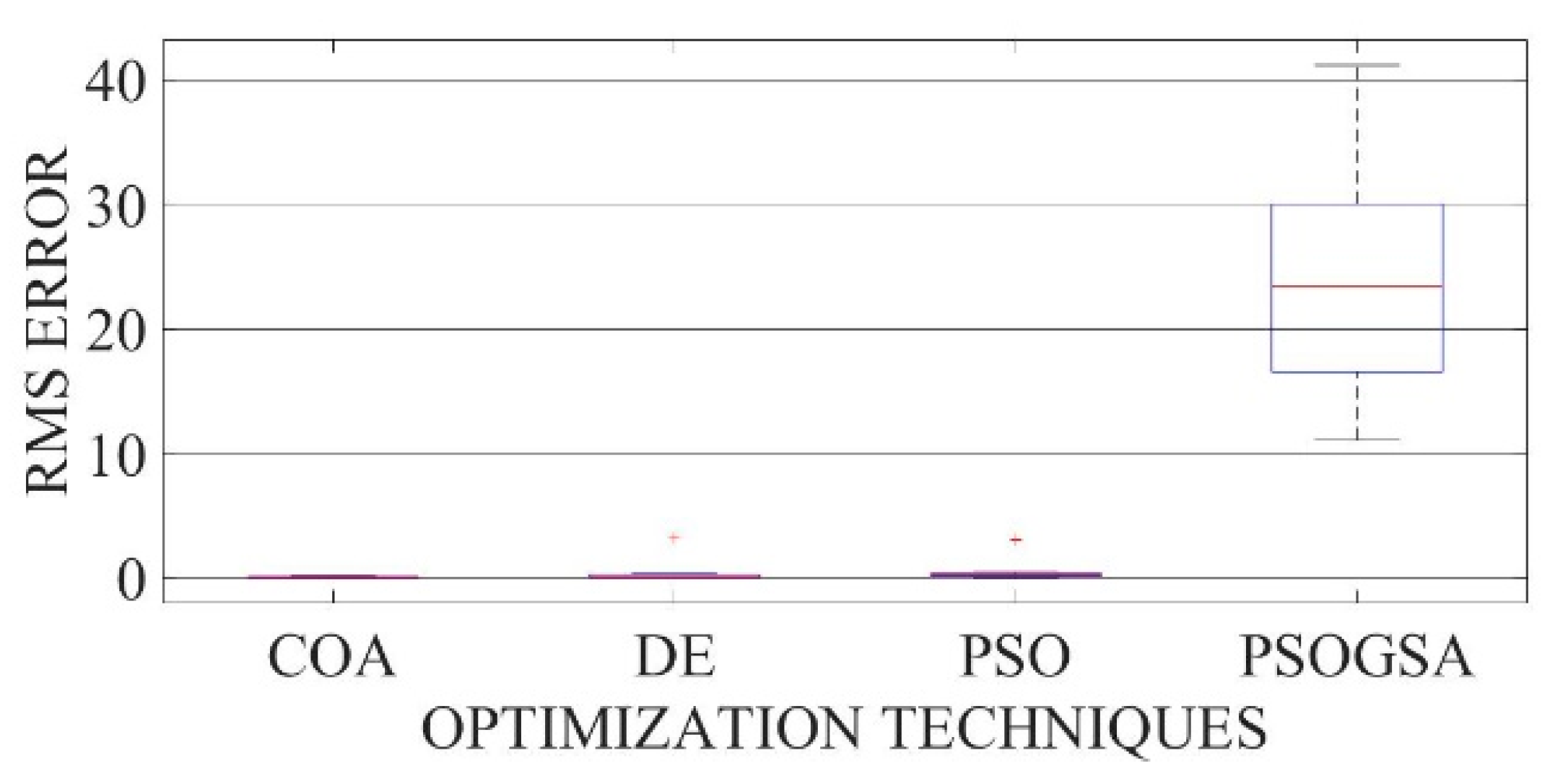
Figure 28.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a thin-film solar cell PVM752 (DDM).
Figure 28.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a thin-film solar cell PVM752 (DDM).
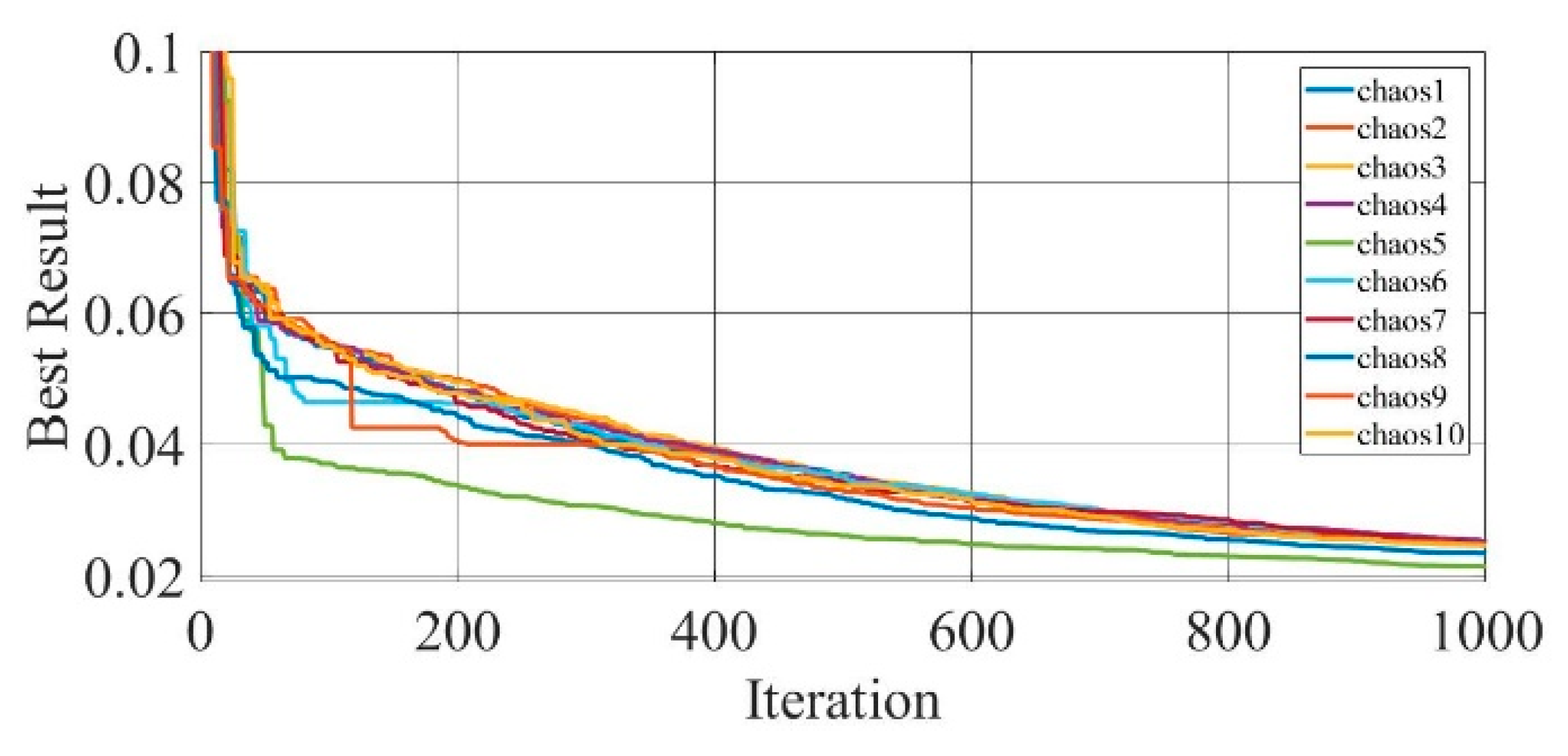
Figure 29.
Convergence curves of chaotic COA optimization technique during parameter extraction for a mono-crystalline solar cell LSM20 module (TDM).
Figure 29.
Convergence curves of chaotic COA optimization technique during parameter extraction for a mono-crystalline solar cell LSM20 module (TDM).
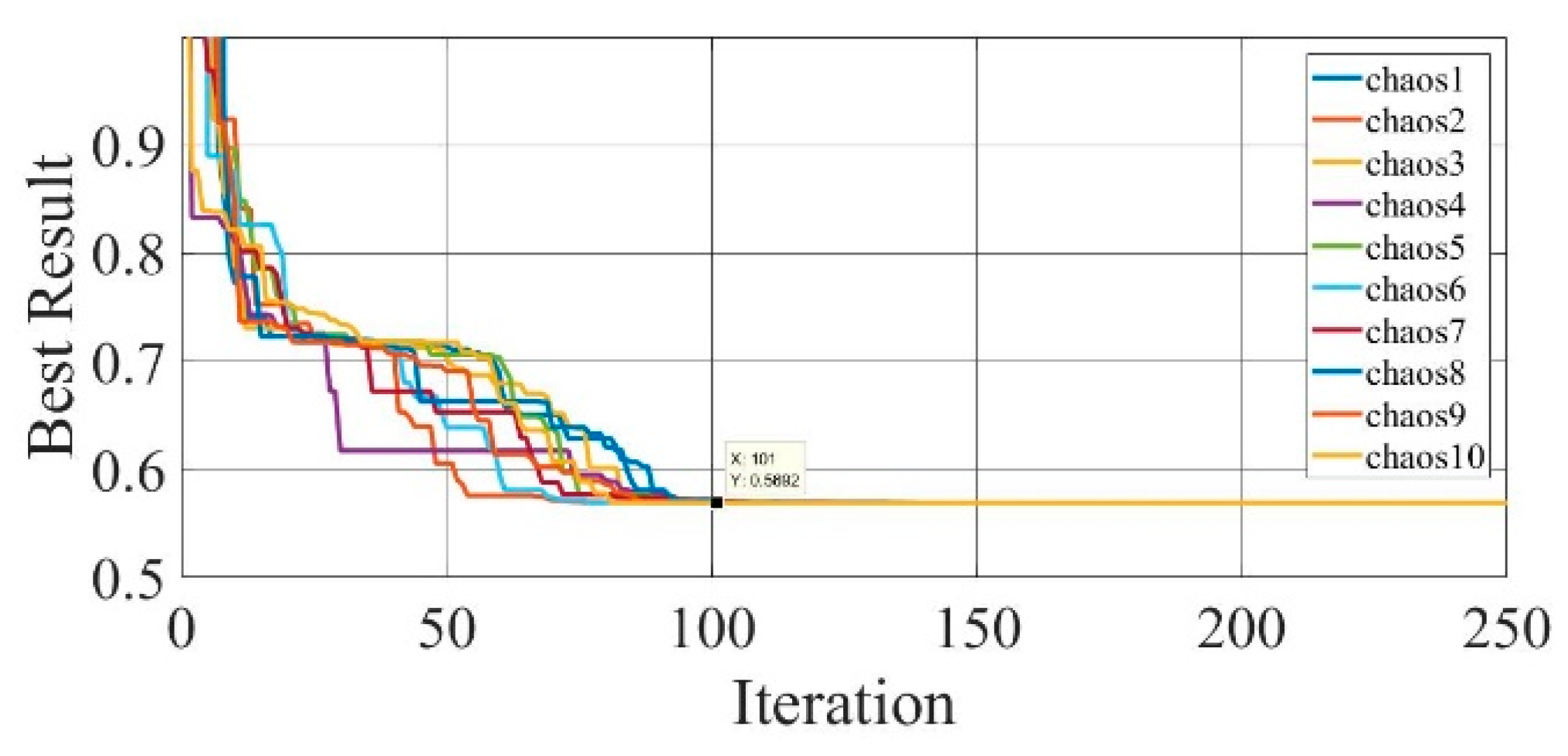
Figure 30.
Convergence curves of chaotic COA optimization technique during parameter extraction for Photowatt-PWP201 solar cell module (TDM).
Figure 30.
Convergence curves of chaotic COA optimization technique during parameter extraction for Photowatt-PWP201 solar cell module (TDM).
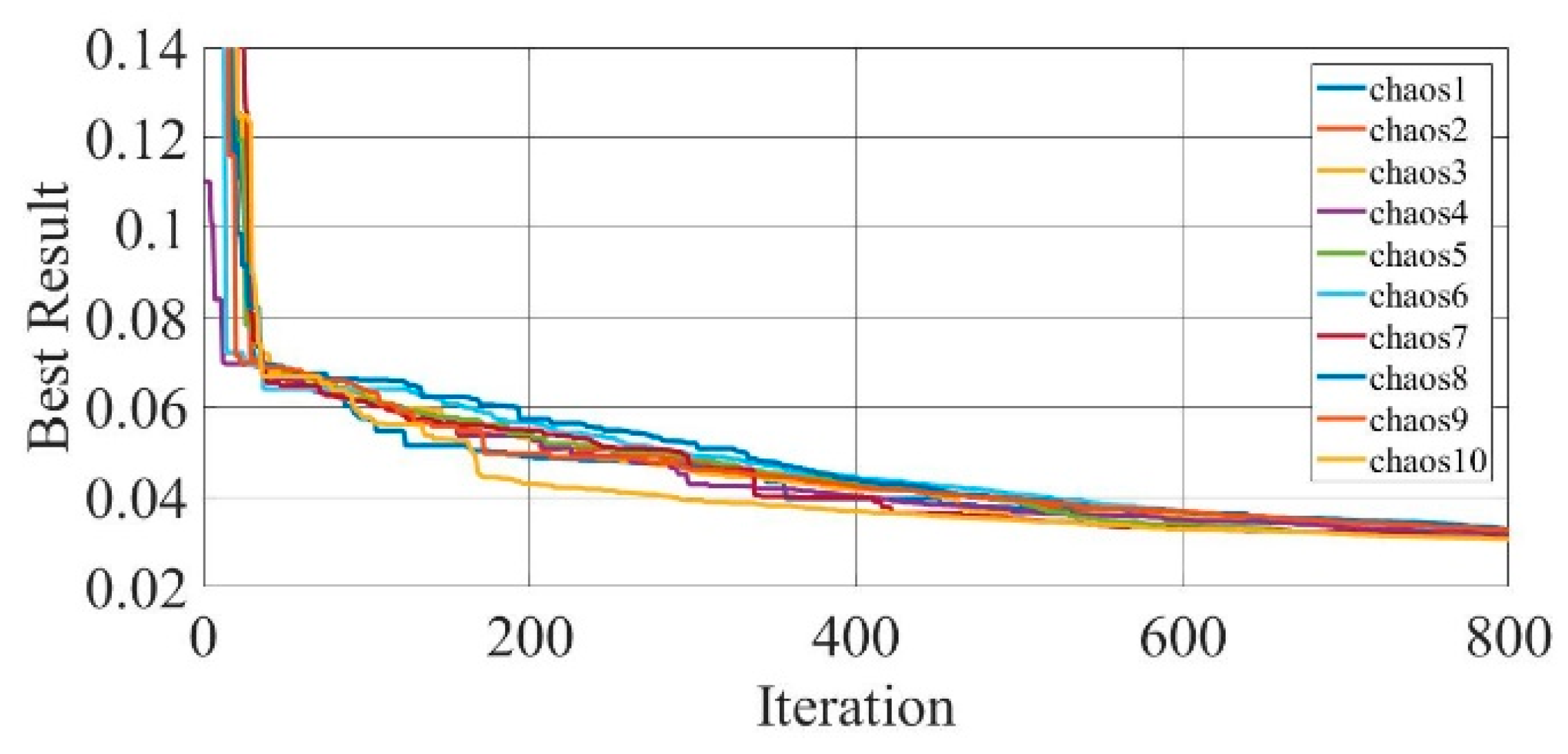
Figure 31.
Convergence curves of chaotic COA optimization technique during parameter extraction for GaAs thin-film solar cell PVM752 (TDM).
Figure 31.
Convergence curves of chaotic COA optimization technique during parameter extraction for GaAs thin-film solar cell PVM752 (TDM).
Figure 32.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a mono-crystalline LSM20 solar cell module (TDM).
Figure 32.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a mono-crystalline LSM20 solar cell module (TDM).
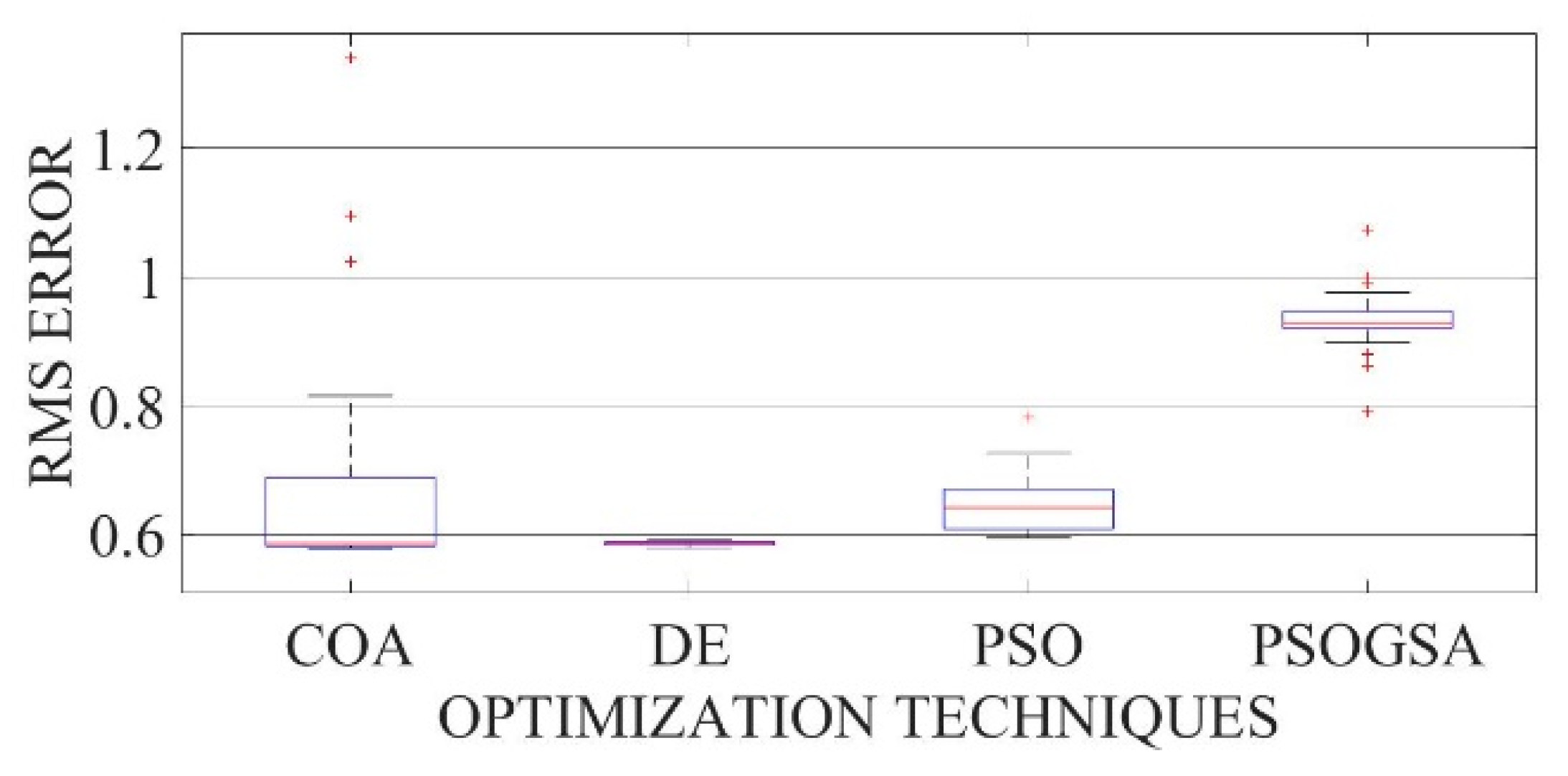
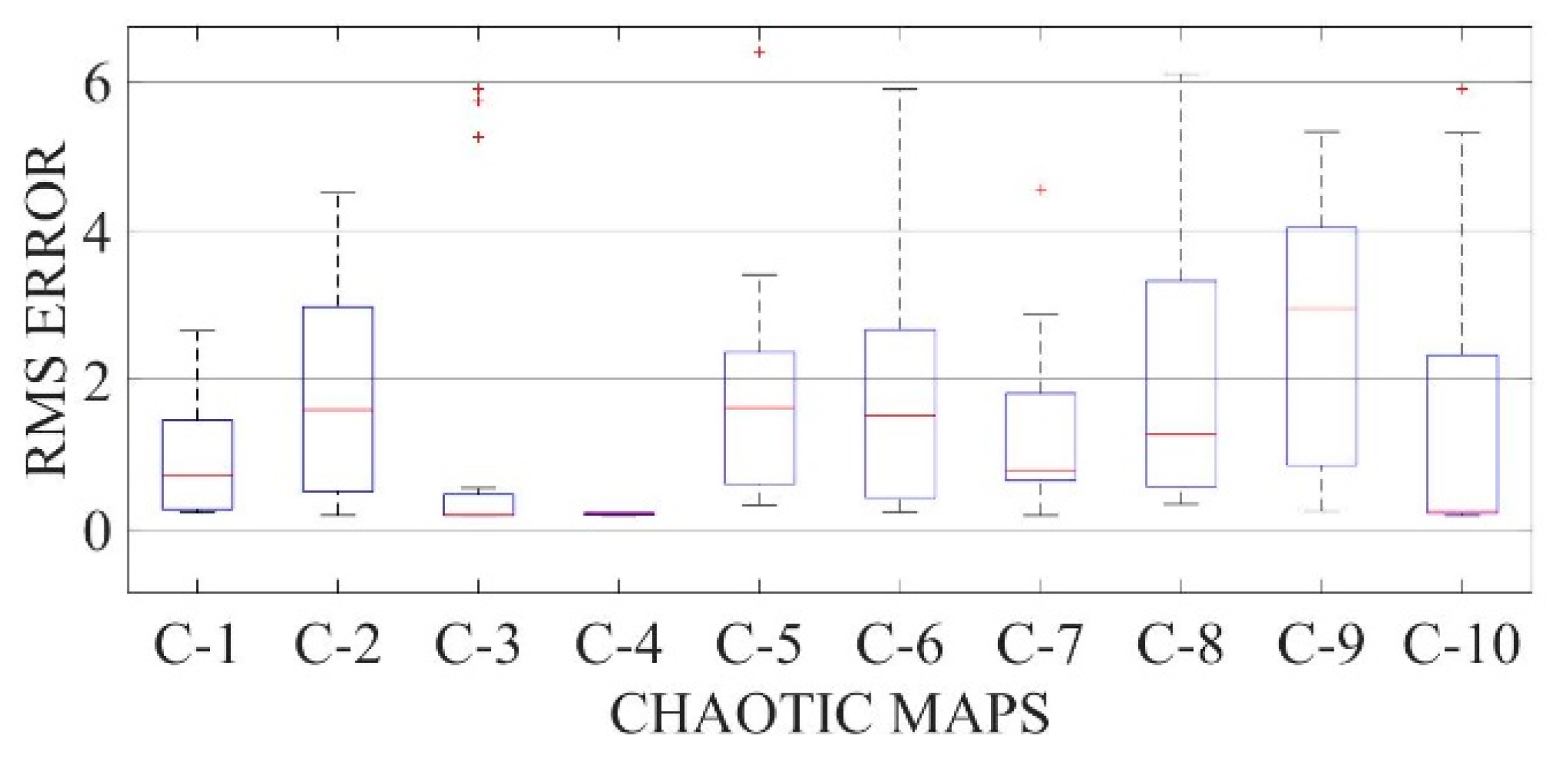
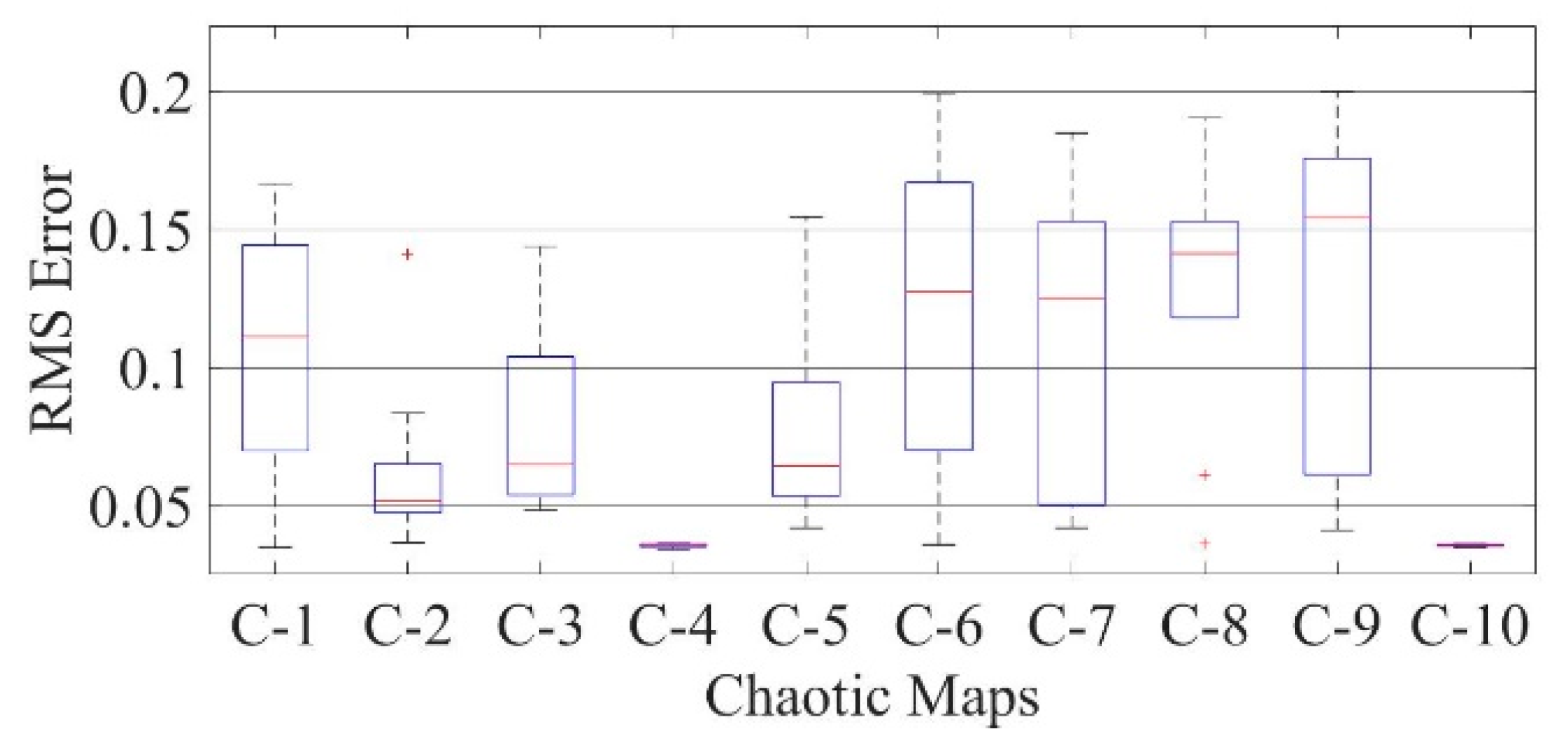
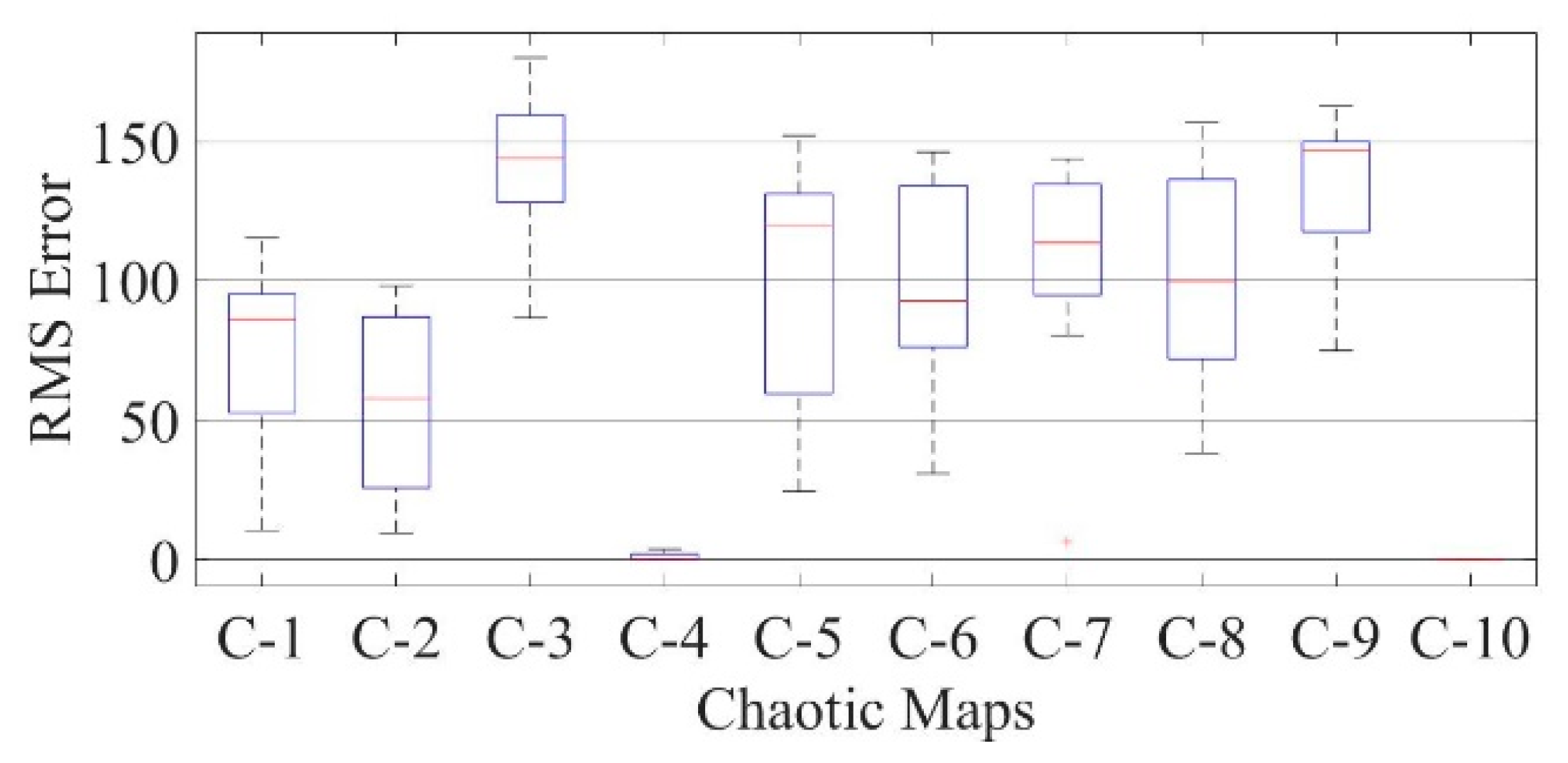
Figure 33.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a polycrystalline PWP-201 solar cell module (TDM).
Figure 33.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a polycrystalline PWP-201 solar cell module (TDM).
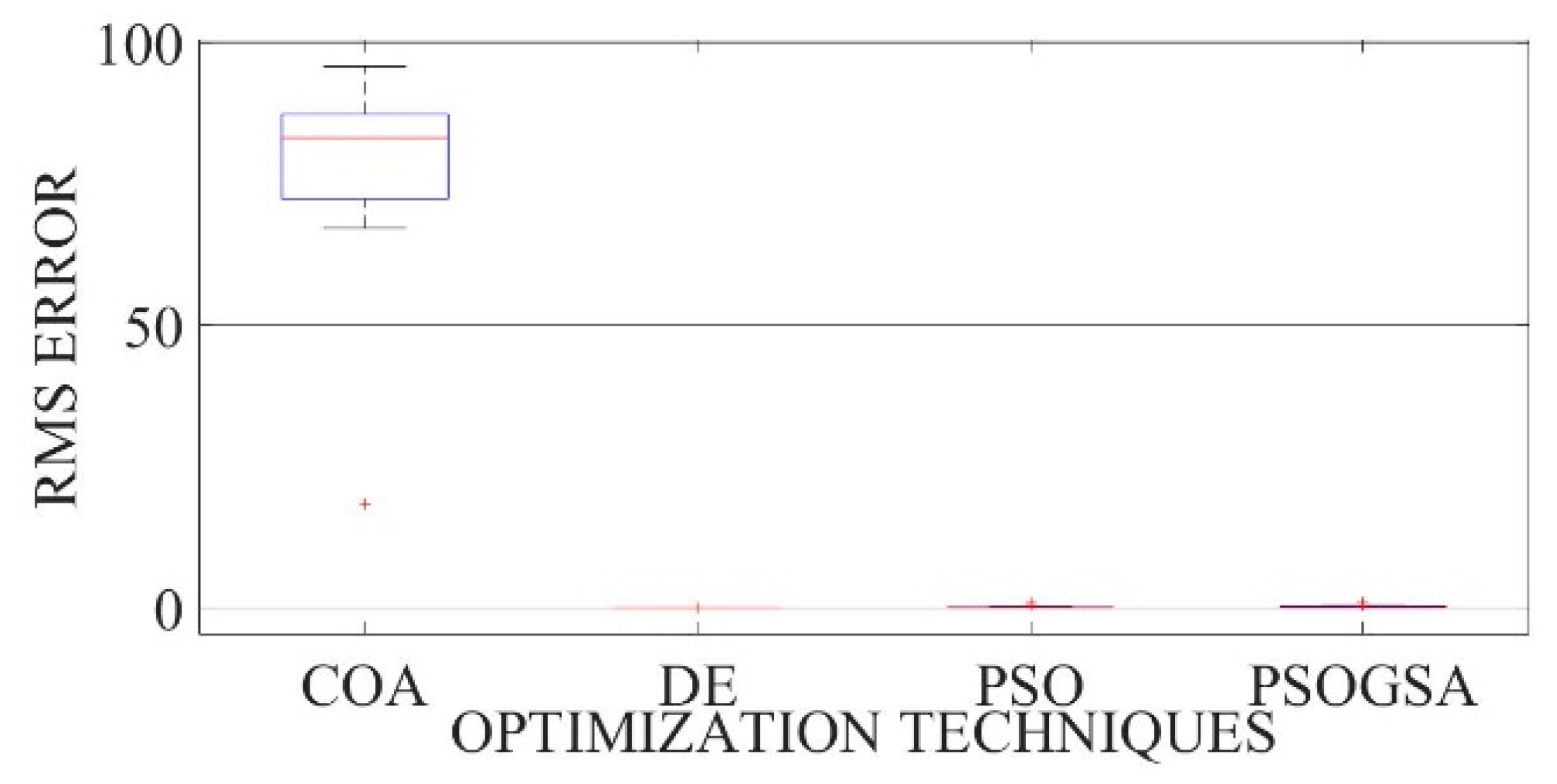
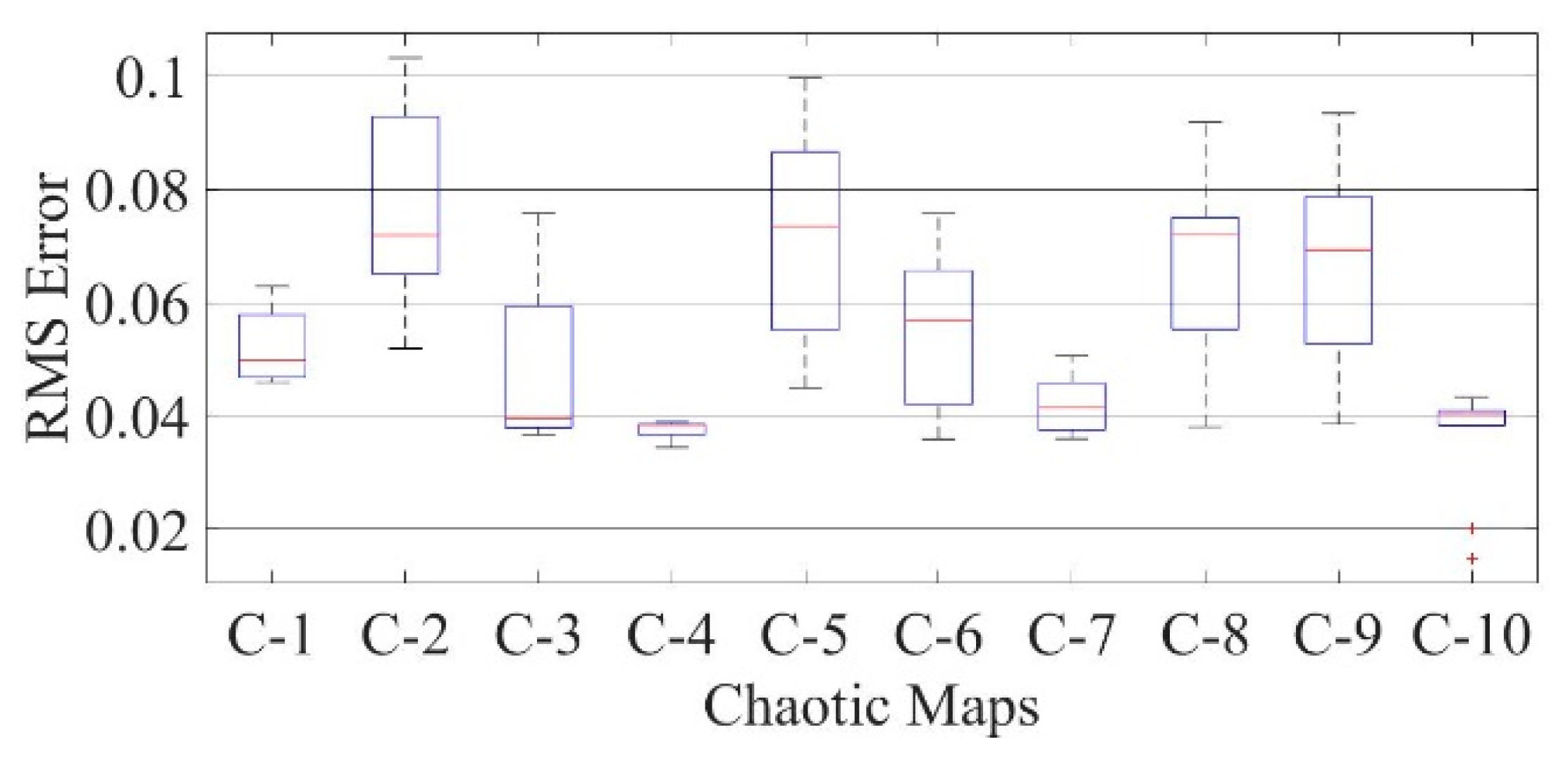
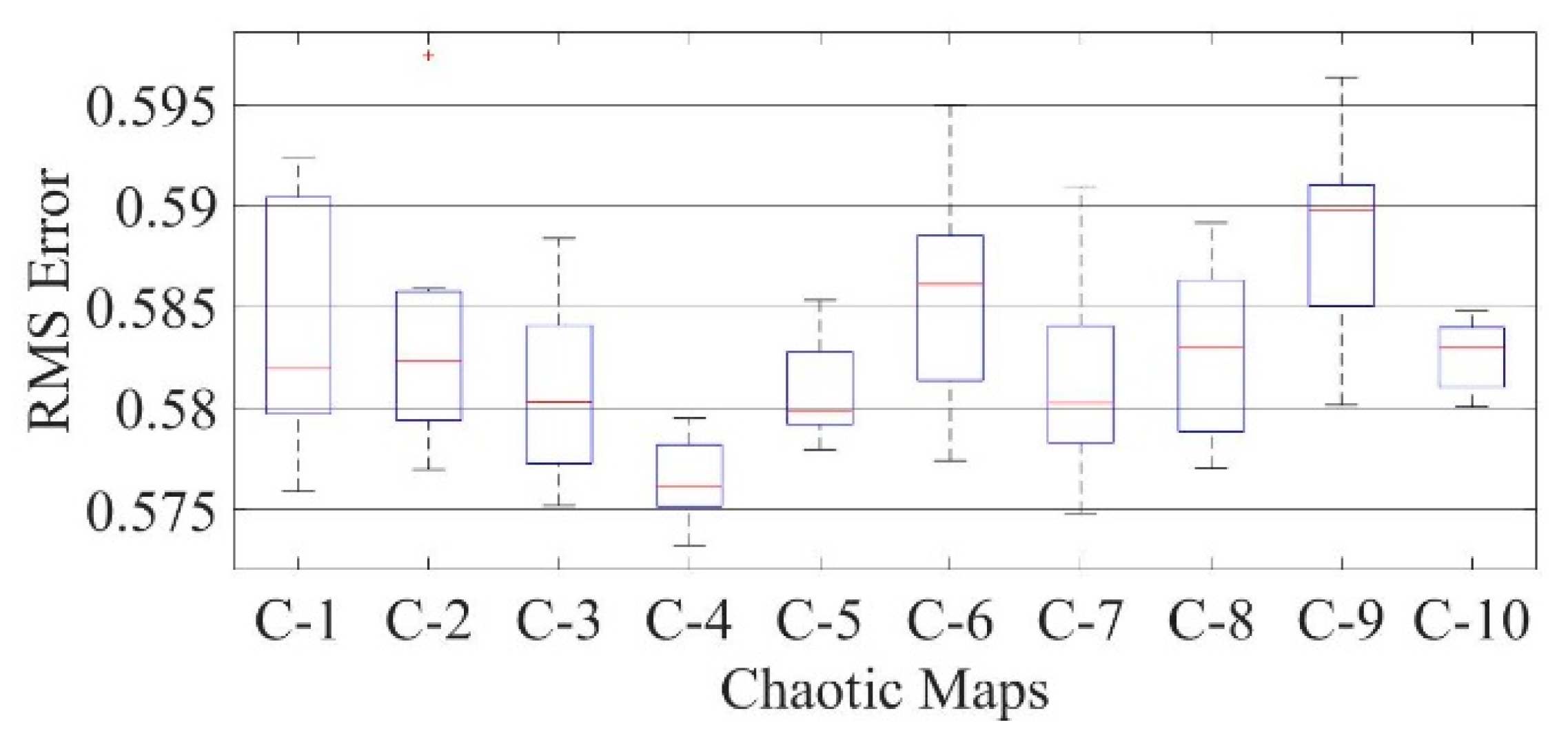
Figure 34.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a thin-film solar cell PVM752 (TDM).
Figure 34.
Boxplot comparing RMSE values using COA with the help of chaotic maps for a thin-film solar cell PVM752 (TDM).
Table 1.
Various classical optimization methods.
Table 1.
Various classical optimization methods.
| S. No. | Optimization Methods |
|---|
| 1. | Least square-based Newton Raphson [17] |
| 2. | Fitting the curve based on iteration [18] |
| 3. | Lambert W based optimization [19,20,21,22,23,24] |
| 4. | Identification by linear least square [25,26] |
| 5. | Linear extrapolation and linear interpolation [27] |
| 6. | Taylor series expansion [28] |
| 7. | Chebyshev polynomials [29] |
| 8. | Padé approximations [30] |
| 9. | Symbolic function [31] |
| 10. | Analytical mathematical method [32] |
Table 2.
Various metaheuristic methods for parameter extraction reported in the literature.
Table 2.
Various metaheuristic methods for parameter extraction reported in the literature.
| S. No. | Metaheuristic Methods |
|---|
| 1. | Flower Pollination Algorithm (FPA) [33] |
| 2. | Firefly Algorithm (FA) [34] |
| 3. | Simulated Annealing (SA) [35] |
| 4. | Particle Swarm Optimization (PSO) [36] |
| 5. | Hybrid Particle Swarm Optimization and Simulated Annealing (HPSOSA) [37] |
| 6. | Differential Algorithm (DE) [38] |
| 7. | Particle Swarm Optimization and Global Search Algorithm (PSOGSA) [39] |
| 8. | Modified and Multiobjective Firefly Algorithm (FA) [40,41,42,43,44,45] |
| 9. | Coyote Optimization Algorithm (COA) [46,47,48,49,50] |
Table 3.
Vectors of solutions (Xi) for SDM and DDM.
Table 3.
Vectors of solutions (Xi) for SDM and DDM.
| Model | Parameters (Xi) |
|---|
| Single Diode Model (SDM) | Rs, Rsh, I0, n, Iph |
| Double Diode Model (DDM) | Rs, Rsh, I01, I02, n1, n2, Iph |
| Three Diode Model (TDM) | Rs, Rsh, I01, I02, I03, n1, n2, n3, Iph |
Table 4.
Parameters extracted for a mono-crystalline LSM20 solar PV module by COA and its comparison with other techniques for SDM.
Table 4.
Parameters extracted for a mono-crystalline LSM20 solar PV module by COA and its comparison with other techniques for SDM.
| Parameters | COA | DE | PSO | PSOGSA |
|---|
| Rs | 0.00 | 0.00 | 0.00 | 0.00 |
| Rsh | 100 | 100 | 96.76659 | 82.205 |
| IL | 0.2023 | 0.2023 | 0.20259 | 0.2026 |
| I0 | 0.00 | 0.00 | 0.0001300 | 0.0001 |
| n | 1 | 1 | 1.08115 | 1.0527 |
| RMSE | 0.17668 | 0.1767446 | 0.1862443 | 0.1802 |
| Time (sec.) | 1.330 | 1.156 | 1.138 | 10.605 |
Table 5.
Parameters extracted for a Photowatt-PWP201 solar PV module by COA and its comparison with other techniques for SDM.
Table 5.
Parameters extracted for a Photowatt-PWP201 solar PV module by COA and its comparison with other techniques for SDM.
| Parameters | COA | DE | PSO | PSOGSA |
|---|
| Rs | 0 | 0 | 0 | 0.0222 |
| Rsh | 0.6379 | 0.635 | 0.6356339 | 3.1774 |
| IL | 1.1201 | 1.1207 | 1.1207088 | 0.7173 |
| I0 | 1 | 1 | 1 | 0.6874 |
| n | 2 | 1.9100 | 1.9109 | 1.6331 |
| RMSE | 0.54732 | 0.55444 | 0.561334 | 0.7224 |
| Time (sec.) | 1.300 | 1.674 | 1.087 | 10.504 |
Table 6.
Parameters extracted for PVM752 GaAs thin-film solar PV cell by COA compared with other techniques for SDM.
Table 6.
Parameters extracted for PVM752 GaAs thin-film solar PV cell by COA compared with other techniques for SDM.
| Parameters | COA | DE | PSO | PSOGSA |
|---|
| Rs | 0 | 0 | 0 | 0.05 |
| Rsh | 10.4707 | 10.4707 | 10.4707052 | 61.0883 |
| IL | 0.1816 | 0.1816 | 0.18156 | 0.1677 |
| I0 | 0 | 0 | 0 | 0.0006 |
| n | 1.5848 | 1 | 1.26827 | 2 |
| RMSE | 0.221817 | 0.22179 | 1.89115 | 0.50266 |
| Time (sec.) | 1.2920 | 1.178 | 1.088 | 10.24 |
Table 7.
Chaos Table.
| S. No. | Name | Chaotic Maps | Range |
|---|
| C 1 | Chebyshev [53] | | (−1, 1) |
| C 2 | Circle [54] | | (0, 1) |
| C 3 | Gauss/mouse [55] | | (0, 1) |
| C 4 | Iterative [56] | | (−1, 1) |
| C 5 | Logistic [56] | | (0, 1) |
| C 6 | Piecewise [57] | | (0, 1) |
| C 7 | Sine [58] | | (0, 1) |
| C 8 | Singer [59] | | (0, 1) |
| C 9 | Sinusoidal [60] | | (0, 1) |
| C 10 | Tent [61] | | (0, 1) |
Table 8.
Time taken by COA with the ten chaotic functions for LSM20 solar module.
Table 8.
Time taken by COA with the ten chaotic functions for LSM20 solar module.
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 0.8600 |
| C 2 | Circle | 0.7540 |
| C 3 | Gauss/mouse | 0.8690 |
| C 4 | Iterative | 0.8240 |
| C 5 | Logistic | 0.8560 |
| C 6 | Piecewise | 0.8650 |
| C 7 | Sine | 0.8260 |
| C 8 | Singer | 0.8530 |
| C 9 | Sinusoidal | 0.8340 |
| C 10 | Tent | 0.6500 |
Table 9.
Time taken by COA with the ten chaotic functions for Photowatt-PWP201 solar cell module (SDM).
Table 9.
Time taken by COA with the ten chaotic functions for Photowatt-PWP201 solar cell module (SDM).
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 0.5510 |
| C 2 | Circle | 0.4300 |
| C 3 | Gauss/mouse | 0.4100 |
| C 4 | Iterative | 0.4020 |
| C 5 | Logistic | 0.4200 |
| C 6 | Piecewise | 0.4340 |
| C 7 | Sine | 0.4250 |
| C 8 | Singer | 0.4280 |
| C 9 | Sinusoidal | 0.4460 |
| C 10 | Tent | 0.4150 |
Table 10.
Time taken by COA with the ten chaotic functions for GaAs thin-film solar cell PVM752 (SDM).
Table 10.
Time taken by COA with the ten chaotic functions for GaAs thin-film solar cell PVM752 (SDM).
| S. No. | Chaotic Maps | Time (seconds) |
|---|
| C 1 | Chebyshev | 0.5420 |
| C 2 | Circle | 0.5250 |
| C 3 | Gauss/mouse | 0.4860 |
| C 4 | Iterative | 0.6490 |
| C 5 | Logistic | 0.6670 |
| C 6 | Piecewise | 0.6700 |
| C 7 | Sine | 0.6550 |
| C 8 | Singer | 0.7920 |
| C 9 | Sinusoidal | 0.6430 |
| C 10 | Tent | 0.6370 |
Table 11.
Time taken by COA with the ten chaotic functions for LSM20 solar module (DDM).
Table 11.
Time taken by COA with the ten chaotic functions for LSM20 solar module (DDM).
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 1.32 |
| C 2 | Circle | 1.26 |
| C 3 | Gauss/mouse | 1.269 |
| C 4 | Iterative | 1.272 |
| C 5 | Logistic | 1.258 |
| C 6 | Piecewise | 1.246 |
| C 7 | Sine | 1.266 |
| C 8 | Singer | 1.251 |
| C 9 | Sinusoidal | 1.308 |
| C 10 | Tent | 1.200 |
Table 12.
Time taken by COA with the ten chaotic functions for Photowatt-PWP201 solar cell module (DDM).
Table 12.
Time taken by COA with the ten chaotic functions for Photowatt-PWP201 solar cell module (DDM).
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 0.6390 |
| C 2 | Circle | 0.6180 |
| C 3 | Gauss/mouse | 0.5940 |
| C 4 | Iterative | 0.6020 |
| C 5 | Logistic | 0.6160 |
| C 6 | Piecewise | 0.580 |
| C 7 | Sine | 0.598 |
| C 8 | Singer | 0.592 |
| C 9 | Sinusoidal | 0.601 |
| C 10 | Tent | 0.596 |
Table 13.
Time taken by COA with the ten chaotic functions for GaAs thin-film solar cell PVM752 (DDM).
Table 13.
Time taken by COA with the ten chaotic functions for GaAs thin-film solar cell PVM752 (DDM).
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 1.292 |
| C 2 | Circle | 0.661 |
| C 3 | Gauss/mouse | 1.268 |
| C 4 | Iterative | 0.912 |
| C 5 | Logistic | 1.314 |
| C 6 | Piecewise | 1.020 |
| C 7 | Sine | 1.052 |
| C 8 | Singer | 1.314 |
| C 9 | Sinusoidal | 1.092 |
| C 10 | Tent | 1.295 |
Table 14.
Time taken by COA with the ten chaotic functions for LSM20 solar module (TDM).
Table 14.
Time taken by COA with the ten chaotic functions for LSM20 solar module (TDM).
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 1.237 |
| C 2 | Circle | 1.26 |
| C 3 | Gauss/mouse | 1.244 |
| C 4 | Iterative | 1.195 |
| C 5 | Logistic | 1.232 |
| C 6 | Piecewise | 1.273 |
| C 7 | Sine | 1.232 |
| C 8 | Singer | 1.247 |
| C 9 | Sinusoidal | 1.262 |
| C 10 | Tent | 1.268 |
Table 15.
Time taken by COA with the ten chaotic functions for Photowatt-PWP201 solar cell module (TDM).
Table 15.
Time taken by COA with the ten chaotic functions for Photowatt-PWP201 solar cell module (TDM).
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 0.6030 |
| C 2 | Circle | 0.5640 |
| C 3 | Gauss/mouse | 0.5790 |
| C 4 | Iterative | 0.5470 |
| C 5 | Logistic | 0.5480 |
| C 6 | Piecewise | 0.5340 |
| C 7 | Sine | 0.5000 |
| C 8 | Singer | 0.5250 |
| C 9 | Sinusoidal | 0.5240 |
| C 10 | Tent | 0.5310 |
Table 16.
Time taken by COA with the ten chaotic functions for GaAs thin-film solar cell PVM752 (TDM).
Table 16.
Time taken by COA with the ten chaotic functions for GaAs thin-film solar cell PVM752 (TDM).
| S. No. | Chaotic Maps | Time (Seconds) |
|---|
| C 1 | Chebyshev | 0.7410 |
| C 2 | Circle | 0.7430 |
| C 3 | Gauss/mouse | 0.7680 |
| C 4 | Iterative | 0.7110 |
| C 5 | Logistic | 0.7470 |
| C 6 | Piecewise | 0.7890 |
| C 7 | Sine | 0.7470 |
| C 8 | Singer | 0.7550 |
| C 9 | Sinusoidal | 0.7490 |
| C 10 | Tent | 0.7360 |
Table 17.
Extracted parameters for a mono-crystalline solar cell module (LSM20) at different temperatures and irradiance of 1000 W/m2.
Table 17.
Extracted parameters for a mono-crystalline solar cell module (LSM20) at different temperatures and irradiance of 1000 W/m2.
| Parameters | 25 °C | 60 °C | 80 °C |
|---|
| Rs | 0.2861 | 0.2973 | 0.2880 |
| Rsh | 6485.3459 | 3711.1515 | 2790.0845 |
| IL | 5 | 1.3536 | 0.5467 |
| I0 | 2.0231 | 0 | 3.873 |
| n | 1.6185 | 1.4837 | 1.4178 |
| RMSE | 1.164391 | 1.1592703 | 1.156579 |
Table 18.
Extracted parameters for Photowatt-PWP201 solar cell module at different temperatures and irradiance of 1000 W/m2.
Table 18.
Extracted parameters for Photowatt-PWP201 solar cell module at different temperatures and irradiance of 1000 W/m2.
| Parameters | 25 °C | 60 °C | 80 °C |
|---|
| Rs | 0.05 | 0.05 | 0.05 |
| Rsh | 8308.43 | 5804.069 | 1107.783 |
| IL | 1.9204 | 5 | 0.7208 |
| I0 | 1.2713 | 0 | 1.1682 |
| n | 1.5441 | 1.4156 | 1.3528 |
| RMSE | 0.88267 | 0.877021 | 0.872806 |
Table 19.
Extracted parameters for GaAs thin-film solar cell at different temperatures and irradiance of 1000 W/m2.
Table 19.
Extracted parameters for GaAs thin-film solar cell at different temperatures and irradiance of 1000 W/m2.
| Parameters | 25 °C | 60 °C | 80 °C |
|---|
| Rs | 1 | 1 | 1 |
| Rsh | 9765.4351 | 5061.5258 | 2720.594 |
| IL | 3.7317 | 5 | 0.1392 |
| I0 | 0.3085 | 0.820 | 3.4280 |
| n | 2.7484 | 2.5197 | 2.4074 |
| RMSE | 1.45346 | 1.4455 | 1.44154 |
Table 20.
Extracted parameters for a mono-crystalline solar cell module (LSM20) at different irradiances and a temperature of 25 °C.
Table 20.
Extracted parameters for a mono-crystalline solar cell module (LSM20) at different irradiances and a temperature of 25 °C.
| Parameters | 200 W/m2 | 500 W/m2 | 800 W/m2 | 1000 W/m2 |
|---|
| Rs | 0.2450 | 0.2979 | 0.3075 | 0.3102 |
| Rsh | 1878.296 | 3095.537 | 2990.48 | 7249.32 |
| IL | 0.0464 | 4.9285 | 1.2624 | 5 |
| I0 | 1.8635 | 2.5201 | 0.7712 | 2.8617 |
| n | 1.68986 | 1.5814 | 1.5311 | 1.5084 |
| RMSE | 0.55417 | 1.701389 | 2.8567 | 3.6297 |
Table 21.
Extracted parameters for a polycrystalline solar cell module (PWP201) at different irradiances and a temperature of 25 °C.
Table 21.
Extracted parameters for a polycrystalline solar cell module (PWP201) at different irradiances and a temperature of 25 °C.
| Parameters | 200 W/m2 | 500 W/m2 | 800 W/m2 | 1000 W/m2 |
|---|
| Rs | 0.05 | 0.05 | 0.05 | 0.05 |
| Rsh | 454.525 | 1713.430 | 3776.4653 | 9997.4275 |
| IL | 4.0432 | 5 | 3.9312 | 1.4427 |
| I0 | 3.1249 | 0.9070 | 5 | 5 |
| n | 1.9233 | 1.6266 | 1.5544 | 1.5250 |
| RMSE | 1.15172 | 0.83263 | 0.75804 | 0.88636 |
Table 22.
Extracted parameters for GaAs thin-film solar cell at different irradiances and a temperature of 25 °C.
Table 22.
Extracted parameters for GaAs thin-film solar cell at different irradiances and a temperature of 25 °C.
| Parameters | 200 W/m2 | 500 W/m2 | 800 W/m2 | 1000 W/m2 |
|---|
| Rs | 1 | 1 | 1 | 1 |
| Rsh | 2253.8709 | 3304.608 | 7208.2173 | 8214.6883 |
| IL | 2.4687 | 0.4442 | 2.4873 | 5 |
| I0 | 0.2695 | 0.7437 | 2.8613 | 0.5273 |
| n | 3.151 | 2.898 | 2.7851 | 2.3494 |
| RMSE | 0.1164 | 0.61287 | 1.11641 | 1.45343 |