Improved Salp Swarm Optimization Algorithm: Application in Feature Weighting for Blind Modulation Identification
Abstract
:1. Introduction
2. Problem Formulation
3. Improvements on Salp Swarm Algorithm
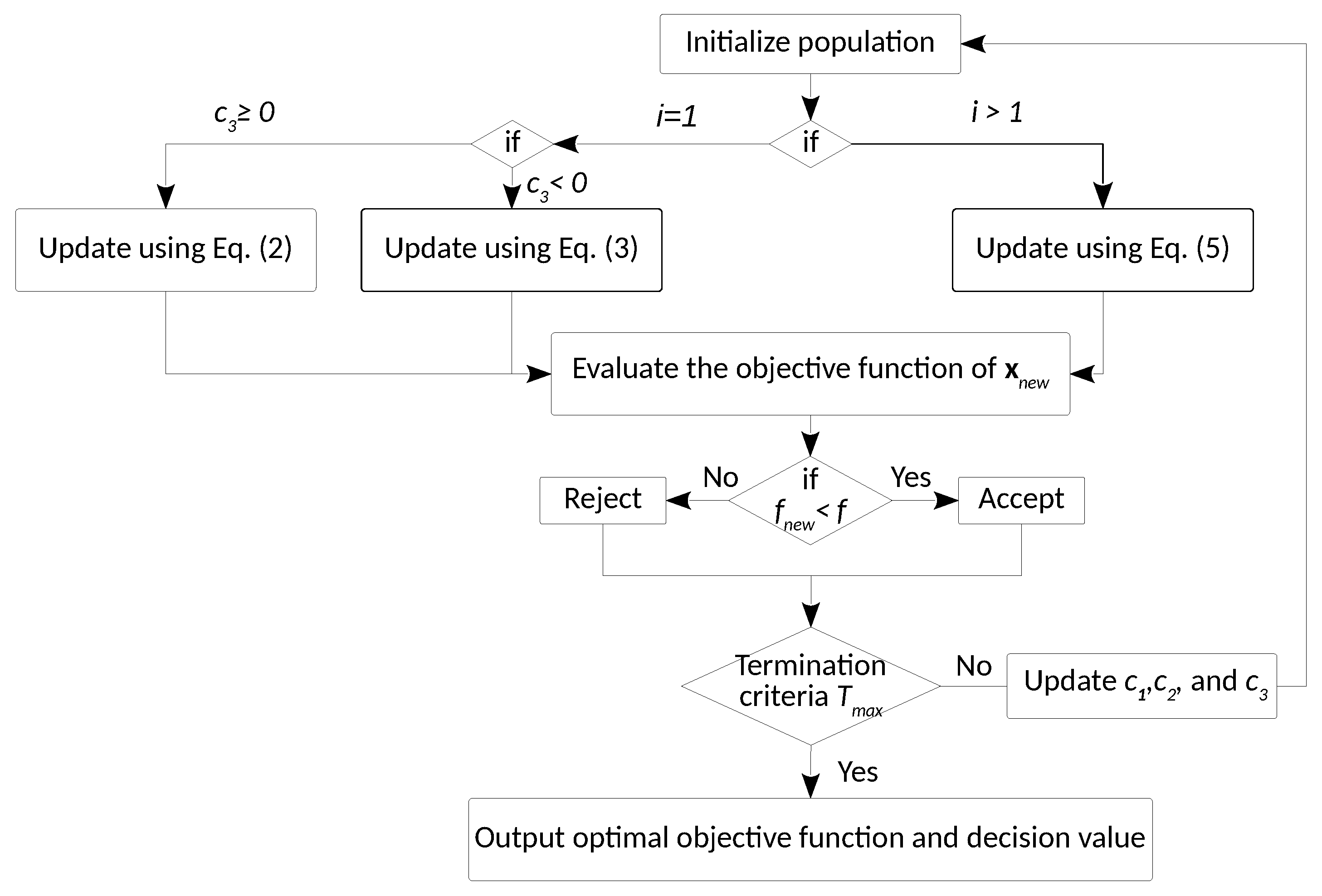
3.1. SSA, the Basic Algorithm
3.2. Motivation and Improvements
4. Comparison Methodology and MATERIALS
4.1. Comparison Methodology
4.2. Materials
5. Benchmarking of SSA and ISSA
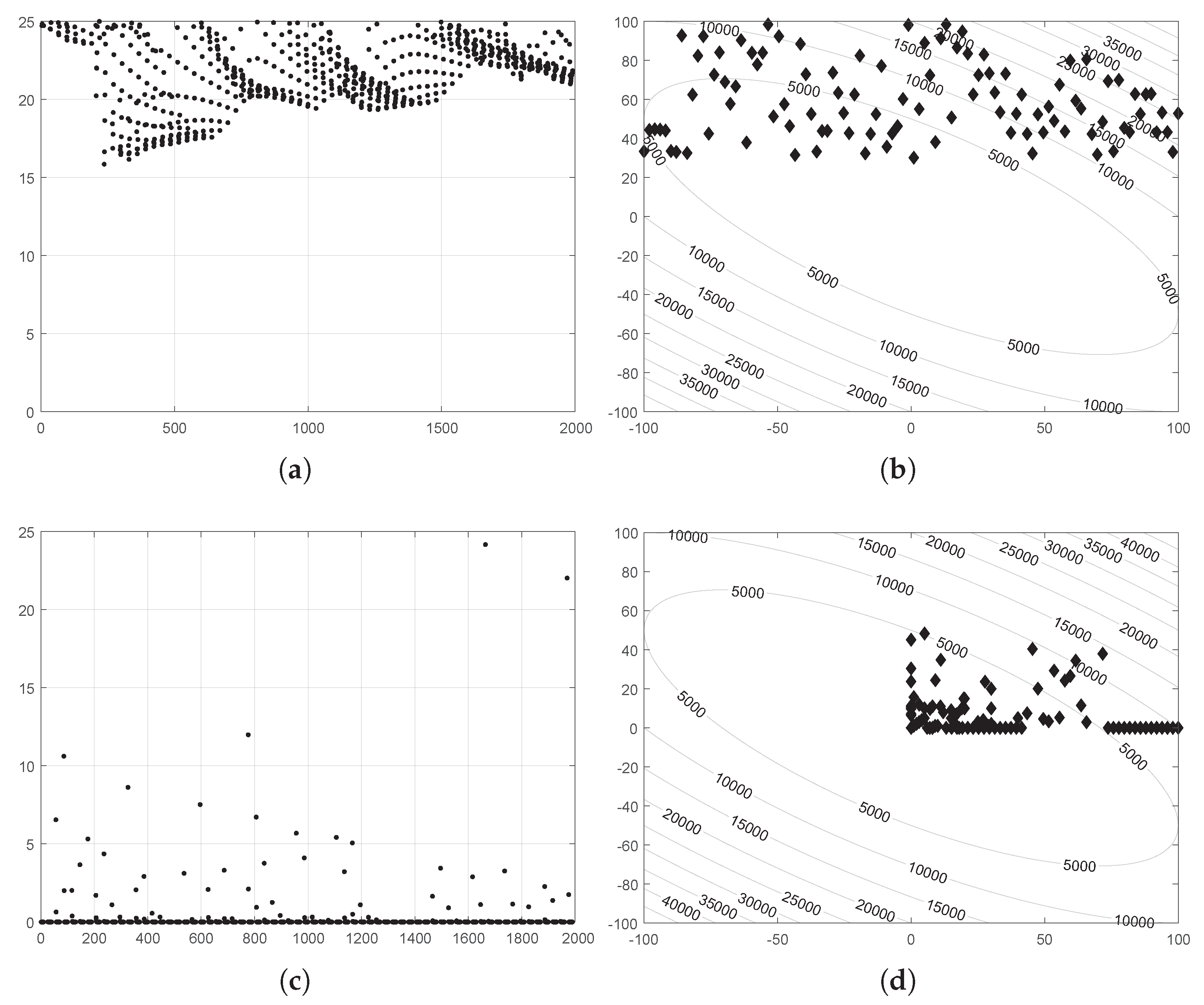
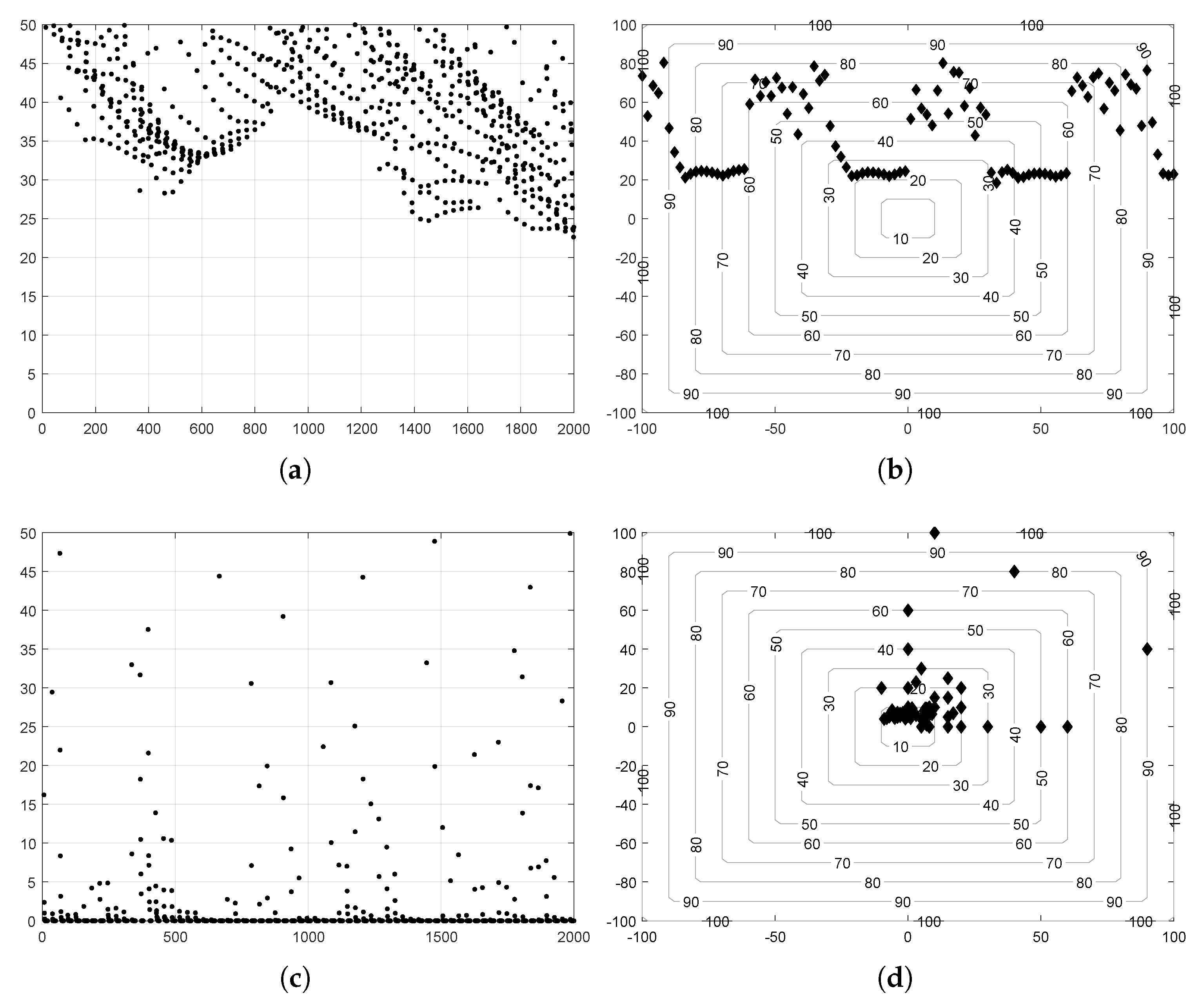
5.1. Comparison Based on Solution Accuracy
5.2. Comparison Based on Convergence
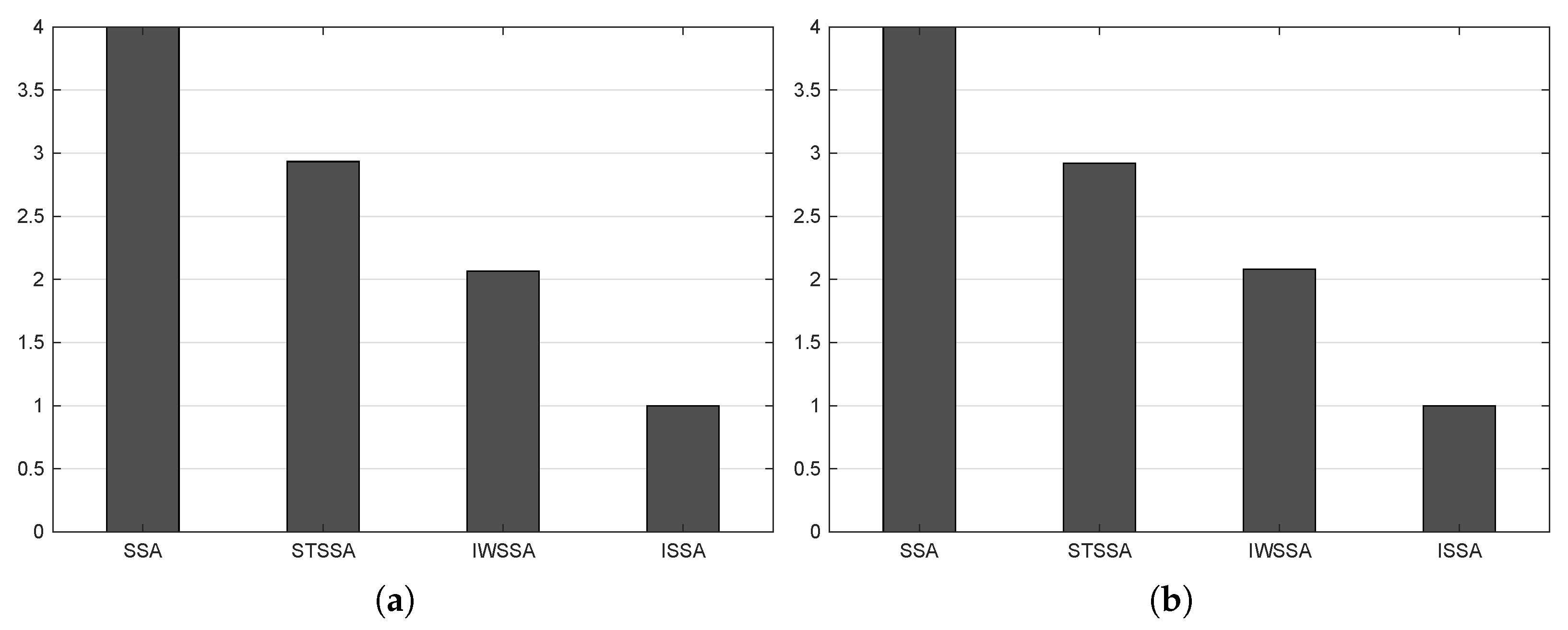
5.3. Statistical Analysis
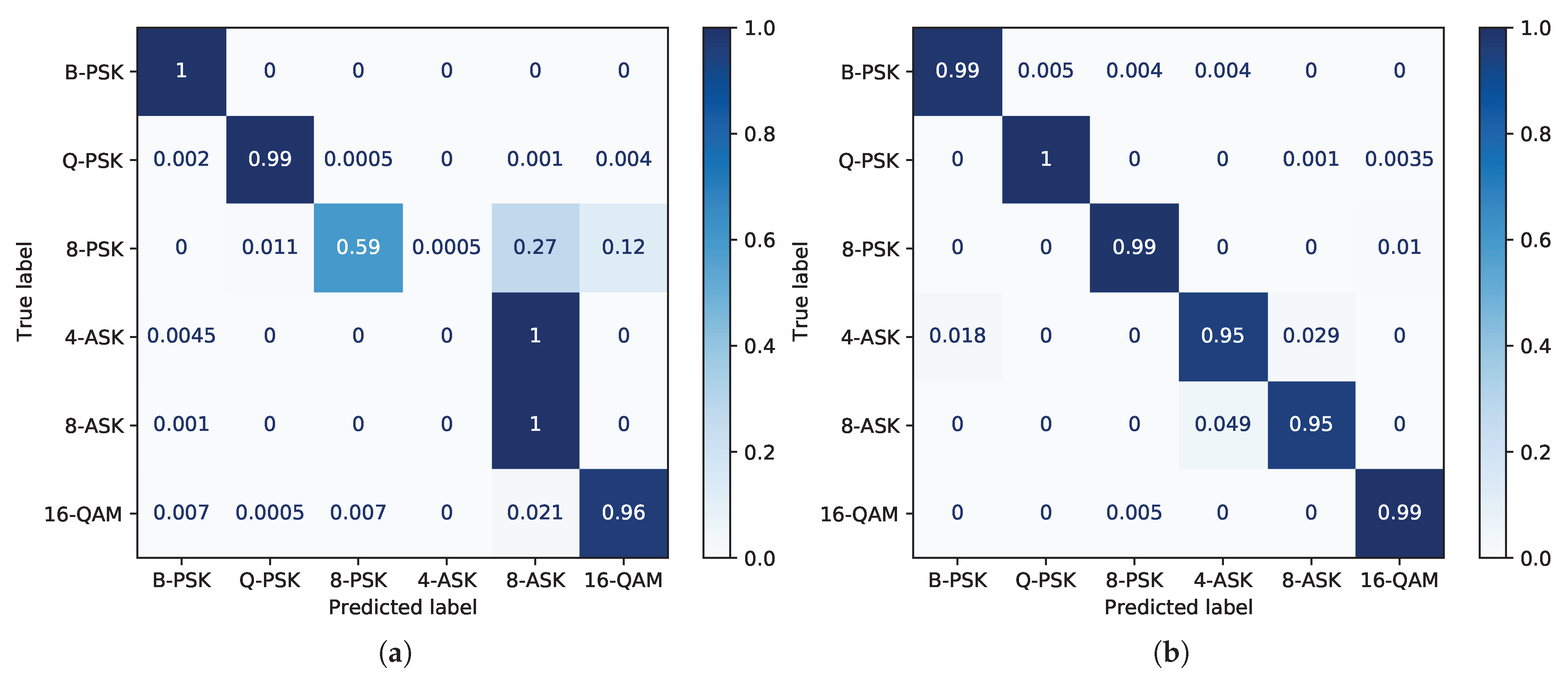
6. ISSA for Feature Weighting in DMI
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ghodratnama, S.; Moghaddam, H.A. Content-based image retrieval using feature weighting and C-means clustering in a multi-label classification framework. Pattern Anal. Appl. 2021, 24, 1–10. [Google Scholar] [CrossRef]
- Nguyen, K.; Todorovic, S. Feature weighting and boosting for few-shot segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 622–631. [Google Scholar] [CrossRef] [Green Version]
- Tubishat, M.; Idris, N.; Shuib, L.; Abushariah, M.A.; Mirjalili, S. Improved Salp Swarm Algorithm based on opposition based learning and novel local search algorithm for feature selection. Expert Syst. Appl. 2020, 145, 113122. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Alabool, H. Salp swarm algorithm: A comprehensive survey. Neural Comput. Appl. 2020, 32, 11195–11215. [Google Scholar] [CrossRef]
- Hodashinsky, I.; Sarin, K.; Shelupanov, A.; Slezkin, A. Feature Selection Based on Swallow Swarm Optimization for Fuzzy Classification. Symmetry 2019, 11, 1423. [Google Scholar] [CrossRef] [Green Version]
- Parpinelli, R.S.; Lopes, H.S. New inspirations in swarm intelligence: A survey. Int. J. Bio-Inspired Comput. 2011, 3, 1–16. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. An overview of evolutionary algorithms in multiobjective optimization. Evol. Comput. 1995, 3, 1–16. [Google Scholar] [CrossRef]
- Biswas, A.; Mishra, K.; Tiwari, S.; Misra, A. Physics-inspired optimization algorithms: A survey. J. Optim. 2013, 2013, 438152. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Panda, N.; Majhi, S.K. Improved Salp swarm algorithm with space transformation search for training neural network. Arab. J. Sci. Eng. 2019, 45, 2743–2761. [Google Scholar] [CrossRef]
- Hegazy, A.E.; Makhlouf, M.; El-Tawel, G.S. Improved salp swarm algorithm for feature selection. J. King Saud Univ. Comput. Inf. Sci. 2020, 32, 335–344. [Google Scholar] [CrossRef]
- Kharbech, S.; Simon, E.P.; Belazi, A.; Xiang, W. Denoising Higher-Order Moments for Blind Digital Modulation Identification in Multiple-Antenna Systems. IEEE Wirel. Commun. Lett. 2020, 9, 765–769. [Google Scholar] [CrossRef]
- Hassan, K.; Dayoub, I.; Hamouda, W.; Nzéza, C.N.; Berbineau, M. Blind digital modulation identification for spatially-correlated MIMO systems. IEEE Trans. Wirel. Commun. 2011, 11, 683–693. [Google Scholar] [CrossRef]
- Kharbech, S.; Dayoub, I.; Simon, E.; Zwingelstein-Colin, M. Blind digital modulation detector for MIMO systems over high-speed railway channels. In Proceedings of the International Workshop on Communication Technologies for Vehicles, Lille, France, 14–15 May 2013; pp. 232–241. [Google Scholar] [CrossRef]
- Mahdavi, S.; Rahnamayan, S.; Deb, K. Opposition based learning: A literature review. Swarm Evol. Comput. 2018, 39, 1–23. [Google Scholar] [CrossRef]
- Ewees, A.A.; Abd Elaziz, M.; Houssein, E.H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst. Appl. 2018, 112, 156–172. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Liu, Z.; Blasch, E.; John, V. Statistical comparison of image fusion algorithms: Recommendations. Inf. Fusion 2017, 36, 251–260. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]





| SSA | STSSA | IWSSA | ISSA | ||
|---|---|---|---|---|---|
| Mean | 4.03 × 10 | 7.12 × 10 | 1.01 × 10 | 0.00 × 10 | |
| SD | 9.52 × 10 | 2.78 × 10 | 3.48 × 10 | 0.00 × 10 | |
| SEM | 1.73 × 10 | 5.08 × 10 | 6.35 × 10 | 0.00 × 10 | |
| Mean | 1.90 × 10 | 8.90 × 10 | 9.00 × 10 | 1.20 × 10 | |
| SD | 7.10 × 10 | 1.54 × 10 | 1.17 × 10 | 0.00 × 10 | |
| SEM | 1.20 × 10 | 2.82 × 10 | 2.13 × 10 | 0.00 × 10 | |
| Mean | 1.93 × 10 | 2.20 × 10 | 1.78 × 10 | 0.00 × 10 | |
| SD | 1.01 × 10 | 1.24 × 10 | 3.61 × 10 | 0.00 × 10 | |
| SEM | 1.84 × 10 | 2.28 × 10 | 6.60 × 10 | 0.00 × 10 | |
| Mean | 1.50 × 10 | 7.73 × 10 | 9.02 × 10 | 2.27 × 10 | |
| SD | 4.17 × 10 | 1.78 × 10 | 9.66 × 10 | 0.00 × 10 | |
| SEM | 7.63 × 10 | 7.63 × 10 | 1.76 × 10 | 0.00 × 10 | |
| Mean | 1.40 × 10 | 89.4 × 10 | 89.2 × 10 | 89.2 × 10 | |
| SD | 3.59 × 10 | 1.60 × 10 | 1.40 × 10 | 1.20 × 10 | |
| SEM | 6.56 × 10 | 0.3 × 10 | 0.2 × 10 | 0.2 × 10 | |
| Mean | 6.31 × 10 | 0.13 × 10 | 6.00 × 10 | 6.30 × 10 | |
| SD | 2.72 × 10 | 3.30 × 10 | 1.40 × 10 | 1.70 × 10 | |
| SEM | 4.98 × 10 | 0.60 × 10 | 0.20 × 10 | 0.30 × 10 | |
| Mean | 0.60 × 10 | 8.19 × 10 | 4.44 × 10 | 4.69 × 10 | |
| SD | 0.40 × 10 | 8.38 × 10 | 4.16 × 10 | 4.58 × 10 | |
| SEM | 0.40 × 10 | 1.53 × 10 | 7.60 × 10 | 8.37 × 10 | |
| Mean | −2.83 × 10 | −2.23 × 10 | −2.093 × 10 | −2.096 × 10 | |
| SD | 2.54 × 10 | 1.91 × 10 | 1.54 × 10 | 1.65 × 10 | |
| SEM | 4.65 × 10 | 3.50 × 10 | 2.82 × 10 | 3.01 × 10 | |
| Mean | 1.94 × 10 | 1.01 × 10 | 0.00 × 10 | 0.00 × 10 | |
| SD | 0.75 × 10 | 3.62 × 10 | 0.00 × 10 | 0.00 × 10 | |
| SEM | 0.13 × 10 | 6.61 × 10 | 0.00 × 10 | 0.00 × 10 | |
| Mean | 7.50 × 10 | 6.17 × 10 | 6.11 × 10 | 8.88 × 10 | |
| SD | 8.10 × 10 | 1.57 × 10 | 8.03 × 10 | 0.00 × 10 | |
| SEM | 1.40 × 10 | 2.87 × 10 | 1.46 × 10 | 0.00 × 10 | |
| Mean | 2.60 × 10 | 9.36 × 10 | 0.00 × 10 | 0.00 × 10 | |
| SD | 1.40 × 10 | 4.36 × 10 | 0.00 × 10 | 0.00 × 10 | |
| SEM | 0.20 × 10 | 7.97 × 10 | 0.00 × 10 | 0.00 × 10 | |
| Mean | 2.70 × 10 | 3.60 × 10 | 1.40 × 10 | 1.30 × 10 | |
| SD | 4.60 × 10 | 1.20 × 10 | 0.50 × 10 | 0.50 × 10 | |
| SEM | 0.80 × 10 | 0.20 × 10 | 0.10 × 10 | 0.10 × 10 | |
| Mean | 0.10 × 10 | 7.00 × 10 | 3.40 × 10 | 3.50 × 10 | |
| SD | 0.30 × 10 | 1.70 × 10 | 0.70 × 10 | 0.90 × 10 | |
| SEM | 0.60 × 10 | 0.30 × 10 | 0.10 × 10 | 0.10 × 10 | |
| Mean | 0.10 × 10 | 0.20 × 10 | 0.14 × 10 | 0.14 × 10 | |
| SD | 1.80 × 10 | 0.11 × 10 | 6.10 × 10 | 6.70 × 10 | |
| SEM | 0.30 × 10 | 2.10 × 10 | 1.10 × 10 | 1.20 × 10 | |
| Mean | 0.10 × 10 | 0.90 × 10 | 0.60 × 10 | 0.60 × 10 | |
| SD | 0.30 × 10 | 0.40 × 10 | 0.10 × 10 | 0.20 × 10 | |
| SEM | 0.60 × 10 | 8.92 × 10 | 3.03 × 10 | 4.32 × 10 | |
| Mean | −10.3 × 10 | −10.3 × 10 | −10.2 × 10 | −10.2 × 10 | |
| SD | 9.59 × 10 | 3.01 × 10 | 0.10 × 10 | 0.20 × 10 | |
| SEM | 1.75 × 10 | 5.49 × 105 | 0.2 × 10 | 0.3 × 10 | |
| Best for | 3/16 | 0/16 | 7/16 | 11/16 | |
| SSA | STSSA | IWSSA | ISSA | ||
|---|---|---|---|---|---|
| MeanFES | 24,699.3 | 23,743.1 | 961.8 | 427.1 | |
| SR (%) | 100 | 100 | 100 | 100 | |
| MeanFES | 29,272.6 | 27,581.9 | 3262.9 | 538.5 | |
| SR (%) | 20 | 100 | 100 | 100 | |
| MeanFES | 24,189.5 | 23,052.8 | 975.5 | 314.3 | |
| SR (%) | 100 | 100 | 100 | 100 | |
| MeanFES | 28,211.3 | 27,320.7 | 2709.9 | 595.5 | |
| SR (%) | 100 | 100 | 100 | 100 | |
| MeanFES | NaN | NaN | NaN | NaN | |
| SR (%) | 0 | 0 | 0 | 0 | |
| MeanFES | 23,569.4 | NaN | NaN | NaN | |
| SR (%) | 100 | 0 | 0 | 0 | |
| MeanFES | NaN | 22,196.0 | 10,977.3 | 16,115.1 | |
| SR (%) | 0 | 70 | 90 | 90 | |
| MeanFES | 6670.3 | 8318.1 | 7208.3 | 7298.2 | |
| SR (%) | 100 | 70 | 40 | 46.7 | |
| MeanFES | NaN | 22,598.3 | 765.4 | 342.9 | |
| SR (%) | 0 | 100 | 100 | 100 | |
| MeanFES | 27,726.4 | 27,119.7 | 2840.9 | 489.7 | |
| SR (%) | 50 | 100 | 100 | 100 | |
| MeanFES | NaN | 23,761.7 | 1082.5 | 339.9 | |
| SR (%) | 0 | 100 | 100 | 100 | |
| MeanFES | 20,934.8 | NaN | NaN | NaN | |
| SR (%) | 63.3 | 0 | 0 | 0 | |
| MeanFES | 21,824.07 | NaN | NaN | NaN | |
| SR (%) | 90 | 0 | 0 | 0 | |
| MeanFES | 6371.1 | 2980.2 | 9078 | 6266.7 | |
| SR (%) | 97 | 16.67 | 20 | 24 | |
| MeanFES | 10,698.4 | 9842.8 | 9280.5 | 11,614.1 | |
| SR (%) | 66.67 | 66.67 | 96.67 | 90 | |
| MeanFES | 10,090.9 | 11,945.7 | 13,526 | 13,367.5 | |
| SR (%) | 100 | 100 | 20 | 33.3 | |
| Best for | MeanFES | 5/16 | 1/16 | 2/16 | 7/16 |
| SR (%) | 9/16 | 8/16 | 9/16 | 8/16 |
| SSA | STSSA | IWSSA | ISSA | |
|---|---|---|---|---|
| Mean | 2.289 × 10 | 2.290 × 10 | 2.29 × 10 | 1.06 × 10 |
| SD | 3.24 × 10 | 2.57 × 10 | 5.5 × 10 | 1.5 × 10 |
| SEM | 5.9 × 10 | 4.7 × 10 | 9.954 × 10 | 2.801 × 10 |
| SSA | STSSA | IWSSA | ISSA | |
|---|---|---|---|---|
| MeanFES | NaN | 10,134 | 810.3 | 2773.7 |
| SR (%) | 0 | 86.67 | 100 | 100 |
| w/o FW | z-Score | SSA | STSSA | IWSSA | ISSA |
|---|---|---|---|---|---|
| 0.1888 | 0.0384 | 0.2418 | 0.0213 | 0.0137 | 0.0089 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Chaabane, S.; Belazi, A.; Kharbech, S.; Bouallegue, A.; Clavier, L. Improved Salp Swarm Optimization Algorithm: Application in Feature Weighting for Blind Modulation Identification. Electronics 2021, 10, 2002. https://doi.org/10.3390/electronics10162002
Ben Chaabane S, Belazi A, Kharbech S, Bouallegue A, Clavier L. Improved Salp Swarm Optimization Algorithm: Application in Feature Weighting for Blind Modulation Identification. Electronics. 2021; 10(16):2002. https://doi.org/10.3390/electronics10162002
Chicago/Turabian StyleBen Chaabane, Sarra, Akram Belazi, Sofiane Kharbech, Ammar Bouallegue, and Laurent Clavier. 2021. "Improved Salp Swarm Optimization Algorithm: Application in Feature Weighting for Blind Modulation Identification" Electronics 10, no. 16: 2002. https://doi.org/10.3390/electronics10162002
APA StyleBen Chaabane, S., Belazi, A., Kharbech, S., Bouallegue, A., & Clavier, L. (2021). Improved Salp Swarm Optimization Algorithm: Application in Feature Weighting for Blind Modulation Identification. Electronics, 10(16), 2002. https://doi.org/10.3390/electronics10162002






