1. Introduction
“Massive MIMO is a reality—What is next?” [
1]. This suggestive paper presents various technologies based on the use of antenna arrays whose evolution will play an increasingly important role in the development of new generations of wireless communication systems (5G and beyond). Among them, the use of extremely large aperture arrays (ELAA) is presented as one of the most promising. Basically, the idea consists of distributing a great number of antennas over an extensive area, such as the roof of a big commercial building, or distributing them over a large geographical area, instead of grouping them into concentrated arrays, as has been the usual case so far. In this way, the user terminals (UTs) are surrounded by antennas belonging to a distributed base station (BS) instead of being covered by a BS with all its antennas concentrated in a classic array. The hybridization of proposals to evolve toward distributed wireless communication systems [
2,
3,
4], together with the idea of massive multiple-input multiple-output (MIMO), has given rise to the concept of distributed massive MIMO [
5,
6,
7,
8,
9,
10] and the cell-free MIMO network concept [
11,
12,
13,
14].
Numerous theoretical works have investigated the performance of distributed massive MIMO (D-mMIMO) systems and their comparison with concentrated massive MIMO (C-mMIMO) systems. Obtaining adequate channel models is one of the difficulties in theoretical analysis of the capacity or spectral efficiency (SE) of distributed systems. Unlike concentrated systems, distributed ones present a great variability between the radio channels that a UT establishes with the different antennas conforming the BS. This is due to various propagation effects such as the path loss, shadowing effects, and degree of obstruction that each radio link experiences. This matter has been treated and modeled in the literature in different ways; see for instance [
2,
15,
16,
17,
18].
Concerning experimental results, far fewer works can be found in the literature, all of them showing the advantages of the D-mMIMO system over the C-mMIMO one. In [
19], an experimental analysis is carried out at 2.6 GHz; a C-mMIMO scheme is compared with another D-mMIMO one in the same indoor–outdoor environment and under non-line-of-sight (NLOS) conditions. It uses two arrays of 32 antennas that are placed together forming a concentrated 64 antenna element array, or two 32 antenna arrays 6.4 m apart, giving rise to a system which is, to a certain extent, distributed (split array). In summary, the conclusions are that the distributed configuration improves both the total throughput as well as the user fairness. In [
20], an improved measurement system with regard to that presented in [
19] is used in an indoor picocell. In this case, several antenna configurations are considered, where arrays consisting of 32 antennas are used, collocated, or distributed. In this case, the work is more focused on the proposal of new user scheduling algorithms than on the comparison of distributed versus collocated antenna configurations. In [
21], an outdoor field experiment at 4.65 GHz of a distributed MIMO system is presented using sub-arrays of 2 × 2 antennas that are deployed on the terrace of a building in four positions 37 m apart. The total throughput is compared to that obtained with a concentrated MIMO system of 4 × 4 antennas. In both cases, eight UTs are considered moving at different speeds along the street surrounding the building. The main conclusion is that distributed MIMO has a better performance when compared with concentrated MIMO in cases of low mobility (5 km/h) and a similar performance in cases of high mobility (40 km/h). In [
22], and using a similar experimental set-up as the one described in [
21], a study is presented in the same frequency band, but now in an indoor environment. In this case, a significant increase in throughput is demonstrated when a distributed MIMO configuration is employed.
This paper presents a measurement-based comparison of distributed and concentrated massive MIMO systems, i.e., D-mMIMO and C-mMIMO systems, in an indoor environment. In both cases, we have considered an array of 64 antennas at the BS and eight simultaneously active UTs. The work focuses on the characterization of the channel in the up-link, considering the analysis of the capacity and the SE achievable by using the zero forcing (ZF) algorithm as the combining method, under the hypothesis of perfect channel state information (CSI). The effect of the power imbalance between the different UTs, and thus, the benefits of performing an adequate power control are also analyzed. In addition, user fairness is considered as another figure of merit in the comparison between both systems. Other important aspects related to the network architecture, such as the backhaul structure, the strategy to obtain CSI with minimal overhead, scheduling strategies, etc., remain outside the scope of this paper.
The channel measurements have been performed in the frequency domain, emulating a massive MIMO system in the framework of a time-domain duplex orthogonal frequency multiple access network (TDD-OFDM-MIMO). Moreover, the measurements have been carried out avoiding the movement of people in the building, considering a 400 MHz bandwidth centered at 3.5 GHz, with a frequency tone separation of 31.25 kHz, which is close to the 30 kHz established in the 5G standard numerology. The characterization of the MIMO channel is based on the virtual array technique for both C-mMIMO and D-mMIMO systems.
The main contributions of this paper are as follows: (i) The differences between the C-mMIMO and D-mMIMO channels are analyzed through the observation of the structure of their respective measured channel matrices, through parameters such as the condition number or the power imbalance between the channels established by each UT. (ii) The sum capacity of both types of channel is calculated and analyzed, and it is related to the structure of the channel matrix. (iii) Two alternative channel normalizations are used, one of which can be interpreted as the implementation by the system of an ideal power control. Thus, we quantify the impact of the power imbalance on the system performance and outline the advantages of carrying out an adequate power control. (iv) Beyond the intrinsic capacity of the channel, the achievable throughput is calculated using ZF as the combination method. (v) The latter allows us to analyze not only the total throughput achievable by each one of the schemes, distributed or concentrated, but also the user fairness that each of the methods offers, as a parameter of great interest when analyzing the pros and cons of both schemes.
The remainder of this paper is organized as follows. In
Section 2, we present the channel characterization methodology for massive MIMO.
Section 3 describes the indoor environment where the measurements are carried out along with the main characteristics of the channel sounders and the measurement settings. In
Section 4, we present and analyze the results obtained from the experimental measurements. Finally, we conclude the paper in
Section 5.
2. Channel Characterization Methodology
Focusing the analysis on the up-link, the massive MIMO system considered is a simple cell system where the BS is equipped with M antennas. The maximum number of active users is Q, and each UT is equipped with a single antenna. It is assumed that the users transmit a total power P. In addition, it is assumed that the BS knows the channel and that the UTs are not collaborating among each other. Furthermore, we consider an OFDM system with Nf sub-carriers, which correspond to the measured tones.
Considering this model, the vector form of the received signal at the BS for the
k-th sub-carrier when the
Q users are active will be given by:
where
y[
k] is a column vector with
M elements corresponding to the
k-th sub-carrier;
G[
k] is the channel matrix of order
M ×
Q, in which each one of its columns corresponds with the narrowband channel of the
q-th user
gq[
k] of order
M × 1;
s[
k] (
Q × 1) is the vector representing the signals vector transmitted from the UTs and normalized in such a way that
, where
E{.} represents the mean or expected value; and
n[
k] is a complex Gaussian noise vector with independent and identically distributed (i.i.d.) unit variance elements. Finally, the
SNR represents the mean signal to noise ratio at the receiver.
The matrix in (1) is normalized in such a way that verifies:
where
is the Frobenius norm.
Moreover, the matrix
G is obtained from the matrix of the raw channel measurements (
Graw) by means of:
The normalization matrix
J is a diagonal matrix of order
Q ×
Q. Different normalizations can be considered, provided they verify (2), which guarantees the conservation of the total transmitted power. Following the proposal and the nomenclature in [
23], we consider two normalizations that we will denote as normalization 1 (N1) and normalization 2 (N2).
On the one hand, in case of using N1, the normalization matrix
J is a diagonal matrix of order
Q ×
Q, whose elements (
jqq) are given by
The elements of the normalization matrix J take different values so that all the columns in G are normalized to one; consequently, the power imbalance between the channels corresponding to each UT is eliminated, although the channel variations between antennas within the receiver array and frequency tones are maintained. The resulting normalized matrix, G, can be interpreted as that associated with a system in which an ideal power control is performed. In this case, the total available power transmitted by the users is not distributed equally, but each UT is assigned the necessary power so that all UTs reach the BS with the same mean power.
On the other hand, N2 is defined in such a way that all the elements of the diagonal matrix
J are equal and thus, the operation in (3) is equivalent to multiplying the matrix by a scalar:
This normalization keeps the difference between the received power from different UTs, receiver antennas, and frequency tones.
Both N1 and N2 normalizations have their pros and cons. N2 preserves the original structure of the channel and the effect that the power imbalance can have on the system. However, if the aim is to isolate the effect of the power imbalance and exclusively analyze the orthogonality of the channel, for example through the condition number, it is mandatory to use N1 [
23].
The SE that massive MIMO systems can achieve depends largely on the degree to which the condition of “favorable propagation” is met, which depends on the extent to which the channels of the different users are orthogonal [
23,
24,
25,
26,
27]. A commonly accepted metric used to weigh up the orthogonality of the columns of a matrix is the condition number,
κ, which is also a measure of the dispersion of the singular values of the matrix. The condition number of a matrix
G is defined by the relationship:
According to (6), a value of κ equal to one corresponds to a channel matrix in which all its columns are orthogonal. Conversely, high values of κ indicate that at least two columns of the matrix will be practically collinear. It is more suitable to interpret the results to use the inverse of the condition number (ICN), which varies between 1 (maximum orthogonality) and 0 (zero orthogonality).
To have a direct measure of the goodness of the channel, we calculate the sum capacity. Under the hypothesis of a perfect knowledge of the channel at the BS, we can obtain the sum capacity of the massive MIMO-OFDM system by means of the breakdown into singular values of the channel matrix as
in which
represents the
q-th eigenvalue of the
GHG matrix, i.e., the square of the
q-th singular value of the
G matrix.
Under favorable propagation conditions, as the number of receiving antennas
M increases, and for a fixed number of transmitters
Q, the capacity of the up-link channel will tend asymptotically to the upper bound [
27]:
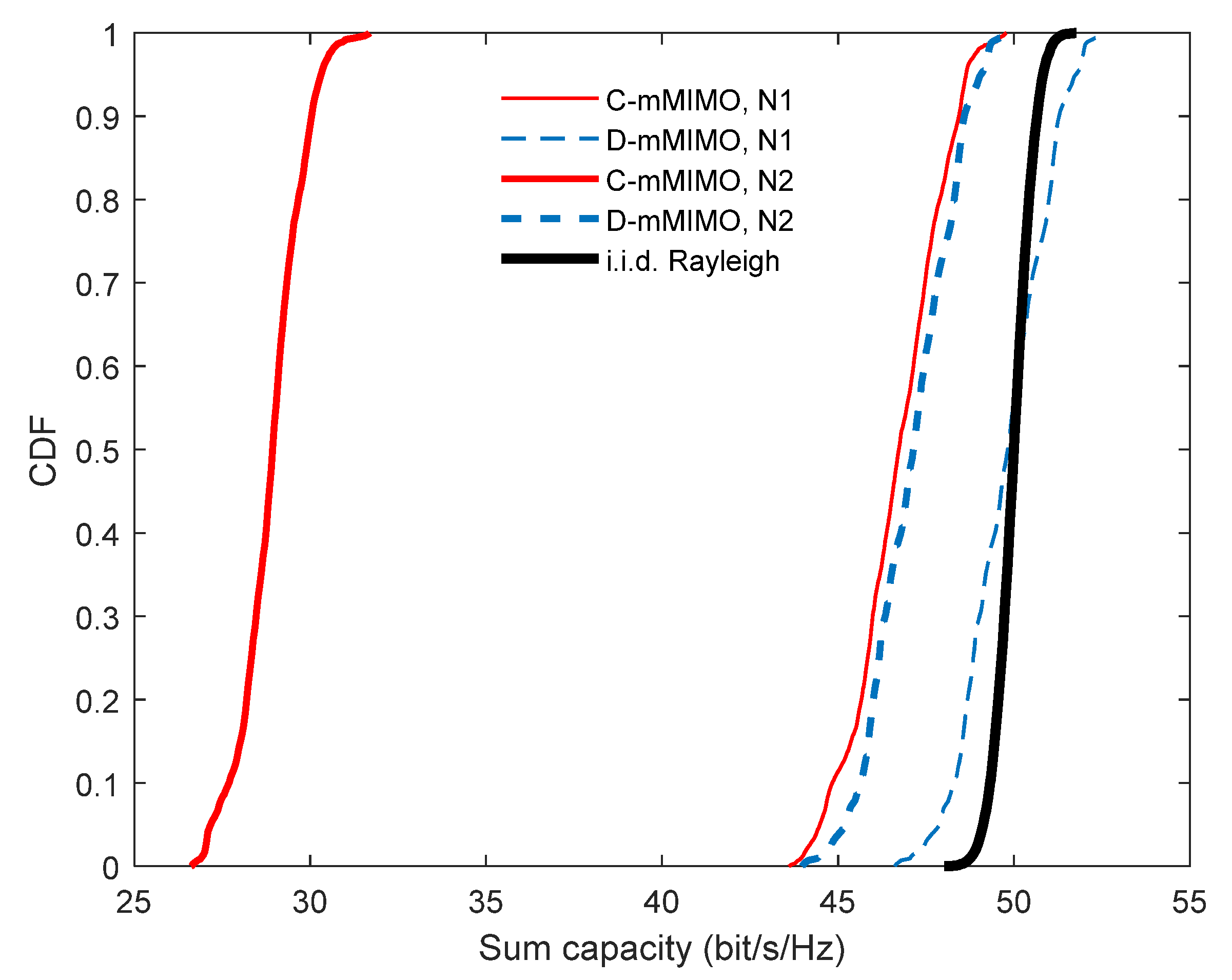
The sum capacity obtained from the concentrated system versus the distributed one allows a global comparison of the behavior of both systems to be made.
Furthermore, the analysis of the channel spectral efficiency provides additional information to compare both C-mMIMO and D-mMIMO systems. In this sense, both the individual SE for each user as well as the sum SE are calculated. Let us consider that the received signal is processed in the receiver by a linear combination method such as the ZF method, which is defined by the matrix
V and expressed as
Then, the processed signal at the receiver can be expressed as
where
[
k] is a column vector with
Q elements that represents the estimation of the signals transmitted by the
Q active users at the
k-th frequency tone.
The signal to interference plus noise ratio (SINR) of the
q-th user on the
k-th sub-carrier is given by:
Using (11), the individual SE of each active UT is calculated as follows:
Finally, the sum SE is expressed as:
Another useful factor available to compare both C-mMIMO and D-mMIMO systems is the user fairness given by Jain’s Fairness Index (JFI) [
28]. This metric is used to analyze the fairness of the channel to share out the overall SE among the active UTs, and it is given by:
where
E{⋅} represents the mathematical expectation evaluated over all the
Nf frequency tones. The JFI takes values between 1/
Q and 1, so that the value 1 corresponds to the maximum fairness among the SE values of the active UTs.
3. Indoor Channel Measurements
In this section, the description of the indoor environment showing the distribution of both UTs and VAs for both situations (C-mMIMO and D-mMIMO), along with a summary including the main characteristics of the channel sounders and the measurement settings are presented.
In order to compare the experimentally obtained performance of both presented C-mMIMO and D-mMIMO configurations, a measurement campaign has been carried out inside a modern office building at the University of Cantabria. The measurements focus on the up-link and consider for the UTs both line-of-sight (LOS) as well as non-line-of-sight (NLOS) positions. Potential locations close to those that might be considered for a real deployment have been chosen for the virtual arrays (VAs) at the BS side. Regarding the channel sounding, we have considered two different measurement setups, both using a vector network analyzer as the main measurement equipment.
3.1. The Indoor Environment
The top view of the indoor measurement environment considered in this work is shown in
Figure 1a. The floor of the building mainly consists of offices and computer laboratories with a large corridor that provides access to those rooms. Regarding the materials of the building, it is made of reinforced concrete, has plasterboard paneled walls and ceiling boards, along with metallic doors in all the indoor rooms. The rooms are characterized by the presence of desks, chairs, and wooden and steel cabinets, along with computers and monitors.
According to the topology of the floor, the measurement campaign has concentrated on that part of the building shown in
Figure 1b, including the details for both UTs and receiver (Rx) VA locations considered. It must be pointed out that there are four circular concrete columns almost centered in the corridor, which influence the multipath contributions reaching the Rx VAs and thus, the locations for such BS VAs must be carefully chosen. In this sense, the C-mMIMO VA consisting of 8 × 8 elements has been located near the main entrance of the building, at a height
hRx for the center of the scanning area, and centered in the lower-widest half of the corridor. Furthermore, concerning the D-mMIMO VA arrangement, it consists of 64 antennas placed at the ceiling board at a height
hRx, uniformly spaced Δ
l, and distributed over two linear trajectories, T1 and T2, which are located at both sides of the columns and linearly shifted from each other Δ
l/2.
Finally, eight potential UTs or transmitter (Tx) positions have been considered, mixing up two well-differentiated channel propagation conditions; some of them are under LOS conditions, i.e., UT
2, UT
6, and UT
8 (though strictly the UT
6 is under NLOS conditions for most of the D-mMIMO VA positions), and the rest are under NLOS conditions, i.e., UT
1, UTs
3-5, and UT
7. In this case, the Tx antenna is placed at a height
hTx. The summary of the main parameters for both C-mMIMO and D-mMIMO virtual arrays, including those concerning the UTs, is presented in
Table 1.
3.2. Measurement Setups
Two channel sounders have been used to carry out the measurements for both massive MIMO configurations. Basically, the two systems use a vector network analyzer (VNA) to measure in the frequency domain and in the frequency band of interest, i.e., 3.3–3.7 GHz, the S21(f) scattering parameter that corresponds with the complex channel transfer function, H(f).
Concerning the C-mMIMO measurements, the automated measurement system used is shown in
Figure 2. The channel sounder consists of a planar scanner and the P5006A VNA from Keysight Technologies, which are both remote controlled from a laptop to measure for a certain UT/Tx the
H(
f) at any Rx position of the VA over the YZ plane. The planar scanner consists of two linear units and the associated servomotors to control the movement in both axes, i.e., BLS-72 and BLS-55 motors from Mavilor. Compared with a previous channel sounder [
29], the fitting of the speed of the motors and the use of the USB-controlled VNA speeds up the measurements significantly, the measurement for every UT position currently taking 20 min.
For the D-mMIMO measurements, we simplified the system used for the C-mMIMO setup by just eliminating the planar scanner. Basically, in this case and as shown in
Figure 3, for every UT/Tx location, the Rx/Bs antenna is fixed to the ceiling board and manually moved to any of the 32 positions that make up both T1 and T2 trajectories. Bearing in mind again that the analysis is focused on the up-link, at every Rx position, the S
21-trace is acquired and, from the post-processing of the traces, a complete characterization of the indoor channel established between that Tx, i.e., an UT, and the Rx VA, i.e., the virtual array at the BS, can be carried out. Concerning the D-mMIMO measurement time, and in spite of the fact that the trace acquisition from the VNA takes less than 15 s per Rx position, the manual movement of the Rx antenna increases the overall measurement time for every UT position up to around one hour on average.
Regarding the antennas used in the measurement campaign, which are all linearly polarized, we have used the EM-6865 model from Electrometrics (a biconical omnidirectional antenna) on the Tx/UT side for both C-mMIMO and D-mMIMO measurements [
29]. Furthermore, either the log-periodic HG2458-08LP [
29] or the multi-band omnidirectional HG35805CUPR-NF antennas, both models from L-Com, have been used on the Rx/BS side for both C-mMIMO and D-mMIMO, respectively. Basically, the EM-6865 antenna operates in the 2–18 GHz frequency range and has a gain of around 1 dB in the band of interest, whereas the HG2458-08LP antenna operates in the 2.3–6.5 GHz frequency range showing a gain higher than 8 dBi and a beam width close to 60°. In [
29], details for both antennas measured at 4 GHz are included. Moreover, the ceiling mount antennas, the HG35805CUPR-NF, show at 3.5 GHz a nearly omnidirectional pattern and a gain of 4.9 dB.
Finally, it must be pointed out that both sets of measurements, with the C-mMIMO and D-mMIMO systems, have been carried out at night to guarantee stationary conditions as the analysis of the effect of people is beyond the scope of this paper, keeping all the doors of the floor closed.
3.3. Measurement Settings
The measurements have been carried out in the 3.3–3.7 GHz frequency range, containing most of the band considered for the current deployments of 5G networks. Regarding the S21-trace, Nf = 12,801 frequency tones, Δf = 31.25 kHz uniformly spaced in the 400 MHz band have been considered; close to 30 kHz, one of the OFDM sub-carrier spacings was adopted in 5G New Radio (NR)-based air interface. The frequency resolution Δf leads to a maximum observable distance of 9.6 km (stated as c0/Δf, in which c0 represents the speed of light), so the multipath contributions are properly considered.
Concerning the VNA, the main settings are summarized in
Table 2. An intermediate frequency (IF) filter bandwidth of 3 kHz along with an averaging factor of three traces have been considered to achieve an appropriate trade-off between acquisition time and dynamic range for the whole set of UTs, those in LOS as well as in NLOS conditions. In fact, the average
SNR observed is always above 35 dB. Moreover, a dwell time of 1 μs has been set in the sweep in order to take into account the propagation delay of the multipath components. Finally, and prior to every measurement session, the VNA has been properly calibrated at the ends of the radio frequency cables, so the S
21 measured takes into account the joint effect of both channel and antennas, which represents the radio channel [
30].
5. Conclusions
Taking as a reference empirical data obtained from channel measurements carried out in an indoor cell, a comparison between D-mMIMO and C-mMIMO systems as deployment alternatives has been reported and discussed. The channel measurements have been performed in the frequency domain, considering a 400 MHz span centered at 3.5 GHz.
The results show that the sum capacity of the D-mMIMO channel always outperforms that achieved by the C-mMIMO channel. In fact, in the particular case of not performing a power control mechanism, the C-mMIMO sum capacity is much lower than that of the D-mMIMO system. The explanation for such differences is obtained from the analysis of the ICN performance and the power imbalance between the sub-channels for both systems. In the case of the C-mMIMO channel, low ICN values are obtained, even in the case of compensating for the power imbalance between sub-channels. On the contrary, in the case of the D-mMIMO channel, the ICN values are always higher, and in the case of performing an ideal power control, they are close to those of an i.i.d. Rayleigh reference channel. Although the power control applied in this work is ideal, it can be inferred that the C-mMIMO channel will always be more dependent on the realistic power control that could be carried out than the D-mMIMO one.
The sum SE reflects the characteristics of the channel that explain the behavior of the capacity. It is observed that the sum SE is always greater for the D-mMIMO system. It can also be stated that the loss of SE with respect to the obtainable capacity is considerably higher for the C-mMIMO system than for the D-mMIMO one. The difference between the SE and the capacity depends on the performance of the ZF combination method. Although ZF removes the interference generated by other users, the application of this combination method introduces an additional noise enhancement. This problem, which degrades the SE, has a greater impact on channels with ill-conditioned G matrices, as is the case of the concentrated channel versus the distributed one, as confirmed from the observation of the measured ICN performance.
Finally, an important parameter in the comparison between both systems is the user fairness. The paper presents the CDF of the SE of each user, and these are related to the distance and degree of obstruction (LOS or NLOS) of each one. Furthermore, the user fairness is quantified with Jain’s Fairness Index. In conclusion, it can be stated that in the case of not performing a power control, the SE of the users is clearly more homogeneous in the D-mMIMO system than in the C-mMIMO one. When a perfect power control is carried out, the situation is equalized between both systems. Nevertheless, it is important to emphasize again that the behavior of this parameter will be much more dependent on the effective power control that can be implemented in practice in a concentrated system than in a distributed one.