Improved ISR for IEEE 802.11ah Nonlinearity Compensation via Adjustable Constellation Borders

Abstract

Iterative subcarrier regularization (ISR) has been recently proposed as a receiver-side remedy for orthogonal frequency division multiplexing (OFDM) nonlinearity. It allows the power amplifier of OFDM transmitters to operate at a lower input back-off for more efficient uplinks. However, the compensation ability cannot align with increasing channel quality, because the standard quadrature amplitude modulation (QAM) used in ISR may eliminate compensation due to erroneous decisions. To solve this issue, an improved version of ISR was proposed to flexibly adjust the constellation borders of QAM and numerically optimize it based on IEEE 802.11ah (hereinafter referred to as 802.11ah) specifications. Simulations show that the proposed scheme not only improves the converged bit error rate of ISR but also accelerates its own convergence, especially in a high channel quality, thereby achieving better power efficiency for Internet of Things clients without additional computational complexity.

1. Introduction

IEEE 802.11ah [1], also known as Wi-Fi HaLow, is a low-power wide-area (LPWA) version of the IEEE 802.11-2007 wireless networking standard [2]. It supports various Internet of Things (IoT) services based on low-power connectivity, such as sensor networks and wearables [3,4]. Although the usage of license-free bands and well-established infrastructures makes 802.11ah more competitive than other LPWA techniques, its orthogonal frequency division multiplexing (OFDM)-based architecture still challenges the necessity for low power consumption due to the high peak-to-average power ratio (PAPR) issue over power amplifiers (PAs) [5]. Therefore, the improvement in power efficiency has become a critical issue for 802.11ah [6,7,8,9,10,11].

The receiver-side remedies for PA nonlinearity in OFDM systems have been widely investigated in the literature [12,13,14,15,16]; however, the increase in processing time makes such iterative methods infeasible due to the high data rate requirement of mobile broadband. Nevertheless, these techniques may come in handy for LPWA uplinks to support machine-type communications, which need to leave all possible complicated operations at base stations for power saving [17,18]. Based on this framework, iterative subcarrier regularization (ISR) [19] has recently been introduced for 802.11ah power-efficient uplink. ISR can compensate for the PA-distorted signals in two ways: regularizing subcarriers iteratively with deterministic prior knowledge only (ISR scheme I, ISR-I) or with both deterministic and probabilistic prior knowledge (ISR scheme II, ISR-II). In ([19], Figure 12), ISR-II outperforms ISR-I in terms of bit error rate (BER) and convergence under a fair channel; however, only ISR-I can further improve the BER by consuming more iterations when the signal-to-noise ratio (SNR) consistently increases.

In this paper, we propose an improved ISR to overcome the saturation of BER improvement and concurrently retain its fast convergence through adjustable constellation borders. The proposed scheme shrinks the decision region of the modulation for ISR only, and, hence, computational complexity is not increased. By using the experimentally optimized hard-decision range, the 802.11ah-based simulation results demonstrate that the proposed scheme can significantly enhance the performance of BER and convergence compared to that of the original ISR-I or ISR-II.

2. System Model

The system structure of the OFDM transceiver with the ISR technique used in this study is fully consistent with that used in [19] for a fair performance comparison, whose block diagram is shown in Figure 1. At the transmitter, the information bits are modulated by $\mathcal{M}$-ary quadrature amplitude modulation (QAM) with average power normalized to one. Subsequently, different types of subcarriers are mapped to generate time-domain OFDM signals $\mathit{x}={\left[x_0, \dots , x_{N-1}\right]}^T$ using an inverse discrete Fourier transform (IDFT), yielding

$$\mathit{x}={\mathcal{F}}_{\mathit{N}}^{\mathit{H}}\mathit{X},$$

(1)

where $\mathit{X}={\left[X_0, \dots , X_{N-1}\right]}^T$ is the transmitted subcarrier vector based on the 802.11ah channel bandwidth 1 (CBW1) specification [1]; ${\mathcal{F}}_{\mathit{N}}$ is the $N\times N$ discrete Fourier transform (DFT) matrix, the entry of which is given by ${\left[{\mathcal{F}}_{\mathit{N}}\right]}_{\left(n,k\right)}\triangleq \frac{1}{\sqrt{N}}{e}^{-j\left(\frac{2\pi }{N}\right)nk}, 0\le n, k\le N-1$; and ${\left[·\right]}^H$ stands for Hermitian transpose. After padding a length-$P$ cyclic prefix (CP), i.e., $\mathit{x}={\left[x_{N-P}, \dots , x_{N-1}, x_0, \dots , x_{N-1}\right]}^T$, the baseband output signal is distorted by Rapp’s PA nonlinearity model [20], whose amplitude-to-amplitude (AM/AM) conversion is featured as

$$G\left(x_n\right)=g·x_n{\left[1+{\left(\frac{g·\left|x_n\right|}{A_{sat}}\right)}^{2p}\right]}^{-\frac{1}{2p}},$$

(2)

where $A_{sat}$ is the saturation level specified by the value of input back-off (IBO, in dB) from $A_{sat}=x_{RMS}·{10}^{IBO/20}$; $x_{RMS}=\sqrt{{{\displaystyle \sum }}_{n=0}^{N-1}{\left|x_n\right|}^2/N}$; $p$ controls the smoothness of conversion; $g$ specifies the voltage gain of the amplifier. In this study, $g=1$ is used for generality, and $p=2$ is used for simulating the low-complexity PA of IoT devices.

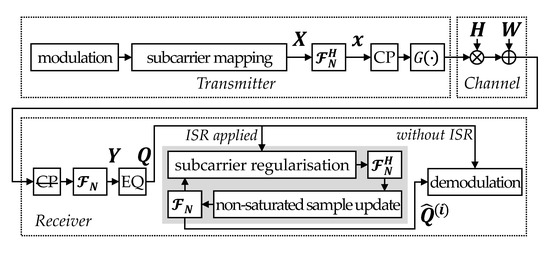
Figure 1. System block diagram of OFDM transceiver with ISR.

At the receiver, after CP removal and performing DFT, the equivalent frequency-domain received signal $\mathit{Y}={\left[Y_0, \dots , Y_{N-1}\right]}^T$ is given by

$$\mathit{Y}=\mathit{H}{\mathcal{F}}_N·G\left({\mathcal{F}}_{\mathit{N}}^{\mathit{H}}\mathit{X}\right)+\mathit{W},$$

(3)

where $\mathit{W}={\left[W_0, \dots , W_{N-1}\right]}^T$, $W_k\in \mathcal{C}\mathcal{N}\left(0, N_{0, F}\right)$ is the frequency-domain noise vector; $\mathcal{C}\mathcal{N}\left(0, {\sigma }^2\right)$ denotes a zero-mean complex Gaussian random variable with variance ${\sigma }^2$; and $\mathit{H}={\left[H_0, \dots , H_{N-1}\right]}^T={\mathcal{F}}_{\mathit{N}}\mathit{h}$ is the frequency-domain fading channel vector, where $\mathit{h}={\left[h_0, \dots , h_{L-1}, 0, \dots , 0\right]}^T$ is the $L$-tap channel impulse response ($L\le P$). Finally, the recovered subcarrier vector ${\widehat{\mathit{Q}}}^{\left(\mathit{i}\right)}={\left[{\widehat{Q}}_0^{\left(i\right)}, \dots , {\widehat{Q}}_{N-1}^{\left(i\right)}\right]}^T$ is gained by performing $i$-iterations of ISR on the equalized subcarrier vector $\mathit{Q}$, where

$$\mathit{Q}=\mathit{Y}{\mathit{H}}^{-\mathbf{1}}=\mathit{H}{\mathcal{F}}_{\mathit{N}}·G\left({\mathcal{F}}_{\mathit{N}}^{\mathit{H}}\mathit{X}\right){\mathit{H}}^{-\mathbf{1}}+\mathit{W}{\mathit{H}}^{-\mathbf{1}}.$$

(4)

3. Improved ISR

3.1. Conventional ISR

As shown in Figure 1, the ISR is an iterative approach to compensate the lost (PA-saturated) samples by updating the prior knowledge both in the data (time) and transformed (frequency) domains [19]. The process can be summarized as following steps.

• Estimate the saturation level by specified IBO:

  $${\widehat{A}}_{sat}=q_{RMS}·{10}^{IBO/20}, q_{RMS}=\sqrt{{{\displaystyle \sum }}_{n=0}^{N-1}{\left|q_n\right|}^2/N}, q_n\in \mathit{q}, \mathit{q}={\mathcal{F}}_{\mathit{N}}^{\mathit{H}}\mathit{Q}.$$

  (5)
• Create time-domain prior knowledge by reserving the non-saturated samples:

  $${\mathit{K}}_{\mathit{D}}^{\mathit{ISR}}={\mathcal{I}}_{\mathit{D}}^{\mathit{ISR}}q, {\left[{\mathcal{I}}_{\mathit{D}}^{\mathit{ISR}}\right]}_{\left(j,j\right)}=\left\{\begin{array}{c}1, q_n<{\widehat{A}}_{sat}\\ 0, q_n\ge {\widehat{A}}_{sat}\end{array}\right., 0\le j, n\le N-1.$$

  (6)
• Take $\mathit{q}$ as an initial guess by denoting ${\widehat{\mathit{q}}}^{\left(\mathit{i}=\mathbf{0}\right)}$.
• Apply frequency-domain prior knowledge from 802.11ah (CBW-1) standards (refer to Table 1 [19]):

  $$\begin{array}{cc}{\widehat{\mathit{q}}}^{\left(\mathit{i}+\mathbf{1}\right)}={\mathcal{F}}_{\mathit{N}}^{\mathit{H}}[(\mathit{I}-\hfill & {\mathcal{I}}_{\mathit{T}}^{\mathit{ISR}}){\mathit{Q}}_{\mathit{H}\mathit{D}}^{\left(\mathit{i}\right)}+{\mathit{K}}_{\mathit{T}}^{\mathit{ISR}}],\hfill \\ \hfill & {\widehat{\mathit{Q}}}_{\mathit{H}\mathit{D}}^{\left(\mathit{i}\right)}=\underset{\mathit{X}\in \mathcal{M}-\mathrm{QAM}}{\arg \min }\left(\Vert {\widehat{\mathit{Q}}}^{\left(\mathit{i}\right)}-\mathit{X}{\Vert }_2\right), {\widehat{\mathit{Q}}}^{\left(\mathit{i}\right)}\in \mathrm{data} \mathrm{subcarriers}.\hfill \end{array}$$

  (7)
  Table 1. 802.11ah (CBW1)-based frequency-domain prior knowledge ($N=32$).

  Vector Element $\left({\mathit{K}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right)$	$\mathbf{Value} \mathbf{of} {\mathit{K}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}$	Labeling Index $\left({\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right)$	Carrier Index	Carrier Type
  $K_T^{ISR}\left(0\right)$	0	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(0,0\right)}=1$	0	DC
  $K_T^{ISR}\left(1\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(1,1\right)}=0$	1	data
  …	…	…	…	…
  $K_T^{ISR}\left(6\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(6,6\right)}=0$	6	data
  $K_T^{ISR}\left(7\right)$	1	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(7,7\right)}=1$	7	pilot 1
  $K_T^{ISR}\left(8\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(8,8\right)}=0$	8	data
  …	…	…	…	…
  $K_T^{ISR}\left(13\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(13,13\right)}=0$	13	data
  $K_T^{ISR}\left(14\right)$	0	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(14,14\right)}=1$	14	guard
  $K_T^{ISR}\left(15\right)$	0	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(15,15\right)}=1$	15	guard
  $K_T^{ISR}\left(16\right)$	0	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(16,16\right)}=1$	−16	guard
  $K_T^{ISR}\left(17\right)$	0	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(17,17\right)}=1$	−15	guard
  $K_T^{ISR}\left(18\right)$	0	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(18,18\right)}=1$	−14	guard
  $K_T^{ISR}\left(19\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(19,19\right)}=0$	−13	data
  …	…	…	…	…
  $K_T^{ISR}\left(24\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(24,24\right)}=0$	−8	data
  $K_T^{ISR}\left(25\right)$	−1	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(25,25\right)}=1$	−7	pilot 1
  $K_T^{ISR}\left(26\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(26,26\right)}=0$	−6	data
  …	…	…	…	…
  $K_T^{ISR}\left(31\right)$	$\mathcal{M}$ kinds	${\left[{\mathcal{I}}_{\mathit{T}}^{\mathit{I}\mathit{S}\mathit{R}}\right]}_{\left(31,31\right)}=0$	−1	data

  ¹ The position of pilot subcarriers may change in each OFDM slot for performing “traveling pilots”.
• Apply time-domain prior knowledge:

  $${\widehat{\mathit{q}}}^{\left(\mathit{i}+\mathbf{1}\right)}=\left(\mathit{I}-{\mathcal{I}}_{\mathit{D}}^{\mathit{ISR}}\right){\widehat{\mathit{q}}}^{\left(\mathit{i}+\mathbf{1}\right)}+{\mathit{K}}_{\mathit{D}}^{\mathit{ISR}}.$$

  (8)
• Return to step 4 for a new iteration.

3.2. Observation for Standard Decision

In the conventional ISR [19], the step of subcarrier regularization in (7) utilizes a typical decision region as the standard $\mathcal{M}$-ary QAM to reset the symbols of data subcarriers to their closest constellation points. Such action may introduce a serious decision errors, even if a symbol only slightly exceeds the constellation borders (in Figure 2a, a received symbol belonging to the alphabet $S_A$ is wrongly demodulated to $S_B$, where $S_A$, $S_B\in \left\{S_0, \dots , S_{\mathcal{M}-1}\right\}$). However, these symbols are likely to be correctly demodulated within the next few iterations if they are reserved as reconstructed samples, similar to saturated signals in the time domain. Once a symbol can be successfully demodulated, it considerably contributes to the restoration process.

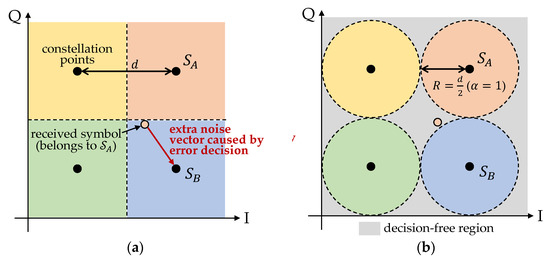
Figure 2. Decision region of data subcarriers for ISR. (a) Conventional constellation borders. (b) Adjustable constellation borders.

3.3. Proposed Scheme

To allow the received symbols located at the decision border to return to their original decision region, it is necessary to design a room for reconstruction before employing a hard decision. As the channel noise added in each subcarrier is a two-dimensional Gaussian distribution, we proposed the decision region in a circle with an adjustable radius $R$. For standard $\mathcal{M}$-ary QAM, the Euclidean distance between two adjacent constellation points is $d=2/\sqrt{K}$, where $K=2\left(\mathcal{M}-1\right)/3$ is the normalization factor. The radius of the decision circle with scaling ratio $\mathsf{\alpha }$ can be defined as

$$R=\alpha ·\frac{d}{2}=\frac{\alpha }{\sqrt{K}}, 0<\alpha \le 1$$

(9)

Therefore, the area of the decision-free region (the grey region in Figure 2b) can be determined by the value of$\alpha$. When$\alpha \to 0$, the decision circle shrinks to a constellation point, where the process of ISR-II becomes the same as that of ISR-I. As there is a trade-off between BER improvement and convergence rate, the proposed scheme helps in designing a flexible structure so that the performances of converged BER and convergence by the parameter $\alpha$ can be adjusted.

3.4. Decision Radius Optimization

To optimize the performance of the proposed scheme, we used Monte Carlo simulation for 802.11ah examples of $\mathcal{M}=16,$ 64, 256 with 3, 4, 5 dB input back-off (IBO), respectively. Note that although $\mathcal{M}=2,$ 4 are also defined in the 802.11ah modulation and coding scheme (MCS) table, both modulations are not considered in this study, because their improvement should be evaluated in low IBO (e.g., 0 dB), whose performance of power spectral density (PSD) exceeds the 802.11ah spectral mask [19]. The converged number of iterations ($i_c$) and converged BER ($BE{R}_{i_c}$) are evaluated when $\alpha =0.01:0.01:1$ with an appropriate convergence threshold $\delta$ (the iteration process stops when $BE{R}_{i_c}-BE{R}_{i_c+1}\le \delta$) and differently normalized SNRs ($E_b/N_0=30, 40, 50$ dB).

Figure 3a–c demonstrate the overall performance evaluation of the converged BER and number of iterations for $\mathcal{M}=16,$ 64, 256, respectively. With a better understanding of the time domain, the converged BER can be optimized when $E_b/N_0$ increases. For $\mathcal{M}=16$, there are three candidates of sub-optimal $BE{R}_{i_c}$ ($\alpha =0.47, 0.58, 0.73$) for $E_b/N_0=50$ dB, and we chose $\alpha =0.73$, as it consumes the lowest number of iterations. The chosen $\alpha$ can achieve optimized $BE{R}_{i_c}$ and $i_c$ for all SNRs, although the optimization of $BE{R}_{i_c}$ is not obvious when the SNR is low. For higher order modulations (i.e., $\mathcal{M}=$ 64 and 256), the improvement decreases due to the shrinking of the decision region. Nevertheless, the proposed scheme does not degrade the performance of ISR in any SNR and can reduce the BER without additional computational complexity, as the alpha can be pre-computed while being independent of the data to transmit.

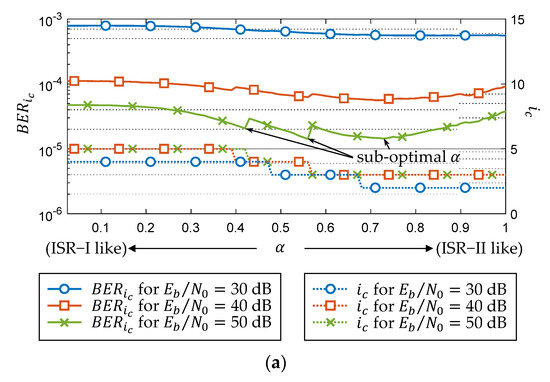
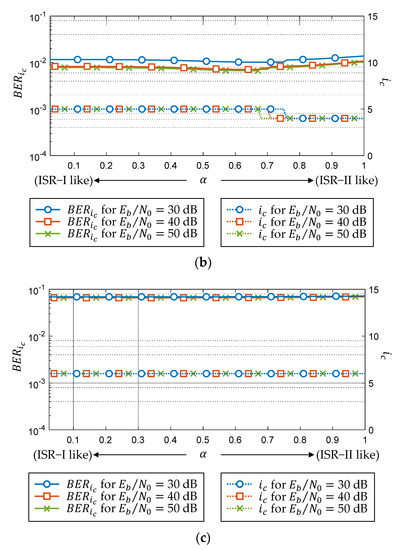
Figure 3. Overall performance evaluation of converged BER and number of iterations for different $\mathsf{\alpha }$: (a) $\mathcal{M}=16$, IBO $=$ 3 dB,$\delta ={10}^{-5}$. (b)$\mathcal{M}=64$, IBO $=$ 4 dB, $\delta ={10}^{-3}$, (c) $\mathcal{M}=256$, IBO $=$ 5 dB, $\delta ={10}^{-3}$.

4. Performance Evaluation

As the proposed scheme mainly contributes at 16-QAM, according to the analysis in the previous section, the effectiveness of the proposed scheme was verified through numerical results based on 802.11ah CBW1 subcarrier mapping with optimized decision region ($\alpha =0.73$) for $\mathcal{M}=16$ and IBO $=$ 3 dB. Figure 4 compares the BER performance of ISR-I, ISR-II, and the proposed scheme for different numbers of iterations ($\mathrm{i}=1, 2, 5$). It can be seen that the BER of the proposed scheme is slightly degraded compared to that of ISR-II for $\mathrm{i}=1$ only but it outperforms ISR-I or ISR-II for $\mathrm{i}>1$, especially when the SNR is increasing. This phenomenon is highly correlated with the SNR and is more obvious in the view of convergence, which can be observed in Figure 5. For $E_b/N_0=30$ dB, the convergence of the proposed scheme is almost the same as that of ISR-II; for $E_b/N_0=40, 50$, the converged BERs compared with ISR-II are remarkably improved with only one or two additional iterations. Although for $E_b/N_0=50$, the BER of ISR-I can be stably reduced with an increasing number of iterations, its convergence is much slower than that of the proposed scheme. According to [19], the number of iterations for the converged BER dominates the complexity of receiver-based solutions due to the usage of FFT/IFFT pairs. There are usually one or two iterations in most schemes, except for in the case of ISR (e.g., [12,13,14,15,16]). In this example, the proposed scheme further enhances the converged BER to ${10}^{-5}$ within five iterations, which consumes two to five times more complexity when compared with the consumption of other schemes. However, ISR aims to reduce the converged BER as much as possible when the high quality of time-domain knowledge (i.e., high SNR) can also contribute to the compensation, taking the processing time as a trade-off for the tolerant latency in IoT networks. From Figure 5, it can be observed that the proposed scheme significantly improves the convergence of ISR but does not increase the complexity.

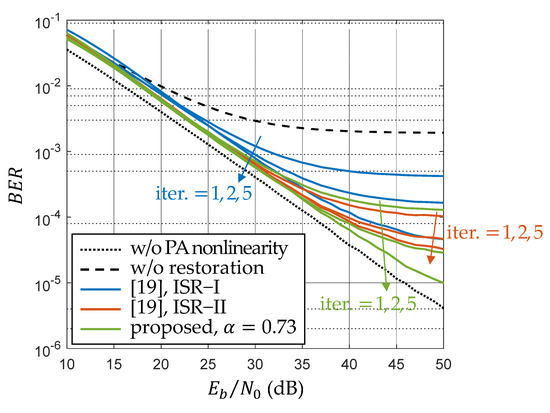
Figure 4. Comparison of BER performance for different ISR schemes ($\mathcal{M}=16$, IBO $=$ 3 dB).

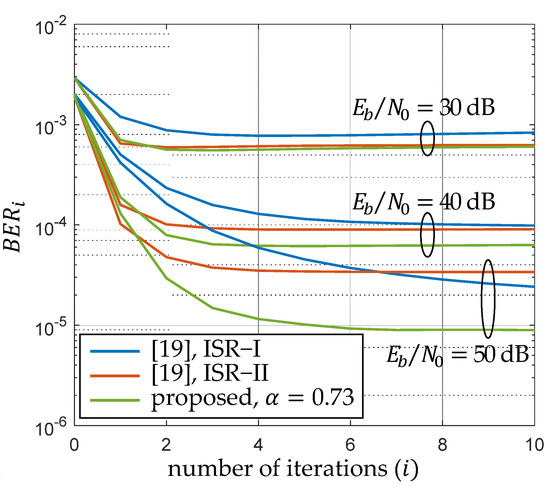
Figure 5. Comparison of convergence for different ISR schemes ($\mathcal{M}=16$, IBO $=$ 3 dB).

5. Conclusions

A novel scheme is proposed to improve the OFDM nonlinearity compensation of ISR when a high SNR is considered. This is achieved by optimizing an adjustable decision-free region for symbols on data subcarriers to reduce the occurrence of erroneous decisions at constellation borders. The simulation results verify that the proposed scheme not only improves the converged BER of ISR but also accelerated its own convergence without additional computational complexity. As most OFDM systems tend to rely on channel coding schemes for robust transmission, the combination of improved ISR and those schemes such as convolutional code in the 802.11ah is considered as our future work.