K-MDTSC: K-Multi-Dimensional Time-Series Clustering Algorithm

Abstract

The increasing capability to collect data gives us the possibility to collect a massive amount of heterogeneous data. Among the heterogeneous data available, time-series represents a mother lode of information yet to be fully explored. Current data mining techniques have several shortcomings while analyzing time-series, especially when more than one time-series, i.e., multi-dimensional timeseries, should be analyzed together to extract knowledge from the data. In this context, we present K-MDTSC (K-Multi-Dimensional Time-Series Clustering), a novel clustering algorithm specifically designed to deal with multi-dimensional time-series. Firstly, we demonstrate K-MDTSC capability to group multi-dimensional time-series using synthetic datasets. We compare K-MDTSC results with k-Shape, a state-of-art time-series clustering algorithm based on K-means. Our results show both K-MDTSC and k-Shape create good clustering results. However, K-MDTSC outperforms k-Shape when complicating the synthetic dataset. Secondly, we apply K-MDTSC in a real case scenario where we are asked to replace a scheduled maintenance with a predictive approach. To this end, we create a generalized pipeline to process data from a real industrial plant welding process. We apply K-MDTSC to create clusters of weldings based on their welding shape. Our results show that K-MDTSC identifies different welding profiles, but that the aging of the electrode does not negatively impact the welding process.

1. Introduction

Thanks to the Internet of Things technology and diversified sensors nowadays, we can collect a huge amount of heterogeneous data. Among the heterogeneous data available, time-series are commonly found in different fields such as sales, stock prices, weather, biomedical measurements, industrial data, audio, and video signals, etc. Time-series collect several subsequent observations of the same sensors, thus creating a large set of ordered samples, possibly having multiple dimensions too. Time-series data fostered many studies in the data mining community to promote novel machine learning algorithms and applications: from time-series forecasting in stock trading [1] or sensors networks [2], to classification time-series for health or video data [3], up to clustering to help the Decision Support Systems while analyzing robots trajectories data in rescue operations [4] to name a few. Frequently, researchers rely on time-series transformations to reduce it or its multi-dimensional nature to solve the course of dimensionality problem. Different distance metrics are used to compute the similarities among the transformed time series [5]. Considering the nature of the data, uni-dimensional time-series involve the analysis of one single time-series per time. However, in many fields, the need to analyze multiple and time-series simultaneously is rising, i.e., multi-dimensional time-series. The industrial field is one of them. With the Industry 4.0 paradigm, we can implement robots with multiple sensors to collect and store a massive amount of data about the manufacturing processes. These robots generate multiple time-series, synchronized over time.

In this paper, we focus on this scenario where synchronous multi-dimensional timeseries are available. Firstly, we propose K-MDTSC (K-Multi-Dimensional Time-Series Clustering), a novel clustering algorithm specifically designed to deal with synchronous multidimensional time-series. Based on a generalized version of K-means [6] and a generalized notion of distance able to handle synchronous multi-dimensional time-series of any dimension, K-MDTSC automatically groups multi-dimensional time-series. In a nutshell, the generalized distance and the synchronous nature of the data allow K-MDTSC creates clusters without the need for any transformation or dimensionality reduction. We compare K-MDTSC performance with k-Shape [7] a state-of-art time-series clustering algorithm based on K-means. We run a thorough validation process using synthetic datasets composed of distinct synchronous multi-dimensional time-series families. We study the impact of the main multi-dimensional time-series data characteristics, i.e., we inject noise-like perturbation, increase the number of families and the number of dimensions. Our results show that both K-MDTSC and k-Shape effectively identify and group multi-dimensional time-series of the same family. However, K-MDTSC outperforms k-Shape when noise increases, a common problem in real data, and families’ numbers grow.

Our second goal is to apply K-MDTSC in a real case scenario. In detail, we employ K-MDTSC in an industrial case study to gain a more profound knowledge of the process and understand if a predictive maintenance strategy can be applied instead of the existing periodic one. To this end, we design a generic pipeline to process the data and fed them into our clustering algorithm. Firstly, in our pipeline, we reduce the eventual presence of noise in each dimension of the multi-dimensional time-series employing a low pass filter. Next, we use two data selection processes to align the multi-dimensional time-series obtaining synchronous time-series having equal duration. Finally, different dimensions may be characterized by time-series having different operational ranges; thus, we run a data normalization process. We employ our generic pipeline and K-MDTSC on a real dataset composed of two-dimensional time-series collected in the body-in-white welding stage of an actual car manufacturing plant. During this stage, different car bodies’ welding spots are soldered together to join the different parts of the car frame. Our results show that the automatic pipeline effectively processes the data so that the K-MDTSC algorithm clearly identifies different welding profiles. Furthermore, we show that there is no negative impact on the welding profiles, suggesting that an increase in the wear and tear of the electrode would be possible.

To support new analyses in similar scenarios where synchronous multi-dimensional time-series are available, we release our synthetic datasets and K-MDTSC code as opensource at [8].

The contributions of this work can be summarized as follows:

• Definition of K-MDTSC (K-Multi-Dimensional Time-Series Clustering) to group multi-dimensional time-series.
• Thorough validation of K-MDTSC and comparison with k-Shape, a state-of-art time-series clustering algorithm.
• Synthetic datasets and K-MDTSC code available at [8].
• Generic pipeline to process time-series data.
• Application in a real case scenario with real data from the Industrial field.

The rest of the paper is organized as follows: In Section 2, we discuss our work in light of past literature for clustering algorithms, predictive maintenance, and applications of clustering algorithms with a focus on time-series data. After, we report the details about K-MDTSC and k-Shape clustering algorithms in Section 3, and present our validation results in Section 4. Next, we present our real case scenario, the available dataset, and detail the steps of our automatic processing pipeline in Section 5. Then, we present the relative clustering results in Section 6. Finally, in Section 7, we draw our conclusions and derive our future directions.

2. Related Work

With the increasing amount of unlabeled data, clustering algorithms have been widely used in the last years to extract knowledge from data in different fields such as image processing [9,10,11,12], text analysis [13,14], network traffic analysis [15,16,17,18], social network data analysis [19,20,21], and medical data [22,23,24]. Along with unlabeled data, the possibility to collect data over time leads to the acquisition of a considerable amount of time-series data. To cluster time-series, authors in [7] proposed k-Shape, a K-means-based clustering algorithm to group uni-dimensional time-series by using a dynamic time warping distance. Like them, authors in [25] used a dynamic time warping approach focusing mainly on how to compute the clusters’ centroid. Authors in [26], instead, studied how to use a partitional clustering algorithm to handle multi-dimensional time-series in case of both categorical and continuous values. Authors in [27] studied how to rely only on part of the time-series to extract local patterns and use them to cluster time-series having different lengths. Authors in [28], instead, proposed a clustering algorithm to group sub-sequences in multi-dimensional time-series. To study how to transform time-series data into different domains, authors in [29] used 38 distinct datasets and evaluated different time-series representations and different similarity measures to assess the pruning power of each solution. Authors in [30], instead, employed an iterative discrete Wavelet Transformation decomposition with a standard K-means algorithm to group time-series. Authors in [31] used a dimensional reduction solution to replace time-series data with global measures describing the time-series characteristics, and authors in [32] used a Principal Component Analysis methodology to segment and cluster multi-dimensional time-series. Regarding the applications, many works applied clustering to time-series: starting from the financial field [33,34,35], in which time-series clustering have been used to find seasonal patterns or expected return-risk pattern; with urban data [36] to analyze time-series about population distribution during a day detecting a similar pattern in population distribution changes in a different location; by using environmental data [37] to identify climate indices and group weather stations located in the same state; focusing on meteorological data [38] to propose a methodology able to group multi-dimensional time-series up to the medical field [39,40] in which cluster of biomedical images have been created for several different medical applications from human brain mapping up to the analysis of suspicious lesions in patients with breast cancer. To give a broad view of literature regarding time-series clustering, in 2005, Liao [41] presented a seminal survey regarding time-series clustering. He summarized the previous studies related to time-series clustering, identifying similarities between time-series, and the employed performance metrics. To update it, in 2015, authors in [5] proposed a new overview of ten years of time-series clustering applied in different fields. While recently, in 2020, authors in [42] benchmark eight different clustering solutions with different distance metrics on over 100 time-series datasets. The increasing amount of data available also fostered an increasing interest in predict maintenance approaches in different fields such as railway [43], electric distribution network [44], aircraft [45], industrial vehicles [46], automotive [47,48], and electrical motors [49] to name a few, as well as in robotics industry [50,51], similarly to our case study. Regarding the application of time-series analysis for predictive maintenance, authors in [52] proposed a predictive maintenance pipeline based on clustering to study the laser melting manufacturing technology. Their study proposed a preprocessing step to transform time-series into statistical features, e.g., minimum, skewness, maximum, mode, etc. Similarly, authors in [53] propose the adoption of custom features and the application of a Principal Component Analysis process to select the most important features. Kulkarni et al. [54,55] use clustering to find outliers and extract features, and then use them with autoregressive or classification models to predict faults in industrial and refrigerator machines. Similarly, authors in [56] employed an iterative K-means solution in the data preprocessing step to reduce the signal to analyze in the final classification step.

The closest work to ours is proposed by authors in [57]. In this work, the authors proposed a methodology to group multi-dimensional time-series using a spectral clustering algorithm. Then, they validated it and compared the clustering performance with a standard K-means implementation employing a synthetic and a networking dataset. Unlike the previous works, in our clustering solution, we do not deal with sub-sequences or time-series re-alignment, as we assume synchronous multi-dimensional time-series having the same length. Moreover, we do not employ any transformation technique to transform time-series data into features or a different domain, e.g., Fourier transforms, wavelet transformation, etc. Instead, we propose a generic multi-dimensional time-series clustering algorithm directly relying on raw synchronous multi-dimensional time-series based on a generalized notion of the euclidean distance. We validate it by comparing the clustering performance with another state-of-art time-series clustering algorithm, i.e., k-Shape.

Furthermore, we propose a generic pipeline to preprocess multi-dimensional time-series and fed them into our generic multi-dimensional time-series clustering algorithm. To the best of our knowledge, we are the first to study a real multi-dimensional time-series dataset from the industrial field and suggest using this clustering approach to perform a predictive maintenance strategy.

3. Time-Series Clustering

This section recalls the K-means clustering algorithm that we use as a building block in K-MDTSC. Then, we present k-Shape as a state-of-art time-series clustering algorithm.

3.1. K-Means

K-means is a classic clustering algorithm born from statistics. It creates central-based clusters such as the points within a cluster are closer (hence more similar) to the centroid of the cluster (i.e., the center of the cluster) they belong to, rather than the centroid of the other clusters. [6]. In K-means, the user specifies a single parameter k, representing the number of desired clusters. Then, starting from the input points, K-means groups them in k clusters, assigning them to the closest centroid. Then, it returns each cluster and the respective centroid.

Initially, K-means randomly extracts k points in the input data space and uses them as initial centroids of the clusters. All the input points are then assigned to the cluster having the shortest distance (usually the Euclidean distance) from the respective centroids. Once K-means assign all the points to a cluster, new centroids are computed and compared with the previous ones. If the centroids do not change, the algorithm stops and returns the generated clusters and centroids. Otherwise, the algorithm restarts reassigning all the points to the clusters based on the new centroids. While traditional K-means represents a simple yet efficient algorithm to group points together, it has some well-known limitations related to the definition of distance and some well-known criticalities, such as creating empty clusters. Most of all, K-means cannot easily deal with time-series.

3.2. k-Shape

k-Shape is one of the state-of-art time-series clustering algorithms based on K-means [7]. To cope with time-series, k-Shape employs a shape-based distance to evaluate the similarity between two curves. In addition, the shape-based distance uses a cross-correlation distance to identify the smallest distance between two curves even if they are not properly aligned. To this end, firstly, it shifts one of them to identify the best alignment leading to the smallest distance. Then to cope with time-series inherent distortions, k-Shape uses a z-normalization process. Finally, k-Shape computes the shape-based distance by normalizing the cross-correlation distance by the geometric mean of the autocorrelations of the individual sequences.

While k-Shape can identify time-series clusters even when they are not aligned, it cannot handle multi-dimensional time-series per se. Indeed, k-Shape gets as input only one-dimension time-series. Here, we adapt it to multi-dimensional time-series to cope with this constraint.

Given a multi-dimensional time-series $X_N\left(z\right)$, where N represent the dimensions, we define $X\left(z\right)$ as a one-dimension time-series by concatenating all the dimensions as follows:

$$X\left(z\right)=\bigcup _{n=0}^N{X}_n\left(z\right)$$

Finally, we give as input the $X\left(z\right)$ time-series to k-Shape.

3.3. K-MDTSC

For our implementation, we base K-MDTSC on the traditional K-means algorithm. Firstly, we define a generalized notion of distance to handle time-series, and in particular multi-dimensional time-series.

Given a pair of multi-dimensional time-series $X_N\left(z\right)$ and $Y_N\left(z\right)$, where z represents the sample in Z samples, and N the dimensions, we define our generalized distance as follow:

$$d(X_N,Y_N)=\sqrt[L]{\sum _{n=0}^N\sum _{z=0}^Z{|X_n\left(z\right)-Y_n\left(z\right)|}^L}$$

where L represents the metric distance. For our implementation, we rely on $L=2$, i.e., the Euclidean distance. We use the distance $d(.)$ to find the closest centroid in the K-means algorithm. Notice that our generalized distance assumes that $X_N\left(z\right)$ and $Y_N\left(z\right)$ are synchronous multi-dimensional time-series. In case the multi-dimensional time-series may present different phases but the same shape, i.e., synchronous but not aligned time-series, in Section 5.2, we present our generic pipeline to align them.

In addition, in our implementation, we introduce the following improvements to the classic K-means algorithm:

• A well-known criticality is related to the choice of the initial centroids. If a random point is chosen as a centroid and lays in part of space where no other points belong, it may create empty clusters. The worst the clustering result is, in the end, instead of k clusters, the user will retrieve $k-1$ clusters. To reduce this situation probability, we choose the k initial centroids among the multi-dimensional time-series directly.
• Secondly, while the first solution reduces the probability of getting empty clusters, some corner cases are still possible, e.g., if two similar multi-dimensional time-series are present and both are used as centroids. To solve this issue, we verify whether any empty cluster exists. If any is present, for each empty cluster, we select from the most prominent cluster the farthest multi-dimensional time-series and take it as a new centroid.

3.4. Performance Metrics

We assess the clustering performance through quality metrics, including the Error Sum of Squares (SSE) and the Adjusted Rand index.

Error Sum of Squares (SSE): The SSE index computes the cluster cohesion [58]. On the one hand, when the points belonging to a cluster lay close to the cluster’s centroid, the cluster is very compact; hence a good clustering result is achieved. On the other hand, when points are far from their cluster’s centroid, the result is bad, as it means that the points have little similarities. Thus, given a cluster $C\in \widehat{C}$ clusters, its multi-dimensional time-series centroid $C_N\left(z\right)$ and the time-series $X_N\left(z\right)\in C$ on N dimensions, we compute the SSE index as follow:

$$SSE=\sum _{C\in \widehat{C}}\sum _{X_N\in C}d(X_N,C_N)$$

Adjusted Rand index: The Adjusted Rand Index [59] measures the clustering algorithm’s ability to separate points belonging to preassigned categories and re-identify them without the category’s notion. This index is bounded between 0 and 1. When the clustering result and the preassigned categories perfectly agree, the Adjusted Rand index is 1. Otherwise if, for random labeling, it gets a value close to 0. Since the Adjusted Rand Index is an external index, hence independent from the clustering algorithm and the distance matrix, we rely on the implementation defined in [60].

4. Results on Synthetic Data

In this section, we present our synthetic dataset, and we evaluate the capability of k-Shape and K-MDTSC to identify groups of homogeneous curves correctly.

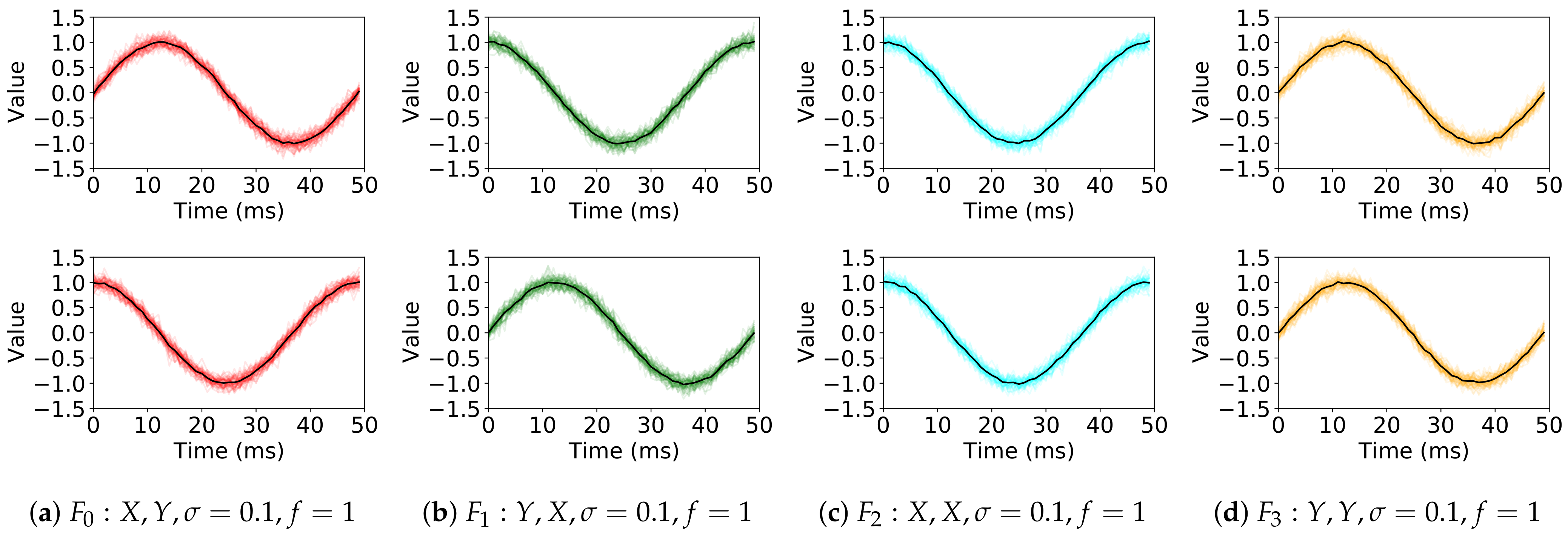
4.1. Synthetic Dataset Generation

We generate synthetic datasets, composed of synchronous multi-dimensional time-series by using as building blocks the following functions:

$$Building Block=\left\{\begin{array}{c}X\left(t\right)=sin\left(2\pi ft\right)+N_{\sigma }\left(t\right)\hfill \\ Y\left(t\right)=cos\left(2\pi ft\right)+N_{\sigma }\left(t\right)\hfill \end{array}\right.$$

where f is the frequency of the sinusoidal curve, $N_{\sigma }\left(t\right)$ is a random normal noise component with zero mean and standard deviation $\sigma$. We add to each curve this perturbation to create time-series having different profiles.

Based on that, we create datasets composed of multi-dimensional time-series. Firstly, we generate a dataset composed of 200 two-dimension time-series, divided in four distinct families. We set $f=1$ and $\sigma =0.1$. In detail, we generate the following families F:

$$Dataset=\left\{\begin{array}{c}{F}_0:(X,Y),f=1,\sigma =0.1\hfill \\ F_1:(Y,X),f=1,\sigma =0.1\hfill \\ F_2:(X,X),f=1,\sigma =0.1\hfill \\ F_3:(Y,Y),f=1,\sigma =0.1\hfill \end{array}\right.$$

(1)

Figure 1 depicts the 4 two-dimension time-series families present in our dataset. Each family F is composed of 50 synchronous two-dimension time-series. From the plots, we can see how each family presents synchronous time-series, each having slightly different profiles, as shown by the resulting thickness of each family.

We then run the k-Shape and K-MDTSC on all samples. We test different values of k to identify whether we achieve the best clustering performance when k is equal to the number of families. Figure 2 reports the SSE score while increasing the number of clusters k. As expected, both algorithms identify the best result starting from $k=4$. To characterize the clustering results, the black curves in Figure 1 report the centroid of each family as returned by K-MDTSC. Similar results hold for k-Shape.

Perturbation Stability: Next, we study the clustering capability to handle a growing perturbation. To this end, we generate datasets composed again of 4 distinct synchronous families of two-dimension time-series. We generate datasets having always the same frequency $f=1$, and characterized by a growing perturbation $\sigma \in [0,2]$ with step $0.1$.

$$Datasets=\left\{\begin{array}{c}{F}_0:(X,Y),f=1,\sigma \in [0,2]\hfill \\ F_1:(Y,X),f=1,\sigma \in [0,2]\hfill \\ F_2:(X,X),f=1,\sigma \in [0,2]\hfill \\ F_3:(Y,Y),f=1,\sigma \in [0,2]\hfill \end{array}\right.$$

(2)

For each dataset, we run the clustering algorithms fixing the parameter $k=4$ as the number of families. Figure 3a reports the trend of the SSE score. As expected, the higher the perturbation, the higher the SSE score, with a $SSE=0$ when no-perturbation is present. Interestingly, K-MDTSC creates more cohesive clusters and better centroids, as shown by the lower SSE score. To evaluate the capability of the clustering algorithm to automatically assign points of the same family to the same cluster, in Figure 3 we compute the Adjusted Rand Index. We can use it in our synthetic dataset as we are aware of each multi-dimensional time-series family. With $\sigma \le 1$, both algorithms create a distinct cluster for each family. With a growing perturbation, k-Shape creates more heterogeneous clusters composed of time-series belonging to different families than K-MDTSC.

Families Stability: Next, we study the stability while increasing the number of families. To this end, we generate datasets composed of $\left|F\right|$ distinct families of two-dimension time-series. We generate datasets with $\left|F\right|\in [2,10]$. We characterize each family with a unique combination of sinusoidal curves and sinusoidal periods. As the initial dataset, we keep $\sigma =0.1$.

$$Datasets=\left\{\begin{array}{c}{F}_{0,4,8}:(X,Y),f\in \{1,2,3\},\sigma =0.1\hfill \\ F_{1,5,9}:(Y,X),f\in \{1,2,3\},\sigma =0.1\hfill \\ F_{2,6}:(X,X),f\in \{1,2\},\sigma =0.1\hfill \\ F_{3,7}:(Y,Y),f\in \{1,2\},\sigma =0.1\hfill \end{array}\right.$$

where the families $F_i$$i>4$ have a combination of sinusoidal curves as the family $i-4$, but with a different frequency f, e.g., with $\left|F\right|=6$ we obtain $F_0:(X,Y),f=1$; $F_1:(Y,X),f=1$; $F_2:(X,X),f=1$; $F_3:(Y,Y),f=1$.; $F_4:(X,Y),f=2$.; and $F_5:(Y,X),f=2$ all having a perturbation $\sigma =0.1$.

For each dataset, we run the clustering algorithms setting the parameter $k=\left|F\right|$ as the number of families. Figure 4a reports the trend of the SSE score. The increasing number of families have only a minor impact on K-MDTSC performance, while k-Shape cannot correctly group elements of the same family together when $\left|F\right|>5$. Looking at the Adjusted Rand index (Figure 4b), k-Shape demonstrates the creation of heterogeneous clusters composed of more than one family. Instead, in most of the cases, K-MDTSC clusters the data correctly.

Dimensions Stability: Finally, we study the stability while increasing the number of dimensions D. To this end, we generate datasets composed of 4 families of D-dimensional time-series. We generate datasets with $D in[2,10]$, where we characterize each family by a unique combination of sinusoidal curves and sinusoidal periods. As the initial dataset, we keep a $\sigma =0.1$.

$$Datasets=\left\{\begin{array}{c}{F}_0:\left\{\begin{array}{c}(X,Y),f=1,\sigma =0.1\hfill \\ (X_i,Y_j),i\in \{2,4,6,8\},j\in \{3,5,7,9\},f=Rnd,Rnd\in [2,10],\sigma =0.1\hfill \end{array}\right.\hfill \\ F_1:\left\{\begin{array}{c}(Y,X),f=1,\sigma =0.1\hfill \\ (Y_i,X_j),i\in \{2,4,6,8\},j\in \{3,5,7,9\},f=Rnd,Rnd\in [2,10],\sigma =0.1\hfill \end{array}\right.\hfill \\ F_2:\left\{\begin{array}{c}(X,X),f=1,\sigma =0.1\hfill \\ (X_i,X_j),i\in \{2,4,6,8\},j\in \{3,5,7,9\},f=Rnd,Rnd\in [2,10],\sigma =0.1\hfill \end{array}\right.\hfill \\ F_3:\left\{\begin{array}{c}(Y,Y),f=1,\sigma =0.1\hfill \\ (Y_i,Y_j),i\in \{2,4,6,8\},j\in \{3,5,7,9\},f=Rnd,Rnd\in [2,10],\sigma =0.1\hfill \end{array}\right.\hfill \end{array}\right.$$

When $D=2$, for each family, we keep the same sinusoidal curves as in Equation (1). When $D>2$, for each family, we repeat the same sinusoidal schema as the first two dimensions but setting the frequency f as a random variable in $[2,10]$. This allows us to create dimensions having different profiles, e.g., when $D=3$, we define family $F_0:(X,Y),f=1,X,f=Rnd,Rnd\in [2,10],\sigma =0.1$. Hence, as first and second dimension X and Y curves having unitary frequency plus random noise perturbation, and a third dimension being a X curve having a random frequency between 2 and 10 plus a random noise perturbation.

We run K-MDTSC and k-Shape fixing $k=4$, equal to the number of families. Both algorithms show that once the clustering algorithm identifies families based on a few dimensions, increasing the dimensions does not impact the performance. Indeed, as expected, the SSE score increases (Figure 5a) with more dimensions; however, the Adjusted Rand Index remains stable (Figure 5b). Still, K-MDTSC offers more cohesive clusters than k-Shape as testified by the SSE score.

Lessons Learned

With synchronous multi-dimensional time-series, the need for alignment drops. When this happens, with a growing noise perturbation or a growing family number, K-MDTSC overcomes k-Shape performance. Indeed, K-MDTSC creates either more cohesive clusters that k-Shape, either more homogeneous clusters composed by single multi-dimensional time-series family. Instead, the number of dimensions does not play a significant role, with both algorithms showing perfect family re-identification.

5. Real Use Case

After evaluating K-MDTSC with a synthetic dataset, we detail the data collection process in our industrial case study. Then, we define our problem and outline the proposed generic pipeline to preprocess multi-dimensional time-series data.

5.1. Data Collection

To collect data about the manufacturing process, we instrument two robots in two different working stations in the body-in-white shop of a car manufacturing production line. Each robot is composed of one or two clamps, each one equipped with a welder soldering different welding spots ($ws$) of the car body.

The robot moves through welding spots in a periodic fashion car body after car body. While welding each welding spot $ws$, for each weldingi, we record the voltage $V_{(ws,i)}\left(z\right)$, and the current$I_{(ws,i)}\left(z\right)$ curves as time-series. Time-series samples t are collected with a frequency of 1 kHz. Figure 6 reports two examples of the voltage and current time-series in two different $ws$. While the same welding spot $ws$ always follows the same welding process, with possibly little differences only in duration, different welding spots are characterized by different welding processes having different shapes and lengths. Based on $V_{\left(ws\right)}\left(z\right)$ and $I_{\left(ws\right)}\left(z\right)$ we define up to two welding phases: warm-up, in which the electrode heat up; and the steady-state when the welder solder the welding spot. Figure 6a,b reports an example of a one-phase and a two-phase welding process (divided by the vertical dashed line), respectively.

While welding, the electrode is continuously exposed to pressure and high temperature, altering the tip geometry. Furthermore, during the welding process, material expulsion may soil the electrode, making it less efficient and worsting the welding performance. Therefore, to reshape the electrode and optimize the welding process, two maintenance operations are performed regularly: a tip dressing operation and an electrode replacement. Firstly, every a fixed number of welds, a tip dressing operation is performed. During a tip dressing operation, part of the electrode material is removed to clean it and restore it to its original shape. For each robot clamp, the tip dressing operation is always performed between the same two welding spots. We refer to these two as the welding spot before $w{s}_b$ and the welding spot after $w{s}_a$ the maintenance operation. After each tip dressing operation, a calibration program $cp$ runs to calibrate the welder. Each robot runs a different calibration program. The calibration program consists of running a welding operation without any material. We record also the time-series of $V_{(cp,i)}\left(z\right)$ and $I_{(cp,i)}\left(z\right)$. Secondly, while the tip dressing operation is fundamental to reset the electrode shape, it also reduces the electrode size. Hence, after a fixed number of tip dressing operations, the electrode is replaced with a new one. For each welding operation and each calibration program, we record the relative wear index (w). The wear index reports the percentage of tip dressing operations performed since the last electrode replacement with respect to the expected number of tip dressing operations per electrode. In a nutshell, the wear represents the age of the electrode. We use this index to track maintenance operations.

Table 1. Monitored Parameters.

Parameter	Description
i	When the weld was performed
$ws$	The welding spot
$I_{(ws,i)}$	Time-series describing the current curve
$V_{(ws,i)}$	Time-series describing the voltage curve
w	Percentage of tip dressing operations with respect to the expected number of tip dressing operation per electrode

summarizes the acquired features.

We collected data from November 2019 to February 2020 from a real FCA pant. In this period, we record more than 60 thousand welding operations from the instrumented robots.

Table 2. Dataset Overview.

Working Station	# Clamps	# Welds	Calibration Program ID
Working Station 1	1	22,746	3
Working Station 2	1	26,546	4
Working Station 2	2	89,857	4

summarizes the main dataset information.

5.2. Problem Definition

Our goal is to study the possibility of using this welding data to migrate from periodic maintenance to a predictive maintenance approach. To this end, we address the following research questions:

• Can we use the welding data to predict the electrode aging and adopt the predictive maintenance?
• Can we infer further information about the welding process to identify possible patterns hinting at problems?

To answer the questions above, we develop the generic pipeline depicted in Figure 7. First, starting from the data of a selected welding point $wp$, we design different preprocessing steps to feed K-MDTSC and identify clusters of welding operations. Finally, we correlate the clusters with external indexes, i.e., the wear, to identify whether different clusters describe different electrode aging.

In detail, we perform the following steps:

• Noise reduction: While K-MDTSC can handle any multi-dimensional time-series, domain experts suggested to us to filter the time-series to remove high-frequency noise that depends mostly on the sensors and collection process.
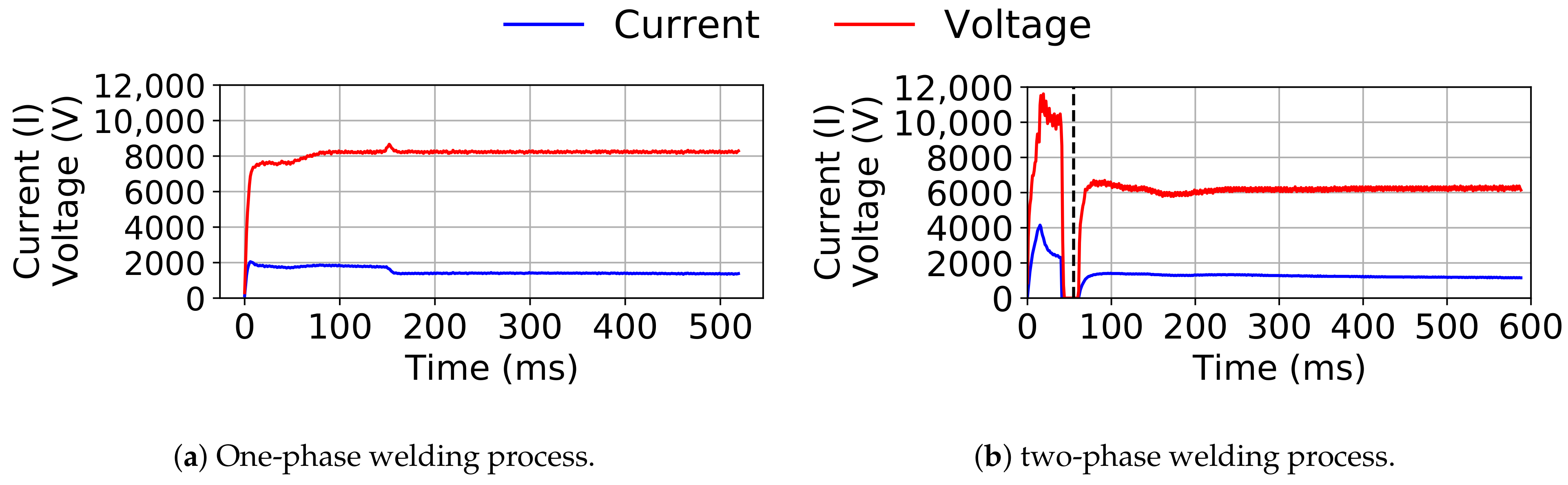
• Data selection: Secondly, weldings may have different durations even within the same welding spot. Moreover, two-phase welding spots are characterized by two distinct periods. Hence, we apply different data selection strategies to extract multi-dimensional time-series having (i) the same duration and (ii) that appear synchronized.
• Data Normalization: Since $V_{(ws,i)}\left(z\right)$ and $I_{(ws,i)}\left(z\right)$ have different operational ranges, we run a classic data normalization process based on z-score.
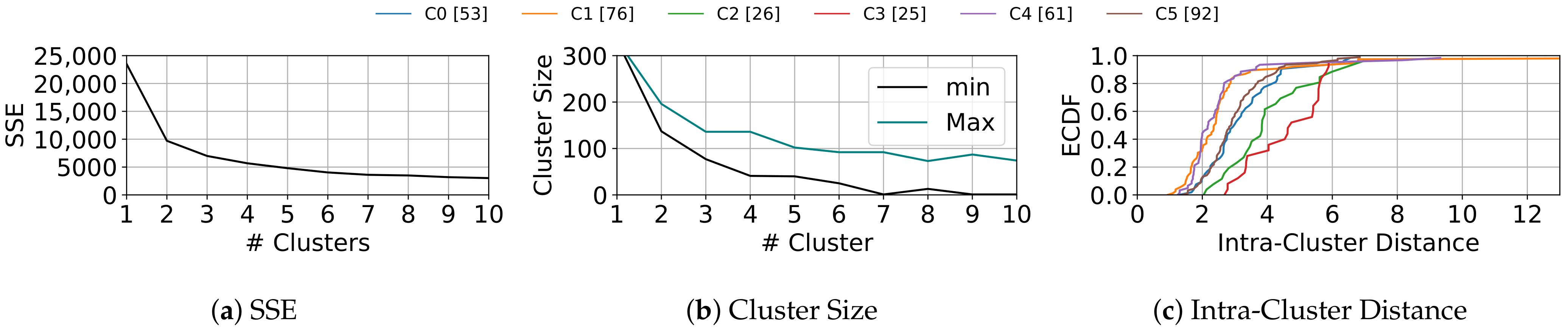
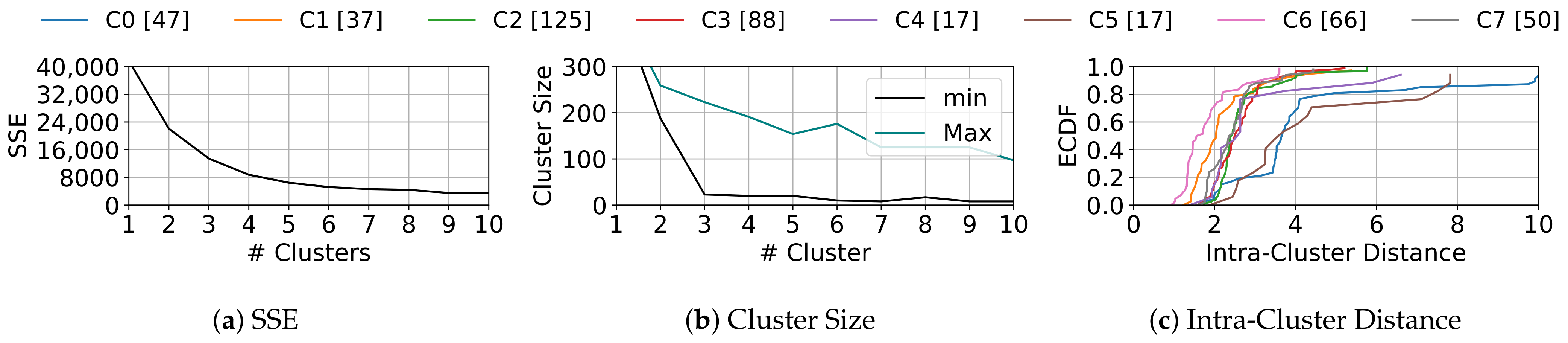
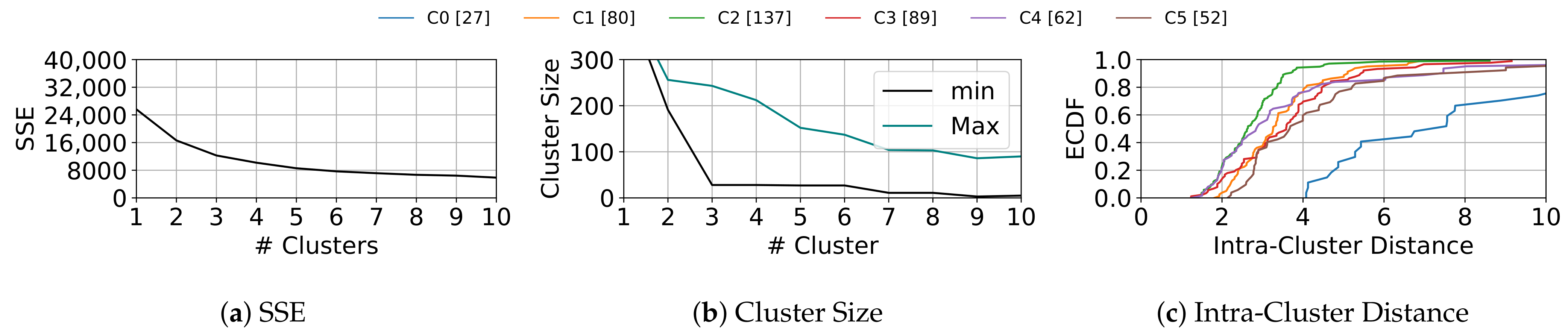
• Time-Series Clustering: We run K-MDTSC to group welding samples and identify different welding shapes within each welding spot.
• Correlation with external indexes: Finally, we study the clusters by using the wear to discover whether different welding shapes are characterized by different tears and wear of the electrode.

In the following we detail each step.

5.3. Noise Reduction

In the data collection the voltage $V_{(ws,i)}\left(z\right)$ and current $I_{(ws,i)}\left(z\right)$ time-series are collected with a frequency of 1 kHz. Such a moderately high frequency allows us to spot sudden and short changes. However, in the presence of noise in the acquisition system, the samples may suffer from frequent changes although the welder’s output remains stable. As such, to remove the noise component, we apply a low pass filter. In detail, given a time-series $X_{(ws,i)}$ with $X\in \{V,I\}$, we relay on a exponential moving average function defined as follows:

$${\overline{X}}_{(ws,i)}(z+1)=\alpha \ast X_{(ws,i)}\left(z\right)+(1-\alpha )\ast {\overline{X}}_{(ws,i)}\left(z\right)$$

where ${\overline{X}}_{(ws,i)}\left(z\right)$ is the value of the exponential moving average at time z, $\alpha$ is the smoothing factor. Notice that the higher $\alpha$, the more weight is given to the recent observation, i.e., the noise component, while the lower the alpha, the more we average the signal. Figure 8 reports an example of the noise reduction effect with $\alpha =0.75$.

5.4. Data Selection

Given a welding point $wp$, the different welding samples i may be described by curves ${\overline{X}}_{(ws,i)}\left(z\right)$ with $\overline{X}\in \{\overline{V},\overline{I}\}$ having different durations. Furthermore, for welding points $wp$ characterized by a two-phases welding process, the steady-state may begin in different instant $z_0$ based on the warm-up duration. Since our clustering solution requires that all the time-series in the input have the same duration and are synchronized, we align all the time-series as follows:

Whole Time-Series: Firstly, we consider the entire time-series. Given a welding point $wp$, we select the entire time-series ${\overline{X}}_{(ws,*)}\left(z\right)$. Next, we select the earliest finish time-series $E_f\left(ws\right)$ as the earliest time for a welding sample to finish.

$$E_f\left(ws\right)=min\left(\right|{\overline{X}}_{(ws,\ast )}\left|\right)$$

Finally, for each time-series $i\in {\overline{X}}_{(ws,\ast )}$, we get ${\widehat{X}}_{(ws,i)}\left(z\right)$ as the time-series lasting $E_f\left(ws\right)$.

$${\widehat{X}}_{(ws,i)}\left(z\right)={\overline{X}}_{(ws,i)}\left(z\right)0\le z\le E_f\left(ws\right)$$

Figure 9a depicts the results of the data selection step for all the time-series of the welding spot shown in Figure 8b.

Steady-State Aligned: Secondly, we focus only on the steady-state as the actual phase when the welder solder. Given a welding spot $wp$, for each time-series ${\overline{X}}_{(ws,i)}\left(z\right)$ we identify the start of the steady-state$S_{st}(ws,i)$ as the time when the welding process starts after the warm-up phase ends. We identify $S_{st}(ws,i)$ based on the current curve ${\overline{I}}_{(ws,i)}\left(z\right)$. Given ${\overline{I}}_{(ws,i)}\left(z\right)$, the warm-up phase ends when the current value drops below a given $Threshol{d}_I$. Next, we identify $S_{st}(ws,i)$ as the time when the current value ${\overline{I}}_{(ws,i)}\left(z\right)$ overcomes the $Threshol{d}_I$ again.

For each time-series $i\in {\overline{X}}_{(ws,\ast )}$, we get the steady-state ${\tilde{X}}_{(ws,i)}$ as follow:

$${\tilde{X}}_{(ws,i)}\left(z\right)={\overline{X}}_{(ws,i)}\left(z\right)z\ge S_{st}(ws,i)$$

After this, the steady-states are aligned, i.e., all ${\tilde{X}}_{(ws,i)}\left(z\right)$ start synchronously. However, since they may have different duration, we compute the earliest finish $\widetilde{E_f}\left(ws\right)$ over all ${\tilde{X}}_{(ws,i)}\left(z\right)$.

Finally, for each time-series $i\in {\tilde{X}}_{(ws,\ast )}$, we get the steady-state${\tilde{X}}_{(ws,i)}\left(z\right)$ lasting $E_f\left(ws\right)$.

$${\tilde{X}}_{(ws,i)}\left(z\right)={\tilde{X}}_{(ws,i)}\left(z\right)0\le z\le \widetilde{E_f}\left(ws\right)$$

Figure 9a depicts the result of the steady-states data selection step for the time-series shown in Figure 8b.

5.5. Data Normalization

After the data selection, the time-series ${\widehat{V}}_{(ws,i)}\left(z\right)$ and ${\widehat{I}}_{(ws,i)}\left(z\right)$ (or ${\tilde{V}}_{(ws,i)}\left(z\right)$ and ${\tilde{I}}_{(ws,i)}\left(z\right)$) are represented with different ranges. As such, we run a standard z-score normalization process as follows.

Given a welding sample $ws$, we select all the time-series ${\widehat{V}}_{(ws,i)}\left(z\right)$ and ${\widehat{I}}_{(ws,i)}\left(z\right)$. We create two time-series ${\widehat{V}}_{ws}\left(z\right)$ and ${\widehat{I}}_{ws}\left(z\right)$, where each one is the union of all ${\widehat{V}}_{(ws,\ast )}\left(z\right)$ and ${\widehat{I}}_{(ws,\ast )}\left(z\right)$ selected in the temporal order, respectively.

$${\widehat{V}}_{ws}\left(z\right)=\bigcup {\widehat{V}}_{(ws,i)}\left(z\right)i\in (1,..,|{\widehat{V}}_{ws}\left|\right)$$

$${\widehat{I}}_{ws}\left(z\right)=\bigcup {\widehat{I}}_{(ws,i)}\left(z\right)i\in (1,..,|{\widehat{I}}_{ws}\left|\right)$$

Next, from ${\widehat{I}}_{ws}\left(z\right)$ and ${\widehat{V}}_{ws}\left(z\right)$, we extract the:

• Mean: $m=\frac{1}{N}{\sum }_{z\in w\left(z\right)}{x}_i\left(z\right)$;
• Standard deviation: $\sigma =\sqrt{\frac{1}{N-1}{\sum }_{z\in w\left(z\right)}{(x_i\left(z\right)-m)}^2}$

Finally, we run the z-score normalization separately for each welding sample i:

$${\widehat{V}}_{ws,i}\left(z\right)=\frac{{\widehat{V}}_{(ws,i)}\left(z\right)-m_V}{{\sigma }_V}i\in (1,..,|{\widehat{V}}_{ws}\left|\right)$$

$${\widehat{I}}_{ws,i}\left(z\right)=\frac{{\widehat{I}}_{(ws,i)}\left(z\right)-m_I}{{\sigma }_I}i\in (1,..,|{\widehat{I}}_{ws}\left|\right)$$

6. Case Study Evaluation

We evaluate the proposed pipeline on the real data collected from a real production line as described in Section 5.

6.1. First Robot

Firstly, we focus on the data of the robot in Working Station 1 composed of a single clamp. Since the maintenance operation’s highest impact should be more evident in the welding point immediately before ($w{p}_b$) or after ($w{p}_a$) the maintenance operation, we focus on them. Considering the welding technique, both use a one-phase welding process, hence after the noise reduction step, we use the Whole Time-Series data selection process.

Focusing on $w{p}_b$, Figure 10a depicts the trend of the SSE score, while Figure 10b reports the trend of the minimum and maximum clusters size while increasing the number of clusters k. We use these two metrics to choose the best k. The SSE score suggests that increasing k by more than 4 gives a marginal benefit as the SSE keeps reducing at a slower pace while increasing k. However, considering the difference between the smallest and the biggest clusters, we can see that with more than 5 clusters, we start having a stable minimum cluster size. In contrast, the maximum cluster size starts reducing at a slower pace. Hence, to study the clustering result, we set $k=6$.

Next, we focus on the intra-cluster distance as a quality metric of the clustering result. We focus on this metric as huge distances may highlight unusual welding shapes, thus requiring maintenance operation. Figure 10c reports the Empirical Cumulative Distribution Function (ECDF) on the $y-axis$ of the intra-cluster distance separately for each cluster. The legend also reports the size of each cluster. Clusters $C0$, $C1$, and $C4$, accounting in total for 248 out of 293 welding samples, show very dense results with limited intra-cluster distance. On the contrary, small clusters show the highest distance. To investigate these results, we focus on each cluster’s centroid separately for the current and the voltage curves. Figure 11a,b show the denormalized current and the voltage centroids, respectively. Cluster $C5$ clearly shows higher values of the current with respect to the other clusters. Clusters $C2$ and $C3$, instead, show a higher deviation from the other clusters by looking at the voltage curves.

To identify whether these differences also reflect on the wear, Figure 11c reports, for each cluster, the ECDF of the wear of the welding samples. In a nutshell, we evaluate whether different clusters are characterized by different wear of the electrode. Thus, if we can use the clustering result to identify welding shapes that clearly point to maintenance needs, in this case, we could trigger the maintenance operation only when such welding shapes appear. Unlike the clustering results, however, the correlation with the wear does not show a clear picture. Clusters tend to be heterogeneous concerning this metric, with welding samples having different wear and tear of the electrode present in all the clusters.

Next, we focus on $w{p}_a$. The SSE score (Figure 12a) reports a trend similar to the previous case. Hence, to identify the best value of k we use the trend of the clusters size (Figure 12b). After $k=5$, the maximum size trend starts stabilizing while the minimum size drops after $k=6$. Thus, we set $k=6$. Differently from the previous case, only a few time-series in clusters have a large distance, as shown by the tail of the distribution in Figure 12c. This suggests a good clustering result with centroids well repressing the respective clusters. Here, cluster $C5$ is the most heterogeneous one, with 25 time-series. Considering the current centroids in Figure 13a, they clearly show differences among them, while voltage centroids in Figure 13b are more similar. By studying the correlation with the wear, in Figure 13c, all clusters contain heterogeneous welding samples. This hints that both the welding points before and after the maintenance operations do not show any particular impact on the electrode’s wear and tear.

Given these results, we also study calibration program 3 of the robot. The results, not shown here for the sake of brevity, highlight that the calibration program is not a good proxy of the maintenance operation. By discussing with domain experts, this may be because the calibration program runs without any material, with limited electrode usage.

6.2. Second Robot

We now repeat the analysis to study whether our results are generalized to the second robot. We focus on a welding point of the robot in the Working Station 2, Clamp 1. We focus on a welding point characterized by a two-phase welding process. We start by employing the Whole Time-Series data selection. Figure 14a reports the trend of the SSE score. The presence of the warm-up phase is immediately visible. The SSE score reaches a maximum value almost twice as much as the previous welding spot. The shape of the SSE score suggests that we should consider at least 4 clusters. Intuitively, Figure 14b shows that the higher k, the smaller is the maximum cluster size. From this metric, we choose $k=8$ as the maximum cluster size presents a plateau while the minimum cluster size presents a maximum local value. By choosing $k=8$, clusters $C0$ and $C5$ present, generally, a higher intra-cluster distance (Figure 14c). Analyzing the clusters’ centroid, we can see that this is due mostly to different peaks in the voltage curve (Figure 15a) rather than in the current curve (Figure 14c). Similarly, with the $w{s}_b$ case in Figure 11c, also in Figure 15c, the wear does not reflect the intra-cluster distance behavior. Indeed, cluster $C0$ presents an ECDF of the wear as the other clusters.

Next, since the warm-up phase demonstrates to drive the clustering, we rely on the Steady-State aligned data selection to focus on the actual welding process. We analyze the same two-phase welding spot to study the differences among the two clustering results. Figure 16a reports the trend of the SSE score. Clearly, the SSE score reaches a lower value than the previous case, slowing down in the reduction pace with at least 4 clusters. Looking at Figure 16b, we set $k=6$, as the minimum cluster size presents a plateau while the maximum cluster size keeps decreasing. Interestingly, the intra-cluster distance in Figure 16c shows that cluster $C0$ groups time-series that are always very far from their centroid. However, the current centroid in Figure 17a shows a shape very similar to the other clusters. Differently, the voltage centroid in Figure 17b, shows a very different shape with a lower voltage value during the actual welding process. As in the other cases, the ECDF of the wear, Figure 17c does not show any particular behavior related to the different welding shapes.

By analyzing the results with domain experts, we discover that current scheduled maintenance is performed with a frequency higher than required. Our results, therefore, confirm that this behavior allows the robots to weld without altering the welding shape while increasing the wear and tear of the electrode. As a result, domain experts plan to increase the time gap between two maintenance operations. This increase will result in a time-reduction of the time spent for the maintenance operations and money-saving due to increased electrodes’ usage.

Lessons Learned

Our automatic pipeline effectively preprocesses and correctly identifies different welding profiles. Different welding profiles are not characterized by homogeneous wear of the electrode. This heterogeneity hints that the manufacturer could postpone current maintenance until the wear does not clearly impact the welding shape. This result is generalized over the different welding points and robots. Furthermore, with the two-phase welding process, the steady-state demonstrates to hold most of the information. Thus, when possible, it is better to study the welding shape only on this part of the welding process.

6.3. Noise Sensitivity

Since K-MDTSC could handle noisy curves, here we study the impact of the noise reduction step introduced in our case study. To this end, we repeat the clustering process of the welding point collected by the robot in Working Station 2. We repeat our generic pipeline, avoiding the noise reduction step and applying the steady-state aligned data selection process. Comparing the SSE score in Figure 16a (with noise reduction) and Figure 18a (without noise reduction), we can see that the curves have a similar trend. However, when we do not apply the noise reduction, the maximum value increases almost three times. The cluster size (Figure 18b), instead, shows both similar trends and clusters cardinality with respect to the case with noise reduction (Figure 16c). Hence, we set $k=6$. The clustering result shows that clusters are much less dense than the case with noise reduction. Indeed, in Figure 18c, we can see how all intra-cluster distances are greater than 4. Instead, in Figure 16c, most of the intra-cluster distances are lower than 4. Considering the cluster centroids, in Figure 19a,b, the identification of different welding shapes is a complex task, as the noise gives a major contribution, especially in the current curve. Finally, as in the previous cases, also here (Figure 19c), different welding shapes do not reflect differences in the electrode’s wear.

Based on these results, on the one hand, K-MDTSC confirms the capability to handle noise data. On the other hand, a noise reduction step demonstrates to ease the analysis of the clustering results.

Lessons Learned

The noise reduction step demonstrates limited benefits, mainly visible while considering the cluster cohesiveness and the centroids representation. Instead, the correlation with the electrode wear does not show any impact of the noise. Indeed, also in this case the electrode wear does not alter the welding shape.

7. Conclusions

This work presented K-MDTSC, a K-means-based clustering algorithm designed to group synchronous multi-dimensional time-series. Firstly, we ran a thorough validation process using synthetic datasets composed of synchronous multi-dimensional sinusoidal curves and compared the results with k-Shape, a state-of-art time-series clustering algorithm K-means-based. Our results showed that:

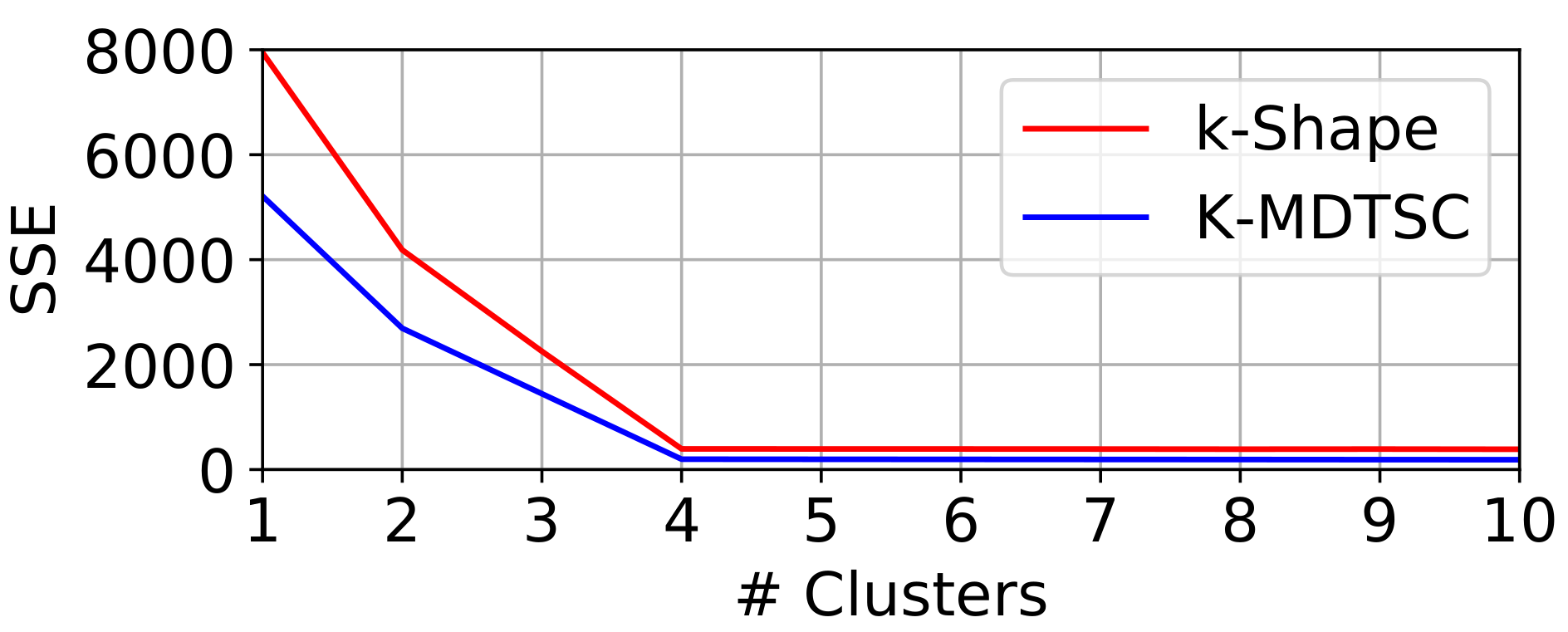
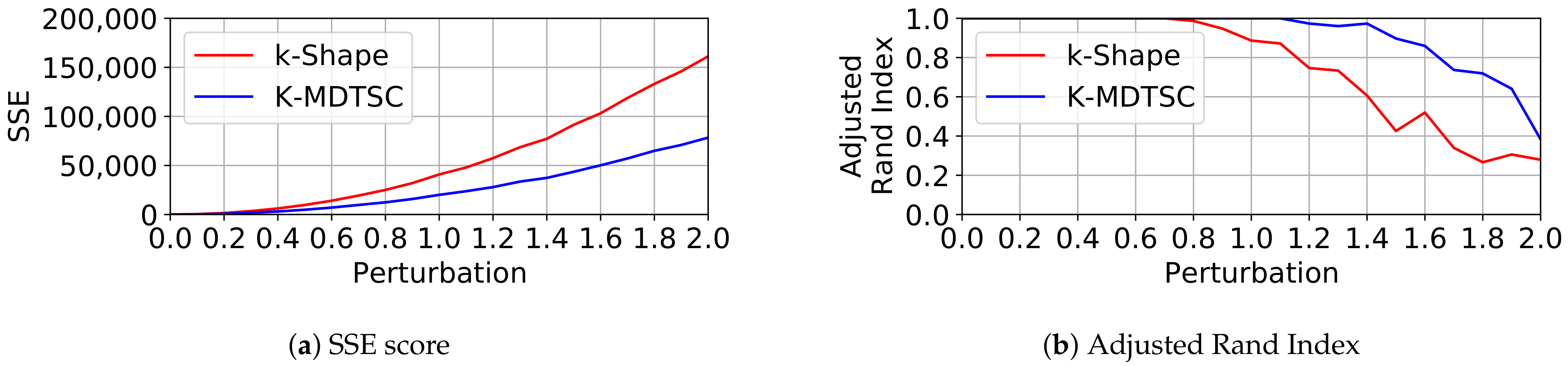
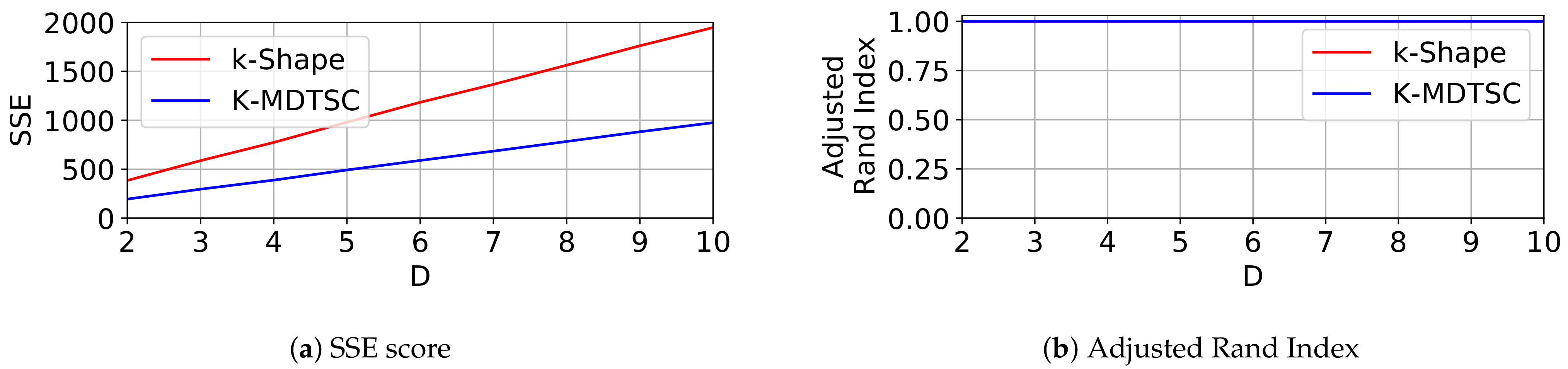
• both K-MDTSC and k-Shape correctly group multi-dimensional time-series;
• however, K-MDTSC overcomes k-Shape performance when a high number of curve families or noise perturbation are present.

Next, we used K-MDTSC to analyze data from the body-in-white welding stage of an actual production plant. To use K-MDTSC with real data, we deploy a generalized pipeline that reduces the noise in the multi-dimensional time-series, realign them if needed to get synchronous multi-dimensional time-series, normalize each dimension separately, and finally fed them into K-MDTSC. Our results show that our automatic pipeline effectively processes the data and that K-MDTSC algorithm identifies different welding profiles. By presenting our results to domain experts, they discover that:

• the wear and tear of the electrode do not negatively impact the welding process;
• considering the different data selection techniques, the wear and tear of the electrode does not negatively impact it neither considering the whole welding process nor considering only the steady-state when the actual welding process is performed;

Based on these results, experts reach the conclusion that current maintenance operations are premature and could be postponed with a reduction of the time spent for maintenance and a resulting money-saving.

To allow other researchers to replicate our results and use K-MDTSC to run similar analyses with synchronous multi-dimensional time-series, we release the K-MDTSC code and our synthetic datasets as open-source at [8].

As future work, we plan to extend our validation process to other public multi-dimensional time-series datasets and run a thoroughly compare K-MDTSC algorithm with other time-series clustering algorithms. For future analysis, we plan to extend our analyses to the new data characterized by postponed maintenance operations.