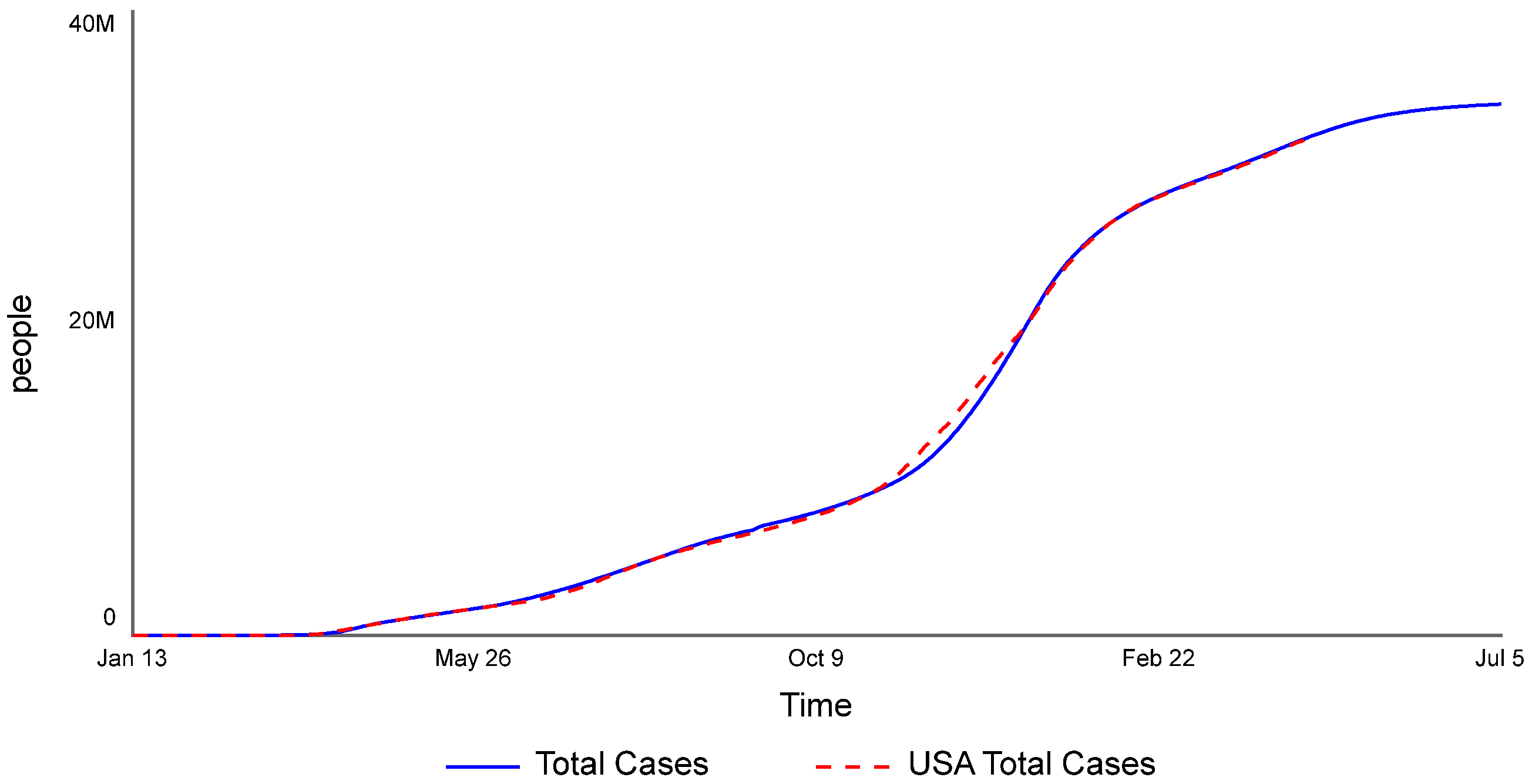
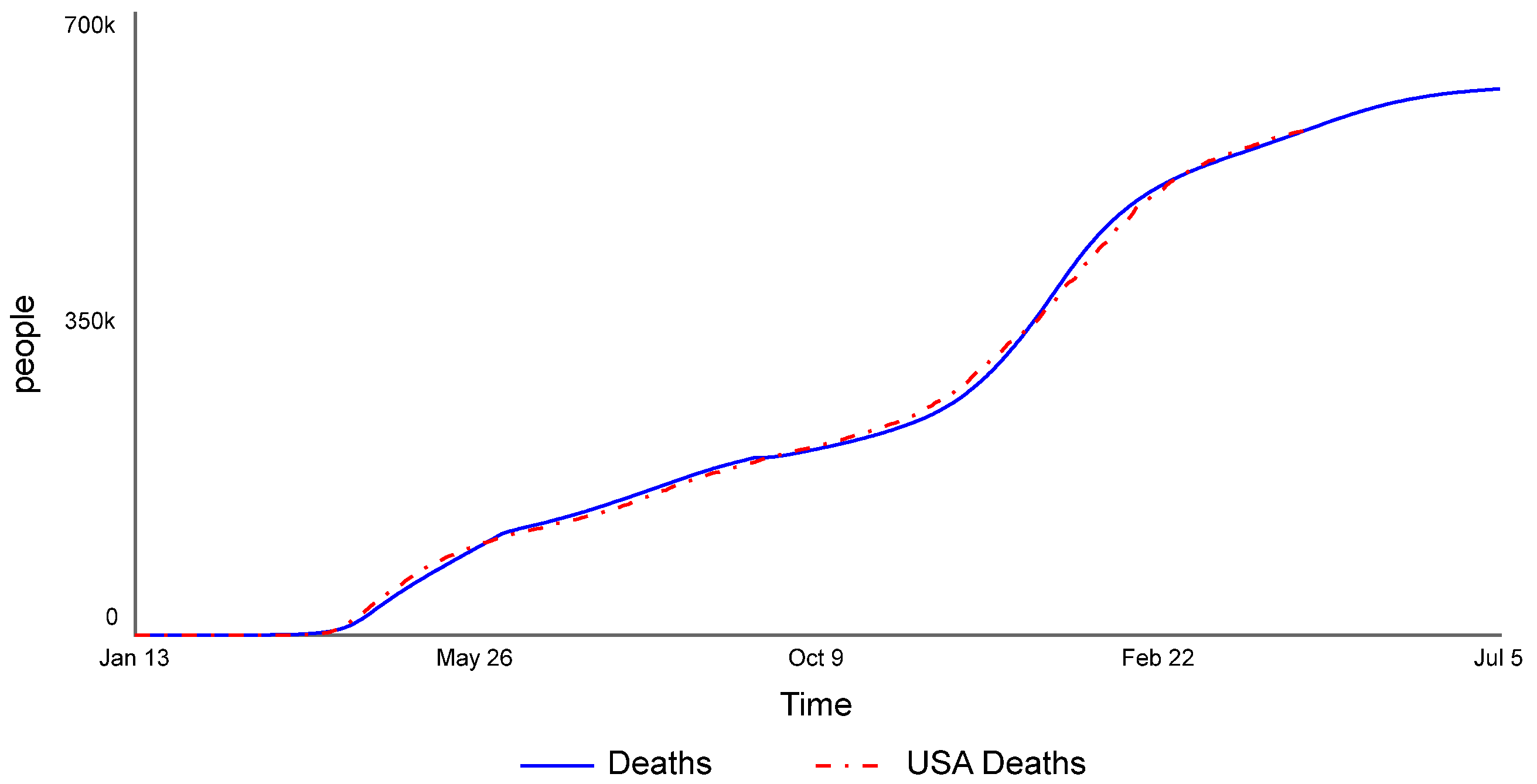
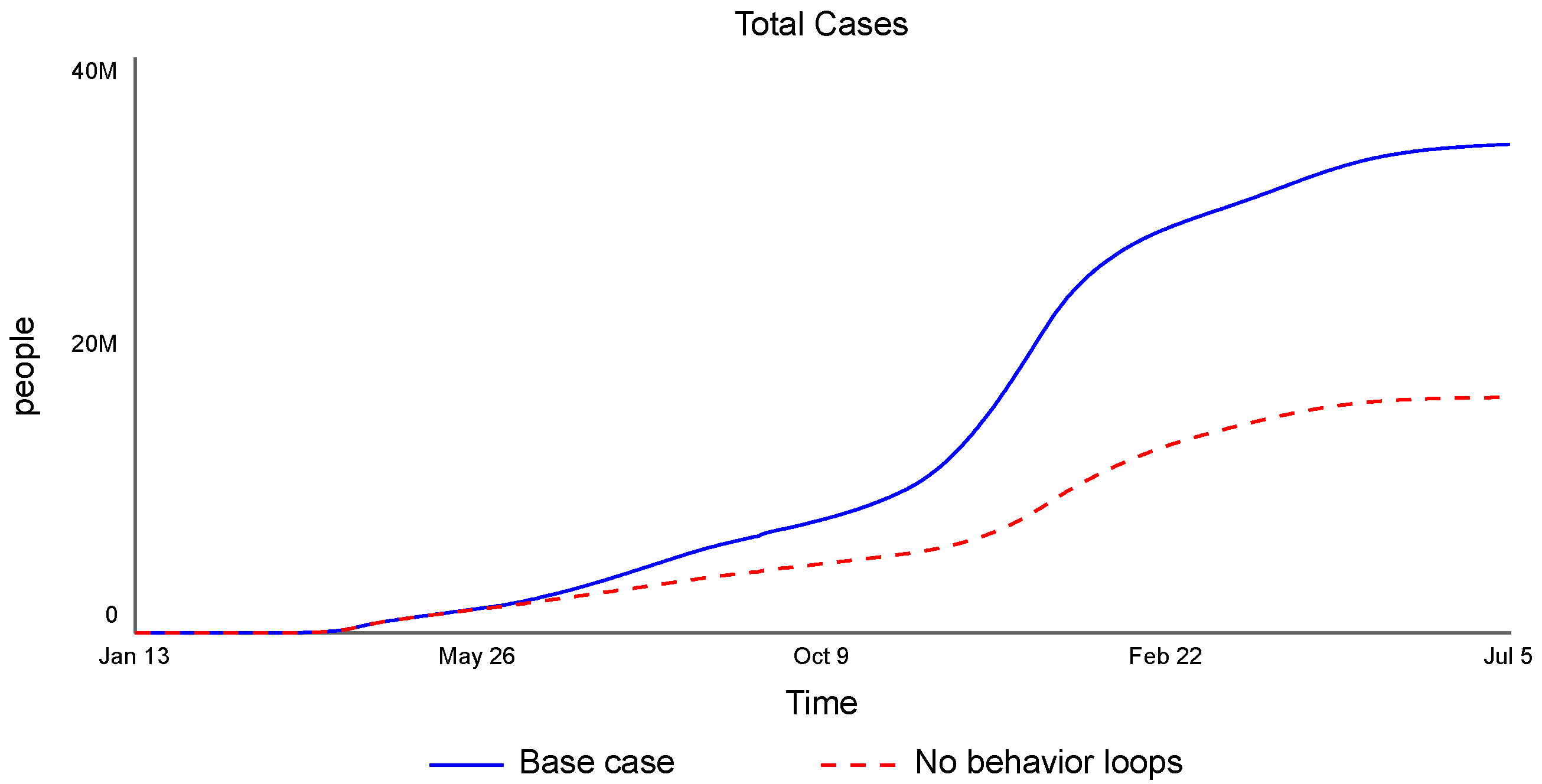
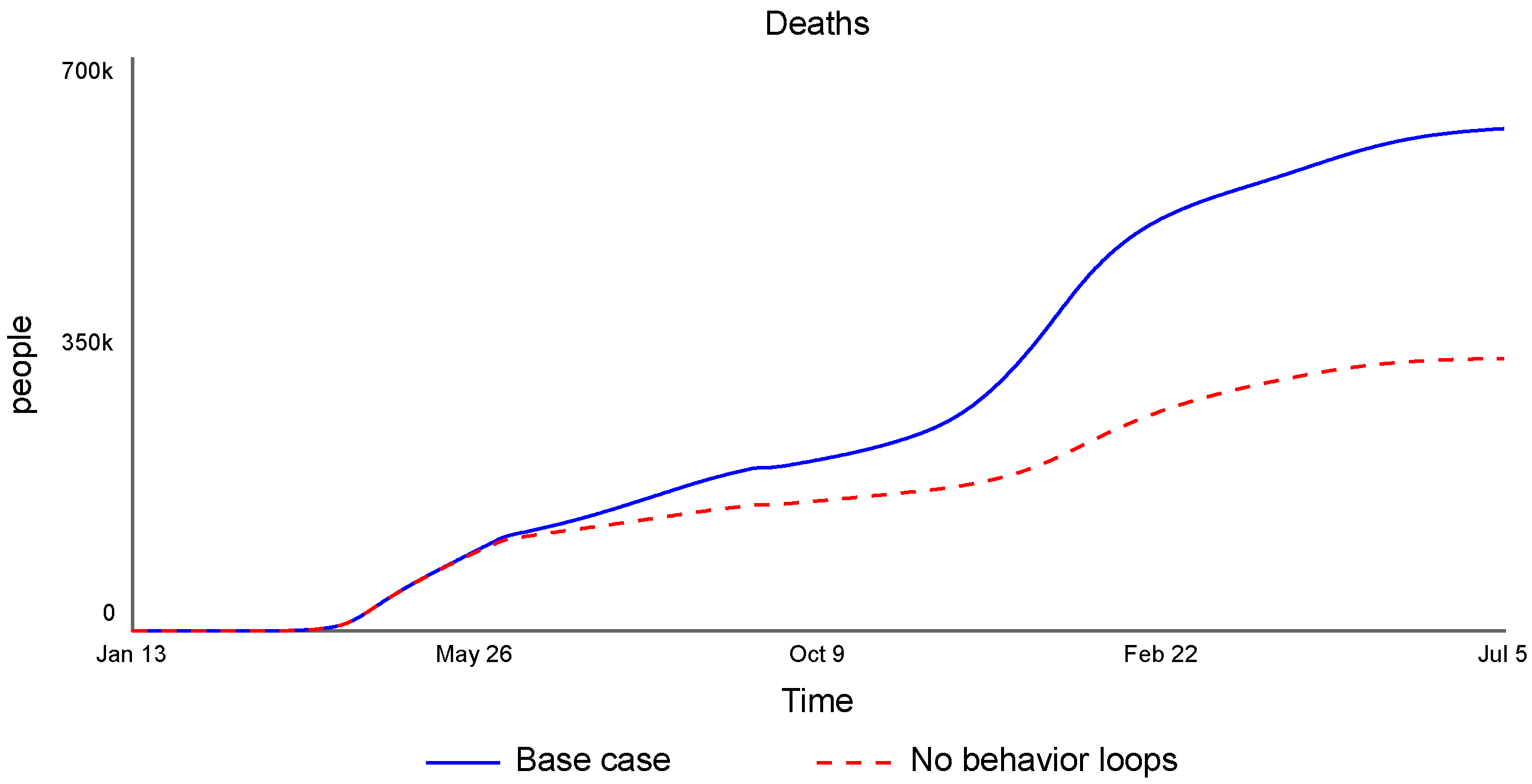
Appendix A. Model Equations without Calibration Settings
Stocks:
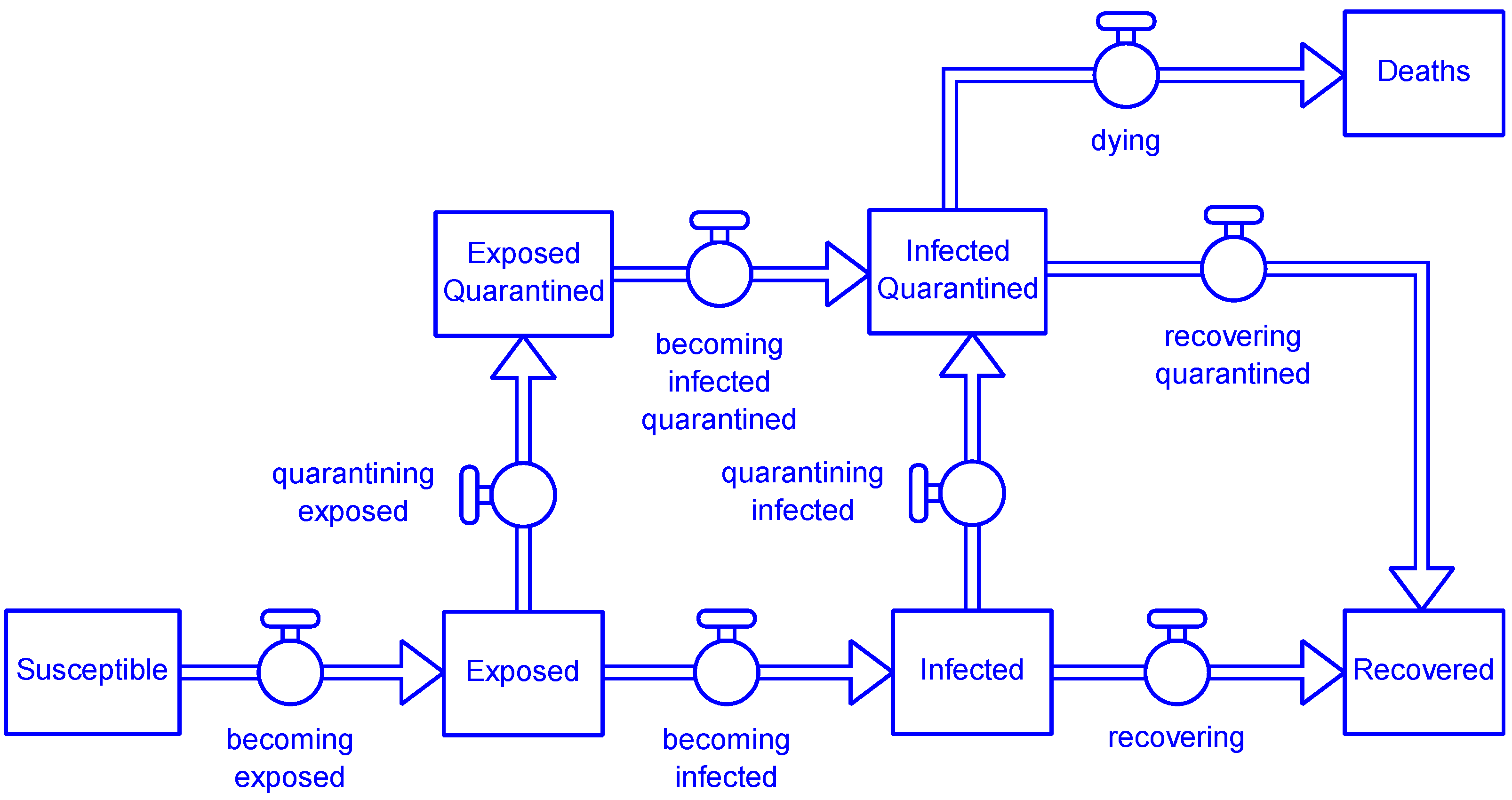
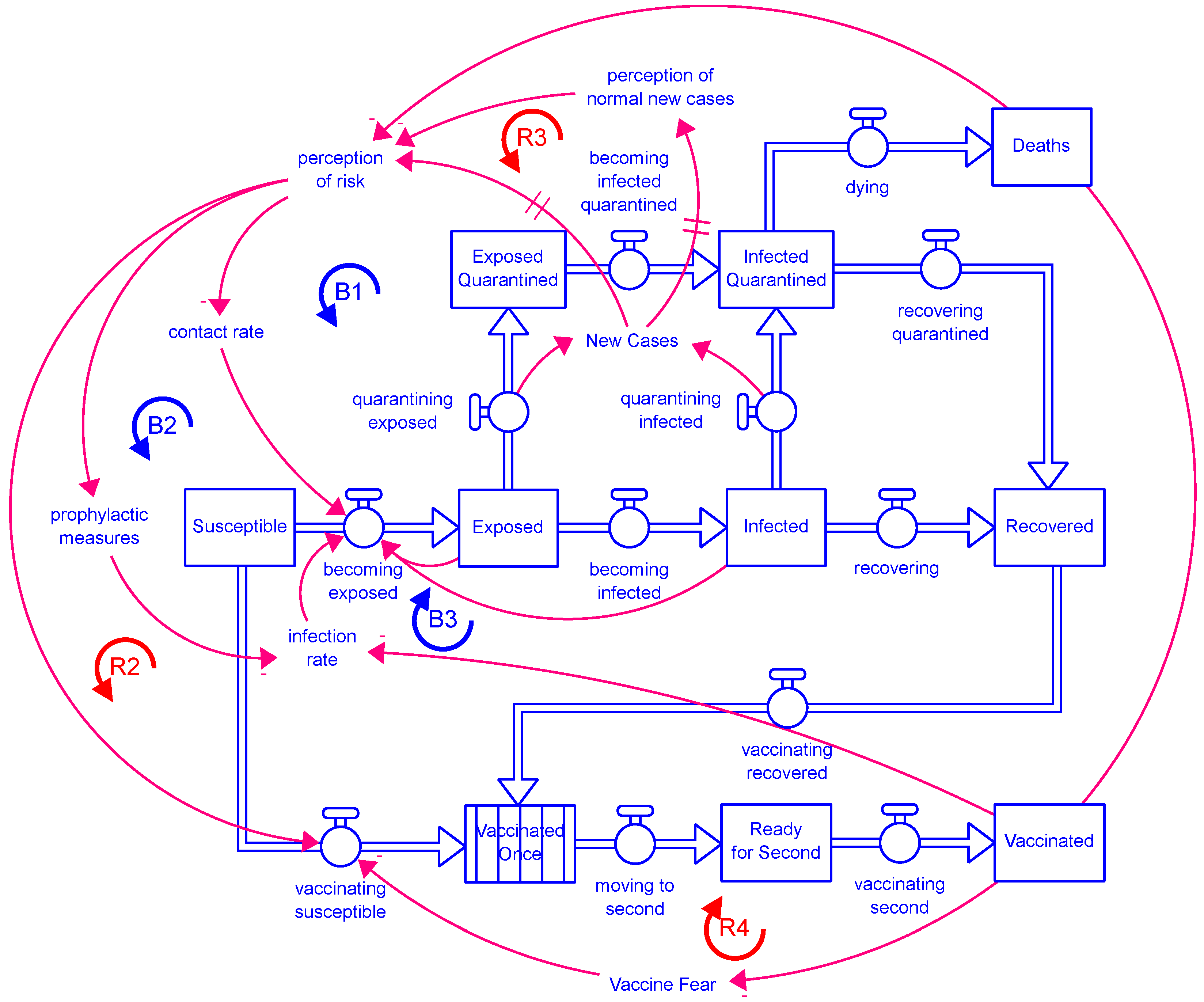
Deaths = ∫(dying[not_yet] + dying[vaccinated])dt
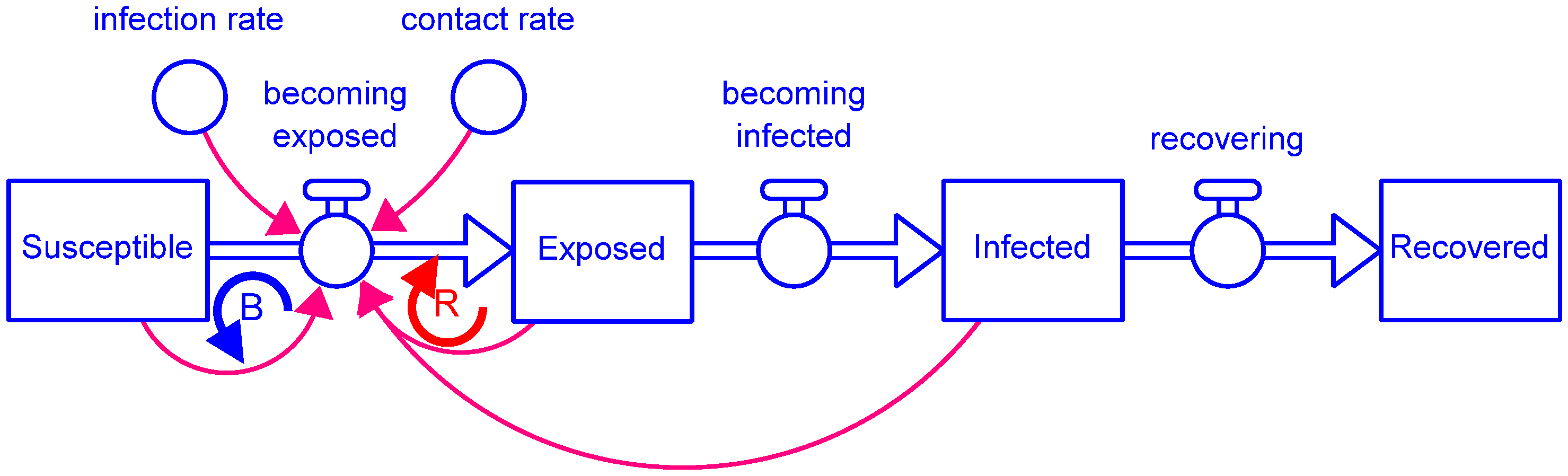
Exposed = ∫(becoming_exposed − becoming_infected − quarantining_exposed)dt
Exposed_Quarantined = ∫(quarantining_exposed − becoming_infected_quarantined)dt
Infected = ∫(becoming_infected − recovering − quarantining_infected)dt
Infected_Quarantined = ∫(quarantining_infected + becoming_infected_quarantined
− recovering_quarantined − dying)dt
Prevalent_Strain = ∫(mutating)dt
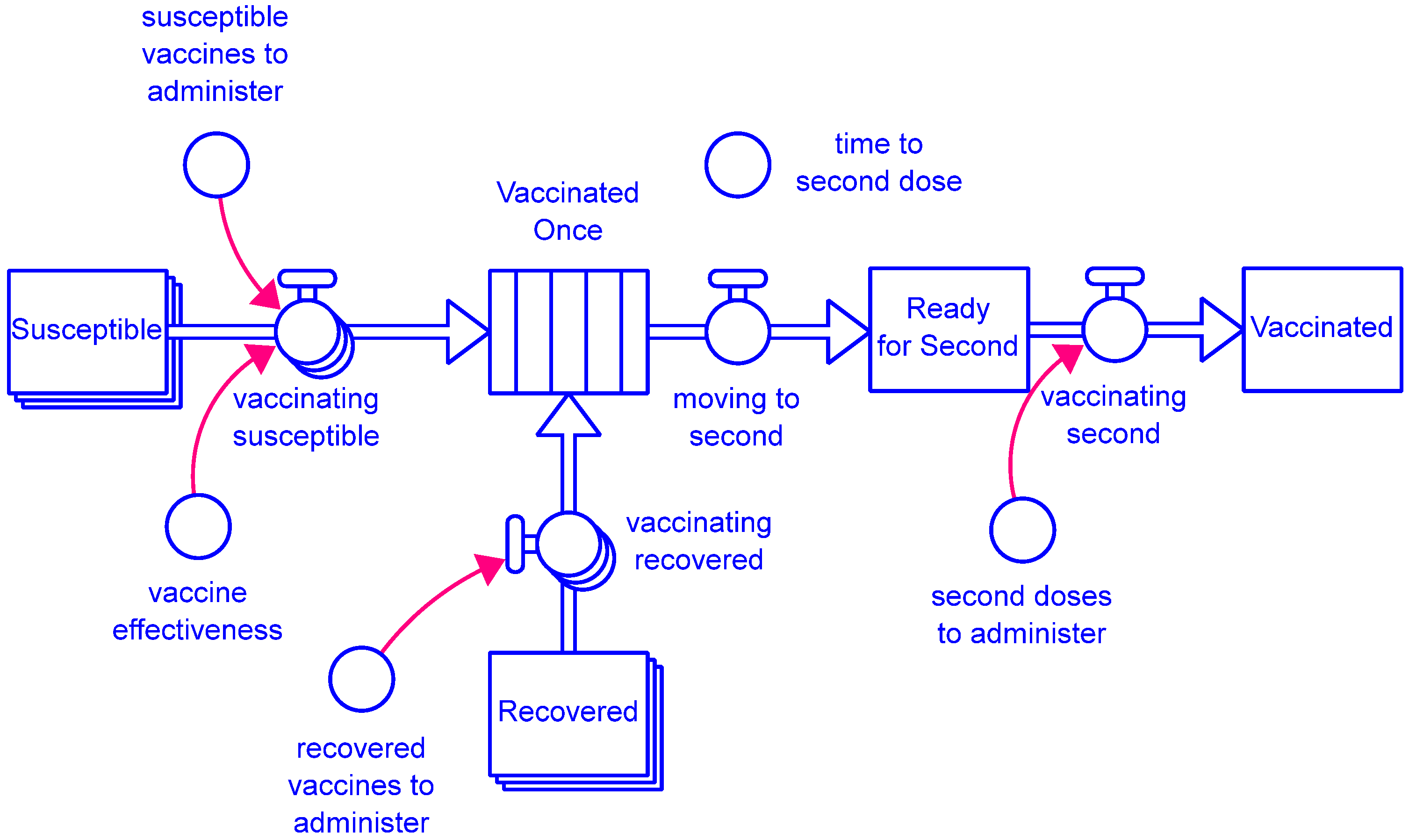
Ready_for_Second = ∫(moving_to_second − vaccinating_second)dt
Recovered = ∫(recovering + recovering_quarantined − vaccinating_recovered − losing_immunity)dt
Susceptible = ∫(becoming_susceptible − becoming_exposed − vaccinating_susceptible)dt
Total_Cases = ∫(adding_cases)dt
Vaccinated = ∫(vaccinating_second − losing_vaccine_immunity)dt
Vaccinated_Once = ∫(vaccinating_recovered_in + vaccinating_susceptible_in
− moving_to_second)dt
transit time(Vaccinated_Once) = time_to_second_dose
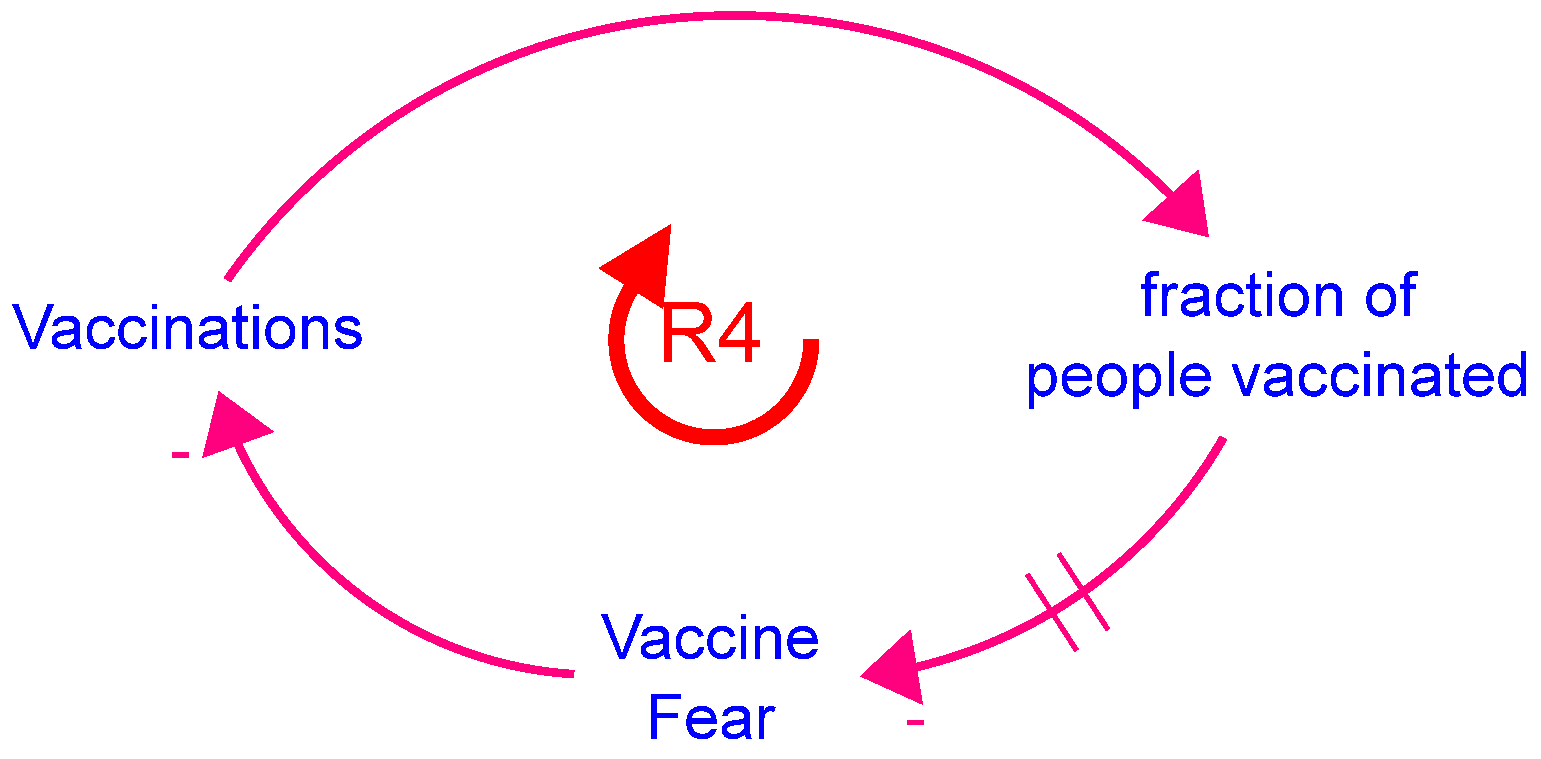
Vaccine_Fear = ∫(-diminishing_fear)dt
Flows:
adding_cases = New_Cases
becoming_exposed = infection_rate × susceptible_contacts_with_infected
becoming_infected = newly_infected_people
becoming_infected_quarantined = Exposed_Quarantined/(time_to_show_symptoms/2)
becoming_susceptible[not_yet] = 0
becoming_susceptible[vaccinated] = (1 − vaccine_effectiveness) × vaccinating_susceptible[not_yet]
diminishing_fear = IF TIME >= vaccine_start THEN Vaccine_Fear/time_to_reduce_fear ELSE 0
dying = DELAYN2OUT(total_infected_quarantining, 1//death_rate, 3, 0,
desired_recovering_quarantined)
moving_to_second = conveyor outflow(Vaccinated_Once)
mutating = mutation_switch × new_mutations_possible/time_to_mutate
quarantining_exposed = DELAYN2OUT2ND(becoming_exposed,
time_to_show_symptoms, distribution, 0, desired_testing)
quarantining_infected = DELAYN2OUT2ND(becoming_infected, time_to_recover, distribution,
0, desired_quarantining)
recovering = DELAYN2OUT(becoming_infected, time_to_recover, distribution,
0, desired_quarantining)
recovering_quarantined = DELAYN2OUT2ND(total_infected_quarantining, 1//death_rate, 3,
0, desired_recovering_quarantined)
vaccinating_recovered = IF Vaccine_Status = Vaccine_Status.not_yet
THEN recovered_vaccines_to_administer ELSE 0
vaccinating_recovered_in = vaccinating_recovered[not_yet]
vaccinating_second = second_doses_to_administer
vaccinating_susceptible = IF Vaccine_Status = Vaccine_Status.not_yet
THEN susceptible_vaccines_to_administer ELSE 0
vaccinating_susceptible_in = vaccine_effectiveness × vaccinating_susceptible[not_yet]
Parameters and other variables:
asymptomatic_fraction = 0.698841227245
base_infection_rate = 0.024
base_prophylactic_reduction_fraction = 0.53
base_quarantine_effectiveness = 0.7
behavior_switch = 1
contact_rate = vaccinated_effect_on_contact_rate × seasonal_effect_on_contact_rate
× quarantine_effect_on_contact_rate × normal_contact_rate
death_rate = overall_death_rate/time_to_recover_quarantined
desired_quarantining = symptomatic_quarantine_effectiveness
× (1 − asymptomatic_fraction) × becoming_infected
desired_recovering_quarantined = Infected_Quarantined/time_to_recover_quarantined
desired_testing = test_effectiveness × probability_exposed × testing_resources_noninfected
distribution = 3
fear_effect_on_vaccinations = f(Vaccine_Fear):
(0.0, 1.0000), (10.0, 0.802192027621), (20.0, 0.66959737847), (30.0, 0.580716527147), (40.0, 0.521137910797), (50.0, 0.481201169942), (60.0, 0.454430771974),
(70.0, 0.436486037575), (80.0, 0.424457322387), (90.0, 0.416394233468),
(100.0, 0.410989383333)
first_dose_demand = ((1 − vaccine_hesitancy_switch) + vaccine_hesitancy_switch
× fear_effect_on_vaccinations) × new_cases_effect_on_vaccinations × first_doses_needed
first_dose_resources = vaccine_resources − second_doses_to_administer
first_doses_needed = vaccine_demand × Vaccine_Ready
first_doses_to_administer = vaccination_switch × MIN(first_dose_resources,
first_dose_demand/time_to_administer)
fraction_12–15 = 0.05212
fraction_16+ = 0.7683
fraction_population_severe = severe_infected/Live_Population
fraction_ready_vaccinated = Total_Vaccinated/Vaccine_Ready
fraction_susceptible = Susceptible[not_yet]//(Susceptible[not_yet] + Recovered[not_yet])
fraction_vaccinated = Total_Vaccinated//Live_Population
holiday_effect_on_contact_rate = (holiday_multiplier − 1) × holiday_season + 1
holiday_multiplier = 1.3
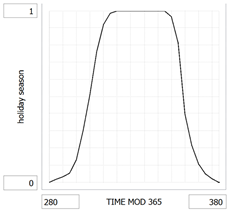
holiday_season = f(TIME MOD 365):
(280.0, 0.000), (284.0, 0.0176), (288.0, 0.0322), (292.0, 0.0534), (296.0, 0.132),
(300.0, 0.303), (304.0, 0.513), (308.0, 0.763), (312.0, 0.921), (316.0, 0.987), (320.0, 1.000), (324.0, 1.000), (328.0, 1.000), (332.0, 1.000), (336.0, 1.000), (340.0, 1.000), (344.0, 1.000), (348.0, 1.000), (352.0, 0.9668), (356.0, 0.8134), (360.0, 0.399), (364.0, 0.2166),
(368.0, 0.108), (372.0, 0.050), (376.0, 0.0208), (380.0, 0.000)
infection_rate = prophylactic_effect_on_infection_rate
× mutation_effect_on_infection_rate × base_infection_rate
Live_Population = Total_Population − Deaths
maximum_fraction_vaccinated = 0.75
Maximum_New_Cases_So_Far = MAXIMUM(New_Cases)
mutation_effect_on_death_rate = f(Prevalent_Strain)
(0.000, 1.0000), (0.300, 1.00976498428), (0.600, 1.02428602211), (0.900, 1.04458679859), (1.200, 1.07050171822), (1.500, 1.1000), (1.800, 1.12949828178), (2.100, 1.15541320141), (2.400, 1.17571397789), (2.700, 1.19023501572), (3.000, 1.2000)
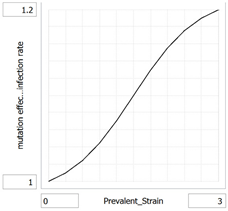
mutation_effect_on_infection_rate = f(Prevalent_Strain)
(0.000, 1.0000), (0.300, 1.00976498428), (0.600, 1.02428602211), (0.900, 1.04458679859), (1.200, 1.07050171822), (1.500, 1.1000), (1.800, 1.12949828178), (2.100, 1.15541320141), (2.400, 1.17571397789), (2.700, 1.19023501572), (3.000, 1.2000)
mutation_switch = 1
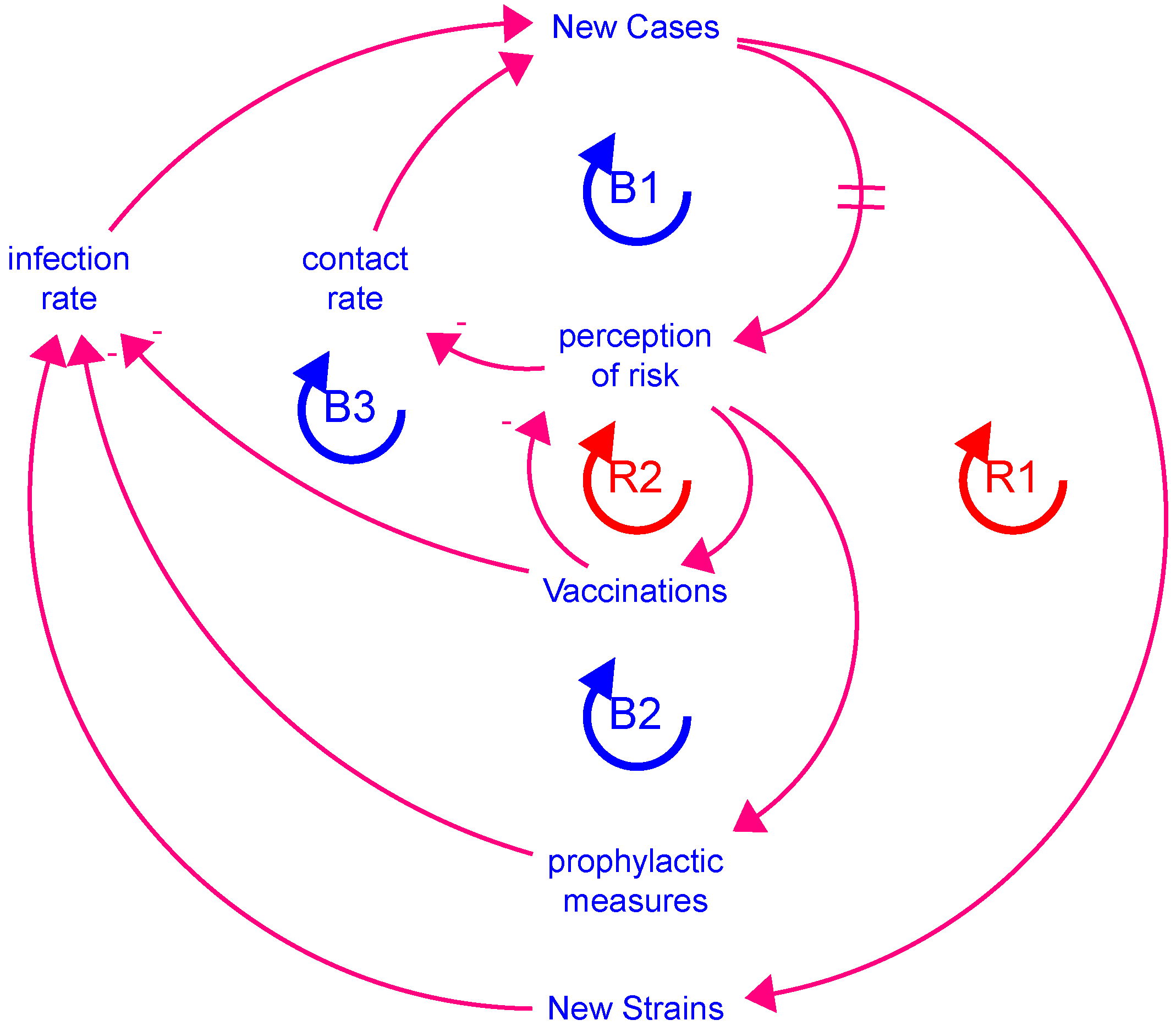
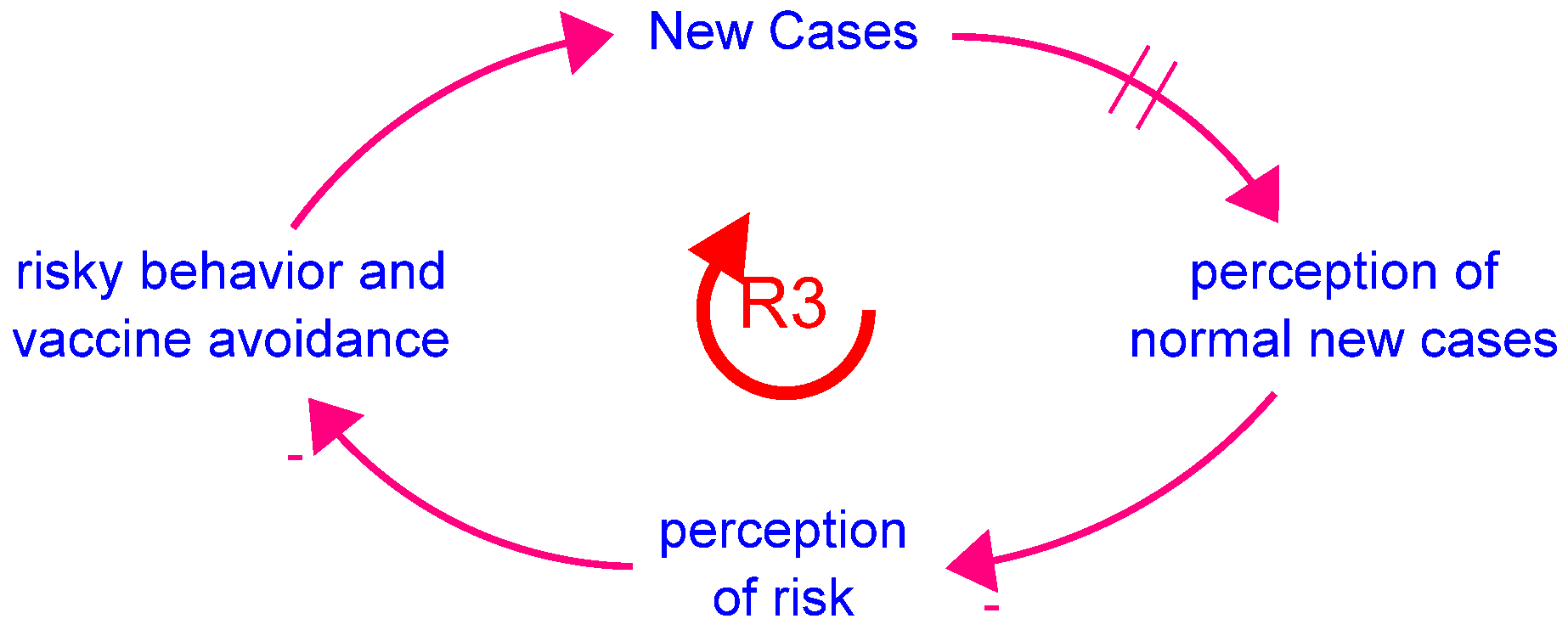
New_Cases = SUM(quarantining_exposed + quarantining_infected)
new_cases_effect_on_prophylactics = f(perception_of_new_cases)
(0.000, 0.000), (0.100, 0.204704191101), (0.200, 0.373647966026), (0.300, 0.51307842386), (0.400, 0.628151338387), (0.500, 0.723121805124), (0.600, 0.801501583626),
(0.700, 0.866188953175), (0.800, 0.919575883568), (0.900, 0.963636483909), (1.000, 1.000)
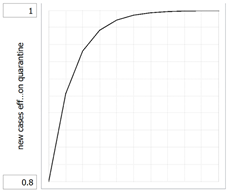
new_cases_effect_on_quarantine = f(perception_of_new_cases)
(0.000, 0.8000), (0.100, 0.902726242763), (0.200, 0.952728473174),
(0.300, 0.97706717163), (0.400, 0.98891408801), (0.500, 0.994680601285),
(0.600, 0.99748746463), (0.700, 0.998853711695), (0.800, 0.999518735537),
(0.900, 0.999842437392), (1.000, 1.0000)
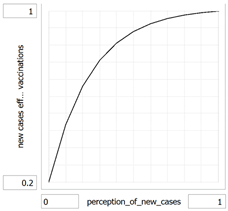
new_cases_effect_on_vaccinations = f(perception_of_new_cases)
(0.000, 0.2000), (0.100, 0.468664729336), (0.200, 0.648756083073), (0.300, 0.7694749276), (0.400, 0.850395189021), (0.500, 0.904637662382), (0.600, 0.940997479623),
(0.700, 0.965370193989), (0.800, 0.981707713005), (0.900, 0.992659079504),
(1.000, 1.0000)
new_mutations_possible = (Total_Exposed + Total_Infected) × probability_of_mutation
newly_infected_people = DELAYN2OUT(becoming_exposed, time_to_show_symptoms,
distribution, 0, desired_testing)
normal_contact_rate = 10.255130942
normal_time_to_reduce_fear = 36.5991817151
overall_death_rate = 0.0696453653012
perception_of_new_cases = SMTH3(relative_fraction_of_new_cases,
time_to_perceive_new_cases, 0)
probability_exposed = SUM(Exposed)/SUM(Susceptible + Exposed)
probability_of_contact_with_susceptible = Susceptible/(Total_Population
− Quarantined_or_Died)
probability_of_mutation = 1/1000000
prophylactic_effect_on_infection_rate = IF (TIME > quarantine_start/2)
AND ((TIME <= 487) OR (NOT remove_masks_switch))
THEN 1 − prophylactic_switch × prophylactic_reduction_fraction ELSE 1
prophylactic_effectiveness = IF quarantine_in_effect THEN 1
ELSE 0.85 − reduced_prophylactic_use_switch × 0.085
prophylactic_reduction_fraction = new_cases_effect_on_prophylactics
× prophylactic_effectiveness × base_prophylactic_reduction_fraction
prophylactic_switch = 1
quarantine_effect_on_contact_rate = 1 − Quarantine_In_Effect × quarantine_effectiveness
quarantine_effectiveness = new_cases_effect_on_quarantine × base_quarantine_effectiveness
quarantine_in_effect = (TIME >= quarantine_start)
AND (TIME < quarantine_start + quarantine_length)
quarantine_length = 64
quarantine_start = 83
Quarantined_or_Died = Deaths + SUM(Exposed_Quarantined) + SUM(Infected_Quarantined)
recovered_vaccines_to_administer = first_doses_to_administer
− susceptible_vaccines_to_administer
reduced_prophylactic_use_switch = 0
relative_fraction_of_new_cases = behavior_switch
× MIN(New_Cases//Maximum_New_Cases_So_Far, 1) + (1 − behavior_switch)
remove_masks_switch = 0
seasonal_effect_on_contact_rate = seasonality_switch × summer_effect_on_contact_rate
× holiday_effect_on_contact_rate + (1 − seasonality_switch)
seasonality_switch = 1
second_doses_to_administer = MIN(vaccine_resources, Ready_for_Second/time_to_administer)
severe_fraction = 0.2
severe_infected = severe_fraction × SUM(Infected_Quarantined)
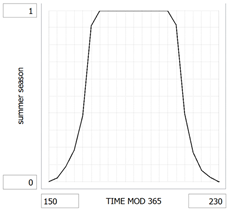
summer_effect_on_contact_rate = (summer_multiplier − 1) × summer_season + 1
summer_multiplier = 1.1
summer_season = f(TIME MOD 365)
(150.00, 0.000), (154.00, 0.022), (158.00, 0.088), (162.00, 0.185), (166.00, 0.386),
(170.00, 0.912), (174.00, 1.000), (178.00, 1.000), (182.00, 1.000), (186.00, 1.000),
(190.00, 1.000), (194.00, 1.000), (198.00, 1.000), (202.00, 1.000), (206.00, 1.000),
(210.00, 0.917), (214.00, 0.399), (218.00, 0.171), (222.00, 0.066), (226.00, 0.026),
(230.00, 0.000)
susceptible_contacts_with_infected = probability_of_contact_with_susceptible
× total_infected_contacts
susceptible_vaccines_to_administer = fraction_susceptible × first_doses_to_administer
symptomatic_quarantine_effectiveness = 0.75
test_effectiveness = 0.8
testing_resources = RAMP(7092.2, testing_start, testing_start + 282)
testing_resources_noninfected = MAX(testing_resources − SUM(quarantining_infected), 0)
testing_start = 45
time_to_administer = 1
time_to_mutate = 2000
time_to_perceive_new_cases = 30
time_to_reach_target = 120
time_to_recover = 18.6059231858
time_to_recover_quarantined = time_to_recover/2
time_to_reduce_fear = vaccination_effect_on_fear_reduction × normal_time_to_reduce_fear
time_to_second_dose = 25
time_to_show_symptoms = 9.91451735291
total_eligible_exposed = “fraction_16+” × (Total_Exposed + Total_Infected)
Total_Exposed = SUM(Exposed) + SUM(Exposed_Quarantined)
Total_Infected = SUM(Infected) + SUM(Infected_Quarantined)
total_infected_contacts = contact_rate × SUM(Exposed + Infected)
total_infected_quarantining = quarantining_infected + becoming_infected_quarantined
Total_Population = 330000000
Total_Recovered = SUM(Recovered)
Total_Susceptible = SUM(Susceptible)
Total_Vaccinated = Exposed[vaccinated] + Exposed_Quarantined[vaccinated]
+ Infected[vaccinated] + Infected_Quarantined[vaccinated] + Ready_for_Second
+ Recovered[vaccinated] + Susceptible[vaccinated] + Vaccinated + Vaccinated_Once
Total_Vaccinated_Infected = Exposed[vaccinated] + Exposed_Quarantined[vaccinated]
+ Infected[vaccinated] + Infected_Quarantined[vaccinated] + Recovered[vaccinated]
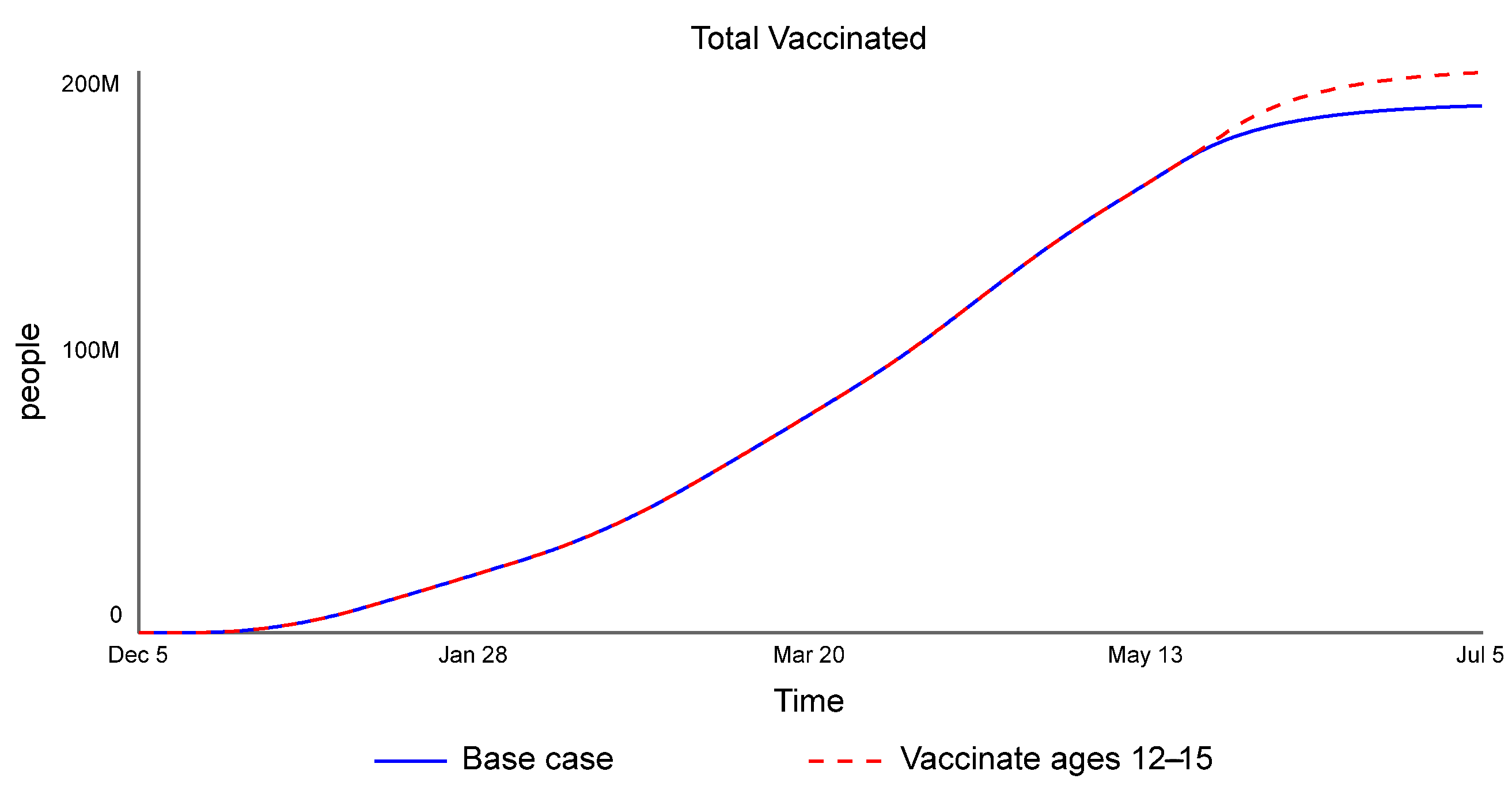
vaccinate_12_to_15_switch = 0
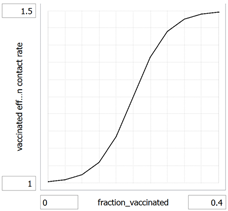
vaccinated_effect_on_contact_rate = f(fraction_vaccinated)
(0.0000, 1.00334642546), (0.0400, 1.00899310498), (0.0800, 1.02371293659),
(0.1200, 1.05960146101), (0.1600, 1.13447071069), (0.2000, 1.2500),
(0.2400, 1.36552928932), (0.2800, 1.44039853899), (0.3200, 1.47628706341),
(0.3600, 1.49100689502), (0.4000, 1.49665357454)
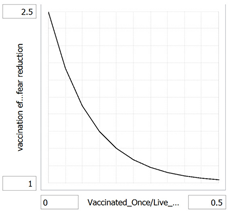
vaccination_effect_on_fear_reduction = f(Vaccinated_Once/Live_Population)
(0.0000, 2.500), (0.0500, 2.00548006905), (0.1000, 1.67399344618),
(0.1500, 1.45179131787), (0.2000, 1.30284477699), (0.2500, 1.20300292485),
(0.3000, 1.13607692993), (0.3500, 1.09121509394), (0.4000, 1.06114330597),
(0.4500, 1.04098558367), (0.5000, 1.02747345833)
vaccination_switch = 1
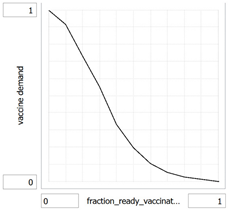
vaccine_demand = f(fraction_ready_vaccinated)
(0.000, 1.000), (0.100, 0.917), (0.200, 0.732), (0.300, 0.553), (0.400, 0.333), (0.500, 0.197), (0.600, 0.105), (0.700, 0.053), (0.800, 0.026), (0.900, 0.013), (1.000, 0.000)
vaccine_dose_target = 3000000
vaccine_effectiveness = 0.9
Vaccine_Eligible = “fraction_16+” × Live_Population + vaccinate_12_to_15_switch
× STEP(“fraction_12–15”, 489) × Live_Population
vaccine_hesitancy_switch = 1
Vaccine_Ready = maximum_fraction_vaccinated × (Vaccine_Eligible − total_eligible_exposed)
vaccine_resources = RAMP(vaccine_dose_target/time_to_reach_target, vaccine_start,
vaccine_start + time_to_reach_target)
vaccine_start = 336
Graphical functions:
fear_effect_on_vaccinations: As fear increases, vaccinations fall.
holiday_season:
mutation_effect_on_death_rate: Later strains have higher death rates
mutation_effect_on_infection_rate: Later strains have higher infection rates
new_cases_effect_on_prophylactics: As perception of risk falls, use of prophylactics falls
new_cases_effect_on_quarantine: As perception of risk falls beyond a certain point, the effectiveness of quarantine diminishes
new_cases_effect_on_vaccinations: As perception of risk falls, the vaccination rate falls
summer_season:
vaccinated_effect_on_contact_rate: As more people are vaccinated, the contact rate increases
vaccination_effect_on_fear_reduction: As more people are vaccinated, the fear of the vaccine falls
vaccine_demand: As more people are vaccinated, demand falls off