1. Introduction
In 1976, the economist and historian Carlo M. Cipolla (1922–2000) wrote an essay titled “The Basic Laws of Human Stupidity”. Initially, it was only a pamphlet circulated among friends [
1], but later it was published as a book [
2]. Written in a tongue in cheek style, Cipolla’s text analyzed human behavior using a semiquantitative model in the form of two individuals (“agents”) interacting with each other in performing economic transaction involving gains and losses.
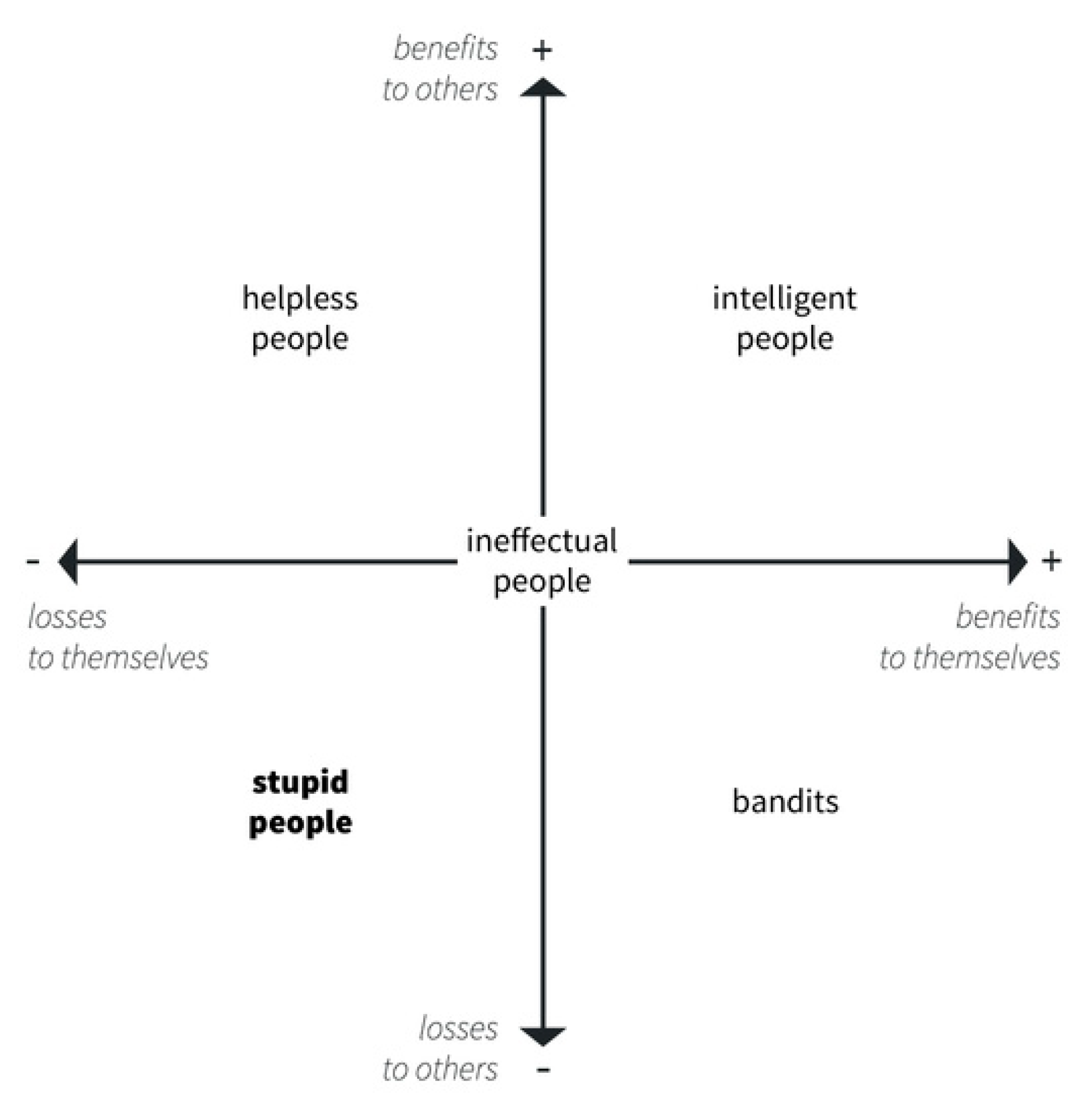
Cipolla reasoned in terms of the payoff of each transaction, arranging the possible outcomes in terms of a quadrant divided into four subsectors. One of the two agents may gain something at the expense of the other, but it may also happen that both agents profit from the exchange. The worst possible situation is the one in which they both lose something. The kind of agents who cause someone else’s loss while also damaging themselves in the process were labelled by Cipolla as “stupid people”.
From there, Cipolla went on to define the five “laws of stupidity” as (1) Always and inevitably everyone underestimates the number of stupid individuals in circulation. (2) The probability that a certain person will be stupid is independent of any other characteristic of that person. (3) A stupid person is a person who causes losses to another person or a group of persons while himself deriving no gain and even possibly incurring losses. (4) Nonstupid people always underestimate the damaging power of stupid individuals, and (5) a stupid person is the most dangerous type of person.
Today, Carlo Cipolla may be better known for his quadrant and the five laws, that he probably thought of as a joke, than for his academic papers. One of the reasons for this popularity is that these ideas make sense in terms of our everyday experience. Indeed, people do behave in stupid ways, and we often don’t understand why. An answer may come from mathematical models and, indeed, Cipolla’s ideas are related to fields of study, such as game theory, that also examine systems involving conflicting behavior among agents, a typical example being the “prisoner’s dilemma” [
3]. Cipolla’s model has been specifically modeled in terms of game theory [
4] and of agent based modelling [
5].
Here, we take a fresh look at Cipolla’s theory using an approach that goes in parallel with those used in other fields of the study of complex systems: we use the model known as “Lotka–Volterra” (LV), also known as the “predator–prey” or “foxes and rabbits” model [
6,
7]. This model is normally presented in textbooks as dealing with biological systems, but it has a wide range of applications. It is worth remembering that Volterra himself developed it not to study an ecosystem, but an economic system: the fisheries of the Adriatic Sea [
8]. Later on, the model was used extensively to describe economic systems by Goodwin, starting in 1965 [
9], although there may have been even earlier applications [
10]. More recently, the LV model has been applied to oil extraction [
11], the 19th century whaling industry [
12], and the production cycle of modern fisheries [
13,
14]. It is a versatile model: playing with the signs of the coefficients it can describe widely different behaviors, such as the attraction of Juliet and Romeo in Shakespeare’s play [
15].
Therefore, we believe it is possible to apply the LV model to the economic model developed by Cipolla. Our examination leads us to propose a “6th law of stupidity” based on equating Cipolla’s definition of “stupidity” with the human tendency to overexploit natural resources. Indeed, we may say that stupidity consists in overexploiting resources to the point of destroying them beyond repair. In this way, the agent damages him/herself, and everyone else in the process. Since humans perform that to an extent much larger than any known species in Earth’s biosphere, we believe that they may rightly deserve the title of “the stupidest species on Earth”.
2. Methods
Cipolla’s approach is illustrated by the quadrant shown in
Figure 1. The orthogonal axes refer to the two agents participating in an economic transaction: positive values indicate “gain”; negative values “loss”.
Typically, the
x−axis refers to the observer (you), while the
y−axis to the second agent (“the other person”). Starting with the top left quadrant, we have a situation in which helpless people damage themselves while providing an advantage to the other person. In the original paper by Carlo Cipolla [
1], the example involved selling an old and valueless pig to another person for a high price. The top right quadrant describes a deal that benefits both participants: you sell a good pig at an honest price to the other person. The bottom right quadrant is that of the bandits: you steal a pig from the other person or pay it much less than it is worth. Finally, the bottom left quadrant is the one dealing with stupidity, a phenomenon that occurs when someone’s action results in damage to both parties involved. In Cipolla’s original paper, stupidity was not illustrated with images of people selling or buying pigs, rather with someone who trips on a ladder causing the person who stands on it to fall, too. However, there are many more possible examples, some of which would still involve pigs. For instance, we might imagine someone who kills the owner of the pig to steal it, and then is arrested and sent to jail for life. In this case, we have a good illustration of how stupidity is related to the search for immediate gains without considering the consequences. This quadrant is the focus of Cipolla’s discussion.
The model can also be seen in wider terms, that is, not just describing monetary transactions in the economy. No economic process could take place without some energy being available and we may see the interactions among agents as involving an exchange of energy [
16]. In this case, the agents are not necessarily human beings, but may be individuals or populations of biological species involved in interactions with other species in the form of a trophic chain. More specifically, the economic process is a form of dissipation of energy potentials [
17]. In this sense, it is not different from most dynamic processes ongoing in the universe. A predator will increase its internal energy by absorbing some energy from the prey, just like an economic agent will increase its monetary stock by obtaining a profit from the transaction. This view is part of the general concept of “biophysics” that deals with dynamic complex systems.
The Lotka–Volterra (LV) model is possibly the simplest mathematical description of a complex system involving two populations: predators and prey, often referred to as “rabbits” and “foxes”. The two species form a two-stage trophic chain where metabolic energy is dissipated in steps: The first level (rabbits) acquires energy from a source supposed to be unlimited (grass). This energy is transferred to the second level (foxes) by the process of predation. Finally, energy is dissipated to the environment in the form of waste heat.
A characteristic of the LV system is the presence of “feedbacks” that govern the energy transfer rate, assumed to be proportional to the size of the stocks. Due to this feature, we can say that this system is autocatalytic. The more a stock grows, the more it draws energy from another stock or the environment, a behavior typical of biological populations. It is also typical of economic entities, such as companies and corporations.
There are several versions of the LV model, see ref. [
18] for a review. The most general form of the model is defined as “Generalized Lotka–Volterra” (GLV) by Solomon [
19]. For the purposes of the present paper, we can start with the simplest, two agent version, described by two coupled differential equations.
L1 represents the population of the first trophic level (the prey, or rabbits). L2 is the population of the second level (the predators, or foxes). a, b, and c are constant coefficients, η is an efficiency parameter that ranges from zero to one. In the standard version of the model, all these coefficients are positive. The interplay of the parameters in the LV model generates continuous oscillations in that the two populations tend to go through cycles of rapid growth and sudden collapses. This periodic behavior is driven by L1L2, originating major nonlinearities when either population become small while the other is large. This allows the minority population to recover and fosters the oscillations.
In a common variant of the model (the so-called “competitive” version) [
18], a further parameter is introduced: the carrying capacity of the system (
N). This parameter sets a limit to the maximum size that a population can reach. We write the equations of the competitive LV model assuming this limit affects only the
L1 (prey) population, while the predator population is effectively regulated by that of the prey:
This model generates a series of damped oscillations that lead the size of the stock to stabilize in a condition called “homeostasis”.
The similarity of the Lotka–Volterra model to Cipolla’s model is qualitatively evident: in a biologic system, the two levels of the trophic chain exchange metabolic energy under the effect of energy potentials. In Cipolla’s model, the agents exchange money or goods under what we may call a “financial potential”. Therefore, we can take the two LV levels as representing the two agents of the Cipolla model, with the levels of the stocks representing their wealth.
3. Results
Now, we need to describe how the LV model can be tuned to reproduce the characteristics of the interactions described by Cipolla. We will examine each quadrant separately.
3.1. First and Third Quadrants: Bandits and Their Helpless Victims
The two diagonally opposite quadrants of Cipolla’s model, those labelled “Helpless”, and “Bandits”, are the same except for their different viewpoints. In both cases, we have a prey/predator interaction, with the bandit as the predator and the victim as the prey. This interaction is well described by the standard LV model with
L1 corresponding to the victim and
L2 to the bandit. The figure below shows how the system evolves in time according to the LV equations, solved iteratively. In the figure, the y−scale represents the level of the stocks and it can be seen as a measure of the monetary wealth of the agents: bandits and victims (
Figure 2).
A qualitative interpretation of these results is that the bandits build up their wealth by depredating (or swindling) their helpless victims, until the victims are so impoverished that the bandits do not make any more a profit by attacking them. That forces the bandits to reduce their activity. At this point, the victims have a chance to rebuild their assets and become again interesting targets for robbery. In more detail, the model tells us that the bandits operate at a certain cost. Just like predators need metabolic energy to outrun their prey, bandits need capital investments in the form of weapons, equipment, transportation, and more. If robberies do not provide a sufficient profit, this capital falls to depreciation.
From the equations of the model, we can say that banditry will be profitable if
dL2/dt > 0. This condition implies
ηbL1/c > 1. This expression is the ROI, the return on the investment in robbery. In a biophysical system, this parameter is called EROI or EROEI (energy return on energy invested) [
20]. According to Cipolla, a “perfect” bandit is one whose gains exactly equals the loss of the victim, but this is not possible in the real world because of the limits set by the laws of thermodynamics (
η must be smaller than 1). Nevertheless, bandits will normally try to maximize their ROI/EROI by being as efficient as possible (
η close to 1). They may also try to decrease the value of the
c coefficient, decreasing the cost of banditry. Another possible strategy for them is to increase the value of the
b coefficient, increasing the intensity of their robbing activity. Note that the formula implies that the return on investment of the bandits is proportional to that of their victims. That agrees with the common wisdom that bandits should always rob rich people (something that Robin Hood understood without the need for mathematical models).
These attempts will not eliminate the oscillations of the systems, although they may change the height of the peaks.
3.2. Second Quadrant: Intelligent Agents
This quadrant, in Cipolla’s model, represents a condition in which both actors involved in a transaction gain something. In a biological system, it describes the condition known as a symbiosis: two species that form an alliance that benefits both in the sense that they both gain some energy. Symbiotic systems are well known in biology, a classic example is the gut microbiota of human beings that receives food from the human organism and helps it to digest it. This system is described by Lynn Margulis using the term “holobiont” [
21].
Holobionts are normally understood as the result of an evolutionary process of adaptation. It may well be that a competitive predator/prey interaction evolves into a symbiosis after many cycles of destructive interactions where the two species gradually “learn” how to respect each other and the physical limits of the system. This phenomenon can be described using the term “evolution”, although not intended strictly in the sense of a change in genetic code generated by natural selection. As argued by Margulis and others, symbiotic evolution may simply be behavioral, or involve an adaptation in the relative sizes of the populations involved.
The competitive version of the Lotka–Volterra model describes this kind of evolution by incorporating the limits of the system, that is, taking into account the maximum size of at least one of the stocks (the “carrying capacity” of the system). The result is that the system converges (or “evolves”) to a well defined attractor in the form of two specific values of the stocks. N is a “memory element” that tells the system how to control itself. Evidently, in real ecosystems, there are physical signals that regulate the growth of both stocks. For instance, rabbits face a dearth of grass that prevents them from growing exponentially even in the absence of foxes. However, that is not the only way to transfer this information to the system and we may imagine intelligent agents who can plan and try to optimize the system even before growth is reined in by physical limitations. In the evolutionary game, these agents would be favored in the long run because they could avoid the crash that follows excessive growth that might bring competitors to extinction.
These considerations provide a justification to the idea of using the competitive Lotka–Volterra model to describe the Cipolla quadrant dealing with intelligent people, whom we may see as able to adapt (evolve) to a condition of symbiosis. We may imagine intelligent bandits who understand that overexploiting their victims is not a good thing. Limiting exploitation activity could also be the result, for instance, of progressive taxation or of the government introducing quotas or other balancing factors in the exploitation of natural resources—again, actions performed by intelligent agents. Once this assumption is inserted in the equations of the model in the form of a finite carrying capacity, we see that the agents/populations tend to reach a condition of homeostasis in terms of stable wealth (
Figure 3).
The initial oscillations reflect an initial phase of reciprocal adaptation. Then, an intelligent buyer and an intelligent seller will agree on a price that benefits both. In this system, there holds the same condition as for the bandits/helpless people (predators/prey) quadrants. That is, the ROI/EROI of the transaction, ηbL1/c, is equal to 1 in homeostatic conditions. In this case, we have that dL1/dt = 0. The consequence is that L2 = a(1 − a/N)/b. The symbionts involved in the energy exchange should try to maximize this expression, which involves a = N/2, that is L2 = N/4b. Since we can express b as a function of L1, we can obtain a relation between L1 and L2 at homeostasis. The result is L2 = ηNL1/4c, which indicates the requirements to maximize the efficiency of symbiosis.
3.3. Fourth Quadrant: Stupid People
In a biological system, the equivalent of stupidity, according to Cipolla’s definition, implies that the parasites/predators destroy their host/prey. In biology, “parasitoids” are defined as parasites that kill their host. However, normally, parasitoids are not stupid: killing the host is part of a strategy that involves moving to another host. Nevertheless, some parasites/predators can operate against their own survival and destroy themselves by killing their host/prey. This kind of behavior is rare in an ecosystem, but it is well known that viruses and bacteria can kill their hosts. An example of stupidity involving vertebrates is the story of Matthew Island in the Northern Pacific Ocean, where a small number of reindeers were introduced by humans in 1944 [
22]. Over about two decades, the reindeer grew in numbers, destroyed their sources of food, lichen and grass, and went extinct as a result. You may argue that the reindeer were not “stupid”, it was rather the humans who introduced them to the island who were stupid. However, this is exactly the point made by Cipolla! In terms of large-scale human stupidity, that is not just limited to two agents, we have plenty of examples, from the destruction of the American bison, to the overfishing of many fish stocks [
13]. In general, these phenomena can be seen in terms of the “Tragedy of the Commons” described by Garrett Hardin [
23]. As interpreted by Hardin, the “tragedy” does not involve individual stupidity, but a collective phenomenon in which each agent acts intelligently in order to maximize his/her individual gains, but where the result is the collapse of the whole economic system.
In terms of the Cipolla quadrant, since the LV model assumes a continuous function for the values of the stocks, they can never go to zero. Therefore, strictly speaking, the model cannot simulate extinction or complete extermination of the prey. This problem is referred to, sometimes, as the “nanorabbits” or “nanofoxes” problem: as long as all the four coefficients of the model are larger than zero, extinction can never take place.
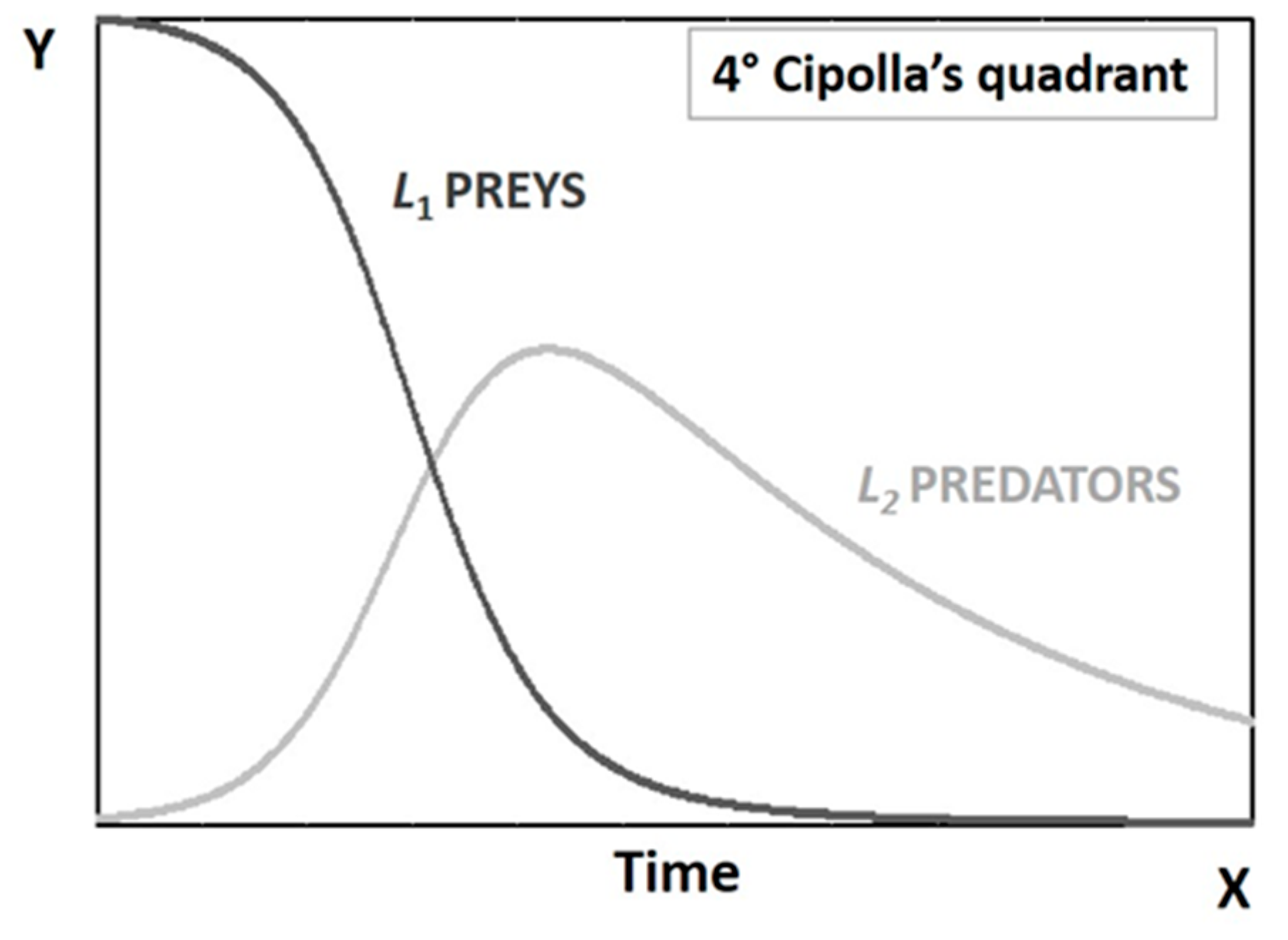
Nevertheless, the first coefficient (
a), the one that describes the reproduction rate of the prey, may be small enough that a new cycle of exploitation is not observed during the time lapse of the simulation. At the limit, we can assume that
a = 0 without losing the generality of the model. For instance, when considering the exploitation of fossil fuels, the time needed for the prey (fuels) to reproduce is of the order of millions of years, so we can effectively set the reproduction coefficient to zero. This situation is shown in the
Figure 4.
In the case of economic agents, stupid people do not optimize the system they exploit, they rather tend to destroy it. In this sense, stupid people behave like bandits, but bandits can survive a crash in their revenues by leaving to their victims sufficient resources to rebuild their wealth. Instead, stupid people completely destroy their sources of revenue, ruining themselves as well. This behavior is equivalent to Cipolla’s definition of stupidity.
There are several examples of this behavior in the history of economics, not just for the case of resources that are considered as “nonrenewable” (e.g., fossil fuels): one is the case of the mining industry which is exploiting resources that will need at least hundreds of thousands of years to reform by geological process if they ever will. It is also the case of industries that exploit slowly reproducing biological resources. A modern example is that of whaling, as demonstrated in previous papers [
12]. The same resource destruction also occurs for other cases of fisheries [
14]. Humans do not seem to need modern tools to destroy the resources they exploit, as shown by the extinction of the Earth’s megafauna [
24], at least in part the result of human actions performed using tools not more sophisticated than stone tipped spears. Overall, the destruction of the resources that enable people to live seems to be much more common than in the case of any other biological species in the natural ecosystem. We believe that this observation justifies the proposed “sixth law of stupidity”, in addition to the five proposed by Carlo Cipolla, that states that “humans are the stupidest species in the ecosphere”.
4. Discussion
Cipolla’s quadrant highlights several fundamental features of those systems that can be described as both “complex” and “autocatalytic”, where the growth rate is proportional to the size of the stocks. These systems include living creatures, biomes, entire ecosystems, as well as human created entities, such as companies, organizations, and entire economic systems.
The analysis of Cipolla’s quadrant carried out using the Lotka–Volterra model shows the substantial unitarity of many phenomena driven by the dissipation of energy potentials: from life to commerce. There are, indeed, some basic laws at work in these systems and when we use the term “law” for a physical system we mean that some factors are at work to keep it, if not perfectly regulated, at least within some boundaries.
Cipolla’s quadrant tells us that these complex systems are all dominated by the same factors but that these factors can operate in different ways. The simplest case is the predator/prey (bandit/victim) relationship, in which the predator seeks only maximum short-term profit. The result is periodical oscillations, and the system never stabilizes. That is, for instance, a typical behavior of financial markets.
This phenomenon is especially destructive with resources that can be renewed only slowly or cannot be renewed at all in times of interest for human beings. This is the case, for instance, for fish stocks (slowly renewable) and fossil fuels (nonrenewable). The result is the dreary phenomenon of “overexploitation” which we propose is the main element that describes human stupidity when the actions of one of the actors in the exchanges lead to doom for everyone and everything. In ecosystems, it is extinction; in economic systems, it is bankruptcy.
The analysis also shows the possibility for these systems to adjust in such a way to attain the condition that Cipolla describes as “intelligent people” and that in ecosystems goes under the name of “symbiosis”. As proposed by Lynn Margulis [
25], symbiotic systems that operate under the name of “holobionts” are the basic unit of the ecosystem. We may extend this definition to all kinds of autocatalytic complex systems, including those forming the human economy.
But if holobionts are an efficient unit of energy dissipation, why does stupidity exist? In particular, why is it so common in the economy? Cipolla’s explanation is that,
“Some are stupid and others are not, and that difference is determined by nature and not by cultural forces or factors. One is stupid in the same way one is red-haired; one belongs to the stupid set as one belongs to a blood group. A stupid man is born a stupid man by an act of Providence.”
What Cipolla calls “an act of Providence” may also be seen as the result of the genetic setup of human beings. Indeed, humans are a relatively recent element of the ecosystem: modern humans are believed to have appeared only some 300,000 years ago, although other hominins practicing the same lifestyle may be as old as a few million years. Yet, this is a young age in comparison to that of most species currently existing in the ecosphere.
Therefore, humankind’s stupidity may be not much more than an effect of the relative immaturity of our species which still has to learn how to live in harmony with the ecosystem. That explains what we called here “the sixth law of stupidity”, stating that humans are the stupidest species on Earth. It is a condition that may lead the human species to extinction, although it is also possible that, if they survive, one day they will learn how to interact with the ecosystem without destroying it.
5. Conclusions
In his essay of 1976 [
1], the economic historian Carlo Cipolla evaluated the degree of human stupidity in terms of a qualitative model of the relationship between benefits and losses that an individual causes to him or herself and benefits and losses caused to others. Inspired by Cipolla’s approach, the authors show that such a theory helps not only in describing the interaction dynamic between humans beings, but also the less or more virtuous attitude of humans toward the exploitation of ecosystem resources. The authors also show that both the original humans–humans and the extended humans–resources relationship laws operate according to a dynamical archetype represented by the Lotka–Volterra model, better known as the prey–predator model. From this extended interpretation, the authors define an additional law, which states that “humans are the stupidest species on Earth” because of their tendence of overexploiting, and eventually destroying, the resources that make them live. This statement should not be taken as pessimistic, it simply reflects the fact that humans are among the most recent creatures on the planet. Our results show that intelligence and stupidity may be two sides of the same coin and that humankind may still learn to live in harmony with the ecosystem.