Comparing Equation-Based and Agent-Based Data Generation Methods for Early Warning Signal Analysis

Abstract

Dynamical systems are known to exhibit sudden state transitions, with abrupt shifts from one stable state to another. Such transitions are widely observed, with examples ranging from abrupt extinctions of species in ecosystems to unexpected financial crises in the economy or sudden changes in medical conditions. Statistical methods known as early warning signals (EWSs) are used to predict these transitions. In most studies to date, EWSs have been tested on data generated using equation-based methods that represent a system’s aggregate state and thus show limitations in considering the interactions of a system at the component level. Agent-based models offer an alternative without these limitations. This study compares the performance of EWSs when applied to data from an equation-based and from an agent-based version of the Ising model. The results provide a reason to consider agent-based modelling a promising complementary method for investigating the predictability of state changes with EWSs.

1. Introduction

Many complex dynamical systems exhibit critical transitions, where states shift abruptly from one stable equilibrium to another [1,2]. These transitions have been studied extensively both in theory [3] and in practice [2]. Real-world examples include the abrupt extinction of species in ecosystems [4,5], the collapse of financial markets into a state of crisis [6], sudden changes in medical conditions such as asthma attacks or epileptic seizures [7,8] and rapid changes in climate and oceanic systems [2,9,10]. Given that many such systems undergo sudden and potentially irreversible transitions to detrimental states, it is important to anticipate their tipping points. With this intention, a set of statistical tools known as early warning signals (EWSs) has been compiled that enables the detection of an impending transition in time. In recent years, research on this topic has intensified, and various metrics have been proposed that qualify as EWSs. Many studies have been devoted to testing and comparing the signals themselves as well as testing and comparing data pre-processing methods to further improve signal performance [11,12,13]. The majority of these studies, however, use equation-based models (EBMs) to generate data for signal testing (further examples: [11,14,15,16]).

This seems somewhat at odds, since equation-based models replicate a system’s aggregate behaviour on a macro level, which expresses the system’s particularities in terms of a mean-field approximation, which is a rather coarse statistical abstraction. It does not consider the system’s actual drivers in detail, particularly the interactions at the system’s component or micro level. Furthermore, the natural fluctuations of these systems are simulated by introducing noise to the equation variables, often without an elaborate concept of what kind of noise is representative (e.g., normally, binomially or uniformly distributed, etc.). This may load the simulation with unjustified estimates. Considering that systems are virtually defined by the fact that they emerge from bottom-up interactions, the focus of EWS research on equation-based methods seems inadequate.

Agent-based models (ABMs) could provide an alternative [17,18] or at least a complementary method [19,20,21]. ABMs focus on defining a minimal ruleset for the system’s components, which allows the particular behaviour of the system (its “eigen-behaviour”) to emerge bottom-up in self-organization. This impacts the way the system’s fluctuations are represented: it is true that not all stochastics in ABMs are always well-justified (such as agent updating or setup positioning, etc.). However, in EBMs, which build on deterministic mathematical means, stochastic aspects must be introduced manually, while in ABMs, fluctuations arise from the interactions of (actually simulated) components, which are core aspects in this type of modelling. Thus, in ABMs, fluctuations are a sort of operating condition. Since it is exactly these fluctuations that are necessary for EWSs to detect a transition, it seems reasonable to investigate whether the modelling approach used for generating test data impacts the performance of EWSs.

This study examined such possible performance differences. The paper is organized as follows: Section 2 introduces the system as used in this study as well as equation-based and agent-based representations for two of its bifurcation types. Section 3 explains details of the data generation and time series comparison. Section 4 introduces the statistical tools used for the EWS analysis. Section 5 shows the results of the analysis. Section 6 discusses the gained insights and some limitations of the study. Section 7 finally summarizes the paper.

2. System Used for Data Generation

To enable comparability across the modelling approaches, this study focused on a system that is known to show topologically equivalent characteristics around the bifurcation points when modelled with EBM and with ABM methods. The Ising model of ferromagnetism [22,23,24] is one such system that is commonly modelled in an equation-based (so-called 1D) EBM version and in a 2D-grid version as an ABM [25]. The system represents the magnetic dipole moments of atomic spins as points on a lattice, which can be in one of two states (+1 or −1), dependent on the ambient temperature T and energy, which is defined as the negative of the sum of the products of a spin with each of its four neighbouring spins. Spins are seeking a low-energy state, causing them to flip, depending on the potential gain in energy, which determines the flipping probability. Consequently, as the temperature increases, flipping to a higher-energy state becomes increasingly likely, but as the energy to be gained by flipping increases, the likelihood of flipping decreases.

As a simplified model of particle behaviour in magnetic metals, the system allows for the identification of phase transitions and is therefore also often used to model social phenomena such as opinion changes [26] or the spreading of rumours [27]. It is known to exhibit a (symmetric) supercritical pitchfork bifurcation at a critical temperature value. By adding an external magnetic field while fixing the temperature well below the bifurcation point, it can also be locked into a bi-stable region with two stable states and one unstable state, thus generating a combined saddle-node bifurcation showing hysteresis by varying the external field. Both possibilities were used in EBM as well as in ABM mode to generate a large number of time series in the onset of critical transitions in order to expose them to EWS analysis (see

Table 1. Overview of model selection for the pitchfork and the hysteresis system.

	Agent-Based Model	Equation-Based Model
Pitchfork system	2D Ising model without external field	Mean-field approximation of 2D Ising model without external field
Hysteresis system	2D Ising model with external field	Mean-field approximation of 2D Ising model with external field

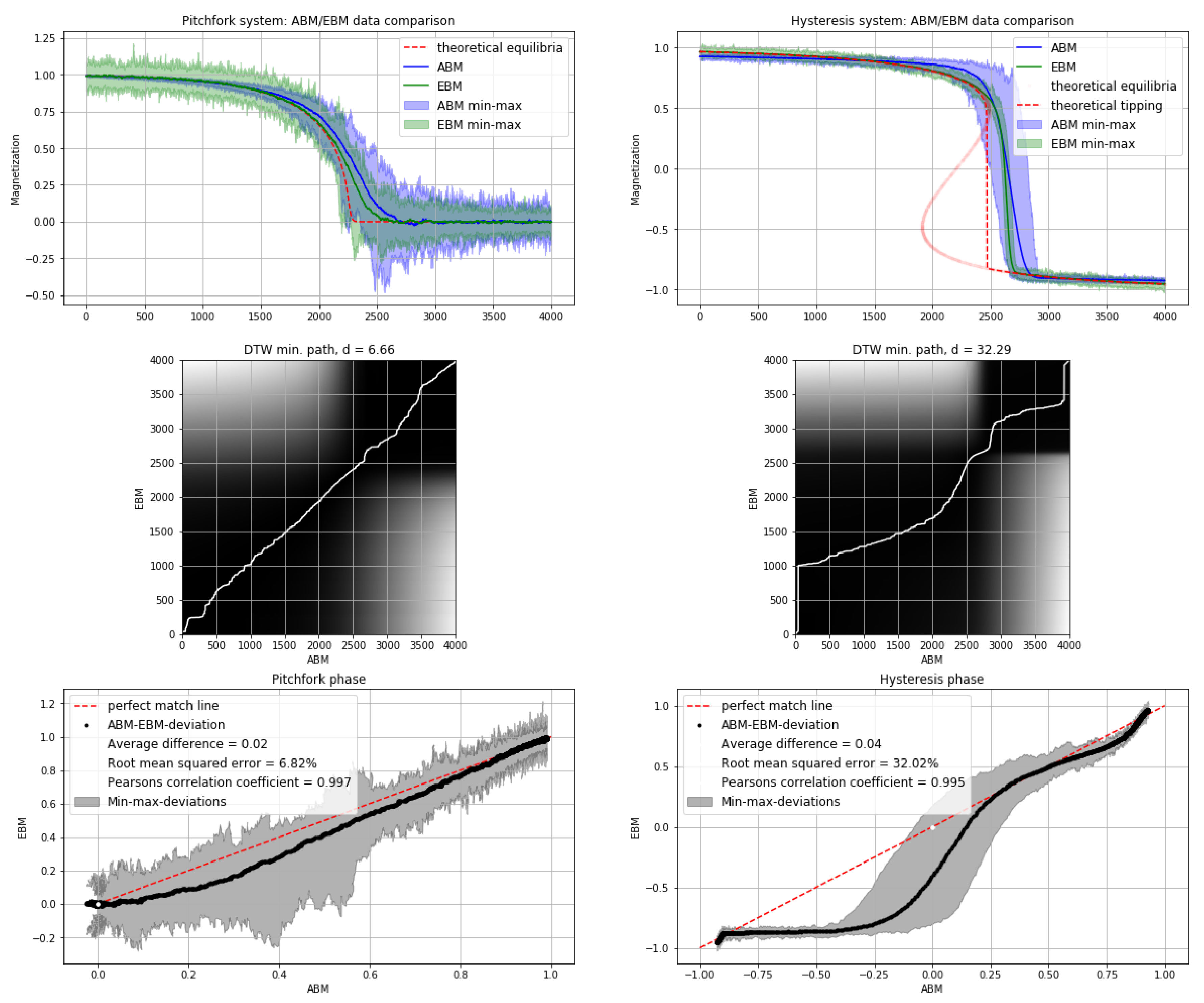
below for an overview and Figure 1 for a comparison).

2.1. Pitchfork System

To generate agent-based test data for the pitchfork system, we used a spatial simulation of the 2D Ising model (see Appendix A). In this case, the system’s temperature T was taken as the critical parameter, which when varied across a certain parameter space generated a pitchfork bifurcation, causing mildly abrupt phase transitions in the system’s magnetization M, which is defined as the average spin of all the spins on the lattice. The model was actuated using the Metropolis algorithm (adapted from [23,28,29]).

To generate equation-based test data, the following difference equation was used as a mean-field approximation of the 2D Ising model (see [23,24]):

$$M_{t+1}=(-M_t+tanh(B·M_t))·∆t+p·N$$

(1)

where M is the system’s state or magnetization at a specific point in time, ∆t is the size of the time step and B is the inverse temperature and also the critical parameter. Variability was added using a standard normal distribution N, where the distribution’s weight is controlled by the parameter p. As mentioned, the selection of this addition was critical since it is rarely well justified. In this case, we oriented to [30], according to whom most physical systems have a limited amount of available energy per time step, i.e., a power limitation. This is equivalent to a limit on the variance of a quantity that can best be modelled with a normal distribution, thus justifying this choice.

2.2. Hysteresis System

To generate the agent-based test data for the hysteresis system, we slightly adapted the Ising model by adding an external magnetic field H, while fixing the temperature well below the bifurcation point (see Appendix A). This locked the system in a bi-stable region with two stable states and one unstable state. The variation of the external field then allowed for the desired hysteresis effect. Depending on the direction of the additional field, this can create a pull or push towards one of the stable states. If the field is strong enough, it will cause the system to shift from its current stable state to the alternative one.

To generate the equation-based test data for the hysteresis system, the following difference equation with an added external magnetic field was used (see [23,24]):

$$M_{t+1}=(-M_t+tanh(B·(M_t+H)))·∆t+p·N$$

(2)

where M is the system’s state or magnetization at a specific point in time, ∆t the size of the time step, B the inverse temperature, and H the external magnetic field and also the critical parameter. Variability was added using a standard normal distribution N, where the distribution’s weight is controlled by the parameter p.

3. Data Generation and Comparison

To generate data for the EWS analysis, 100 time series were generated for each model and for each bifurcation type, all of which showed the respective state transition. Every simulated time series consisted of 5000 time steps, of which the first 1000 time steps were discarded to remove the initial transient to the starting equilibrium. The bifurcation’s characteristic transition was generated by linearly decreasing the critical parameter (the temperature for the pitchfork system and external magnetic field for the hysteresis system) across its bifurcation point, so that in each timestep, the critical parameter was incrementally increased/decreased along evenly spaced numbers over an interval [a, b]. The dynamics of each simulation run were slightly altered by varying the model parameters to increase the overall sample variety. The considered parameter ranges are summarized in

Table 2. Parameter ranges for the equation-based and agent-based pitchfork models.

Agent-Based Pitchfork Model		Equation-Based Pitchfork Model
Temperature T (critical parameter)	Over [1.42, 3.12]	Inverse temp. B (critical parameter)	Over [2.7, −0.3]
Lattice size N	50 < N < 100	Time step ∆t	0.1
		Weight of normal distribution p	0.01 < p < 0.02

and

Table 3. Parameter ranges for the equation-based and agent-based hysteresis models.

Agent-Based Pitchfork Model		Equation-Based Pitchfork Model
External field H (critical parameter)	Over [−0.2, 0.2]	External field H (critical parameter)	Over [0.6, −0.5]
Lattice size N	50 < N < 100	Time step ∆t	0.1
Temperature T	2.12	Inverse temp. B	1.3
		Weight of normal distribution p	0.004 < p < 0.008

, which together with the analytical data comparison (see Figure 1) were used to uniformly and randomly select combinations of parameter values for each simulation run.

As the ABM and EBM exhibit the desired behaviour in different parameter ranges, the data had to be equated, which was performed with respect to the theoretical equilibria of the systems following arguments of topological equivalence [23,24,31]. In order to maximize the comparability, the model parameters were tweaked in this regard, with the problem that the core model parameters (the temperature T, external magnetic field H and lattice size N in the case of the ABM, and the inverse temperature B, external magnetic field H, step size Δt and weight of the standard normal distribution p in the case of the EBM) differ in number and quality and are therefore not directly comparable. Additionally, the system’s reaction time to perturbations is governed by the parameter Δt in the EBM case, whereas in the ABM case, it is, in a sense, naturally built in. Therefore, efforts with respect to the comparability remained limited to fitting the macroscopic trend and the bandwidth of all the data samples, which was performed on the basis of an extensive analysis, considering a range of indicators typically applied to time series comparisons [32]. Figure 1 (the second and bottom row plots) shows the results for the average difference, the root mean squared error, Pearson’s correlation coefficient (r) and dynamic time warping [33].

4. Early Warning Signal Analysis

Early warning signals build on the premise that a system close to a sudden state transition shows different behaviour from a system further away [12]. More specifically, early warning signals exploit the fact that a system’s stability landscape changes as it approaches a bifurcation [2]. Considering that the stability landscape also determines how the system behaves when it is out of equilibrium, we can search for changes in the system’s fluctuations around its stable states to gain information about the proximity of a bifurcation and, thus, a possible state transition [2].

For the EWS analysis, a set of commonly used indicators was applied to the generated time series to forecast the imminent regime shift in the system’s dynamics. Most of these EWS indicators build on a phenomenon known as “critical slowing down” (CSD). CSD implies that systems near a tipping point take longer to recover from perturbations than those at distances further from the tipping point.

The system experiences a loss of resilience, which slows down the return to the stable state before perturbation [34]. CSD shows in the statistical properties of the time series from a system’s dynamics taken at various states of equilibrium. An increase in autocorrelation at lag = 1 (AC-1), for example, indicates a higher “short-term memory” for the system, related to changes in the correlation structure close to a tipping point [11]. Additionally, the standard deviation (STD) and its trend-independent pendant, the coefficient of variation (CV), can increase before a critical transition, caused by the system’s tendency to move further away from its stable state when losing stability. Moreover, the proximity to an alternative equilibrium and the resulting attraction can cause so-called flickering, that is, asymmetries in variance and the occurrence of short jumps to states further away from the stable state and back. These effects show in changes in the skewness (S) and kurtosis (K) of the analysed time series. Serial correlations between successive time samples can also induce changes in the spectral density, so-called reddening (R), measured by spectral analysis. Finally, correlations over timescales longer than those detectable with AC-1 can be measured by detrended fluctuation analysis (DFA) [35]. In order to minimize the possibility of false positives [12] and to make data more comparable across different modelling approaches, time series were considered in their original form as well as in a detrended form, using moving averages of window size 10 to remove their global trend.

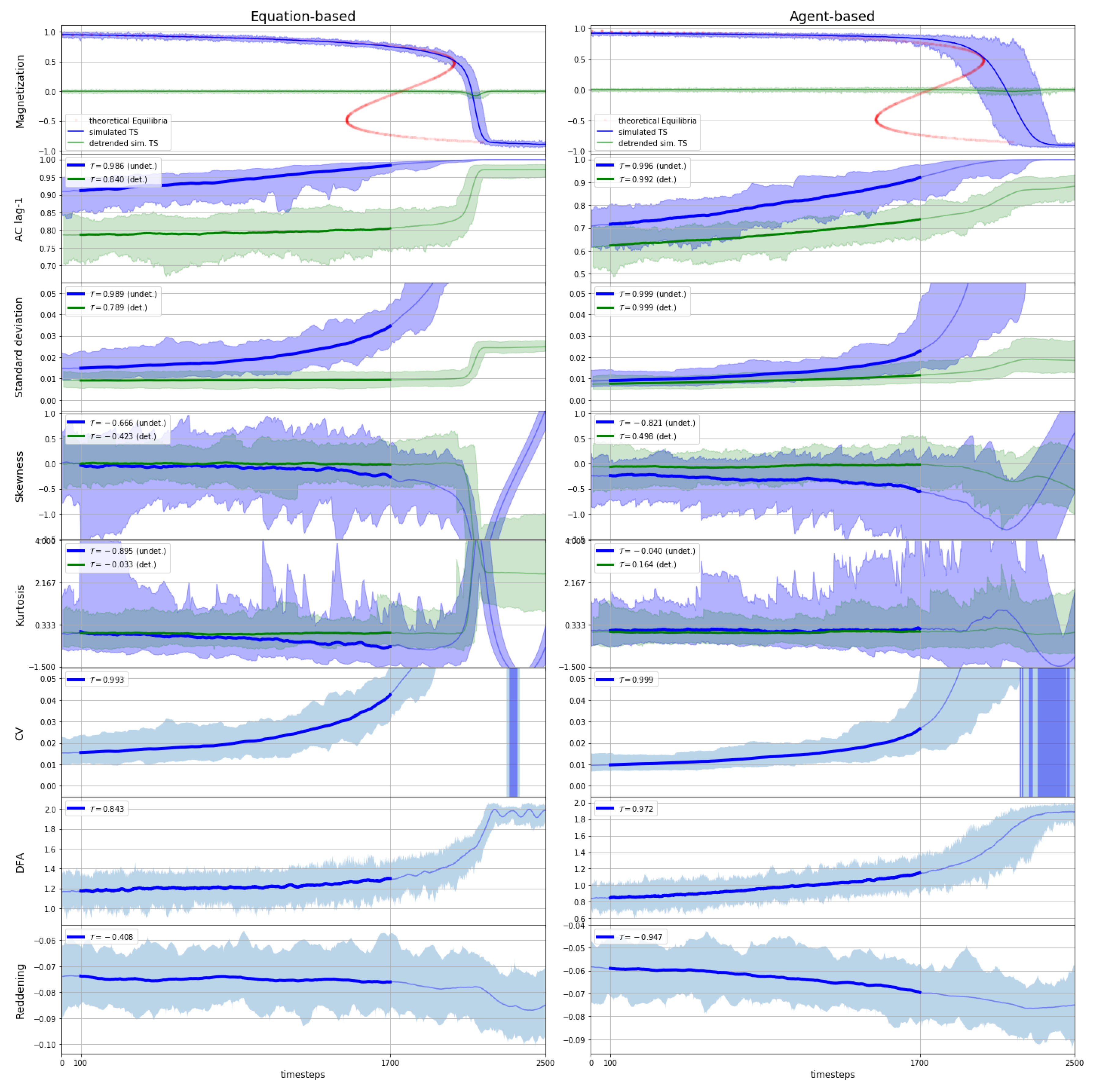
The above-mentioned EWS indicators were applied to the time series while sweeping over the considered parameter ranges (see Table 2 and Table 3) in rolling windows of size 500. For the obtained signals, the mean as well as the maximum and minimum was calculated (see Figure 2 and Figure 3). Additionally, the overall performance of a signal time series was evaluated using Kendall’s rank correlation coefficient τ ([36,37]), following suggestions by [11,38] (the insets in Figure 2 and Figure 3 show the averages of τ of 100 time series in each case). The Kendall’s τ coefficients were calculated over 1600 time steps, starting at time step 100 and stopping some distance before the actual tipping at time step 1700. Note that Kendall’s τ coefficient is a correlation measure for ordinal data. This means that it is a useful measure for determining the overall distinctiveness of an increasing or decreasing trend. It does not, however, take the steepness of the signal into account. It is also incapable of differentiating between linear and higher-order trends. As a result, it is possible to obtain a rather low τ value on a visually steep signal and vice versa.

A positive EWS and thus an indication of an imminent critical transition can be expected when the AC-1, STD, CV and DFA clearly increase; R decreases; and S and K either increase or decrease. In many studies to date, the approach of tipping is diagnosed when at least two of these indicators show the expected behaviour.

5. Results

5.1. Pitchfork System

As can be seen in Figure 2, the results of the EWS analysis applied to un-detrended as well as to detrended pitchfork data can be regarded as meeting the expectations. All the indicators show more-or-less clear indications of imminent tipping, maybe with the exception of S and K when applied to the detrended data. In most cases, however, the ABM data seem to trigger slightly more decisive signals, with Kendall’s tau values often equal or close to 1 (or −1 in the case of R), indicating a strong correlation with respect to the expected trend.

5.2. Hysteresis System

Figure 3 shows the results of the EWS EBM/ABM comparison applied to un-detrended and detrended hysteresis data. Again, the results can be regarded as meeting expectations. The EWS indicators allow for an anticipation of imminent tipping, maybe again with the exception of kurtosis on detrended data. In most cases, the signals derived from the ABM data seem to indicate the approach of a critical transition more clearly.

6. Discussion and Limitations

The results show differences in EWS performance between the ABM and EBM modelling paradigms. Specifically, the EWS analysis showed more distinct signals for the data generated by the ABM. This suggests that the ABM should be used as a complementary method to investigate EWS analysis, despite the fact that most EWS studies to date have used the EBM as the preferred method. Since EWSs are ultimately meant to be applied to real data in order to prepare for or to prevent unwanted regime shifts, it makes sense to assess their performance on the most appropriate means available. Our results provide a reason to consider the ABM among these means and to further extend EWS research in this direction, for example, to consider systems for data generation, where component interaction is analytically represented in the form of networks (see [17]) and thus allows for higher resolution in regard to social details.

It should, however, be emphasized that this recommendation for the ABM is not directly based on the fact that the EWS analysis produced clearer signals for the ABM-generated data than for the EBM-generated data. It arises from the fact that the EWS analysis showed different results for modelling approaches that attempted to essentially model the same system type or bifurcation.

The results in this study were obtained from the very basic structure of an abstracted particle interaction process as represented by the Ising model. Considering the limited scope of this model, it is clear that our results need further confirmation. Additionally, the procedure by which the ABM and EBM data were equated offers room for improvement. Despite the assumption of the topological equivalence of the two-dimensional Ising model’s mean-field approximation, the model’s parameters needed to be tweaked to some extent to achieve similar time series data. Due to this tweaking, the stability landscape across the modelling approaches may not be exactly the same, thus impacting the performance of the indicators tested on it. Limitations also arise from the comparability of the parameters. The agent-based model includes three core parameters: the temperature T, the external magnetic field H and the lattice size N. The equation-based model holds five core parameters: the inverse temperature B, external magnetic field H, step size Δt and weight of the standard normal distribution p. Consequently, it is not possible to equate the model parameters or to relate the parameter ranges in all regards. Efforts were thus limited to fitting the macroscopic trend and the bandwidth of the data samples and trying to optimize the comparability statistically. For future work, these limitations and uncertainties, particularly with regard to the comparability of models, must be addressed. To further confirm the perceived tendency of better signal performance on agent-based data, the results need to be backed up by testing additional models.

7. Summary

The objective of this study was to assess the performance differences of statistical indicators for predicting critical transitions in complex systems, which have recently been encompassed by the term early warning signals, when applied to time series data generated by agent-based and by equation-based methods. Two different bifurcation types relevant to many ecological systems were considered and simulated with an equation-based and an agent-based version of the well-known Ising model, thus generating a large set of time series data, which was applied to EWS analysis. The results show differences in most EWS indicators when applied to agent-based generated data, suggesting that the modelling approach, even among comparable models, impacts signal performance. Regarding the methodology, the results have to be considered against the background of the difficulties in aligning the models, where efforts remained limited to achieving topologically equivalent behaviour, but not parameter equality. Future work will need to test more and different systems and refine the possibilities for making the model data comparable.