1. Introduction
System dynamics (SD) is a modeling and simulation approach with wide ranging applications in various disciplines such as management [
1], constructions [
2] and agriculture [
3]. The need to improve efficiencies in the model building process and to deal with the explosion of data have already been acknowledged in the SD literature [
4,
5,
6]. Several opportunities exist for recent advances in computational intelligence (CI) and machine learning techniques to be leveraged to support and improve the model building process. Although such techniques do not replace human cognition, they do alleviate some of the tedious tasks, such as data analysis, knowledge extraction, model calibration and model validation. This may lead to significant improvements in saving resources, dealing with large amounts of data and exploring large model spaces. The use of data driven approaches, specifically the CI methods, in SD modeling is not entirely new. In recent years, several studies have reported on the application of CI methods to SD modeling. Salient examples of such works include: the use of fuzzy logic (FL) for knowledge acquisition and representation [
7] and identification of key system variables [
8]; the application of echo state networks (ESNs) [
9] and evolutionary echo state networks [
10,
11] for generating causal loop diagrams (CLDs); the use of a hybrid approach combining recurrent neural networks (RNNs) and genetic algorithms (GA) for generating stock and flow diagrams (SFDs) as well as for parameter estimation [
12]; the application of genetic programming (GP) [
13,
14,
15] and a hybrid of feed forward neural networks (FFNNs) and GA [
16] for generating model equations and parameter estimation; the application of GA [
17], fuzzy multiple objective programming (FMOP) [
18] and bootstrapping methods [
19] for parameter estimation; the application of particle swarm optimization (PSO) [
20], grammatical evolution (GE) [
21], simulated annealing (SA) [
22], decision trees [
23] and differential games [
24] for policy optimization; and the use of GA [
25,
26] and FL [
27] for model validation and testing. A clear trend that can be observed from the above works is that the application of CI methods has been limited to specific stages of the model building process, with greater attention paid to model parameter estimation and policy optimization stages. Furthermore, the application of these methods to generate conceptual and formal models (often represented by CLDs and SDFs, respectively) or the underlying mathematical equations is rare.
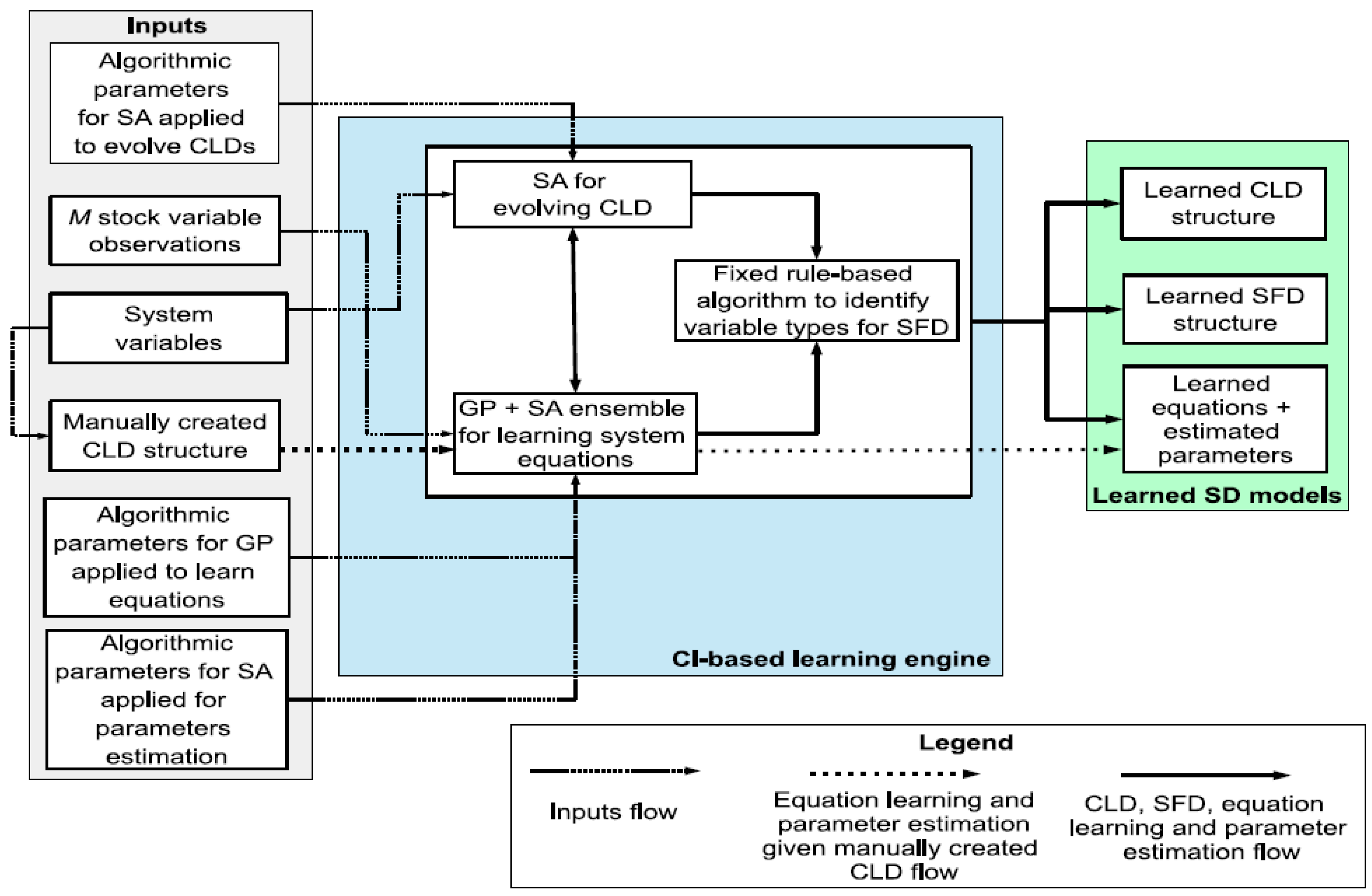
This paper presents our progress towards developing an integrated CI-based, SD modeling support system to facilitate modelers through the model building stages. In particular, the learning engine of the support system builds upon several CI techniques, namely Cartesian genetic programming (CGP), GP ensemble learning, standard SA and fixed rule-based heuristics, to support the building of system CLDs, SFDs, equations and calibration of the model. A prototype of the proposed support system is provided as an easy to use executable tool. The tool provides a graphical user interface to feed data into the learning engine and to visually present the automatically inferred models. The minimum required knowledge that needs to be present before starting the automated modeling effort includes: the list of key variables, identification of stock variables, time series data capturing system observations for the stock variables, and the parameter settings of different CI methods.
Genetic programming (GP) is a population-based evolutionary algorithm, representing individual solutions as programs instead of a string of bits, as in a genetic algorithm (GA) [
28], in which the evolving structures are represented as hierarchical trees. GP uses notions of functional (
F) and terminal (
T) sets to represent and evolve such structures, where all internal nodes are elements of
F and all leaf nodes are elements of
T. The generation of the initial population in a typical GP algorithm could be created in three different ways according to Koza [
28]: full method, grow method and ramped half-and-half. Similar to other evolutionary algorithms, GP evolves the structures using selection, crossover, and mutation operators. The selection mechanisms most commonly used include tournament and roulette wheel selection. In crossover, random subtrees are selected from the parents and exchanged to generate the offspring. During mutation, each node is selected with a certain probability and the associated subtree is either replaced with a randomly generated one (subtree mutation) or the node type is simply changed (point mutation). Therefore, each solution has a fitness that measures the output error between target outputs and generated outputs. Standard GP suffers from several issues, the major one being bloating [
29,
30]. Bloating refers to the production of solutions with large amounts of unnecessary code that increases over the evolutionary process without providing any improvement [
31]. Cartesian genetic programming (CGP) is a special, flexible and highly efficient type of GP algorithm that encodes a graphic representation of a computer program and uses only point mutation operator without applying the crossover operator [
32]. It has several advantages over standard GP: it finds good solutions after only a few evaluations; it decodes solutions efficiently; it does not bloat; and it is easy to implement. Simulated annealing (SA) is a global optimization algorithm inspired from the cooling process of a material. During temperature reduction, the molecules of a material slow down and align to a crystallized form that represents the lowest energy state of the system [
33]. Standard SA evolves one solution over time, unlike evolutionary algorithms that are population-based. The algorithm starts with an initial random solution, which is followed by a newly generated solution based on the initial one. The next step is the acceptance or rejection of the newly created solution. If the newly created solution shows an improvement in the objective function, it is accepted. If it shows an increase in the objective function, it is either rejected or accepted, with a probability based on the difference between objective values for current and newly created solutions. SA has the following advantages: able to deal with arbitrary cost functions, able to skip from local minimas, simple to implement, and can be applied to continuous and discrete problem domains.
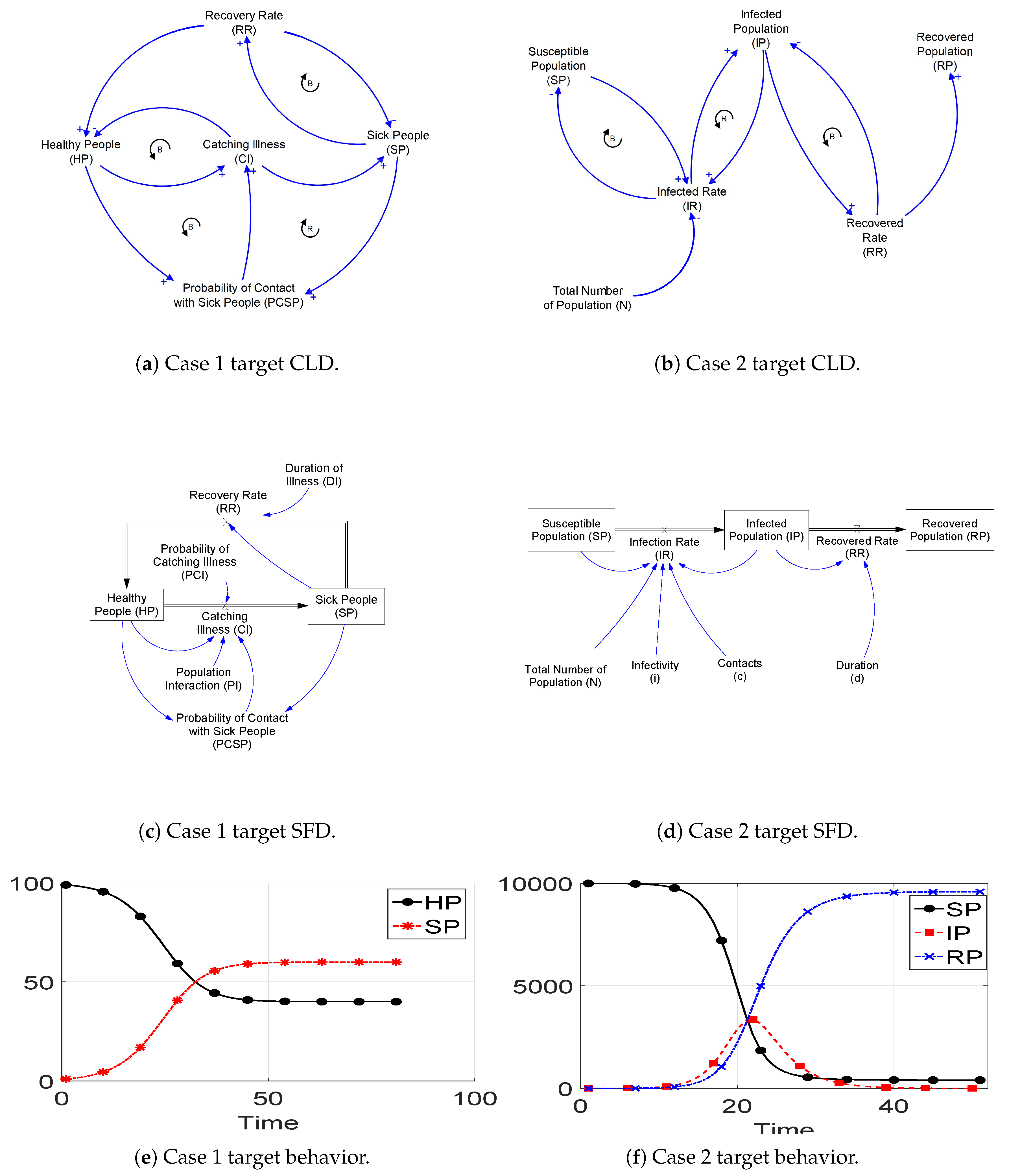
We have demonstrated the ability of the modeling support system to generate useful models and equations by conducting experiments with two synthetic reality case studies taken from the SD literature. Our goal is to use CI methods in the SD field to support the modeling process with complex and large scale models. In this paper, however, we report on our progress using small models involving two and three stocks. In our opinion, the work presented here could be extended to improve the proposed support system and applied to complex models with a lot of data. To the best of our knowledge, this proposal is one of the first attempts to provide an SD modeling support system.
This paper is organized as follows: an overview of the proposed support system is followed by a description of how the different components work. The next section presents the experimental setup and describes the case studies used to demonstrate the performance of the support system. Lastly, we discuss the experimental results and limitations, draw conclusions and summarize future directions for this work.
4. Results and Analysis
4.1. Setup 1
Setup 1 results for Case 1 and Case 2 are shown in
Table 1 and
Table 2, respectively. Each equation set shows the target equations, followed by equations generated by the GP ensemble in the presence and absence of the depth controller parameter
. The observation was made that each stock variable’s generated equation contained the correct variables. This was because the knowledge of causalities among the variables was known from the predefined CLD. This knowledge defines the terminal set for each GP ensemble member and determines how the generated equations will look. The comparison between target and generated behaviors from Case 1 inferred equations (
Table 1) and Case 2 inferred equations (
Table 2), with and without applying the depth controller, is shown in
Figure 5 and
Figure 6, respectively.
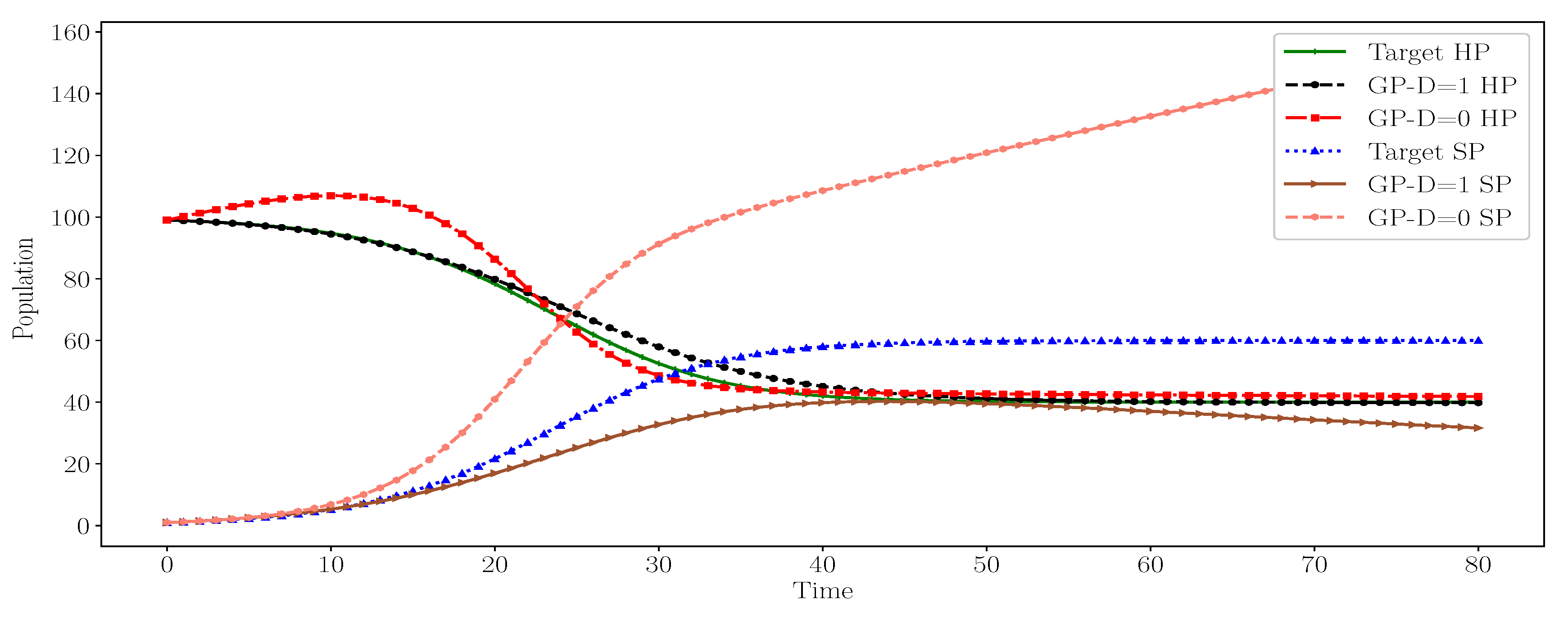
4.1.1. Case 1
For Case 1 with and without the depth controller, an obvious difference between the target equations and generated ones resides in the values of model parameters in all generated equations. Additional parameter values were added to the
stock variable’s generated equations in the presence and absence of
. In addition, additional parameter values were added to the
stock variable’s generated equation only in the absence of
. For the generated equation structures, the GP ensemble is able to generate equations for both
and
stock variables similar to the target equations in the presence and absence of the depth controller parameter. However, the denominator term
is missing in the generated equations, as shown in
Table 1. Since this term is the sum of both populations (total number of population), it could be considered a normalization term. The inferred equations with depth controller generate behaviors more similar to those of the targets than in the absence of depth controller, as shown in
Figure 5.
A possible explanation for the absence of this term from the generated equations using depth controller is that the depth controller restricts the GP generated tree to not exceed the terminal set size. This encourages the GP to converge toward solutions with small and balanced trees. This is illustrated by the term in the generated equation where its tree size is one and the first multiplication operator is the tree root. In the generated equation, the tree size is two and the second multiplication operator is the tree root, as shown by term. For the generated equations, without the depth controller, the absence of this term causes the generation of large and more unbalanced GP trees, as shown by the term in the generated equation. Its tree size is three and the first multiplication operator is the tree root, similarly for the term whose tree size is three and the plus operator is the tree root. In terms of model parameters and equation structures, there is no obvious advantage to apply the depth controller over not applying it. However, we consider it best to apply the depth controller to the generated equations because the resulting behavior is closer to the target behavior.
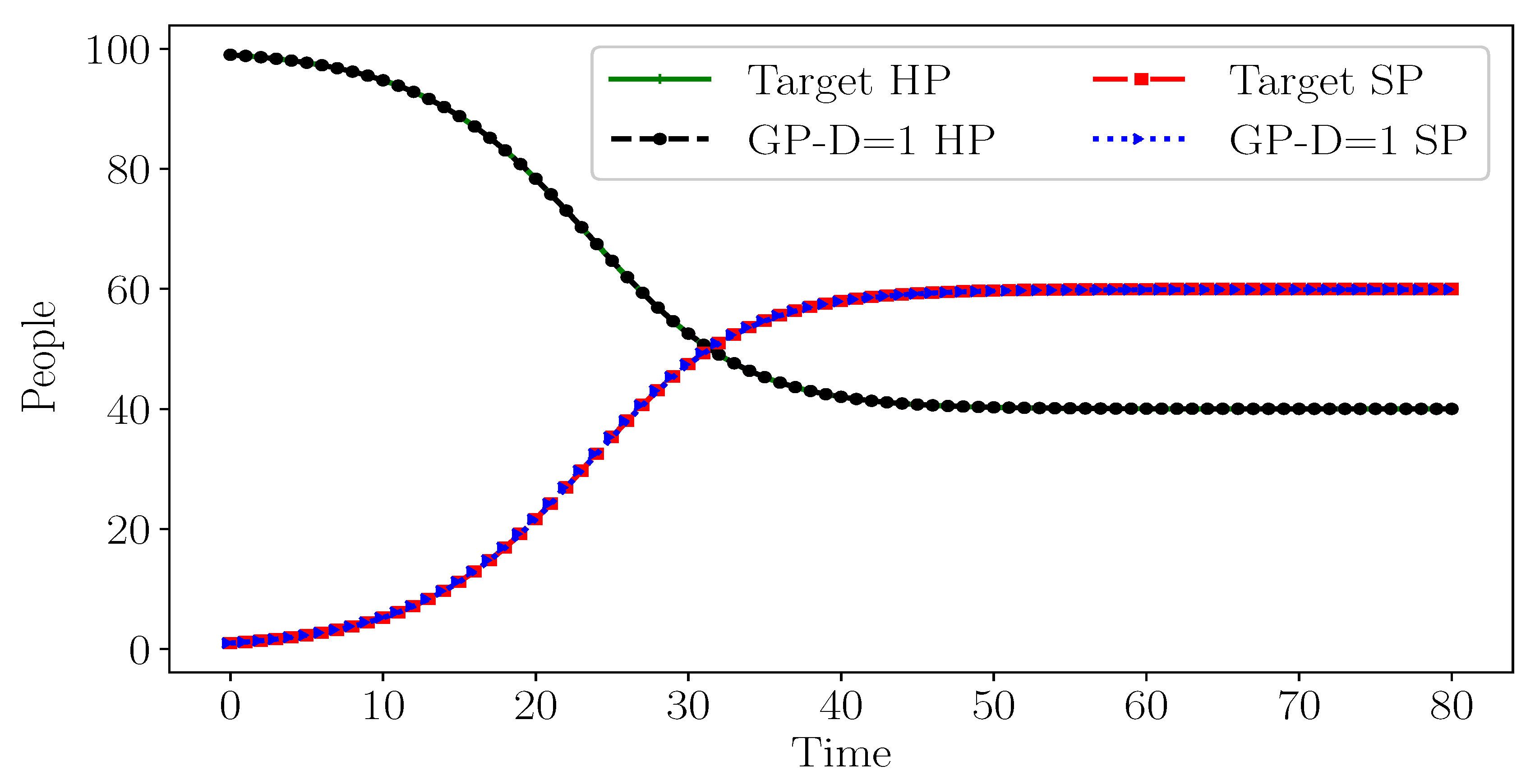
4.1.2. Case 2
For Case 2, the GP ensemble is able to generate the exact target equations, including the correct values for model parameters, with and without the depth controller, as shown in Equation (2). A possible explanation for the ability of GP to generate these exact similar structures is that the target equation has maximum depth of two with smaller algebraic operators compared to the operators in Case 1’s equation. GP, with and without the depth controller, results in small and balanced trees similar to the target equations. The generated behaviors from inferred equations exactly match the target behaviors, as shown in
Figure 6. This is expected since the inferred equations exactly match the structure of the target equations.
4.2. Setup 2
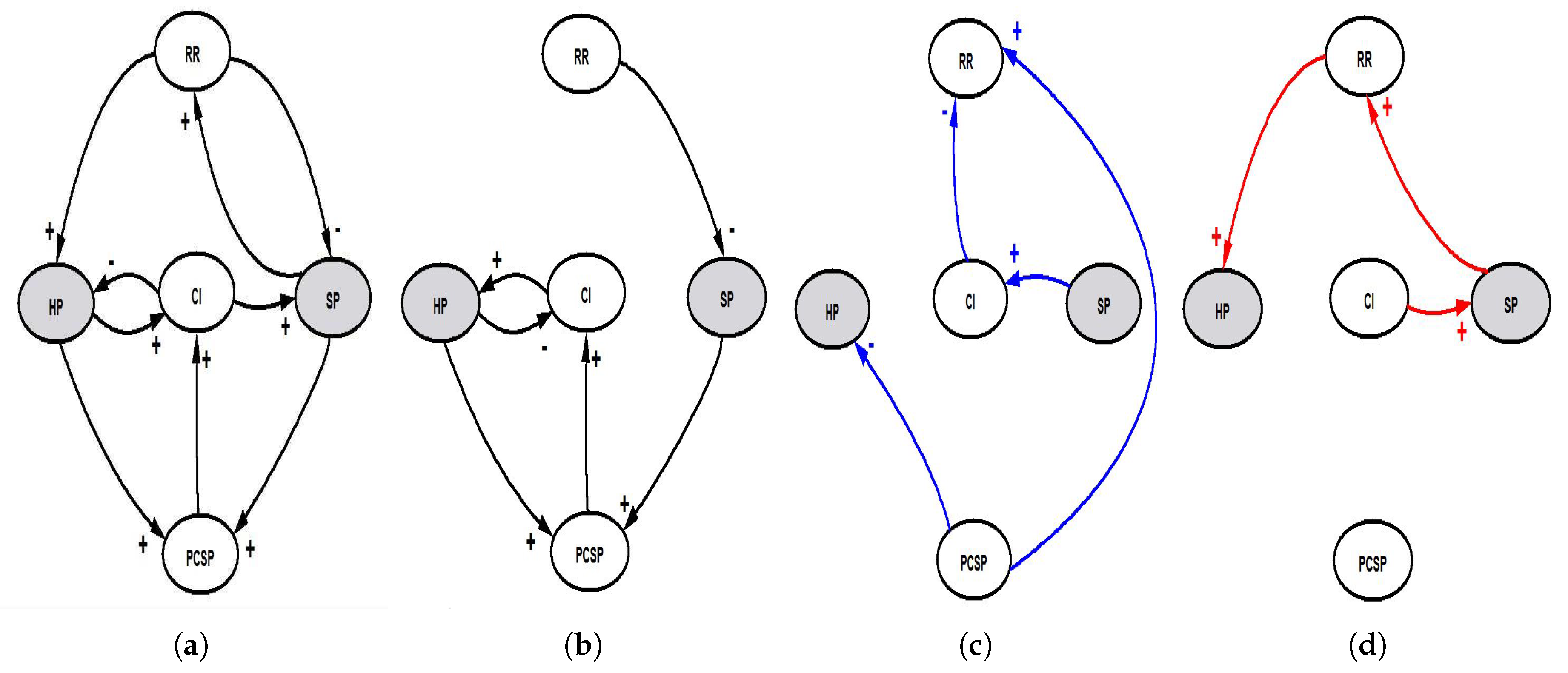
For each case in Setup 2, we compared the best generated CLD, SFD and equation structures with the target structures. The comparison between target and generated behaviors from Case 1 inferred equations (
Table 3), with and without applying the depth controller, is shown in
Figure 7. The best generated CLD for Case 1 was compared to the target structure by illustrating the correctly predicted, additional and missing links, as shown in
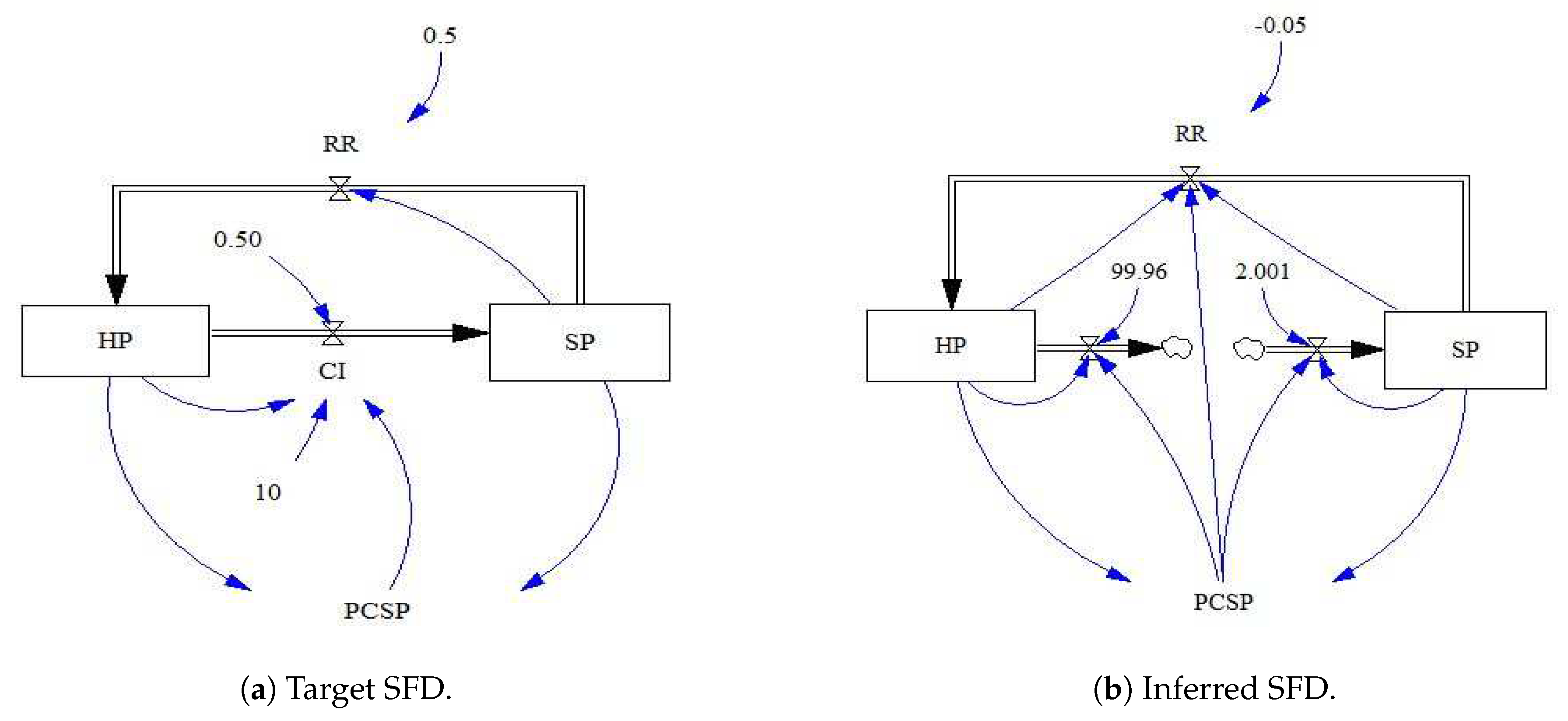
Figure 8. The best generated SFD for Case 1 was compared to target one, as shown in
Figure 9. The comparison between target and generated behaviors from Case 2 inferred equations (
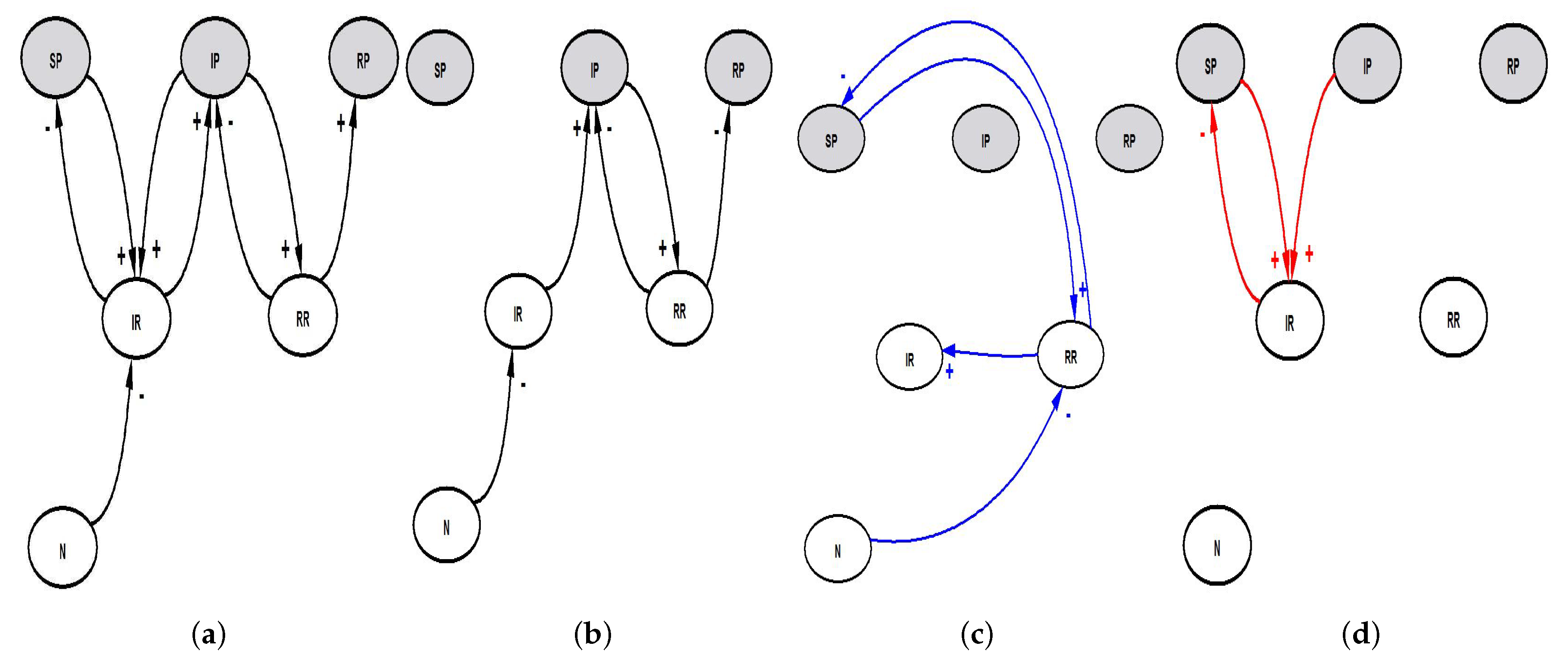
Table 4), with and without applying the depth controller, is shown in
Figure 10. The best generated CLD for Case 2 was compared to the target structure by illustrating the correctly predicted, additional and missing links, as shown in
Figure 11. The best generated SFD for Case 2 was compared to target one, as shown in
Figure 12. In contrast to Setup 1, in Setup 2, the defined terminal sets for each GP ensemble member depend upon the evolved CLD links by the SA algorithm. We generated SFD by applying predefined rules to mark variable types as either stock, flow, auxiliary or model parameters.
4.2.1. Case 1
An obvious difference between the target equations and generated equations, in Case 1, lies in the values of the model parameters for the generated equations. Additional parameter value is added to the second term of the
stock variable’s generated equation. The inferred CLD has six correct links (
Figure 8b) out of nine, three missing (
Figure 8d) and four additional (
Figure 8c). It can be seen from the values of different generated links in the CLD that the SA algorithm is able to predict most of the correct links. This is because it is a global optimization algorithm. The constructed SFD for this case (
Figure 9b) is quite similar to the target one with some additional links and flow variables. This is because the SFD is based on the generated CLD and equations. Evolving the CLD by flipping randomly chosen links to either on or off affects the defined terminal sets for the GP ensemble that also affects the evaluation of how accurate the CLD is. The accuracy of CLD is the output error between the behavior generated from inferred equations and the target ones. Given the best generated CLD, the terminal sets defined for the GP ensemble that generates the
stock equation will be
for both equation terms. The terminal sets defined for the GP ensemble that generates the
stock equation will be
for first equation term and
for second equation term. The presence of
symbol in the first term of
stock variable’s generated equation could be explained by the defined terminal set
for both terms in
stock generated equation and the restriction for each GP ensemble member to include all symbols defined in the terminal set. This provide us with correct symbols in the second term of
stock variable’s generated equation. Given the correct defined terminal sets for
stock variable’s generated equation terms, the generated equation is quite similar to the target one. However, we made the same observation with Setup 1: in the absence of the denominator term
, for both stocks,
and
generated equations. This is the effect of applying the depth controller to restrict the tree size to the size of the terminal sets. In the absence of this term, the equation structure still valid since it could be considered as a normalization term. The generated behaviors from inferred equations exactly match the target. This is despite the addition of
symbol in the first term of stock variable
inferred equation and the minus operator between the symbols in the second term. This observation was not expected since the inferred equations in Setup 1 looks more similar to the target equations than the inferred equations in Setup 2.
4.2.2. Case 2
In Case 2, the differences between the target equations and generated equations reside in the values of model parameters. A possible explanation for these differences and additional parameter values is the presence of the additional symbols in these generated equations, specifically in the
stock generated equation. The GP algorithm will have more numeric values if there are many symbolic terms in the tree. This is because the GP tree is constructed in a random manner from the terminal set and crossover and mutation operators. The inferred CLD has five correct links out of eight (
Figure 11b), three missing (
Figure 11d) and four additional (
Figure 11c). Similar to Case 1, the SA algorithm is able to predict most of the correct links, causing the generated equations to be more similar to target equations. Since generating the SFD is based on the generated CLD and equations, the constructed SFD for this case (
Figure 12b) closely matches the target one with two additional links. Given the best generated CLD, GP ensemble members that generated all stock variables’ equations were using
as their terminal set. The correctly defined terminal set for the GP ensemble that generates the
stock equation enables generation of the same structure as the target equation—similarly for the correctly defined terminal set for the
stock generated equation, which also results in the same structure as the target equation. However, the incorrect defined terminal set with additional symbols
and
N for the both
and
stock generated equations causes the presence of these symbols and generates different structures than target equations. Even with applying the depth controller to restrict the tree depth size, the presence of these symbols in the terminal sets forces the GP ensemble members to reject any tree structure lacking these symbols. The generated behaviors from inferred equations exactly match the target behaviors. This was not expected since the inferred equations have additional terms added to
and
stock variables’ inferred equations.
4.3. Runtime Analysis
We used Java version 1.8.0_91 to develop the algorithms. The experiments were run on an Intel Core i7 CPU 3.4 GHz, with 16 GB of RAM and Windows 7 (64 bit) machine (Dell, Canberra, Australia). The execution time for one run of the GP ensemble for equation learning and parameter estimation (Setup 1) and SA + GP ensemble for inferring CLD (Setup 2) was recorded for each case, as shown in
Table 5.
For Setup 1, cases 1 and 2 execution times are around 6.2 and 6.9 min, respectively. Cases 1 and 2 have five and six total variables, respectively, and two and three stock variables, respectively. Since the GP ensemble is constructed based on the number of stock variables, we believe that number of stock variables effects the execution time. In addition, the complexity of relationships among variables also has an effect on the execution time. We think this an acceptable time to learn such models, given the ability of the support system to navigate through the modeling space by producing a large number of models. In order to judge if the execution time of the GP ensemble is reliable, the time taken by a human modeler to come up with these models should be recorded.
For Setup 2, execution times for cases 1 and 2 are around 4 and 5 h, respectively. Since CLD and equation structures are inferred with parameter estimation, both number of stocks and relationship complexity influence execution time. In addition, the execution time for this Setup is longer than Setup 1 which makes sense. From the perspective of modeling time, we think this an acceptable time to infer such models. It is probably much quicker to generate CLD, SFD, equations and their parameters, with the ability to navigate and produce a large number of models, than to develop these models manually. However, the human-based modeling has the benefit of producing more meaningful and structurally valid models than the CI-based methods can do. In order to determine whether the execution time in this Setup is reliable, it should be compared with the time taken by a human modeler to come up with these case models.
4.4. Limitations
The concept of structural validity of method under development generated models is not applied in this paper, where graphical or topological error measures are only applied to compare the generated models against the target synthetic models. The structural credibility of models was assessed by asking the following questions: Do the equations make causal sense? Do they have a real-life causal meaning? Do they possess unit consistency? Do units of the equations naturally yield the units of the output variable, without adding any dummy ‘fudging’ coefficients? Do the equations yield logical extreme values, under extreme input values? Are the equations robust/valid under high and low parameter values?
The GP ensemble used to generate the model equations suffers from two main issues: first, the predefined functional sets that list the mathematical operators and functions used to build the GP trees. In our experimental setups, we defined these sets according to our knowledge of case study models nature. However, this assumption is a weak point in the proposed GP ensemble which could be fixed either by defining functional sets that contain a large collection of algebraic and nonlinear functions, or by learning these sets during the evolution process. Second, the defined fitness function relies on the output error between the target behavior and generated behavior. The main purpose of the proposed GP ensemble is to generate models that have valid structures and not just models that generate behavior similar to that of the target. As we see from the results, for Case 2 in particular, two different model structures inferred in both Setup 1 and 2 can generate the same behavior despite having different equation structures. The main purpose of using ensemble learning method is to avoid inferring the whole system equations all at once given the time-series observations. This could lead to generate too large equations for the sake of matching the target ones since the fitness function is mainly derived by output error. This problem is a well-known issue in the literature called bloating [
29]. Furthermore, the balance between the model structure and generated behaviors should be preserved as much as we can to provide SD modelers with model equations that make sense at least in terms of equations size.
Our proposed methodology relies mainly on the CLDs to generate both SFD and equations. In Setup 1, we assume that target CLD is given and based on this we generate the equations. In Setup 2, we learn CLD and underlying equations simultaneously, and, after the SFD is built, by annotating each variable in the CLD. Although CLDs play an important role in the SD modeling process, such as enabling the smooth transition to the final SFDs and early engagement with system stakeholders, they are not in themselves the complete SD models. From the perspective of the SD modeling process, it makes more sense to use SFDs instead of CLDs to generate the equations, where CLD can be generated easily from SFD for presentation purposes. The reason for choosing to learn the model equations based on the CLDs and not SFDs is due to the smaller search space needed to infer CLDs than to infer SFDs. With CLDs, we are only interested in the links between variables, whereas, with SFDs, we aim to identify the variable types (e.g., stock, in/out flow, auxiliary) and the links between them. This could make the overall inferring process more complicated and costly.
The integration of the SA and GP ensemble algorithm to generate both CLD and equations simultaneously is still a costly process. The reason is that both processes are nested and the quality of the CLD depends on the generated equations that should be simulated first to generate behavior. This nested process could be avoided by determining how to evaluate the CLD independently, before giving it to the GP ensemble to generate the underlying equations. Furthermore, we need to use a wide range of case studies that scale from simpler to more complicated ones to see how the proposed CI methods’ calculation time scale for large scale cases.
We assume that the stocks are known and that time series observations will be available for all of them. This assumption is necessary for two purposes: for the GP ensemble methodology which is used to generate the mathematical representation, with differential equations, of system stock variables; and for SFD inferring where the identification of the remaining system variables starts from knowing the stocks. However, the system observations could refer to stock variables or to any other variables, such as flows or auxiliaries. In addition, the availability of the observations for all system variables, regardless of their types, is not always known.
5. Conclusions
Our ability to store and process increasing amounts of data and then to utilize CI methods to turn this data into useful information is driving a revolution across the SD field. SD is a powerful tool used in the modeling of complex dynamical systems. It is extensively applied to dynamic phenomena emerging in industrial, economic, social, ecological and transportation systems, as well as being used for a variety of tasks, such as policy analysis and design, learning and training, decision-making and forecasting. This paper contributes to a growing field of interest that aims to facilitate and improve the efficiency of the SD modeling process by developing a CI-based modeling support system to generate SD models from system observations. The core component of the support system is the learning engine which builds upon different CI methods. These can be invoked in two different inferring modes: inferring only the underlying equations and their parameters using the GP ensemble; and inferring CLDs, SFDs, equations and estimating their parameters by the integration of the GP ensemble and SA algorithms. Based on the inferred CLD and system equations, the SFD was created by applying a fixed rule-based system to identify the variable types as either inflows, outflows, auxiliaries or parameters.
To illustrate how the support system could be applied to generate SD models close to target models, we chose two synthetic reality cases from the epidemics domain. Two main setups were applied, Setup 1 for generating the system equations and estimating their parameters given the target CLD, and Setup 2 for generating CLD, SFD, equations and estimating the model parameters. The experimental results from Setup 1 show the ability of the GP ensemble to match the target equations and generate the same behaviors for Case 2. Although the generated equations for Case 1 have missing terms, these inferred equations are able to generate a very close match to the target behavior. These differences in the generated equations are affected by the depth controlled parameter that controls the GP tree depth. It has the advantage of preventing the generated equations from growing and at the same time generates the desired behavior since the fitness function is mainly derived from the output error between the generated and target behaviors. The results from Setup 2 show that the inferred CLDs, SFDs and equations have some similarities to the target ones. There are additional and missing links in the generated CLD and SFD, and additional terms in the inferred equations. The inferred structures generate behaviors which match those of the target because the GP fitness function is derived from the output error. In order to guide the GP inferring process to generate valid structures in addition to minimizing the output error, a structural measure needs to be integrated with the output error fitness. This structural measure should be inspired and derived from structural validation tests applied to SD models built by SD practitioners and modelers. The performance of the GP ensemble is verified with specific conditions, where all system stocks, their observations and the mathematical nature of the target equations are known. Changing one of these conditions will have an effect on the performance of GP ensemble, in addition to the uncertainty in the system observations which could also affect the robustness of GP algorithm. Regarding the conducted runtime analysis, the scale of the problem affects the evolution process of the CI algorithms—specifically if we want to infer different model parts synchronously such as CLDs, SFDs or equations which are tightly coupled through the SD modeling process.
The proposed support system in this paper shows great promise to support SD modeling process which will enable the modelers to save time and effort in building an SD model by providing the SD modeler with an inferred model where the modeler could check and validate. Several directions can be taken to extend this work:
Most pressing is the need to work towards enhancing the ability of the methods to generate models with minimal structures that can characterize the data. The methods under development should be robust and scalable with the ability to handle big data.
It is crucial to integrate the necessary semantic domain knowledge, about the system or problem of interest, with the CI-based methods to generate valid structures. This will add a new dimension to the capability of the CI-methods for generating valuable models, especially for real-life systems where we do not have any idea about how the target model looks.
Identification of which variables to include in the model, as part of the support system’s inference engine, is challenging because, for each variable set selected, a SD model should be built and simulated to evaluate those selected. Therefore, the efficiency of the modeling process would be greatly enhanced by finding a method which bypassed the need to build the whole SD model.
Generating an SD model without prior knowledge of the types of variables and only limited observations is a challenging task too. However, the ability to handle these conditions since they are common in real world applications is an important feature to be added to the support system. Generating SD models under these conditions will require not only a search for the set of causal and mathematical relationships, but a search for the types of variables and for the mathematical equations for those variables that do not have any observations.