Categorification of the Müller-Wichards System Performance Estimation Model: Model Symmetries, Invariants, and Closed Forms

Abstract

The Müller-Wichards model (MW) is an algebraic method that quantitatively estimates the performance of sequential and/or parallel computer applications. Because of category theory’s expressive power and mathematical precision, a category theoretic reformulation of MW, i.e., CMW, is presented in this paper. The CMW is effectively numerically equivalent to MW and can be used to estimate the performance of any system that can be represented as numerical sequences of arithmetic, data movement, and delay processes. The CMW fundamental symmetry group is introduced and CMW’s category theoretic formalism is used to facilitate the identification of associated model invariants. The formalism also yields a natural approach to dividing systems into subsystems in a manner that preserves performance. Closed form models are developed and studied statistically, and special case closed form models are used to abstractly quantify the effect of parallelization upon processing time vs. loading, as well as to establish a system performance stationary action principle.

1. Introduction

In the late 1980s, D. Müller-Wichards proposed a concise novel approach for estimating the total performance of computer-based (but machine independent) applications by algebraically combining the known performance estimates of the individual arithmetic, data movement, and delay elements that comprise the applications in a manner that also accounts for various degrees of parallelism that can occur during processing [1]. The essence of the mathematical framework upon which the Müller-Wichards model (MW) is based is abstracted by the expression $\phi :H\to P$, where $H$ is a monoid (i.e., a semigroup with identity) representation of the application, $P$ is the Müller-Wichards performance algebra (also a monoid), and $\phi$ is a monoid homomorphism. The image $\phi \left(h\right)$ in $P$ of a single application element $h$ in $H$ provides a numerical performance measure for $h$. The total numerical performance estimate for the application results naturally from the associative binary operations in $H$ and $P$ and the homomorphism property of $\phi$, which algebraically combines the performance estimates for each application element in $H$.

Every area of mathematics (e.g., group theory, topology) is described by numerous definitions, theorems, and constructions. However, many common mathematical concepts occur naturally with only slight variation in the various areas of mathematics. Category theory is that branch of mathematics which identifies and studies these common concepts and provides formal mechanisms for mapping them from one area of mathematics to another. More specifically, a category (e.g., the category of sets) consists of a class of objects (e.g., sets), morphisms between objects (e.g., maps between sets), an identity morphism for each object (e.g., the set identity map), and a rule for associatively composing morphisms (e.g., composition of maps). Functors provide formal maps between categories (e.g., from the category of groups to the category of sets) by associating objects and morphisms in different categories subject to the constraints that morphism composition and object identities are preserved.

Because of its generality category, theory has found application in recent years in such diverse areas as physics (e.g., [2,3,4,5]), design specification (e.g., [6,7]), data fusion (e.g., [8]), computer science (e.g., [9]), computer security (e.g., [10,11]), systems engineering (e.g., [12]), manufacturing (e.g., [13]), theoretical biology (e.g., [14,15,16]), network theory (e.g., [17]), multi-agent systems models (e.g., [18]), concurrent system design verification (e.g., [19]), emergence (e.g., [20]), and artificial general intelligence (e.g., [21]). Motivated by category theory’s mathematical precision and expressive power, this paper introduces a new category theoretic application useful for numerical systems engineering modelling and analysis via a very simple straightforward categorification of MW for the case that the application monoid $H$ is a free monoid generated by a finite set of basis processes, i.e., $H$ is the set of all finite sequences of basis processes, including the empty sequence-where each sequence represents a system and each basis process corresponds to either an arithmetic process, a data movement process, or a delay process-and catenation of systems serves as the associative binary operation. The categorified MW-denoted by CMW-is comprised of three components: a single object category of systems that is specified by $H$ and has elements of $H$ as its set of morphisms; a single object performance category that is specified by $P$ and has the elements of $P$ as its set of morphisms; and a performance functor specified by $\phi$ with the category of systems as its domain and the performance category as its codomain.

CMW is effectively numerically equivalent to MW with the added benefit that the formalism introduced by categorification provides a precise vocabulary useful for identifying and discussing certain fundamental properties of both the model and the systems modelled by it. In particular, the CMW fundamental symmetry group is introduced and the category theoretic formalism is used to facilitate the identification of associated symmetry invariants found in the model. In addition, the formalism provides a natural approach to system factorization-i.e., dividing a system into subsystems in a manner that maintains its integrity-i.e., preserves the performance of the undivided system.

As indicated above, the objective of this paper is to provide a categorified version of the MW model and exploit the associated category theoretic vocabulary to provide additional insights into properties of the MW model, as well as the systems modelled by it. In order to make this paper reasonably self-contained, relevant definitions, terminology, and preliminary lemmas are summarized in the next section (for additional depth and clarification the reader is invited to consult such references as [22,23,24]). The remainder of this paper is organized as follows: The Müller-Wichards performance categories are defined, and their category theoretic properties discussed in Section 3. The category of systems and the Müller-Wichards performance functors are introduced in Section 4. The CMW fundamental symmetry group is defined and its associated model invariants are identified in Section 5. System factorization and a “product of categories” performance model are discussed in Section 6. Closed form models are developed in Section 7 and several aspects of closed form models are studied statistically in Section 8. Special case closed form models are developed in Section 9. These special case closed form models are applied in Section 10 to abstractly demonstrate the effect of parallelization on system processing time vs. loading and to obtain a stationary action principle for system performance. Concluding remarks comprise the final section of this paper. To avoid disrupting the flow of the text, proofs for all theorems (including those for the special case closed form models) are consigned to Appendix A.

2. Definitions, Terminology, and Preliminary Lemmas

2.1. Categories and Morphisms

A category $\mathit{C}$ consists of a collection $Ob{j}_{\mathit{C}}$ of objects such that ([22], p. 2)

• For every pair of objects $X,Y\in Ob{j}_{\mathit{C}}$ there is a (possibly empty) set $Mo{r}_{\mathit{C}} \left(X,Y\right)$ of morphisms from $X$ to $Y$;
• For any $X,Y,Z\in Ob{j}_{\mathit{C}}$ there is a composition “$\circ$” of morphisms

  $$\circ : Mo{r}_{\mathit{C}}\left(X,Y\right)\times Mo{r}_{\mathit{C}}\left(Y,Z\right)\to Mo{r}_{\mathit{C}}\left(X,Z\right)$$

  (1)

  given by $\left(f,g\right)\mapsto g\circ f$ with the properties:
• For every $X\in Ob{j}_{\mathit{C}}$ there is an identity morphism $1_X\in Mo{r}_{\mathit{C}}\left(X,X\right)$ such that for $f\in Mo{r}_{\mathit{C}}\left(X,Y\right)$ and $g\in Mo{r}_{\mathit{C}}\left(Y,X\right)$, $f\circ 1_X=f$ and $1_X\circ g=g$;
• When defined, composition of morphisms is associative, i.e., $\left(f\circ g\right)\circ h=f\circ \left(g\circ h\right)$.

To illustrate this definition, consider the following canonical examples of categories:

• The category $\mathit{S}\mathit{e}\mathit{t}$ where $Ob{j}_{\mathit{S}\mathit{e}\mathit{t}}$ is the collection of all sets, the morphisms are the ordinary mappings between sets, and $\circ$ is the usual composition of maps.
• The category $\mathit{G}\mathit{r}\mathit{p}$ where $Ob{j}_{\mathit{G}\mathit{r}\mathit{p}}$ is the collection of all groups, the morphisms are the ordinary group homomorphisms, and $\circ$ is the usual composition of homomorphisms.

It is easily verified that $\mathit{S}\mathit{e}\mathit{t}$ and Grp satisfy items 3 and 4 above.

A category $\mathit{C}$ is a subcategory of a category $\mathit{D}$ if ([22], p. 7): every object of $\mathit{C}$ is an object of $\mathit{D}$; for all objects $X,Y$ of $\mathit{C}$, $Mo{r}_{\mathit{C}}\left(X,Y\right)\subseteq Mo{r}_{\mathit{D}}\left(X,Y\right)$; the composition of two morphisms in $\mathit{C}$ is the same as their composition in $\mathit{D}$; and for all objects $X$ of $\mathit{C}$, $1_X$ is the same in $\mathit{D}$ as it is in $\mathit{C}$. If $Ob{j}_{\mathit{C}}$ is a set, then $\mathit{C}$ is a small category ([22], p. 6) and if $Mo{r}_{\mathit{C}}\left(X,Y\right)\ne \varnothing$ for all $X,Y\in Ob{j}_{\mathit{C}}$, then $\mathit{C}$ is a connected category ([22], p. 19).

Morphisms are classified in a variety of ways according to their composition properties. Of interest here are monic and epic morphisms. A morphism $f$ is monic ([22], p. 11) if $f\circ g=f\circ h$ implies $g=h$ and it is epic ([22], p. 12) if $g\circ f=h\circ f$ implies $g=h$. For example, in the category $\mathit{S}\mathit{e}\mathit{t}$ injective maps are monic morphisms and surjective maps are epic morphisms. A morphism that is both monic and epic is a bimorphism ([22], p. 15). A morphism $h$ is factorizable ([22], p. 43) if $h=f\circ g$, where $f$ is monic and $g$ is epic.

Another useful notion involving morphisms is the sieve ([25], p. 206) on an object. For some $X\in Ob{j}_{\mathit{C}}$ consider the set of morphisms ${\Psi }_X=\left\{f:f\in Mo{r}_{\mathit{C}}\left(X,Y\right) forall Y\in Ob{j}_{\mathit{C}}\right\}$ and observe that ${\Psi }_X$ is closed under left composition, i.e., $g\circ f\in {\Psi }_X$ when $f\in {\Psi }_X$ and $g\in Mo{r}_{\mathit{C}}\left(Y,Z\right)$ for any $Z\in Ob{j}_{\mathit{C}}$. An $X-$sieve is the subset $\Psi \subseteq {\Psi }_X$ that is closed under left composition, i.e., $g\circ f\in \Psi$ when $f\in \Psi$. Note that there are at least two sieves for every $X\in Ob{j}_{\mathit{C}}$, namely ${\Psi }_X$ and the empty sieve $\varnothing$.

2.2. Functors

Functors can be regarded as morphisms between categories and-in a sense-they provide a “picture” of what one category looks like in another. If $F$ is a covariant functor-or simply a functor (contravariant functors are not used here) ([22], p. 73)-from category $\mathit{C}$ to category $\mathit{D}$ (denoted $F:\mathit{C}\to \mathit{D}$), then it assigns to every $X\in Ob{j}_{\mathit{C}}$ an $FX\in Ob{j}_{\mathit{D}}$ and to every $f\in Mo{r}_{\mathit{C}}\left(X,Y\right)$ an $Ff\in Mo{r}_{\mathit{D}}\left(FX,FY\right)$ such that:

• $F{1}_X=1_{FX}$ for every $X\in Ob{j}_{\mathit{C}}$; and
• When $f\circ g=h$ is defined in $\mathit{C}$, then $Ff\circ Fg=Fh$ is defined in $\mathit{D}$ and $Ff\circ Fg=F\left(f\circ g\right)= Fh$.

$F$ is full ([22], p. 97) if for all $X,Y\in Ob{j}_{\mathit{C}}$ the mapping $Mo{r}_{\mathit{C}}\left(X,Y\right)\to Mo{r}_{\mathit{D}}\left(FX,FY\right)$ defined by $f\mapsto Ff$ is surjective, and is faithful ([22], p. 97) if this mapping is injective. Simple examples of functors include:

• The identity functor $1_{\mathit{C}}:\mathit{C}\to \mathit{C}$ which makes the assignments $1_{\mathit{C}}X=X$ for every $X\in Ob{j}_{\mathit{C}}$ and $1_{\mathit{C}}f=f$ for every $f\in Mo{r}_{\mathit{C}}\left(X,Y\right)$.
• The forgetful functor $U :\mathit{G}\mathit{r}\mathit{p}\to \mathit{S}\mathit{e}\mathit{t}$ which assigns to every group $G\in Ob{j}_{\mathit{G}\mathit{r}\mathit{p}}$ its underlying set $UG\in Ob{j}_{\mathit{S}\mathit{e}\mathit{t}}$ and to each homomorphism $f\in Mo{r}_{\mathit{G}\mathit{r}\mathit{p}}\left(G,H\right)$ the set map $Uf\in Mo{r}_{\mathit{S}\mathit{e}\mathit{t}}\left(UG,UH\right)$ (i.e., $U$ forgets group structure going from $\mathit{G}\mathit{r}\mathit{p}$ to $\mathit{S}\mathit{e}\mathit{t}$).

It can be determined by inspection that these functors satisfy the required properties given above by items 1 and 2.

Preservation and reflection are two important features of functors. A functor $F:\mathit{C}\to \mathit{D}$ preserves a categorical property ([22], p. 97) $\pi$ if-whenever an object, morphism, or diagram has property $\pi$ in $\mathit{C}$, then the image under $F$ of that object, morphism, or diagram has property $\pi$ in $\mathit{D}$. Similarly, $F$ reflects property ([22], p. 97) $\pi$ if-whenever the image under $F$ of an object, morphism, or diagram has property $\pi$ in $\mathit{D}$, then that object, morphism, or diagram has property $\pi$ in $\mathit{C}$.

It is readily deduced from item (2) that, in general, functors preserve commutative triangles of morphisms. For example, if Figure 1 is the commutative triangle for $f\circ g=h$ in $\mathit{C}$, then it must be

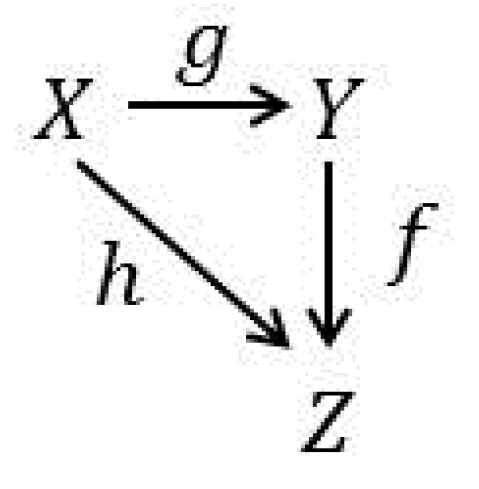
Figure 1. The commutative triangle for $f\circ g=h$ in C.

the case that the commutative triangle in Figure 2 is the preserved image of Figure 1 under the functor:

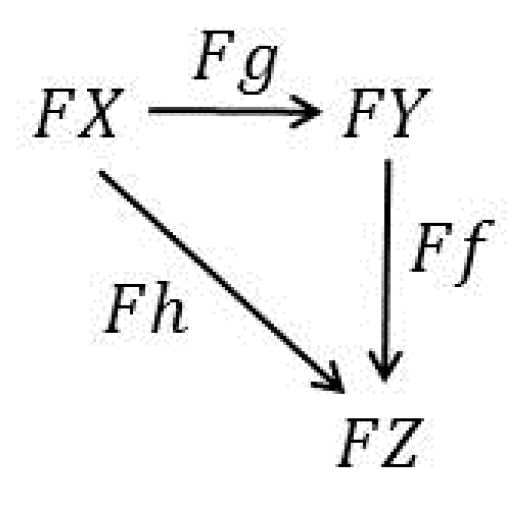
Figure 2. The preserved image of Figure 1 under $F$ in D.

$F$ in $\mathit{D}$. Note that Figure 1 is a factorization of $h$ when $f$ is monic and $g$ is epic.

2.3. Preliminary Lemmas

The following lemmas are needed to prove and discuss the main results of this paper. They have been established elsewhere and are stated here without proof for the reader’s convenience.

Lemma 1 [9].

Any monoid$M$specifies a category$\mathit{M}$with$M$as its only object, the elements of$M$as its only set of morphisms, and the binary operation on$M$as its composition of morphisms.

Lemma 2 [9].

Each monoid homomorphism$f:M\to N$specifies a functor$F:\mathit{M}\to \mathit{N}$with$FM=N$and Fx$\in Mo{r}_{\mathit{N}}\left(N,N\right)=N$for$x \in Mo{r}_{\mathit{M}}\left(M,M\right)=M$such that$Fx\circ Fy=Fz$in$\mathit{N}$when$x\circ y=z$in$\mathit{M}$.

Lemma 3 [24].

Let${ℱ}_X$be the free monoid on a set$X$and$S$be any monoid. If${\phi }_0$is any mapping of$X$into$S$, then${\phi }_0$can be extended in one and only one way to a homomorphism$\phi$of${ℱ}_X$into$S$as$\phi \left(x_1{x}_2\cdots x_n\right)={\phi }_0\left(x_1\right){\phi }_0\left(x_2\right)\cdots {\phi }_0\left(x_n\right)$.

Lemma 4 [22].

Every faithful functor reflects monics, epics, and commutative triangles.

Lemma 5 [24].

A free monoid${ℱ}_X$is cancellative (i.e., $uv=uw$ and $vu=wu$ implies $v=w$ for$u,v,w\in {ℱ}_X$) and equidivisible (i.e., $uv=wz$ implies there exists an$x$ such that either$u=wx$ and$z=xv$ or$w=ux$ and$v=xz$ for$u,v,w,x,z\in {ℱ}_X$).

As an example of equidivisibility, suppose $uv=wz$ is a commutative square in a free monoid with $u=a_1{a}_2{a}_3{a}_4{a}_5$, $v=a_6{a}_2{a}_4{a}_7$, $w=a_1{a}_2$, and $z=a_3{a}_4{a}_5{a}_6{a}_2{a}_4{a}_7$. Then there exists an $x=a_3{a}_4{a}_5$ such that $u=wx$ and $z=xv$.

3. The Müller-Wichards Performance Categories

As mentioned in the introduction, in 1988 Dieter Müller-Wichards posited a (computing) machine independent “performance algebra” designed to estimate the total performance of a specific implementation of an application on a machine using the (known) performance characteristics of its individual building blocks. This approach enabled trade-off studies and analyses of applications using its various decompositions and implementations [1]. As indicated above, similar studies and analyses can be performed using CMW to estimate the numerical performance of any system that can be represented as sequences of arithmetic, data movement, and delay processes.

The Müller-Wichards performance algebra consists of a set whose elements are ordered in triples along with an associative binary operation, which defines how the elements of the set are to be multiplied. These elements are partitioned into three distinct subsets depending upon whether they are arithmetic, data movement, or delay elements. The first and second entries in each triple correspond to a performance value (e.g., a processing or data movement rate) and a weight value (e.g., the number of operations to be performed or the amount of data to be moved), respectively (delay elements are a special case—see below). The third entry is either a $0$-which defines the element as a data movement or delay element-or a $1$-which defines the element as an arithmetic element. Multiplication of an arithmetic element by any element produces another arithmetic element, whereas the product of a data movement element with a data movement element or a delay element is a data movement element. The set of delay elements is closed under this multiplication.

Multiplication is defined in terms of a positive real valued parameter $q$, which provides a family of (“skewed” time) results that interpolate between completely sequential and completely parallel execution of the associated application. The value of this parameter can be selected to account for execution time “speedup” or for degrees of machine and application parallelism.

The sets that define the Müller-Wichards performance algebra are:

$${ℝ}_{+}\equiv \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{positive}\mathrm{real}\mathrm{numbers},$$

(2)

$$C\equiv {ℝ}_{+}\times {ℝ}_{+}\times \left\{1\right\}\equiv \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{arithmetic}\mathrm{elements},$$

(3)

$$D\equiv {ℝ}_{+}\times {ℝ}_{+}\times \left\{0\right\}\equiv \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{data}\mathrm{movement}\mathrm{elements},$$

(4)

$$V\equiv \left({ℝ}_{+}{\displaystyle \cup }\{\infty \}\right)\times \left\{i\right\}\times \left\{0\right\}\equiv \mathrm{the}\mathrm{set}\mathrm{of}\mathrm{delay}\mathrm{elements} ,$$

(5)

where $i=\sqrt{-1}$,

$$\wp \equiv C{\displaystyle \cup }D{\displaystyle \cup }V,$$

(6)

and

$${\wp }^{\prime }\equiv C{\displaystyle \cup }D.$$

(7)

Each element in $C,D,$ and $V$ is a triple $g=\left(r,w,u\right)$, where $r$ is a performance value, $w$ is a weight value, and $u\in \left\{0,1\right\}$ determines the element type (i.e., $C$, $D$, or $V$).

Let $1\le q\le \infty ,$ and define the operation ${\otimes }^q$ as follows:

• If $g_1=\left(r_1,w_1,u_1\right)\in \wp$ and $g_2=\left(r_2,w_2,u_2\right)\in {\wp }^{\prime }$, then $g_1{\otimes }^q{g}_2=\left(r,w,u\right)$, where

  $$u=u_1˅ u_2,$$

  (8)

  $$w=Re\left[u_1{w}_1+u_2{w}_2+\neg u\left(w_1+w_2\right)\right],$$

  (9)

  and

  $$r=\{\begin{array}{c}\frac{\left|w\right|}{{\left[{\left(\frac{\left|w_1\right|}{r_1}\right)}^q+{\left(\frac{\left|w_2\right|}{r_2}\right)}^q\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$q$}\right.}} , q<\infty \\ \frac{\left|w\right|}{\underset{}{\max }\left[\frac{\left|w_1\right|}{r_1},\frac{\left|w_2\right|}{r_2}\right]} , q=\infty \end{array}$$

  (10)
• If $g_1,g_2\in V$, then $g_1{\otimes }^q{g}_2=\left(r,i,u\right),$ where $u$ and $r$ are given by Equations $\left(8\right)$ and $\left(10\right)$, respectively.

The elements $g_1,g_2$ are comparable if $g_1,g_2\in C$ or $g_1,g_2\in D$ or $g_1,g_2\in V$. If $g_1,g_2\in \wp$, then $g_1\le g_2$ when $g_1,g_2$ are comparable and either $\frac{\left|w_2\right|}{r_2}<\frac{\left|w_1\right|}{r_1}$ or $\frac{\left|w_2\right|}{r_2}=\frac{\left|w_1\right|}{r_1}$ and $r_2\ge r_1$.

Theorem 1.

$\left(\wp ,{\otimes }^q\right)$is a commutative monoid$M_q$with identity$e=\left(\infty ,i,0\right)$.

Since $\left(\wp ,{\otimes }^q\right)$ is the monoid $M_q$, then $\left(\wp ,{\otimes }^q\right)$ specifies a category according to the prescription given by the next theorem.

Theorem 2.

$\left(\wp ,{\otimes }^q\right)$specifies the Müller-Wichards performance category${\mathit{\wp }}_{\mathit{q}}$with$M_q$as its only object,$Mo{r}_{{\mathit{\wp }}_{\mathit{q}}}\left(M_q,M_q\right)=\wp$as its only morphism set, and composition of morphisms defined by${\otimes }^q$.

In order to identify additional categorical properties derived from the algebraic structure of $\left(\wp ,{\otimes }^q\right)$, let ${\wp }^C\equiv$ $C{\displaystyle \cup }\left\{e\right\}, {\wp }^D=D{\displaystyle \cup }\left\{e\right\},$ ${\wp }^{CD}={\wp }^{\prime }{\displaystyle \cup }\left\{e\right\}$, and ${\wp }^V=V$.

Theorem 3.

$\left({\wp }_q^X,{\otimes }^q\right), X\in \left\{C,D,CD,V\right\}$, are submonoids of$\left(\wp ,{\otimes }^q\right)$.

This leads to the following result:

Theorem 4.

If$X\in \left\{C,D,CD,V\right\}$, then$\left({\wp }^X,{\otimes }^q\right)$specifies the Müller-Wichards performance category${\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}$with$M_q^X$as its only object,$Mo{r}_{{\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}}\left(M_q^X,M_q^X\right)={\wp }^X$as its only morphism set, and composition of morphisms defined by${\otimes }^q$.

Note that although $Mo{r}_{{\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}}\left(M_q^X,M_q^X\right)\mathit{\subset }\mathit{M}\mathit{o}{r}_{{\wp }_q}\left(M_q,M_q\right)$, ${\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}$ is not a subcategory of ${\mathit{\wp }}_{\mathit{q}}$ because $M_q^X\ne M_q$.

Theorem 5.

Each of the categories${\mathit{\wp }}_{\mathit{q}}$and$$are small and connected.

Theorem 6.

Every morphism in${\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}, X\in \left\{C,D,V\right\},$is a bimorphism.

The following result is included for completeness and is a category theoretic statement of the fact that multiplication in the performance algebra is biased towards arithmetic elements, i.e., the product of any element in set $\wp \equiv C{\displaystyle \cup }D{\displaystyle \cup }V$ with an element in set $C$ is an element in $C$.

Theorem 7.

The set$C$is an$M_q$- sieve in category${\mathit{\wp }}_{\mathit{q}}$.

4. The Category of Systems and the Müller-Wichards Performance Functors

In this section, the category of systems is obtained from the free monoid ${ℐ}_A$ generated by a finite set $A$ of basis processes. Although this approach is similar to that employed in [1] to define $H$, for simplicity the catenation operation in ${ℐ}_A$ is used here instead of the two operations $\otimes$ and $\oplus$ used in $H$ to distinguish between portions of an application that have sequential and parallel implementations. A product of categories construction will be introduced for this purpose in Section 6.

Recall from Section 1 that ${ℐ}_A$ consists of all finite sequences of basis processes of $A \mathrm{called}\mathrm{s}ystems.$ The catenation of systems $u,v\in {ℐ}_A$ is the system $w=uv\in {ℐ}_A$ and $u$ and $v$ are subsystems of $w$. The empty system $\epsilon \in {ℐ}_A$ is the system with no basis processes and serves as the identity element for ${ℐ}_A$ with $\epsilon u=u\epsilon =u$.

The category of systems ${\mathit{\Im }}_{\mathit{A}}$ associated with a basis process set $A$ is obtained from ${ℐ}_A$, as prescribed in the following theorem.

Theorem 8.

${ℐ}_A$specifies the category of systems${\mathit{\Im }}_{\mathit{A}}$with${ℱ}_A$as its only object,$Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)={ℐ}_A$as its only morphism set, and composition of morphisms defined by catenation of systems.

Thus, a morphism in ${\mathit{\Im }}_{\mathit{A}}$ is a system and composition of morphisms in ${\mathit{\Im }}_{\mathit{A}}$ is catenation of systems.

Theorem 9.

${\mathit{\Im }}_{\mathit{A}}$is a small connected category.

Theorem 10.

Every morphism in${\mathit{\Im }}_{\mathit{A}}$is a bimorphism.

Any functor from ${\mathit{\Im }}_{\mathit{A}}$ into ${\mathit{\wp }}_{\mathit{q}}$ or ${\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}, X\in \left\{C,D,CD,V\right\},$ is referred to here as a Müller-Wichards performance functor for ${\mathit{\Im }}_{\mathit{A}}$ and the performance for any system in ${\mathit{\Im }}_{\mathit{A}}$ is its image under a Müller-Wichards performance functor in ${\mathit{\wp }}_{\mathit{q}}$ or ${\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}, X\in \left\{C,D,CD,V\right\}$. These functors are defined by unique extensions of gauge maps from the set of basis processes into the associated Müller-Wichards performance monoids as described by the following theorem (here “gauge” emphasizes the fact that these maps set the performance gauge for each basis process).

Theorem 11.

For any gauge map${\phi }_0:A\to \left(\wp ,{\otimes }^q\right)$ [${\phi }_0:A\to \left({\wp }^X,{\otimes }^q\right),X\in \left\{C,D,CD,V\right\}$] there is a unique Müller-Wichards performance functor $F_{{\phi }_0}:{\mathit{\Im }}_{\mathit{A}}\to {\mathit{\wp }}_{\mathit{q}} \left[F_{{\phi }_0}^X:{\mathit{\Im }}_{\mathit{A}}\to {\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}\right]$ such that

$$F_{{\phi }_0}{a}_1{a}_2\cdots a_n={\phi }_0\left(a_1\right){\otimes }^q{\phi }_0\left(a_2\right){\otimes }^q\cdots {\otimes }^q{\phi }_0\left(a_n\right)$$

(11)

$$[ F_{{\phi }_0}^X{a}_1{a}_2\cdots a_n={\phi }_0\left(a_1\right){\otimes }^q{\phi }_0\left(a_2\right){\otimes }^q\cdots {\otimes }^q{\phi }_0\left(a_n\right) ]$$

(12)

where $a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$.

5. The CMW Fundamental Symmetry Group and Associated Invariants

Based upon the discussion above, it is clear that CMW can be abstracted by the functor expressions $F_{{\phi }_0}:{\mathit{\Im }}_{\mathit{A}}\to {\mathit{\wp }}_{\mathit{q}}$ and $F_{{\phi }_0}^X:{\mathit{\Im }}_{\mathit{A}}\to {\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}, X\in \left\{C,D,CD,V\right\}$. In this section, the CMW fundamental symmetry group is introduced and associated model invariants (which at an abstract level can be viewed as invariants of the modelled system) are identified. Recall that, in general, a symmetry associated with a “situation” is related to an “immunity to change” for some aspect of the “situation”. In order for a “situation” to have a symmetry: (i) the aspect of the “situation” remains unchanged or invariant, when a change or symmetry transformation acts upon the “situation”; and (ii) it must be possible to perform the change, although the change does not actually have to be performed [26]. Here, symmetry and symmetry transformation are used interchangeably.

An automorphism of ${\mathit{\Im }}_{\mathit{A}}$ is a bijection $\alpha :Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)\to Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$, which preserves the catenation operation in ${ℐ}_A$. Since $Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$ remains unchanged under $\alpha$ and it is possible-but not necessary-to apply $\alpha$, then items (i) and (ii) above are satisfied and $\alpha$ is a ${\mathit{\Im }}_{\mathit{A}}$ symmetry. The set of all such symmetries under the operation composition of bijections forms the automorphism group $Aut({\mathit{\Im }}_{\mathit{A}}$). This group is the CMW fundamental symmetry group.

Theorem 12.

The CMW fundamental symmetry group is isomorphic to the group of permutations of the set$A$of basis processes.

The following corollary is obvious and is stated without proof.

Corollary 1.

$\left|Aut\left({\mathit{\Im }}_{\mathit{A}}\right)\right|=\left|A\right|!$

A CMW invariant is a CMW property that remains unchanged after every symmetry in the CMW fundamental symmetry group has been applied to $Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$.

Theorem 13.

The images of${\mathit{\Im }}_{\mathit{A}}$in${\mathit{\wp }}_{\mathit{q}}$and${\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}$under the Müller-Wichards performance functors$F_{{\phi }_0}$and$F_{{\phi }_0 }^X, X\in \left\{C,D,CD,V\right\},$respectively, are CMW invariants.

Theorem 14.

If$\Delta$is a commutative triangle in${\mathit{\Im }}_{\mathit{A}}$, then$\Delta$and its image under Müller-Wichards performance functors are CMW invariants.

6. System Factorization and Product Performance Models

Recall from Section 2 that a morphism $h$ is factorizable if $h=f\circ g$, where $f$ is a monic morphism and $g$ is an epic morphism. In the category of systems, this means that when a system $w$ is factorizable as $w=uv$, then $w$ can be divided into the two subsystems $u$ and $v$ without affecting the order and content of the base processes in $w$. The integrity of a factorization is maintained if the performance of $w$ is identical to that of $uv$.

Theorem 15.

Every commutative triangle in${\mathit{\Im }}_{\mathit{A}}$corresponds to a system factorization, which maintains its integrity.

A commutative square in ${\mathit{\Im }}_{\mathit{A}}$ corresponds to an equation $uv=wz$, where $u,v,w,z\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$.

Theorem 16.

For every commutative square in${\mathit{\Im }}_{\mathit{A}}$there are two systems in the square, which have factorizations that maintain their integrity.

Corollary 2.

Whenever$uv=wz$is a commutative square in${\mathit{\Im }}_{\mathit{A}}$, then either$F_{{\phi }_0}^{X}u$and$F_{{\phi }_0}^{X}z$or$F_{{\phi }_0}^{X}w$and$F_{{\phi }_0}^{X}v$are factorizable in${\mathit{\wp }}_{\mathit{q}}^{\mathit{X}}$,$X\in \left\{C,D,V\right\}.$

Corollary 3.

If$F_{{\phi }_0}u=F_{{\phi }_0}v{\otimes }^q{F}_{{\phi }_0}w$, then$u$is factorizable in${\mathit{\Im }}_{\mathit{A}}$and maintains its integrity when$F_{{\phi }_0}$is faithful.

Results similar to Corollary 3 also apply for $F_{{\phi }_0}^X,$ $X\in \left\{C,D,CD,V\right\}$.

Additional modelling flexibility can be obtained using products of categories when a system is comprised of subsystems that have different sequential and/or parallel characteristics. Here, two basis sets $A$ and $B$ of processes and two morphism compositions ${\otimes }^q$ and ${\otimes }^p$ form the product category of systems ${\mathit{\Im }}_{\mathit{A}\mathit{B}}={\mathit{\Im }}_{\mathit{A}}\times {\mathit{\Im }}_{\mathit{B}}$ and the associated Müller-Wichards product performance category ${\mathit{\wp }}_{\mathit{q}\mathit{p}}={\mathit{\wp }}_{\mathit{q}}\times {\mathit{\wp }}_{\mathit{p}}$, respectively. For the product category ${\mathit{\Im }}_{\mathit{A}\mathit{B}}$ the single object is the pair $Ob{j}_{{\mathit{\Im }}_{\mathit{A}\mathit{B}}}=Ob{j}_{{\mathit{\Im }}_{\mathit{A}}}\times Ob{j}_{{\mathit{\Im }}_{\mathit{B}}}=\left\{\left({ℱ}_A,{ℱ}_B\right)\right\}\equiv \left\{{ℱ}_{AB}\right\},$ the set of morphisms are ordered pairs $Mo{r}_{{\mathit{\Im }}_{\mathit{A}\mathit{B}}}\left({ℱ}_{AB},{ℱ}_{AB}\right)=Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)\times Mo{r}_{{\mathit{\Im }}_{\mathit{B}}}\left({ℱ}_B,{ℱ}_B\right)$ such that for $\left(f_A,f_B\right)\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}\mathit{B}}}\left({ℱ}_{AB},{ℱ}_{AB}\right)$, $f_A:{ℱ}_A\to {ℱ}_A$ and $f_B: {ℱ}_B\to {ℱ}_B$ with composition performed component wise. Similarly, for the product category ${\mathit{\wp }}_{\mathit{q}\mathit{p}}$ the object is the pair $Ob{j}_{{\mathit{\wp }}_{\mathit{q}\mathit{p}}}=Ob{j}_{{\mathit{\wp }}_{\mathit{q}}}\times Ob{j}_{{\mathit{\wp }}_{\mathit{p}}}=\left\{\left(M_q,M_p\right)\right\}\equiv \left\{M_{qp}\right\}$, the set of morphisms are ordered pairs $Mo{r}_{{\mathit{\wp }}_{\mathit{q}\mathit{p}}}\left(M_{qp},M_{qp}\right)=Mo{r}_{{\mathit{\wp }}_{\mathit{q}}}\left(M_q,M_q\right)\times Mo{r}_{{\mathit{\wp }}_{\mathit{p}}}\left(M_p,M_p\right)$ such that for $g_{qp}\equiv \left(g_q,g_p\right)\in Mo{r}_{{\mathit{\wp }}_{\mathit{q}\mathit{p}}}\left(M_{qp},M_{qp}\right)$, and $g_p: M_p\to M_p$ with composition performed component wise. It is easily verified that ${\mathit{\Im }}_{\mathit{A}\mathit{B}}$ and ${\mathit{\wp }}_{\mathit{q}\mathit{p}}$ are categories where $1_{{ℱ}_{AB}}=\left(\epsilon ,\epsilon \right)$ and $1_{M_{qp}}=\left(\left(\infty ,i,0\right),\left(\infty ,i,0\right)\right)$ are the object identities.

Now use the gauge maps ${\phi }_0:A\to \left(\wp ,{\otimes }^q\right)$ and ${\theta }_0:B\to \left(\wp ,{\otimes }^p\right)$ to define $F_{{\phi }_0,{\theta }_0}:{\mathit{\Im }}_{\mathit{A}\mathit{B}}\to {\mathit{\wp }}_{\mathit{q}\mathit{p}}$ as $F_{{\phi }_0,{\theta }_0}\equiv F_{{\phi }_0}\times F_{{\theta }_0}=\left(F_{{\phi }_0},F_{{\theta }_0}\right)$ such that $F_{{\phi }_0,{\theta }_0}{ℱ}_{AB}=\left(F_{{\phi }_0}{ℱ}_A,F_{{\theta }_0}{ℱ}_B\right)=\left(M_q,M_p\right)=M_{qp}$ and for $f\equiv \left(f_A,f_B\right)\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}\mathit{B}}}\left({ℱ}_{AB},{ℱ}_{AB}\right)$, $F_{{\phi }_0,{\theta }_0}f=\left(F_{{\phi }_0}{f}_A,F_{{\theta }_0}{f}_B\right)=\left(g_q,g_p\right)=g_{qp}$. It is readily seen that $F_{{\phi }_0,{\theta }_0}$ is a functor because $F_{{\phi }_0,{\theta }_0}{1}_{{ℱ}_{AB}}=\left(F_{{\phi }_0}\epsilon ,F_{{\theta }_0}\epsilon \right)=\left(\left(\infty ,i,0\right),\left(\infty ,i,0\right)\right)=1_{M_{qp}}$ and for $h,k\equiv \left(h_A,h_B\right),\left(k_A,k_B\right)\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}\mathit{B}}}\left({ℱ}_{AB},{ℱ}_{AB}\right)$, if, then $F_{{\phi }_0,{\theta }_0}f\circ h=F_{{\phi }_0,{\theta }_0}\left(f_A\circ h_A,f_B\circ h_B\right)=\left(F_{{\phi }_0}{f}_A\circ h_A,F_{{\theta }_0}{f}_B\circ h_B\right)=\left(F_{{\phi }_0}{k}_A,F_{{\theta }_0}{k}_B\right)=F_{{\phi }_0,{\theta }_0}k$.

Thus:

$$\begin{array}{c}{F}_{{\phi }_0,{\theta }_0}{a}_1{a}_2\cdots a_m,b_1{b}_2\cdots b_n=\left(F_{{\phi }_0}{a}_1{a}_2\cdots a_m,F_{{\theta }_0}{b}_1{b}_2\cdots b_n\right)\\ =\left({\phi }_0\left(a_1\right){\otimes }^q{\phi }_0\left(a_2\right){\otimes }^q\cdots {\otimes }^q{\phi }_0\left(a_m\right),{\theta }_0\left(b_1\right){\otimes }^p{\theta }_0\left(b_2\right){\otimes }^p\cdots {\otimes }^p{\theta }_0\left(b_n\right)\right)\\ =\left(g_q,g_p\right)\end{array}$$

(13)

Of course, a similar construction can be made using products of a finite number of categories of systems and Müller-Wichards performance categories.

Thus, generally distinct performance triples $g_q\equiv \left(r_q,w_q,u_q\right)$ and $g_p\equiv \left(r_p,w_p,u_p\right)$ are obtained, which yield separate performance estimates for systems comprised of $A$ basis processes and for systems comprised of $B$ basis processes, respectively. Obviously, unless $q=p$, $g_q$ and $g_p$ cannot be properly combined algebraically to obtain a single performance estimate for a process comprised of both $A$ and $B$ basis processes. However, an inequality can be established by letting $g_1=g_q, g_2=\left(\infty ,i,0\right)=g_3,$ and $g_4=g_p$ in Lemma 2.6 in [1]. These yields $g_q{\otimes }^p{g}_p\ge g_q{\otimes }^q{g}_p$ when $1\le q\le p\le \infty$. An alternative approach is to estimate the combined processing time for systems composed of $A$ processes and for systems composed of $B$ processes from $g_q$ and $g_p$ using $t_{AB}=t_A+t_B$, where $t_A=\frac{\left|w_q\right|}{r_q}$ and $t_B=\frac{\left|w_p\right|}{r_p}$.

7. Closed Form Models

In this section, the above theory is used to develop general closed form system performance estimation models where a system’s performance $r$ and weight $w$ are explicit functions of the performances and weights of the processes that comprise the system. The next theorem provides models for systems comprised entirely of a finite number of arithmetic processes or data movement processes. In what follows, let $N=\left\{1,2,\cdots ,n\right\}$.

Theorem 17.

Let$a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right).$If${\phi }_0\left(a_i\right)\in C, i\in N,$or${\phi }_0\left(a_i\right)\in D, i\in N,$then

$$F_{{\phi }_0}^X{a}_1{a}_2\cdots a_n=\left(r_1,w_1,x\right){\otimes }^q\left(r_2,w_2,x\right){\otimes }^q\cdots {\otimes }^q\left(r_n,w_n,x\right)=\left(r,w,x\right),$$

(14)

where$x=1$or$0$when$X=C$or$D$, respectively,$w={{\displaystyle \sum }}_{i=1}^n{w}_i$, and

$$r=\frac{w}{{\left[{{\displaystyle \sum }}_{i=1}^n{\left(\frac{w_i}{r_i}\right)}^q\right]}^{\frac{1}{q}}}$$

(15)

Now consider systems comprised entirely of a finite number of delay processes.

Theorem 18.

Let$a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right).$If${\phi }_0\left(a_i\right)\in V, i\in N,$then

$$F_{{\phi }_0}^V{a}_1{a}_2\cdots a_n=\left(r_1,i,0\right){\otimes }^q\left(r_2,i,0\right){\otimes }^q\cdots {\otimes }^q\left(r_n,i,0\right)=\left(r,i,0\right),$$

(16)

where

$$r=\frac{1}{{\left[{{\displaystyle \sum }}_{i=1}^n{\left(\frac{1}{r_i}\right)}^q\right]}^{\frac{1}{q}}}.$$

(17)

The last two theorems can be used to construct closed form models for systems comprised of finite numbers of arithmetic, data movement, and delay processes.

Theorem 19.

Suppose the system$a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$is comprised of$n_C$arithmetic processes,$n_D$data movement processes, and$n_V$delay processes such that$n_C+n_D+n_V=n$. Then

$$F_{{\phi }_0}{a}_1{a}_2\cdots a_n=\left(r_C,w_C,1\right){\otimes }^q\left(r_D,w_D,0\right){\otimes }^q\left(r_V,i,0\right)=\left(r,w_C,1\right),$$

(18)

where

$$r=\frac{w_C}{{\left[{\left(\frac{w_C}{r_C}\right)}^q+{\left(\frac{w_D}{r_D}\right)}^q+{\left(\frac{1}{r_V}\right)}^q\right]}^{\frac{1}{q}}} ,$$

(19)

with$r_C$and$w_C$given by Theorem 17 when$X=C$and$n=n_C;$$r_D$and$w_D$given by Theorem 17 when$X=D$and$n=n_D;$and$r_V$given by Theorem 18 when$n=n_V$.

8. Statistical Properties of $r$ for Closed Form Models

Since system performance studies are often stochastic in nature, it is instructive to examine the statistical characteristics of the system performance variable $r$ for several cases using the closed form models of Theorem 17 for arithmetic and data movement elements.

8.1. Fixed Rates and Independent Random Weights

Assume that for both element types each rate $r_i=r_I, i\in N,$ where $r_I$ is a fixed value, and each weight $w_i, i\in N,$ is an independent random variable described by the same Poisson distribution with mean $\lambda$. In this case-for a fixed $q$, $n$, and λ-Equation (15) can be written as:

$$r=r_I\frac{{{\displaystyle \sum }}_{i=1}^n{w}_i}{{\left({{\displaystyle \sum }}_{i=1}^n{w}_i^q\right)}^{\frac{1}{q}}}$$

(20)

Note that it necessarily follows that ${{\displaystyle \sum }}_{i=1}^n{w}_i$ is also Poisson distributed with mean $n\lambda$.

Using these assumptions, ${10}^4$ trials were generated for each $\lambda$ and $q$ combination, where $\lambda \in \left\{10,20,40\right\}$ and $q\in \left\{1.5, 2, 2.5, 3, 4, \infty \right\}$, when$n=10$ and $r_I=1$. A kernel estimator of the probability density function (pdf) for the overall system rate $r$ associated with each combination is shown in Figure 3. Observe from Equation (20) that since this figure is generated using $r_I=1$, the horizontal axes of this figure can be interpreted as the ratio $r/r_I$. Thus, multiplying each pdf by $0<r_I\ne 1$ yields the pdf for the associated $r_I$.

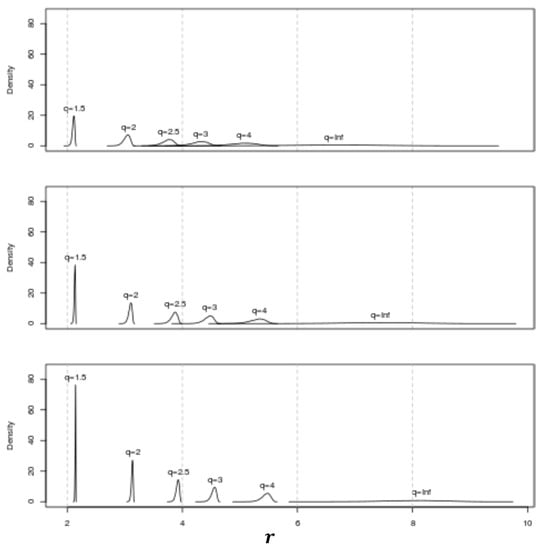
Figure 3. Probability density functions for $r$ for various $q$ values when $r_I=1, n=10,$ and $\lambda =10,20,40$ (top to bottom).

Inspection of Figure 3 quantifies-for a system comprised of a fixed number of basis processes and a fixed processing rate-the intuitively pleasing facts that: (i) for a fixed $q$ value, the peak value of the pdf increases, the $r$ value of the peak of the pdf effectively remains fixed, and the width of the pdf narrows as the mean process weight λ increases (i.e., the probability that the value of the overall system rate $r$ will be within a small fixed interval about the peak $r$ value increases with increasing mean process weight); and (ii) for a fixed mean process weight, the peak value of the pdf for $r$ increases and the width of the pdf broadens as $q$ increases in value (i.e., the overall peak system rate $r$ increases and the probability that $r$ will be within a small interval about the peak rate decreases with increasing system “speedup” or parallelism).

Kernel estimator pdfs were also obtained for $r$ using ${10}^4$ trials and Equation (20) with $r_I=1$ for $n\in \left\{2,4,8,10,16\right\}$ and $q\in \left\{1.5,2,2.5,3,4,\infty \right\}$. The weights for each trial were determined from a Poisson distribution with $\lambda =10$. These results are presented in Figure 4 where-as expected from the Figure 3 results-it is seen for each $n$ that the peak $r$ value increases, the distribution broadens, and the value of the pdf peak decreases with increasing $q$. Also expected is the fact that-although the pdf peak values and distribution width effectively remain the same-the distributions shift to larger $r$ values with increasing $q$ as $n$ increases.

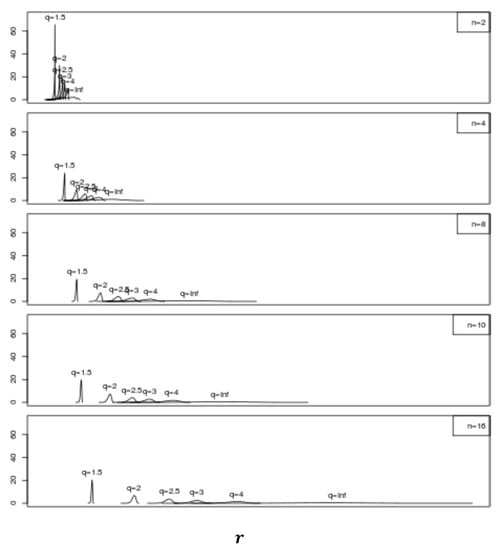
Figure 4. Probability density functions for $r$ when $r_I=1, q\in \left\{1.5,2,2.5,3,4,\infty \right\}$, and $n\in \left\{2,4,8,10,16\right\}.$

8.2. Random Rates and Random Weights

Now consider trials where for each trial—in addition to having Poisson distributed random weights as just described—the rates $r_i$ in Equation (15) are also randomly assigned using the exponential distribution:

$$f\left(x,\gamma \right)=\{\begin{array}{c}\gamma e^{-\gamma x}, x\ge 0\\ 0, \mathrm{otherwise}\end{array}.$$

(21)

Using this methodology, kernel estimator pdfs for $r$ were obtained using ${10}^4$ trials per combination for a range of $\gamma$ values and each $q\in \left\{1.5,2,2.5,3,4,\infty \right\}$ when $\lambda =10$ and $n=10$. These results are presented in Figure 5 for $\gamma \in \left\{2,10\right\}$ and in Figure 6 when $q$ is also unity and $\gamma \in \left\{1,2,3\right\}$. Each of the pdfs in the two lower Figures in Figure 6 are scaled by their $\gamma$ values, i.e., all of the resulting $r$ values are divided by their respective $\gamma$ values, so that the pdfs for all $\gamma$ values fit on the same horizontal axis value range.

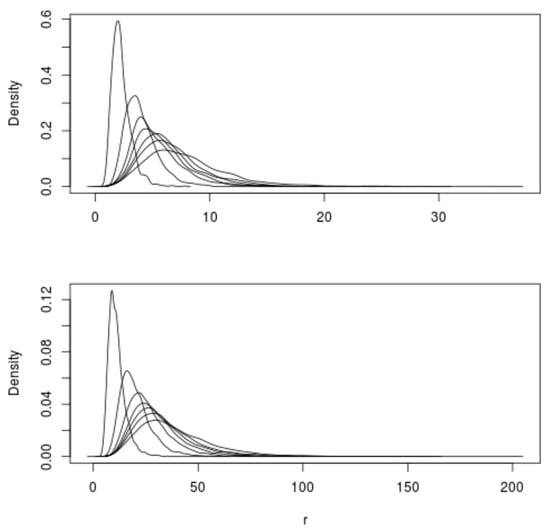
Figure 5. Probability density functions for $r$ when $n=10, \lambda =10, \gamma =2 \left(top\right),$ $\gamma =10$ (bottom) and $q\in \left\{1.5,2,2.5,3,4,\infty \right\}$ (left to right).

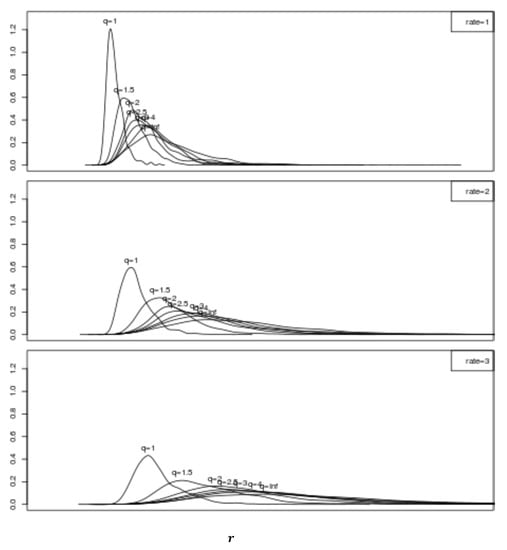
Figure 6. Probability density functions for $r$ when $n=10, \lambda =10, \gamma \in \left\{1,2,3\right\},$ and $q\in \left\{1,1.5,2,2.5,3,4,\infty \right\}$. Each $r$ value for $\gamma \in \left\{2,3\right\}$ has been divided by the associated value of $\gamma$.

Observe from these figures that—when compared with the previous results for fixed $r_I$—the inclusion of random rates causes the $q$ parameterized pdfs to be closer together and overlap. The presence of randomness increases the variance associated with each $r$ pdf and, interestingly, tends to significantly decrease the sensitivity of the pdfs to the value of $q$. This comparison is made more clear in Figure 7 where the graphs of the pdfs for $n=10, \lambda =10,$ and $q\in \left\{1.5,2,2.5,3,4\right\}$ are placed one above the other for the case where both the rates and weights are randomly selected as above when $\gamma =10$ (upper Figure) and the case where the rates all have unit value and only the weights are Poisson distributed (lower Figure). Each of the pdfs in the upper Figure are scaled by the associated $\gamma =10$ value.

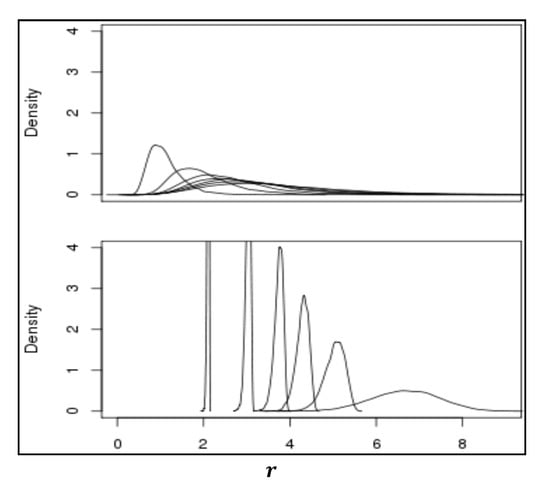
Figure 7. Probability density functions for $r$ when $n=10, \lambda =10 \mathrm{and}q\in \left\{1.5,2,2.5,3,4\right\}$.

9. Special Case Closed Form Models

Here, Theorems 17–19 are used to produce several closed form models when the performance values and the weight values are assumed to be equal for all processes in a system. Such processes are equal processes and the associated system models are special case closed form models (SCCFMs).

SCCFM 1.

If $a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$ is a system such that ${\phi }_0\left(a_i\right)=\left(\rho ,\lambda ,1\right)\in C, i\in N$, then $F_{{\phi }_0}^C{a}_1{a}_2\cdots a_n=\left(r,w,1\right)$, where $w=n\lambda$ and $r=n^{1-\frac{1}{q}} \rho$. The time required for the system to complete its arithmetic operations is $t_q^C=n^{\frac{1}{q}}\left(\frac{\lambda }{\rho }\right)$.

Since the next model is also a direct consequence of Theorem 17 and its proof follows that of the previous model, it is stated without proof.

SCCFM 2.

If $a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$ is a system such that ${\phi }_0\left(a_i\right)=\left(\sigma ,\omega ,0\right)\in D, i\in N$, then $F_{{\phi }_0}^D{a}_1{a}_2\cdots a_n=\left(r,w,0\right)$, where $w=n\omega$ and $r=n^{1-\frac{1}{q}} \sigma$. The time required for the system to complete moving all of its data is $t_q^D=n^{\frac{1}{q}}\left(\frac{\omega }{\sigma }\right)$.

SCCFM 3.

If $a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$ is a system such that ${\phi }_0\left(a_j\right)=\left(\delta ,i,0\right)\in V, j\in N$, then $F_{{\phi }_0}^V{a}_1{a}_2\cdots a_n=\left(r,i,0\right)$, where $r=n^{-\frac{1}{q}} \delta$. The time delay for this system is $t_q^V=n^{\frac{1}{q}}\left(\frac{1}{\delta }\right)$.

Note that: (i) when $q=1$, the processing is sequential and as required, the time $t_1^X, X\in \left\{C,D,V\right\},$ for the systems to complete their processing is the sum of the $n$ individual times required to complete each process in the system; (ii) when $1<q<\infty$, the processing time is “skewed” or “compressed” and $t_q^X<t_1^X$.

SCCFM 4.

Suppose the system $a_1{a}_2\cdots a_n\in Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$ is comprised of $n_C$ equal arithmetic processes, $n_D$ equal data movement processes, and $n_V$ equal delay processes such that $n_C+n_D+n_V=n$. Then:

$$F_{{\phi }_0}{a}_1{a}_2\cdots a_n=\left(r_C,w_C,1\right){\otimes }^q\left(r_D,w_D,0\right){\otimes }^q\left(r_V,i,0\right)=\left(r_{CDV},n_C\lambda ,1\right),$$

(22)

where $r_C$ and $w_C$ are given by SCCFM 1 when $n=n_C;$ $r_D$ and $w_D$ are given by SCCFM 2 when $n=n_D;$ ${\mathrm{r}}_{\mathrm{V}}$ given by SCCFM 3 when $n=n_V$; and:

$$r_{CDV}=\frac{n_C\lambda }{{\left[n_C{\left(\frac{\lambda }{\rho }\right)}^q+n_D{\left(\frac{\omega }{\sigma }\right)}^q+n_V{\left(\frac{1}{\delta }\right)}^q\right]}^{\frac{1}{q}}} .$$

(23)

The time required for this system to complete its processing is:

$$t_q^{CDV}={\left[{\left(t_q^C\right)}^q+{\left(t_q^D\right)}^q+{\left(t_q^V\right)}^q\right]}^{\frac{1}{q}} .$$

(24)

Again, note that when $q=1$, $t_1^{CDV}$ is the sum of the system delays, the time required for the system to complete processing its arithmetic operations, and the time required for the system to complete its data movement operations.

10. Applications of Special Case Closed Form Models

Special case closed form models are useful for understanding and describing fundamental properties and dynamics of CMW system performance models. The following subsections provide several examples of this.

10.1. The Effect of $q$ Upon the $t_q^X-n_X$ Dependence, $X\in \left\{C,D,V\right\}$

It is easily seen from SCCFM1-SCCFM3 that the differential of $t_q^X$ (with respect to $n_X$) can be written as:

$$d{t}_q^X=\frac{1}{q}{t}_q^X\frac{d{n}_X}{n_X}, X\in \left\{C,D,V\right\}.$$

(25)

Dividing both sides of this equation by $t_q^X$ yields:

$$\frac{d{t}_q^X}{t_q^X}=\frac{1}{q}\frac{d{n}_X}{n_X}$$

(26)

which can be written as

$$d\ln t_q^X=\frac{1}{q}d\ln n_X$$

(27)

or as

$$\frac{d\ln t_q^X}{d\ln n_X}=\frac{1}{q}.$$

(28)

It follows from this that for these SCCFMs, $\ln t_q^X$ varies linearly with $\ln n_X$ with an associated slope of $q^{-1}$. This implies the intuitively pleasing result that for SCCFM1-SCCFM3, increasing the system’s parallelization (i.e., increasing the $q$ value) decreases the processing time $t_q^X$-regardless of the number $n_X$ of basis processes that must be processed.

10.2. A Stationary Action Principle for SCCFM4 System Performance

Consider SCCFM4, assume for fixed $q$ that $\left[{\left(t_q^C\right)}^q+{\left(t_q^D\right)}^q+{\left(t_q^V\right)}^q\right]=\chi \left(t\right)\equiv \chi$ is time dependent, and let the function:

$${ℒ}_q\equiv {ℒ}_q\left(\chi ,\dot{\chi }\right)=\frac{1}{q}{\chi }^{\frac{1-q}{q}}\dot{\chi },$$

(29)

where $\dot{\chi }\equiv \frac{d\chi }{dt}$, describe the system’s performance with time. Using Equation (29), it is found that:

$$\frac{d}{dt}\left(\frac{\partial {ℒ}_q}{\partial \dot{\chi }}\right)=\frac{\partial {ℒ}_q}{\partial \chi },$$

(30)

i.e., ${ℒ}_q$ satisfies the Euler-Lagrange equation. Consequently, ${ℒ}_q$ is the performance Lagrangian for the system, Equation (30) is the associated equation of motion for the system’s performance, and the integral

$${{\displaystyle \int }}_0^{\tau }{ℒ}_{q}dt$$

(31)

is stationary so that its first variation $\delta$ vanishes (e.g., [27]). This has the following interpretation: If $\sum$ is the configuration space $\chi \times t\subset {ℝ}_{+}\times {ℝ}_{+}$ and processing begins at $t=0$ and is completed at $t=\tau$, then the actual processing path followed by $\left[{\left(t_q^C\right)}^q+{\left(t_q^D\right)}^q+{\left(t_q^V\right)}^q\right]$ in $\sum$ during the fixed processing interval $\left[0,\tau \right]$ is such that:

$$\delta {{\displaystyle \int }}_0^{\tau }{ℒ}_{q}dt=0$$

(32)

with respect to all path variations in $\sum$, which vanish at the end-points of the interval.

10.3. Invariance of the Equation of Motion

Note that for any arbitrary (twice differentiable) function $\varphi \left(\chi \right)$, the transformed performance Lagrangian

$${ℒ}_q^{\#}\equiv {ℒ}_q+\dot{\varphi }$$

(33)

also describes the processing path followed by $\left[{\left(t_q^C\right)}^q+{\left(t_q^D\right)}^q+{\left(t_q^V\right)}^q\right]$ in $\sum$ during the fixed processing interval $\left[0,\tau \right]$ since:

$$\delta {{\displaystyle \int }}_0^{\tau }{ℒ}_q^{\#}dt=\delta {{\displaystyle \int }}_0^{\tau }{ℒ}_{q}dt+\delta {\left[\varphi \right]}_0^{\tau }=\delta {{\displaystyle \int }}_0^{\tau }{ℒ}_{q}dt=0.$$

(34)

Thus, although the performance Lagrangian is not unique, by extension, it can be concluded that the equation of motion for the system’s performance is invariant under all transformations of the performance Lagrangian of the form given by Equation (33).

11. Concluding Remarks

This paper has presented a category theoretic reformulation of the Müller-Wichards system performance model. The use of category theoretic terminology provides a precise and efficient mathematical vocabulary for defining categories of systems, system performance, and system performance functors. These functors were shown to be useful for discussing factorizing systems without changing their performance and identifying model symmetries and invariants. Such formal mathematical properties of models tend to characterize aspects of the real systems that the models represent.

A practical feature of the model is that it can be implemented in a relatively straightforward manner as a software package. A user can assign to each basis process—via a gauge map—its numerical triple in the performance category. This defines for each basis process its type (arithmetic, data movement, or delay element), rate, and weight. The associated performance functor then uses these assignments to automatically generate a final performance triple for any system (string of basis processes) in the category of systems defined by the process basis set. Several other useful features of the model include using closed form performance models to provide “quick” performance estimates, as well as to provide “sanity checks” for results obtained from software implementations of the model; generating stochastic-based performance studies by treating rates and weights as random variables (as illustrated in Section 8); and applying closed form models to abstractly characterize aspects of system performance (as illustrated in Section 10).

Future research involves defining an appropriate metric $d$ on $Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right)$ that measures the similarity between systems; and finding an approach for classifying subsets of interest in the associated metric space $\left(Mo{r}_{{\mathit{\Im }}_{\mathit{A}}}\left({ℱ}_A,{ℱ}_A\right),d\right)$ such that the systems within such a class are very similar [28]. An implementation of this classification scheme in a software package, which also uses $F_{{\phi }_0}$ to automatically evaluate in ${\mathit{\wp }}_{\mathit{q}}$ the performance of the systems in such a class can be useful for scheduling analysis, as well as for making informed high level system engineering design trade-offs.