Nonlinear Phenomena in Cournot Duopoly Model
Abstract
1. Introduction
- there is more than one company, and all the companies produce a homogenous product (there is no product differentiation);
- the companies do not cooperate (there is no collusion);
- the companies have a market power (each company’s output decision affects the goods’ price);
- the number of companies is fixed;
- the companies compete in quantities and choose the quantities simultaneously;
- the companies are economically rational and act strategically, usually seeking to maximize the profit given by their competitors’ decision.
- there are at least two companies producing a homogeneous product, and they cannot cooperate in any way;
- the companies compete by setting the prices simultaneously, and consumers want to buy everything from the company that offers a lower price;
- both companies have the same constant unit cost of the production, then marginal and average costs are the same, and they are equal to the competitive prices (as long as the price is above the unit cost, the company is willing to supply any amount that is demanded; if the price is equal to the unit cost, then it is indifferent to how much the company sells; the company will never want to set a price below the unit cost).
- the leader must know ex ante that the follower observes his/her action;
- the follower must have no means of reacting to the next leader’s action, and the leader must know that (if the follower could react to the leader’s action and the leader knew this, the leader’s best response would be to play the follower’s action).
- In the Cournot model, the quantity produced by every duopoly will be and the price on the market will be ; therefore, the profit of every duopolist will be
- In the Bertrand model, the quantity produced by every duopolist will be and in a very absurd way, the market price will be zero (therefore, the profit of every duopolist will also be zero);
- In the Stackelberg model, the leader will sell a quantity at the price (and the profit will be ), when the follower will sell a quantity at the same price as the leader (and the profit will be ).
2. Materials and Methods
- Firstly, a stationary solution to (1) is found. For the given , the stationary solution can be found as a solution to the equation
- Next, the stationary solution having been found , the behavior of solutions that start near this solution can be examined. Therefore, we consider the following difference that measures the deviation from at time The corresponding difference equation with stationary solution of 0 is The simplification of the latter equation is its linear approximation by the Taylor theorem Neglecting the higher order terms of the following linear system of difference, we can consider the equations:where is the Jacobian matrix evaluated for stationary solution and at the given value of the parameter.
- Finally, the stability of the stationary solution can be assessed. When using Jacobian matrix , its eigenvalues can be found. The values of these eigenvalues determine the character of the stationary solution For details, see [15].
2.1. Bifurcation Diagram
- A limit set X of a point where W is an open set in state space, is the set of all points for which a sequence of natural numbers characterized by exist, and By the notation , it is meant that the map (1) is composed of itself times.
- A compact set is called the attractor if there is such a neighborhood U of A in which A is the limit set of all initial values
- (i)
- Choose the initial value of of the parameter set M of the map (1).
- (ii)
- Randomly choose the initial value of the map (1).
- (iii)
- Calculate several first iterations of (1) and ignore them.
- (iv)
- Calculate several next iterations of (1) and plot them.
- (v)
- Increment the value of the parameter of the map (1), and repeat all the above given steps until you reach the end of the parameter sets
2.2. Lyapunov Exponent
- If , then , which means that two initially close trajectories can move away from each other, and the system (1) is sensitively dependent on the initial conditions.
- On other side, if , then , which means that two initially close trajectories can stay close to each other, and the system (1) is not sensitively dependent on the initial conditions.
- (i)
- Start with an initial orthonormal basis of the space that sufficiently characterizes the initial circle
- (ii)
- Compute the vectors and
- (iii)
- Use the vectors and the Gram–Schmidt orthogonalization method to find a new orthogonal basis .
- (iv)
- Set , and consider the basis for further computation.
- (v)
- Repeat (ii), (iii) and (iv) for a sufficiently large number of steps At each step, use (1), compute the following state and use it instead of in the Jacobian matrix in Step (ii).
- (vi)
- The good approximation for the total expansion in the direction where is vector Thus, a good approximation of the Lyapunov number is where is the Euclidean norm.
3. Model
3.1. Fundamental Principles of the Dynamics Cournot Oligopoly Model
3.2. Dynamics of Cournot Model
3.3. Linear Model
3.4. Nonlinear Model
- the quantity demanded is reciprocal to the price,
- the companies operate under constant unit costs.
4. Discussion
4.1. The Equilibrium of the Linear Model and Its Properties
4.2. Equilibrium of the Nonlinear Model and Its Properties
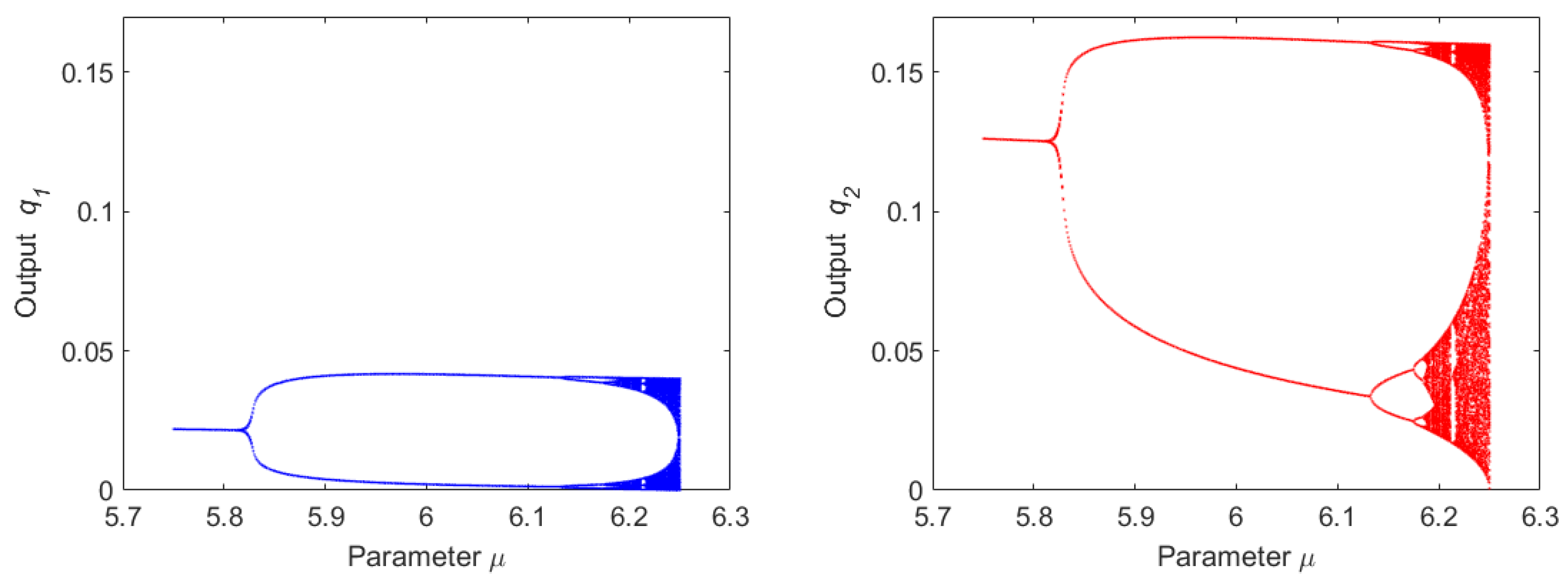
4.3. Bifurcation Diagram of the Duopoly Model
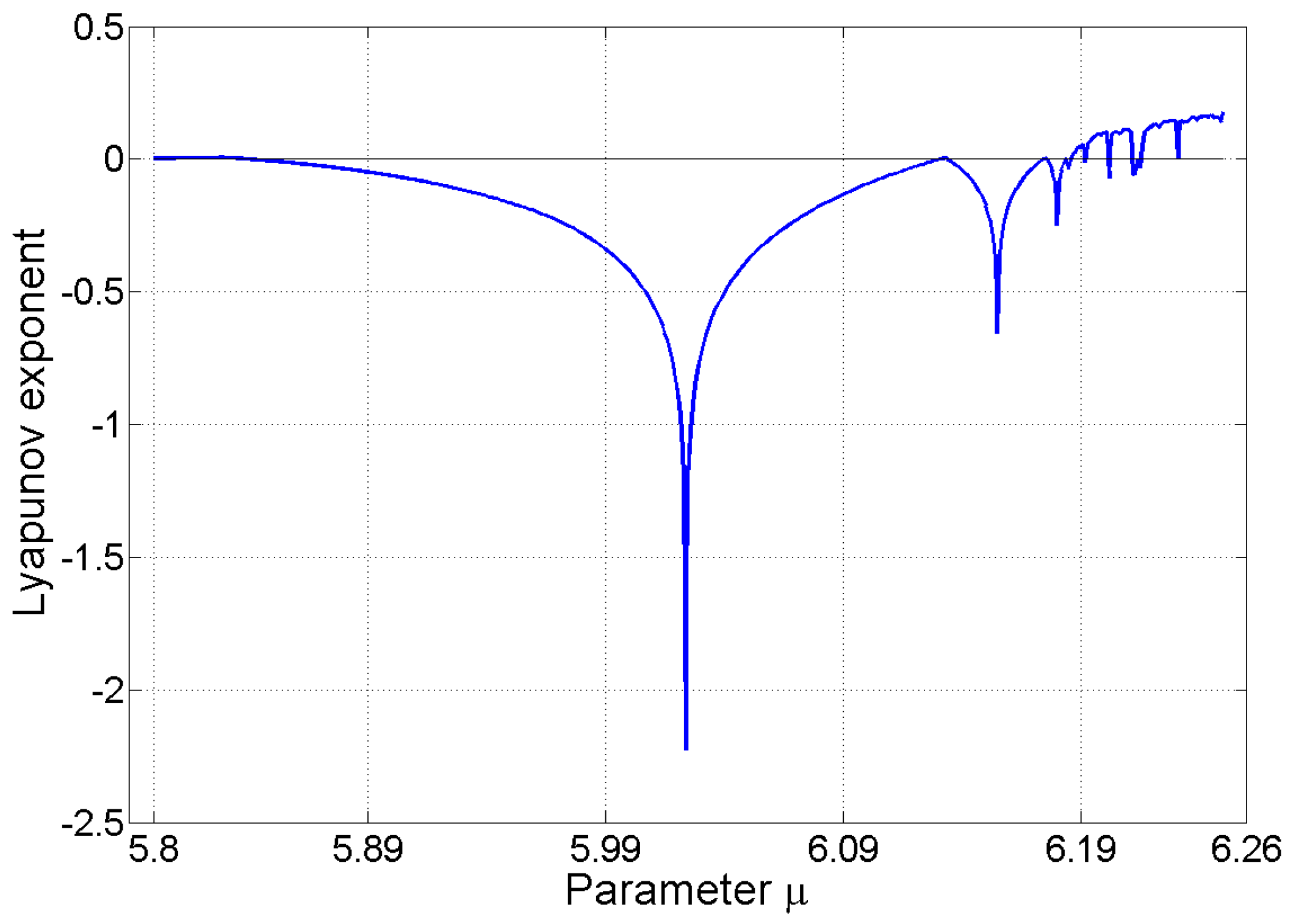
4.4. Lyapunov Exponent of the Duopoly Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. MATLAB Implementation of the Bifurcation Diagram for the Duopoly Map

Appendix B. MATLAB Implementation of the Lyapunov Exponent for the Duopoly Map


References
- Pražák, P. On a Dynamic Model of Revenue Maximizing Firm. In Mathematical Methods in Economics 2010, Part II; University of South Bohemia: České Budějovice, Czech Republic, 2010; pp. 542–547. ISBN 978-80-7394-218-2. [Google Scholar]
- Rand, D. Exotic phenomena in games and duopoly models. J. Math. Econ. 1978, 5, 173–184. [Google Scholar] [CrossRef]
- Kopel, M. Simple and complex adjustment dynamics in Cournot duopoly models. Chaos Solitons Fractals 1996, 7, 2031–2048. [Google Scholar] [CrossRef]
- Puu, T. Chaos in Duopoly Pricing. Chaos Solitons Fractals 1991, 1, 573–581. [Google Scholar] [CrossRef]
- Puu, T. Attractors, Bufurcations and Chaos, Nonlinear Phenomena in Economics; Springer: Berlin, Germany, 2003; ISBN 3-540-40226-8. [Google Scholar]
- Pražák, P. Nonlinear Cournot Duopoly Game. In Hradec Economic Days; University of Hradec Králové: Hradec Králové, Czech Republic, 2018; Volume 8, pp. 188–195. ISBN 978-80-7435-701-5. [Google Scholar]
- Bischi, G.I.; Chiarella, C.; Kopel, M.; Szidarovszky, F. Nonlinear Oligopolies, Stability and Bifurcations; Springer: Berlin, Germany, 2010; ISBN 978-3-642-02105-3. [Google Scholar]
- Zhang, J.; Da, Q.; Wang, Y. Analysis of nonlinear duopoly game with heterogeneous players. Econ. Model. 2007, 24, 138–148. [Google Scholar] [CrossRef]
- Varian, H.R. Intermediate Microeconomics: A Modern Approach; W. W. Norton & Company: New York, NY, USA, 2006; ISBN 0-393-92702-4. [Google Scholar]
- Cournot, A. Récherces Sur Les Principes Mathématiques de la Théorie des Richesses; Hachette: Paris, France, 1838. (In French) [Google Scholar]
- Betrand, J. Théorie des Richesses: revue de Théories mathématiques de la richesse sociale par Léon Walras et Recherches sur les principes mathématiques de la théorie des richesses par Augustin Cournot. J. Savants 1883, 67, 499–508. (In French) [Google Scholar]
- Stackelberg, H.F. Marktform und Gleichgewicht; Springer: Berlin, Germany, 1934. (In German) [Google Scholar]
- Kulenovic, M.R.S.; Merino, O. Discrete Dynamical Systems and Difference Equations with Mathematica; Chapman & Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos, An Introduction to Dynamical Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Elaydi, S. An Introduction to Difference Equations; Springer: New York, NY, USA, 2005; ISBN 0-387-23059-9. [Google Scholar]
- Boeing, G. Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction. Systems 2016, 4, 37. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Gibbons, R. Game Theory for Applied Economists; Princeton University Press: Princeton, NJ, USA, 1992; ISBN 0-691-04308-6. [Google Scholar]
- Varian, H.R. Microeconomic Analysis; W. W. Norton & Company: New York, NY, USA, 1992; ISBN 0-393-95735-7. [Google Scholar]
- Huang, J. Demand Functions in Decision Modeling: A Comprehensive Survey and Research Directions. Decis. Sci. 2013, 44, 557–609. [Google Scholar] [CrossRef]
- Song, Y.Y.; Ray, S.; Li, S.L. Structural properties of buyback contracts for price-setting newsvendors. Manuf. Serv. Oper. Manag. 2008, 10, 1–18. [Google Scholar] [CrossRef]
- Jeuland, A.P.; Shugan, S.M. Channel of distribution profits when channel members form conjectures. Mark. Sci. 1988, 7, 202–210. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pražák, P.; Kovárník, J. Nonlinear Phenomena in Cournot Duopoly Model. Systems 2018, 6, 30. https://doi.org/10.3390/systems6030030
Pražák P, Kovárník J. Nonlinear Phenomena in Cournot Duopoly Model. Systems. 2018; 6(3):30. https://doi.org/10.3390/systems6030030
Chicago/Turabian StylePražák, Pavel, and Jaroslav Kovárník. 2018. "Nonlinear Phenomena in Cournot Duopoly Model" Systems 6, no. 3: 30. https://doi.org/10.3390/systems6030030
APA StylePražák, P., & Kovárník, J. (2018). Nonlinear Phenomena in Cournot Duopoly Model. Systems, 6(3), 30. https://doi.org/10.3390/systems6030030




