Abstract
The economic world is very dynamic, and most phenomena appearing in this world are mutually interconnected. These connections may result in the emergence of nonlinear relationships among economic agents. Research discussions about different markets’ structures cannot be considered as finished yet. Even such a well-known concept as oligopoly can be described with different models applying diverse assumptions and using various values of parameters; for example, the Cournot duopoly game, Bertrand duopoly game or Stackelberg duopoly game can be and are used. These models usually assume linear functions and make analyses of the behavior of the two companies. The aim of this paper is to consider a nonlinear inverse demand function in the Cournot duopoly model. Supposing there is a sufficiently large proportion among the costs of the two companies, we can possibly detect nonlinear phenomena such as bifurcation of limit values of production or deterministic chaos. To prove a sensitive dependence on the initial condition, which accompanies deterministic chaos, the concept of Lyapunov exponents is used. We also point out the fact that even though some particular values of parameters are irrelevant for the above-mentioned nonlinear phenomena, it is worth being aware of their existence.
1. Introduction
One of the impacts of globalization is the existence of very rich and powerful corporations in the economic world. These corporations are usually multinational and of a considerable size, and they can have a significant impact on setting the prices in particular markets [1]. Consequently, trading can be completely controlled by several companies. This is the reason why the oligopoly structure of markets and their different models are constantly studied and modified. Different nonlinear versions of oligopoly models can be found in [2] or [3], where the assumption of unimodal reaction functions was established. The papers [4,5,6] worked with the assumption that the quantity of demanded goods is reciprocal to their price. Many specific details of dynamical oligopoly models can be found in [7]. A nonlinear version of duopoly for heterogeneous players is introduced in [8]. It is well known that oligopoly markets consider a few producers of the same goods or perfectly substitutable goods. Each company must reflect not only on the market demand, but also on the competitors’ activities, which is the property that is known as interdependence. Before a nonlinear duopoly model is presented, results based on static linear models will be briefly reminded [9]. As was mentioned above, several different theoretical models about oligopoly exist, such as the Cournot duopoly game, Bertrand duopoly game or Stackelberg duopoly game.
Antoine Augustin Cournot (1801–1877) formulated his model in 1838 with the following assumptions [10]:
- there is more than one company, and all the companies produce a homogenous product (there is no product differentiation);
- the companies do not cooperate (there is no collusion);
- the companies have a market power (each company’s output decision affects the goods’ price);
- the number of companies is fixed;
- the companies compete in quantities and choose the quantities simultaneously;
- the companies are economically rational and act strategically, usually seeking to maximize the profit given by their competitors’ decision.
In the typical Cournot duopoly game with the linear price formula, another assumption about the constant marginal costs (i.e., 0) was formulated. Cournot constructed a profit function for each company, and then, partial differentiation was used to construct a function representing the company’s best response to the given output levels of other firms on the market. A stable equilibrium occurs where these functions intersect. Consequently, if the equilibrium is reached, each company’s expectations of how other companies will act appear to be correct, and no company wants to change its output decision. The strategy of the duopoly game works in the following way: when the first company assumes the output of the second company is zero, then that first company deals with the total market demand (the demand for the products of the first company is the market demand) and, with respect to non-perfect competition, chooses the output. Consequently, the second company assumes the output of the first company as given; the demand for the production of this company is half of the market, and this company will set up its quantity. The first company assumes the output of the second company as given and will reduce its production, while the second company will increase its production.
Joseph Louis Francois Bertrand (1822–1900) formulated his model in 1883 [11]. While Cournot analyzed quantity in his model, Bertrand focused on price. This model made the following very specific assumptions:
- there are at least two companies producing a homogeneous product, and they cannot cooperate in any way;
- the companies compete by setting the prices simultaneously, and consumers want to buy everything from the company that offers a lower price;
- both companies have the same constant unit cost of the production, then marginal and average costs are the same, and they are equal to the competitive prices (as long as the price is above the unit cost, the company is willing to supply any amount that is demanded; if the price is equal to the unit cost, then it is indifferent to how much the company sells; the company will never want to set a price below the unit cost).
If both the companies set the competitive price at the level of the price equal to the marginal costs, neither of them will earn any profits. However, if one company sets the price equal to the marginal costs, then if the other company raises its price above the unit costs, it will earn nothing, since all consumers will buy the goods from the company still setting the competitive price. If both the companies set the same price above the unit costs and share the market, then either of them has a stimulus to undercut the other company by an arbitrarily small amount, and then, it can capture the whole market and at the same time almost double its profits. Therefore, there can be no equilibrium with both the companies setting the same price above the marginal costs. There can be no equilibrium with the companies setting different prices, as well. The company setting the higher price will earn nothing (the company offering lower prices serves all of the customers); therefore, it will want to lower its price to undercut the lower priced company. Hence, the only equilibrium in the Bertrand model occurs when both companies set the price equal to the unit costs.
Heinrich Freiherr von Stackelberg (1905–1946) introduced his duopoly model in 1934 [12]. In his model, one player is the leader, and the other player is the follower; they compete in the sphere of quantity. In a way, this model is a modification of the Cournot model. However, there are some constraints on sustaining Stackelberg’s equilibrium:
- the leader must know ex ante that the follower observes his/her action;
- the follower must have no means of reacting to the next leader’s action, and the leader must know that (if the follower could react to the leader’s action and the leader knew this, the leader’s best response would be to play the follower’s action).
Two companies may get engaged in Stackelberg’s competition if one of them has a sort of advantage enabling it to move first (more generally, the leader must have commitment power). Moving observably first is the most obvious means of commitment. Once the leader has made his/her move, he/she cannot undo it (he/she is committed to that action). Holding excess capacity is another means of commitment. The mutual comparison of the above-mentioned linear models (where a presents fixed costs and b average variable costs) brings the following results [9]:
- In the Cournot model, the quantity produced by every duopoly will be and the price on the market will be ; therefore, the profit of every duopolist will be
- In the Bertrand model, the quantity produced by every duopolist will be and in a very absurd way, the market price will be zero (therefore, the profit of every duopolist will also be zero);
- In the Stackelberg model, the leader will sell a quantity at the price (and the profit will be ), when the follower will sell a quantity at the same price as the leader (and the profit will be ).
The above-described models are static, and they usually assume a linear inverse demand function and a linear cost function. The aim of this paper is to consider a nonlinear inverse demand function in a dynamic Cournot duopoly model. Supposing there is a sufficiently large proportion among the costs of the two companies, it is possible to detect nonlinear phenomena such as the bifurcation of limit values of production or deterministic chaos. To prove a sensitive dependence on the initial condition, the concept of the Lyapunov exponent is introduced. The computation of the Lyapunov exponent of the introduced nonlinear Cournot model can be considered as an important complement to the earlier published results in [3,4,5,7,13].
The paper is organized in the following way: First, basic concepts and methods connected with discrete dynamical systems are introduced in Section 2. Second, a general dynamical model of oligopoly based on the treatise in [13] is introduced in Section 3. Then, a nonlinear Cournot duopoly model is presented. In contrast to the classical Cournot duopoly game, a nonlinear inverse demand function is considered. These issues are studied in [2,5]. Similar properties as in [4] are considered in this paper. The final part, Section 4, presents a discussion based on solutions to both the linear model and the nonlinear one. The main aim of the simultaneous presentation of the results brought by the linear model and the nonlinear model is to emphasize the big difference between these two types of models and to illustrate this difference in one place.
2. Materials and Methods
The dynamics of a discrete dynamical system with state space and parameter space can be given as a system of difference equations:
where is a state of the system at time is a parameter and is a map. Usually, the initial condition is also given. Provided that map F is nonlinear, the formula of the solution to (1) cannot be found. As an alternative, it is possible to consider only a qualitative solution to the system (1). The fundamental steps of this procedure are briefly introduced [14,15]:
- Firstly, a stationary solution to (1) is found. For the given , the stationary solution can be found as a solution to the equation
- Next, the stationary solution having been found , the behavior of solutions that start near this solution can be examined. Therefore, we consider the following difference that measures the deviation from at time The corresponding difference equation with stationary solution of 0 is The simplification of the latter equation is its linear approximation by the Taylor theorem Neglecting the higher order terms of the following linear system of difference, we can consider the equations:where is the Jacobian matrix evaluated for stationary solution and at the given value of the parameter.
- Finally, the stability of the stationary solution can be assessed. When using Jacobian matrix , its eigenvalues can be found. The values of these eigenvalues determine the character of the stationary solution For details, see [15].
The characteristics of the solution to (1) obviously depend on the value of parameter In this case, it is necessary to take into account the phenomenon called bifurcation [13,14].
2.1. Bifurcation Diagram
Only necessary concepts are introduced here, and details can be found in [14]. The bifurcation diagram shows the relationship between the values of a parameter and the values of stationary points, or values of periodic orbits of the given dynamical system. More generally, asymptotically-stable stationary points and periodical points are special types of attractors that can be briefly characterized in two steps as follows:
- A limit set X of a point where W is an open set in state space, is the set of all points for which a sequence of natural numbers characterized by exist, and By the notation , it is meant that the map (1) is composed of itself times.
- A compact set is called the attractor if there is such a neighborhood U of A in which A is the limit set of all initial values
In other words, the attractor is a set of all points to which trajectories starting from initial points in a neighborhood of the set will converge. The parameter space is confined to the case of in this paper. Now it is possible to characterize the bifurcation diagram in more details: if is a parameter of dynamical System (1) and is a set of all attracting points for the given value of then the bifurcation diagram is the graph of the relation This figure shows the birth, evolution and extinction of attracting sets [14]. The algorithm for plotting a bifurcation diagram is based on the direct application of the attractor’s definition; instead of computing exact limit points, only points for a sufficiently large number of iterations of the map (1) are considered. The algorithm can be described as follows:
- (i)
- Choose the initial value of of the parameter set M of the map (1).
- (ii)
- Randomly choose the initial value of the map (1).
- (iii)
- Calculate several first iterations of (1) and ignore them.
- (iv)
- Calculate several next iterations of (1) and plot them.
- (v)
- Increment the value of the parameter of the map (1), and repeat all the above given steps until you reach the end of the parameter sets
More details can be found in [14]. The given algorithm for the duopoly model was implemented in MATLAB; see Appendix A. Notes about the visual analysis of nonlinear dynamical systems are introduced in [16].
2.2. Lyapunov Exponent
The bifurcation diagram can also point out the phenomenon called deterministic chaos. In this case, almost all intervals seem to be filled with the plot. Once such a phenomenon is observed, it is useful to compute Lyapunov exponents for special values of parameter This method can formally identify the sensitive dependence of the given system on the initial conditions, which is one of the characteristic attributes of chaotic behavior. This exponent measures the exponential rate of the separation of very close trajectories.
Only a concise characterization based on [14] is provided here. Let F be the map on , similarly as in (1), and provided where is an initial point, the given value of the parameter and the first derivative of the map F with respect to In other words, J is the Jacobian matrix of the map For , let be the length of the k-th longest orthogonal axis of the ellipsoid where is the dimensional unit sphere with the center This means that the value measures the expansion or contraction in the neighborhood of the orbit starting at during the first m iterations. If the following limit:
exists, it is called the k-th Lyapunov number, and moreover, the k-th Lyapunov exponent of is
- If , then , which means that two initially close trajectories can move away from each other, and the system (1) is sensitively dependent on the initial conditions.
- On other side, if , then , which means that two initially close trajectories can stay close to each other, and the system (1) is not sensitively dependent on the initial conditions.
The concept of the Lyapunov exponent allows us to characterize chaotic orbits (cf. [14]): the orbit is chaotic if it is not asymptotically periodic, no Lyapunov exponent is exactly zero and The particular algorithm for computing approximations of Lyapunov exponents uses an indirect approach. It is based on ideas given in [14,17]. If the state space is which is the case that is required in this paper, it can be briefly described as follows:
- (i)
- Start with an initial orthonormal basis of the space that sufficiently characterizes the initial circle
- (ii)
- Compute the vectors and
- (iii)
- Use the vectors and the Gram–Schmidt orthogonalization method to find a new orthogonal basis .
- (iv)
- Set , and consider the basis for further computation.
- (v)
- Repeat (ii), (iii) and (iv) for a sufficiently large number of steps At each step, use (1), compute the following state and use it instead of in the Jacobian matrix in Step (ii).
- (vi)
- The good approximation for the total expansion in the direction where is vector Thus, a good approximation of the Lyapunov number is where is the Euclidean norm.
The given algorithm is not applicable to the real numerical computation because it uses very large and small numbers. To avoid this complication, it is possible to use an orthonormal basis at each step (iv); it is possible to use the unit vector where Notice further that If we take the logarithm of the latter relationship, we can summarize that the formula:
provides a good approximation of the k-th largest Lyapunov exponent The given algorithm can be implemented in MATLAB (see Appendix B), and it can be used for the nonlinear duopoly model.
3. Model
A classical model of oligopoly can be briefly reminded [18,19], and in particular, the Cournot duopoly assumptions are presented [10]. Then, we can introduce a special nonlinear demand function [4] that allows us to present some complex phenomena of the duopoly game.
3.1. Fundamental Principles of the Dynamics Cournot Oligopoly Model
Let be the number of companies in the given market. Denote a finite set, and let be the company that produces the homogeneous output at the given time period All companies make plans for their production in the subsequent time period in order to maximize their expected profit or expected utility, which is related to the expected total supply. This process will be developed in detail.
The profit of each company depends on the price at which the goods are sold in the period t, and this price depends on the total supply according to the given inverse demand function:
To simplify the further considerations, we introduce the following notation:
which represents the total output of the rest of the industry expected by the company in the given period Notice that the relation is valid for all The profit of the company in the given period t can be now expressed as:
where is the cost function of the company Moreover, the production for the next period of the company can be found as a solution to the following optimization problem:
where represents the total output of the rest of the industry expected by the company for the next time period and is the strategy set, which is used for the selection of the optimal production of the company The principal assumption of the model concerns some particular expectations about the production of other companies. The original Cournot assumption is a simple naive expectation:
for all
3.2. Dynamics of Cournot Model
Let all problems (6) have their unique solutions. If (7) is applied, we can state:
where is the reaction function of the company , or the best response by the company, or the best reply mapping the firm To study this dynamical problem in more detail, more specific forms of inverse demand functions and costs functions are necessary.
3.3. Linear Model
To be able to see the strange behavior of the nonlinear duopoly model, it is necessary to have a notion about the properties of the linear model. The contrast between the simple behavior of the solution to the linear model and the erratic behavior of the solution to a nonlinear model will be presented later. This is the reason why the linear model is introduced in this subsection. For further details, cf. [7]. In the linear model, it is considered that the inverse demand function is a decreasing linear function of the industry output. Particularly, it is assumed that (3) has the following form:
where and are real constants (as was already mentioned, a presents fixed costs, and b presents average variable costs in this model). Substituting this relation to formula (5) for profit of company , we gain:
where is a constant unit, average costs of the company are and x substitutes for a specific value of the period Now, it is possible to solve the problem of the profit maximization (6). The first order conditions of this problem are as follows:
which means that the reaction function is:
The reaction x is positive provided that:
If not, then the negative outcome has to be replaced by a sufficiently small and nonzero outcome which allows us to construct the resulting reaction functions for the dynamics (8). For all , we can consider:
3.4. Nonlinear Model
The behavior of the solution to the linear Cournot duopoly model is very simple. The model has only one asymptotically-stable equilibrium as is introduced in Section 4.1. If a nonlinear inverse function is used instead of (9), a more complex behavior of the Cournot duopoly model can emerge. The nonlinear inverse demand function means that also the demand function is nonlinear. Different types of nonlinear demand functions can be found in [20,21,22]. In [4], it is considered that:
- the quantity demanded is reciprocal to the price,
- the companies operate under constant unit costs.
The latter assumptions will be partly modified, relaxed and generalized in this subsection. The first assumption is modified in (15), and the second one is relaxed in (16). Instead of the linear inverse demand function (9), it is assumed that a nonlinear decreasing function of the industry output is given. In [20,22], the algebraic demand function is considered. Its inverse function, which can be substituted into (3), has the form:
where and are real constants. Notice that if , then , which means that parameters and c determine the intersection of the graph of the inverse demand function with the horizontal axis that represents the total supply Instead of (5), it is possible to write the profit function in the form:
where are exogenous average unit costs of the company within a specific time period t and x substitutes for this time period. Now, it is possible to solve the problem of the profit maximization (6). If the time period t is fixed, the first order conditions of this problem are:
To be able to find an explicit solution to the latter Equation (17), it is necessary to consider that If this setting is not valid, a numerical method for the solution to a nonlinear Equation (17) has to be applied; however, this difficulty is not considered here. Assuming further that:
Equation (17) can be solved for Particularly, it is possible to find the reaction function:
The reaction x is positive provided that:
If not, then the negative outcome has to be replaced by a sufficiently small and nonzero outcome which allows us to construct the resulting reaction functions for the dynamics (8). For all , we put:
4. Discussion
In the remaining part of this paper, a special case of a duopoly game will be considered. In this case, , and immediately from (4), we have:
If duopolists partially adjust their quantities towards their best replies according to (8) and (22), the dynamical system is generated by the iteration of the map:
where and are the reaction functions of the companies and given by (21). If the initial conditions are given, the trajectory:
is generated by the t-th iteration of the map (23), and it produces the Cournot tatonnement [13].
4.1. The Equilibrium of the Linear Model and Its Properties
If there is a fixed point on the map (23), it is called the Cournot–Nash equilibrium [18]. In Section 2, it was already mentioned that this equilibrium can be found as a solution to the following system of equations With the particular form of the reaction functions (14) and (22), it is possible to find the following nonzero equilibrium:
As was pointed out in Section 2, the stability of this stationary point can be determined from the Jacobian matrix of the map (14) enumerated at the stationary point (25); see [15]. It is possible to find:
The eigenvalues of the matrix (26) are:
Since the stationary point is always asymptotically stable (cf. [15]), no matter what the values of parameters and are. As soon as the average costs of companies are zero ( in (25)), the equilibrium is which corresponds to the known result for the static Cournot duopoly model introduced in Section 1.
4.2. Equilibrium of the Nonlinear Model and Its Properties
To be able to find the equilibrium of a nonlinear model (21), it is necessary to consider an autonomous system. This means that it is assumed that average unit costs in this model are a constant function of time which can be written in the form:
where and are real constants. With the particular form of reaction functions (21) and (22), it is possible to solve the equation for the stationary point and find a nonzero Cournot–Nash equilibrium:
The stability of this stationary point can be determined from the Jacobian matrix of the map (23) enumerated at the stationary point, [15]. It is possible to find:
which means that at the stationary point (29), we have:
The eigenvalues of the matrix (31) are imaginary as follows:
The stationary point is asymptotically stable provided that for details, see [15]. Solving this problem, we can observe that such a situation happens when the following relation for the ratio of unit costs is valid:
If the ratio of the unit costs falls outside these intervals, the stationary point is not stable. Then, a more complex behavior of the model can be detected. To observe such phenomena, a bifurcation diagram can be used.
Let us finally return to the problem with nonconstant companies’ average costs briefly. Let us suppose that during a finite time period the company’s costs are functions of time Specifically, let them change exponentially as where and are real constants. Further, let us suppose that the costs functions stay constant for the rest of the time, which means that:
Then, the new stationary point of the model (21) is:
4.3. Bifurcation Diagram of the Duopoly Model
As (23) depends symmetrically on two parameters and corresponding to a company’s cost prices and the parameter of the inverse demand function, the price ratio is considered as a bifurcation parameter. Without loss of generality, it is possible to fix as a price unit for particular computations. Other values of the constant could be used, and the same structure of the bifurcation would be observed. The algorithm for the construction of a bifurcation diagram was described in Section 2.1. It was implemented in MATLAB (See Appendix A), and its results are illustrated in Figure 1. The domain for the parameter was selected similarly as in [4], where more details can be found. Since which is the upper limit of the parameter for the asymptotic stable stationary point of the map (23), it is assumed that
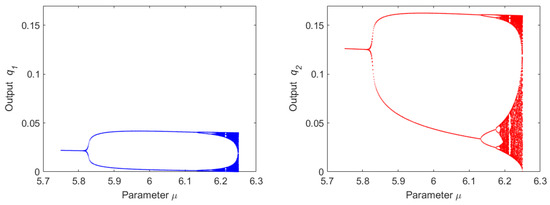
Figure 1.
The bifurcation diagram of the map (23) with the inverse demand function (15), where and . The left diagram describes the dependence of the limit points of the variable on the parameter , and similarly, the right diagram describes the limit points of the variable Source: computation in MATLAB; cf. Appendix A.
The analysis of Figure 1 shows that the results are really interesting from the economic point of view. The basic Cournot linear duopoly model, as described in the Introduction and Section 4.1, has the only unique stable equilibrium for both companies. However, as was mentioned above, if the ratios of the unit costs fall outside the presented intervals, the stationary point is not stable. The companies will behave differently. It is possible that both the companies will try to sell a higher amount of products, which will result in the supply exceeding the demand, and then, a certain amount of unsold goods will occur on the market. Consequently, both companies will decrease their supply simultaneously, which will result in the demand exceeding the supply, and the demand of the market will not be satisfied. The companies will cyclically repeat their behavior. Moreover, if the ratio of the unit costs becomes really high (more than 6.1, as described in Figure 1), the behavior of the companies will be really unstable, chaotic and unpredictable. The basic idea and basic conclusion of the Cournot duopoly game with linear functions (one stable solution) will not work at that moment.
4.4. Lyapunov Exponent of the Duopoly Model
The bifurcation diagrams in Figure 1 provide only graphical evidence of chaotic behavior. To present quantitative evidence of this issue, Lyapunov exponents of the map (23) are computed here. The concept of Lyapunov exponents was introduced in Section 2.2. The described algorithm for the map (23) was implemented in MATLAB; see Appendix B. It was found that Lyapunov exponents for the bifurcation parameter can be approximated by the values and , respectively, after iterations. In this computation, the initial state and parameter were used. If the process of the computation of Lyapunov exponents converges, then it does not depend on the initial value This phenomenon was tested with different initial values. Since at least one value of Lyapunov exponents is positive, we can conclude that for the given value of the parameter , the map (23) is sensitive to the initial conditions. This means that it is possible to consider the fact that the given map shows features typical of deterministic chaos. The same computations can be used for different values of the bifurcation parameter In this way, the diagram of the largest Lyapunov exponent can be found. If , the diagram in Figure 2 can be constructed step by step.
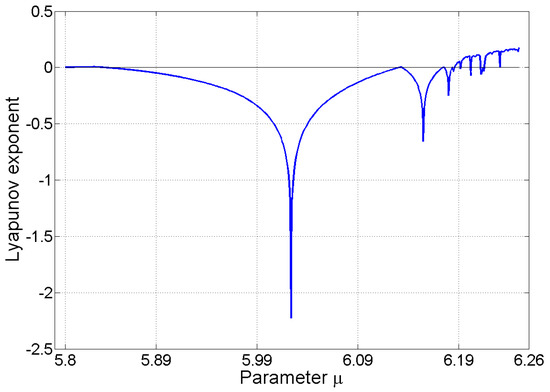
Figure 2.
Diagram of the largest Lyapunov exponent of the map (23) with the inverse demand function (15), where and . Bifurcation parameter Source: computation in MATLAB; essential steps of the algorithm are given in Appendix B.
The diagram depicts that there are values of the bifurcation parameter for which the largest Lyapunov exponent is positive. For these values, the system given by the maps (23) and (21) is sensitively dependent on initial values, and deterministic chaos can emerge. Similarly as in the case of the bifurcation diagram in Figure 1, it is possible to observe that this phenomenon is present for large values of the bifurcation parameter which represents the ratio of both the companies’ unit costs. Since such high ratios are not very likely in economic systems, it can be summarized that the erratic behavior of the duopoly model can be rather rare.
5. Conclusions
The paper introduced both a linear and a nonlinear version of the Cournot duopoly model. The reason for presenting these versions together was given by the overall goal to compare the differences in the behavior of their possible solutions. The essential assumption linked with the nonlinear model is that of a nonlinear inverse demand function. A similar assumption as in [4] was used. Instead of the unique inverse demand function given in [4], a more general function (15) was proposed and used. The equilibrium was found, and the conditions for its stability were established. The shift of the Cournot–Nash equilibrium caused by exogenous development of the companies’ cost function was examined. Provided there is a sufficiently large proportion between the unit costs of the two companies in the duopoly game, it was shown that there are nonlinear phenomena such as bifurcation of limit values of the production or deterministic chaos. To prove a sensitive dependence on the initial conditions that accompanies deterministic chaos, the concept of Lyapunov exponents was used. Moreover, a diagram for the largest Lyapunov exponent was also introduced in Figure 2. MATLAB implementations of the bifurcation diagram and calculation of Lyapunov exponents are introduced in Appendices Appendix A and Appendix B, respectively. In our future work, we would like to deal with the chaos control linked with the presented model (29). We would also like to improve the algorithm for the computation of Lyapunov exponents to make it more accurate.
Author Contributions
P.P. carried out the computations and wrote the paper. J.K. suggested the economic interpretations of results.
Funding
This work was supported by the Faculty of Informatics and Management, University of Hradec Králové grant of Specific Research number 8/2018.
Acknowledgments
Special thanks to Kateřina Frončková for her technical help and assistance.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. MATLAB Implementation of the Bifurcation Diagram for the Duopoly Map

Appendix B. MATLAB Implementation of the Lyapunov Exponent for the Duopoly Map


References
- Pražák, P. On a Dynamic Model of Revenue Maximizing Firm. In Mathematical Methods in Economics 2010, Part II; University of South Bohemia: České Budějovice, Czech Republic, 2010; pp. 542–547. ISBN 978-80-7394-218-2. [Google Scholar]
- Rand, D. Exotic phenomena in games and duopoly models. J. Math. Econ. 1978, 5, 173–184. [Google Scholar] [CrossRef]
- Kopel, M. Simple and complex adjustment dynamics in Cournot duopoly models. Chaos Solitons Fractals 1996, 7, 2031–2048. [Google Scholar] [CrossRef]
- Puu, T. Chaos in Duopoly Pricing. Chaos Solitons Fractals 1991, 1, 573–581. [Google Scholar] [CrossRef]
- Puu, T. Attractors, Bufurcations and Chaos, Nonlinear Phenomena in Economics; Springer: Berlin, Germany, 2003; ISBN 3-540-40226-8. [Google Scholar]
- Pražák, P. Nonlinear Cournot Duopoly Game. In Hradec Economic Days; University of Hradec Králové: Hradec Králové, Czech Republic, 2018; Volume 8, pp. 188–195. ISBN 978-80-7435-701-5. [Google Scholar]
- Bischi, G.I.; Chiarella, C.; Kopel, M.; Szidarovszky, F. Nonlinear Oligopolies, Stability and Bifurcations; Springer: Berlin, Germany, 2010; ISBN 978-3-642-02105-3. [Google Scholar]
- Zhang, J.; Da, Q.; Wang, Y. Analysis of nonlinear duopoly game with heterogeneous players. Econ. Model. 2007, 24, 138–148. [Google Scholar] [CrossRef]
- Varian, H.R. Intermediate Microeconomics: A Modern Approach; W. W. Norton & Company: New York, NY, USA, 2006; ISBN 0-393-92702-4. [Google Scholar]
- Cournot, A. Récherces Sur Les Principes Mathématiques de la Théorie des Richesses; Hachette: Paris, France, 1838. (In French) [Google Scholar]
- Betrand, J. Théorie des Richesses: revue de Théories mathématiques de la richesse sociale par Léon Walras et Recherches sur les principes mathématiques de la théorie des richesses par Augustin Cournot. J. Savants 1883, 67, 499–508. (In French) [Google Scholar]
- Stackelberg, H.F. Marktform und Gleichgewicht; Springer: Berlin, Germany, 1934. (In German) [Google Scholar]
- Kulenovic, M.R.S.; Merino, O. Discrete Dynamical Systems and Difference Equations with Mathematica; Chapman & Hall/CRC: Boca Raton, FL, USA, 2002. [Google Scholar]
- Alligood, K.T.; Sauer, T.D.; Yorke, J.A. Chaos, An Introduction to Dynamical Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Elaydi, S. An Introduction to Difference Equations; Springer: New York, NY, USA, 2005; ISBN 0-387-23059-9. [Google Scholar]
- Boeing, G. Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction. Systems 2016, 4, 37. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Gibbons, R. Game Theory for Applied Economists; Princeton University Press: Princeton, NJ, USA, 1992; ISBN 0-691-04308-6. [Google Scholar]
- Varian, H.R. Microeconomic Analysis; W. W. Norton & Company: New York, NY, USA, 1992; ISBN 0-393-95735-7. [Google Scholar]
- Huang, J. Demand Functions in Decision Modeling: A Comprehensive Survey and Research Directions. Decis. Sci. 2013, 44, 557–609. [Google Scholar] [CrossRef]
- Song, Y.Y.; Ray, S.; Li, S.L. Structural properties of buyback contracts for price-setting newsvendors. Manuf. Serv. Oper. Manag. 2008, 10, 1–18. [Google Scholar] [CrossRef]
- Jeuland, A.P.; Shugan, S.M. Channel of distribution profits when channel members form conjectures. Mark. Sci. 1988, 7, 202–210. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).