From Systems to Organisations
Abstract
:1. Introduction
- The number of variables is moderate but it is not possible to hold all but two or three variables with fixed values;
- There are fundamental aspects that are non-quantitative or elude identification and measurement;
- Aspects observed are entangled, invalidating assumptions about superposition and independence;
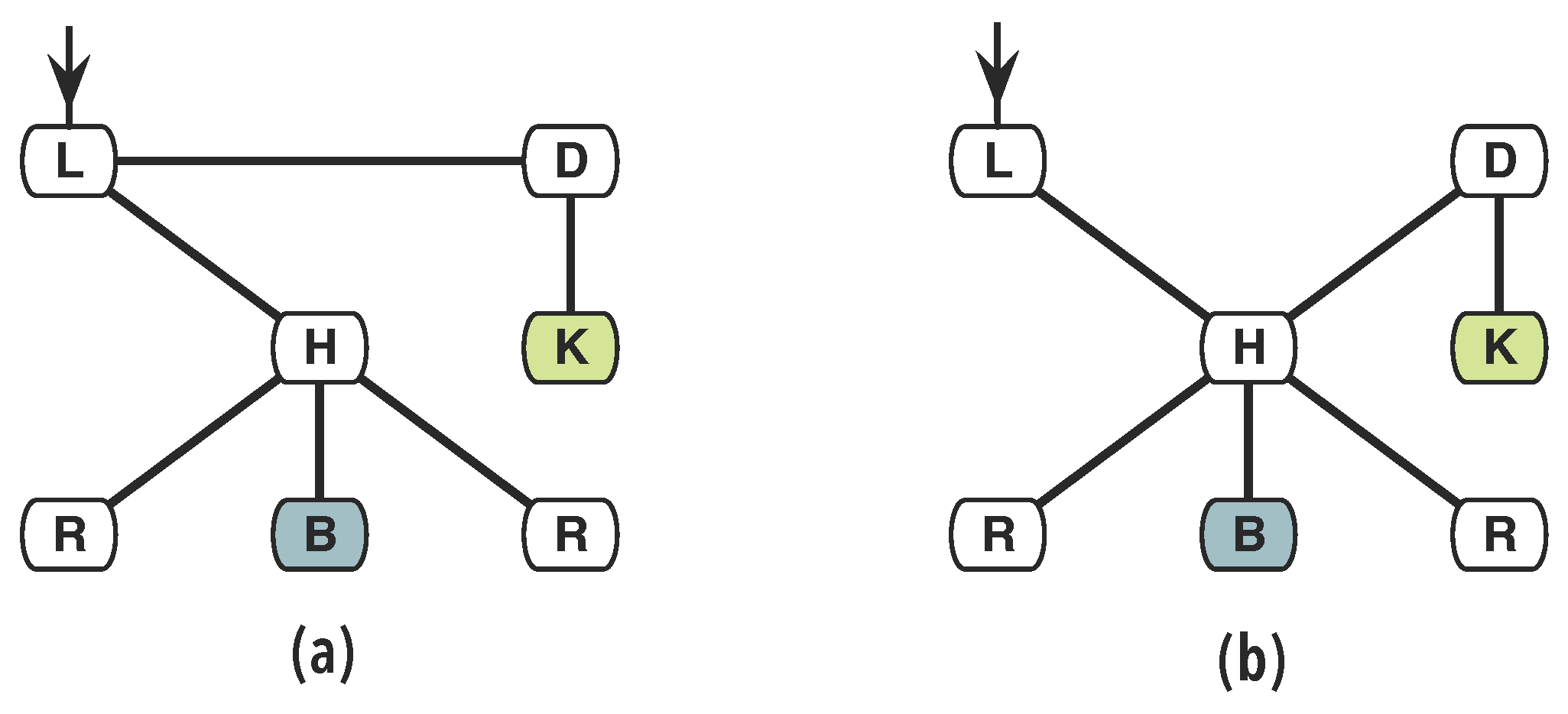
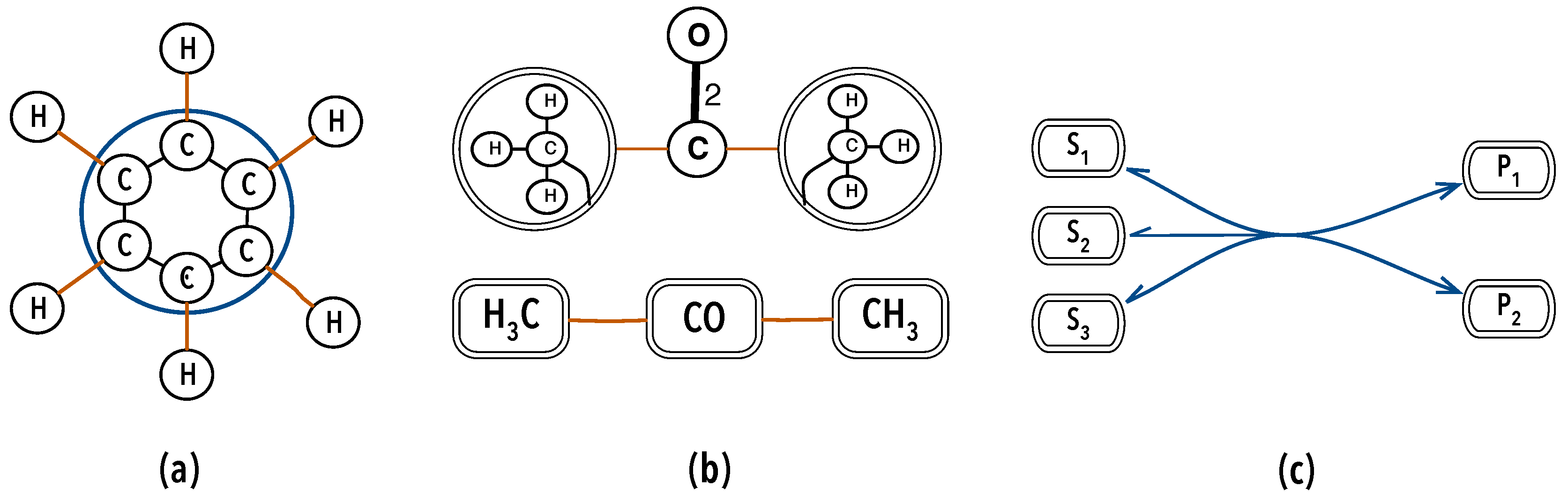
- A collection of things interrelated in a stable and individuated manner may act as an aggregate thing, a whole, interacting with other things at the same or at different aggregation levels;
- Interrelations and possible channels of interaction among elements change, affecting the phenomenon propensities or behaviour; and
They are problems which involve dealing simultaneously with a seizable number of factors which are interrelated into an organic whole.
2. Organisation and Information in Life Systems and Sciences
3. Theoretical Framework: The Organisation Perspective
3.1. Biological Organisation: A Minimalist Snapshot
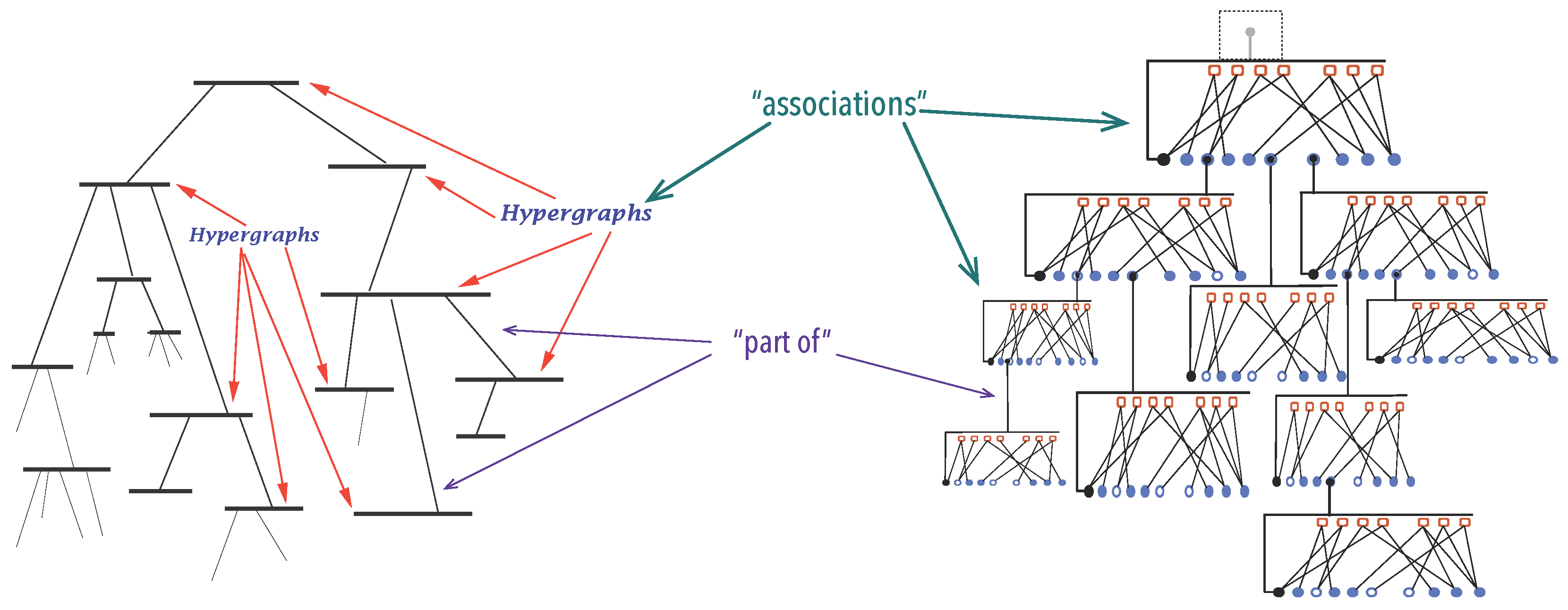
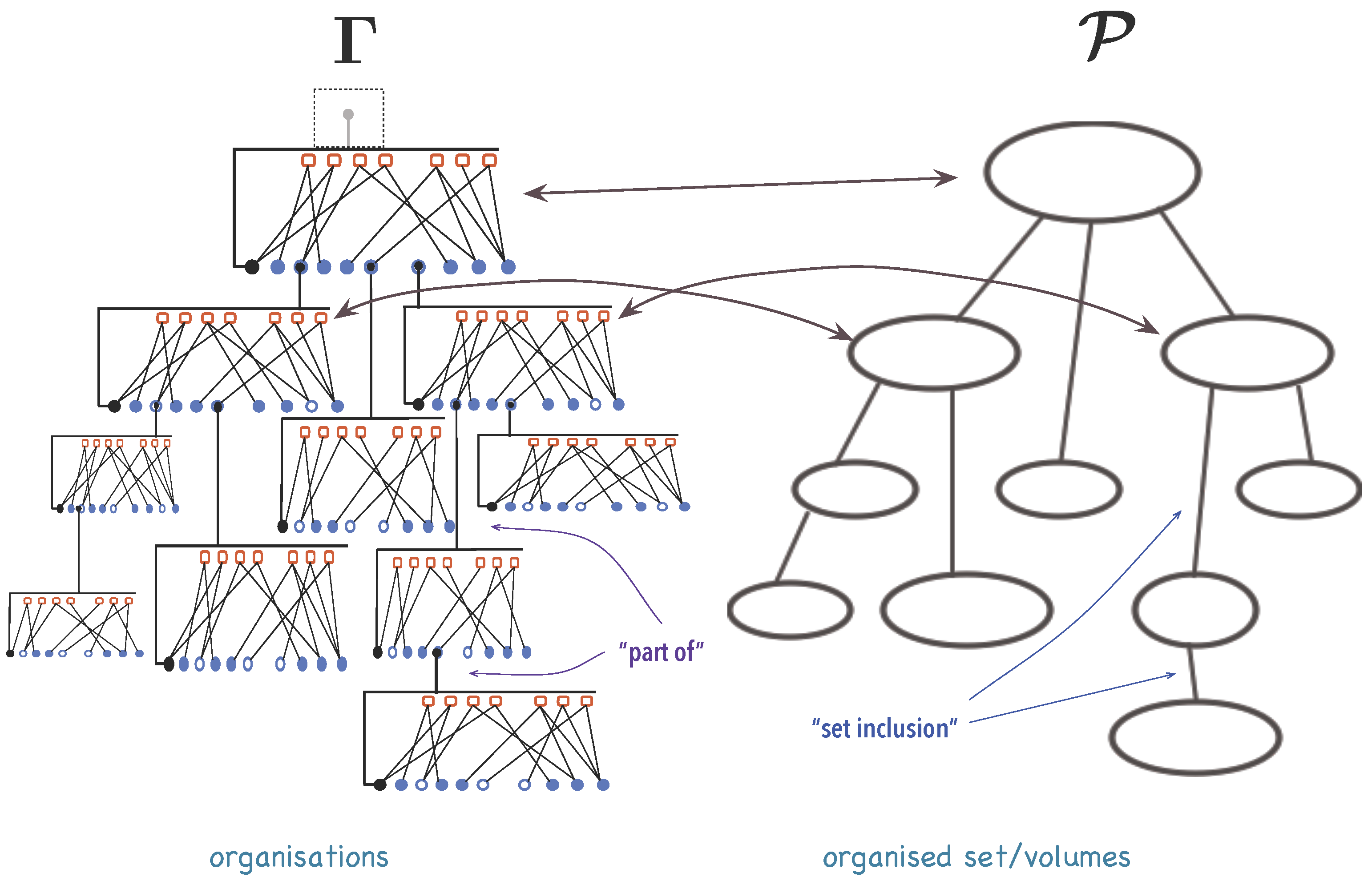
3.1.1. Organisations
- an atom;
- a set of organisations;
- a group of organisations put somehow in relation to one another;
- nothing else.
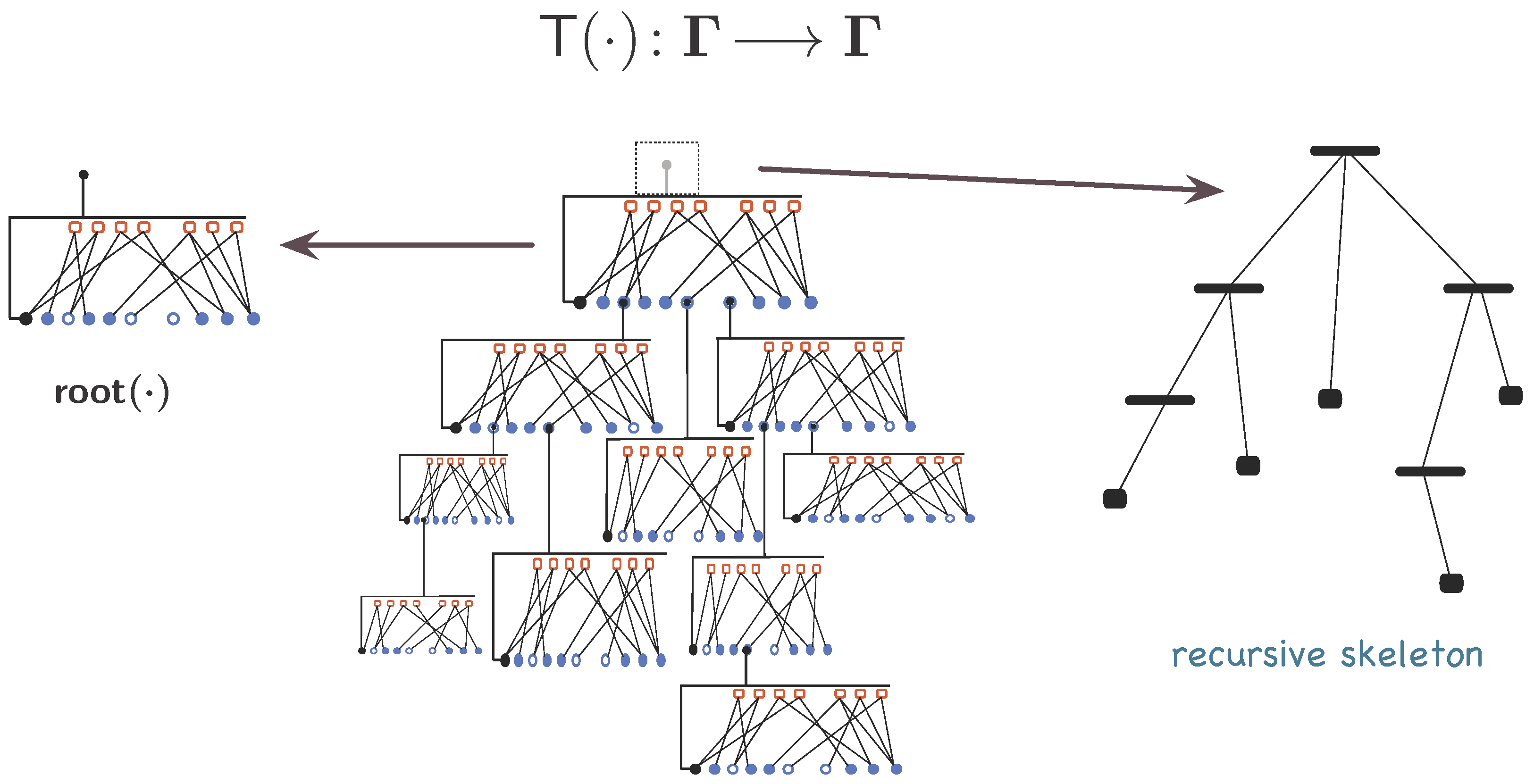
3.1.2. A Mathematical Model for Organisations
- 1.
- ,
- 2.
- ,
- 3.
- nothing else.
- 1.
- 2.
- Note that since then . Moreover, can be identified with and with through the following injectionand the immersionshows that .
- If , then . Let be a set of k meta-variables and let be identified to by the procedure in step 1. Thenis an element of Γ.
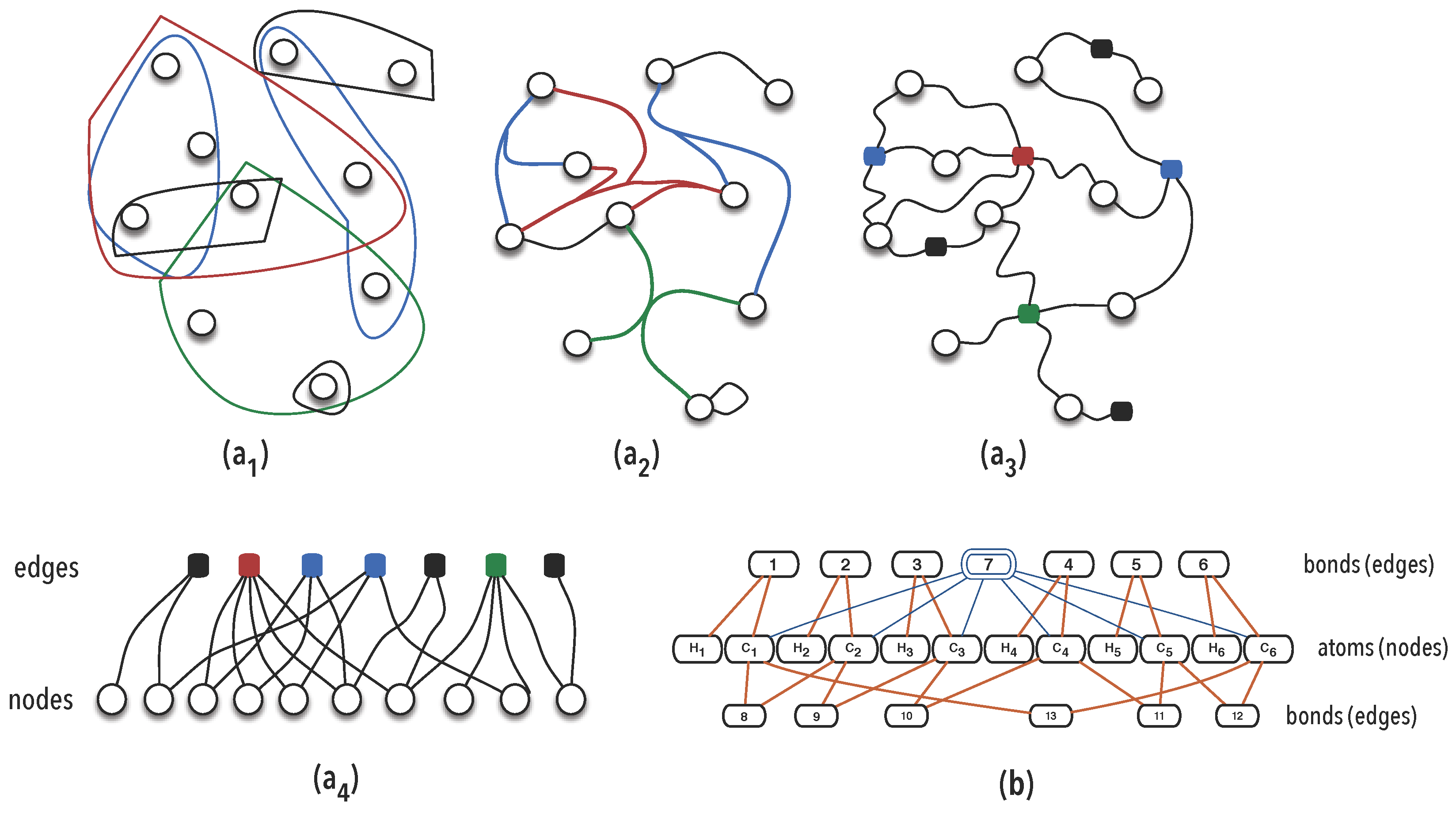
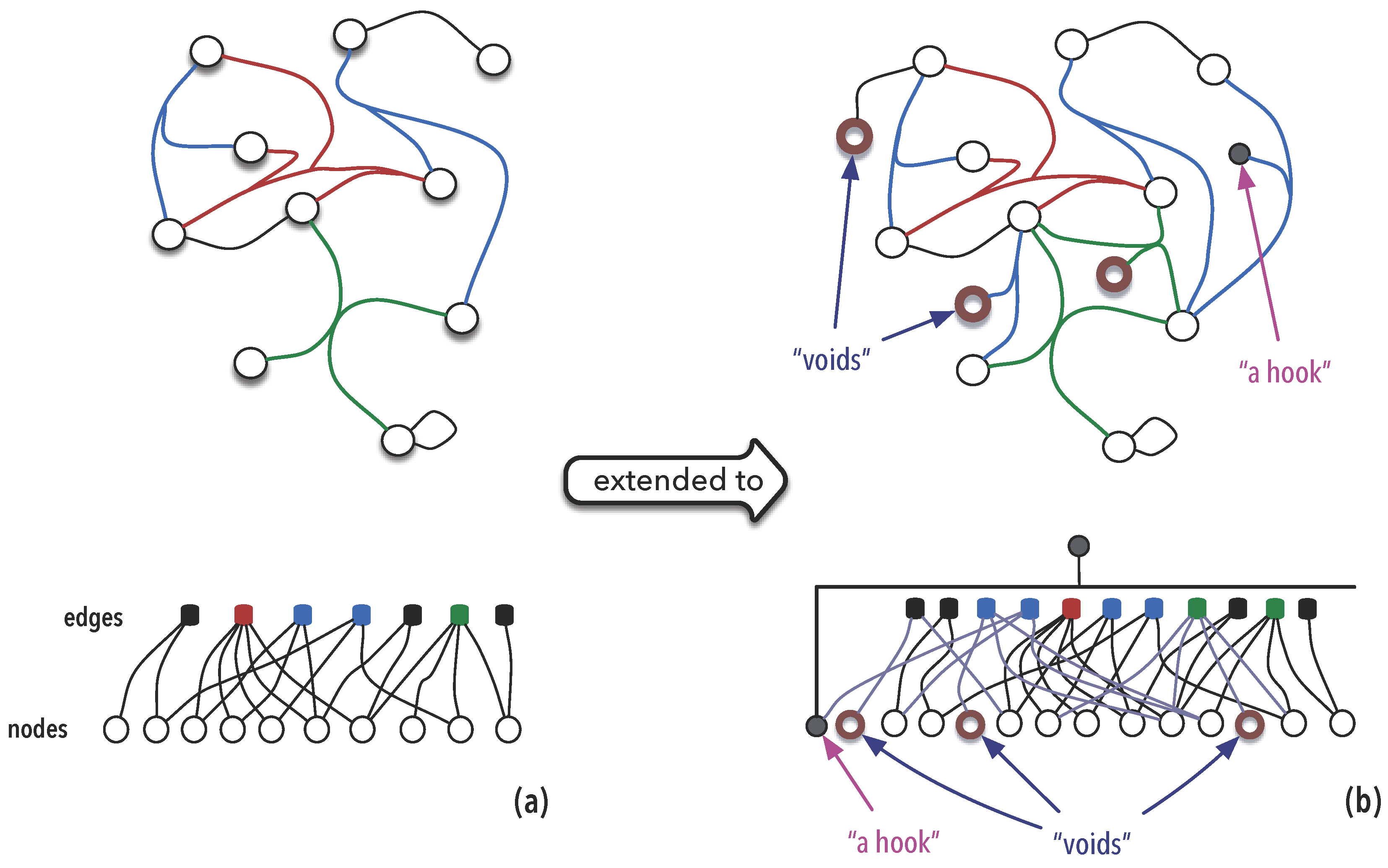
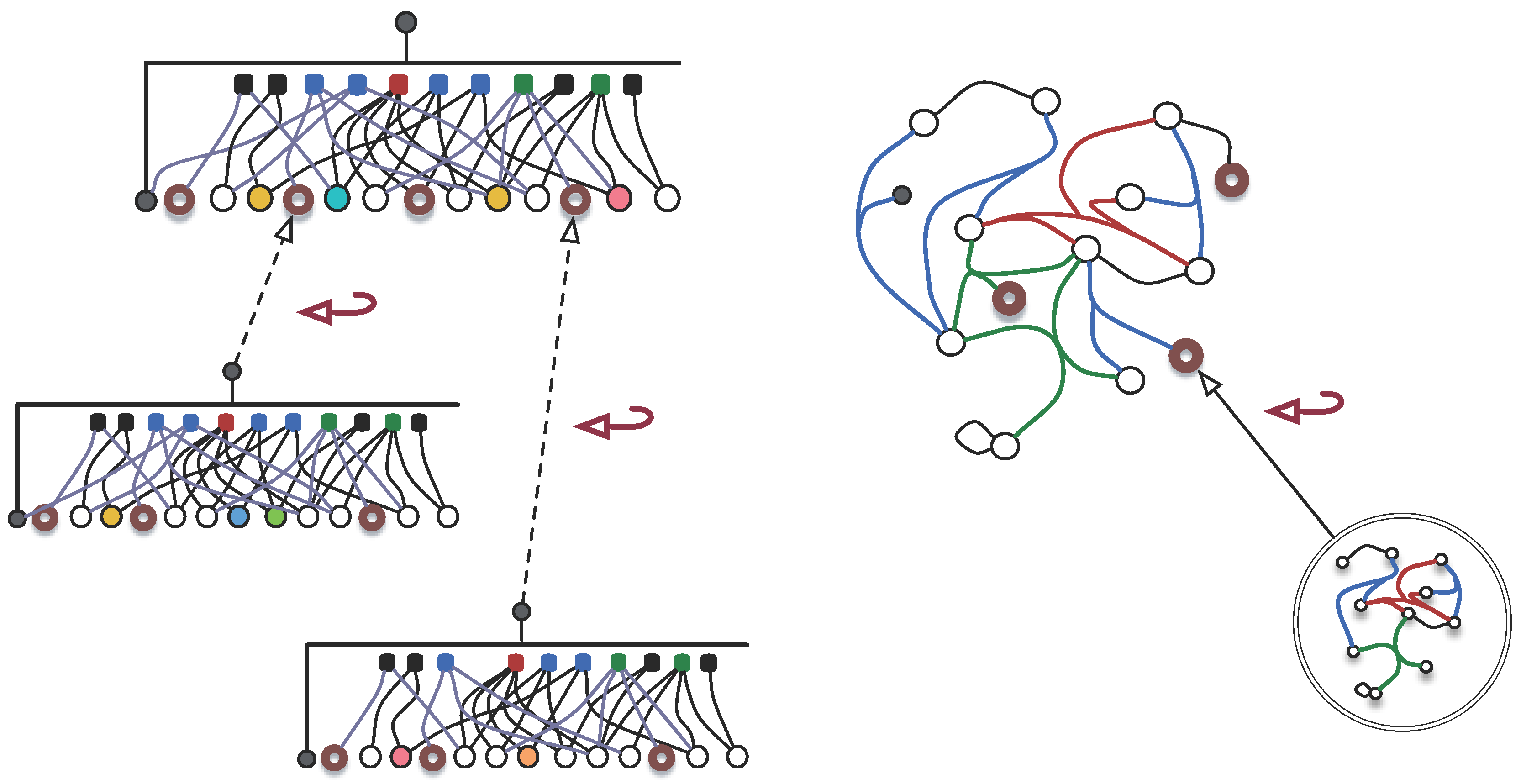
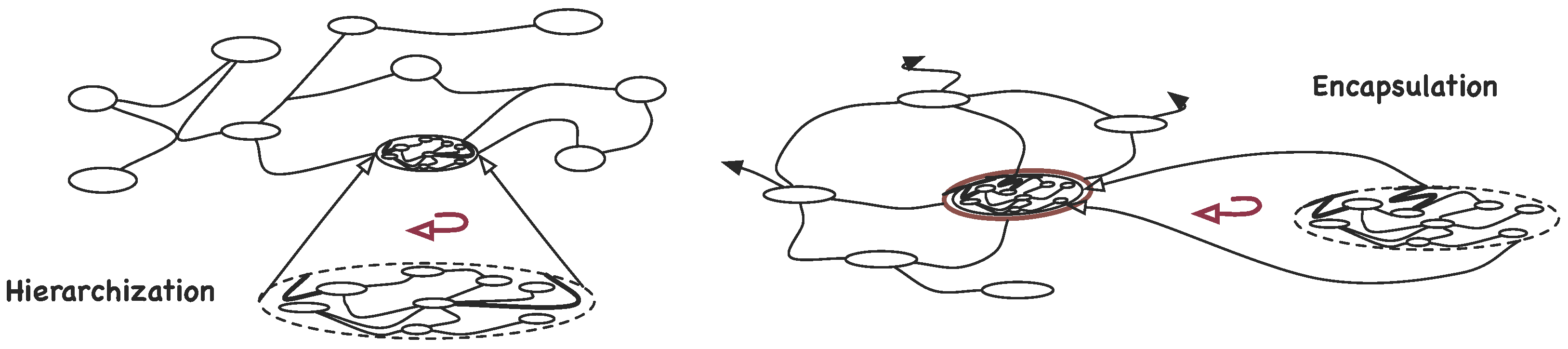
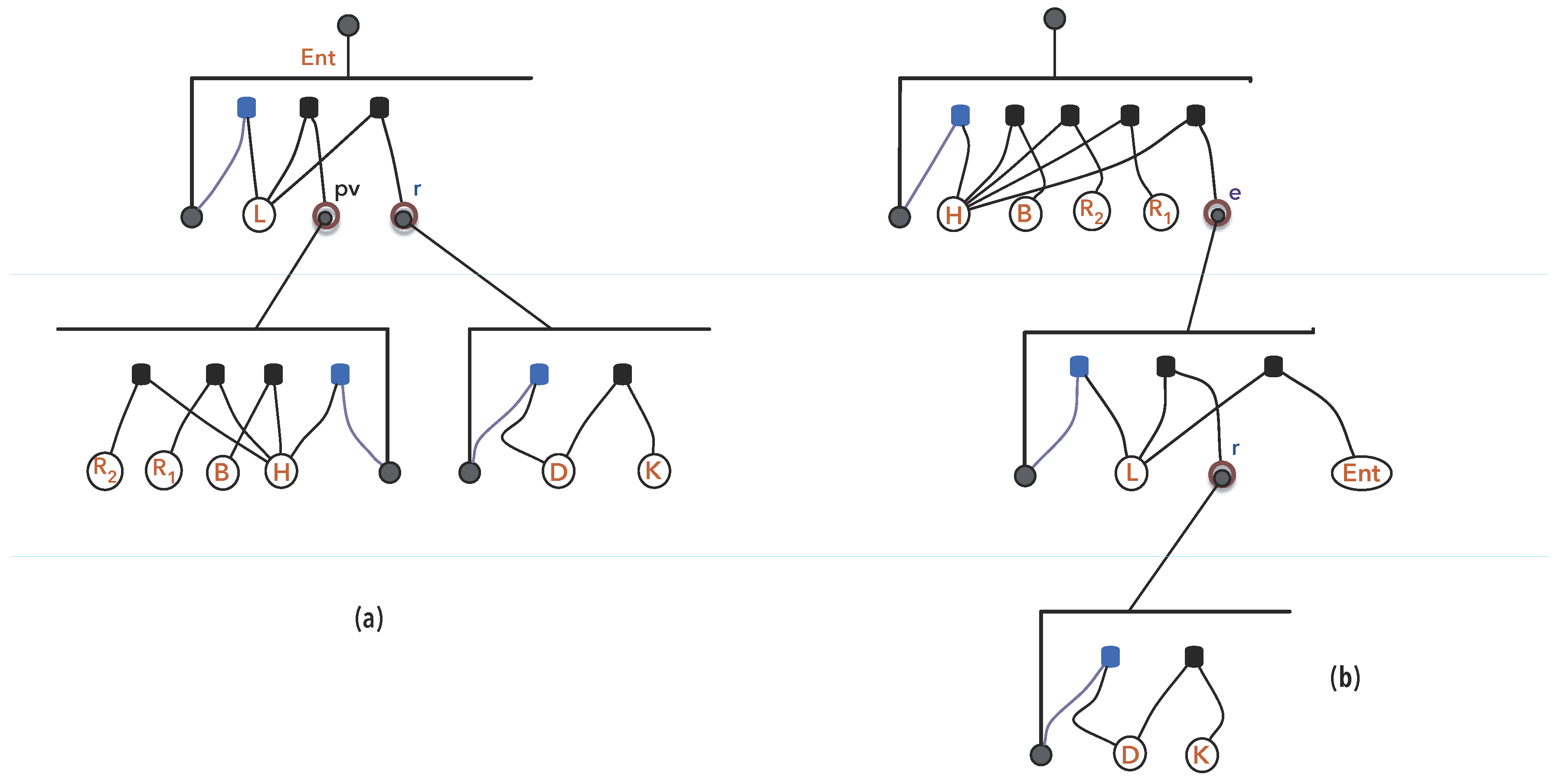
3.1.3. Synexions
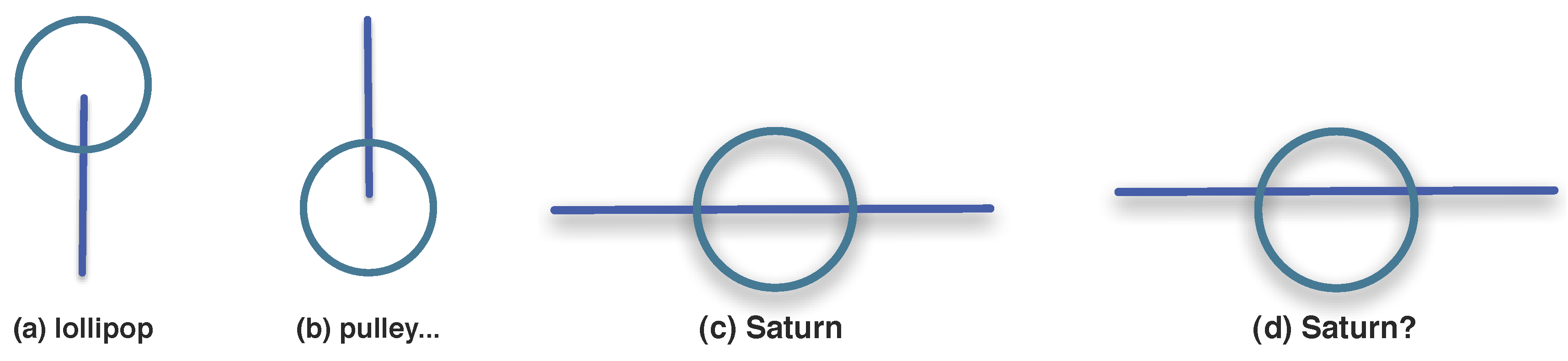
3.1.4. Further Basic Constructions
- 1.
- and , as elements of ;
- 2.
- and
- ,
- ,
- 1.
- If , then , as elements of .
- 2.
- If then if either condition holds:
- or
- .
- 3.
- Else, .
- 1.
- If , , where and ;
- 2.
- if , then
- 3.
- nothing else.
- 1.
- If , then , where
- 2.
- If , , , then , whereand the latter are modifications of and given, respectively, by:
3.2.
3.2.1. Perceptions
- ▸
- Any signal encountering sensory apparatuses (in the skin) of a biological entity at time and transmitted into it provokes (localised) changes in its organisation.
- ▸
- Moreover, if another signal encounters the same biological entity at time and tends to provoke the same change in the organisation of as signal , is recognised as being the same signal as .
3.2.2. and Interpretation
- A.
- Any biological entity or process may be represented in .
- B.
- All biological and life-related entities or processes .
- C.
- Perceptions are unique for a given biological entity or process—same signal, same imprint;
- D.
- Biological organisations emit signals that uniquely characterise them, that is, they may be recognised by means of the signals they emit.
- A signal reaching two different biological entities and , represented by and may provoke different imprints in their organisations, even if , and , are similar. However, if the collection of signals associated with imprints and is the same, that is, if any signal leading to the first imprint will also lead to the second imprint, the perception should be considered same for and ;
- Stabilised imprints are models for signals or collections of signals;
- A travelling molecule is a signal, because it is a localised variation in density, mass and other aspects concentrated in time and space;
- Pressure and concentration variations, being more diffuse and collective perturbations of environment attributes, may not be always taken as signals. This suggests that environmental variations depend on scale sensitivities as well as the complexity of the perturbation and the perceiver to be considered as signals. Signal and perception are thus relative concepts;
- Encountering is always due to relative motion. Either the signal propagates or the organism is moving and reaches a resting obstacle that acts as a perturbation in the perceived environment. What is important is that signal and organism approach each other in space and time for an encounter to occur.
4. Ontological Considerations
4.1. Space, Time and
4.1.1. Cognitive Domain
4.1.2. Molecular Scale
4.1.3. Cellular Scale
4.1.4. Physiology and Behaviour
4.1.5. Cultural Domain
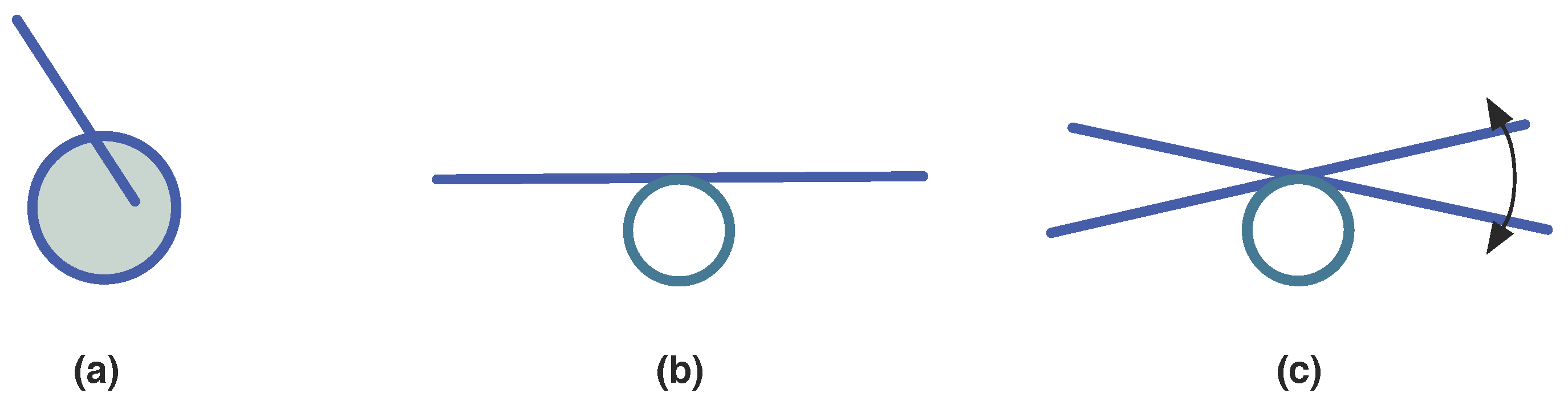
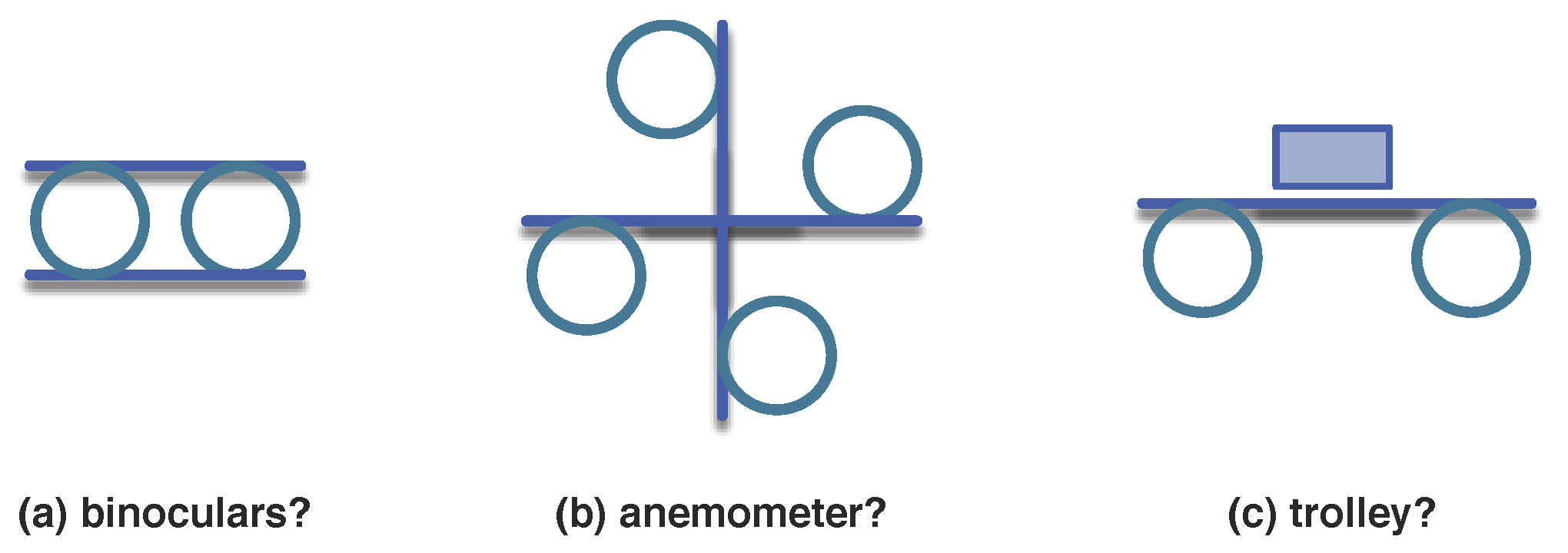
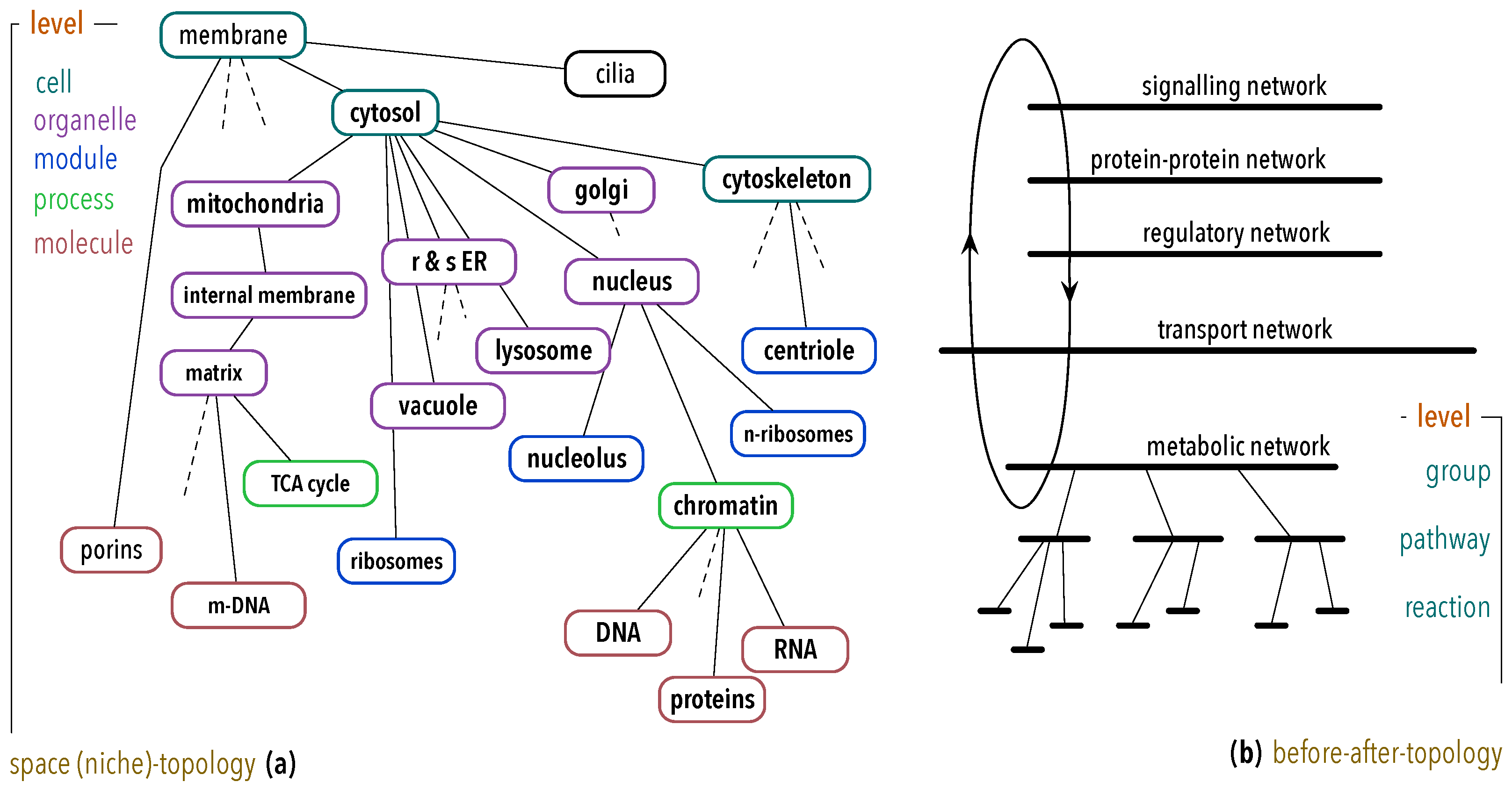
4.2. Organisation and Complexity
- The more associations there are in a -graph, higher its complexity is;
- ;
- The more detailed an organisation is, that is, deeper the hierarchical levels go or bigger the number of its parts is, higher its complexity is;
- The finiteness of and the existence of self-similar , require that the contribution of deeper levels in the hierarchy decays rapidly, e.g., .
- 1.
- By definition, ;
- 2.
- If then , since ;
- 3.
- does not imply that ;
- 4.
- It is possible that and , or even that .
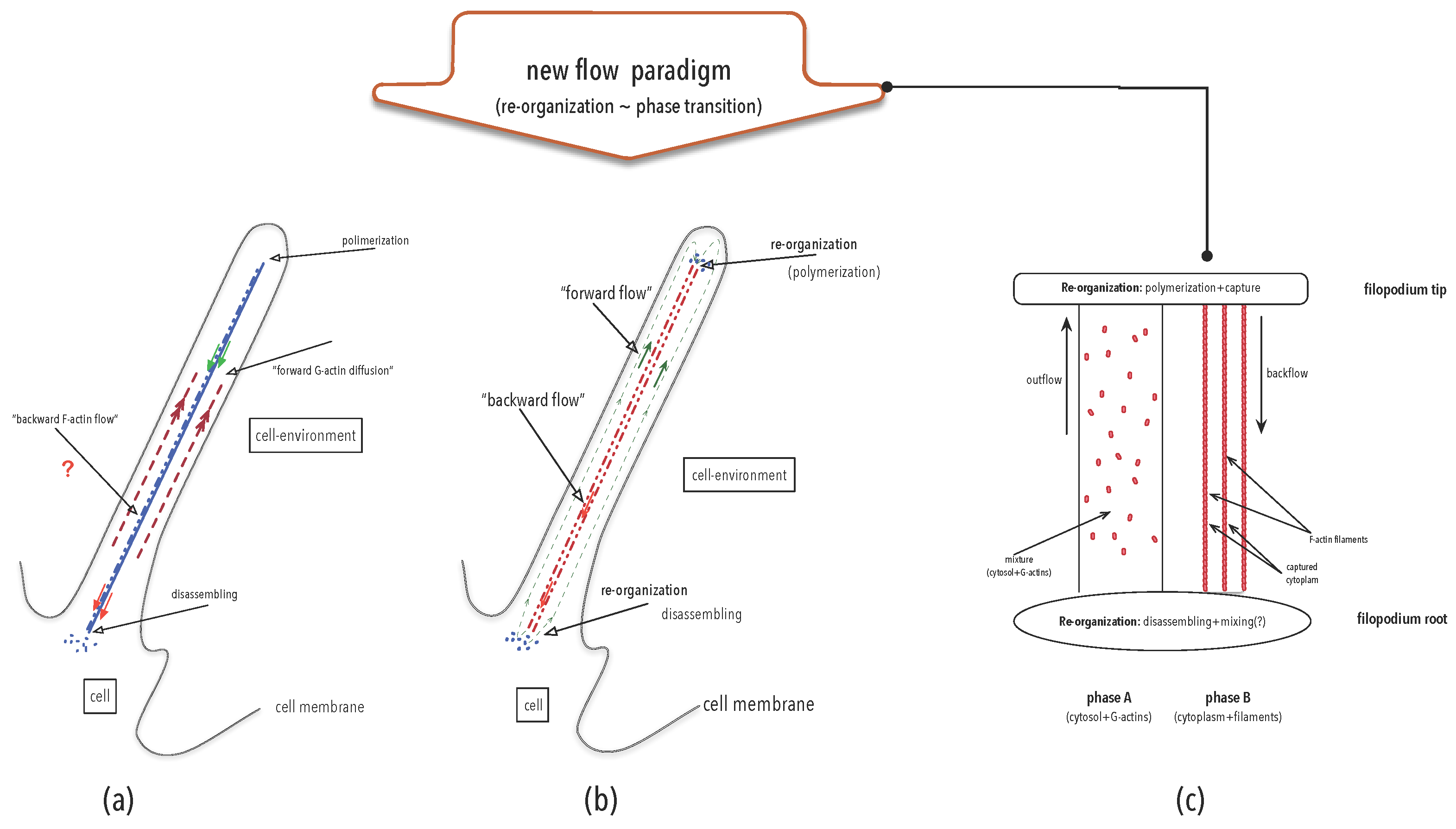
4.3. Organisation Perspective in Action: Re-Thinking Flows
5. Interacting Organisations: Biological and Complex Phenomena
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Weaver, W. Science and Complexity. Am. Sci. 1948, 36, 536–544. [Google Scholar] [PubMed]
- Miller, J.G. Living Systems; McGraw-Hill Book Co., Inc.: New York, NY, USA, 1978. [Google Scholar]
- Kritz, M.V. Boundaries, Interactions and Environmental Systems. Mec. Comput. 2010, 29, 2673–2687. [Google Scholar]
- Mohler, R.R.; Ruberti, A. (Eds.) Recent Developments in Variable Structure Systems, Economics and Biology; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1978; Volume 162.
- Junk, W.J. (Ed.) The Central Amazon Floodplain: Ecology of a Pulsating System; Springer: New York, NY, USA, 1997.
- De Ruiter, P.C.; Wolters, V.; Moore, J.C. (Eds.) Dynamic Food Webs : Multi-species Assemblages, Ecosystem Development, and Environmental Change; Theoretical Ecology Series; Academic Press: Boston, MA, USA; Elsevier: Amsterdam, The Netherlands, 2005.
- Pascual, M.; Dunne, J.A. Ecological Networks: Linking Structure to Dynamics in Food Webs; Studies in the Sciences of Complexity, Santa Fe Institute, Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Rosen, R. Life Itself: A Comprehesive Inquiry into the Nature, Origin, and Fabrication of Life; Complexity in Ecological Systems Series; Columbia University Press: New York, NY, USA, 1991. [Google Scholar]
- Hofmeyr, J.H.S. The biochemical factory that autonomously fabricates itself: A systems biological view of the living cell. In Systems Biology: Philosophical Foundations; Elsevier B.V.: Amsterdam, The Netherlands, 2007; pp. 217–242. [Google Scholar]
- Miller, J.G. Living Systems: The Organization. Behav. Sci. 1972, 17, 1–182. [Google Scholar] [CrossRef] [PubMed]
- Harold, F.M. The Way of the Cell: Molecules, Organisms and the Order of Life; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Lillie, R.S. Living Systems and Non-living Systems. Philos. Sci. 1942, 9, 307–323. [Google Scholar] [CrossRef]
- Ulanowicz, R.E. On the nature of ecodynamics. Ecol. Complex. 2004, 1, 341–354. [Google Scholar] [CrossRef]
- Harold, F.M. Molecules into Cells: Specifying Spatial Architecture. Microbiol. Mole. Biol. Rev. 2005, 69, 544–564. [Google Scholar] [CrossRef] [PubMed]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Mathematical and Computational Biology, Chapman & Hall/CRC: London, UK, 2007. [Google Scholar]
- Boogerd, F.C.; Bruggeman, F.J.; Hofmeyr, J.H.S.; Westerhoff, H.V. Systems Biology: Philosophical Foundations; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Krakauer, D.C.; Collins, J.P.; Erwin, D.; Flack, J.C.; Fontana, W.; Laubichler, M.D.; Prohaska, S.J.; West, G.B.; Stadler, P.F. The challenges and scope of theoretical biology. J. Theor. Biol. 2011, 276, 269–276. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.; Jeldtoft-Jensen, H.; Oliveira, L.P.; Sibani, P. Evolution in complex systems. Complexity 2004, 10, 49. [Google Scholar] [CrossRef]
- Roberts, A.J. Model Emergent Dynamics in Complex Systems; Mathematical Modeling and Computation, SIAM, Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2015. [Google Scholar]
- Bailly, F.; Longo, G. Extended Critical Situations: The Physical Singularity of Life Phenomena. J. Biol. Syst. 2008, 16, 309–336. [Google Scholar] [CrossRef]
- Watson, D.L. Biological Organization. Q. Rev. Biol. 1931, 6, 143–166. [Google Scholar] [CrossRef]
- Mesarović, M.D. (Ed.) System Theory and Biology; Springer: New York, NY, USA, 1968.
- Klir, G.J. Facets of Systems Science, 2nd ed.; Plenum Press: New York, NY, USA, 2001. [Google Scholar]
- Balescu, R. Equilibrium and Non-Equilibrium Statistical Mechanics; A Wiley-Interscience Publication, John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Rosen, R. On interactions between dynamical systems. Math. Biosci. 1975, 27, 299–307. [Google Scholar] [CrossRef]
- Kritz, M.V.; dos Santos, M.T. Dynamics, Systems, Dynamical Systems and Interaction Graphs. In Dynamics, Games and Science II; Peixoto, M.M., Rand, D., Pinto, A.A., Eds.; Springer: Berlin, Germany, 2011; pp. 507–541. [Google Scholar]
- Ashby, W.R. Principles of the Self-Organizing System. In Principles of Self-Organization: Transactions of the University of Illinois Symposium; von Foster, H., Zopf, G.W., Jr., Eds.; University of Illinois, Pergamon Press: London, UK, 1962; pp. 255–278. [Google Scholar]
- Rosen, R. Biological Systems as Organizational Paradigms. Int. J. Gen. Syst. 1974, 1, 165–174. [Google Scholar] [CrossRef]
- Varela, F.G.; Maturana, H.R.; Uribe, R. Autopoiesis: The Organization of Living Systems, Its Characterization and a Model. Biosystems 1974, 5, 187. [Google Scholar] [CrossRef]
- Miller, J.G. Living Systems: Basic Concepts. Behav. Sci. 1965, 10, 193–237. [Google Scholar] [CrossRef] [PubMed]
- Auger, P. The Methods and Limits of Scientific Knowledge. In On Modern Physics; Clarkson N. Potter, Inc. Publisher: New York, NY, USA, 1961; pp. 79–108. [Google Scholar]
- Miller, J.G. Living systems. Curr. Mod. Biol. 1971, 4, 55–256. [Google Scholar] [CrossRef]
- Miller, M.B.; Bassler, B.L. Quorum Sensing In Bacteria. Ann. Rev. Microbiol. 2001, 55, 165–199. [Google Scholar] [CrossRef] [PubMed]
- Stoney, R.A.; Ames, R.M.; Nenadic, G.; Robertson, D.L.; Schwartz, J.M. Disentangling the multigenic and pleiotropic nature of molecular function. BMC Syst. Biol. 2015, 9, S3. [Google Scholar] [CrossRef] [PubMed]
- Oyeyemi, O.J. Modelling HIV-1 Interaction with the Host System. Ph.D. Thesis, University of Manchester, Manchester, UK, 2016. [Google Scholar]
- Prokop, A.; Beaven, R.; Qu, Y.; Sánchez-Soriano, N. Using fly genetics to dissect the cytoskeletal machinery of neurons during axonal growth and maintenance. J. Cell Sci. 2013, 126, 2331–2341. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zheng, H. Organized modularity in the interactome: Evidence from the analysis of dynamic organization in the cell cycle. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 1264–1270. [Google Scholar] [CrossRef] [PubMed]
- Brownridge, P.; Lawless, C.; Payapilly, A.B.; Lanthaler, K.; Holman, S.W.; Harman, V.M.; Grant, C.M.; Beynon, R.J.; Hubbard, S.J. Quantitative analysis of chaperone network throughput in budding yeast. Proteomics 2013, 13, 1276–1291. [Google Scholar] [CrossRef] [PubMed]
- Peacocke, A.R. An Introduction to the Physical Chemistry of Biological Organization; Clarendon Press: Oxford, UK, 1983. [Google Scholar]
- Atlan, H. Entre le Cristal et la Fumée. Essay sur l’Organization du Vivant; Éditions du Seuil: Paris, France, 1986. [Google Scholar]
- Kritz, M.V. Creating Bio-Mathematical Worlds. P&D Report 29/95, LNCC/MCT, Petrópolis, 1995. In Proceedings of the 13th European Meeting on Cybernetics and Systems Research, Vienna, Austria, 9–12 April 1996.
- Bizzarri, M.; Palombo, A.; Cucina, A. Theoretical aspects of Systems Biology. Prog. Biophys. Mol. Biol. 2013, 112, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Kitto, K. High end complexity. Int. J. Gen. Syst. 2008, 37, 689–714. [Google Scholar] [CrossRef]
- Waddington, C.H. (Ed.) Biological Organization, Cellular and Sub-cellular; Pergamon Press: London, UK, 1959.
- Berg, H. Motile behavior of bacteria. Phys. Today 2000, 53, 24–29. [Google Scholar] [CrossRef]
- Blanchoin, L.; Boujemaa-Paterski, R.; Sykes, C.; Plastino, J. Actin Dynamics, Architecture, and Mechanics in Cell Motility. Physiol. Rev. 2014, 94, 235–263. [Google Scholar] [CrossRef] [PubMed]
- Needham, J. On the dissociability of the fundamental processes in ontogenesis. Biol. Rev. 1933, 8, 180–233. [Google Scholar] [CrossRef]
- Rosen, R. Structural And Functional Considerations in the Modelling of Biological Organization; Technical Report 77 25; The Center for Theoretical Biology, SUNY: Buffalo, NY, USA, 1977. [Google Scholar]
- Schweitzer, F. (Ed.) Self-Organization of Complex Structures: From Individual to Collective Dynamics; CRC Press, Taylor and Francis Group, LLC.: Boca Raton, FL, USA, 1997.
- Vinson, V.J. Proteins in Motion. Science 2009, 324, 197. [Google Scholar] [CrossRef] [PubMed]
- Longo, G.; Miquel, P.A.; Sonnenschein, C.; Soto, A.M. Is information a proper observable for biological organization? Prog. Biophys. Mol. Biol. 2012, 109, 108–114. [Google Scholar] [CrossRef] [PubMed]
- von Bertalanffy, L. General Systems Theory; Allen Lane The Penguin Press: London, UK, 1968. [Google Scholar]
- Fontana, W.; Buss, L. The Barrier of Objects: From Dynamical Systems to Bounded Organizations. In Boundaries and Barriers; Casti, J.L., Karlqvist, A., Eds.; Addison-Wesley Publishing Company, Inc.: Reading, MA, USA, 1996; pp. 55–115. [Google Scholar]
- Letelier, J.C.; Soto-Andrade, J.; Guíñez Abarzúa, F.; Cornish-Bowden, A.; Luz Cárdenas, M. Organizational invariance and metabolic closure: Analysis in terms of systems. J. Theor. Biol. 2006, 238, 949–961. [Google Scholar] [CrossRef] [PubMed]
- Cornish-Bowden, A. Tibor Gánti and Robert Rosen: Contrasting approaches to the same problem. J. Theor. Biol. 2015, 381, 6–10. [Google Scholar] [CrossRef] [PubMed]
- de la Escosura, A.; Briones, C.; Ruiz-Mirazo, K. The systems perspective at the crossroads between chemistry and biology. J. Theor. Biol. 2015, 381, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Montévil, M.; Mossio, M. Biological Organization as Closure of Constraints. J. Theor. Biol. 2015, 372, 179–191. [Google Scholar] [CrossRef] [PubMed]
- Dittrich, P.; di Fenizio, P.S. Chemical Organisation Theory. Bull. Math. Biol. 2007, 69, 1199–1231. [Google Scholar] [CrossRef] [PubMed]
- Kauffman, S.A. At Home in the Universe: The Search for Laws of Self-Organization and Complexity; Oxford University Press: New York, NY, USA; Oxford, UK, 1995. [Google Scholar]
- Kauffman, S.A. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: New York, NY, USA; Oxford, UK, 1993. [Google Scholar]
- Rashevsky, N. Life, information theory, and topology. Bull. Math. Biol. 1955, 17, 229–235. [Google Scholar] [CrossRef]
- Atlan, H. Application of information theory to the study of the stimulating effects of ionizing radiation, thermal energy, and other environmental factors. Preliminary ideas for a theory of organization. J. Theor. Biol. 1968, 21, 45–70. [Google Scholar] [CrossRef]
- Walker, I. The Evolution of Biological Organization as a Function of Information; Editora INPA: Manaus, Brazil, 2005. [Google Scholar]
- Rashevsky, N. Topology and life: In search of general mathematical principles in biology and sociology. Bull. Math. Biol. 1954, 16, 317–348. [Google Scholar] [CrossRef]
- Atlan, H. On a formal definition of organization. J. Theor. Biol. 1974, 45, 295–304. [Google Scholar] [CrossRef]
- Pahl-Wostl, C. The Dynamic Nature of Ecosystems, Chaos and Order Entwined; John Wiley & Sons: Chichester, UK, 1995. [Google Scholar]
- Maturana, H. The Organization of the Living: A Theory of the Living Organization. Int. J. Hum. Comput. Stud. 1999, 51, 149–168. [Google Scholar] [CrossRef]
- Louie, A.H. (M,R)-Systems and their Realizations. Axiomathes 2006, 16, 35–64. [Google Scholar] [CrossRef]
- Kineman, J.J. Relational Science: A Synthesis. Axiomathes 2011, 21, 393–437. [Google Scholar] [CrossRef]
- Baas, N.A. On structure and organization: An organizing principle. Int. J. Gen. Syst. 2013, 42, 170–196. [Google Scholar] [CrossRef]
- Baas, N.A. On higher structures. Int. J. Gen. Syst. 2016, 45, 747–762. [Google Scholar] [CrossRef]
- Hellerman, L. The Animate—Inanimate Relationship. Int. J. Gen. Syst. 2016, 45, 734–746. [Google Scholar] [CrossRef]
- Baas, N.A. Self-organisation and Higher Order Structures. In Self-organisation of Complex Structures: From Individual to Collective Dynamics; Schweitzer, F., Ed.; CRC Press: Boca Raton, FL, USA, 1997; pp. 71–81. [Google Scholar]
- Bohr, N.H.D. Light and Life. Nature 1933, 131, 457–459. [Google Scholar] [CrossRef]
- Maynard Smith, J. The Concept of Information in Biology. Philos. Sci. 2000, 67, 177–194. [Google Scholar] [CrossRef]
- Adami, C. Information theory in molecular biology. Phys. Life Rev. 2004, 1, 3–22. [Google Scholar] [CrossRef]
- Atlan, H.; Cohen, I.R. Self-organization and meaning in immunology. In Self-Organization and Emergence in Life Sciences; Feltz, B., Crommelinck, M., Goujon, P., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 121–139. [Google Scholar]
- Hauhs, M.; Lange, H. Ecosystem dynamics viewed from an endoperspective. Sci. Total Environ. 1996, 183, 125–136. [Google Scholar] [CrossRef]
- Jablonka, E.; Lamb, M.J. Evolution in Four Dimensions: Genetic, Epigenetic, Behavioral, and Symbolic Variaton in the History of Life. In Life and Mind: Philosophical Issues in Biology and Psycology, A Bradford Book; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Roederer, J.G. Information and its Role in Nature; The Frontiers Collection; Springer: Berlin, Germany, 2005. [Google Scholar]
- Adamatzky, A.; Armstrong, R.; Jones, J.; Gunji, Y.P. On creativity of slime mould. Int. J. Gen. Syst. 2013, 42, 441–457. [Google Scholar] [CrossRef]
- Chaitin, G. To a Mathematical Definition of ‘LIFE’. SIGACT News, 1970; 4, 12–18. [Google Scholar] [CrossRef]
- Chaitin, G.J. Toward a Mathematical Definition of “Life”. In Maximum Entropy Formalism; Levine, R.D., Tribus, M., Eds.; M.I.T. Press: Cambridge, MA, USA, 1979; pp. 477–498. [Google Scholar]
- Pattee, H.H. Simulations, Realizations, and Theories of Life. In Artificial Life; Number VI in SFI Series in the Sciences of Complexity; Langton, C., Ed.; Addison-Wesley Publishing Company, Inc.: Redwood City, CA, USA, 1989; pp. 63–77. [Google Scholar]
- Atlan, H.; Koppel, M. The cellular computer DNA: Program or data. Bull. Math. Biol. 1990, 52, 335–348. [Google Scholar] [CrossRef] [PubMed]
- Emmeche, C. The Computational Notion of Life. Theoria 1994, 9, 1–30. [Google Scholar]
- Griffiths, P.E. Genetic Information: A Metaphor in Search of a Theory. Philos. Sci. 2001, 68, 394–412. [Google Scholar] [CrossRef]
- Jablonka, E. Information: Its interpretation, its inheritance, and its sharing. Philos. Sci. 2002, 69, 578–605. [Google Scholar] [CrossRef]
- Thaller, B. Advanced Visual Quantum Mechanics; Springer Science+Business Media Inc.: New York, NY, USA, 2005. [Google Scholar]
- Scott Kelso, J.A. Dynamic Patterns: The Self-Organization of Brain and Behaviour; The MIT Press, A Bradford Book: Cambridge, MA, USA, 1999. [Google Scholar]
- Bruggeman, F.J.; Westerhoff, H.V.; Boogerd, F.C. BioComplexity: A pluralist research strategy is necessary for a mechanistic explanation of the “live” state. Philos. Psychol. 2002, 15, 411–440. [Google Scholar] [CrossRef]
- Lloyd, E.K. Counting Isomers and Isomerizations. In Graph Theory and Its Applications: East and West, Proceedings of the First China_USA International Graph Theory Conference, Jinan, China, June 9–20, 1986; Annals of the New York Academy of Sciences; Capobianco, M.F., Guan, M., Hsu, D.F., Tian, F., Eds.; The New York Academy of Sciences: New York, NY, USA, 1989; Volume 576, pp. 377–384. [Google Scholar]
- Dobrowolski, J.C. The chiral graph theory. MATCH Commun. Math. Comput. Chem. 2015, 73, 347–374. [Google Scholar]
- Barwise, J. Admissible Sets and Structures; Springer: Berlin, Germany, 1975. [Google Scholar]
- Kritz, M.V. On Biology and Information; P&D Report 25/91; LNCC/MCTI: Petrópolis, Brazil, 1991. [Google Scholar]
- Hartwell, L.H.; Hopfield, J.J.; Leibler, S.; Murray, A.W. From molecular to modular cell biology. Nature 1999, 402, C47–C52. [Google Scholar] [CrossRef] [PubMed]
- Berge, C. Graphs and Hypergraphs; North-Holland: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Schmidt, G.; Ströhlein, T. Relations and Graphs: Discrete Mathematics for Computer Scientists; EACTS Monagraphs on Theoretical Computer Science; Springer: Berlin, Germany, 1993. [Google Scholar]
- Klamt, S.; Haus, U.U.; Theis, F. Hypergraphs and Cellular Networks. PLoS Comput. Biol. 2009, 5, e1000385. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, M.T.; Kritz, M.V. On the Hierarchical Organization of Metabolic Networks: An Underlying Mathematical Model. In Proceedings of the International Symposium on Mathematical and Computational Biology (BIOMAT 2005); Mondaini, R., Dilão, R., Eds.; E-papers Serviços Editoriais Ltda.: Rio de Janeiro, Brazil, 2006; pp. 221–241. [Google Scholar]
- Manna, Z. The Mathematical Theory of Computation; McGraw-Hill Co.: New York, NY, USA, 1974. [Google Scholar]
- Bailly, A. Dictionnaire Grec Français, 26th ed.; Librairie Hachette: Paris, France, 1963; (1e Édition, 1894). [Google Scholar]
- Arnol’d, V.I. Mathematical Methods of Classical Mechanics; Vol. 60, Graduate Texts in Mathematics; Springer: Berlin, Germany, 1978. [Google Scholar]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Kritz, M.V. On Relations between i-graphs and Data Structures. Logique Analyse 1996, 39, 153–164. [Google Scholar]
- Kritz, M.V. Biological Organizations. In Proceedings of the IV Brazilian Symposium on Mathematical and Computational Biology (BIOMAT IV); Mondaini, R., Ed.; BIOMAT Consortium, E-papers Serviços Editoriais Ltda.: Rio de Janeiro, Brazil, 2005; Volume 2, pp. 89–103. [Google Scholar]
- Mitchell, A.; Romano, G.H.; Groisman, B.; Yona, A.; Dekel, E.; Kupiec, M.; Dahan, O.; Pilpel, Y. Adaptive prediction of environmental changes by microorganisms. Nature 2009, 460, 220–224. [Google Scholar] [CrossRef] [PubMed]
- Nuñez, J.K.; Lee, A.S.Y.; Engelman, A.; Doudna, J.A. Integrase-mediated spacer acquisition during CRISPR-Cas adaptive immunity. Nature 2015, 519, 193–198. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, A.A.K.; Der, B.S.; Shin, J.; Vaidyanathan, P.; Paralanov, V.; Strychalski, E.A.; Ross, D.; Densmore, D.; Voigt, C.A. Genetic circuit design automation. Science 2016, 352, aac7341. [Google Scholar] [CrossRef] [PubMed]
- Stonier, T. Information and the Internal Structure of the Universe; Springer: London, UK, 1990. [Google Scholar]
- Fenzl, N.; Hofkirchner, W. Information Processing in Evolutionary Systems. In Self-organisation of Complex Structures: From Individual to Collective Dynamics; Schweitzer, F., Ed.; CRC Press: Boca Raton, FL, USA, 1997; pp. 59–70. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Hoath, S.B. Considerations on the Role of the Skin as the Boundary of an Autopoietic System. In Proceedings of the Biology, Language, Cognition and Society: International Symposium on Autopoiesis, Belo Horizonte, Brazil, 18–21 November 1997.
- Santra, T.; Kolch, W.; Kholodenko, B.N. Navigating the multilayered organization of eukaryotic signaling: A new trend in data integration. PLoS Comput. Biol. 2014, 10, e1003385. [Google Scholar] [CrossRef] [PubMed]
- Nadin, M. Anticipation and dynamics: Rosen’s anticipation in the perspective of time. Int. J. Gen. Syst. 2010, 39, 3–33. [Google Scholar] [CrossRef]
- Iyer, K.V.; Pulford, S.; Mogilner, A.; Shivashankar, G.V. Mechanical activation of cells induces chromatin remodeling preceding MKL nuclear transport. Biophys. J. 2012, 103, 1416–1428. [Google Scholar] [CrossRef] [PubMed]
- Gerritsen, V.B. Moody wallpaper. Protein Spotlight 2003, 33. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.616.8546&rep=rep1&type=pdf (accessed on 1 March 2017). [Google Scholar]
- Ai, C.; Li, Y.; Wang, Y.; Chen, Y.; Yang, L. Insight into the effects of chiral isomers quinidine and quinine on CYP2D6 inhibition. Bioorg. Med. Chem. Lett. 2009, 19, 803–806. [Google Scholar] [CrossRef] [PubMed]
- Levinson, H.; Mori, K. The Pheromone Activity of Chiral Isomers of Trogodermal for Male Khapra Beetles. Naturwissenschaften 1980, 67, 148–149. [Google Scholar] [CrossRef]
- Barrangou, R.; Marraffini, L.A. CRISPR-Cas Systems: Prokaryotes Upgrade to Adaptive Immunity. Mol. Cell 2014, 54, 234–244. [Google Scholar] [CrossRef] [PubMed]
- Simon, H.A. The Sciences of the Artificial, 3rd ed.; The MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Lenneberg, E.H. Biological Foundations of Language, reprint ed.; Robert E. Krieger Publ. Co.: Malabar, FL, USA, 1984; (Original edition and copyright: John Wiley & Sons, Inc., 1967.). [Google Scholar]
- Casti, J.L.; Karlqvist, A. (Eds.) Complexity, Language, and Life: Mathematical Approaches; Vol. 16, Lecture Notes in Biomathematics; Springer: Berlin, Germany, 1986.
- Weinberg, G.M. An Introduction to General Systems Thinking; Dorset Hause Publishing: New York, NY, USA, 2001. [Google Scholar]
- Bosch, O.; Maani, K.; Smith, C. Systems Thinking—Language of Complexity for Scientists and Managers; The University of Queensland: Queensland, Australia, 2007; pp. 57–66. [Google Scholar]
- Corning, P.A.; Szathmáry, E. “Synergistic selection”: A Darwinian frame for the evolution of complexity. J. Theor. Biol. 2015, 371, 45–58. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Complexity, Entropy, and the Physics of Information. In Santa Fe Institute Studies in the Sciences of Complexity; Perseus Publishing: Cambridge, MA, USA, 1990. [Google Scholar]
- Watkins, J.J. Number Theory: A Historical Approach; Princeton University Press: Princeton, NJ, USA; Oxford, UK, 2014. [Google Scholar]
- Rosen, R. Complexity and System Descriptions. In Systems, Approaches, Theories, Applications; Hartnett, W., Ed.; D. Reidel Publishing Co.: Dordrecht-Holland, The Netherlands, 1977; pp. 169–178. [Google Scholar]
- Shao, X.; Li, Q.; Mogilner, A.; Bershadsky, A.D.; Shivashankar, G.V. Mechanical stimulation induces formin-dependent assembly of a perinuclear actin rim. Proc. Natl. Acad. Sci. USA 2015, 112, E2595–E2601. [Google Scholar] [CrossRef] [PubMed]
- Ditlev, J.A.; Mayer, B.J.; Loew, L.M. There is More Than One Way to Model an Elephant. Experiment-DrivenModeling of the Actin Cytoskeleton. Biophys. J. 2013, 104, 520–532. [Google Scholar] [CrossRef] [PubMed]
- Erban, R.; Flegg, M.B.; Papoian, G.A. Multiscale Stochastic Reaction–Diffusion Modeling: Application to Actin Dynamics in Filopodia. Bull. Math. Biol. 2013, 76, 799–818. [Google Scholar] [CrossRef] [PubMed]
- Mogilner, A.; Rubinstein, B. The physics of filopodial protrusion. Biophys. J. 2005, 89, 782–795. [Google Scholar] [CrossRef] [PubMed]
- De Moura, C.A.; Kritz, M.V.; Leal, T.F.; Prokop, A. Mathematical-computational Simulation of Cytoskeletal Dynamics. In Modeling and Computational Intelligence in Engineering Applications; Santiago, O.L., da Silva-Neto, A.J., Silva, G., Eds.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Callebaut, W.; Rasskin-Gutman, D. Modularity: Understanding the Development and Evolution of Natural Complex Systems; The Viena Series in Theoretical Biology; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Simon, H.A. The Architecture of Complexity. Proc. Am. Philos. Soc. 1962, 106, 467–485. [Google Scholar]
- Ehret, C.F. Organelle Systems and Biological Organization. Science 1960, 132, 115–123. [Google Scholar] [CrossRef] [PubMed]
- Herrgård, M.J.; Swainston, N.; Dobson, P.; Dunn, W.B.; Arga, K.Y.; Arvas, M.; Büthgen, N.; Borger, S.; Costenoble, R.; Heinemann, M.; et al. A consensus yeast metabolic network reconstruction obtained from a community approach to systems biology. Nat. Biotechnol. 2008, 26, 1155–1160. [Google Scholar] [CrossRef] [PubMed]
- Lambert, A.; Dubois, J.; Bourqui, R. Pathway Preserving Representation of Metabolic Networks. Comput. Graph. Forum 2011, 30, 1021–1030. [Google Scholar] [CrossRef]
- Kritz, M.V.; dos Santos, M.T.; Urrutia, S.; Schwartz, J.M. Organizing Metabolic Networks: Cycles in Flux Distribution. J. Theor. Biol. 2010, 265, 250–260. [Google Scholar] [CrossRef] [PubMed]
- Keung, A.J.; Khalil, A.S. A unifying model of epigenetic regulation. Science 2016, 351, 661–662. [Google Scholar] [CrossRef] [PubMed]
- Breinig, F.; Sendzik, T.; Eisfeld, K.; Schmitt, M.J. Dissecting toxin immunity in virus-infected killer yeast uncovers an intrinsic strategy of self-protection. Proc. Natl. Acad. Sci. USA 2006, 103, 3810–3815. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, M.J.; Breinig, F. Yeast viral killer toxins: Lethality and self-protection. Nat. Rev. Microbiol. 2006, 4, 212–221. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Cousiño, N.; Maqueda, M.; Ambrona, J.; Zamora, E.; Esteban, R.; Ramírez, M. A new wine Saccharomyces cerevisiae killer toxin (Klus), encoded by a double-stranded rna virus, with broad antifungal activity is evolutionarily related to a chromosomal host gene. Appl. Environ. Microbiol. 2011, 77, 1822–1832. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A.; Polak, E. System Theory, Vol. 8, Inter-University Electronics Series; TATA McGraw-Hill Publishing Co. Ltd.: Bombay/New Delhi, India, 1969. [Google Scholar]
- Louie, A.H. Anticipation in (M,R)-systems. Int. J. Gen. Syst. 2012, 41, 5–22. [Google Scholar] [CrossRef]
- Burstein, G.; Negoita, C.; Kranz, M. Postmodern Fuzzy System Theory: A Deconstruction Approach Based on Kabbalah. Systems 2014, 2, 590–605. [Google Scholar] [CrossRef]
- Igamberdiev, A.U. Anticipatory dynamics of biological systems: From molecular quantum states to evolution. Int. J. Gen. Syst. 2015, 44, 631–641. [Google Scholar] [CrossRef]
- Kritz, M.V. Biological Information and Knowledge; Relatório de P&D 23/2009; LNCC/MCT: Petrópolis, Brazil, 2009. [Google Scholar]
- Kritz, M.V. Biological Organization, Biological Information, and Knowledge. bioRxiv 2014, 2014, 012617. [Google Scholar]
- Johnson, J. A Theory of Stars in Complex Systems. In Complexity, Language, and Life: Mathematical Approaches; Lecture Notes in Biomathematics; Casti, J.L., Karlqvist, A., Eds.; Springer: New York, NY, USA, 1986; Volume 16, pp. 21–61. [Google Scholar]
- Bergareche, A.M.; Ruiz-Mirazo, K. Metabolism and the problem of its universalization. BioSystems 1999, 49, 45–61. [Google Scholar] [CrossRef]
- Holland, J.H. Studying complex adaptive systems. J. Syst. Sci. Complex. 2006, 19, 1–8. [Google Scholar] [CrossRef]
- Letelier, J.C.; Cárdenas, M.L.; Cornish-Bowden, A. From L’Homme Machine to metabolic closure: Steps towards understanding life. J. Theor. Biol. 2011, 286, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Emmeche, C. A Bio-semiotic Note on Organisms, animals, machines, Cyborgs, and the Quasi-autonomy of Robots. Pragmat. Cogn. 2007, 15, 455–483. [Google Scholar]
- Luz Cárdenas, M.; Letelier, J.C.; Gutiérrez, C.; Cornish-Bowden, A.; Soto-Andrade, J. Closure to efficient causation, computability and artificial life. J. Theor. Biol. 2010, 263, 79–92. [Google Scholar] [CrossRef] [PubMed]
- Villani, M.; Filisetti, A.; Graudenzi, A.; Damiani, C.; Carletti, T.; Serra, R. Growth and Division in a Dynamic Protocell Model. Life 2014, 4, 837–864. [Google Scholar] [CrossRef] [PubMed]
- Shrager, J. The fiction of function. Bioinformatics 2003, 19, 1934–1936. [Google Scholar] [CrossRef] [PubMed]
- Brownlee, J. Complex Adaptive Systems; CIS Technical Report 070302A; Complex Intelligent Systems Laboratory, Centre for Information Technology Research: Melbourne, Australia, 2007. [Google Scholar]
- Wolkenhauer, O. Systems biology: The reincarnation of systems theory applied in biology? Brief. Bioinform. 2001, 2, 258–270. [Google Scholar] [CrossRef] [PubMed]
- Szathmáry, E. Founder of systems chemistry and foundational theoretical biologist: Tibor Gánti (1933-2009). J. Theor. Biol. 2015, 381, 2–5. [Google Scholar] [CrossRef] [PubMed]
- Lazebnik, Y. Can a biologist fix a radio?—Or, what I learned while studying apoptosis. Cancer Cell 2002, 2, 179–182. [Google Scholar] [CrossRef]
- Boogerd, F.; Bruggeman, F.; Jonker, C.; de Jong, H.L.; Tamminga, A.; Treur, J.; Westerhoff, H.; Wijngaards, W. Inter-level relations in computer science, biology, and psychology. Philos. Psychol. 2002, 15, 463–471. [Google Scholar] [CrossRef]
- Mayr, E. This Is Biology: The Science of the Living World; Belknap Press/Havard University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Kitto, K. A Contextualised General Systems Theory. Systems 2014, 2, 541–565. [Google Scholar] [CrossRef]




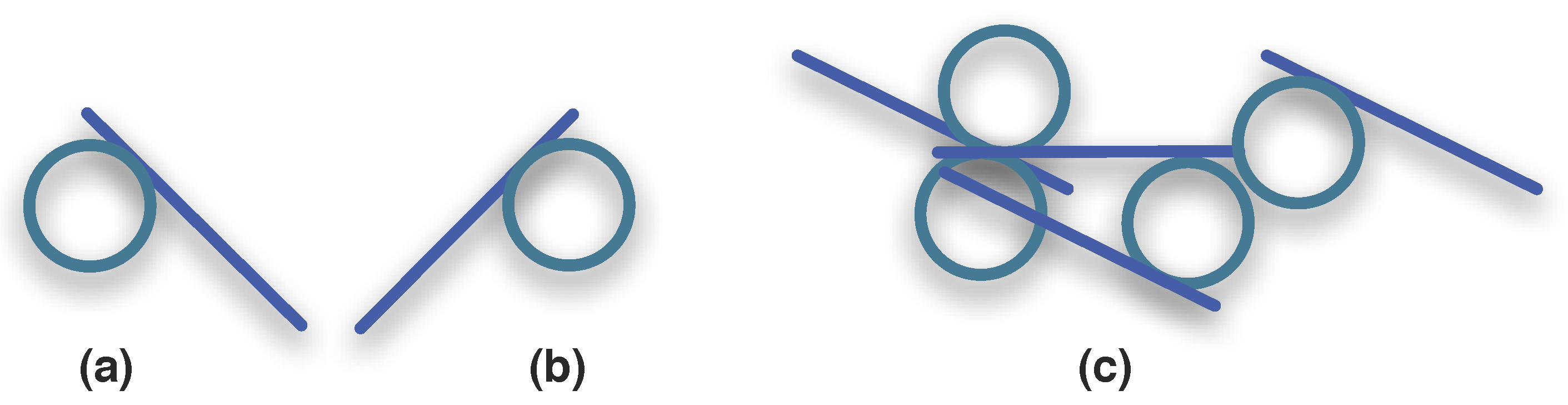
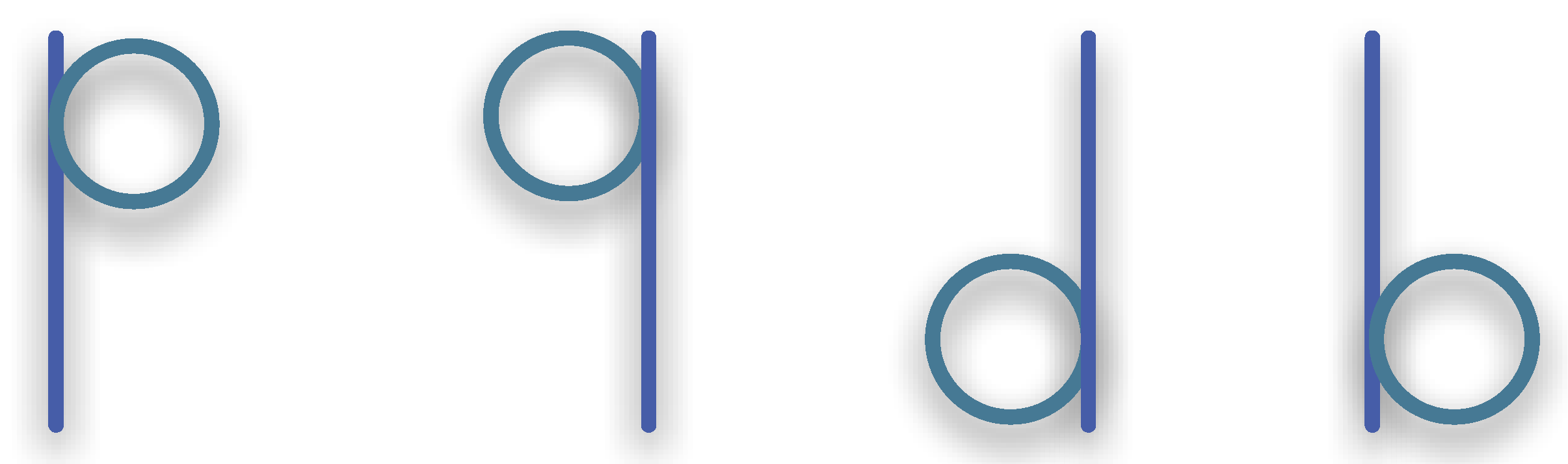
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kritz, M. From Systems to Organisations. Systems 2017, 5, 23. https://doi.org/10.3390/systems5010023
Kritz M. From Systems to Organisations. Systems. 2017; 5(1):23. https://doi.org/10.3390/systems5010023
Chicago/Turabian StyleKritz, Maurício. 2017. "From Systems to Organisations" Systems 5, no. 1: 23. https://doi.org/10.3390/systems5010023
APA StyleKritz, M. (2017). From Systems to Organisations. Systems, 5(1), 23. https://doi.org/10.3390/systems5010023




