Using Optimization Models for Scheduling in Enterprise Resource Planning Systems

Abstract

Companies often use specially-designed production systems and change them from time to time. They produce small batches in order to satisfy specific demands with the least tardiness. This imposes high demands on high-performance scheduling algorithms which can be rapidly adapted to changes in the production system. As a solution, this paper proposes a generic approach: solutions were obtained using a widely-used commercially-available tool for solving linear optimization models, which is available in an Enterprise Resource Planning System (in the SAP system for example) or can be connected to it. In a real-world application of a flow shop with special restrictions this approach is successfully used on a standard personal computer. Thus, the main implication is that optimal scheduling with a commercially-available tool, incorporated in an Enterprise Resource Planning System, may be the best approach.

1. Introduction

Operative production planning and scheduling in Enterprise Resource Planning Systems are incorporated in hierarchical production planning, consisting of master production scheduling, material requirements planning (MRP), and scheduling (see Kurbel [1] or Vollmann [2]). Since capacity considerations in master production scheduling and material requirements planning cause incorrect estimations of lead times, out-of-stock and tardiness, respectively, can be substantially reduced by scheduling. Due to the so called “no free lunch theorem” (see Wolpert and Macready [3]), the performance of an algorithm can only be high if (correct) problem-specific knowledge is used (about the structure of the optimization problem). This explains why there are still many publications about scheduling algorithms for specific production systems. This fits to the observation that companies produce small batches on specially-designed production systems which are changed from time to time. Thus, such production systems have special technological restrictions. For example, in cell manufacturing, a buffer could be non-existent due to limited space and storage facilities. So, in recent years, a considerable amount of research for no-buffer (blocking) scheduling problems and for no-wait scheduling problems are published. However, real-world problems often have more restrictions; for example, a limited amount of production aids such that they are even more difficult to schedule. Therefore, it is very time consuming to get an appropriate algorithm: either by developing a new one or by finding one in the literature (since the information about the runtime is, if published, usually outdated, satisfying a runtime restriction can just be tested by an implementation of the algorithm.).

This paper proposes that a linear optimization model is developed for a scheduling problem and it is solved with a commercially-available tool. Several tools are available. In this paper, the tool ILOG, which is available in the SAP system, is used. As an alternative, Baker uses, in [4], the Risk Solver Platform (RSP), which is an Excel add-in, developed by Frontline Systems, Inc. (Incline Village, NV, USA). Thus, an appropriate tool is either available in an Enterprise Resource Planning Systems (ILOG is in the SAP system, for example) or can be connected to it.

The approach is applied on permutation flow shop problems with technology restrictions. A real-world example serves as a test problem. As usual, in industrial practice, the planning is executed in a rolling-horizon environment. For this, a production-planning and control (PPC) system simulation is implemented. In this simulation, a customer order arrival process is generated. Material requirements planning (as usual) determines production orders. These are scheduled by the approach at the company site, by priority rules and by solving an optimization model. Because a standard personal computer is used, this real-world application shows that optimal scheduling is applicable in industrial practice. With each new generation of hardware (or improved software for solving an optimization model) more complex scheduling problems can be optimally solved under the conditions at the company site. For research this means that optimal solutions can serve as a benchmark—not only for small test problems. Thus, the main implication is that optimal scheduling with a commercially-available tool, incorporated in an Enterprise Resource Planning System, will, in the future, be more often the best approach.

This paper is organized as follows. First, the real-word problem is explained (Section 2). An optimization model is developed (Section 3) and a literature review about published optimal and heuristic solutions is given (Section 4). This section also explains the priority rules which serve as comparison to the optimal scheduling. Then, simulation of the rolling horizon planning together with the input data is presented and computational results are analyzed (Section 5). Some conclusions are given at the end (Section 6).

2. Real-World Problem

The problem is a modification of a partly-automated production line at Fiedler Andritz in Regensburg, Germany, to produce filters (baskets) with a lot size of one. They are mainly sold to customers directly or assembled in other products. All filters have unified construction. They differ in varying heights of the baskets and there exist different designs.

The production line consists of four stations which are shown in Figure 1. Station 1 assembles six single batons (called consoles) on an assembly ground plate to a skeleton of a filter basket. Baton profiles are assembled into the provided slots of the filter basket skeletons. At the plunge station a wire coil is contrived in the device of a lining machine. The lining machine straightens the wire and inserts batons into the slots. To ensure stability, a worker installs span belts in inflow filter baskets and span cores in outflow filter baskets. To install a span core is more time consuming; this is the only difference in the processing times between and outflow filter baskets. There are enough span belts but just one span core for each outflow filter type. Then, the filter basket is lifted from the assembly ground plate and is transported to the welding station, at which the baton profiles are welded on the filter basket skeletons. The completed filter basket leaves the production line. Prior to this, the span medium is removed. An overhead travelling crane lifts a filter basket out of a station, transports it to the next station and inserts it directly in this station. This is just possible if this station is free. So, there is no buffer in the production line. Due to other operational issues, the crane can just be moved if all stations are inactive. Since an operation cannot be interrupted, the transport has to be performed after the completion of all operations on the stations in the flow shop. Due to further operational issues this restriction has to also applied be for the first and the last station; note, that the crane loads S1 and unloads S4 as well. In summary, all stations are loaded and unloaded with filters during a common process and this process starts with the last station S4, followed by station S3, S2, until station S1 is reached. It is allowed that a station is empty; then this station is skipped (may be partially) in this process.

The processing times of the 10 filter types for inflow (if) and outflow (of) are listed in

Table 1. Routings for the real-world application in minutes.

Filter Type	Station 1	Station 2	Station 3		Station 4	Sum of Processing Times
			if	of		if	of
1	65	5	15	20	10	95	100
2	300	50	55	60	15	420	425
3	255	125	60	67	75	515	522
4	295	45	245	259	15	600	614
5	135	195	295	313	105	730	748
6	75	305	20	25	305	705	710
7	255	285	205	215	75	820	830
8	255	275	195	209	230	955	969
9	50	290	250	263	290	880	893
10	270	300	235	247	300	1105	1117

. The duration of loading (unloading) a station is negligible compared to the duration of the operation as well as it is independent of the allocation (or loading) of the other stations and it is included in the duration of the operation.

Single filters (lot size 1) are sold to customers directly or assembled in other products. In both cases, these products are components in a large product. Thus, the due dates of the demands are in the future. This also happens due to contracts with customers about filter types in the future. For demands of single filters material requirements planning determine production orders. With “just in time” production a storage of these expensive filters are avoided as much as possible. The production orders are scheduled by a simple priority rule. Each working day consists of one shift with a net working time of seven hours—there are breaks of in total one hour in each shift. Material requirements planning is executed before each shift for all known demands. The priority rule is executed on the queue of waiting orders if the first station in the production line becomes idle.

The general (single) scheduling problem consists of M stations and a pool of N jobs, which may change at any time, with known earliest possible starting times being, respectively, release dates ${\mathrm{a}}_{\mathrm{i}}$ $\left(1\le \mathrm{i}\le \mathrm{N}\right)$ and due dates ${\mathrm{f}}_{\mathrm{i}}$ $\left(1\le \mathrm{i}\le \mathrm{N}\right)$, as well as duration ${\mathrm{t}}_{\mathrm{i},\mathrm{j}}$ of operation $\left({\mathrm{o}}_{\mathrm{i},\mathrm{j}}\right)$ j $\left(1\le \mathrm{j}\le \mathrm{M}\right)$ of job i $\left(1\le \mathrm{i}\le \mathrm{N}\right)$, which is worked on station j. Critical at the customer site is the tardiness of a customer order and the tardiness of a filter which will be assembled in other products should be as small as possible. Thus, minimizing total tardiness and analyzing average tardiness $\left({\mathrm{T}}_{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n}}\right)$ and standard deviation of tardiness $\left({\mathrm{T}}_{\mathsf{\sigma }}\right)$ is in line with other studies; see Mouelhi-Chibani and Pierreval [5] or Rajendran and Alicke [6] for generated scheduling problems, as well as Voß and Witt [7] for a real-world application.

The time between two consecutive executions of the load process is determined by the maximum of the duration of the operations on the stations in the flow shop; this is called cycle time. This “load”-restriction, the no-buffer condition, and the capacity of the stations are the main restrictions. Set-up times are relatively small compared to operation times and they are included in operation times.

The no-buffer condition means a relaxation of the scheduling problem with the (above) “load”-restriction. A good survey of scheduling problems with the no-buffer condition was given by Hall and Sriskandarajah [8]. There it is proved that this problem is NP-hard in the strong sense for more than two stations. Thus, the problem class with this real-world application as an example is NP-hard in the strong sense as well.

3. A Linear Optimization Model

3.1. Literature Review

There are two main approaches (see Sundaramoorthy and Maravelias [9]): sequence-based models (a sequence of jobs is determined) or discrete time models (those discrete periods are determined, in which the jobs are completed). In many cases, the modeling of restrictions, especially for a limited storage capacity, require more complicated constraints for sequence-based models than for discrete time models. On the other hand, sequence-based models have normally shorter run times. In the literature there are two ways to express such a sequence: in the so-called assignment formulation the key decision variable $\left({\mathrm{x}}_{\mathrm{i},\mathrm{p}}\right)$ is set to 1, if job i is at position p in the permutation, and in the so called precedence formulation the key decision variable $\left({\mathrm{x}}_{\mathrm{i},\mathrm{p}}\right)$ is set to 1, if job i precedes job p in the sequence. Due to Gupta et al. [10] the assignment formulation requires less computation time than the precedence formulation. In their study makespan is minimized. As can be seen below, for the class of problems regarded in this paper restrictions can be formulated by quite simple constraints, so that a sequence-based model seems to be the best choice. Nevertheless, in many papers, see Gicquel et al. [11] for example, an integer model with discrete time periods is used. If general precedence constraints occur then flow shop problems are modelled by the well-known resource constrained scheduling problem (RCPSP, sometimes referred to as a project shop; see e.g., Morton and Pentico [12]); an example is in Voß and Witt [7]. Thus, the following model extends the ones in the literature by restrictions ensuring the “load”-restriction, restrictions for the special treatment of the first and the last cycles, restrictions for the rolling planning environment, and restrictions to ensure that a span core is used not more than once.

3.2. Model

Already, the no-buffer restriction means that all feasible schedules are a permutation of the N jobs of the scheduling problem. The problem is modeled as an assignment problem with additional restrictions.

Parameters:

M:

number of stations; $1\le \mathrm{j}\le \mathrm{M}$.

N:

number of jobs; $1\le \mathrm{i}\le \mathrm{N}$.

NE:

number of artificial jobs; $1\le \mathrm{i}\le \mathrm{N}$.

${\mathrm{a}}_{\mathrm{i}}$:

release date of job i for all $1\le \mathrm{i}\le \mathrm{N}$.

${\mathrm{f}}_{\mathrm{i}}$:

due date of job i for all $1\le \mathrm{i}\le \mathrm{N}$.

${\mathrm{o}}_{\mathrm{i},\mathrm{j}}$:

operation j of job i $\left(1\le \mathrm{i}\le \mathrm{N}\right)$ which is worked on station j for all $1\le \mathrm{i}\le \mathrm{N}$ and $1\le \mathrm{j}\le \mathrm{M}$.

${\mathrm{t}}_{\mathrm{i},\mathrm{j}}$:

duration of operation j of job i $\left({\mathrm{o}}_{\mathrm{i},\mathrm{j}}\right)$ which is worked on station j for all $1\le \mathrm{i}\le \mathrm{N}$ and $1\le \mathrm{j}\le \mathrm{M}$

Decision variables:

${\mathrm{x}}_{\mathrm{i},\mathrm{p}}$:

position of job i in the permutation: job i is at position p for all $1\le \mathrm{i},\mathrm{p}\le \mathrm{N}$.

(Decision) variables for intermediate results:

$\mathrm{F}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$:

upper bound of the realised finish time of the job at position p in a permutation on station j for all $1\le \mathrm{p},\mathrm{j}\le \mathrm{N}$.

$\mathrm{F}{\mathrm{T}}_{\mathrm{p},0}$:

release date of the job at position p for all $1\le \mathrm{p}\le \mathrm{N}$.

$\mathrm{S}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$:

earliest starting time for job p in a permutation on station j for all $1\le \mathrm{p}\le \mathrm{N}$; i.e., $\mathrm{S}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}=\mathrm{F}{\mathrm{T}}_{\mathrm{p}-1,\mathrm{j}}$.

$\mathrm{S}\mathrm{R}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$:

realized starting and finish time of the job at position p in a permutation on station j for all $1\le \mathrm{p},\mathrm{j}\le \mathrm{N}$.

$\mathrm{F}\mathrm{R}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$:

realized starting and finish time of the job at position p in a permutation on station j for all $1\le \mathrm{p},\mathrm{j}\le \mathrm{N}$.

$\mathrm{T}\mathrm{y}{\mathrm{p}}_{\mathrm{p},\mathrm{k}}^{\mathrm{O}\mathrm{F}}$:

job at position p in the permutation has type k and is an outflow filter for all $1\le \mathrm{p}\le \mathrm{N}$ and for all $1\le \mathrm{k}\le 10$.

${\mathrm{T}}_{\mathrm{p}}$:

upper bound for the tardiness of the job at position p for all $1\le \mathrm{p}\le \mathrm{N}$.

Restrictions:

(1)

${\mathrm{x}}_{\mathrm{i},\mathrm{p}}=\{\begin{array}{cc}1,& \mathrm{j}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{t}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{u}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}$ for all $1\le \mathrm{i},\mathrm{p}\le \mathrm{N}$.

Each job i and each position p is handled once:

(2)

${\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{N}}{\mathrm{x}}_{\mathrm{i},\mathrm{p}}}=1$ for all $1\le \mathrm{i}\le \mathrm{N}$.

(3)

${\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{x}}_{\mathrm{i},\mathrm{p}}}=1$ for all $1\le \mathrm{p}\le \mathrm{N}$.

The “load”-restriction is ensured as follows. For each job there is a timeframe in which the execution takes place; by (4, 5). The jobs, which are together in a cycle, have the same timeframe; by (6–8).

In a timeframe the capacity restriction is ensured by (4) (remember: $\mathrm{F}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ is an upper bound of the realized finish time of the job at position p in a permutation on station j):

(4)

$\mathrm{F}{\mathrm{T}}_{\mathrm{p},\mathrm{j}-1}+{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{t}}_{\mathrm{i},\mathrm{j}}\cdot {\mathrm{x}}_{\mathrm{i},\mathrm{p}}}\le \mathrm{F}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ for all $1\le \mathrm{p}\le \mathrm{N}$ and for all $1\le \mathrm{j}\le \mathrm{M}$ (remember: $\mathrm{F}{\mathrm{T}}_{\mathrm{p},0}$ is the release date of the job at position p).

Linear inequalities (5) ensure that the orders of jobs on each station are identical:

(5)

$\mathrm{F}{\mathrm{T}}_{\mathrm{p}-1,\mathrm{j}}+{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{t}}_{\mathrm{i},\mathrm{j}}\cdot {\mathrm{x}}_{\mathrm{i},\mathrm{p}}}\le \mathrm{F}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ for all $1\le \mathrm{p}\le \mathrm{N}$ and for all $1\le \mathrm{j}\le \mathrm{M}$ with $\mathrm{F}{\mathrm{T}}_{0,\mathrm{j}}$ being the availability of station j for all $1\le \mathrm{j}\le \mathrm{M}$.

Now, all jobs in a cycle should have identical timeframes:

(6)

$\mathrm{F}{\mathrm{T}}_{\mathrm{p}+\left(\mathrm{j}-1\right),\mathrm{M}-\left(\mathrm{j}-1\right)}=\mathrm{F}{\mathrm{T}}_{\mathrm{p}+\mathrm{j},\mathrm{M}-\mathrm{j}}$ for all $1\le \mathrm{p}\le \mathrm{N}-\mathrm{M}+1$ and for all $1\le \mathrm{j}\le \mathrm{M}-1$.

At the beginning $\left(1\le \mathrm{p}\le \mathrm{M}-1\right)$ and at the end $\left(\mathrm{N}-\mathrm{M}+2\le \mathrm{p}\le \mathrm{N}-1\right)$ of a permutation, not all stations are occupied. So, the linear inequalities are adapted as follows.

For $1\le \mathrm{p}\le \mathrm{M}-1$ restriction (6) is:

(7)

$\mathrm{F}{\mathrm{T}}_{1+\left(\mathrm{j}-1\right),\left(\mathrm{M}-\mathrm{p}\right)-\left(\mathrm{j}-1\right)}=\mathrm{F}{\mathrm{T}}_{1+\mathrm{j},\left(\mathrm{M}-\mathrm{p}\right)-\left(\mathrm{j}-1\right)-1}$ for all $1\le \mathrm{p}<\left(\mathrm{M}-1\right)$ and for all $1\le \mathrm{j}<\mathrm{M}-\mathrm{p}$.

and for $\mathrm{N}-\mathrm{M}+2\le \mathrm{p}\le \mathrm{N}-1$ restriction (6) is:

(8)

$\mathrm{F}{\mathrm{T}}_{\mathrm{p}+\left(\mathrm{j}-1\right),\mathrm{M}-\left(\mathrm{j}-1\right)}=\mathrm{F}{\mathrm{T}}_{\mathrm{p}+\mathrm{j},\mathrm{M}-\mathrm{j}}$ for all $\mathrm{N}-\mathrm{M}+1<\mathrm{p}<\mathrm{N}$ and for all $1\le \mathrm{j}\le \mathrm{N}-\mathrm{p}$.

So, $\mathrm{F}{\mathrm{T}}_{\mathrm{p}-1,\mathrm{j}}$ is the earliest starting time for job p in a permutation on station j, as decision variable $\mathrm{S}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ $\left(=\mathrm{F}{\mathrm{T}}_{\mathrm{p}-1,\mathrm{j}}\right)$. With the following linear inequalities, additional decision variables for the real processing times (remember: $\mathrm{S}\mathrm{R}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ and $\mathrm{F}\mathrm{R}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ are realized starting and finishing time of the job at position p in a permutation on station j) are set correctly in the timeframe of a cycle and each job starts at the beginning of a cycle.

(9)

$\mathrm{S}\mathrm{R}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}+{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{t}}_{\mathrm{i},\mathrm{j}}\cdot {\mathrm{x}}_{\mathrm{i},\mathrm{p}}}=\mathrm{F}\mathrm{R}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}\le \mathrm{F}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ for all $1\le \mathrm{p}\le \mathrm{N}$.

(10)

$\mathrm{S}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}=\mathrm{S}\mathrm{R}{\mathrm{T}}_{\mathrm{p},\mathrm{j}}$ for all $1\le \mathrm{j}\le \mathrm{M}$.

Note: The idle time of a job in a cycle can be used to start later, for example, if a worker is not available. Set up times can be integrated if needed.

Just one span core for each outflow filter type (used on the consecutive stations S3 and S4) means that there occurs no two consecutive orders in a permutation having the same outflow filter type. To ensure this, the type of an order in position p in the permutation is determined by:

(11)

$\mathrm{T}\mathrm{y}{\mathrm{p}}_{\mathrm{p},\mathrm{k}}^{\mathrm{O}\mathrm{F}}=\{\begin{array}{cc}1,& \mathrm{j}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{u}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{k}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}$ for all $1\le \mathrm{p}\le \mathrm{N}$ and for all $1\le \mathrm{k}\le 10$.

The above condition is not met, if $\mathrm{T}\mathrm{y}{\mathrm{p}}_{\mathrm{p},\mathrm{k}}^{\mathrm{O}\mathrm{F}}+\mathrm{T}\mathrm{y}{\mathrm{p}}_{\mathrm{p}+1,\mathrm{k}}^{\mathrm{O}\mathrm{F}}>1$ for one k, $1\le \mathrm{k}\le 10$, and one p, $1\le \mathrm{p}\le \mathrm{N}$.

Thus, the condition is met by

(12)

$\mathrm{T}\mathrm{y}{\mathrm{p}}_{\mathrm{p},\mathrm{k}}^{\mathrm{O}\mathrm{F}}+\mathrm{T}\mathrm{y}{\mathrm{p}}_{\mathrm{p}+1,\mathrm{k}}^{\mathrm{O}\mathrm{F}}\le 1$ for all $1\le \mathrm{p}<\mathrm{N}-1$ and for all $1\le \mathrm{k}\le 10$.

(13)

${\mathrm{x}}_{\mathrm{i},\mathrm{p}}\in \left\{0,1\right\}$ for all $1\le \mathrm{i}\le \mathrm{N}$ and for all $1\le \mathrm{p}\le \mathrm{N}$.

(14)

$\mathrm{T}\mathrm{y}{\mathrm{p}}_{\mathrm{p},\mathrm{k}}^{\mathrm{O}\mathrm{F}}\in \left\{0,1\right\}$ for all $1\le \mathrm{p}\le \mathrm{N}$ and for all $1\le \mathrm{k}\le 10$.

Linear inequalities (15, 16) ensure upper bounds for the variable tardiness $\left({\mathrm{T}}_{\mathrm{p}}\right)$.

(15)

${\mathrm{T}}_{\mathrm{p}}\ge 0$ for all $1\le \mathrm{p}\le \mathrm{N}$.

(16)

${\mathrm{T}}_{\mathrm{p}}\ge \mathrm{F}{\mathrm{T}}_{\mathrm{p},\mathrm{M}}-{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{f}}_{\mathrm{i}}\cdot {\mathrm{x}}_{\mathrm{i},\mathrm{p}}}$ for all $1\le \mathrm{p}\le \mathrm{N}$.

Then

(17)

Minimize $\left({\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{p}}}\right)$

minimizes the average tardiness.

An empty station in a cycle is achieved by an artificial order i whose duration time on each station is zero, and whose release date is less than the release dates of all normal jobs, so i can start immediately. With a large due date, no tardiness occur; so, i does not affect the objective function (17). That this is beneficial is analyzed in the section “results and discussion”.

For the linear inequalities, which affects the cycles—as (6–8), there is a distinction between the first (M − 1) cycles, the last (M − 1) cycles and the ones in between. This implies a minimum number of jobs—i.e., of N. A smaller number (of N) of jobs is extended by one or more artificial jobs. For the sake of simplicity, there are always (M − 1) artificial jobs at the beginning and (M − 1) artificial jobs at the end of the to be determined permutation; i.e., the decision variable x. This is achieved with the linear inequalities

(18)

${\mathrm{x}}_{\mathrm{p},\mathrm{p}}=1$ for all $1\le \mathrm{p}\le \left(\mathrm{M}-1\right)$

in the case of the (M − 1) artificial jobs at the beginning and

(19)

${\mathrm{x}}_{\mathrm{N}+\left(\mathrm{M}-1\right)+\mathrm{N}\mathrm{E}+\mathrm{p},\mathrm{N}+\left(\mathrm{M}-1\right)+\mathrm{N}\mathrm{E}+\mathrm{p}}=1$ for all $1\le \mathrm{p}\le \left(\mathrm{M}-1\right)$

in the case of the (M − 1) artificial jobs at the end, where NE is the number of artificial jobs with each of them an empty station in a cycle is realized.

3.3. Model Extension for a Rolling Planning Environment

The entire planning hierarchy is executed in a rolling planning environment. This means (for all scheduling procedures) that a sequence of scheduling problems are solved. Each solution of a single scheduling problem is added to a permutation P of the jobs scheduled so far. The starting point is a sequence S of jobs—determined by material requirements planning. The jobs of one single scheduling problem (i.e., workload) consists of those jobs in S. The actual permutation P is extended by the permutation of the jobs due to the first c cycles, $\mathrm{c}\in \mathrm{N}$, also $\mathrm{c}\ge 1$, in an optimal solution, which are not already in P. Assume that p is the period in which the last of these c cycles is finished. Then the next workload consists of the jobs from S with a release date less than or equal to p + r and which are not already in P, of course. For a production line of M stations this means for the calculation of the new solution (NS): The last (M − 1)-jobs in P (A₁, …, A_{M − 1}) are partially part of the first (M − 1) cycles of NS. A₁, …, A_{M − 1} determine a minimum length of the first (M − 1) cycles of NS. For cycle j, $1\le \mathrm{j}\le \left(\mathrm{M}-1\right)$, of these cycles, this minimum length is the maximum of the durations of the jobs in A₁, …, A_{M − 1} which are executed in cycle j and it is denoted by $\mathrm{T}\mathrm{Z}{\mathrm{B}}_{\mathrm{j}}$. In addition, these first (M − 1) cycles of NS determine the (realized) due dates of A₁, …, A_{M − 1} which is denoted by $\mathrm{S}\mathrm{E}{\mathrm{T}}_{\mathrm{i}}$ for job A_i, $1\le \mathrm{i}\le \left(\mathrm{M}-1\right)$.

The model is extended as follows:

Parameters:

P: Permutation of the jobs scheduled so far due to the rolling planning environment.

A₁, …, A_{M − 1}: last (M − 1)-jobs in P.

$\mathrm{T}\mathrm{Z}{\mathrm{B}}_{\mathrm{j}}$: lower bound for the duration of cycle j for all $1\le \mathrm{j}\le \left(\mathrm{M}-1\right)$.

Note: the other parameters of the model in Section 3.2 are filled by the release procedure explained above.

(Decision) variables for intermediate results:

$\mathrm{S}\mathrm{E}{\mathrm{T}}_{\mathrm{i}}$: due date of job A_i for all $1\le \mathrm{i}\le \left(\mathrm{M}-1\right)$.

Restrictions:

The following restrictions—see (20)—ensure that the first (M − 1) cycles are longer than $\mathrm{T}\mathrm{Z}{\mathrm{B}}_{\mathrm{j}}$. In our approach, the jobs A₁, …, A_{M − 1} are not scheduled, but substituted by the above mentioned artificial jobs. So, the positions M until (M+ M − 1− 1) have to be regarded and the finishing time is, related to station 1, i.e., $\left(\mathrm{F}{\mathrm{T}}_{\left(\mathrm{M}-1\right)+\mathrm{j},1}\right)$. This corresponds to the first (M − 1) cycles of NS—without the (M − 1) artificial jobs. Then the linear inequalities

(20)

$\mathrm{T}\mathrm{Z}{\mathrm{B}}_{\mathrm{j}}\le \mathrm{F}{\mathrm{T}}_{\left(\mathrm{M}-1\right)+\mathrm{j},1}-\mathrm{F}{\mathrm{T}}_{\left(\mathrm{M}-1\right)+\left(\mathrm{j}-1\right),1}$ for all $1\le \mathrm{j}\le \left(\mathrm{M}-1\right)$

are needed.

Since the first (M-1) cycles of the new solution (NS)—again (as with $\mathrm{T}\mathrm{Z}{\mathrm{B}}_{\mathrm{j}}$) without the (M − 1) artificial jobs—can increase the (realized) due dates of A₁, …, A_{M − 1}, so that their adapted delay have to be integrated in the objective function. With $\mathrm{S}\mathrm{E}{\mathrm{T}}_{\mathrm{i}}$ being the due date of the job which is finished in cycle i (of NS) – i.e., A_i—the linear inequalities (21, 22) ensure upper bounds for the variable tardiness $\left({\mathrm{T}}_{\mathrm{i}}\right)$ or $\left({\mathrm{T}}_{{\mathrm{A}}_{\mathrm{i}}}\right)$, respectively.

(21)

${\mathrm{T}}_{\mathrm{i}}\ge 0$ for all $1\le \mathrm{i}\le \left(\mathrm{M}-1\right)$.

(22)

${\mathrm{T}}_{\mathrm{i}}\ge \mathrm{F}{\mathrm{T}}_{\left(\mathrm{M}-1\right)+\mathrm{i},1}-\mathrm{S}\mathrm{E}{\mathrm{T}}_{\mathrm{i}}$ for all $1\le \mathrm{i}\le \left(\mathrm{M}-1\right)$.

Then, the sum of these tardiness variables has to be added in the objective function:

(23)

Minimize $\left({\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{N}}{\mathrm{T}}_{\mathrm{p}}}+{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}-1}{\mathrm{T}}_{\mathrm{i}}}\right)$.

Technically, $\mathrm{T}\mathrm{Z}{\mathrm{B}}_{\mathrm{j}}$ is calculated by the scheduling algorithm as the maximum of the durations of the jobs in A₁, …, A_{M − 1} which are executed in cycle j. For this, there exists a so called simulation algorithm which simulates the execution of a permutation of jobs on the flow shop. This simulation algorithm can be used to ensure restrictions outside the optimization model; then the simulation algorithm ensures a feasible schedule and calculates the correct completion times for example. This is helpful for restrictions in industrial practice which are difficult to formulate by a linear inequality (or linear inequalities) or for a linear inequality (or linear inequalities) which increases the runtime significantly.

The rolling planning environment implies that there are linear inequalities which ensures that no job starts before its realized date (i.e., $\mathrm{S}\mathrm{R}{\mathrm{T}}_{\mathrm{p},1}\ge$ release date of p) and that the availability of the stations are met (i.e., $\mathrm{S}\mathrm{R}{\mathrm{T}}_{1,\mathrm{j}}\ge$ availability of the station j).

4. Optimal and Heuristic Scheduling

Since the scheduling problem is NP-hard (in the strong sense, see above), research over the last decades focuses increasingly on heuristic methods—from simple priority rules to sophisticated metaheuristics. For flow shop scheduling, the development of the research is traced in Gupta et al. [10]. In more detail, Vallada et al. [13], even though it is focused on heuristics and metaheuristics, provides a careful review of previous research.

As said earlier, the real application is close to the class of no-buffer (blocking) scheduling problems. Solutions for the no-buffer (blocking) scheduling problems are presented in various papers already. Just one example for the blocking flow shop scheduling with makespan criterion is the paper of Wang et al. [14]. They propose a harmony search algorithm together with a new NEH heuristic (Nawaz et al. [15], which several researchers name as best constructive heuristic to minimize the makespan in the flow shop with blocking (see Framinan et al. [16] as one example only), based on the reasonable premise, that the jobs with less total processing times should be given higher priorities.

To the best of my knowledge, just a few studies investigate algorithms for the total tardiness objective (for flow shops with blocking). Ronconi and Henriques [17] describe several versions of a local search. First, with the NEH algorithm they explore specific characteristics of the problem. A more comprehensive local search is developed by a GRASP-based (greedy randomized adaptive search procedure) search heuristic.

Optimal solutions are often achieved by a branch-and-bound algorithm, normally, with a lower bound (-s) which reduces the number of nodes significantly. This algorithm is a heuristic if the CPU time of a run is limited. An example for the total tardiness objective is the work of Ronconi and Armentano [18]; a more effective one is presented in Ronconi [19], but for minimizing makespan.

Exact methods, like branch and bound approaches—for alternatives see Brucker andKnust [20]—can just be applied to problems with a small number of stations; for a review see e.g., Brucker [21]. For example, Kim [22] described a branch and bound algorithm for minimizing mean tardiness in two machine flow shops. Typically, for a small number of stations lower bounds for pruning the search tree (i.e., reducing the search (space)) are developed (and often proven), see e.g., Gharbi et al. [23]. As shown in the literature, see e.g., Brucker [21], the performance criteria affect the complexity of algorithms for scheduling problems. In this sense minimizing makespan is the easiest problem; for example, the two-machine flow shop problem with minimizing makespan is solved in polynomial time by the Johnson algorithm but the 2 machine flow shop problem with minimizing mean tardiness is NP hard. So, it can be expected that additional requirements from industrial practice cause additional runtime consumption.

For flowshop problems, in general, a careful review is provided in the recent paper of Baker [4]. My own search about the last two years show that there is nothing to add. Especially, due to Baker [4], the most effective branch and bound algorithm for the flow shop tardiness problem is developed by Chung, Flynn, and Kirca [24]. The review in Baker [4] says: “Kim [22] examined problems with different values of m and was able to solve problems as large as $14\cdot 4$ and $13\cdot 8$ within a time limit of 1 h. Roughly a decade later, Chung, Flynn, and Kirca [24] also considered different values of m and were able to solve most problems containing 15 jobs (and as many as 8 machines), but several 20-job instances in their testbed went unsolved. Instead of using a time limit, they terminated their algorithm on the basis of nodes visited in the branch-and-bound (BB) algorithm, using a limit of four million nodes. Based on the results of these studies, the state of the art among specialized BB algorithms appears to be the solution of problems with up to about 15 jobs and 8 machines. Clearly, improvements in hardware have occurred since the Chung paper appeared, but that does not necessarily mean that we should expect to solve much larger problems today.”

Using priority rules for scheduling is still state of the art in industrial practice; see, for example, El-Bouri [25] or Chiang and Fu [26], and is used at Fiedler Andritz in Regensburg as well. Thus, in this paper, optimal scheduling is compared with established priority rules from the literature. As is known, tardiness is improved by assigning jobs with a small slack; the slack for job i is defined by ${\mathrm{f}}_{\mathrm{i}}-\mathrm{t}-\mathrm{t}{\mathrm{t}}_{\mathrm{i}}$, where t is the current time and ${\mathrm{f}}_{\mathrm{i}}$ is the due date of job i and $\mathrm{t}{\mathrm{t}}_{\mathrm{i}}$ is the sum of the processing times of the operations of job i—or an alternative assessment of the lead time. Investigations (see e.g., Engell et al. [27]) show that for many job shop problems the rules $\mathrm{CR}+\mathrm{SPT}=\{\begin{array}{c}\begin{array}{ll}\frac{{\mathrm{f}}_{\mathrm{i}}-\mathrm{t}}{\mathrm{t}{\mathrm{t}}_{\mathrm{i}}},& {\mathrm{f}}_{\mathrm{i}}-\mathrm{t}-\mathrm{t}{\mathrm{t}}_{\mathrm{i}}>0\end{array}\\ \begin{array}{cc}\mathrm{t}{\mathrm{t}}_{\mathrm{i}},& {\mathrm{f}}_{\mathrm{i}}-\mathrm{t}-\mathrm{t}{\mathrm{t}}_{\mathrm{i}}\le 0\end{array}\end{array}$, $\mathrm{t}{\mathrm{t}}_{\mathrm{i}}$ means the shortest processing time (SPT) rule, ODD, which is identical with the EDD-rule (i.e., earliest due date) for the class of job shop problems in this investigation, and $\mathrm{S}\mathrm{L}/\mathrm{O}\mathrm{P}\mathrm{N}=\frac{{\mathrm{f}}_{\mathrm{i}}-\mathrm{t}-\mathrm{t}{\mathrm{t}}_{\mathrm{i}}}{\mathrm{M}}$ (where a low value is always preferred) are Pareto optimal to the average, the variance, and the maximum tardiness (see Engell et al. [27]). This explains why SL/OPN and CR+SPT are often used as benchmark; according to Raghu and Rajendran [28] other combinations deliver worse results for flow shop problems. In addition, newer rules are regarded. One is RR, originally defined in Raghu and Rajendran [22] and used, slightly modified, in Rajendran and Holthaus [29]. The priority index is $\left({\mathrm{f}}_{\mathrm{i}}-\mathrm{t}-\mathrm{t}{\mathrm{t}}_{\mathrm{i}}\right)\cdot {\mathrm{e}}^{-\mathsf{\eta }}+{\mathrm{e}}^{\mathsf{\eta }}\cdot \mathrm{t}{\mathrm{t}}_{\mathrm{i}}$, with utilization level $\mathsf{\eta }$ of the entire flow shop defined by $\mathsf{\eta }=\frac{\mathrm{b}}{\mathrm{b}+\mathrm{j}}$, with b being the busy time and j being the idle time of the entire flow shop, and the job with the lowest priority index is processed next. The other rule (RM) is based on the development of a weighted slack-based scheduling rule in Rachamadugu and Morton [30]. Modifications of this rule deliver very good results for flow shop and job shop problems with weighted tardiness criteria (see Vepsatainen and Morton [31]). The rule was successfully adapted to resource-constrained project scheduling problems (RCPSP) in Voß and Witt [7]. Since there is no weight in our problem, the priority index is $\frac{1}{{\mathsf{\pi }}_{\mathrm{i}}}\cdot {\mathrm{e}}^{\frac{\mathrm{k}}{\overline{\mathrm{t}}}\cdot \left({\mathrm{f}}_{\mathrm{i}}-\mathrm{t}-\mathrm{t}{\mathrm{t}}_{\mathrm{i}}\right)}$, with resource costs ${\mathsf{\pi }}_{\mathrm{i}}$, motivated by Voß and Witt [7], and k is an empirically determined “look-ahead” parameter. As local processing time costing we use ${\mathsf{\pi }}_{\mathrm{i}}^{\mathrm{l}}=\mathrm{t}{\mathrm{t}}_{\mathrm{i}}$, called RM local, and as global processing time we use ${\mathsf{\pi }}_{\mathrm{i}}^{\mathrm{g}}={\displaystyle \sum _{\mathrm{i}\in {\mathrm{U}}_{\mathrm{t}}}\mathrm{t}{\mathrm{t}}_{\mathrm{i}}}$, where ${\mathrm{U}}_{\mathrm{t}}$ is the set of unfinished jobs in the pool of orders, including job i, called RM global; note that, in the literature, additional costs are regarded (see Lawrence and Morton [30]).

5. Results and Discussion

In the real-world application the number of demands per period is between 3 and 9 and there are long sequences of successive periods with a similar number of demands. By scheduling with FIFO this causes a lead time for part types 1 to 5, which is almost always below one period, and a lead time for part types 6 to 10, which is always below two periods. Thus, these values are used as lead times in the material requirements planning. The hierarchical planning of material requirements planning followed by optimal scheduling is denoted by MRP-OS and, if priority rules are used for scheduling, it is denoted by MRP-Rule with the name of the rule in brackets, e.g., MRP-Rule (SL/OPN) in the case of the SL/OPN rule. Both alternatives are simulated in a rolling environment. From an optimal schedule just the first order is finally assigned on the production line; i.e., parameter C, see Section 3, is 1. This minimizes the impact of uncertain demand.

The number of demands per period are clustered in five cases: Case 1 between 3 to 5, Case 2 between 5 and 6, Case 3 between 6 and 8, Case 4 between 8 or 9, and a randomly-generated number between 3 to 9. In addition, the demand at the customer site over the last two years is used. These different workloads per period cause different number of late jobs in case of scheduling with the “first-in-first-out” priority rule. Approximately, they are 30% with Case 1, 48% with Case 2, 71% with Case 3, and 82% with Case 4. With all demand scenarios and parameter settings a steady state for both performance criteria—${\mathrm{T}}_{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n}}$ and ${\mathrm{T}}_{\mathsf{\sigma }}$—is reached by a simulation horizon of less than 2500 periods. Therefore, in all experiments a simulation horizon of 3000 periods is used; in the case of historical data, they are repeated. To avoid errors from start-up and rundown, the first and the last 10 periods are disregarded. In literature, an alternative is applied, which is implemented as well: the length of the warm-up period of the simulation model is determined using the MSER-5 heuristics of White, Cobb, and Spratt [32] and cut off. In addition, confidence intervals are calculated; for example, using the overlapping batch means heuristic proposed by Meketon and Schmeiser [33] combined with the optimal batch size heuristic from Song [34]. Since a steady state is always achieved, confidence intervals are not needed.

In this investigation optimal scheduling is executed by IBM-ILOG—version 12.6.2—and the tests are executed on a PC with an Intel 3.3 GHz CPU and 64 GB of RAM. ILOG is often used in academic and industrial practice. Probably, Excel is more accepted in industrial practice. With the Excel add-in Risk Solver Platform (RSP) the optimal model can be implemented, as Baker [4] shows; RSP is developed by Frontline Systems, Inc. (Incline Village, NV, USA) and is available with several textbooks and is widely used by students and practitioners. Thus, OS is feasible in industrial practice.

In the literature the sensitivity of the optimal schedule (OS) to changes in the (forecasted) demands which is characteristic for a rolling planning environment is addressed—see for example Bredström et al. [35]. In a preliminary investigation this effect is analyzed for the real-world application. For this, OS is applied on the above explained different workloads with the parameter setting r = 0 (this means that just the jobs with a release date in the actual period are released (of course the entire workload contains the backlog as well)), with r = 1 (compared to r = 0 also demand in the following period is known) and with r = 2 (i.e., an additional period is regarded as well). Since mean tardiness is optimized, just this criteria is analyzed.

Table 2. Relative differences to r = 1 with “+” means a higher value (worse) and “−“ means a lower value (better) for the six demand scenarios.

OS	Case 1	Case 2	Case 3	Case 4	Case 5	Historical
r = 0	20.8%	23.9%	30.4	39.1%	29.9%	32.8%
r = 2	0%	−0.01%	−0.01%	0.1%	0	0%

contains the relative difference to r = 1: “+” means a higher value (worse) and “−” means a lower value (better). The results with r = 0 are significantly worse than the ones with r = 1. Moreover, the results for r = 2 are very close to the ones of r = 1. The high time pressure in Case 4 shows that a larger release horizon occasionally causes a decrease of the mean tardiness, but overall—i.e., after a full simulation—the number of tardy jobs is slightly smaller. Thus, a much higher runtime due to a larger release horizon is not beneficial and r = 1 is used for the demand scenarios.

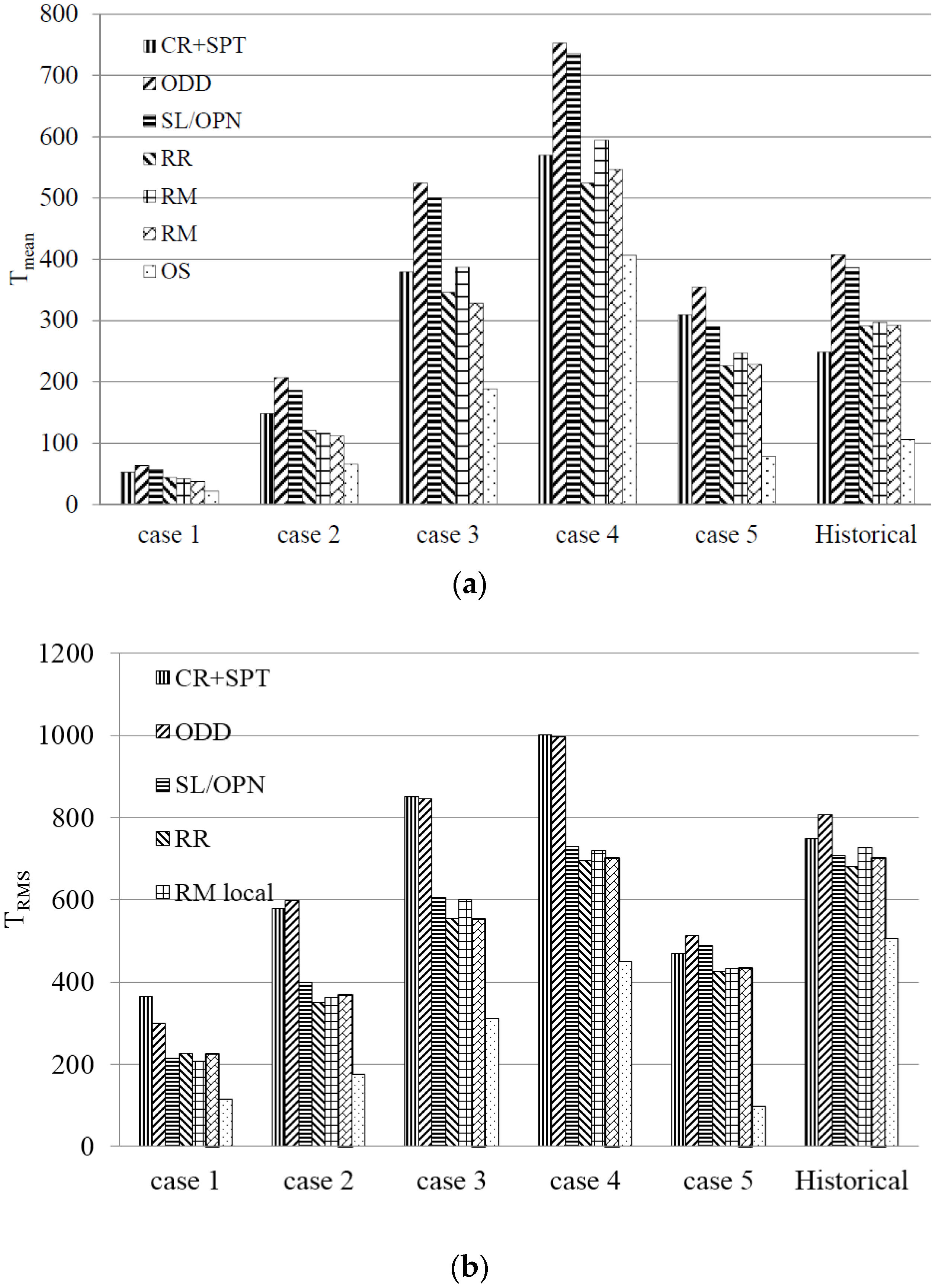
The results by the priority rules and the optimal scheduling are shown in Figure 2. The values for ${\mathrm{T}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ determines a sequence of rules, which is in accordance with the results in literature, like Voß and Witt [7], Raghu and Rajendran [28], Rajendran and Holthaus [29], Lawrence and Morton [36], and Engell et al. [27].

In accordance with the expectation (see Engell et al. [27]) CR + SPT delivers a small ${\mathrm{T}}_{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n}}$ at the expense of a higher ${\mathrm{T}}_{\mathrm{R}\mathrm{M}\mathrm{S}}$ and the opposite is true for SL/OPN. As said earlier, the first behavior is typical for a SPT-based rule, and the second for a slack-based rule. The other three rules, RR, local RM, and global RM, avoid large ${\mathrm{T}}_{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{n}}$ and ${\mathrm{T}}_{\mathrm{R}\mathrm{M}\mathrm{S}}$, respectively, which is in accordance with the results in the literature, but they do not always deliver the best value. Nevertheless, the rule RR combines the rules SPT and slack better than the CR + SPT rule. Further experiments indicate that the application of the exponential function on the slack in the (two versions of the) RM rule, partially modified by constants, uses the slack more effective than the other slack-based rules and delivers good results even if it is beneficial to prefer the job with the smallest processing time. However, this is not enough to ensure that both RM rules deliver better results than RR—indeed half of the figures for RR are better than the ones for RM local. The better processing time costing of RM global compared to RM local results in RM global always delivering the best results.

6. Conclusions

This paper presents an optimization model for a real world flow shop scheduling problem with specific restrictions, which are not covered by the restrictions in the classification of scheduling problems normally used in literature (see e.g., Brucker [21]). This optimization model is solved in a rolling planning environment (called OS) as at the company site. The best solution—i.e., real optimal solution—is achieved if all orders (of the entire simulation in our case) are known. In this case, such an optimal solution is nearly delivered by OS in a runtime which is acceptable for this company. So, this paper presents an application of a solver of linear optimization problems on a real-world problem. Baker [4] expects that such a procedure will be applied in the future more often.

Further studies indicate that in the general case (especially, the job shop problem) there is typically a relatively larger deviation between the schedule delivered by OS and the one to the (real) optimal solution—together with a strong deviation in the performance criteria. This is caused by a higher sensitivity (of the optimal schedule) to changes in the (forecasted) demands than in this study. As a consequence, the needed horizon of known (and unchanged) orders to eliminate this effect is longer. With tuning the material requirements planning the sensitivity of the optimal schedule to the uncertain demand is significantly reduced. Thus, this paper contributes to a robust scheduling in a rolling environment. An extension of this approach to the general job shop problem or the realization of other ideas, may be derived from the ones of Stadtler [37] who solved this problem for the single uncapacitated lot-sizing problem or a control of workload, for which, typically, a release procedure is used, are left to future investigations.