Abstract
In dynamic environments, when faced with a choice of which learning strategy to adopt, do people choose to mostly explore (maximizing their long term gains) or exploit (maximizing their short term gains)? More to the point, how does this choice of learning strategy influence one’s later ability to control the environment? In the present study, we explore whether people’s self-reported learning strategies and levels of arousal (i.e., surprise, stress) correspond to performance measures of controlling a Highly Uncertain or Moderately Uncertain dynamic environment. Generally, self-reports suggest a preference for exploring the environment to begin with. After which, those in the Highly Uncertain environment generally indicated they exploited more than those in the Moderately Uncertain environment; this difference did not impact on performance on later tests of people’s ability to control the dynamic environment. Levels of arousal were also differentially associated with the uncertainty of the environment. Going beyond behavioral data, our model of dynamic decision-making revealed that, in actual fact, there was no difference in exploitation levels between those in the highly uncertain or moderately uncertain environments, but there were differences based on sensitivity to negative reinforcement. We consider the implications of our findings with respect to learning and strategic approaches to controlling dynamic uncertainty.
1. Introduction
Consider the following issue: Every day, managers must decide what works and what does not work for organizational performance and effectiveness. For example, a team manager needs to make choices about how to motivate her subordinates, such as providing encouragement, delegating responsibility, offering rewards, or punishing shirking. Likewise, senior management decides upon how much to invest into research and development, into brand building, or into skill development of employees. Decision-making in such situations is challenging because managers usually only have an incomplete understanding of how their choices affect performance outputs. Their current knowledge may not lead to superior outputs. They need to explore by experimenting with novel approaches to learn about causal relationship between their new strategies and ultimately how this improves performance, but the value of exploration itself is unclear, particularly when the broader environmental conditions (e.g., markets) are constantly changing. It may instead be more effective if the team manager renews efforts to exploit current policies and strategies rather than seek to change them.
There are multitude of mundane (e.g., figuring out diet/exercise plan to implement) to highly consequential (e.g., figuring out how much money to invest in stock and bonds) non-stationary decision contexts in which individuals have to solve problems, much like the example above; this translates into what is commonly referred to as the exploration vs. exploitation trade-off. This distinction is informed by the pioneering work of Sutton and Barto [1]. Their conceptualization of reinforcement learning is that an agent interacts with an environment with the aim of achieving as much rewards as possible (i.e., maximize cumulative reward). They can employ a maximizing choice rule such that they always pick the alternative from a range of options that is currently associated with the highest expected payoff in the agent’s representation (Exploitation), which is also referred to as greedy action selection. Alternatively, an agent employing a strategy designed to learn about the environment is focused essentially on reducing uncertainty rather than maximizing their rewards (at least in the short term) [1,2,3,4]. Generally, the distinction between the two concerns situations in which a decision-maker implements a policy (or the strategy) that they have already learnt (Exploit), which seems to be the best choice at the time, or they seek to test out an alternative policy which can potentially improve on the policy that is their current best choice (Explore).
The examples we present here highlight what is key to the distinction, which is that there is uncertainty attached to the choice of policy that is implemented. Exploiting may seem like a safe bet because, in the short term, uncertainty is reduced because of past knowledge of the successes and failures of the strategy, but that does not mean it is a safe bet in the future. Exploring may seem like a risky bet, because in the short term it is not clear what the consequences are to changing the strategy. However, typically, the argument follows that exploration is better because seeking more information and adapting strategies will lead to long-term future gains [5,6,7]. Moreover, the argument also follows that when the conditions of the environment are stable, one should exploit, and when the conditions are unstable, one should explore (though this is not without challenge—see [8,9]).
To date, there are no empirical studies that have examined people’s explicit choice behavior when it comes to implementing an exploratory or exploitative learning strategy under different types of dynamically uncertain environmental conditions. In addition, the aim of this study is to also explore an issue that has been of interest in the domain of decision-making, but for which there is virtually no empirical work actually looking at the relationship between affective experiences in varying levels of dynamic uncertainty of an environment people are attempting to control. Thus, the aim of the present study is to examine the impact that highly uncertain and moderately uncertain dynamic environments have on learning approaches (i.e., exploration/exploitation), strategic behavior, control performance, and affect. In addition, we propose a model of dynamic decision-making in order to capture decision-making profiles and to examine the extent to which self-reported learning approaches correspond to those described formally by the model.
1.1. Bandit Tasks
A typical way of examining exploration and exploitation is to use bandit tasks. These are situations in which there are a fixed number of choice alternatives (e.g., two-arm bandits, like a slot machine in a casino) and each bandit has a fixed rate of reward, which is unknown to the decision maker. From trial to trial the decision-maker receives information (outcome-feedback/reward) from their choice between the alternatives, and their job is to reliably select sequentially from the alternatives so that they maximize their cumulative rewards [10]. The tasks not only involve discrete choices between two options [11,12], but can also include four [13] six [14], or even eight options [15].
Overall, the appeal of bandit tasks is that they are versatile and can be used to study a variety of behaviors. For instance, these tasks have been extended to examine choice behavior with non-human participants (rats/pigeons) (e.g., [15]), and in non-stationary versions as well [16]. For both animals and humans, it appears that the amount of trials spent exploring is dependent on the payoff differentials [17], so that the better arm is found quicker (i.e., in fewer trials) the larger the differentials are. In addition, another factor that leads to more exploration is the familiarity with the environment [18]. Moreover, in non-stationary versions of bandit task people do learn the changes in pay-off, but rate of learning is slower than stationary environments [5], and usually only increases when the changes in pay-offs are explicitly signaled to the participant [15]. In general, the behavioral work, and more recently neuropsychological work examining activations in brain regions associated with choice behavior in bandit tasks [13,19], has been successfully modeled by reinforcement learning models [2,20,21].
1.2. IOWA Gambling Task
A commonly studied variant of the bandit task is the IOWA gambling task. In the IOWA gambling task there are four decks of cards, two of which are bad decks (high rewards, but very high losses) and good decks (low rewards, low losses). As with the bandit task, people have to choose a card from each deck, and they receive feedback on their choices, which is used to help them decide on which decks to sample from to maximize their cumulative rewards [22]. In general the findings suggest that participants perseverate over an exploration strategy and rarely move from this to a stage of exploitation [23,24,25,26,27,28]. The reasons for this may be because decisions in the IOWA gambling task are predominately based on a variety of models of the environment and emotional factors (e.g., [22]), which we discuss in Section 1.3. For instance, one view is that card selection strategies are likely to change over time because people construe the IOWA gambling task as a non-stationary environment, despite the fact that it is a stationary one [27,29,30]. However, there has been considerable debate recently concerning the validity of the task and the reliability of the findings and whether much can actually be made of the learning profiles of participants in the task [27,29,30].
1.3. Affective Experience in Decision-Making under Uncertainty
Affect, by which we refer to emotional arousal directed towards someone or something, plays an important role in the way in which people make decisions under uncertainty in a variety of situations. The most popular work examining the link between arousal and decision-making has focused on the way in which arousal is indicative of rapid evaluations of the goodness of their choices prior to making their choices. Studies examining this typically use the IOWA gambling task [22,31,32]. Healthy participants performing the task first displayed arousal towards both positive and negative outcomes of their decisions; arousal here was measured using skin conductance responses which is a method in which arousal is indexed as a physiological response through the amount of sweat produced in a participants’ fingers. Over the course of repeated trials increases in (negative) arousal was associated with poor choices [33]. This work suggests that people make decisions based on appraisals of prospective outcomes, as described by Bechara [34] and [35], in which the ventromedial prefrontal cortex (VM) coordinates external stimulus information (i.e., task information) with internal information about affective states provided by brainstem nuclei, somatosensory and insular cortex, and the amygdala. That the patients with damage to putative emotional centers [36] and VM fail to exhibit any learning, and made poor choices in the IOWA gambling task, also provides complementary empirical support. The claim being made here is that damage to core brain regions prevents the integration of cognitive appraisals of the valence of prospective choices, and cumulative physiological signals (e.g., [35,37]). In line with this account, Botvinick and Rosen [38] examined the association between skin conductance responses and the differentiation in costs, in this case are not monetary outcomes but the result of cognitive demands. The findings indicated an elevated arousal in association with the anticipation of imminent cognitive costs when choosing bad decks which in turn affects subsequent choices.
Alternative accounts, based on studies also measuring arousal using skin conductance responses, suggest that arousal tracks reward feedback from choices made, rather than just anticipatory appraisals of the outcome of prospective choices [39,40]. For instance, Tomb et al. [40] reported a decline of arousal (lower skin conductance responses) over the course of performing the IOWA gambling task as more feedback from choices was experienced, and better choice behavior was achieved. In addition, other interpretations of the IOWA gambling results suggest arousal reflects the level of uncertainty in experiencing gains and losses, and as experience with the task increases, uncertainty decreases, as does arousal [40,41]. Otto, Knox, Markman and Love [42] investigated levels of arousal in a task designed to examine the exploration–exploitation trade-off in a “leapfrog” task. They manipulated task uncertainty and demonstrated that skin conductance responses were larger for exploratory choices than exploitative choices. Again, the idea here being that there is greater uncertainty attached to exploratory choices with potentially inferior rewards compared to prior choices with known associated rewards, and this in turn was associated with greater arousal. Moreover, they also assessed the hypothesis that skin conductance responses could help differentiate between optimal and suboptimal choices, and in support found that arousal increased when choices deviated from optimal.
The insights from work currently examining the association between arousal and choice behavior, in both risky and uncertain decision-making environments, clearly suggest that arousal signals anticipatory appraisals of outcomes, tracking actual outcome feedback, and task uncertainty. A natural extension of this work is to examine whether arousal is associated with choice behavior in a dynamic environment in which the goal is to control a dynamically uncertain outcome, which to the authors’ knowledge has not been empirically explored.
1.4. Dynamic Decision Making Tasks
While often referred to as complex dynamic tasks, or complex problem solving tasks (for review see [43,44,45]), the basic set-up of a dynamic decision making task is fairly uncomplicated. Participants are presented with a system (a set of input–output variables—typically continuous) and from trial to trial they are required to manipulate the input variables in order to bring the output variables to a specific target level. Once they have reached the target level, they must maintain it for a specified length of trials. The difficulty in achieving this comes from not knowing in advance what the underlying input-output relationship is (e.g., linear, non-linear), what the causal structure of the input-output links are, and the fact that the observed dynamic changes to the state of the system can either be exogenous (the result of participant’s actions), endogenous (the result of internal mechanisms in the system) or a combination of both. In addition, controlling the output to a target value may carry a separate reward. That is, successful interventions on the inputs that lead to an output value that reaches the target value, or incrementally gets closer to the target value from trial to trial, may in turn be rewarded [46].
Exploration and exploitation take on different meanings in this paradigm than they do in bandit tasks. Typically, in dynamic decision-making tasks, investigators divide up the tasks into a training session and a testing session [47,48,49,50]. One key manipulation is the type of goal that participants pursue during training, which has been shown to have a significant effect on later decision-making performance in testing sessions [48,49,50,51,52,53]. Training to a specific goal involves participants learning to select the appropriate actions that will enable them to reach the target output value (which can be treated as maximizing one’s reward); this then would approximate exploitation. Training to a non-specific goal involves participants actively learning about the system through hypothesis testing; this form of learning is unconstrained and approximates exploration. However, in dynamic decision-making tasks, there is no cost to exploration, and rewards are entirely subjective and based on the individual’s assessment of the accuracy of their knowledge [50]. Nevertheless, one can argue that there may well be an intrinsic motivation to gather more relevant information from a task, such as the kind faced by those taking part in a dynamic decision-making task in which there are several sources of uncertainty. In other words, when there is no imposed external goal which could act as a motivator, people may switch to an active learning strategy because they are intrinsically motivated to reduce uncertainty [54,55,56,57]. Overall, across several studies comparing non-specific goal with specific goal set-ups, a non-specific goal is shown to be the most effective learning strategy, and leads to more accurate knowledge of the system, and better control of the outputs [48,49,50,51,52,53].
1.5. Differences between Bandit Type Tasks and Dynamic Decision-Making Tasks
There are several important differences between dynamic decision-making tasks and bandit type tasks (including the IOWA gambling task). The most critical of which is that in dynamic decision-making tasks there is a causal structure that connects inputs to outputs, whereas in bandit tasks, each arm is usually independent of the other, and there is no causal structure that associates the arms. Thus, an action taken in a dynamic decision-making task has consequences and can affect the state of the system, whereas for bandit tasks (even those that attempt to blend bandit with dynamic decision-making tasks—e.g., [58]) an action does not change the actual state of the system, it just changes the reward value. In addition, the presence of a causal structure in a dynamic decision-making task has important implications for explorative behavior, because decision-makers may actively manipulate the system in order to improve their understanding and enhance their ability to control the output(s) reliably over time. These interventions can be more or less extensive. For example, a decision-maker could substantially change the states of multiple input variables at the same time or restrict gradual changes to just one variable. One might view the former approach of extensive changes to the system corresponds to more explorative learning than the latter strategy (e.g., [59,60,61]); though this is an unorthodox extension of the common formation of exploration in the reinforcement learning/machine learning domain. In dynamic decision-making tasks, exploration and exploitation also differ in terms of how a decision-maker manipulates the system. In the behavioral literature on dynamic decision-making, exploration is associated with more extensive changes to input variables, which may lead to considerable variations in current control performance. Exploitation, in contrast, corresponds to minor, localized changes and variations in current performance tend to be less pronounced [48,49,50,51]. This trade-off between more or less radical changes to a system figures prominently in other literature, such as management (e.g., [62,63]), but has attracted much less attention in the psychology literature. Importantly, it is virtually impossible to study the impact of strategic interventions on input variables with a view to controlling outputs in the classic bandit task.
1.6. Computational Model: The Single Limited Input, Dynamic Exploratory Responses (SLIDER) Model
The aim of the present study is not only to examine behaviorally the kinds of learning strategies that people adopt with the aim of eventually controlling a dynamic environment, our aim is also to formally describe this behavior. We seek to characterize the basic properties of the reinforcement learning, which drives action selection in the present dynamic decision-making task. To do so, we present a model which utilizes reinforcement learning to produce a probabilistic action selection distribution. The Single Limited Input, Dynamic Exploratory Responses (SLIDER) model takes in information regarding the state of the environment, integrates this information, and selects responses that then go on to impact the state of the environment.
The SLIDER model draws upon established concepts in the computational modeling of reinforcement learning, towards a novel adaptation, which allows partial and intermittent state information to drive the unique action selection procedure in the dynamic decision-making task. In this way, we are able to characterize critical mechanisms of reinforcement learning. These mechanisms are (1) the integration of partial information over multiple response options, (2) the trade-off between exploitative and exploratory action selections, (3) associative learning rates, and (4) continuous action selection functions. The overall structure of the SLIDER model is presented in Figure 1.
Reinforcement learning is at the heart of many different forms of computational modeling approaches to human decision-making. Behaviorists implemented formalized representations of two stages of learning in order to describe many aspects of learning, from neuronal level to the behavioral decision making level. First, an associative learning stage pairs information received from the environment with actions made by the decision process. Second, the difference between observed and predicted information received from the environment is used to compute a prediction error. This prediction error is used to update the associative learning process, resulting in better decisions over time [64]. In this way, reinforcement learning has been used to successfully model learning from the neural level to the behavioral level.
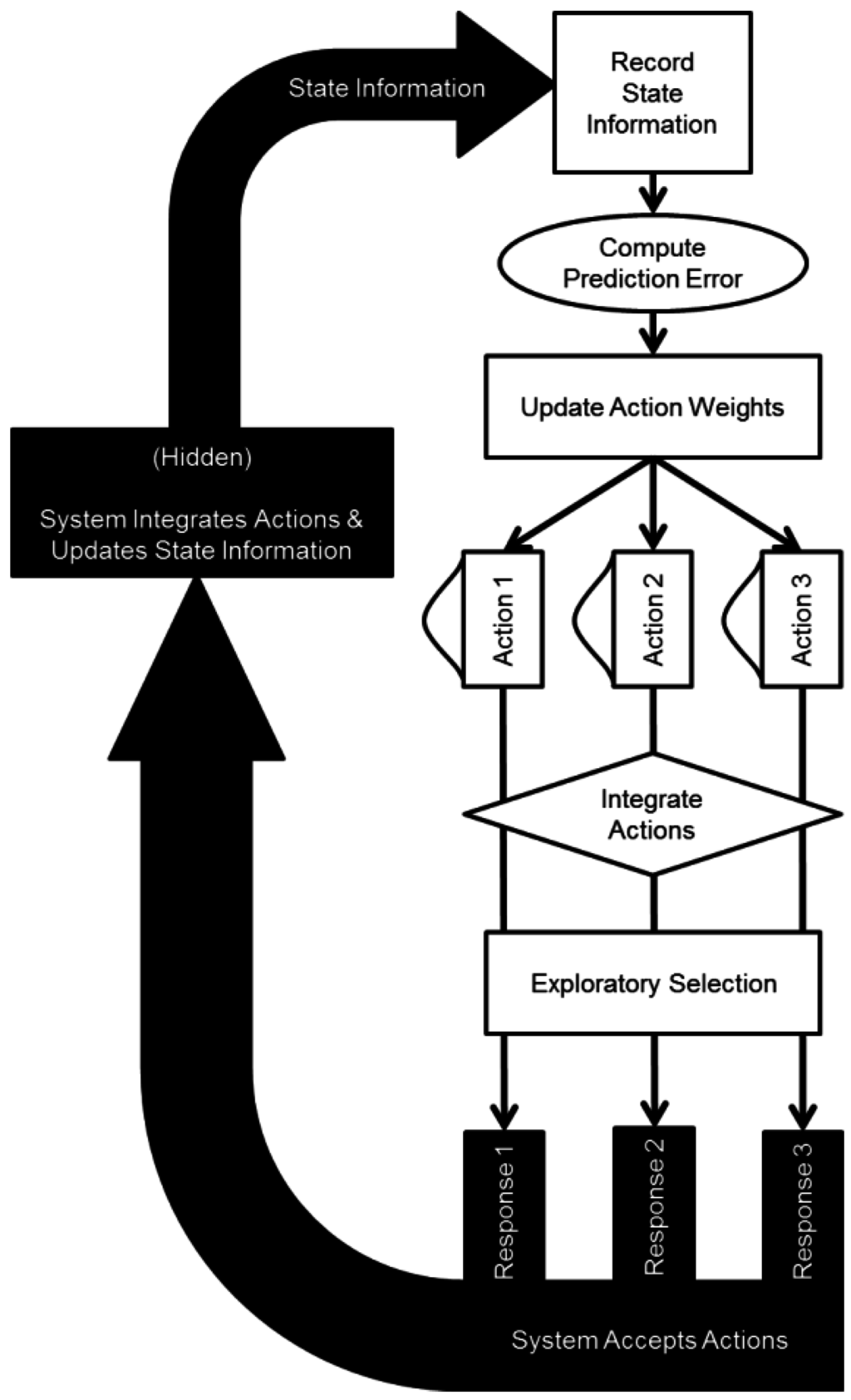
Figure 1.
Overall structure of the Single Limited Input, Dynamic Exploratory Responses (SLIDER) model, and its dynamic interaction with the environment.
The integration of partial information over multiple sources is a critical aspect of many formulations of action selection models. Typically, multiple information sources are combined to generate a single output response [65,66]. Here, the SLIDER model takes in a single information source and propagates the information over multiple output responses. In doing so, the model parameterizes the weights given to different response options, similar to classification models, which weigh and summate different perceptual dimensions [67].
Importantly, the SLIDER model can be adapted for any number and type of response options, due to the nature of the integration procedure and the continuous function used to describe the expected values. Continuous response options have been used to model response selection for graded response modalities [68]. By utilizing a continuous response function, the SLIDER implementation is scalable to other DDM paradigms with different response features.
Sutton and Barto [1] characterize the exploration-exploitation trade-off as the decision to rely on previously learned policies (exploitation) versus considering alternative actions, which may result in improved overall learning (exploration). In this way, the trade-off can be considered a meta-strategy, which drives action selection and learning. In the SLIDER model, the reinforcement history becomes the basis for a probabilistic action selection function using Luce’s choice; this is a Softmax rule developed by Luce [69]. This function includes a temperature parameter that controls the exploration-exploitation trade-off. This meta-strategic mechanism is a critical part of many computational models of learning and behavior. Thus, it is important to characterize the level of participants’ exploration in the present dynamic decision-making task.
By combining these basic mechanisms into a model designed to react to and learn from the present dynamic decision-making paradigm, we are able to specify a computational model which can be used to describe response selections on a participant by participant basis. Computational models can be useful tools for analyzing task behavior beyond what can be construed from trial-by-trial responses [70,71]. This is achieved by formally defining a computational system, which can, in its own right, complete the task at hand. Then, parameters of the model are fit to empirical data in order to determine behavioral characteristics, which describe the empirical data. The parameters included in the SLIDER model are summarized in Table 1, and explained below.

Table 1.
Free parameters of the SLIDER model.
| Parameter | Symbol | Description | Min, Max |
|---|---|---|---|
| Memory-Updating Reinforcement Strength | γs | Learning weight which determines how learned selection probabilities are combined with newly computed selection probabilities | 0, 1 |
| Inter-Input Parameter | β | The gating mechanism which determines the level at which learning regarding one response selection bleeds over to the other response selections | 0, 1 |
| Exploitation Parameter | K | Determines the temperature of the Softmax action selection function. At 1, the function will select the action with the highest expected value. At 0, the function will select randomly from all options. | 0, 1 |
1.7. Memory-Updating Reinforcement Strengths
After each trial of our dynamic control task, the computational model determines whether the input values it selected resulted in the outcome value moving towards or away from the goal. For each input, a Gaussian curve with a mean equal to the chosen input is constructed (Equation (1)).
where Pupdate (v) is the probability of selecting a value of v when the previous selected value was vp, and σ is the constant standard deviation, here set to 10.
This curve is then summed to (successful trial) or subtracted from (unsuccessful trial) the input’s former reinforcement history. A free parameter (one for successful trials, one for unsuccessful trials) determines the relative weight of the updating summation. For example, if the memory-updating positive reinforcement strength is 0.8, then the reinforcement history is updated such that 80% of the new reinforcement history reflects the current input value choice and 20% reflects the previous reinforcement history (Equation (2)).
where PHistory(v) is the input selection probability history for input value v, γs is the memory-updating reinforcement strength for feedback s (positive or negative), and R is the change in the outcome value’s distance to the goal from the previous trial.
In summary, there are two memory-updating reinforcement strengths, one for positive outcomes and one for negative outcomes. Each strength represents the weight with which current choices impact choice history (see Figure 2).
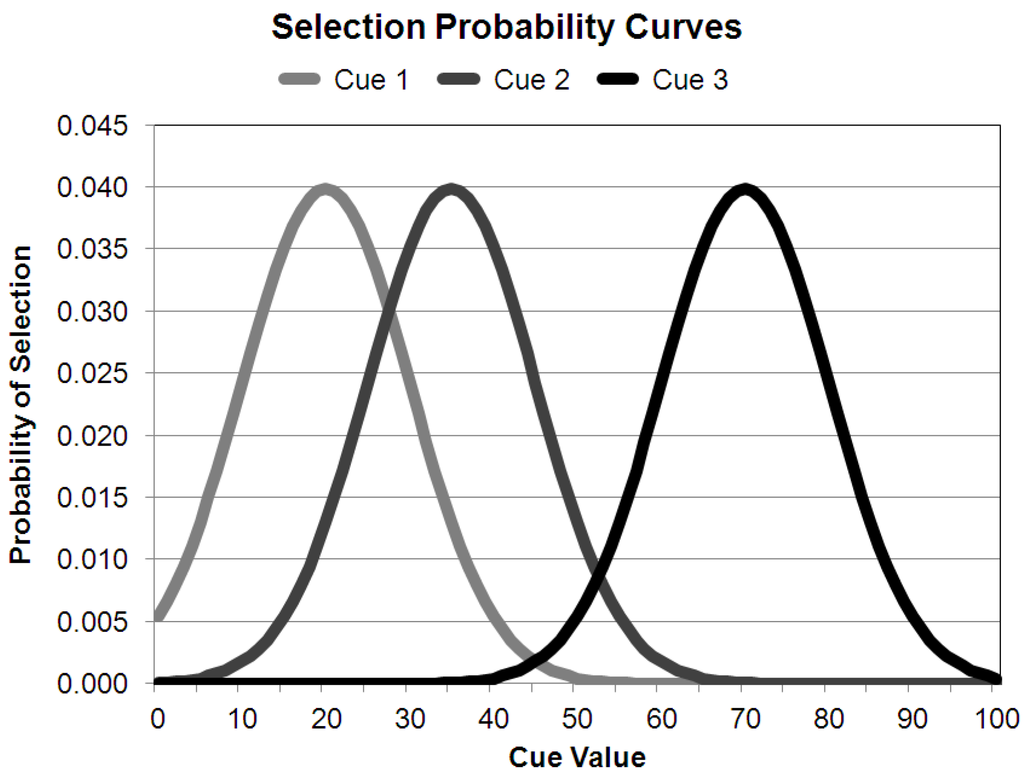
Figure 2.
Sample probability density curves of selecting a given value for a given cue. Over the course of a block, the curves will alter in various ways depending on the model parameters, trial success, and uncertainty inherent in the outcome value.
1.8. Inter-Input Parameter
Before the final probabilistic selection of the input value occurs, for each of the three inputs, the reinforcement history of the two other inputs are taken into consideration. The level of this consideration is controlled by an inter-input parameter. This parameter determines the strength at which the reinforcement history of other two inputs will influence the action selection of the input at hand. This is done using a gating equation, which weighs the alternate inputs using the inter-input parameter (Equation (3)).
where PInterinput(vcA) is the probability of selecting value v for input cA (e.g., input 1), β is the inter-input parameter, and cA and cB are the other two inputs (e.g., input 2 and 3). At high values of the inter-input parameter, the computational model is more likely to pick similar input values for all three inputs. As the inter-input parameter approaches 0, the model is less likely to select an action for one input based on the reinforcement history of the other two.
1.9. Exploitation Parameter
On each trial, the computational model evaluates the reinforcement history of each input to generate the probability of selecting each of the 100 input value options. From these options, a single value is chosen using the Softmax decision rule (Equation (4)). The equation’s exploitation parameter, K, determines the level of determinism in the choice process [72]. As K approaches ∞, the process is more likely to choose the most probable option (i.e., exploit); and as K approaches 0, the process is more likely to pick a less probable option (i.e., explore). The exploitation parameter can be converted to an exploration parameter using the inverse (i.e., 1/K).
where PFinal (vi) is the final probability of selecting input value vi, K is the exploitation parameter, and vj are all the input values from 0 to 100 for each given input.
1.10. Present Study
Given these issues, the present study is able to make several inroads in understanding exploration and exploitation in dynamic environment by using the dynamic decision-making paradigm. It is, for example, unclear whether environmental instability promotes more or less exploratory behavior. One argument that has been proposed is that there should be more exploratory behavior under highly unstable compared to stable conditions; in fact there is evidence that people do indeed explore more under dynamically unstable environments in bandit type tasks (e.g., [59,60,61]). The present study examines the extent to which this pattern generalizes to dynamic decision-making tasks, and also examines the extent to which this learning behavior impacts on control performance at test. In addition, we examine the extent to which self-reports of learning strategies (exploration, exploitation) correspond with formal descriptions of learning behaviors (i.e., rate of exploitation).
The present study also examines the association between affective experiences and dynamic decision-making behavior. Decision-making in uncertain environment is speculated to be supported by endogenous information of feelings experienced at the decision moment, which are in effect valuations of anticipated outcomes [73]. Moreover, studies have shown that in repeated choice tasks in which frequent outcome feedback is experienced, which is the case for dynamic decision-making tasks, people show increased affective responses (indexed by physiological arousal) for negative [33], as well as positive outcomes [35]. Therefore, the aim of the present study is to examine the extent to which self-reported levels of arousal (i.e., Surprise, Stress) correspond with successful and unsuccessful control performance throughout the dynamic decision-making task.
2. Methods
In the present study we manipulated a noise parameter in our dynamic control task in order to induce two levels of uncertainty—as experienced by the participant as a fluctuating outcome value, and a noise input(s)-output relationship (describe in more detail in the Design section). In the Highly Uncertain condition (i.e., High-Uncertainty), the environment would undergo relatively large autonomous changes, while in the Moderately Uncertain condition (i.e., Moderate-Uncertainty) condition the environment was stable (Condition 2). We then examined the extent to which environmental instability (and thus experienced level of dynamic uncertainty) impacted on decision-makers’ learning strategies and control test performance, as well as affective experiences.
2.1. Participants
A total of 47 participants were randomly allocated to one of two conditions. In the High-Uncertainty condition a total of 23 participants (10 female) took part, and in the Moderate-Uncertainty condition 24 participants (11 female) took part. Mean age of participants was 23 (SD 8.3). Participants were students recruited from the Queen Mary University of London subject pool, and were contacted via email. They were each given a flat fee of £7 ($11.01) as reimbursement for taking part in the experiment.
2.2. Design
The experiment was divided into two sessions: The Learning session comprised a total of 100 training trials during which participants were instructed to learn about the dynamic system in order to gather the relevant information to control the system to criterion at test. In the Test session participants were presented with two Control Tasks each 20 trials long in which they were required to control the outcome to criterion. In Control Task 1, the goal criterion was the same as the one presented during the learning session, and the goal of Control Task 2 was set differently in order to examine the extent to which participants could generalize their ability to control an outcome to a different criterion.
High-Uncertainty and Moderate-Uncertainty conditions were identical but for the difference in perturbation in the control task environment. The dynamic task environment consisted of three inputs and one output. One of the inputs increased the output value and one of the inputs decreased the output value. The third input had no effect on the output. More formally, the task environment can be described by the following Equation (5):
in which y(t) is the output on trial t, x1 is the positive input, x2 is the negative input, and e a random noise component, normally distributed with a zero mean and standard deviation of 16 (Moderate Uncertainty) or 32 (High Uncertainty). The null input x3 is not included in the equation as it had no effect on the output. The reason for including the null input was to add difficulty to controlling the task environment.
2.3. Procedure
Learning session: All participants were presented with a cover story before they began the main experiment. They were told that they were part of a medical research team that would be conducting tests in which they would be introducing a combination of three hormones (labeled as hormones A, B and C; these are the three input variables of the system) into a patient, with the aim of maintaining a specific safe level of neurotransmitter release (this is the output variable) in the patient. They were also informed that the tests were part of a training program in which simulations of the effects of hormones on neurotransmitter release in a patient were examined, and that no patient would actually be harmed. Participants were specifically told that in the first half of the experiment they would be learning about the effects of the hormones on the release of neurotransmitter X, but that they could choose how to learn about the task. They were then told that the knowledge that they had gained in the learning session would be useful later in the test session. They were informed that they would be expected to make decisions about which of the hormones they needed to inject and the amount by which they needed to inject each hormone in order to achieve and maintain a specific level of neurotransmitter release. They were then shown screen shots of the experiment along with details regarding what they could manipulate and where to look to track the effects of their choices on the computer screen.
Figure 3 presents a screen shot of a learning trial as experienced by a participant in the experiment (the control tests were identical to this). The task was performed on a desktop computer, using custom software written in C# for the .NET framework. Recall that the learning session consisted of a total of 100 trials, and the testing session consisted of 40 trials, with each test of control being 20 trials long.
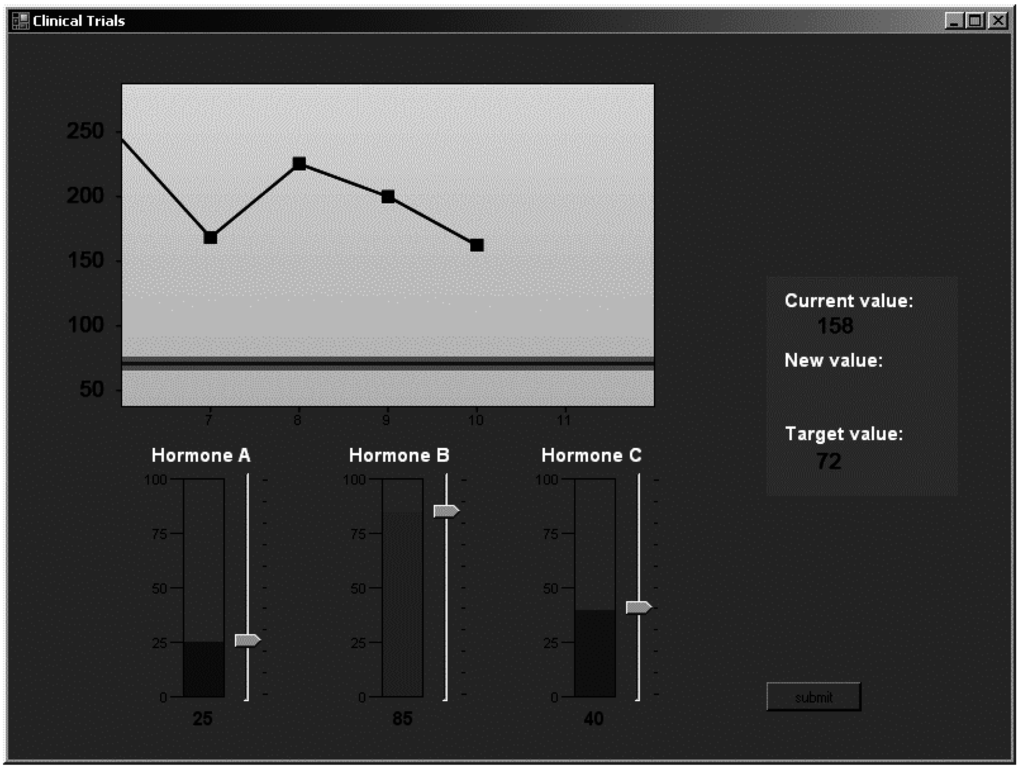
Figure 3.
Screenshot of the dynamic decision-making task used in the present study.
After being presented with the instructions and indicating that they were confident about what was required of them. Participants were then provided detailed instructions describing two modes of learning; exploration, and exploitation. They were told that they would have practice trials of 10 trials long to make exploration choices in the task, and then 10 trials to make exploitative choices in the task. Broadly, participants were told that they could interact with the computer task by “learning by testing out your ideas” (Exploration), or by “learning by trying to fulfill the goal of the task” (Exploitation); this is in line with the types of conceptualizations of exploration and exploitation choices typically referred to in the dynamic decision-making literature (e.g., [48]). More precisely what we mean by an exploratory choice is that the reward (in this case accurately maintaining the output variable to target reliably over a course of trials) is not relevant, and so the actions taken by the participant have no consequence. An exploitation choice was treated as one in which the reward is relevant, and the actions taken by the participant will impact the extent to which the reward is experienced; in this case this a positive reward means achieving an output that is closer to target compared to the previous trial, a negative reward means achieving an output that is further away from target compared to the previous trial. After having completed their familiarization of exploring and exploiting choices, participants were told that at the end of the learning session they would be asked to report the number of trials in which they explored and the number of trials they exploited, and what learning strategy they planned to start with as they embarked the learning session from the point of trial 30. This forewarning was designed to flag to participants that they needed to be vigilant and make a mental note of their approaches to learning the dynamic task.
At the start of the learning session, the cue values were set to ‘0’ and the output value was 178. Thereafter, on each trial, participants adjusted a slider corresponding to each input variable to decide which, and by how much of each hormone to release (a value between 0 and 100). After confirming their decision, the effect on the output value was revealed visually on the output graph. On the next trial, the input values were reset to 0, but the output value was retained from the previous trial. The effects on the output value were cumulative from one trial to the next trial. The information was shown as a trial history on-screen, which contained the output values of last five trials.
2.3.1. Testing Session
Both tests were the same for both High-Uncertainty and Moderate-Uncertainty conditions. In Control Test 1 participants were required to control the output to the same criterion as in the learning session (i.e., target value of 62) for the length of 20 trials. Control Test 2 involved a different output target (target value of 74) in order to examine transfer of knowledge to controlling a system to a different criterion (total 20 trials).
2.3.2. Affect and Experienced Uncertainty
At the end of the learning session, and again at the end of the testing session, participants were required to provide self-reports of their affective experiences. They were asked the following: Please indicate your experience when your score (i.e., the level of neurotransmitter release) was further away from the goal of the task with regards to the following states: Surprise (not at all surprised to highly surprised), Stress (not at all stressed to highly stressed), Uncertainty (not at all certain of the task, highly certain about the task), each on a 7 point scale. They were also asked the same questions for experiences in which their score was close to the goal.
2.4. Scoring
Input-Manipulation: We identified four simple methods by which participants tend to interact with the dynamic control task and develop strategies of manipulating the inputs on each trial both during learning and test [74]. The Input-Manipulation methods include: Not changing any inputs on a trial (No-intervention-method), Changing one input on a trial (One-input), Changing two inputs on a trial (Two-inputs), and Changing all inputs cues on a trial (All-inputs). During learning and test the proportion of trials on which each strategy was implemented was calculated for each participant and formed the data for the input manipulation strategy analyses.
Control performance: Control performance was measured as the absolute difference between the expected achieved and best possible outcome:
in which G(t) is the goal on trial t: either the target output if achievable on that trial, or the closest achievable output. For each participant, a score based on this procedure was used on each trial of each session, though only optimality scores during the test session was uses as the main basis for assessing control performance, since during learning different approaches to learning to control the system were adopt it was not deemed appropriate to use this as a key performance indicator.
3. Results
3.1. Learning Session
3.1.1. Self-Reported Starting Strategy
After the initial two blocks were completed participants were asked to reveal what their learning strategy was (explore or exploit) for the first couple of blocks of the learning session. Approximately 80% of participants in both the High-Uncertainty and Moderate-Uncertainty conditions revealed that their preferred starting strategy was exploring the dynamic environment first. A chi-square analysis revealed that there was no difference between preferences for starting strategy between conditions, p > 0.05.
3.1.2. Self-Reported Learning Profiles
Participants were also asked to report overall the proportion of trials (out of 80 trials during the learning session) that they allocated to exploration, and the rest to exploitation. A one way ANOVA revealed a significant effect of condition, F(1,44) = 4.4, p < 0.05, η2 = 0.09, indicating that participants reported that they explored less frequently in the High-Uncertainty (M = 36.48, SD = 19.89) than the Moderate-Uncertainty condition (M = 48.09, SD = 17.55).
3.1.3. Self-Reported Affect and Experienced Uncertainty
In addition to self-reported learning behaviors, participants were asked to provide self-reports at the end of the learning session regarding their affect and their experience of uncertainty. For each participant a Positive Arousal Score and a Negative Arousal Score that was generated based on the averaged response to items examining affect (level of surprise, level of stress) separately for periods when the output was deviating frequently from target, and when the output was frequently close to target. In addition, participants also reported their experience of uncertainty, again under situations in which the output deviated from target Uncertainty under Negative Experiences, or headed towards target, and level of Uncertainty under Positive Experiences. Though participants were not specifically instructed to control the output to criterion during the training session (and so this was not used as a key indicator of performance), but to learn how to control it, learning was scored according to deviation from target on each trial in order to map their behavior during learning to affective experiences and experiences of uncertainty. The idea was to examine whether self-reports of arousal corresponded meaningfully with actual experiences of deviating or achieving target. Therefore, we conducted exploratory analyses in which positive and negative affect scores were correlated with learning performance over the last 80 trials of the learning session separately for each condition. There was a significant positive correlation between control performance in the High-Uncertainty condition and Negative Arousal (M = 4.8, SD = 1.2), r(23) = 0.42, p < 0.05. For the Moderate-Uncertainty condition there was a significant negative correlation between Positive Arousal (M = 3.4, SD = 1.2) and control performance, r(23)= −0.45, p < 0.05. No other analyses were significant. The pattern here suggests that self-insight into emotional experiences track performance differentially in high and moderate uncertainty conditions.
3.1.4. Input-Manipulation Method
Figure 4 presents the mean proportion of occasions per 10 trials (minus the first two training blocks in the Learning session) in which each of the four different input-manipulation strategies were prevalent. For the purposes of analyzing the data we collapsed across blocks and conducted a 2 × 4 × 2 ANOVA was conducted with Type of self-reported strategy (Exploration, Exploitation), Input-manipulation (No Intervention, One Input, Two Inputs, All inputs) as within-subject factors, and Condition (High-Uncertainty, Moderate-Uncertainty) as the between-subject factor 4. There was a main effect of Input-manipulation, F(1,44) = 57.84, p < 0.0005, η2 = 0.57. In addition, with the exception of comparisons between manipulating Two Inputs or All inputs, (t < 1), all other comparisons between types of Input manipulations were significant, with Bonferoni correction (t(39), p < 0.001). From Figure 4, one can see that overall the most popular strategy during the learning session was manipulating one input at a time. There also appears to be minor differences between the second most popular strategy, which for the High-Uncertainty condition was manipulating two inputs at once in the High-Uncertainty, and for the Moderate-Uncertainty was manipulating all inputs at once. The analysis also revealed an Input-manipulation x Condition interaction, F(3,123) = 8.88, p < 0.0005, η2 = 0.17. However, follow up analyses failed to locate the source of the interaction suggesting that generally that pattern of strategic behavior was different between High-Uncertainty and Moderate-Uncertainty, indicating some form of compensatory behavior in response to the levels of uncertainty in the dynamic task environment.
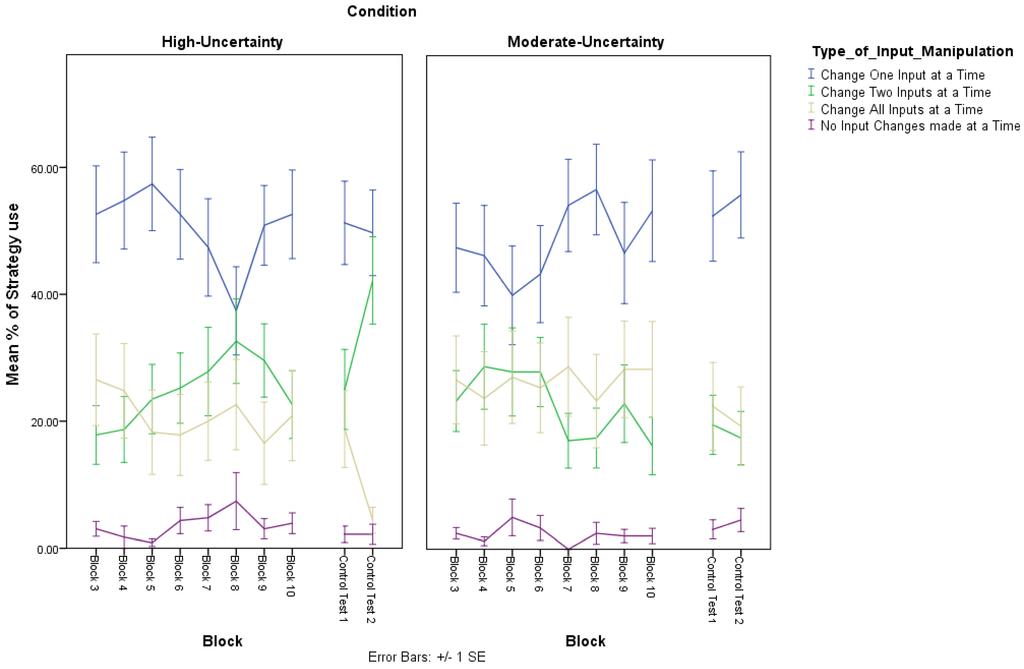
Figure 4.
Mean proportion of occasions (i.e., % of times in blocks of 10 trials in the learning session, and % of times in blocks of 20 trials in each testing session respectively) in which the four different input strategy manipulations were implemented in each Condition (High-Uncertainty, Moderate-Uncertainty) during the learning session (Blocks 3–10) and during the testing session (i.e., Control Test 1, Control Test 2).
3.2. Test Session
3.2.1. Control Performance
The Test session provided the first opportunity to compare the two conditions according to their ability to control the output to the same criterion (See Figure 5). Each Control test (Control test 1, Control test 2) comprised a total of 20 trials which were divided into two blocks of 10 trials each. The following analyses are based on participants' average control performance scores in each block and for each control test. A 2 Control Test (Control Test 1, Control Test 2) × 2 Block (Block 1, Block 2) × Condition (High-Uncertainty, Moderate-Uncertainty) ANOVA was conducted. There was a main effect of Control Test, suggesting that participants’ ability to control the dynamic task improved with more exposure to the testing session, F(1,44) = 17.17, p < 0.0005, η2 = 0.28. There was also a main effect of Block, again suggesting that there were general practice effects within each test, such that performance improved with more exposure to trials during each control test, F(1,44) = 7.34, p < 0.01, η2 = 0.14. No other analyses were significant suggesting that the ability to control the output to criterion was no different between High-Uncertainty and Moderate-Uncertainty conditions.
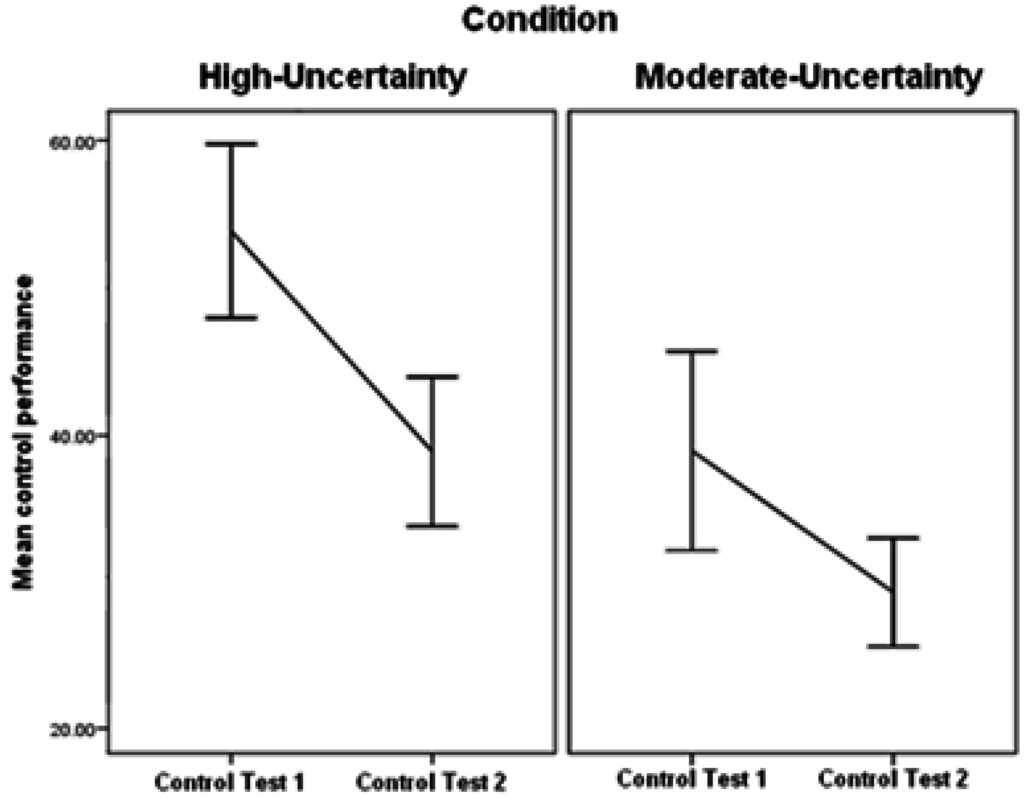
Figure 5.
Mean control performance score overall in the Test session; both Control Test (1, 2) for each condition (High-Uncertainty, Moderate-Uncertainty) (SE 1 +/−).
3.2.2. Input-Manipulation Method
Figure 4 shows the mean proportion of occasions in which each of the four input manipulation strategies were used in each of the two control tests in the test session. To examine the pattern of input manipulation strategies, a 2 × 4 × 2 ANOVA was conducted with Control Test (Control Test 1, Control Test 2), Input-manipulation (No Intervention, One Input, Two Inputs, All inputs) as within-subject factors, and Condition (High-Uncertainty, Moderate-Uncertainty) as the between-subject factor 4. There was a main effect of strategy, suggesting that the occasions in which the four different strategies were implemented was different, F(1,44) = 24.32, p < 0.0005, η2 = 0.39. Overall, as with the learning session, in the test session, manipulating one input at a time was the most popular input manipulation strategy. With the exception of comparisons between manipulating Two Inputs or All inputs, and the comparison between All Inputs and No Intervention (t < 1), all other comparisons between types of Input manipulations were significant, with Bonferoni correction (t(39), p < 0.05). There was a Control Test × Strategy × Condition interaction, F(3,111) = 3.54, p < 0.05, η2 = 0.02. In Control Test 2 there were fewer occasions in which participants manipulated all three inputs in the High-Uncertainty condition, compared to the Moderate-Uncertainty conditions, F(1,44) = 4.42, p < 0.05, and those in the High-Uncertainty condition manipulated two inputs more often than the Moderate-Uncertainty condition, F(1,44) = 9.84, p < 0.005.
3.2.3. Self-Reported Affect and Experienced Uncertainty
As with learning, after both Control tests participants reported their affective experience, and for each a Positive Arousal Score and a Negative Arousal Score and Experienced Uncertainty was generated, and was correlated with averaged control performance across Control Test 1 and Test 2. For those in the high condition, there was a significant positive correlation between Uncertainty under Negative Experiences and control performance, r(23)= 0.45, p < 0.05, and also Uncertainty under Positive Experiences and control performance, r(23)= 0.54, p < 0.005. No other analyses were significant.
3.3. Model Based Analysis
We entered the Exploitation parameter for learning blocks, Control Test 1, and Control Test 2 into a 3 Period (Learning, Control Test 1, Control test 2) × Condition (High-Uncertainty, Moderate-Uncertainty) ANOVA. There was a main effect of period, suggesting that exploitation was lower during learning than either of the Control tests, F(2, 88) = 4.50, p < 0.05, η2 = 0.09. However, there was no indication that levels of exploitation differed between conditions (F < 1).
For the inter-input parameter, there was a similar difference between periods, F(2, 88) = 4.16, p < 0.05, η2 = 0.09, suggesting that inter-input parameter values in the test session were higher compared with the learning session. Overall people were likely to select similar input values for the three inputs during test as compared to Learning. Again, there was no evidence from this analysis that condition impacted on the choice of input values selected by condition.
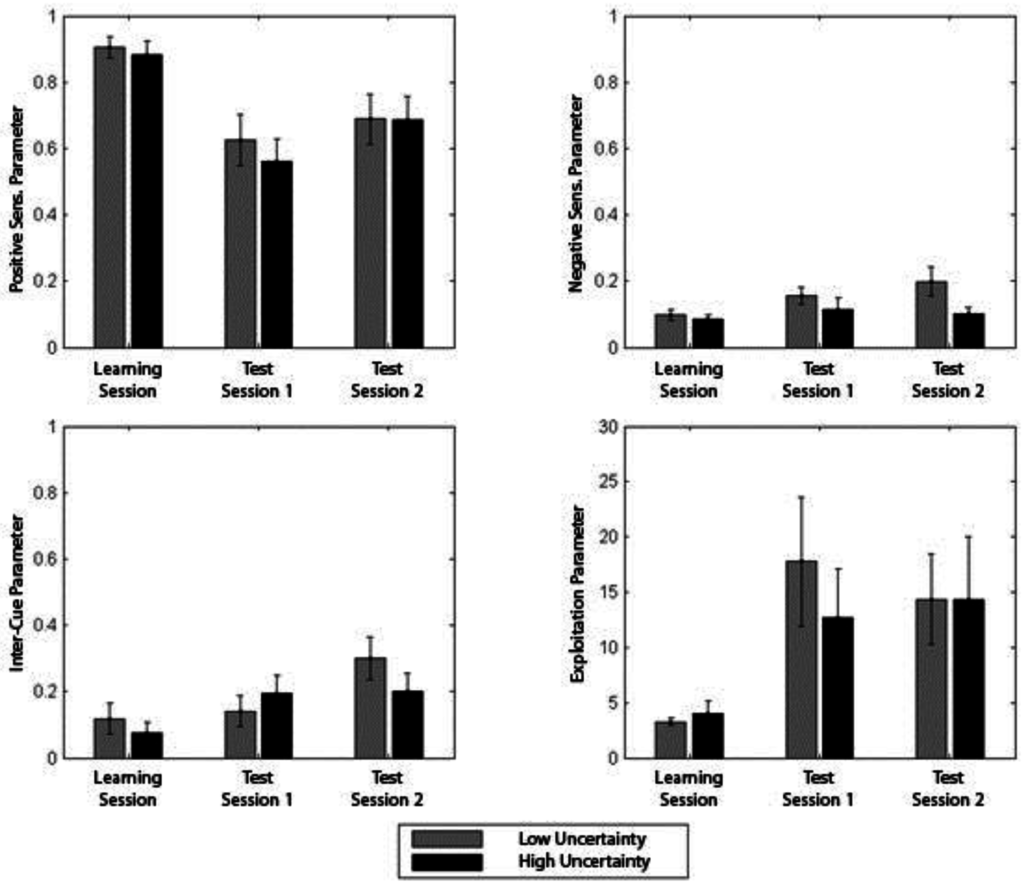
Figure 6.
Best fitting computational model parameters by session (Learning, Test), and by condition (High-Uncertainty, Moderate-Uncertainty) (SE 1 +/−).
The analysis concerning positivity-sensitivity parameter suggested that people were less sensitive to positive reinforcement in the control tests as compared to the learning session, F(2, 88) = 12.73, p < 0.01, η2 = 0.22. For the negative-sensitivity parameter, people appeared to be somewhat more sensitive to negative reinforcement in the control tests than during learning, F(2, 88) = 2.64, p = 0.08, η2 = 0.06. Here there was evidence that there were differential effects on sensitivity to type of reinforcement experienced depending on condition. The main effect of condition, F(1, 44) = 4.43, p < 0.05, η2 = 0.09, suggested that overall the Moderate-Uncertainty condition was more sensitive to negative reinforcement than the High-Uncertainty condition. Figure 6 illustrates the best fitting parameter values for each condition.
4. General Discussion
The aim of this present study was to examine several important factors regarding learning approaches to controlling a dynamically uncertain environment varying in degree of instability. To begin with, we considered the extent to which instability promotes more exploratory behavior. Participants were given explicit choice over the relative amount of exploitative or exploratory trials they wanted to employ during the learning session. In self-reports, after the learning session, they indicated their preference for starting with an exploratory strategy, but that thereafter those in the High-Uncertainty condition preferred to exploit more than explore. However when considering the results of the SLIDER model, there was nothing to suggest that there were differences in levels of exploitation resulting from the instability of the task environment. In turn, this suggests that, (1) retrospective self-reports are not especially accurate at indicating learning strategies, (2) people generally are not especially insightful as to their learning behavior, or (3) our methods of tutoring people as to the differences between exploitation and exploration were not successful. Currently there is no sufficient evidence to be able to answer definitively which of these possible explanations is most appropriate, however, given the correspondence between affective experiences and performance, there is nothing to suggest from this evidence that people lack personal insight into their mental and emotional states. Therefore it is possible that the differences between self-reported learning behavior and model descriptions is down to the method of measuring self-reports and perhaps the stage at which self-reports were introduced (i.e., retrospectively rather than a trial by trial report of whether they were implementing an exploratory or exploitative strategy). Crucially, based on our model analyses, the learning profiles during the learning session were similar, with regards to exploitation, and in turn control performance was similar for the High-Uncertainty and Moderate-Uncertainty condition, also indicated the instability of the environment did not impact on general ability to control it.
The strategy analysis during the learning session suggested that there were differences overall in the input manipulation strategy profiles of those in the High-Uncertainty condition and the Moderate-Uncertainty condition. Similarly, during the test session there were also differences in the strategy profiles between conditions; in particular, concerning the frequency with which all inputs were manipulated or two of them were manipulated. It may be the case that the differences in input manipulation profiles indicated that participants were developing compensatory strategies to cope with the level of instability they were dealing with. Alternatively it could have been that participants were given sufficient learning trials in which they could acquire enough information to control the outcome relatively successfully, or alternatively, the differences between High-Uncertainty and Moderate-Uncertainty was not sufficiently different enough to lead to profound behavioral changes. However, Osman and Speekenbrink [74] also presented participants with a control system in which they manipulated instability to the same levels and reported differences in control performance; though in their study there were no specific learning instructions whereas in the present study there were. This difference may also have contributed to later success in control performance of the High-Uncertainty condition in the present study. This is because the learning instructions presented to them may have cued them to be especially vigilant about how they were interacting with the task during learning.
Moreover, there also differences in affective experience as a result of the instability of the task environment. There was an association between negative arousal and learning behavior in the High-Uncertainty condition, whereas learning behavior was associated with positive arousal in the Moderate-Uncertainty condition. Additionally, while at test affective state was not associated with control performance, experiences of uncertainty were associated with control performance, but only in the High-Uncertainty condition.
Overall it appears that there are differences in some behavioral measures regarding the way in which people interact with highly unstable environments, as well their experiences of emotional arousal and uncertainty, however, instability did not drive any fundamental differences in learning strategies or actual ability to control a dynamic outcome. The remainder of this discussion considers the implication of these findings.
4.1. Causality and Agency
We draw the reader’s attention to a key finding from the computational modeling analysis that may reveal an important insight into the impact of the instability of the environment on one’s sense of agency. Those in the Moderate-Uncertainty condition demonstrated higher values on the negative sensitivity parameter. This result has intriguing implications for causal agency in dynamic decision making [45]. Those in the Moderate-Uncertainty condition were more sensitive to negative feedback, which could be interpreted as evidence for a higher sense of agency relative to those in the High-Uncertainty condition. In other words, on trials when the outcome value moved away from the target value, those in the moderate noise condition were more likely to avoid those cues in the following trials. Suggesting that by continuing to do so, they believed that they could still effectively impact on the fluctuating output value. This could indicate that they interpreted their actions as more responsible for the outcome, whereas those in the High-Uncertainty condition interpreted negative changes in the environment as coming from a different source. In addition, evidence from self-reports of emotional arousal suggest that feedback indicating poor performance (i.e., generating an outcome deviating further from target) was associated with negative arousal in the High-Uncertainty, and with an overall state of high uncertainty compare to the Moderate-Uncertainty in the test session. This lends support to view that those in the High-Uncertainty may have believed that they were less able to control the environment when experiencing negative outcomes, which led to higher negative arousal and greater states of uncertainty. This result can only partially be explained by theories that propose more accurate memory for negatively valenced occurrences [75], because the effect relied on the level of environmental noise.
The difference in sensitivity to reinforcement indicates that there may be a relationship between a sense of agency and environmental stability, which is moderated by characteristics of the reward information. To explore this further, future studied could involve further manipulations of stability in the task environment, in order test whether the more stable the environment is, the more people tend to rely on negative feedback to control the outcome.
4.2. Insights from the SLIDER Model
The SLIDER model provided a basic characterization of the reinforcement learning properties underlying performance in this dynamic decision-making task. Importantly, participants were more exploratory during learning, subsequently shifting to a more exploitative strategy in the test sessions. This suggests that future work should consider whether participants shift from a model-free to a model-based strategy during the course of learning in a dynamic-decision making task [76]. In addition to a relative increase in exploration during learning, participants were also better fit by model parameters representing independent learning for each of the three response options. This demonstrates that decision-makers attempt to determine the function of the response options during learning, then integrate this learning at test. Prior work has demonstrated increased exploitation as time on task increases [42].
In relation to sensitivity to positive feedback (successful trials) versus negative feedback (unsuccessful trials), participants were more sensitive to positive feedback at learning and somewhat more sensitive to negative feedback at test. This suggests at a meta-strategy shift that occurs after learning, and should be considered for future modeling work. Under Low-Uncertainty, participants were more sensitive negative feedback, which also occurred less frequently. Thus, under High-Uncertainty, participants change their behavior less in response to negative feedback than during Low-Uncertainty. These basic insights regarding the reinforcement learning underlying dynamic decision-making demonstrate that further modeling should consider shifts in performance depending on context and uncertainty.
4.3. Differences Between Dynamic Decision-Making and Bandit Tasks
The findings from the present study suggest that overall exploration/exploitation behavior during learning does not affect the control performance, and the trade-off between exploration and exploitation does not differ on the basis of the stability of the environment. These findings depart somewhat from those reported in typical bandit tasks. The main difference between the dynamic decision-making task used in the present study and typical bandit tasks is that the task environment we used was dynamic, there is a causal structure that defines the relationship between inputs and outputs, there is an embedded goal structure, and there was no monetary incentive/reward structure. As discussed earlier, the presence of a causal structure may mean that learning behavior that can generate a state change carries more information about the behavior of the environment and how to control it, as compared to a typical bandit task. In fact, the presence of a causal structure may make the environment easier to learn. In fact, people only required 100 trials to learn about the system, whereas participants in Gureckis and Love’s study [77] required 500 trials in order to learn their system. Though it is hard to directly compare, this may in fact indicate that an embedded causal structure (such as the simple one that underpins the dynamic control task used in the present study) can facilitate the rate of learning. Another crucial factor is that in bandit tasks people are required to learn to maximize, while in dynamic decision-making tasks people are presented with a goal structure. This played an important role in the way people approached the different sessions of the task, when it came to acquisition of knowledge people did explore more than exploit, but when it came to implementation of knowledge exploitation was far more pronounced. Clearly people tend to know how to intervene with the task in order to adapt to the requirements that are expected of them.
5. Conclusions
Unlike typical exploration–exploitation tasks (bandit tasks), the present study was designed to investigate exploration-exploitation behavior in a dynamically highly unstable and moderately unstable environment, in which there was an underlying causal structure. People were required to decide on their approach to knowledge acquisition in order to support their eventual control of the environment. This is a familiar problem to many in applied situations. The findings from the present study suggest that during learning people tend to report that they explore less in highly unstable dynamic environments compared to moderately unstable ones, but that in actual fact in formal computational analyses levels of exploration were equivalent. Crucially, the model analysis suggests that the stability of the environment does not change the pattern of learning behavior, and does not impair people’s ability to control the environment. However, the findings suggest that learning behaviors are highly sensitive to the goals of the task, that feedback is utilized in different ways in order to track and adapt one’s knowledge, that instability does lead to differences in compensatory strategies, which may in turn account for why control performance was the same under both conditions, and finally affective experiences do track decision-making behavior in a dynamic control task.
Acknowledgments
This study was supported by the Engineering and Physical Sciences Research Council (EP/F069626/1; http://www.epsrc.ac.uk/Pages/default. Aspx)
Author Contributions
M.O. prepared the first and final draft of the manuscript and conducted the analyses. Z.H. collected the data and co-developed and co-designed experiments with M.O.; Z.H. performed the experiments, and contributed to analysis of data, writing of manuscript and editing. B.D.G. developed and conducted the computational modeling analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Audibert, J.Y.; Munos, R.; Szepesvári, C. Exploration—Exploitation tradeoff using variance estimates in multi-armed bandits. Theor. Comput. Sci. 2009, 410, 1876–1902. [Google Scholar] [CrossRef]
- Dam, G.; Körding, K. Exploration and exploitation during sequential search. Cognit. Sci. 2009, 33, 530–541. [Google Scholar] [CrossRef] [PubMed]
- Humphries, M.; Khamassi, M.; Gurney, K. Dopaminergic control of the exploration-exploitation trade-off via the basal ganglia. Front. Neurosci. 2012, 6. [Google Scholar] [CrossRef] [PubMed]
- Rakow, T.; Miler, K. Doomed to repeat the successes of the past: History is best forgotten for repeated choices with nonstationary payoffs. Mem. Cognit. 2009, 37, 985–1000. [Google Scholar] [CrossRef] [PubMed]
- Stahlman, W.D.; Roberts, S.; Blaisdell, A.P. Effect of reward probability on spatial and temporal variation. J. Exp. Psychol. Anim. Behav. Process. 2010, 36, 77–91. [Google Scholar] [CrossRef] [PubMed]
- Stahlman, W.D.; Young, M.E.; Blaisdell, A.P. Response variability in pigeons in a Pavlovian task. Learn. Behav. 2010, 38, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Keller, G.; Rady, S. Optimal experimentation in a changing environment. Rev. Econ. Stud. 1999, 66, 475–507. [Google Scholar] [CrossRef]
- Posen, H.; Levinthal, D. Chasing a moving target: Exploitation and exploration in dynamic environments. Manage. Sci. 2012, 58, 587–601. [Google Scholar] [CrossRef]
- Steyvers, M.; Lee, M.D.; Wagenmakers, E. A Bayesian analysis of human decision-making on bandit problems. J. Math. Psychol. 2009, 53, 168–179. [Google Scholar] [CrossRef]
- Brand, H.; Woods, P.J.; Sakoda, J.M. Anticipation of reward as a function of partial reinforcement. J. Exp. Psychol. 1956, 52, 18–22. [Google Scholar] [CrossRef] [PubMed]
- Brand, H.; Sakoda, J.M.; Woods, P.J. Effects of a random versus pattern reinforcement instructional set in a contingent partial reinforcement situation. Psychol. Rep. 1957, 3, 473–479. [Google Scholar] [CrossRef]
- Daw, N.D.; O'Doherty, J.P.; Dayan, P.; Seymour, B.; Dolan, R.J. Cortical substrates for exploratory decisions in humans. Nature 2006, 441, 876–879. [Google Scholar] [CrossRef] [PubMed]
- Payzan-LeNestour, É.; Bossaerts, P. Do not bet on the unknown versus try to find out more: Estimation uncertainty and “unexpected uncertainty” both modulate exploration. Front. Neurosci. 2012, 6, 150. [Google Scholar]
- Racey, D.; Young, M.E.; Garlick, D.; Ngoc-Minh, P.J.; Blaisdell, A.P. Pigeon and human performance in a multi-armed bandit task in response to changes in variable interval schedules. Learn. Behav. 2011, 39, 245–258. [Google Scholar] [CrossRef] [PubMed]
- Jepma, M.; Te Beek, E.T.; Wagenmakers, E.; Van Gerven, J.; Nieuwenhuis, S. The role of the noradrenergic system in the exploration–exploitation trade-off: A pharmacological study. Fronti. Hum. Neurosci. 2010, 4, 170. [Google Scholar] [CrossRef] [PubMed]
- Lea, S.; McLaren, I.; Dow, S.; Grafta, D. The cognitive mechanisms of optimal sampling. Behav. Process. 2011, 89, 77–85. [Google Scholar] [CrossRef] [PubMed]
- Plowright, C.M.S.; Shettleworth, S.J. Time horizon and choice by pigeons in a prey-selection task. Anim. Learn. Behav. 1991, 19, 103–112. [Google Scholar] [CrossRef]
- Dayan, P.; Niv, Y. Reinforcement learning: the good, the bad and the ugly. Curr. Opin. Neurobiol. 2008, 18, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Auer, P.; Ortner, R.; Szepesvári, C. Improved rates for the stochastic continuum-armed bandit problem. In Learning Theory; Springer Berlin Heidelberg: Berlin, German, 2007; pp. 454–468. [Google Scholar]
- Bechara, A.; Damasio, A.R.; Damasio, H.; Anderson, S.W. Insensitivity to future consequences following damage to human prefrontal cortex. Cognition 1994, 50, 7–15. [Google Scholar] [CrossRef]
- Fernie, G.; Tunney, R.J. Some decks are better than others: The effect of reinforcer type and task instructions on learning in the Iowa Gambling Task. Brain Cognit. 2006, 60, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Fridberg, D.J.; Queller, S.; Ahn, W.-Y.; Kim, W.; Bishara, A.J.; Busemeyer, J.R.; Stout, J.C. Cognitive mechanisms underlying risky decision-making in chronic cannabis users. J. Math. Psychol. 2010, 54, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Kjome, K.L.; Lane, S.D.; Schmitz, J.M.; Green, C.; Ma, L.; Prasla, I.; Moeller, F.G. Relationship between impulsivity and decision making in cocaine dependence. Psychiatry Res. 2010, 178, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Premkumar, P.; Fannon, D.; Kuipers, E.; Simmons, A.; Frangou, S.; Kumari, V. Emotional decision-making and its dissociable components in schizophrenia and schizoaffective disorder: A behavioural and MRI investigation. Neuropsychologia 2008, 46, 2002–2012. [Google Scholar] [CrossRef] [PubMed]
- Steingroever, H.; Wetzels, R.; Horstmann, A.; Neumann, J.; Wagenmakers, E.J. Performance of healthy participants on the Iowa Gambling Task. Psychol. Assess. 2013, 25, 180–193. [Google Scholar] [CrossRef] [PubMed]
- Wood, S.; Busemeyer, J.; Koling, A.; Cox, C.R.; Davis, H. Older adults as adaptive decision makers: Evidence from the Iowa Gambling Task. Psychol. Aging 2005, 20, 220–225. [Google Scholar] [CrossRef] [PubMed]
- Konstantinidis, E.; Shanks, D.R. Don’t bet on it! Wagering as a measure of awareness in decision making under uncertainty. J. Exp. Psychol. Gen. 2014, 143, 2111–2134. [Google Scholar] [CrossRef] [PubMed]
- Horstmann, A.; Villringer, A.; Neumann, J. Iowa Gambling Task: There is more to consider than long-term output. Front. Neurosci. 2012, 6, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Bechara, A.; Tranel, D.; Damasio, H.; Damasio, A.R. Failure to respond autonomically to anticipated future outcomes following damage to prefrontal cortex. Cereb. Cortex 1996, 6, 215–225. [Google Scholar] [CrossRef] [PubMed]
- Damasio, A.; Dolan, R.J. The feeling of what happens. Nature 1999, 401, 847–847. [Google Scholar]
- Bechara, A.; Damasio, H.; Tranel, D.; Damasio, A.R. Deciding advantageously before knowing the advantageous strategy. Science 1997, 275, 1293–1295. [Google Scholar] [CrossRef] [PubMed]
- Bechara, A. Neurobiology of decision-making: risk and reward. Semin. Clini. Neuropsychiatry 2001, 6, 205–216. [Google Scholar] [CrossRef]
- Carter, S.; Smith Pasqualini, M. Stronger autonomic response accompanies better learning: A test of Damasio's somatic marker hypothesis. Cognit. Emot. 2004, 18, 901–911. [Google Scholar] [CrossRef]
- Bechara, A.; Damasio, H.; Damasio, A.R.; Lee, G.P. Different contributions of the human amygdala and ventromedial prefrontal cortex to decision-making. J. Neurosci. 1999, 19, 5473–5481. [Google Scholar] [PubMed]
- Palomäki, J.; Kosunen, I.; Kuikkaniemi, K.; Yamabe, T.; Ravaja, N. Anticipatory electrodermal activity and decision making in a computer poker-game. J. Neurosci. Psychol. Econ. 2013, 6, 55–70. [Google Scholar] [CrossRef]
- Botvinick, M.M.; Rosen, Z.B. Anticipation of cognitive demand during decision-making. Psychol. Res. PRPF 2009, 73, 835–842. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Hirota, A.; Takasawa, N.; Shigemasu, K. Application of the somatic marker hypothesis to individual differences in decision making. Biol. Psychol. 2003, 65, 81–88. [Google Scholar] [CrossRef]
- Tomb, I.; Hauser, M.; Deldin, P.; Caramazza, A. Do somatic markers mediate decisions on the gambling task? Nat. Neurosci. 2002, 5, 1103–1104. [Google Scholar] [CrossRef] [PubMed]
- Dunn, B.D.; Dalgleish, T.; Lawrence, A.D. The somatic marker hypothesis: A critical evaluation. Neurosci. Biobehav. Rev. 2006, 30, 239–271. [Google Scholar] [CrossRef] [PubMed]
- Otto, A.R.; Knox, W.B.; Markman, A.B.; Love, B.C. Physiological and behavioral signatures of reflective exploratory choice. Cognit. Affect. Behav. Neurosci. 2014, 14, 1167–1183. [Google Scholar] [CrossRef] [PubMed]
- Osman, M. Controlling Uncertainty: A review of human behavior in complex dynamic environments. Psychol. Bull. 2010, 136, 65–86. [Google Scholar] [CrossRef] [PubMed]
- Osman, M. Controlling Uncertainty: Learning and Decision Making in Complex Worlds; Wiley-Blackwell Publishers: Oxford, UK, 2010. [Google Scholar]
- Osman, M. Future-Minded: The Psychology of Agency and Control; Palgrave MacMillian: London, UK, 2014. [Google Scholar]
- Osman, M. The role of feedback in dynamic decision making. Front. Decis. Neurosci. Hum. Choice 2012, 6, 56–61. [Google Scholar]
- Berry, D. The role of action in implicit learning. Q. J. Exp. Psycholo. 1991, 43, 881–906. [Google Scholar] [CrossRef]
- Burns, B.D.; Vollmeyer, R. Goal specificity effects on hypothesis testing in problem solving. Q. J. Exp. Psychol. 2002, 55, 241–261. [Google Scholar] [CrossRef] [PubMed]
- Osman, M. Observation can be as effective as action in problem solving. Cognit. Sci. 2008, 32, 162–183. [Google Scholar] [CrossRef] [PubMed]
- Osman, M. Evidence for positive transfer and negative transfer/Anti-learning of problem solving skills. J. Exp. Psychol. Gen. 2008, 137, 97–115. [Google Scholar] [CrossRef] [PubMed]
- Osman, M. Seeing is as good as doing. J. Probl. Solving 2008, 2, 29–40. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load during problem solving: Effects of learning. Cognit. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Vollmeyer, R.; Burns, B.D.; Holyoak, K.J. The impact of goal specificity and systematicity of strategies on the acquisition of problem structure. Cognit. Sci. 1996, 20, 75–100. [Google Scholar] [CrossRef]
- Barto, A.G. Intrinsic motivation and reinforcement learning. In Intrinsically Motivated Learning in Natural and Artificial Systems; Springer Berlin Heidelberg: Berlin, German, 2013; pp. 17–47. [Google Scholar]
- Gottlieb, J.; Oudeyer, P.Y.; Lopes, M.; Baranes, A. Information-seeking, curiosity, and attention: Computational and neural mechanisms. Trends Cognit. Sci. 2013, 17, 585–593. [Google Scholar] [CrossRef] [PubMed]
- Şimşek, Ö.; Barto, A.G. An intrinsic reward mechanism for efficient exploration. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25 June 2006; pp. 833–840.
- Schmidhuber, J. Formal theory of creativity, fun, and intrinsic motivation. IEEE Trans. Auton. Ment. Dev. 2010, 2, 230–247. [Google Scholar] [CrossRef]
- Gureckis, T.M.; Love, B.C. Learning in noise: Dynamic decision-making in a variable environment. J. Math. Psychol. 2009, 53, 180–193. [Google Scholar] [CrossRef] [PubMed]
- Busemeyer, J.R.; Gerald, I.D.; Douglas, L.M. Evaluation of exemplar-based generalization and the abstraction of categorical information. J. Exp. Psychol. Learn. Mem. Cognit. 1984, 10, 638–648. [Google Scholar] [CrossRef]
- Kauffman, S.; Lobo, J.; Macready, W.G. Optimal search on a technology landscape. J. Econ. Behav. Organ. 2000, 43, 141–166. [Google Scholar] [CrossRef]
- Billinger, S.; Stieglitz, N.; Schumacher, T.R. Search on rugged landscapes: An experimental study. Organ. Sci. 2013, 25, 93–108. [Google Scholar] [CrossRef]
- Stuart, T.E.; Podolny, J.M. Local search and the evolution of technological capabilities. Strateg. Manag. J. 1996, 17, 21–38. [Google Scholar] [CrossRef]
- Katila, R.; Ahuja, G. Something old, something new: A longitudinal study of search behavior and new product introduction. Acad. Manag. J. 2002, 45, 1183–1194. [Google Scholar] [CrossRef]
- Silvetti, M.; Verguts, T. Reinforcement Learning, High-Level Cognition, and the Human Brain; INTECH Open Access Publisher: Rijeka, Croatia, 2012; pp. 283–296. [Google Scholar]
- Ashby, F.G.; and Maddox, W.T. Human category learning 2.0. Ann. N.Y. Acad. Sci. 2011, 1224, 147–161. [Google Scholar] [CrossRef] [PubMed]
- Cain, N.; Shea-Brown, E. Computational models of decision making: Integration, stability, and noise. Curr. Opin. Neurobiol. 2012, 22, 1047–1053. [Google Scholar] [CrossRef] [PubMed]
- Nosofsky, R.M.; Palmeri, T.J. An exemplar-based random walk model of speeded classification. Psychol. Rev. 1997, 104, 266–300. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, T.L.; Chater, N.; Kemp, C.; Perfors, A.; Tenenbaum, J.B. Probabilistic models of cognition: Exploring representations and inductive biases. Trends Cognit. Sci. 2010, 14, 357–364. [Google Scholar] [CrossRef] [PubMed]
- Luce, R.D. On the possible psychophysical laws. Psychol. Rev. 1959, 66, 81–95. [Google Scholar] [CrossRef] [PubMed]
- Fum, D.; Missier, F.D.; Stocco, A. The cognitive modeling of human behavior: Why a model is (sometimes) better than 10,000 words. Cognit. Syst. Res. 2007, 8, 135–142. [Google Scholar] [CrossRef]
- Lewandowsky, S. The rewards and hazards of computer simulations. Psychol. Sci. 1993, 4, 236–243. [Google Scholar] [CrossRef]
- Daw, N.D.; Doya, K. The computational neurobiology of learning and reward. Curr. Opin. Neurobiol. 2006, 16, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Loewenstein, G.; Lerner, J.S. The role of affect in decision making. In Handbook of Affective Sciences; Oxford University Press: Oxford, UK, 2003; pp. 619–642. [Google Scholar]
- Osman, M.; Speekenbrink, M. Cue utilization and strategy application in stable and unstable dynamic environments. Cognit. Syst. Res. 2011, 12, 355–364. [Google Scholar] [CrossRef]
- Kensinger, E.A. Negative emotion enhances memory accuracy behavioral and neuroimaging evidence. Curr. Direct. Psychol. Sci. 2007, 16, 213–218. [Google Scholar] [CrossRef]
- Gläscher, J.; Daw, N.; Dayan, P.; O'Doherty, J.P. States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron 2010, 66, 585–595. [Google Scholar] [CrossRef] [PubMed]
- Gureckis, T.; Love, B. Short-term gains, long-term pains: How inputs about state aid learning in dynamic environments. Cognition 2009, 113, 293–313. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).