A Fractional Probability Calculus View of Allometry
Abstract
:1. Background of Allometry
1.1. The Empirical Equation
1.2. Fractals and Scaling
1.3. Preview
2. Empirical Allometry
2.1. Living Networks
2.1.1. Biology
2.1.2. Physiology
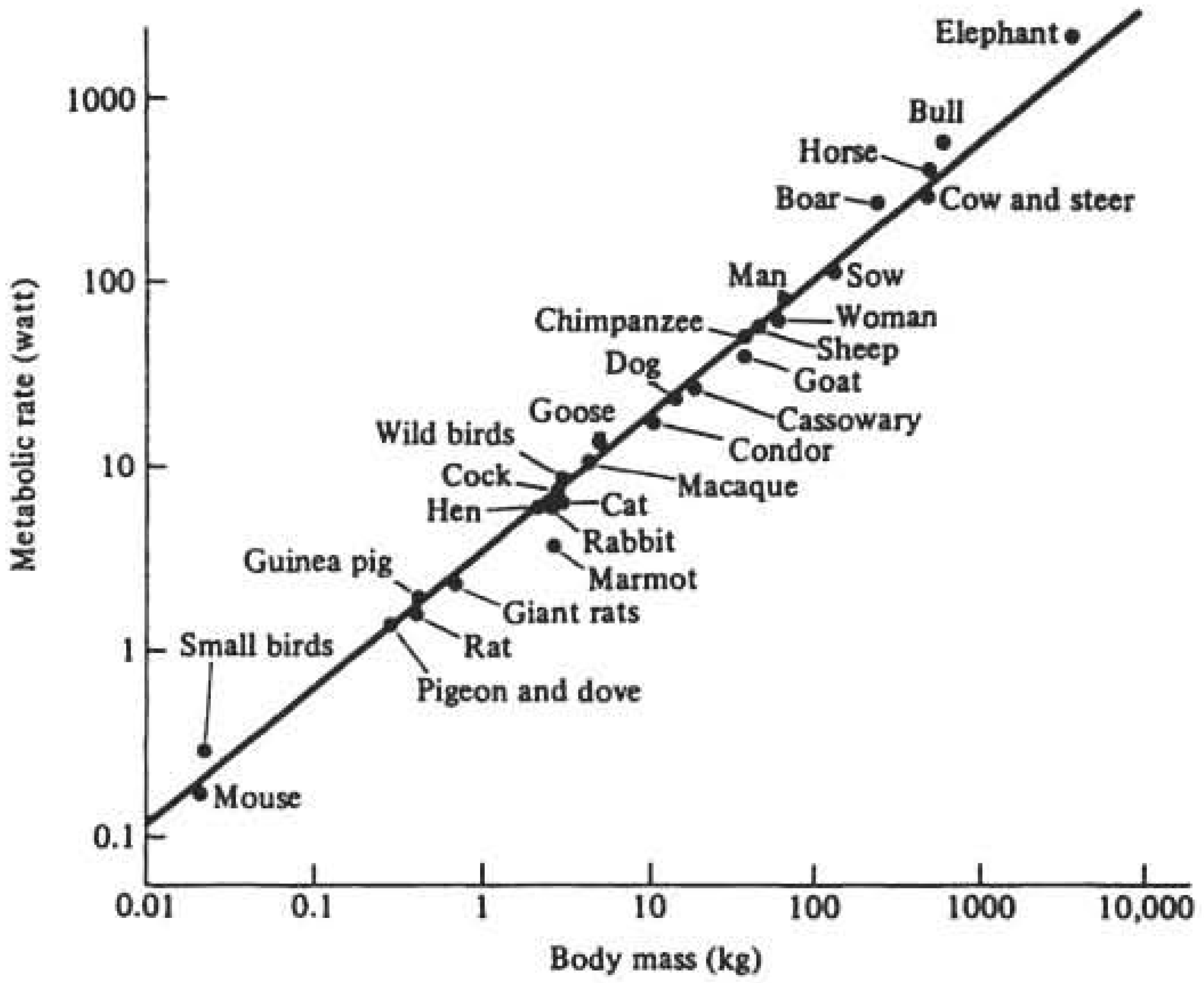
2.1.3. Physiological and/or Biological Time
2.1.4. Information Transfer Hypotheses
2.1.5. Botany
2.1.6. Computers and Brains
2.2. Physical Networks
2.2.1. Hydrology
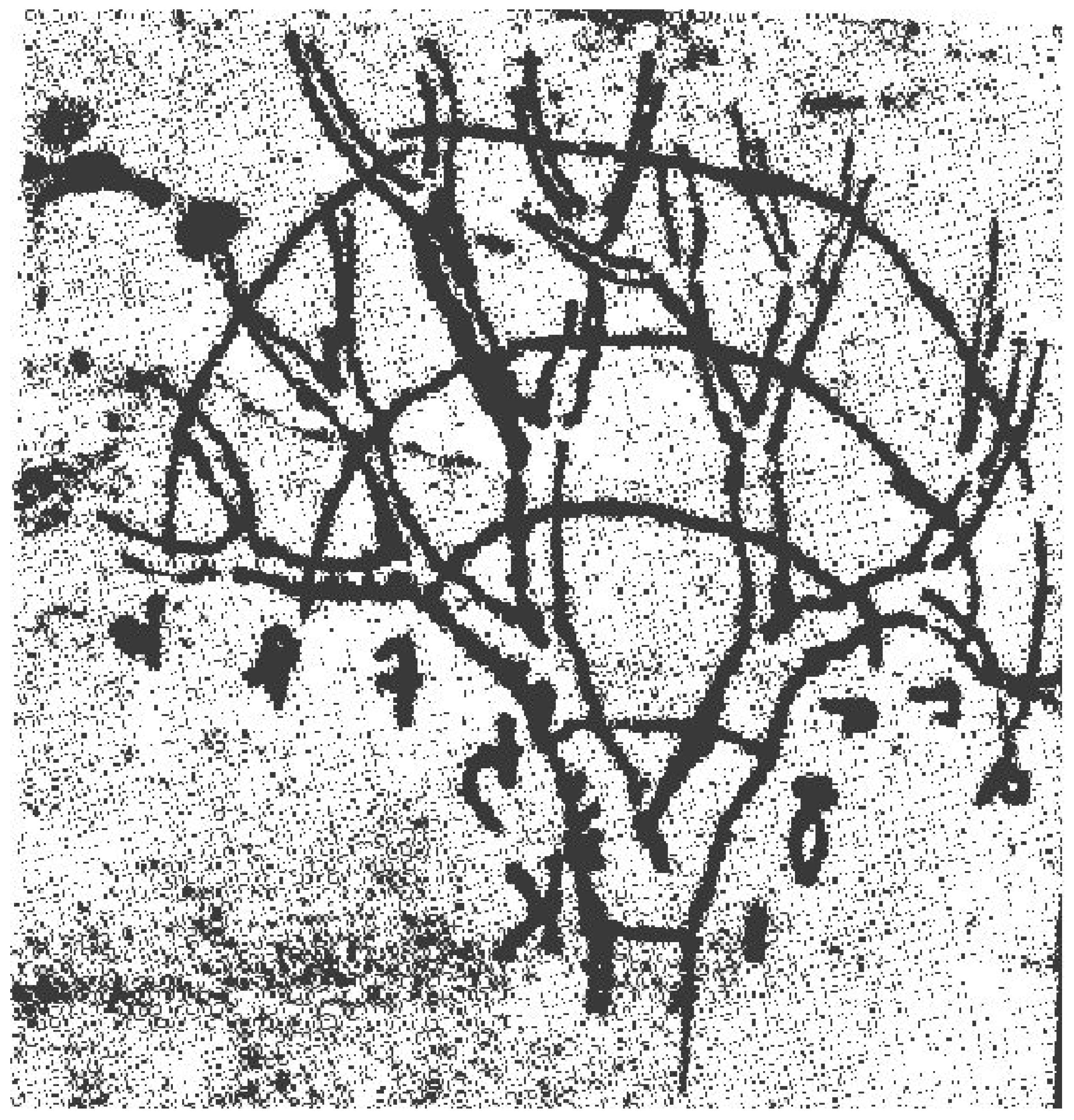
2.2.2. Geology
2.3. Natural History
2.3.1. Ecology
2.3.2. Acoustic Allometry
2.3.3. Paleontology
2.4. Sociology
2.4.1. Effect of Crowding
2.4.2. Urban Allometry
2.4.3. Health, Wealth and Innovation
3. Fractional Calculus
3.1. Subordination
3.2. Fractional Phase Space Equations
3.2.1. Statistics of Allometry Parameters
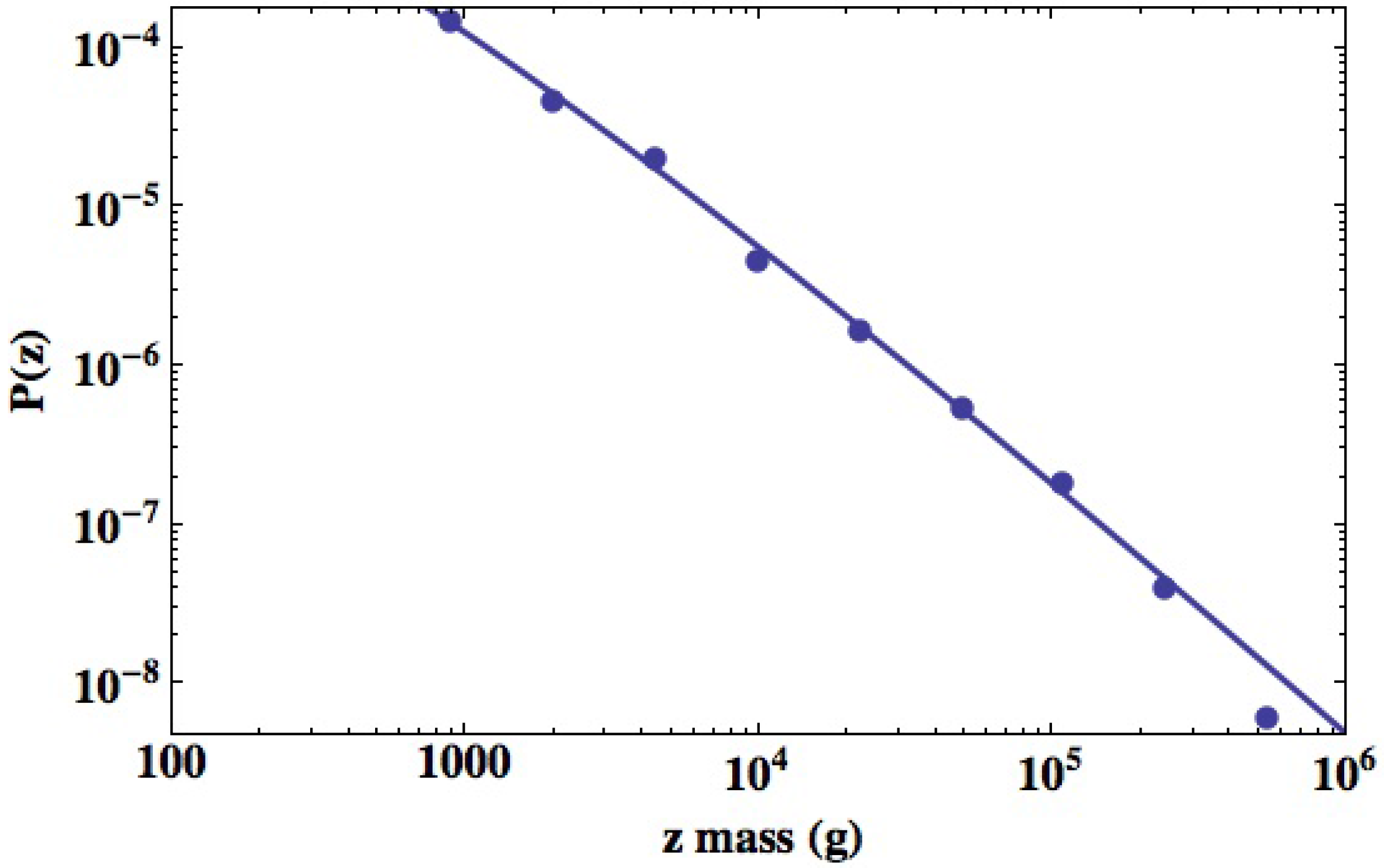
3.2.2. Urban Variability
3.2.3. Scaling Solution
3.2.4. Allometry Relations
4. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
References
- Gould, S.J. Allometry and size in ontogeny and phylogeny. Biol. Rev. Cam. Philos. Soc. 1966, 41, 587–640. [Google Scholar] [CrossRef]
- Reiss, M.J. The Allometry of Growth and Reproduction; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Thompson, D.W. On Growth and Form, The Complete Revised Edition; Dover: New York, NY, USA, 1992. [Google Scholar]
- Huxley, J.S. Problems of Relative Growth; Dial Press: New York, NY, USA, 1931. [Google Scholar]
- Lorenz, E.N. The Essence of Chaos; University of Washington Press: Seattle, WA, USA, 1993. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Lindenberg, K.; West, B.J. The Nonequilibrium Statistical Mechanics of Open and Closed Systems; VCH: New York, NY, USA, 1990. [Google Scholar]
- Calder, W.W., III. Size, Function and Life History; Harvard University Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Schmidt-Nielsen, K. Scaling, Why is Animal Size so Important? Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Banavar, J.R.; Damuth, J.; Maritan, A.; Rinaldo, A. Allometric cascades. Nature 2003, 421, 713–714. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122–124. [Google Scholar] [CrossRef] [PubMed]
- Weissman, M.B. 1/f noise and other slow, nonexponential kinetics in condensed matter. Rev. Mod. Phys. 1988, 60, 537–571. [Google Scholar] [CrossRef]
- West, B.J.; Geneston, E.L.; Grigolini, P. Maximizing information exchange between complex networks. Phys. Rept. 2008, 468, 1–99. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals, Form and Chance; W.H. Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- West, D.; West, B.J. On allometry relations. Int. J. Mod. Phys. 2012, 26, 1230013–1230014. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Self-Affine Fractal Sets. In Fractals in Physics; Pietronero, L., Tosatti, E., Eds.; North-Holland: Amsterdam, The Netherlands, 1986; pp. 3–28. [Google Scholar]
- Mandelbrot, B.B. Fractals and Scaling in Finance; Springer: New York, NY, USA, 1997. [Google Scholar]
- Mantegna, R.N.; Stanley, H.E. Econophysics; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Allegrini, P.; Paadissi, P.; Menicci, D.; Gemignani, A. Fractal complexity in spontaneous EEG metastable-state transitions: New vistas on integrated neural dynamics. Front. Physiol. 2010, 1. [Google Scholar] [CrossRef] [PubMed]
- Werner, G. Frctals in the nervous system: Conceptual implications for theoretical neuroscience. Front. Physiol. 2010, 1. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- West, B.J. Fractal physiology and the fractional calculus: A perspective. Front. Physiol. 2010, 1. [Google Scholar] [CrossRef]
- West, B.J.; Grigolini, P. Complex Webs: Anticipating the Improbable; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Beran, J. Statistics of Long-Memory Processes. In Monographs on Statistics and Applied Probability; Chapman & Hall: New York, NY, USA, 1994; Volume 61. [Google Scholar]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Zolotarev, V.M. One-Dimensional Stable Distributions; Translations of Mathematical Monographs, American Mathematical Society: Providence, RI, USA, 1986; Volume 65. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House: Redding, CT, USA, 2006. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Klafter, J.; Metzler, R. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rept. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J.; Blumen, A. Fractional kinetics. Phys. Today 2002, 55, 48–54. [Google Scholar] [CrossRef]
- West, B.J.; Bologna, M.; Grigolini, P. Physics of Fractal Operators; Springer: Berlin, Germany, 2003. [Google Scholar]
- West, B.J.; West, D. Origin of Allometry Hypothesis. In Fractal Dynamics; Recent Advances; Klafter, J., Lin, S.C., Metler, R., Eds.; World Scientific: Singapore, 2011. [Google Scholar]
- West, B.J.; West, D. Fractional Dynamics of Allometry. Frac. Calc. App. Anal. 2012, 15, 70–96. [Google Scholar] [CrossRef]
- Banavar, J.R.; Damuth, J.; Maritan, A.; Rinaldo, A. Modeling universality and scaling. Nature 2002, 420, 626–627. [Google Scholar] [CrossRef] [PubMed]
- West, G.B.; Brown, J.H.; Enquist, B.J. The fourth dimension of life: Fractal geometry and allometric scaling of organisms. Science 1999, 284, 11677–1679. [Google Scholar] [CrossRef]
- Gayon, J. History of the concept of allometry. Am. Zool. 2000, 40, 748–758. [Google Scholar] [CrossRef]
- Cuvier, G. Recherches sur les Ossemens Fossils; Chez G. Dufour et E. d’Ocagne: Paris, France, 1821. [Google Scholar]
- Snell, O. Die Abhängigkeit des Hirngewichts von dem Körpergewicht und den geistigen Fähigkeiten. Arch. Psychiatr. 1892, 23, 436–446. [Google Scholar] [CrossRef]
- Tower, D.B. Structural and functional organization of mammalian cerebral cortex the correlation of neurone density with brain size. J. Comput. Neurol. 1954, 101, 9–52. [Google Scholar]
- Changizi, M.A. Principles underlying mammalian neocortical scalling. Biol. Cybern. 2001, 84, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Sarrus, R. Rapport sur un memoire adresse a L’Academie Royle de Medcine. Commissaires Robiquet et Thillarye, rapporteurs. Bull. Acad. Roy. Med. (Paris) 1838–1839, 3, 1094–1000. [Google Scholar]
- Rubner, M. Ueber den Einfluss der Körpergrösse auf Stoffund Kraftwechsel. Z. Biol. 1883, 19, 353–358. [Google Scholar]
- Kleiber, M. Body size and metabolism. Hilgarida 1932, 6, 315–353. [Google Scholar] [CrossRef]
- Brody, S. Bioenergetics and Growth; Reinhold: New York, NY, USA, 1945. [Google Scholar]
- Hemmingsen, A.M. The relation of standard (basal) energy metabolism to total fresh weight of living organisms. Rep. Steno. Mem. Hosp. (Copenhagen) 1950, 4, 1–58. [Google Scholar]
- Dodds, P.S.; Rothman, D.H.; Weitz, J.S. Re-examination of the 3/4-law of metabolism. J. Theor. Biol. 2001, 209, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. Beyond the ‘3/4-power law’: Variation in the intra- and interspecific scaling of metabolic rate in animals. Biol. Rev. 2005, 80, 611–662. [Google Scholar] [CrossRef] [PubMed]
- Glazier, D.S. A unifying explanation for diverse metabolic scaling in animals and plants. Biol. Rev. 2010, 85, 111–138. [Google Scholar] [CrossRef]
- Heusner, A.A. Size and power in mammals. J. Exp. Biol. 1991, 160, 25–54. [Google Scholar] [PubMed]
- Bejan, A. The tree of convective heat streams: Its thermal insulation function and the predicted 3/4-power relation between body heat loss and body size. Int. J. Heat Mass Trans. 2001, 44, 699–704. [Google Scholar] [CrossRef]
- Glazier, D.S. The 3/4-power law is not universal: Evolution of isomeric, ontogenetic metabolic scaling in pelagoic animals. BioScience 2006, 56, 325–332. [Google Scholar] [CrossRef]
- West, D.; West, B.J. Stochastic origin of allometry. EPL 2001, 94. [Google Scholar] [CrossRef]
- Hill, A.V. The dimensions of animals and their muscular dynamics. Sci. Prog. 1950, 38, 209–230. [Google Scholar]
- Lindstedt, S.L.; Calder, W.A., III. Body size and longevity in birds. Condor 1976, 78, 91–94. [Google Scholar] [CrossRef]
- Lindstedt, S.L.; Miller, B.J.; Buskirk, S.W. Home range, time and body size in mammals. Ecology 1986, 67, 413–418. [Google Scholar] [CrossRef]
- Lindstedt, S.L.; Calder, W.A., III. Body size, physiological time, and longevity of homeothermic animals. Quart. Rev. Biol. 1981, 36, 1–16. [Google Scholar] [CrossRef]
- Ballard, F.J.; Hanson, R.W.; Kronfeld, D.S. Gluconeogenesis and lipogenesis in tissue from ruminant and nonruminant animals. Fed. Proc. 1969, 28, 218–231. [Google Scholar] [PubMed]
- Sacher, G.A. Relation of Lifespan to Brain Weight and Body Weight in Mammals. In Ciba Foundation Colloquium on Aging; Wolstenholme, G.E.W., Ed.; John Wiley and Sons: Chichester, UK, 1959; Volume 1. [Google Scholar]
- Heusner, A.A. Energy metabolism and body size: I. Is the 0.75 mass exponent of Kleiber’s equation a statistical artifact? Resp. Physiol. 1982, 4, 1–12. [Google Scholar] [CrossRef]
- Savage, V.M.; Gillooly, J.P.; Woodruff, W.H.; West, G.B.; Allen, A.P.; Enquist, B.J.; Brown, J.H. The predominance of quarter-power scaling biology. Func. Ecol. 2004, 18, 257–282. [Google Scholar] [CrossRef]
- West, D.; West, B.J. Physiologic time: A hypothesis. Phys. Life Rev. 2013, 10, 210–224. [Google Scholar] [CrossRef] [PubMed]
- Hempleman, S.C.; Kilgore, D.L.; Colby, C.; Bavis, R.W.; Powell, F.L. Spike firing allometry in avian intrapulmonary chemoreceptors: Matching neural code to body size. J. Exp. Biol. 2005, 208, 3065–3073. [Google Scholar] [CrossRef] [PubMed]
- Niklas, K.J. Plant allometry: Is there a grand unifying theory? Biol. Rev. 2004, 79, 871–889. [Google Scholar] [CrossRef] [PubMed]
- Reich, P.B.; Tjoelker, M.G.; Marchado, J.; Oleksyn, J. Universal scaling of respiratory metabolsim, size and nitrogen in plants. Nature 2006, 439, 457–461. [Google Scholar] [CrossRef]
- Enquist, B.J. Universal scaling in tree and vascular plant allometry: Towards a general quantitative theory linking plant form and function from cells to ecosystems. Tree Phys. 2002, 22, 1045–1064. [Google Scholar] [CrossRef]
- Bassett, D.S.; Greenfield, D.L.; Meyer-Lindenberg, A.; Weinberger, D.R.; Moore, S.W.; Bullmore, E.T. Efficient physical embedding of topologically complex information processing networks in brains and computer circuits. PLoS Comput. Biol. 2010, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Schlenska, G. Volumen und Oberflachenmessungen an Gehiren verschiedener Saugetiere im Vergleich su einem errechneien Modell. J. Hirnforsch 1974, 15, 401–408. [Google Scholar]
- Beiu, V.; Ibrahim, W. Does the brain really ouperfofrm Rent’s rule? In Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS 2008), Seattle, WA, USA, 18–21 May 2008; pp. 640–643.
- Richter, J.P. The Notebooks of Leonardo da Vinci; Dover: New York, NY, USA, 1970; Volume 1, Unabridged edition of the work first published in London in 1883. [Google Scholar]
- Hack, J.T. Studies of longitudianl profiles in Virginia and Maryland. Geol. Surv. Prof. Pap. 1957, 294-B, 1–52. [Google Scholar]
- Feder, J. Fractals; Plenum: New York, NY, USA, 1988. [Google Scholar]
- Rinaldo, A.; Banavar, J.R.; Maritan, A. Trees, networks and hydrology. Water Resour. Res. 2006, 42, 1–19. [Google Scholar] [CrossRef]
- Rigon, R.; Rodriguez-Iturbe, I.; Rinaldo, A. Feasible optimality implies Hack’s law. Water Resour. Res. 1998, 32, 3367–3374. [Google Scholar] [CrossRef]
- Sagar, B.S.; Tien, T.L. Allometric power-law relationships in a Hortonian fractal digital elevation model. Geophys. Res. Lett. 2004, 31, L06501:1–L06501:4. [Google Scholar] [CrossRef]
- Maritan, A.; Rigon, R.; Banavar, J.B.; Rinaldo, A. Network allometry. Geophys. Res. Lett. 2001, 29, 1508. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dierich, W.E. Channel initiation and the problem of landscape scale. Science 1992, 255, 826–832. [Google Scholar] [CrossRef] [PubMed]
- Horton, R.E. Erosional development of streams and their drainage basins: Hydophysical approach to quantitative geomorphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Brown, J.H.; Gupta, V.K.; Li, B.; Milne, B.T.; Restrepo, C.; West, G.B. The fractal nature of nature: Power laws, ecological complexity and biodiversity. Phil. Trans. R. Soc. Lond. B 2002, 357, 619–626. [Google Scholar] [CrossRef] [PubMed]
- Peckham, S. New results for self-similar trees with appllications to river networks. Water Resour. Res. 1995, 31, 1023–1029. [Google Scholar] [CrossRef]
- Peckham, S.D.; Gupta, V.K. A reformulation of Horton’s law for large river networks in terms of statistical self-similarity. Water Resour. Res. 1999, 35, 2763–2777. [Google Scholar] [CrossRef]
- Dodds, P.S.; Rothman, D.H. Scaling, universality and geomorphology. Ann. Rev. Earth Planet. Sci. 2000, 28, 1–41. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Rinaldo, A. Fractal River Basins. Chance and Self-organization; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Woodward, G.; Ebenman, B.; Emmerson, M.; Montoya, J.M.; Olesen, J.M.; Valido, A.; Warren, P.H. Body size in ecological networks. Trends Ecol. Evol. 2005, 20, 402–409. [Google Scholar] [CrossRef]
- Cohen, J.E.; Jonsson, T.; Carpenter, S.R. Ecological community description using the food web, spcies abundance, and body size. Proc. Natl. Acad. Sci. USA 2003, 100, 1781–1786. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Toward a metabolic theory of ecology. Ecology 2004, 85, 1771–1789. [Google Scholar] [CrossRef]
- Brown, J.H.; Gillooly, J.F.; Allen, A.P.; Savage, V.M.; West, G.B. Response to forum commentary on Toward a metabolic theory of ecology. Ecology 2004, 85, 1818–1821. [Google Scholar] [CrossRef]
- Jonsson, T.; Cohen, J.E.; Carpenter, S.R. Food webs, body size and species abundance in ecological community description. Adv. Ecol. Res. 2005, 36, 1–84. [Google Scholar]
- Preston, F.W. The canonical distribution of commonness and rarity. Ecology 1962, 43, 185–215. [Google Scholar] [CrossRef]
- Willis, J.C. Age and Area; Cambridge University Press: Cambridge, UK, 1922. [Google Scholar]
- Brown, J.H. Macroecology; University of Chicago Press: Chicago, IL, USA, 1995. [Google Scholar]
- Williams, C.B. Patterns in the Balance of Nature and Related Problems in Quantitative Ecology; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Fitch, W.T. Skull dimensions in relation to body size in nonhuman mammals: The causal bases for acoustic allometry. Zoology 2000, 103, 40–58. [Google Scholar]
- Martin, R.D.; Harvey, P.H. Brain Size Allometry: Ontogeny and Phylogeny. In Size & Scaling in Primate Biology; Jungers, W.L., Ed.; Plenum Press: New York, NY, USA, 1985. [Google Scholar]
- Shea, B. Relative growth of the limbs and trunk in the African apes. Am. J. Phys. Anthopol. 1981, 56, 179–202. [Google Scholar] [CrossRef] [PubMed]
- Pilbeam, D.; Gould, S.J. Size and scaling in human evoluton. Science 1974, 186, 892–901. [Google Scholar] [CrossRef] [PubMed]
- Cope, E.D. The Primary Factors of Organic Evolution; Open Court Publishing Company: London, UK, 1896. [Google Scholar]
- Galileo, G. This is in the Dialogue of the Second Day in the Discorsi of 1638, the work Galileo wrote while under house arrest by the Inquisition. It was translated as Dialogues Concerning Two New Sciences by H. Crew and A De Salvor in 1914 and reprinted by Dover, New York, 1952.
- Jerison, H.J. Quantitative analysis of evolution of the brain in mammals. Science 1961, 133, 1012–1014. [Google Scholar] [CrossRef] [PubMed]
- White, J.F.; Gould, S.J. Interpretation of the coefficient in the allometric equation. Am. Nat. 1965, 99, 5–18. [Google Scholar] [CrossRef]
- Gould, S.J. Geometric similarity in allometric growth: A contribution to the problem of scaling in the evolution of size. Am. Nat. 1971, 105, 113–136. [Google Scholar] [CrossRef]
- Alberch, P.; Gould, S.J.; Oster, G.F.; Wake, D.B. Size and shape in ontogeny and phylogeny. Paleobiology 1979, 5, 296–317. [Google Scholar]
- Eldredge, N.; Gould, S.J. Punctuated Equilibria: An Alternative to Phyletic Gradualism. In Models in Paleobiology; Schopf, T.J.M., Ed.; Freeman, Cooper and Co.: San Francisco, CA, USA, 1972; pp. 82–115. [Google Scholar]
- Eldredge, N. Time Frames; Princeton University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Sneppen, K.; Bak, P.; Flybjerg, H.; Jensen, M.H. Evolution as a self-organized critical phenomenon. Proc. Natl. Acad. Sci. USA 1995, 92, 5209–5213. [Google Scholar] [CrossRef] [PubMed]
- Bak, P.; Boettcher, S. Self-organized criticality and punctuated equilibrium. Phys. D 1997, 107, 143–150. [Google Scholar] [CrossRef]
- West, D.; West, B.J. Are allometry and macroevolution related? Phys. A 2011, 390, 1733–1736. [Google Scholar] [CrossRef]
- Batty, M.; Longley, P. Fractal Cities; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Milgrim, S. The experience of living in cities. Science 1970, 167, 1461. [Google Scholar] [CrossRef]
- Brownlee, J. Density of death rate: Farr’s law. J. Roy. Soc. Stat. Soc. 1920, 83, 280–283. [Google Scholar] [CrossRef]
- Farr, W. A report on the mortality of lunitacs. J. Stat. (London) 1841, 9, 17–33. [Google Scholar]
- Humphreys, N.A. Vital Statistics: A Memorial Volume of Selections from the Reports and Writings of William Farr; The Sanitory Institute of Great Britian: London, UK, 1885. [Google Scholar]
- Batty, M.; Carvalho, R.; Hudson-Smith, A.; Milton, R.; Smith, D.; Steadman, P. Geometric Scaling and Allometry in Large Cities. In Proceedings of the 6th International Space Syntax Symposium, Istanbul, Turkey, 2007.
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kuhnert, C.; West, G.B. Growth, innovation, scaling and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef] [PubMed]
- Nelson, T.R.; West, B.J.; Goldberger, A.L. The fractal lung: Universal and species-related scaling patterns. Experientia 1990, 46, 251–254. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R. Symmorphosis: On Form and Function in Shaping Life; Harvard University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- West, B.J.; Barghava, V.; Goldberger, A.L. Beyond the principle of similitude: Renormaization in the bronchial tree. J. Appl. Physiol. 1986, 60, 1089–1097. [Google Scholar] [PubMed]
- Hausdorff, J.M.; Purdon, P.L.; Peng, C.-K.; Ladin, Z.; Wei, J.Y.; Goldberger, A.L. Fractal dynamics of human gait: Stability of long-range correlations. J. Appl. Physiol. 1996, 80, 1448–1457. [Google Scholar] [PubMed]
- West, B.J. The Lure of Modern Science: Fractal Thinking; Studies of Nonlinear Phenomena in Life Science; World Scientific: Singapore, 1999; Volume 3. [Google Scholar]
- Peng, C.-K.; Mistus, J.; Hausdorff, J.M.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Long-range anti-correlations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 1993, 70, 1343–1346. [Google Scholar] [CrossRef]
- Jensen, J.L.W.V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math. 1906, 30, 175–193. [Google Scholar] [CrossRef]
- Svenkeson, A.; Beig, M.T.; Turalska, M.; West, B.J.; Grigolini, P. Fractional trajecories: Decorrelation verus friction. Phys. A 2013, 392, 5663–5672. [Google Scholar] [CrossRef]
- Pramukkul, P.; Svenkeson, A.; Grigolini, P.; Bologna, M.; West, B.J. Complexity and the Fractional Calculus. Adv. Math. Phys. 2013, 2013, 498789:1–498789:7. [Google Scholar] [CrossRef]
- Weiss, G.H. Aspects and Applications of the Random Walk; North-Holland: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Montroll, E.W.; Weiss, G. Random walks on lattices. II. J. Math. Phys. 1965, 6, 167–181. [Google Scholar] [CrossRef]
- Sokolov, I.M.; Klafter, J. From diffusion to anomalous diffusion: A centruy after Einstein’s Brownian motion. Chaos 2005, 15, 026103–026109. [Google Scholar] [CrossRef] [PubMed]
- Seshadri, V.; West, B.J. Fractal dimensionality of Lévy processes. Proc. Natl. Acad. Sci. USA 1982, 79, 4501–4505. [Google Scholar] [CrossRef] [PubMed]
- Montroll, E.W.; West, B.J. On an Enriched Collection of Stochastic Processes. In Fluctuation Phenomena; Montroll, E.W., Lebowitz, J.L., Eds.; North-Holland: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Mainardi, F.; Mura, A.; Pagnini, G.; Gorenflo, R. Time-fractional diffusion of distributed order. J. Vib. Control 2007, 10, 269–308. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Lobo, J.; Strumsky, D.; West, G.B. Urban scaling and its Deviations: Revealling the structure of wealth, innovation and crime across cities. PLoS ONE 2010, 5, e1354. [Google Scholar] [CrossRef] [PubMed]
- Warton, D.I.; Wright, I.J.; Falster, D.S.; Westoby, M. Bivariate line fitting methods for allometry. Biol. Rev. 2006, 85, 259–291. [Google Scholar] [CrossRef] [PubMed]
- White, C.R.; Cassey, P.; Blackburn, T.M. Metabolic allometry exponents are not universal. Ecology 2007, 88, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Uchaikin, V.V. Montroll-Weiss problem, fractional diffusion equations and stable distribution. Int. J. Theor. Phys. 2000, 39, 3805–3813. [Google Scholar] [CrossRef]
- Banavar, J.R.; Damuth, J.; Maritan, A.; Rinaldo, A. Scaling in ecosystems and the linkage of macroecological laws. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
West, B.J. A Fractional Probability Calculus View of Allometry. Systems 2014, 2, 89-118. https://doi.org/10.3390/systems2020089
West BJ. A Fractional Probability Calculus View of Allometry. Systems. 2014; 2(2):89-118. https://doi.org/10.3390/systems2020089
Chicago/Turabian StyleWest, Bruce J. 2014. "A Fractional Probability Calculus View of Allometry" Systems 2, no. 2: 89-118. https://doi.org/10.3390/systems2020089
APA StyleWest, B. J. (2014). A Fractional Probability Calculus View of Allometry. Systems, 2(2), 89-118. https://doi.org/10.3390/systems2020089



