Abstract
The integration of renewable energy into the grid has led to problems such as low utilization rate of energy storage resources (“underutilization after construction”) and insufficient system stability. This paper studied the co-evolution mechanism of power market entities empowered by shared energy storage. Based on the interaction among power generation enterprises, power grid operators, and government regulatory agencies, this paper constructed a three-party evolutionary game model. The model introduced a dynamic reward and punishment mechanism as well as a random interference mechanism, which makes it more in line with the actual situation. The stability conditions of the game players were analyzed by using stochastic differential equations, and the influences of key parameters and incentive mechanisms on the stability of the game players were investigated through numerical simulation. The main research results showed the following: (1) The benefits of shared energy storage and opportunistic gains had a significant impact on the strategic choices of power generation companies and grid operators. (2) The regulatory efficiency had significantly promoted the long-term stable maintenance of the system. (3) Dynamic incentives were superior to static incentives in promoting cooperation, while the deterrent effect of static penalties is stronger than that of dynamic penalties. (4) The increase in the intensity of random disturbances led to strategy oscillation. This study suggested that the government implement gradient-based dynamic incentives, maintain strict static penalties to curb opportunism, and enhance regulatory robustness against uncertainty. This research provided theoretical and practical inspirations for optimizing energy storage incentive policies and promoting multi-subject coordination in the power market.
1. Introduction
Building a new type of power system with new energy as the main body was a key support for achieving the goals of “carbon peak and carbon neutrality”. New energy storage technology, as its core equipment, was crucial for stabilizing the fluctuations of new energy power generation and enhancing the flexibility and stability of the system [1]. Governments of various countries had successively adopted policies on energy storage to promote its stable and sustainable development. The National Energy Administration’s “Implementation Plan for the Development of New Energy Storage during the 14th Five-Year Plan Period” clearly set the strategic goal of promoting the development of new energy storage in the direction of “scale, industrialization and marketization”. The U.S. Department of Energy has released the “Energy Storage Strategy and Roadmap”, aiming to address current and future energy demands, promote the stability of the energy storage supply chain, and facilitate the full commercialization of the energy storage industry. However, the current development was facing significant bottlenecks. Power stations are constrained by the high cost of independent energy storage allocation. Their enthusiasm for participating in energy storage was generally low, leading to frequent phenomena such as “unwilling to allocate energy storage”, “assigned energy storage”, and even “built but not used”. These result in severe idleness of energy storage resources and the predicament of improving system stability [2]. In 2023, the average utilization rate indices of grid-side, user-side, and new energy mandatory storage projects were 38%, 65%, and 17%, respectively, resulting in severe idleness of energy storage resources [3]. The actual available regulation capacity of power generation enterprises was far lower than the planned expectations. The peak shaving and frequency regulation pressure on the power grid had not been fundamentally alleviated by the distribution of energy storage. It still relied on traditional coal-fired units, creating a predicament for improving the stability of the power system [4]. Meanwhile, the majority of the energy storage revenue for power grid operators came from capacity leasing. The low leasing rate of power generation enterprises made it difficult for them to recover the management costs of shared energy storage [5,6]. Solving the problems of low participation willingness of power stations and cost recovery of power grids has become a core issue in promoting the healthy development of new energy storage.
Against this backdrop, “shared energy storage” emerged as an innovative model. Relying on the concept of the sharing economy, it built a unified management platform to provide energy storage services for multiple entities by integrating scattered resources and separating ownership from usage rights [7]. Shared energy storage had broken the traditional one-to-one correspondence between energy storage stations and power stations, shifting to a one-to-N relationship [8]. Shared energy storage effectively reduced users’ energy storage costs and alleviates the grid connection pressure of large-scale new energy power [9]. The participation of power generation enterprises in shared energy storage effectively improved energy storage efficiency and enhanced the stability of the power system [10]. Bian, Li, and Qiu have deeply explored the driving factors of enterprise participation, the economic benefits of business models, and the mechanisms by which enterprises promote the large-scale consumption of new energy. They had confirmed that shared energy storage can effectively reduce user costs and enhance the economic efficiency and flexibility of the system [11,12,13]. Power stations could significantly reduce initial investment and operation costs, effectively smooth out fluctuations in new energy output, and enhance the stability of their own power generation through leasing or co-construction [14]. Chen pointed out that shared energy storage was conducive to the optimal dispatching of the power system by multiple virtual power plants [15]. The power grid could efficiently coordinate energy storage resources to optimize their key role in peak shaving, distribute load pressure, and enhance the resilience and reliability of the system. Wang demonstrated that shared energy storage in industrial parks can effectively smooth out the uncertainty and volatility of renewable energy, thereby achieving stable power consumption [16]. However, Xie’s research indicated that decisions among shared energy storage operators, electricity consumers, and distribution network operators are influenced by the complex relationships of network topologies [17]. The safe and stable operation of the new power system highly depended on the collaborative efforts of the power generation side to provide stable power and the grid side to efficiently dispatch and transmit power [18]. For this reason, power generation enterprises need to rely on advanced prediction technologies and energy storage systems to ensure the stable and reliable output of electrical energy. The power grid must build a new type of power system with intelligent dispatching at its core, achieving precise control of complex power flows and coordinated interaction among power sources, grids, and storage.
However, in practice, factors such as information asymmetry, lax supervision, and imperfect market mechanisms could easily induce opportunistic behaviors like “free-riding” [19]. Energy storage facilities played a crucial role in peak shaving, frequency regulation, and enhancing system stability. However, “free-riding” behavior may distort its investment and utilization benefits. Steinle pointed out that in the cooperation and competition among enterprises, social capital was prone to induce opportunistic behaviors of both buyers and sellers [20]. Some power generation enterprises may tend to overly rely on shared energy storage invested in by the power grid to smooth out their output fluctuations, thereby transferring the system balance cost to the entire power grid. On the other hand, power grid enterprises may also rely on power generation enterprises to solve the problem of unstable power generation on their own, thereby reducing the necessary investment in key public energy storage projects. Therefore, there existed opportunistic behavior between power generation enterprises and power grids, and contractual agreements can effectively curb the occurrence of opportunism. Zhao indicated that the contract has a binding effect on opportunism. Compared with post-event contracts, pre-event contracts had the most significant weakening effect on opportunism [21]. This two-way shirking of responsibility and cost transfer stems from a lack of a clear market mechanism and regulatory rules that define the value contribution and cost sharing of energy storage [22]. Therefore, the government must fulfill its regulatory duties and curb the occurrence of opportunistic behavior through a penalty mechanism. The government could also encourage power generation enterprises to participate in shared energy storage and support the active management of energy storage power stations by the power grid through incentives. Galvi and Chen indicated that government regulation was a key force in curbing the opportunism that could not be eliminated by alliance contracts and promoting the reform of the electricity market [23,24]. They emphasized that incentive mechanisms can promote participation in shared energy storage, and supervision mechanisms can ensure the fulfillment of responsibilities. However, excessive incentives may increase financial pressure and potential rent-seeking risks. Excessive penalties imposed negative constraints on corporate behavior [25,26]. The government urgently needed to design effective incentive strategies to enhance the participation of power stations and establish a strong regulatory mechanism to curb opportunistic behavior. In addition, external factors also had a certain impact on the decision-making of the power station to participate in shared energy storage, such as the electricity demand in the power market, the rental price of energy storage, and the market trading mechanism [27]. This was a key issue that urgently needed to be addressed in the construction of the new power system.
To explore the complex relationships among power generation enterprises, power grids, and the government in the electricity market, this paper adopted evolutionary game theory to analyze the decision-making interaction relationships among the various subjects. Evolutionary game theory was widely used to study the strategy interaction problems among multiple agents because it could conform to the behavioral characteristics of “bounded rationality” and “trial-and-error learning” of market entities [28]. Especially in the power market environment under the shared energy storage mode, the uncertainties and complexities faced by the system are extremely significant. Evolutionary games offered a dynamic perspective, depicting the adaptive process in which the game players, unable to obtain the optimal strategy instantaneously [29], gradually adjust their behavioral strategies through continuous trial and error, learning, and imitation [30]. For instance, scholars such as Yi and Yang constructed an evolutionary game model involving power generation enterprises, power grids, and users. They conducted an in-depth analysis of the significant impact of sharp fluctuations in the marginal demand for external electricity on the quotation strategy of the power generation side [31,32]. In addition, the evolutionary game framework could effectively simulate the interaction and evolution trajectory of the strategies of all parties, and dynamically present the changing trend of the proportion of different strategy groups [33]. Dynamic trends helped identify the long-term stable equilibrium state that the shared energy storage ecosystem may reach under the influence of multiple factors such as changes in technology costs, adjustments in market rules, and policy interventions [34]. Sun introduced Gaussian white noise to simulate the random interference of external factors and pointed out that the fluctuation of environmental information affects the information disclosure decision-making behavior of the government, enterprises, and the public [35]. Dong and Kang also pointed out that the risks of information leakage, market fluctuations, and policy changes have interfering effects on the decision-making behaviors of game players, and the greater the volatility of external factors, the more significant the interfering effects [36,37]. Therefore, evolutionary games with random disturbances were suitable for revealing the inherent laws and equilibrium conditions of multi-agent co-evolution in a complex electricity market environment.
In current research, most of the focus was on the direct impact of enterprises’ own economic benefits on the electricity market, such as return on investment and cost allocation. The impact of the key non-price factor of “power supply stability level” between power generation enterprises and power grid enterprises on their strategic interaction and long-term cooperation willingness under the shared energy storage model has not been systematically and deeply analyzed. Furthermore, existing research lacked studies on the impact of the evolution laws of opportunistic behaviors that may occur during the process of jointly ensuring the reliability of the system on the participation of shared energy storage in decision-making. Power supply stability is not only concerned with the safe operation of the power grid and the quality of electricity usage for users, but also directly affects the effectiveness of energy storage capacity configuration and the market reputation mechanism. If the feedback relationship between it and behavioral strategies was ignored, it would be difficult to truly reveal the sustainable development path of shared energy storage systems. The random evolution game theory was applied to the shared energy storage system in the power market to reveal the strategic interaction and dynamic evolution mechanism among multiple entities, such as power generation enterprises, power grid enterprises, and the government. It remained an important field that has not been fully studied at present. Especially in the context of introducing government regulatory mechanisms such as dynamic rewards and punishments, the decision-making behaviors of power market entities under external random interference still need in-depth exploration and modeling analysis.
Based on this, this paper focuses on the collaborative evolution mechanism of the three game players, namely the power station, power grids, and the government, under the shared energy storage model. The core research issues of this article include the following: (1) How do the three-party game players make decisions under external uncertainties such as market, technological, and policy disturbances? (2) How do the stable operation benefits of the system and opportunistic benefits affect the main strategy? (3) How can the government design an efficient dynamic reward and punishment mechanism to balance the incentive effect and fiscal sustainability? To this end, this paper constructed a three-party evolutionary game model that integrates dynamic reward and punishment mechanisms with random disturbances simulating external uncertainties. It used stochastic differential equations to analyze stability conditions and the decision-making behaviors of all parties involved. This paper also explored how the incentives and strategic interactions among stakeholders evolve over time and used numerical simulation to reveal the influence of key parameters and the effects of different incentive mechanisms.
The contributions of this article were mainly reflected in the following three aspects. First, this paper introduces Gaussian white noise into the three-party game model of shared energy storage. It deeply depicted the impact of external random disturbances such as market fluctuations, information asymmetry, and technological innovation on game subject decisions, and enhanced the model’s explanatory power for complex realities. Secondly, this paper quantitatively analyzed from the cost-benefit perspective the differentiated impact of the synergistic benefits brought by the stable operation of the power system and the opportunistic benefits obtained by “free-riding” on the strategic choices of the main body. It revealed the key micro-drivers affecting the stable power supply level of the system. Thirdly, in response to the issue that continuous government subsidies may lead to fiscal unsustainability, a variety of reward and punishment mechanisms for balancing expenditures were innovatively proposed and analyzed. This paper quantitatively evaluated the effects of different mechanisms on the evolution trend of the three-party strategy and the stability of the system.
The remainder of the research in this paper was arranged as follows: In Section 2, we describe the game relationship among power stations, power grids, and the government, provide hypothetical conditions, and formulate the game process. On this basis, a traditional evolutionary game model was constructed. In Section 3, we analyze the three-party evolutionary game model and use Gaussian white noise to improve the traditional evolutionary game model. In Section 4, we use simulation tools to analyze the decision-making behaviors of the game players in the shared energy storage mode under behavioral evolution. In Section 5, we further explore the impact of dynamic reward and punishment mechanisms on three-party game decision-making and comparatively analyze different government reward and punishment mechanisms. In Section 6, this paper presents the conclusions, suggestions, and limitations of this article.
2. Model Construction and Hypothesis Setting
2.1. Problem Description
As the optimal operator of shared energy storage, the power grid had strong financial resources to build and operate shared energy storage power stations. Under the grid-side shared energy storage model, the power grid could fully utilize energy storage resources for peak shaving and voltage regulation, and lease capacity to recover investment costs. In this mode, the function of independent shared energy storage operators was replaced by the power grid. There were multiple consumers of shared energy storage. As the power supplier of the power grid, the power generation fluctuations of power generation enterprises directly affect the power supply stability level of the power system. Large industrial and commercial consumers own certain photovoltaic power generation equipment, and the electricity generated is mainly used for their own consumption. Compared with power generation enterprises, its photovoltaic power generation was relatively small and had a lesser impact on the stability of the power system. As the supervisor and incentivizer of shared energy storage, the government formulated corresponding policies to encourage power generation enterprises and power grids, such as capacity subsidies and electricity price subsidies. This paper explored the co-evolution mechanism of power market entities under the grid-side shared energy storage model. Therefore, the game subjects considered in this paper were power generation enterprises, power grids, and the government.
The stable operation of the power system is jointly maintained by the power station and the power grid. A power station that needs to configure energy storage capacity can participate in shared energy storage. It utilizes shared energy storage resources to reduce the volatility of power generation and improve the stability of power supply on the power generation side. The power grid is responsible for the allocation and transmission of power resources. Grid management plays a decisive role in the stability of the power system and directly affects the stability of the power supply on the grid side. When power stations and power grids make efforts to ensure the stable operation of the power system, they also gain additional benefits. However, when one party makes efforts to ensure the stable operation of the power system while the other does not, a “free-rider” behavior will occur at this time. The party that does not make efforts will gain opportunistic benefits. As the supervisory department of the electricity market, the government formulated corresponding reward and punishment mechanisms based on the behaviors of power stations and power grids. The government encouraged and guided power stations and power grids to promote the stable operation of the power system and prevent the occurrence of “free-riding” behaviors. The specific interaction processes of various subjects in the model of this paper are shown in Figure 1.
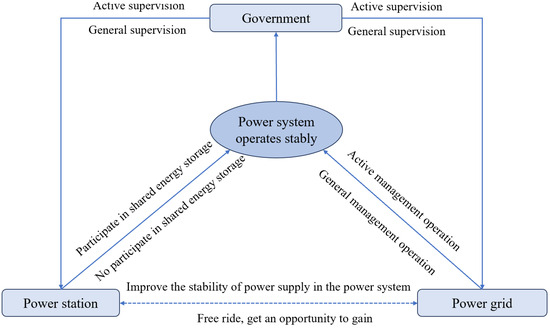
Figure 1.
Schematic diagram of the game logic of shared energy storage entities.
2.2. Assumptions
This article mainly discussed three issues: (1) whether power stations participate in shared energy storage under the dynamic reward and punishment mechanism of the government; (2) how the power grid manages shared energy storage power stations; (3) which incentive and supervision methods the government chooses.
This issue involves three entities: the government, the power station, and the power grids. Among them, the government made strategic choices on the intensity of subsidies based on the development status of shared energy storage and its financial strength. Power stations made decisions based on their energy storage demands and the intensity of government subsidies and penalties. The power grid managed shared energy storage power stations according to the energy storage intentions of each power station. Based on the above problem description, the following assumptions were made:
Hypothesis 1.
Under the shared energy storage mode, the probability of a power station choosing to participate in shared energy storage was , and the probability of not participating in shared energy storage was . The probability of active management of the power grid was , and the probability of ordinary management was . The probability of active government supervision was , and the probability of routine supervision was .
Hypothesis 2.
The cost for a power station to participate in shared energy storage was , and the service fee of the shared management platform was . The cost for a power station not participating in shared energy storage was , and the maintenance and management costs were . The additional income that power stations participating in shared energy storage gain by using their energy storage capacity to enter the power market was . This income needs to be shared, with a sharing coefficient of . The power stations that do not participate in the shared energy storage will exclusively enjoy the additional income.
Hypothesis 3.
Power stations participating in shared energy storage may face the problem of tight energy storage resources during peak hours and be unable to fully reduce the “abandoned wind and abandoned solar” electricity. Power stations not participating in shared energy storage can make full use of their own energy storage equipment to reduce the “abandoned wind and abandoned solar” electricity. The power generation of the two modes was and , respectively. The unit electricity sales revenue was . The participation of a power station in shared energy storage is beneficial to the stability of the power supply in the power system. The unit electricity sales revenue will increase, with a revenue increase coefficient of .
Hypothesis 4.
The power grid conducts active management, adjusts power supply and demand, and makes full use of energy storage equipment resources based on real-time conditions. At this point, the power supply stability level of the power system was , and the initial power supply stability level was . The unit electricity sales revenue was , and the electricity sales volume was .
Hypothesis 5.
The collaborative promotion of stable operation of the system by the power station and the power grid will generate additional economic benefits. The revenue obtained by the power station was , and the revenue obtained by the power grid was .
Hypothesis 6.
Due to the limitations of information and technology, opportunism may occur. When power stations do not participate in shared energy storage but the power grid actively manages to improve the stability of power supply in the power system, the opportunistic benefits obtained by the power station was . When power stations participate in shared energy storage, but the power grid ordinarily manages to improve the stability of power supply in the power system, the opportunistic benefits obtained by the power grid was .
Hypothesis 7.
The government provides subsidies to power stations participating in shared energy storage and actively manages power grids. The upper limits of the reward subsidies were and , and the subsidy coefficients were and , respectively. According to the current penalty design for free-riding, when one party improves the stability level of power supply in the power system, the other party that does not improve the stability level of power supply in the power system will be punished. The upper limit of the penalty was , and the efficiency of government supervision was .
Hypothesis 8.
In the process of the government’s active development of shared energy storage, the management cost of policy formulation and supervision behavior was , and the good reputation benefit obtained was . When power stations participate in shared energy storage and the active management of the power grid, the economic and social benefits that the government will obtain was .
This chapter provided certain explanations on the cost expenditures, benefits, and related parameters of power generation enterprises, power grids, and the government under various circumstances. These parameters facilitated the subsequent calculation of the game players’ returns and the return payment matrix.
2.3. Revenue Payment Matrix
Based on the assumed conditions and the game relationship among power stations, power grids, and the government, a revenue payment matrix was constructed. Each game player has two strategic options, thus forming the benefit functions in eight scenarios, as shown in Table 1.

Table 1.
Income payment matrix table.
This paper explained the meanings of variable symbols in the random evolution model and set up a variable symbol assignment table, as shown in Table 2.

Table 2.
The variable symbol assignment table.
3. Model Solving and Analysis
3.1. Construction of Dynamic Replication Equations
The benefit value perception of power stations participating in shared energy storage was , the benefit value perception obtained from not participating in shared energy storage was , and the average benefit value perception was .
The repeated dynamic equation of the power station was
Power grid enterprises benefit value perception obtained by active management was , benefit value perception obtained by general management was , and average benefit value perception was .
The repeated dynamic equation of power grid enterprises was
The value perception obtained by the government’s active supervision was , the value perception obtained by ordinary supervision was , and the average value perception was .
The repeated dynamic equation of government was
3.2. Analysis of the Random Evolution Game Model
Due to the uncertainty of the external environment, this paper introduced Gaussian white noise into the replication dynamic equation to describe the random interference of the game system, as shown below:
The above equation was a system of non-linear stochastic differential equations; was a one-dimensional standard Brownian motion, a continuous random motion process. , was the step length, was the Gaussian white noise, and were the random interference terms for each subsystem of the game model. represents the disturbance strength, and ; the random disturbance was the largest, which is relatively consistent with the real performance. In group decision, the herd effect tended to be made with high probability and a large proportion of selectors. So the decision was more susceptible to external interference factors.
3.3. Equilibrium Solution and Stability Analysis
Considering the existence of uncertainty in reality, the model could reflect the reality of environmental credit regulation. Therefore, the random perturbation was introduced to analyze and judge the stability of the random evolution, and the stability of the judgment theorem is as follows:
Given a one-dimensional stochastic differential equation,
Assuming the existence function with the normal number sum makes .
If , then the zero solution P moment of the equation is exponentially stable, .
If , ; otherwise, the zero solution P moment of the equation was exponentially unstable, .
So,
If the zero solution moment index of the above Formulas (17)–(19) were stable, then the following formula holds:
Since nonlinear stochastic differential equations are not explicitly solved, the stochastic differential equations are expanded using a Taylor expansion by setting . Referring to the interpretation laws of Xu Xinyang et al., set . Use the Euler method to expand the formula; its random Taylor expansion is .
4. Numerical Simulation Analysis
In order to reveal the key elements in the evolution of highly uncertain events and all possible future development trends, this paper used the 2024b version of the software MATLAB to conduct numerical simulations of the evolutionary game model with random disturbance. This paper referred to the data in the research literature of Han [38] and Tao [39], as well as conducted on-site investigations of power generation enterprises and consultations with power grid workers to obtain relatively accurate power data. We chose to consult the management personnel regarding the operation mechanism and strategy selection of grid-side energy storage. This helped us understand the decisions made by the power grid regarding the operation of energy storage and the relevant subsidies and penalties given by the government. In addition, in order to collect genuine, timely, and operational-level information obtained from the policy implementation end and the front line of grid-side energy storage work, we consulted the on-site operators. On-site actual data often contains many detailed scenarios and unexpected situations that are not captured in administrative documents. This helps us to have a more comprehensive understanding of the implementation status of government policies in practice and the practical challenges they face. This research not only required data and information at the strategic level, but also specific operational data of power generation enterprises and power grids. Therefore, collecting relevant data from the management personnel and on-site operators of the power grid is conducive to forming bottom-up evidence support, enhancing the practicality and ecological validity of the research. In addition, to facilitate the simulation of the article model, we carried out certain processing, but did not change the proportional relationship among the various data. Therefore, the data we selected is proportionally close to the real data. The specific relevant data is shown in Table 3. Considering the random disturbance, the participant will show the fluctuation around a certain strategy, which conforms to the reality situation. The subsequent analysis mainly takes time when the probability of the subject strategy first converges to 1 as the criterion of the strategy selection.

Table 3.
Initial value assignment table of variables.
4.1. The Impact of Different Initial Probabilities on the Strategies of the Game Players
Set to represent the initial probability levels of low, medium, and high for the strategy choices of each entity. The strategy evolution for power stations, power grids, and the government is shown in Figure 2.
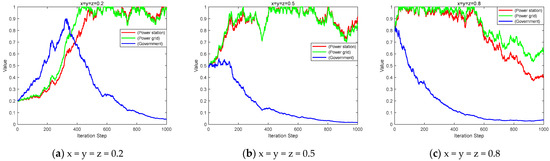
Figure 2.
Evolution trend under different subsidy intensity.
In the power system, when the initial participation probability is low, power stations, power grids, and the government all gradually evolve towards shared energy storage participation, active management, and active supervision. Notably, the government’s evolutionary drive is particularly pronounced. This indicated that in the early stages, the government’s effective supervision significantly increased the probability of power stations participating in shared energy storage and adopting active management. However, over time, the subsidy costs borne by the government continuously mount, while the reputation benefits gained through active supervision remain relatively limited. Consequently, the government tended to shift towards a routine supervision model. When the initial participation probability was at a medium level, power stations and power grids continued to evolve towards shared storage participation and active management. However, the subsidy costs incurred by the government were relatively high, exceeding the reputation benefits. Simultaneously, the government can directly obtain social and economic benefits through routine supervision. Therefore, the government preferred to choose routine supervision. When the initial participation probability was relatively high, power stations and power grids gained significant benefits by promoting the stable operation of the power system. Consequently, their strategies initially evolved towards energy storage participation and active management. However, as the government did not implement subsidies, the benefits for power stations and power grids decreased, leading their strategies to gradually shift. On the other hand, the government faced substantial incentive subsidy costs and significant economic pressure. Furthermore, the reputation benefits obtained from active supervision are far less than the combined costs of active supervision and subsidies. Therefore, the government also opted for routine supervision.
Furthermore, due to the existence of random interference, the strategies of the game players experience “oscillations”. The stability strategies of power generation enterprises fluctuate around the “participation in shared energy storage” strategy. This indicated that the decisions of power generation enterprises were disturbed by the external environment of the electricity market, such as the fluctuations in green electricity prices, the continuity of policies, and the instability of the energy storage market. The power grid was also affected by the price fluctuations of energy storage equipment, policy changes, and the way power generation enterprises install energy storage. The main objective of the government is to promote the participation of power generation enterprises in shared energy storage and the active management of energy storage power stations by the power grid. Therefore, fluctuations in the electricity market and the energy storage market have a relatively small impact on the implementation of its policies.
4.2. The Impact of Reward and Punishment Mechanisms and Regulatory Efficiency on the Strategies of Game Players
Taking , represents the three low, medium, and high states of the government’s subsidy intensity, respectively. Taking represents the three low, medium, and high states of the government’s regulatory efficiency. The level of the government’s regulatory efficiency was used to indicate the intensity of the government’s penalties for the “free-riding” behavior of power enterprises. Its impact on the strategic evolution of the three participating entities is shown in Figure 3 and Figure 4.
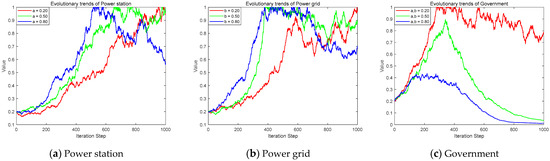
Figure 3.
The evolution trend under different subsidy intensities.
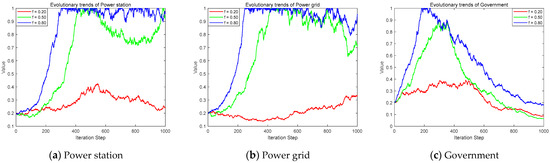
Figure 4.
The evolution trend under different regulatory efficiencies.
As the government gradually raised subsidies for power stations and power grids to promote power system stability, the evolution of power stations towards shared energy storage participation accelerated significantly. The pace at which power grids moved towards active management also quickened markedly. This indicated that government subsidy policies played a significant role in incentivizing both parties to enhance system stability. However, as the subsidy level increased, the government’s fiscal pressure grew accordingly. The reputation benefits gained through active supervision gradually became insufficient to offset the costs of incentive subsidies. As a result, the government shifted its regulatory strategy from active to routine supervision. Therefore, while subsidy policies exerted a positive incentive effect on power stations and power grids, they also heightened the fiscal burden. It thus became necessary to maintain subsidy intensity at a moderate level to avoid excessive fiscal pressure.
As government regulatory efficiency improved, power stations, power grids, and the government all showed a clear trend. They evolved towards participating in shared energy storage, adopting active management, and implementing active supervision. Government regulatory efficiency influenced the potential penalty losses for both power stations and power grids. It also directly affected the government’s own economic revenue. Even under high-efficiency regulation, the initial participation rate of power stations and power grids in shared storage and active management remained low. In this phase, the government increases its revenue through penalty mechanisms and thus tends to adopt an active supervision strategy. As the penalty mechanism takes effect, power stations and power grids gradually evolve towards participating in shared storage and active management until reaching a stable state. At this stage, the government’s penalty mechanism no longer generated penalty revenue, but the government must provide substantial incentive subsidies. Consequently, its regulatory strategy shifts from active supervision to routine supervision. This demonstrated that regulatory efficiency positively promotes decision-making among all three stakeholders. Therefore, it was necessary for the government to enhance its regulatory efficiency.
4.3. The Impact of Additional Gains and Opportunistic Gains on the Strategies of Game Players
(1) Take different values of , , . They respectively represent the benefits, opportunistic benefits, and the increase coefficient of unit electricity sales price brought to the power station by the stable operation of the power system. The impact of the evolution of power station strategies is shown in Figure 5.
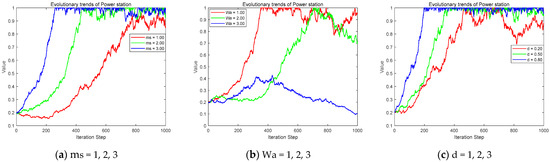
Figure 5.
The evolution trend of power stations under different income levels.
Power station’ participation in shared energy storage enhances the stability of the power supply system, yielding economic benefits. Additionally, the unit electricity price premium significantly boosts their willingness to participate. The benefits of contributing to system stability increased. The unit price premium also rose. As a result, the evolution of power stations towards participating in shared storage sped up. Conversely, sometimes the grid actively managed the system. However, the power station did not participate in shared storage. In this situation, the grid obtained opportunity gains. These gains then deterred the station’s willingness to participate. As opportunity gains increase, the station’s strategies evolved away from participation towards non-participation. This revealed a “free-riding” mentality among stations, which were willing to risk penalties from government regulators to capture the opportunistic benefits stemming from the grid’s active management. Opportunistic gains have hindered power generation enterprises from participating in shared energy storage. Therefore, to incentivize power stations to participate in shared energy storage and promote power system supply stability, the benefits they receive from system stability should be increased. Simultaneously, the government needs to enhance regulatory efficiency, strictly supervise “free-riding” behavior by stations, and ensure that their participation enthusiasm remains unaffected.
(2) Take different values of , , . They respectively represent the benefits, opportunistic benefits, and the increase coefficient of unit electricity sales price brought to the power grid by the stable operation of the power system. The impact of the evolution of power grid strategies is shown in Figure 6.
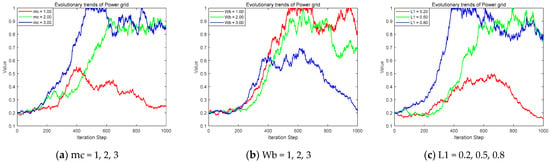
Figure 6.
The evolution trend of the power grid under different income levels.
Proactive grid management enhanced the stability of the power system. The resulting benefits and the improvement in the grid’s own power supply stability significantly strengthened the incentive for the grid to adopt proactive management. The benefits from system stability gradually increased. The level of supply stability achieved through proactive management also rose. As a result, the grid’s management strategy evolved more rapidly. It shifted from ordinary management towards proactive management. The greater the gains from proactive management, the faster this evolutionary process. Sometimes, the grid employed ordinary management. Meanwhile, the power station participated in shared energy storage to promote system stability. In this scenario, the grid obtained opportunity gains. These gains then inhibited its adoption of a proactive management strategy. The increase in the benefits of opportunistic behavior promotes power grids to tend to choose common management strategies. The higher the opportunity of profit gained, the faster the evolution towards ordinary management. This revealed a “free-riding” mentality within the grid. The grid was willing to risk penalties from government regulators. It sought to capture these opportunity gains. This behavior negatively inhibited proactive grid management. Therefore, to promote the construction of an advanced and stable transmission grid, the benefits that the grid receives from system stability need to be increased. Additionally, the grid should be supported in improving its service quality by enhancing its power supply level. Simultaneously, the government needs to enhance regulatory efficiency, strictly oversee grid management practices, and prevent the grid from opting for “free-riding” to obtain opportunity gains for the purpose of reducing management costs, thereby undermining the market environment.
4.4. The Impact of Incentive Costs and Penalty Intensities on the Strategies of the Game Players
Taking different probabilities respectively, it indicates that the cost for the government in formulating an active supervision strategy and the reputation benefits obtained from active supervision gradually increase. The impact of the government’s strategy evolution is shown in Figure 7.
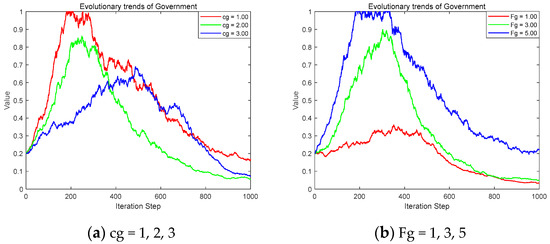
Figure 7.
The evolution trend of the government under different income levels.
As the cost of proactive government supervision gradually increased, the government’s evolutionary trend followed an inverted U-shaped curve. It initially evolved towards proactive supervision, reached a peak, then gradually shifted towards ordinary supervision, and finally stabilized. In the early stages, the probability of a power station participating in shared energy storage was low. The grid’s adoption of proactive management was also limited. During this period, the reputational gains the government obtained from proactive supervision exceeded its incentive subsidy expenditures. Consequently, the government tended to evolve towards a proactive supervision strategy. However, over time, the subsidy costs borne by the government continued to escalate, while the reputational gains from proactive supervision were limited. This led the government to shift towards an ordinary supervision strategy. Government supervision costs exerted a negative inhibitory effect on the proactive supervision strategy. As supervision costs continuously rise, the speed of evolution towards proactive supervision gradually slows down. The probability of the government adopting proactive supervision decreases accordingly. Conversely, the government’s reputation is enhanced positively, promoting the adoption of a proactive supervision strategy. The higher the reputational gain, the faster the evolution towards proactive supervision, and the greater the probability of its adoption. As the regulatory body, the government bears the responsibility of supervision and management. However, substantial subsidies impose significant fiscal pressure. The government needs to guide and encourage power stations and the power grid. They need to collaborate to enhance the stable operation of the power system. At the same time, the government also needs to formulate appropriate subsidy policies. This helps alleviate its own financial burden.
5. Dynamic Reward and Punishment Model
The gradual reduction in government subsidies was a common phenomenon in the development process of enterprises. This was not only a sign that policies were promoting the market to mature, but also a test for enterprises to enhance their market competitiveness. For instance, in order to promote the development of the new energy vehicle industry, the Chinese government initially provided CNY 300 billion in support funds. However, many enterprises relied too much on the subsidies, and eventually, the government stopped the subsidy policy. The new energy enterprise industry shifted from policy-driven to market-driven. The photovoltaic industry also underwent a transformation from subsidy-driven to market-driven. The government cancelled subsidies for photovoltaic electricity prices and encouraged them to enter the market for free competition. The original intention of subsidies was not to provide permanent support. Instead, their purpose was to help enterprises get through the high-risk start-up stage. The ultimate goal was to enable these enterprises to develop independently in market competition.
The government’s penalties change in response to market fluctuations, which is a common strategy for optimizing the business environment. The core of dynamic penalties was to stimulate market vitality through prudent supervision. After enterprises’ participation increased, the government reduced the severity of the penalties. This was not a relaxation of supervision but a shift in regulatory thinking. The government’s reduction in interference with the normal operation of enterprises could effectively enhance regulatory efficiency. The government focuses its limited law enforcement resources on enterprises and fields with higher risks.
Shared energy storage belongs to the new energy development industry, considering that the government’s subsidy for shared energy storage would gradually decrease. Initially, the number of power generation enterprises participating in shared energy storage was relatively small. Therefore, the government’s subsidy was relatively large. This aimed to encourage more enterprises to join. It also helped stimulate market vitality. As the number of participants from power generation enterprises increased, the shared energy storage market gradually improved. The government would gradually reduce the subsidy intensity. At this time, power generation enterprises would not withdraw from shared energy storage due to the reduction in subsidy intensity. In addition, when opportunistic behaviors in the shared energy storage market decreased, the government reduced the severity of penalties, focusing its limited regulatory resources on higher-risk markets. Therefore, this paper assumed that the government’s rewards and subsidies for power generation enterprises and power grids were related to their strategies. The government’s penalties were also related to its strategies.
5.1. Dynamic Reward and Static Penalty Model
In the early stage, the government provided rewards and subsidies to power stations to increase their enthusiasm for participating in shared energy storage. As the number of power stations participating in shared energy storage increased and the shared energy storage model improved, the rewards and subsidies were gradually reduced to alleviate the financial pressure. The government provided subsidies to the power grid to promote active management and enhance the power supply stability of the power system. As the power supply stability of the power grid increased, the rewards and subsidies for the power grid were gradually reduced to alleviate the financial pressure.
We conducted an extensive and in-depth review of the relevant literature and found that many existing studies generally adopt linear relationships to describe the interaction between policy intensity and the strategies of game players. For instance, when Zhang explored the impact of government subsidies and penalties on the quality synergy of shared manufacturing, he established a dynamic incentive model based on linear assumptions [40]. When Fu explored the impact of the government’s dynamic reward and punishment mechanism on the innovative behavior of digital financial enterprises, it also represented dynamic subsidies and penalties with a linear structure [41]. These studies provide us with important theoretical references and methodological inspirations. The introduction of linear relations, on the one hand, helped to simplify the model structure and highlight the interaction between the core mechanisms and key variables in the game process. On the other hand, it was also convenient for solving the equilibrium state and conducting numerical simulation, thereby more clearly revealing the intrinsic connection between policy effects and behavioral feedback. The purpose of this article was to explore the impact of the government’s dynamic rewards and punishments on the decision-making of power generation enterprises and power grids. There was a linear correlation between subsidy intensity and strategy, which could more intuitively reflect the impact of changes in subsidy intensity and penalty intensity on the decision-making of power generation enterprises and power grids. Therefore, in the model construction of this study, drawing on this common practice was also to maintain a certain degree of continuity and result comparability with existing research.
Based on this, the government’s rewards and subsidies for power stations and power grids were set as and , respectively. Under the scenario of the government’s dynamic reward and punishment strategy, the two-dimensional evolutionary game analysis of power stations, power grids, and the government is shown in Figure 8.
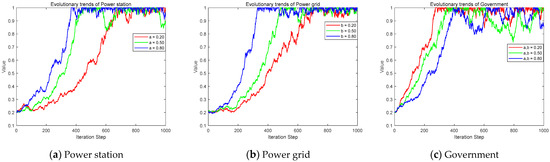
Figure 8.
The evolution trend under dynamic rewards and static penalties.
The impact of a dynamic incentive–penalty mechanism adopted by the government on the strategic choices of power stations and the grid is relatively limited. The government intensified its reward and subsidy efforts. As a result, generation stations evolved more rapidly towards participating in shared energy storage. At the same time, the grid also moved faster towards proactive management. The reward and subsidy intensity were increased. As a result, generation stations required less time to reach a stable state of participating in shared storage. Similarly, the grid also reached a stable state of proactive management more quickly. However, the dynamic incentive–penalty mechanism significantly influenced the government’s choice of supervision strategy. Under a static incentive–penalty mechanism, increased reward and subsidy efforts exacerbated the government’s financial burden, leading its supervision strategy to evolve from proactive towards ordinary supervision. Conversely, under a dynamic mechanism, increased rewards and subsidies may delay the government’s evolution towards proactive supervision. It ultimately still tended towards a proactive supervision strategy and reached a stable state. Under the dynamic mechanism, the probability of generation stations participating in shared storage became high. At the same time, the power grid implemented proactive management effectively. As a result, the power system’s supply stability improved accordingly. At this point, the government’s expenditure on rewards and subsidies for the station and the grid decreases correspondingly. This not only helped reduce government costs but also incentivized the government to adopt proactive supervision to gain greater benefits (such as reputational gains). Therefore, the dynamic incentive–penalty mechanism helped promote the positive evolution of shared storage entities. These entities included generation enterprises and the grid. Additionally, this mechanism exerted a positive influence on the government’s supervision strategy. Its effect was superior to that of a static mechanism.
5.2. Static Reward and Dynamic Penalty Models
In the early stage, the government strengthened the supervision and management of power stations and power grids, imposing relatively severe penalties. The enthusiasm of power stations to participate in shared energy storage has increased. The willingness of power grids to actively manage also grew. As a result, the stability level of the power supply in the system has improved. The government reduced the regulatory penalties on power stations and power grids. The purpose of this article was to explore the impact of the government’s dynamic rewards and punishments on the decision-making of power generation enterprises and power grids. There was a linear correlation between subsidy intensity and strategy, which can more intuitively reflect the impact of changes in penalty intensity on the decision-making of power generation enterprises and power grids. In the model construction of this study, drawing on this common practice was also to maintain a certain degree of continuity and result comparability with existing research. The penalties imposed by the government on power stations and power grids were set as and , respectively. The efficiency of government supervision indicated the intensity of government penalties for the “free-riding” behavior of power stations and power grids. Under the scenario of the government’s dynamic reward and punishment strategy, the two-dimensional evolutionary game analysis of power stations, power grids, and the government is shown in Figure 9.
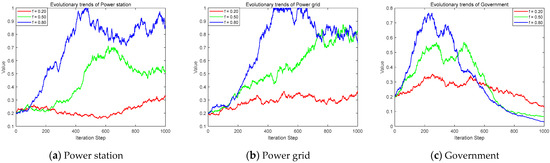
Figure 9.
The evolution trend under static rewards and dynamic penalties.
The government’s dynamic incentive–penalty mechanism exerts a significant influence on the strategic choices of the power station, the power grid, and the government itself. Under the dynamic penalty mechanism, the government’s regulatory efficiency improved. As a result, power stations gradually evolved towards participating in shared energy storage. At the same time, power grids moved towards adopting proactive management. However, when the probability of power station participation and proactive grid management became high, the government reduced the penalty intensity for “free-riding” behavior accordingly. This led stations to tend towards non-participation in shared storage to capture opportunity gains from the stable operation of the power system. Simultaneously, the power grid also tended towards adopting an ordinary management strategy to secure similar opportunity gains. It was noteworthy that the power grid’s evolutionary trend under the dynamic penalty mechanism resembles that of the station. As the government strengthened penalties for “free-riding,” the power grid’s strategy evolved from ordinary management towards proactive management. The greater the penalty intensity, the faster the evolution towards proactive management. The dynamic penalty mechanism also significantly impacted the government’s supervision strategy. In the initial phase of evolution, due to the low probability of power station participation and power grid proactive management, the government can obtain substantial penalty revenue. However, over time, the government gradually reduced the penalty intensity, leading to a corresponding decrease in penalty revenue. This, in turn, drives the government’s supervision strategy to evolve towards ordinary supervision. The purpose of government subsidies was to encourage power generation enterprises to participate in shared energy storage. The purpose of the government’s penalties was to curb opportunistic behavior in the electricity market. Static penalties always maintained a high level of punishment intensity and had a significant inhibitory effect on opportunistic behaviors. The intensity of dynamic penalties will decrease as the number of power generation enterprises participating in shared energy storage in the market increases. At this point, the relatively low penalty intensity had given rise to a sense of luck among some power generation enterprises, and the benefits of opportunism far outweigh the penalty intensity. Therefore, some power generation enterprises would take the risk of penalties to gain opportunistic profits. Compared with a static penalty mechanism, the dynamic mechanism exerted more effective regulatory influence in the initial evolutionary phase. Nevertheless, as time progressed, government penalty revenue decreased under the dynamic mechanism. This reduction hindered its positive evolution towards proactive supervision. It also weakened governmental oversight effectiveness. Furthermore, dynamic penalties may induce complacency in the station and the grid, encouraging them to opt for “free-riding” to capture opportunity gains. This not only impeded the positive evolution of the shared storage entities (generation enterprises and the grid) but also obstructed the government’s cost recovery under a proactive supervision strategy. However, static penalties during the mature stage of shared energy storage development would lead to an increase in government regulatory costs and a waste of law enforcement resources. Therefore, in the early stage of the development of the shared energy storage market, static penalties were applicable. When the market gradually matures, power generation enterprises actively participate in shared energy storage, and the incidence of opportunism is relatively low, the government should adopt dynamic penalties. The government should focus its supervisory resources on other markets where opportunism occurs more frequently.
5.3. Dynamic Reward Subsidy and Dynamic Penalty Model
Suppose that the government’s rewards, subsidies, and penalties for power stations and power grids are related to their strategies. The enthusiasm of power stations to participate in shared energy storage increases. At the same time, the willingness of power grids to actively manage strengthens. As a result, subsidies and penalties for both entities are reduced. This helps alleviate the financial pressure on the government. In the model construction of this study, drawing on this common practice helped to maintain a certain degree of continuity and result comparability with the existing research. The government’s rewards and subsidies for power stations and power grids were set as and , respectively. The penalties for power generation enterprises and power grids were set as and , respectively. The intensity of the government’s penalties for the “free-riding” behavior of power generation enterprises and power grids was indicated by the efficiency of government supervision. Under the scenario of the government’s dynamic reward and punishment strategy, the two-dimensional evolutionary game analysis of power generation enterprises, power grids, and the government is shown in Figure 10 and Figure 11.
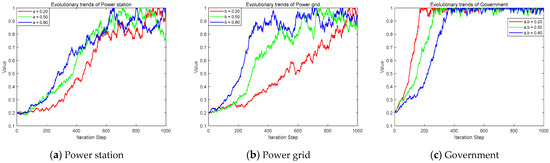
Figure 10.
The evolution trend of increasing rewards in dynamic rewards and penalties.
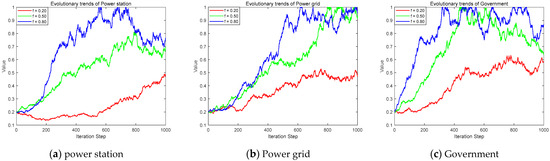
Figure 11.
The evolution trend of increasing penalties in dynamic rewards and penalties.
The dynamic incentive–penalty mechanism significantly influenced the strategic choices of power stations, power grids, and the government. Power stations tend towards the strategy of participating in shared energy storage, the power grid leans towards adopting proactive management, while the government’s supervision strategy evolves towards proactive oversight. Compared to the static mechanism, the ultimate evolutionary trend for generation enterprises and the grid remains unchanged. But the government reduced both the intensity of rewards and subsidies for promoting power system stability and the penalties for “free-riding” behavior. This dampened the enthusiasm of generation enterprises and the grid for enhancing power system supply stability. This consequently slowed down the speed at which both parties evolved towards the equilibrium state of shared storage participation and proactive management strategies. The dynamic mechanism reduced the government’s subsidy costs but also diminished its penalty revenue. However, compared to the static mechanism, the government’s overall benefits under a proactive supervision strategy increase. Therefore, the government’s supervision strategy evolved from ordinary to proactive oversight. Moreover, the smaller the subsidy intensity and the higher the regulatory efficiency, the faster the government evolves towards a proactive supervision strategy.
Under the dynamic mechanism, the government effectively promoted power stations’ participation in shared storage and encouraged the power grid to implement proactive management. As the intensity of rewards and penalties weakened, the impetus for positive evolution in power stations and the grid was suppressed. This fostered “free-riding” behavior. Nevertheless, this mechanism alleviates the government’s financial burden, incentivizing it to choose proactive supervision. Specifically, the dynamic incentive component reduces government cost expenditures, while the dynamic penalty component decreases government penalty revenue. Combinedly, they generally lessen the government’s financial burden, propel the government towards proactive supervision, and facilitate the positive evolution of generation enterprises and the grid. However, under the dynamic incentive–penalty mechanism, the speed of positive evolution for the shared storage entities (generation enterprises and the grid) was relatively slow. This finding indicated that the dynamic mechanism was less effective than the static mechanism. It did not promote the synergistic efforts of generation enterprises and the grid as strongly. These efforts were aimed at ensuring power system stability under the shared storage model.
6. Conclusions
6.1. Conclusions and Implications
This study revealed the internal mechanism of the co-evolution among power stations, power grids, and the government under the shared energy storage mode. It achieved this by constructing a three-party evolutionary game model. The model integrated dynamic rewards and punishments as well as random disturbances. Empirical results showed the economic benefits of shared energy storage. These included the stable operation benefits of the system and the electricity price increase coefficient. These benefits were the core factors. They drove the positive strategies of both power stations and power grids. Opportunistic behavior hinders the willingness of both sides to cooperate. Government regulation can effectively curb opportunistic behavior. The stability control effect of static punishment was better than that of dynamic punishment. The dynamic reward mechanism effectively reduced the long-term fiscal pressure on the government through a gradient design, promoting its continuous selection and active supervision. However, dynamic punishment, due to its weakening of deterrence, had a weakened inhibitory effect on opportunism. In addition, external random disturbances would increase the volatility of the strategy, such as fluctuations in green electricity prices, price fluctuations of energy storage equipment, market instability, and changes in energy storage methods. External interference factors also highlight the systemic risks of fluctuations in the output of new energy and policy adjustments. In conclusion, the healthy development of shared energy storage relies on the triangular support of shared benefits, shared risks, and coordinated regulation. The government needs to play the dual roles of a “guide” and a “night watchman”. The government should ignite market vitality with dynamic incentives. It should also solidify the bottom line of fairness with static penalties. These measures would ultimately achieve the triangular goals of safety, economy, and low carbon in the new power system.
Based on the above findings, this paper proposes the following policy implications. The government needs to construct differentiated reward and punishment combination strategies in accordance with local conditions and the current situation. The government should enhance the net income expectations of the main body through electricity price sharing and high initial subsidies. At the same time, the government should set a lower limit for penalties to maintain rigid constraints on opportunism. It is necessary to respond to random disturbances. The real-time dispatching capacity of the power grid needs enhancement. A linkage mechanism between the electricity and carbon markets also requires exploration. Policy design should be adapted to the development stage of shared energy storage. In the initial stage, strong incentives should be provided to guide large-scale participation. In the mature stage, market-driven approaches should be adopted while maintaining the stability of penalty standards, thereby balancing the demands of fiscal sustainability and system resilience.
6.2. Limitations and Prospects
This paper studied the factors that influence the collaborative promotion of stable power system operation. It focused on power stations participating in shared energy storage and the grid’s active management within the power market. The study did not consider the consumption behavior of other market entities. It also did not examine the energy storage needs of different types of power stations. Furthermore, the impact of various shared energy storage methods on power supply stability was not analyzed. In the future, further research should be conducted on how shared energy storage supports power system stability. Studies should consider perspectives from power generation, the grid, and users. Different types of power generation enterprises should be included, such as renewable energy plants, coal-fired power plants, and distributed generation operators. Various shared energy storage methods and electricity market types also need to be analyzed. Research should focus on how these factors affect both the enterprises’ own generation stability and the overall power supply stability of the system.
Author Contributions
Conceptualization, X.W. and B.L.; methodology, Z.X.; software, C.S.; validation, Z.X., C.S. and X.W.; formal analysis, B.L.; investigation, Z.X.; resources, C.S.; data curation, X.W.; writing—original draft preparation, Z.X. and C.S.; writing—review and editing, Z.X.; visualization, C.S.; supervision, B.L.; project administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Basic Research Program of Shaanxi “Research on the Strengthening Mechanism and Enhancement Countermeasures for the Resilience of the Coal Industry Chain and Supply Chain under the Dual Constraints of Energy Security and Carbon Neutrality”. (grant numbers 2024JC-YBQN-0749).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sayed, E.T.; Olabi, A.G.; Alami, A.H.; Radwan, A.; Mdallal, A.; Rezk, A.; Abdelkareem, M.A. Renewable energy and energy storage systems. Energies 2023, 16, 1415. [Google Scholar]
- He, J.; Cao, L.; Cui, J.; Fu, G.; Jiang, R.; Xu, X.; Guan, C. Flexible energy storage devices to power the future. Adv. Mater. 2024, 36, 2306090. [Google Scholar] [CrossRef]
- Pei, N.; Song, X.; Zhang, Z.; Peña-Mora, F. Optimizing the operation and allocating the cost of shared energy storage for multiple renewable energy stations in power generation side. Energy Convers. Manag. 2024, 302, 118148. [Google Scholar] [CrossRef]
- Jaeyeon, J.; Jinkyoo, P. Demand-side management with shared energy storage system in smart grid. IEEE Trans. Smart Grid 2020, 11, 4466–4476. [Google Scholar] [CrossRef]
- Xie, Y.-S.; Lee, Y.; Chang, X.-Q.; Yin, X.; Zheng, H. Research on the transaction mode and mechanism of grid-side shared energy storage market based on blockchain. Energy Rep. 2022, 8, 224–229. [Google Scholar] [CrossRef]
- Duan, S.; Lv, T.; Li, J.; Shi, W.; Zhang, Y. Methodology for assessing the benefits of shared energy storage systems considering the whole life cycle. J. Energy Storage 2025, 133, 118051. [Google Scholar]
- Yong, X.; Wu, Y.; Zhou, J.; Tao, Y.; Chen, W. Prospects and barriers analysis framework for the development of energy storage sharing. Sustain. Cities Soc. 2023, 89, 104368. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Dong, L. Low carbon-oriented planning of shared energy storage station for multiple integrated energy systems considering energy-carbon flow and carbon emission reduction. Energy 2024, 290, 130139. [Google Scholar]
- Liu, J.; Hu, H.; Yu, S.S.; Trinh, H. Virtual power plant with renewable energy sources and energy storage systems for sustainable power grid-formation, control techniques and demand response. Energies 2023, 16, 3705. [Google Scholar] [CrossRef]
- Dai, R.; Esmaeilbeigi, R.; Charkhgard, H. The utilization of shared energy storage in energy systems: A comprehensive review. IEEE Trans. Smart Grid 2021, 12, 3163–3174. [Google Scholar] [CrossRef]
- Bian, Y.; Xie, L.; Ye, J.; Ma, L.; Cui, C. Peer-to-peer energy sharing model considering multi-objective optimal allocation of shared energy storage in a multi-microgrid system. Energy 2024, 288, 129864. [Google Scholar] [CrossRef]
- Li, J.; Fang, Z.; Wang, Q.; Zhang, M.; Li, Y.; Zhang, W. Optimal operation with dynamic partitioning strategy for centralized shared energy storage station with integration of large-scale renewable energy. J. Mod. Power Syst. Clean Energy 2024, 12, 359–370. [Google Scholar] [CrossRef]
- Qiu, W.; Zhou, S.; Yang, Y.; Lv, X.; Lv, T.; Chen, Y.; Huang, Y.; Zhang, K.; Yu, H.; Wang, Y.; et al. Application prospect, development status and key technologies of shared energy storage toward renewable energy accommodation scenario in the context of China. Energies 2023, 16, 731. [Google Scholar] [CrossRef]
- Leonard, M.D.; Michaelides, E.E.; Michaelides, D.N. Energy storage needs for the substitution of fossil fuel power plants with renewables. Renew. Energy 2020, 145, 951–962. [Google Scholar] [CrossRef]
- Chen, W.; Xiang, Y.; Liu, J. Optimal operation of virtual power plants with shared energy storage. IET Smart Grid 2023, 6, 147–157. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Zhao, Y.; Xu, B. Incorporate robust optimization and demand defense for optimal planning of shared rental energy storage in multi-user industrial park. Energy 2024, 301, 131721. [Google Scholar] [CrossRef]
- Xie, Y.; Li, L.; Hou, T.; Luo, K.; Xu, Z.; Dai, M.; Zhang, L. Shared energy storage configuration in distribution networks: A multi-agent tri-level programming approach. Appl. Energy 2024, 372, 123771. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, Y.; Liu, J.; Yin, S.; Chen, X.; She, L.; Fu, Z.; Liu, H. Distributed shared energy storage double-layer optimal configuration for source-grid co-optimization. Processes 2023, 11, 2194. [Google Scholar] [CrossRef]
- Culiberg, B.; Abosag, I.; Čater, B. Psychological contract breach and opportunism in the sharing economy: Examining the platform-provider relationship. Ind. Mark. Manag. 2023, 111, 189–201. [Google Scholar] [CrossRef]
- Steinle, C.; Schiele, H.; Bohnenkamp, T. Does supplier opportunism lead to buyer opportunism? A social capital perspective. J. Bus. Ind. Mark. 2020, 35, 362–384. [Google Scholar] [CrossRef]
- Zhao, D.; Gu, F.F.; Wang, L. The impact of contractual governance on forms of opportunism. Ind. Mark. Manag. 2022, 102, 89–103. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, H.; Yang, N.; Sun, S. How contract enforcement reduces opportunism? The paradoxical moderating effect of interfirm guanxi. Ind. Mark. Manag. 2021, 97, 115–125. [Google Scholar] [CrossRef]
- Galvin, P.; Tywoniak, S.; Sutherland, J. Collaboration and opportunism in megaproject alliance contracts: The interplay between governance, trust and culture. Int. J. Proj. Manag. 2021, 39, 394–405. [Google Scholar] [CrossRef]
- Cheng, C.-Y.; Lee, Y.J.; Murray, G.; Noh, Y.; Urpelainen, J.; Van Horn, J. Vested interests: Examining the political obstacles to power sector reform in twenty Indian states. Energy Res. Soc. Sci. 2020, 70, 101766. [Google Scholar] [CrossRef]
- Zhu, J.; Baker, J.S.; Song, Z.; Yue, X.-G.; Li, W. Government regulatory policies for digital transformation in small and medium-sized manufacturing enterprises: An evolutionary game analysis. Humanit. Soc. Sci. Commun. 2023, 10, 751. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, W.; Ni, Y. EPR system based on a reward and punishment mechanism: Producer-led product recycling channels. Waste Manag. 2020, 103, 198–207. [Google Scholar] [CrossRef] [PubMed]
- Sheng, Y.; Liu, J.; Wei, D.; Song, X. Heterogeneous Study of Multiple Disturbance Factors Outside Residential Electricity Consumption: A Case Study of Beijing. Sustainability 2021, 13, 3335. [Google Scholar] [CrossRef]
- Shan, S.-N.; Zhang, Z.-C.; Ji, W.-Y.; Wang, H. Analysis of collaborative urban public crisis governance in complex system: A multi-agent stochastic evolutionary game approach. Sustain. Cities Soc. 2023, 91, 104418. [Google Scholar] [CrossRef]
- Wang, G.; Chao, Y.; Cao, Y.; Jiang, T.; Han, W.; Chen, Z. A comprehensive review of research works based on evolutionary game theory for sustainable energy development. Energy Rep. 2022, 8, 114–136. [Google Scholar] [CrossRef]
- Lin, J.; Huang, C.; Dai, Q.; Yang, J. Evolutionary game dynamics of combining the payoff-driven and conformity-driven update rules. Chaos Solitons Fractals 2020, 140, 110146. [Google Scholar] [CrossRef]
- Yi, X.; Lu, S.; Li, D.; Liu, W. Manufacturing enterprises digital collaboration empowered by Industrial Internet Platform: A multi-agent stochastic evolutionary game. Comput. Ind. Eng. 2024, 194, 110415. [Google Scholar] [CrossRef]
- Yang, H.; Mo, J. Research on the bidding behavior of generation-side enterprises based on stochastic evolutionary games. IEEE Trans. Power Syst. 2021, 37, 3693–3703. [Google Scholar] [CrossRef]
- Liu, Z.; Lang, L.; Li, L.; Zhao, Y.; Shi, L. Evolutionary game analysis on the recycling strategy of household medical device enterprises under government dynamic rewards and punishments. Math. Biosci. Eng. MBE 2021, 18, 6434–6451. [Google Scholar]
- Shi, Y.; Han, B.; Zeng, Y. Simulating policy interventions in the interfirm diffusion of low-carbon technologies: An agent-based evolutionary game model. J. Clean. Prod. 2020, 250, 119449. [Google Scholar] [CrossRef]
- Sun, T.; Di, K.; Cai, Q.; Du, H. The study of the random evolutionary game model and policy effects of carbon information disclosure by Chinese listed companies. J. Environ. Manag. 2025, 391, 126369. [Google Scholar] [CrossRef]
- Dong, C.; Liu, J.; Mi, J. How to enhance data sharing in digital government construction: A tripartite stochastic evolutionary game approach. Systems 2023, 11, 212. [Google Scholar] [CrossRef]
- Kang, K.; Bai, L.; Zhang, J. A tripartite stochastic evolutionary game model of complex technological products in a transnational supply chain. Comput. Ind. Eng. 2023, 186, 109690. [Google Scholar] [CrossRef]
- Han, X.; Li, J.; Zhang, Z. Dynamic game optimization control for shared energy storage in multiple application scenarios considering energy storage economy. Appl. Energy 2023, 350, 121801. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S.; Zhao, J. Renewable energy certificates and electricity trading models: Bi-level game approach. Int. J. Electr. Power Energy Syst. 2021, 130, 106940. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Su, C.; Sun, L. Evolutionary game analysis of shared manufacturing quality synergy under dynamic reward and punishment mechanism. Appl. Sci. 2022, 12, 6792. [Google Scholar] [CrossRef]
- Fan, R.; Wang, Y.; Lin, J. Study on multi-agent evolutionary game of emergency management of public health emergencies based on dynamic rewards and punishments. Int. J. Environ. Res. Public Health 2021, 18, 8278. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).