Port Investment Optimization and Its Application Under Differentiated Port and Industrial Risks Along the Maritime Silk Road
Abstract
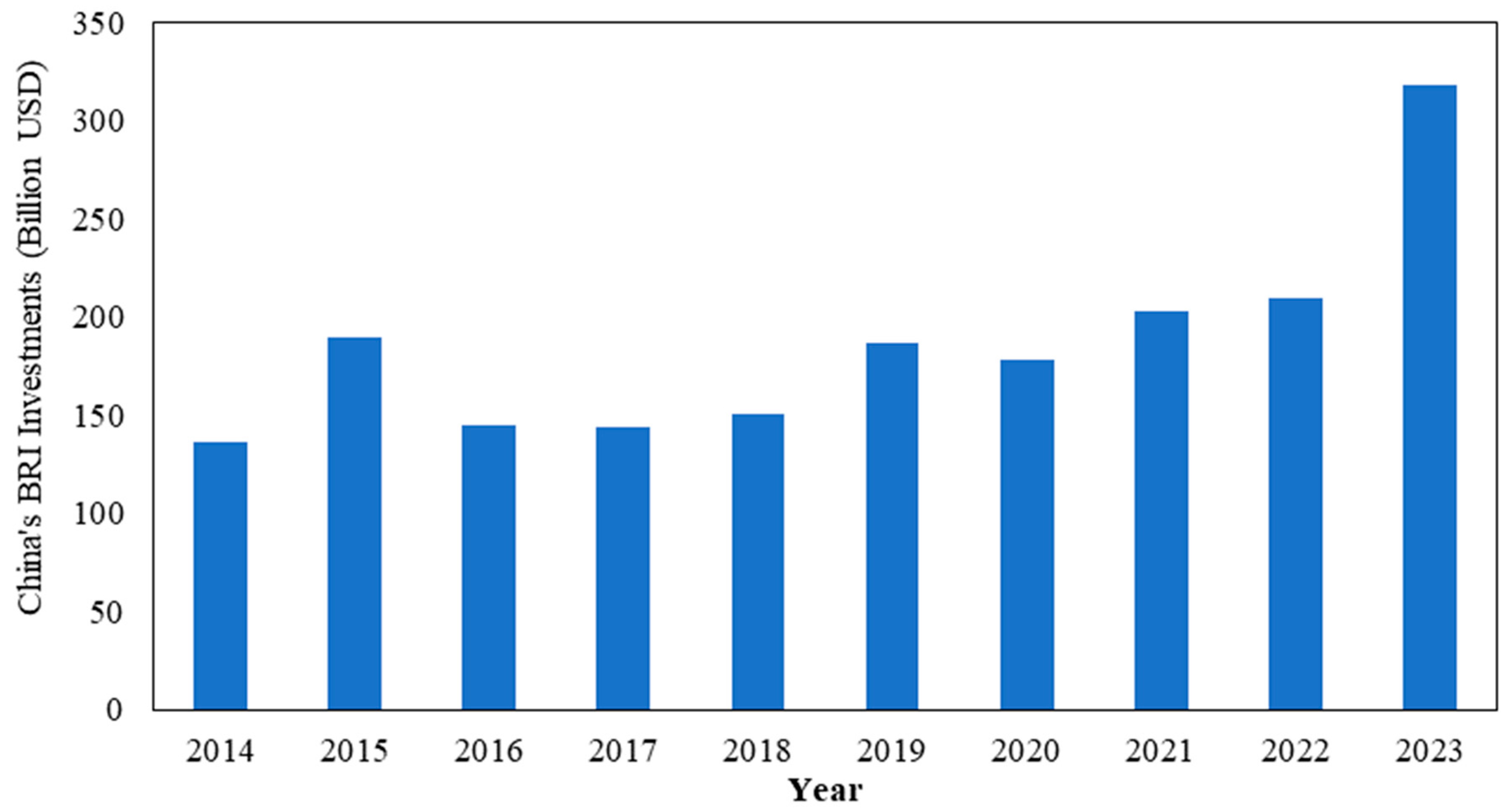
1. Introduction
2. Literature Review
2.1. Research on Port Investment
2.2. Research on Industrial Relocation
3. Problem Description
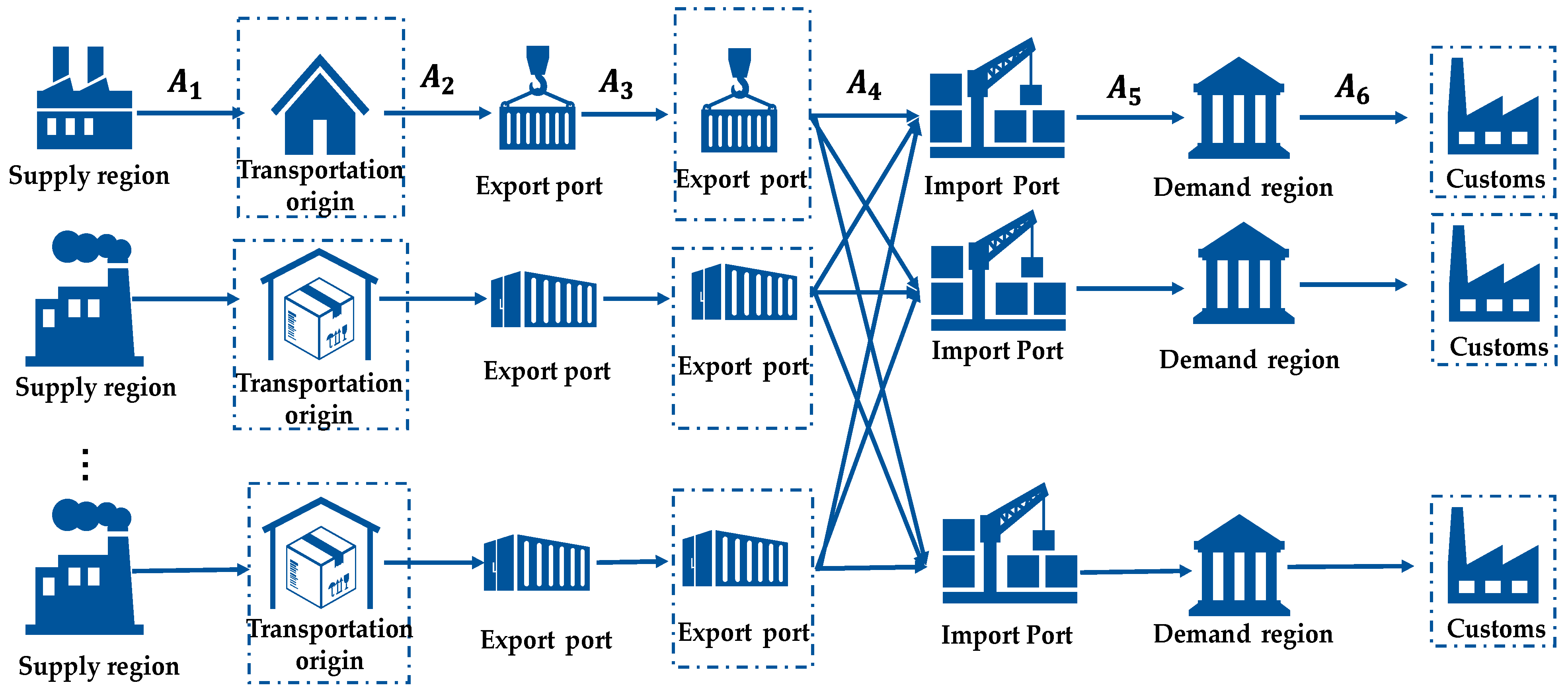
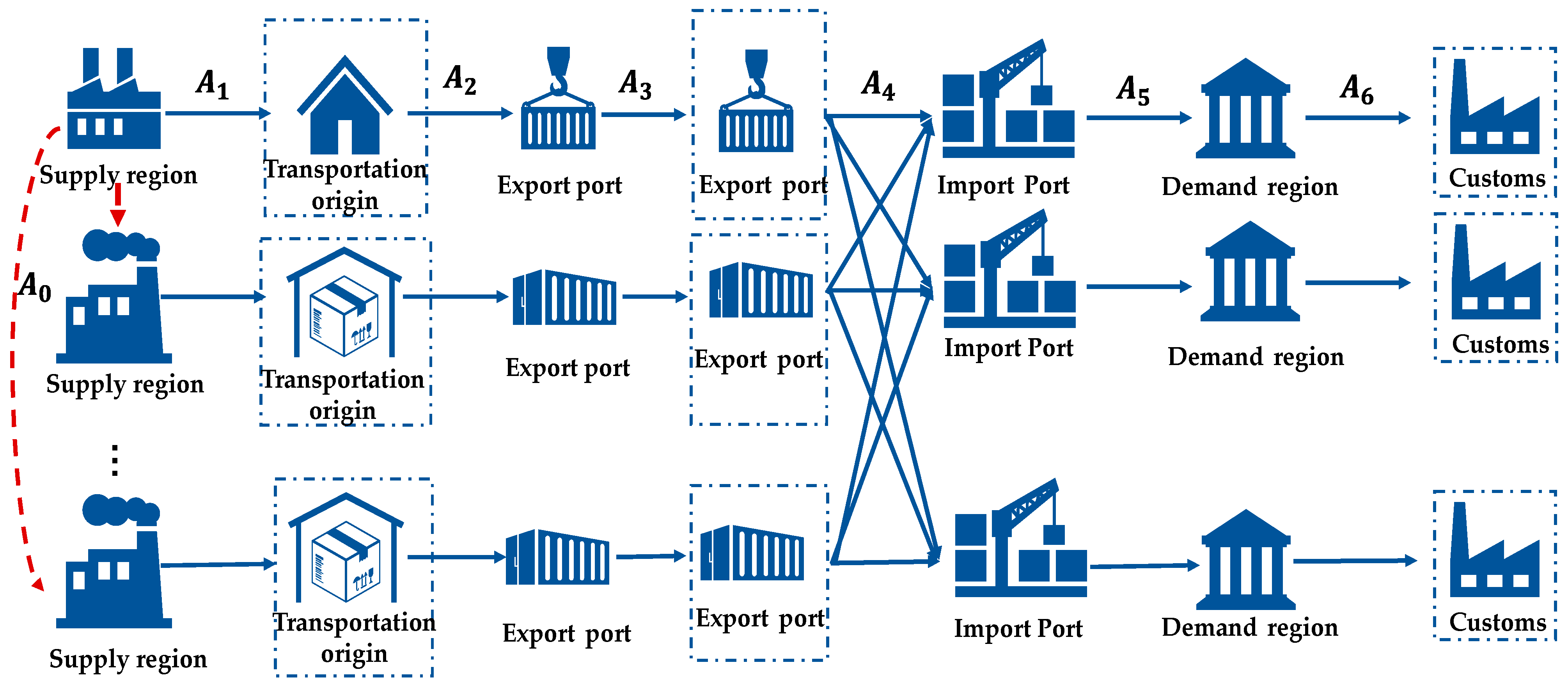
3.1. Research Framework
3.2. Networks and Collections
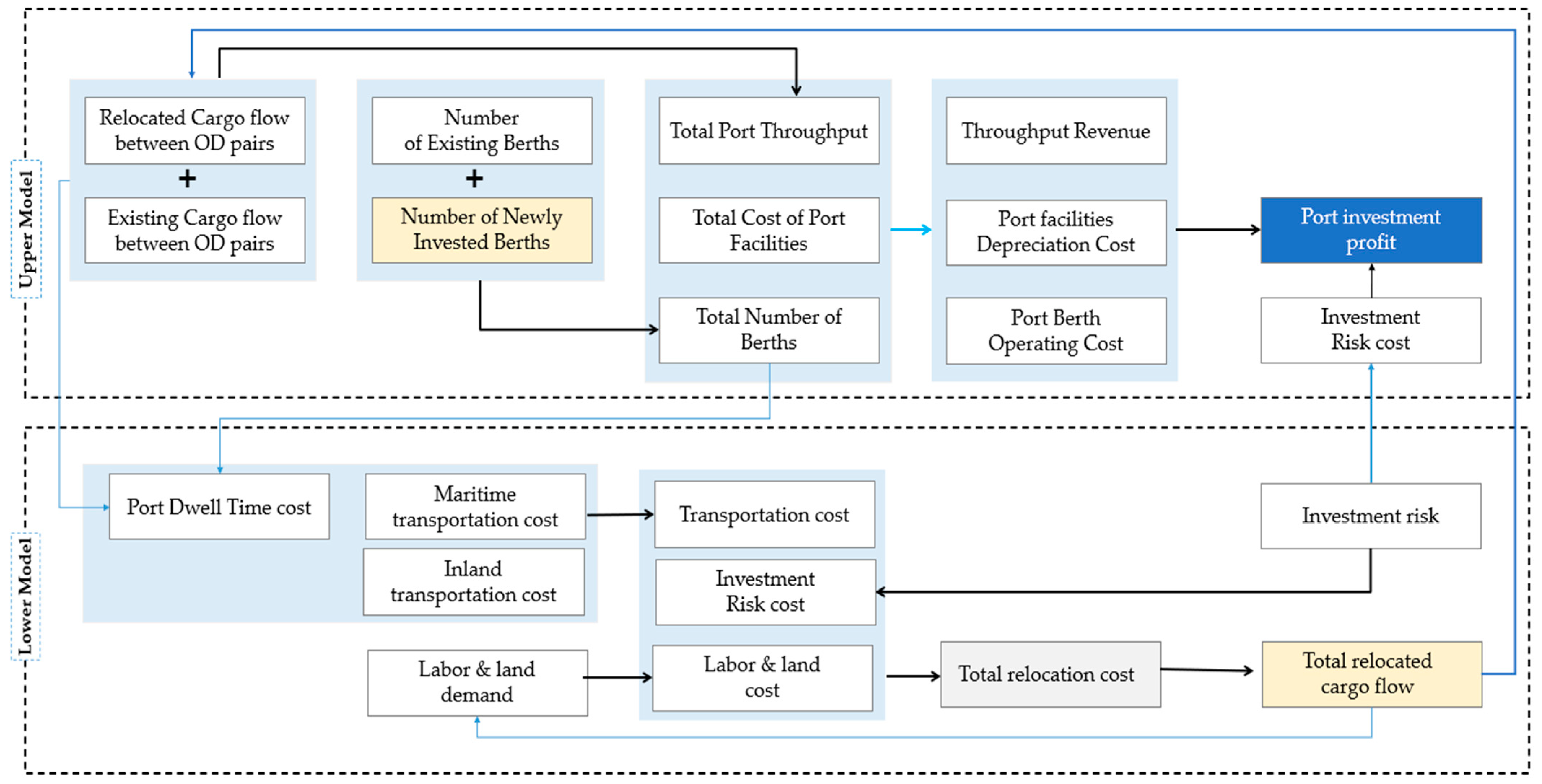
4. Model Building
- Compared to simple integrated optimization: The upper-level and lower-level models correspond to the decisions of different stakeholders, respectively, and these distinct decisions themselves are inherently suitable for the bi-level structure. In contrast, simple integrated optimization relies on a single objective function, which fails to capture the independent decision-making of the upper and lower levels and also cannot reflect the interactive relationships between the two decision-makers.
- Compared to agent-based modeling (ABM): ABM excels at simulating the “emergence” of micro-level heterogeneity, but its results are statistical and often struggle to converge to the specific macro-level Nash equilibrium that is the focus of our study. The bi-level structure, through the user equilibrium condition at the lower level, allows for an analytical solution to this equilibrium state, avoiding the uncertainty and complexity associated with the extensive parameter calibration required in ABM.
4.1. Upper-Level Model
- Gross operating profit: . It represents the gross profit from the operating income generated by the new and existing throughput after deducting variable costs.
- Facility maintenance cost: . It refers to the annual fixed cost incurred to maintain the normal operation of all berths (including newly built and existing ones).
- Amortization of investment capital: C/T. It represents the annual allocation cost of the total initial investment capital for port construction during the payback period.
- Risk cost: CL. This is a key item, representing the expected loss of investment risk calculated by the binary logit model and is used to quantify the potential economic consequences of uncertain factors such as international relations.
4.2. Lower-Level Model
4.3. Algorithm Design
5. Case Study
5.1. Data Sources
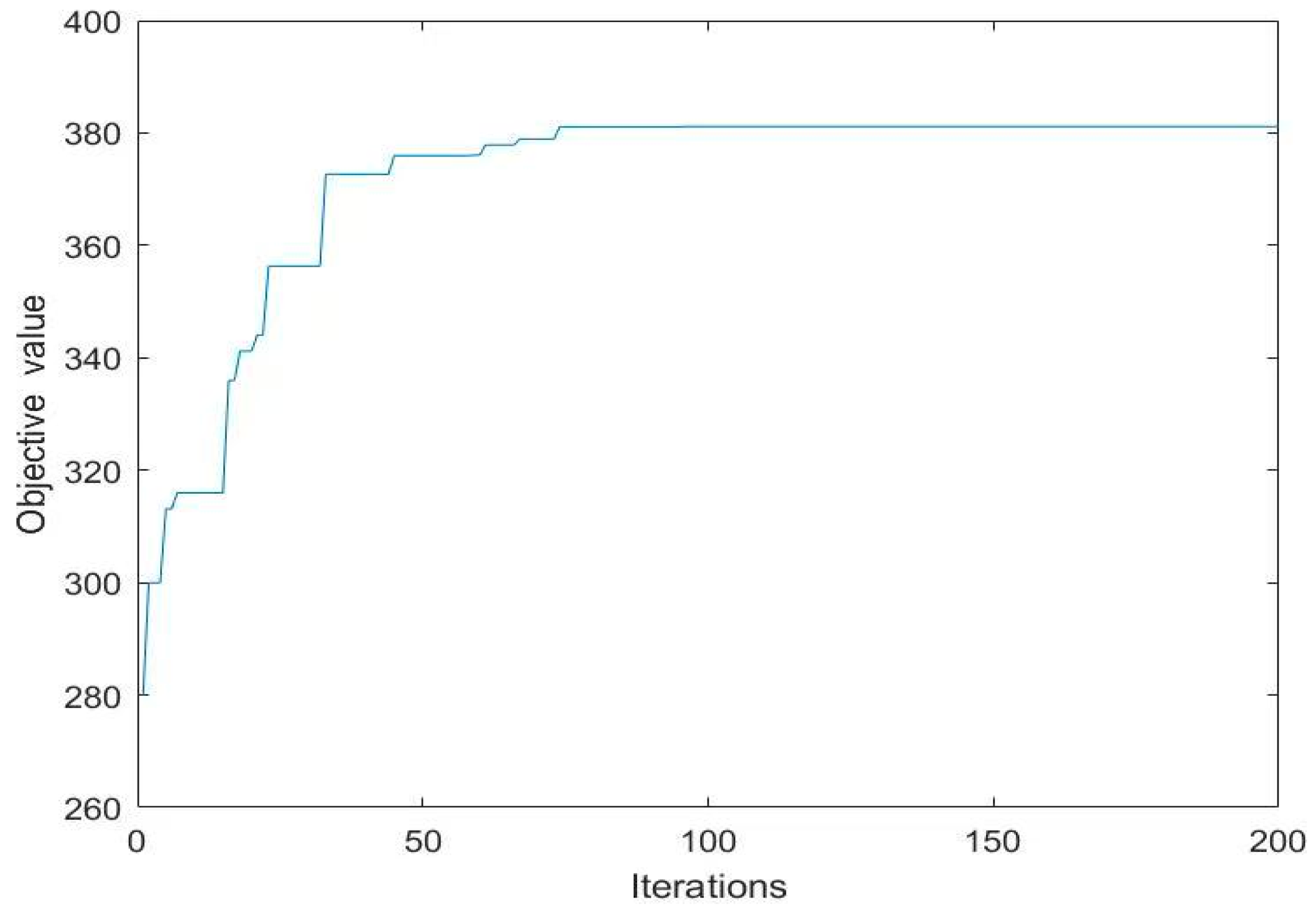
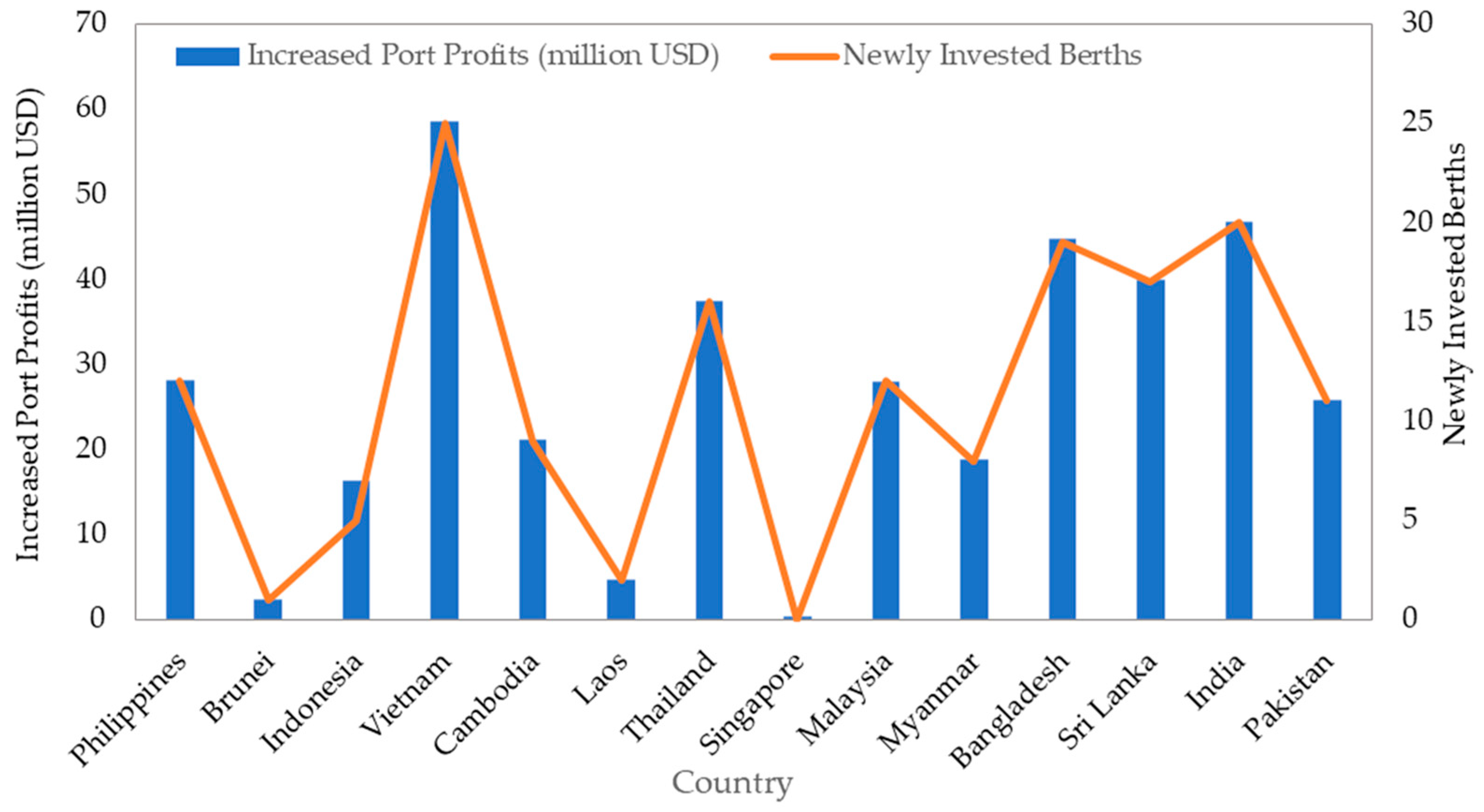
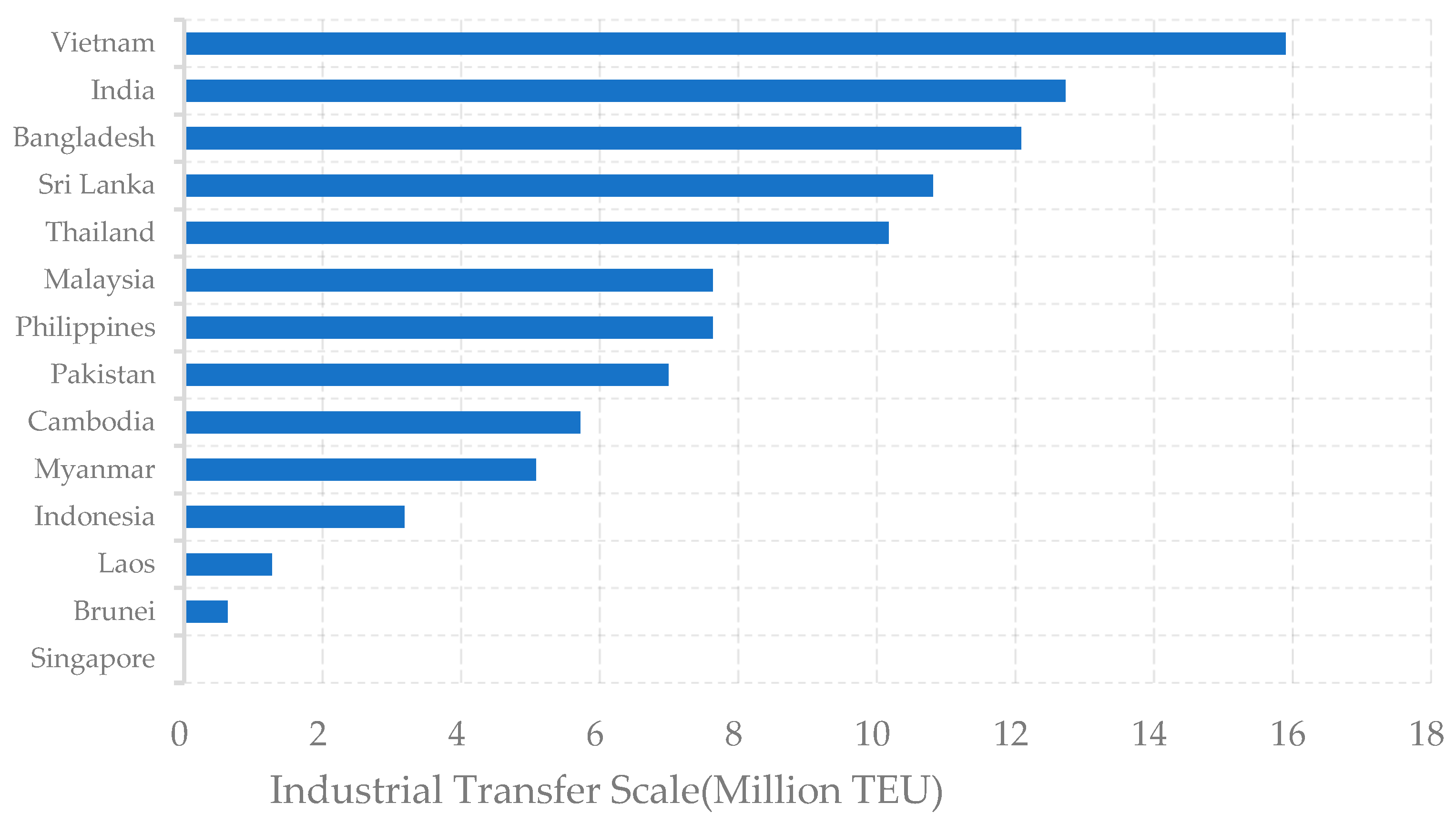
5.2. Optimization Result Analysis
5.2.1. Port Investment Plan
5.2.2. Analysis of Industrial Relocation Scale
5.2.3. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameters Used in the Paper
| Parameter | Definition |
| NQ1 | the number of newly constructed container berths, which is decision variable |
| the original throughput capacity of the port in country j | |
| the freight flow between origin–destination (OD) pairs | |
| the average revenue per container handled at port p | |
| the variable cost per container | |
| the annual average maintenance cost per container berth | |
| NQ0 | the original number of berths |
| C | the total investment cost for berth construction and supporting facilities |
| T | investment payback period |
| CL | the risk cost associated with port investment |
| NQ | the maximum number of berths that can be constructed |
| hc | the average cost of constructing each container berth and its associated supporting facilities |
| the impedance (generalized cost) on link a | |
| the flow on path k between country i and country j | |
| the total flow between origin i and destination j | |
| the total flow on link a | |
| a binary variable used to determine whether link a is included in path k between i and j | |
| tax rate at origin | |
| pv | unit value of containerized products (USD/TEU) |
| daily wage level at origin (USD/person/day) | |
| nh | labor required to produce one TEU of goods (persons) |
| ns | land area required to produce one TEU of goods |
| share of highway transport from origin i to port p | |
| highway freight rate (USD/km/TEU) | |
| railway freight rate (USD/km/TEU) | |
| base railway fee (USD/TEU) | |
| value of time (USD/hour/TEU) | |
| road distance from origin i to port p | |
| rail distance from origin i to port p | |
| average highway speed | |
| average railway speed | |
| congestion coefficient | |
| port capacity | |
| cargo throughput of the port | |
| probability of industrial investment risk | |
| total investment amount of the industrial project | |
| the GDP of country i after relocation | |
| k | the marginal propensity to consume |
| the GDP before investment | |
| the wage level after relocation | |
| the coefficient linking wage to GDP | |
| the change in GDP before and after investment | |
| the original land cost in region i (USD/m2) | |
| the land cost after relocation in region i (USD/m2) | |
| the coefficient relating land price to GDP | |
| crossover rate | |
| mutation rate | |
| population size | |
| H | maximum number of iterations |
References
- Xu, L.; Huang, J.C.; Chen, J.H. How does the initiative of the 21st century Maritime Silk Road incentive logistics development in China’s coastal region. Ocean Coast. Manag. 2023, 239, 106606. [Google Scholar] [CrossRef]
- Chen, D.X.; Yang, Z.Z. Investment in container ports along the Maritime Silk Road in the context of international industry trans fer: The case of the port of Colombo. Marit. Econ. Logist. 2019, 21, 241–257. [Google Scholar] [CrossRef]
- Zhang, Y.; Notteboom, T. The economic impact of Chinese port investments on host countries: Evidence from the Port of Piraeus. Marit. Econ. Logist. 2022, 22, 228–247. [Google Scholar]
- Chen, D.X.; Yang, D.; Yang, Z.Z. Port investment along the Maritime Silk Road considering mutual selections of the industries planned for transfer and recipient countries with location advantage. Marit. Policy Manag. 2022, 51, 1229–1251. [Google Scholar] [CrossRef]
- Feng, L.; Li, X.; Ng, A.K.; Jia, P.; Kuang, H.; Zhang, X. Can port systems be enhanced by government promotion? The case of port cooperation along the maritime silk road. Ocean Coast. Manag. 2023, 242, 100669. [Google Scholar] [CrossRef]
- Jiang, M.; Liu, Y.; Lu, J.; Qu, Z.; Yang, Z. Risk assessment of maritime supply chains within the context of the Maritime Silk Road. Ocean Coast. Manag. 2023, 231, 106380. [Google Scholar] [CrossRef]
- Fudan University, China and Neighboring Countries Relations Research Center. Research on China’s Neighboring Diplomacy; World Knowledge Press: Beijing, China, 2019; pp. 109–135. [Google Scholar]
- Li, X.; Wang, Y.; Liu, Z. Political risk propagation and contractual resilience in BRI port-city projects: Evidence from Colombo. Marit. Policy Manag. 2022, 49, 345–362. [Google Scholar]
- Zhang, L.; Notteboom, T.; Pallis, A.A. Geopolitical risks and port governance under the BRI: The case of Port of Piraeus. Transp. Policy 2020, 95, 1–12. [Google Scholar]
- Murillo, S.D.C.; Henrique, F.P. ESG performance scoring method to support responsible investments in port operations. Case Stud. Transp. Policy 2022, 10, 664–673. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, K.; Li, Z.C.; Fu, X.; Chan, F.T. Subsidy or minimum requirement? Regulation of port adaptation investment under disaster ambiguity. Transp. Res. Part B 2021, 150, 457–581. [Google Scholar] [CrossRef]
- Yang, Z.; He, Y.; Zhu, H.; Notteboom, T. China’s Investment in African Ports: Spatial Distribution, Entry Modes and Investor Profile. Res. Transp. Bus. Manag. 2020, 37, 100571. [Google Scholar] [CrossRef]
- Xia, W.Y.; Lindsey, R. Port adaptation to climate change and capacity investments under uncertainty. Transp. Res. Part B 2021, 152, 180–204. [Google Scholar]
- Wang, C.X.; Xie, F.J.; Xu, L. Which terminals should expand investment: A perspective of internal non-cooperative competition in a port. Marit. Policy Manag. 2020, 47, 718–735. [Google Scholar] [CrossRef]
- Tan, Z.; Zeng, X.; Wang, T.; Wang, Y.; Chen, J. Capacity investment of shore power berths for a container port: Environmental incentive and infrastructure subsidy policies. Ocean Coast. Manag. 2023, 239, 106582. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, L.; Li, W.; Fu, X.; Li, D. Priority analysis of port investment along the 21st-Century Maritime Silk Road region: The case of Southeast Asia. Marit. Policy Manag. 2022, 49, 1116–1134. [Google Scholar]
- Quy, M.N.; Rehan, S.; Lucjan, G. Simulation-Based Performance Assessment Framework for Optimizing Port Investment. J. Waterw. Port Coast. Ocean. Eng. 2021, 147, 04021010. [Google Scholar]
- Zhao, G.; Wang, K.; Yu, F.; Kuang, H. Port Multi-Period Investment Optimization Model Based on Supply-Demand Matching. J. Syst. Sci. Inf. 2015, 3, 77–85. [Google Scholar]
- Kurtulus, E. Optimizing inland container logistics and dry port location-allocation from an environmental perspective. Res. Transp. Bus. Manag. 2023, 48, 100839. [Google Scholar]
- Ma, Q.; Ma, B.; He, Y.; Sun, W. An optimization approach to the scale of port cold-chain dedicated terminals considering uncertainties. Eng. Optim. 2022, 54, 1887–1902. [Google Scholar] [CrossRef]
- Tu, N.; Adiputranto, D.; Fu, X.; Li, Z.C. Shipping network design in a growth market: The case of Indonesia. Transp. Res. Part E 2017, 117, 108–125. [Google Scholar] [CrossRef]
- Wei, H.; Dong, M. Import-export freight organization and optimization in the dry-port-based cross-border logistics network under the Belt and Road Initiative. Comput. Ind. Eng. 2019, 130, 472–484. [Google Scholar] [CrossRef]
- Yang, D.; Pan, K.; Wang, S. On service network improvement for shipping lines under the one belt one road initiative of China. Transp. Res. Part E 2017, 117, 82–95. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Wang, H.; Jin, X.; Du, L. Intermodal transportation hub location optimization with governments subsidies under the Belt and Road Initiative. Ocean Coast. Manag. 2023, 231, 106414. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Luan, J.; Li, X.; Jia, P. An Analysis of the Impact of Government Subsidies on Emission Reduction Technology Investment Strategies in Low-Carbon Port Operations. Systems 2024, 12, 134. [Google Scholar] [CrossRef]
- Wang, B.; Chin, K.S.; Su, Q. Port investments to address diversified risks under risk-sensitive behavior: Prevention or adaptation. Comput. Ind. Eng. 2023, 179, 109153. [Google Scholar] [CrossRef]
- Itoh, R.; Zhang, A.M. How should ports share risk of natural and climate change disasters. Analytical modelling and implications for adaptation investments. Econ. Transp. 2023, 33, 100301. [Google Scholar] [CrossRef]
- Gómez-Fuster, M.J.; Jiménez, P. Probabilistic risk modelling for port investments: A practical approach. Case Stud. Transp. Policy 2020, 8, 822–831. [Google Scholar] [CrossRef]
- Whitman, M.; Baroud, H.; Barker, K. Multicriteria risk analysis of commodity-specific dock investments at an inland waterway port. Eng. Econ. 2019, 64, 346–367. [Google Scholar] [CrossRef]
- Wang, B.; Kwai, S.C.; Su, Q. Prevention and adaptation to diversified risks in the seaport-dry port system under asymmetric risk behaviors: Invest earlier or wait. Transp. Policy 2022, 125, 11–36. [Google Scholar] [CrossRef]
- Balliauw, M.; Meersman, H.; Van de Voorde, E.; Vanelslander, T. Towards improved port capacity investment decisions under uncertainty: A real options approach. Transp. Rev. 2019, 39, 531–552. [Google Scholar] [CrossRef]
- Lewin, A.Y.; Massini, S.; Peeters, C. Why are companies offshoring innovation? The emerging global race for talent. J. Int. Bus. Stud. 2009, 40, 901–925. [Google Scholar] [CrossRef]
- Wang, Z.B.; Zhong, M.; Pan, X.F. Optimizing multi-period freight networks through industrial relocation: A land-use transport interaction modeling approach. Transp. Policy 2024, 158, 112–124. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Xu, D.F. Service on the rise, agriculture and manufacturing in decline: The labor market effects of high-speed rail services in Spain. Transp. Res. Part A 2023, 171, 103617. [Google Scholar] [CrossRef]
- Yan, L.N.; Tu, M.; Chagas, A.L.S.; Tai, L.F. The impact of high-speed railway on labor spatial misallocation—Based on spatial difference-in-differences analysis. Transp. Res. Part A 2022, 164, 82–97. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Y.; Fang, J.; Jing, Y.; Liu, Y.; Liu, Y. Characterizing pollution-intensive industry transfers in China from 2007 to 2016 using land use data. J. Clean. Prod. 2019, 223, 424–435. [Google Scholar] [CrossRef]
- Tate, W.L.; Ellram, L.M.; Schoenherr, T.; Petersen, K.J. Global competitive conditions driving the manufacturing location decision. Bus. Horiz. 2014, 57, 381–390. [Google Scholar] [CrossRef]
- Ghodratnama, A.; Arbabi, H.R.; Azaron, A. Production planning in industrial townships modeled as hub location-allocation problems considering congestion in manufacturing plants. Comput. Ind. Eng. 2019, 129, 479–501. [Google Scholar] [CrossRef]
- Duan, H.S.; Zhang, Y.; Huang, Z.Q. Production line location strategy for foreign manufacturer when selling in a market lag behind in manufacturing. Comput. Ind. Eng. 2024, 198, 110678. [Google Scholar] [CrossRef]
- Li, Y.; Wu, X.Q.; Bauer, J.; Aurich, J.C. Facility location optimization with market segmentation for additive manufacturing material supplier network using quantum annealing. Digit. Eng. 2024, 2, 100011. [Google Scholar] [CrossRef]
- Sharma, P.; Singh Ghatorha, K.; Kang, A.S.; Cepova, L.; Kumar, A.; Phanden, R.K. Strategic insights in manufacturing site selection: A multi-method approach using factor rating, analytic hierarchy process, and best worst method. Front. Mech. Eng. 2024, 10, 1392543. [Google Scholar] [CrossRef]
- Hofstede, G.; Hofstede, G.J.; Minkov, M. Cultures and Organizations: Software of the Mind, 4th ed.; McGraw-Hill: New York, NY, USA, 2023; pp. 192–195. [Google Scholar]
- Chen, D.; Yang, Z. Systematic optimization of port clusters along the Maritime Silk Road in the context of industry transfer and production capacity constraints. Transp. Res. Part E Logist. Transp. Rev. 2018, 109, 174–189. [Google Scholar] [CrossRef]
- World Bank. World Development Indicators 2023; World Bank: Washington, DC, USA, 2023. [Google Scholar]
- International Transport Forum (ITF). ITF Transport Statistics: Freight Transport. OECD. 2023. Available online: https://www.itf-oecd.org/transport-data-and-statistics (accessed on 1 January 2025).
| Area | Port Projects | Years |
| Southeast Asia and South Asia | COSCO—New Port Terminal | 2012 |
| Colombo International Container Terminal | 2012 | |
| Hambantota Port | 2012 | |
| West Asia and North Africa | Djibouti Port in Djibouti | 2013 |
| Suez Canal Terminal | 2012 | |
| Kumport Container Terminal, Istanbul Port, Türkiye | 2015 | |
| Jeddah, Saudi Arabia | ||
| Khalifa Marina, Abu Dhabi, United Arab Emirates | 2018 | |
| New container terminal at Sokhna Port, Egypt | 2023 | |
| Port Sudan Livestock Terminal | 2023 | |
| Haifa New Port | 2023 | |
| Europe | Port of Antwerp | 2012 |
| Port of Piraeus | 2012 | |
| Euromax Terminal Rotterdam | ||
| Terminal Link | ||
| Wado Pier | 2019 | |
| Noatum Port Company | ||
| Odessa Terminal Holdco Ltd. | 2020 | |
| Rotterdam World Gateway | 2020 | |
| Port of Zeebrugge | 2022 | |
| Container Terminal Tollerort, Port of Hamburg | 2023 | |
| Africa | Togo Lomé Container Terminal Company | 2012 |
| Nigeria Tinkan International Container Terminal | ||
| Bokai Mining Terminal | ||
| Container berth at Kribi Deepwater Port in Cameroon | ||
| Lomé Container Terminal, Togo | ||
| Nigeria Tinkan International Container Terminal | ||
| Oceania and the Americas | Port Melbourne | |
| Port of Newcastle | ||
| Darwin Port | 2015 | |
| Seattle Pier | ||
| Puerto Margarita Island, Panama | ||
| Paranagua Port, Brazil | 2018 | |
| Ruchankay Marina | 2019 | |
| Kingston Freeport Terminal Limited | 2020 |
| Profit-Oriented Investment Strategies (Category I) | |||
| References | Model | Factors to Consider | Research Findings |
| Murillo and Henrique [10] | Clustering analysis, Comparative importance matrix | ESG performance, stakeholder demands | Identifies optimal investment strategies for high-performing ports based on ESG metrics. |
| Zheng et al. [11] | Economic model with fuzzy probabilities | Disaster probabilities, spillover externalities, regulation | Analyzes how regulatory interventions influence port investment strategies under uncertainty. |
| Yang et al. [12] | Descriptive model specialization | Enterprise characteristics, host country development, port attributes | Identifies EPC + F + I and PPP as common investment models requiring strategic alignment. |
| Xia and Lindsey [13] | Interdependence model | Investment capacity, protection decisions, port charges, timing | Assesses trade-offs between profitability and social welfare in capacity investment. |
| Wang et al. [14] | Non-cooperative game model | Port congestion, capacity expansion | Offers strategies for achieving investment stability under varying decision-making conditions. |
| Tan et al. [15] | Bi-level optimization model | Government subsidies, emissions reduction, profit margins | Shows a feedback loop where subsidies encourage emission reduction investments that also improve profits. |
| Zheng et al. [16] | Random-walk link prediction | Economic factors, political factors, regional cooperation | Prioritizes port construction projects based on their network and strategic importance. |
| Quy [17] | Three-stage optimization model | External shocks, port performance, cost analysis | Derives optimal investment strategies through sequential safety, performance, and cost evaluation. |
| Zhao et al. [18] | Dynamic programming model | Supply-demand balance, ecological capacity, profit-loss constraints | Provides a framework for multi-period investment decision-making under multiple constraints. |
| Chen and Yang [2] | Bi-level programming model | Investment return, investment scale, industrial relocation costs | Maximizes upper-level returns by considering lower-level industrial relocation feedback. |
| Chen et al. [4] | Bi-level matching model | Locational advantages, source–host country dynamics, social benefits | Optimizes social benefits by simulating industrial-host selection matching. |
| Kutulu [19] | Mixed-integer linear programming | Empty container emissions, total costs | Optimizes inland logistics and dry port locations to minimize both costs and emissions. |
| Ma et al. [20] | Stochastic programming model | Ship type uncertainty, arrival time uncertainty, storage requirements | Determines optimal cold-chain terminal size under operational uncertainties. |
| Tu et al. [21] | Integrated model | Shipper route choice, carrier profit, government welfare | Applies a multi-stakeholder model to optimize Indonesian port and network investments. |
| Zheng et al. [16] | Link-prediction-based random walk | BRI contribution, shipping networks | Ranks port projects based on their strategic value for efficient, policy-aligned investment. |
| Wei and Dong [22] | Bi-objective mixed-integer programming | Freight cost, freight time | Enhances inland logistics and trade volumes by minimizing cost and time simultaneously. |
| Yang et al. [23] | Bi-level planning model | Liner profits, shipper costs | Demonstrates that shipping network improvements under the BRI increase profits and reduce costs. |
| Li et al. [24] | Two-stage mixed-integer model | Hub construction cost, transport cost, transshipment cost | Shows that hub construction can minimize total social costs in a network. |
| Li et al. [25] | Game-theoretic framework | Government subsidies, low-carbon preferences, cost-sharing | Reveals that ports and shipping companies respond differently to subsidies and green market demands. |
| Risk-Oriented Analyses (Category II) | |||
| References | Model | Factors to Consider | Research Findings |
| Wang et al. [26] | Two-period model | Congestion, climate change risks, risk aversion, investment budget, scale and timing | Risk-averse port authorities prioritize investments differently as budgets increase. Provides management insights for port and government decision-makers. |
| Itoh and Zhang [27] | Risk-sharing model | Natural disaster risks, port privatization, profit maximization | Risk-sharing among ports can reduce shipper risk, but private investors still base decisions primarily on profit maximization. |
| Gómez-Fuster and Jiménez [28] | Game theory, AHP, Entropy weight method | Risk management, economic-financial analysis | A generic method integrating risk analysis into financial models is effective for assessing risk in port investment projects, as validated in a case study. |
| Whitman et al. [29] | Dynamic risk interdependence model, Weighted MCDA | Resource allocation, economic loss, GDP, decision-maker risk aversion | MCDA helps prioritize port investments based on criteria like GDP and risk aversion, improving port preparedness and resource allocation. |
| Wang et al. [30] | Two-period game model | Fuzzy and asymmetric risk behavior, competitive environment, risk prevention | Investigates investment decisions in conventional and disruption risk prevention under competition and varying risk behaviors. |
| Balliauw et al. [31] | A real options approach | Technological change, market cycles | This method has a positive effect on socio-economic impacts such as regional employment and connectivity. |
| The Determinants of Industrial Relocation (Category I) | |||
| References | Model | Factors to Consider | Research Findings |
| Lewin et al. [32] | Empirical analysis | Skilled professional availability, Labor cost differentials | The availability of skilled professionals is a more critical determinant of offshore outsourcing locations than labor cost arbitrage. |
| Wang et al. [33] | Land use-transport interaction model, bi-level programming | Freight network investment policies, Location utility sensitivity | Freight investment policies affect relocation patterns, and their effectiveness is moderated by the sensitivity of location utility. |
| Zhang and Xu [34] | Difference-in-differences approach | High-speed rail services, Employment growth | High-speed rail promotes employment growth in the service sector while reducing it in agriculture and manufacturing. |
| Yan et al. [35] | Improved spatial difference-in-differences method | High-speed rail, Labor misallocation, Spatial spillover effects | High-speed rail alleviates local labor misallocation and generates significant positive spatial spillover effects. |
| Hu et al. [36] | Index measurement, hotspot analysis | Environmental regulations, Regional resource endowments | Environmental regulations and resource endowments jointly drove the shift of pollution-intensive industries from eastern to central/western China. |
| Tate et al. [37] | Empirical study of multinational firms | Customer proximity, Exchange rate volatility, Labor costs, Transportation expenses | Customer proximity, exchange rates, labor, and transport costs jointly influence location decisions, with a noted trend of reshoring to the US. |
| The Location Selection of Different Types of Facilities (Category II) | |||
| References | Model | Factors to Consider | Research Findings |
| Ghodratnama et al. [38] | Bi-objective hub location–allocation model | Congestion, Total cost, Total product waiting time | The model effectively optimizes production plans, with outcomes sensitive to parameter changes, balancing cost and time efficiency. |
| Duan et al. [39] | Game–theoretic model | Tariffs, Negative country-of-origin branding | Higher tariffs may make overseas locations more favorable, challenging conventional wisdom on offshoring high-end production. |
| Li et al. [40] | Multi-objective optimization framework | Geographically segmented supplier networks, Market sizes, Inventory planning | Optimizing facility location and market segmentation improves service and inventory efficiency, enhancing overall supply chain performance. |
| Sharma et al. [41] | Factor Rating Method (FRM), AHP, Best–Worst Method (BWM) | Raw material availability, Location, Labor, Transportation, Utilities, Environmental impact | Identified and prioritized key site selection factors, with raw material availability receiving the highest weight. |
| Parameter | Definition | Value | Data Source |
|---|---|---|---|
| Crossover rate | 0.9 | Ghodratnama et al. (2019) [38] | |
| Mutation rate | 0.01 | ||
| Population size | 30 | Chen et al. (2019) [2] | |
| H | Maximum number of iterations | 500 | Zheng et al. (2021) [11] |
| Country | GDP (USD) | Port Collection and Distribution Modes | |
|---|---|---|---|
| Highway Share Rate (%) | Railway Share Rate (%) | ||
| Philippines | 430,232.80 | 99 | 1 |
| Brunei | 13,147.04 | 100 | 0 |
| Indonesia | 1,178,932.01 | 99 | 1 |
| Vietnam | 378,876.06 | 99 | 1 |
| Cambodia | 36,329.79 | 100 | 0 |
| Laos | 20,303.70 | 95 | 5 |
| Thailand | 459,498.91 | 99 | 1 |
| Singapore | 391,555.14 | 97 | 3 |
| Malaysia | 401,479.16 | 80 | 20 |
| Myanmar | 63,756.97 | 96 | 4 |
| Bangladesh | 323,279.98 | 96 | 4 |
| Sri Lanka | 87,374.94 | 99 | 1 |
| India | 3,265,719.70 | 98 | 2 |
| Pakistan | 400,065.45 | 96 | 4 |
| North America | Oceania | Africa | South America | Europe | Asia | |
|---|---|---|---|---|---|---|
| China | 145,182.11 | 618.67 | 130.93 | 1555.82 | 691.37 | 79.36 |
| Philippines | 0.31 | 3.47 | 0.23 | 4.07 | 4.62 | 0.31 |
| Brunei | 0.00 1 | 0.01 | 0.00 | 9.64 | 0.02 | 1.38 |
| Indonesia | 0.09 | 7.41 | 0.12 | 7.07 | 4.26 | 0.21 |
| Vietnam | 7.06 | 26.88 | 2.94 | 165.59 | 22.81 | 4.25 |
| Cambodia | 0.001 | 0.21 | 0.00 | 6.15 | 0.40 | 0.32 |
| Laos | 7.18 | 35.90 | 1.93 | 210.48 | 29.36 | 10.21 |
| Thailand | 0.06 | 0.73 | 0.03 | 11.34 | 2.92 | 0.04 |
| Singapore | 0.23 | 12.35 | 0.40 | 50.95 | 9.20 | 0.65 |
| Malaysia | 6.32 | 42.12 | 3.43 | 334.72 | 42.24 | 2.23 |
| Myanmar | 6.84 | 43.05 | 4.84 | 167.59 | 27.53 | 12.89 |
| Bangladesh | 3.21 | 101.6 | 6.30 | 159.81 | 49.72 | 5.16 |
| Sri Lanka | 0.45 | 9.26 | 0.43 | 7.41 | 24.37 | 1.03 |
| India | 37.88 | 75.08 | 12.00 | 179.53 | 75.37 | 7.59 |
| Pakistan | 1.49 | 6.44 | 0.37 | 9.91 | 10.04 | 0.38 |
| Host Country | Port | Number of Berths | Host Country | Port | Number of Berths |
|---|---|---|---|---|---|
| Philippines | Manila Port | 26 | Singapore | Singapore Port | 54 |
| Brunei | Muara Port | 3 | Malaysia | Port Klang | 4 |
| Indonesia | Jakarta Port | 24 | Myanmar | Yangon Port | 13 |
| Vietnam | Ho Chi Minh Port | 14 | Bangladesh | Chittagong Port | 11 |
| Cambodia | Sihanoukville Port | 9 | Sri Lanka | Colombo Port | 4 |
| Laos | Yong’an Port | 3 | India | Mundra Port | 42 |
| Thailand | Laem Chabang Port | 8 | Pakistan | Karachi Port | 30 |
| Country | Rank | Country | Rank |
|---|---|---|---|
| Philippines | 14 | Singapore | 13 |
| Brunei | 11 | Malaysia | 5 |
| Indonesia | 9 | Myanmar | 3 |
| Vietnam | 1 | Bangladesh | 6 |
| Cambodia | 8 | Sri Lanka | 10 |
| Laos | 2 | India | 12 |
| Thailand | 7 | Pakistan | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Liu, F.; Wu, T.; Xu, X.; Wei, J.; Lai, F.; Lin, Y. Port Investment Optimization and Its Application Under Differentiated Port and Industrial Risks Along the Maritime Silk Road. Systems 2025, 13, 794. https://doi.org/10.3390/systems13090794
Chen D, Liu F, Wu T, Xu X, Wei J, Lai F, Lin Y. Port Investment Optimization and Its Application Under Differentiated Port and Industrial Risks Along the Maritime Silk Road. Systems. 2025; 13(9):794. https://doi.org/10.3390/systems13090794
Chicago/Turabian StyleChen, Dongxu, Feng Liu, Tong Wu, Xin Xu, Jingyi Wei, Fuyu Lai, and Yu Lin. 2025. "Port Investment Optimization and Its Application Under Differentiated Port and Industrial Risks Along the Maritime Silk Road" Systems 13, no. 9: 794. https://doi.org/10.3390/systems13090794
APA StyleChen, D., Liu, F., Wu, T., Xu, X., Wei, J., Lai, F., & Lin, Y. (2025). Port Investment Optimization and Its Application Under Differentiated Port and Industrial Risks Along the Maritime Silk Road. Systems, 13(9), 794. https://doi.org/10.3390/systems13090794





